
Model-based Generation of Hazard-driven Arguments and Formal
Verification Evidence for Assurance Cases
Fang Yan
1 a
, Simon Foster
1 b
, Ibrahim Habli
1 c
and Ran Wei
2 d
1
Department of Computer Science, University of York, York, U.K.
2
School of Artificial Intelligence, Dalian University of Technology, Dalian, China
Keywords:
Assurance Case, Automatic Generation, Model-based Engineering, Model Transformation, Model Query,
Formal Assertion Generation.
Abstract:
Assurance cases (ACs) are an established practice for arguing confidence in critical system properties such as
safety and security in high-risk industries. ACs use system artifacts to argue the aforementioned properties.
Due to the iterative nature of system development, we need to update ACs to maintain assurance validity as
a system evolves. For example, a changed design or an added hazard would result in re-evaluation of claims
or a new claim to be verified. Thus, the generation and maintenance of ACs is a labour-intensive process.
With the growing application of Model-based Engineering (MBE) in system development, it is beneficial to
generate ACs from design models because this captures traceability, and enables automatic AC creation and
update driven by model modification. Accordingly, the contribution of this paper is an automatic approach
to AC generation and assembly from both unstructured design artifacts and UML-like design models within
Eclipse. This approach also supports AC evidence generation by formal verification facilitated by automat-
ically generated assertions. The realization of AC assembly and verification is supported by model query
and model transformation. We apply our approach to an autonomous underwater robot with the RoboChart
robotics modelling language.
1 INTRODUCTION
Assurance of properties, such as safety, security, re-
liability, is vital for the system operation, especially
in high-risk industries such as automotive and health-
care. The assurance is designed into the system and
verified along the system development. An Assur-
ance Case (AC) provides a way to argue, based on
evidence, that certain properties are exhibited by the
system. ACs are a useful tool for communication
between different stakeholders and often required by
safety standards, such as ISO26262 (ISO, 2011).
AC processes should proceed along system devel-
opment. The process takes system development arti-
facts such as hazard analysis results, system architec-
ture, verification methods and results, etc., as inputs
to construct ACs. For example, hazard analysis and
risk assessments give rise to a set of safety require-
a
https://orcid.org/0000-0001-5603-3467
b
https://orcid.org/0000-0002-9889-9514
c
https://orcid.org/0000-0003-2736-8238
d
https://orcid.org/0000-0003-2191-1359
ments which a system must exhibit. A safety AC is
used to both justify these requirements, with reference
to the hazards and other contextual data, and to show
how these requirements are satisfied with reference to
various artifacts created during development, such as
models and codes. We can then use various kinds of
evidence to substantiate our claims, e.g. that model
checking demonstrates the correctness of the model.
Due to the iterative nature of system development,
after creation, ACs need to be updated to maintain
claim validity during system development. For in-
stance, a design change will drive the re-verification
and therefore the updated verification results may no
longer support the claims; an added function intro-
duces a new hazard, then a new claim shall be created
and substantiated. Moreover, a change in a single de-
sign artifact raises the issue of artifact synchronisa-
tion due to the inner relationships among these arti-
facts. Specifically, a coherent AC requires us to keep
a large number of artifacts synchronised. Every time
one artifact changes, we potentially need to review
and update all the others related. Therefore, maintain-
ing ACs is labour-intensive and vulnerable to human
252
Yan, F., Foster, S., Habli, I. and Wei, R.
Model-based Generation of Hazard-driven Arguments and Formal Verification Evidence for Assurance Cases.
DOI: 10.5220/0010847300003119
In Proceedings of the 10th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2022), pages 252-263
ISBN: 978-989-758-550-0; ISSN: 2184-4348
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

error. And this is aggravated by the trends of Robotics
and Autonomous Systems (RAS) whose operational
boundary is usually uncertain at design time and re-
quires higher frequency of updates than the traditional
safety-critical systems. This leads to a desire for au-
tomatic management of traceability between AC ele-
ments and design artifacts which may further enable
the automation of AC generation.
As the application of Model-based Engineering
(MBE) grows rapidly, it becomes feasible and ben-
eficial to generate model-based ACs from design ar-
tifacts automatically. As the basis of this automation,
the automatic establishment of traceability mentioned
above between ACs models and system artifacts can
be realized by MBE techniques such as model query.
Compared to ACs with no MBE support, e.g., pure
graphical or textural ACs, the advantage of model-
based ACs is the strong support of MBE techniques
and tools to manage ACs in an efficient way. The
application of MBE on AC process is a potential so-
lution for automation with the benefit of workload
reduction and error proofing. Much research effort
(Denney and Pai, 2018; Hawkins et al., 2015; Gacek
et al., 2014) has been put into this field. The survey
work (Yan et al., 2021) shows that the application of
MBE on AC process varies in terms of the MBE tech-
niques exploited, the phases of process applied to, and
the automation degree, etc.
However, the conclusions are drawn that there is
not a full automation approach for the AC process.
Specifically, (i) no solution is available to generate
integrated AC arguments from system artifacts of dif-
ferent formats, such as spreadsheets, models, etc. The
available approaches cover either the AC generation
from design models, or from structured design arti-
facts excluding design models and the unstructured
design artifacts. The unstructured data in this paper
refers to the data which is not backed by a meta-
model. Also, the AC generation from design models
is limited to specific modelling notations and develop-
ment environments; (ii) formal verification is widely
used in AC evidence generation, but the automation
of the whole AC process is hindered by the formal as-
sertion generation which usually is a manual process
and requires expertise. This results in a gap in the
automation loop; (iii) the AC metamodels designed
in different work vary and are mainly based on Goal
Structuring Notation (GSN) (OMG, 2021). Extra ef-
fort is needed for unification when exploiting these
different methods in one application. Meanwhile, the
unified AC metamodel ‘Structured Assurance Case
Meta-Model’ (SACM) (OMG, 2020) is both stan-
dardised and flexible and can be the solution for uni-
fication. In particular, it allows much more depth in
describing artifact links and therefore supports more
possibilities for artifacts synchronisation.
Our paper contributes a model-based approach
(Fig.1) that assembles and verifies the SACM-
compliant AC models in an automatic way. We design
an AC pattern for the property to be argued. Then,
we convert the unstructured system artifacts to EMF
models, create AC model structure by instantiating an
AC pattern with EMF models, and also by querying
design models. These AC models are assembled as
an integrated module. Further, for the evidence of
claims that can be generated by formal verification,
we generate automatically the assertions using MBE
techniques for model checking. The evidence models
will be created from the verification results and inte-
grated into the AC module. An example for the above
process can be that (i) a safety requirement ‘Opera-
tor can obtain the system control when required.’ in
a hazard table spreadsheet is converted to an EMF
model, (ii) a claim ‘ The safety requirement {Operator
can obtain the system control when required.} shall be
implemented.’ is created by instantiating AC pattern
with the EMF model of this safety requirement, (iii)
a formal assertion ‘System
S::State Operator Control
is reachable in System S.’ is derived from the claim,
then checked with a formal verification tool, (iv) the
evidence ‘The formal verification result is true.’ is
created by AC pattern instantiation with the verifica-
tion results, and is integrated into the AC module.
Different verification techniques can be involved
in the provision of evidence to AC claims. This work
primarily addresses the automated formal verifica-
tion. Other possible techniques for automation will
be addressed in future work. We have applied our ap-
proach to an autonomous underwater vehicle to eval-
uate the effectiveness.
Figure 1: Automating Assembly and Verification of ACs.
The main contributions of our paper are:
1. An approach for generating and assembling
SACM-compliant AC models from both UML-
like models and unstructured artefacts.
2. A solution for automatic generation of AC ev-
Model-based Generation of Hazard-driven Arguments and Formal Verification Evidence for Assurance Cases
253

idence by formal verification. The MBE tech-
niques are explored to automate the generation
of formal assertions to reduce the need of Formal
Methods (FM) expertise.
3. A case study has been carried out as an example
using RoboChart (Miyazawa et al., 2019).
We organize the paper as follows. §2 provides the
required background on AC and MBE. §3 details the
approach step by step. §4 shows the case study on an
autonomous underwater vehicle. §5 discusses related
work, and we conclude in §6.
2 PRELIMINARIES
2.1 Assurance Case Notations
ACs can be in various formats e.g., text, graphics,
and machine-readable models. One of the popular
forms is graphical notations (e.g., GSN and Claims-
Arguments-Evidence (CAE) (Adelard, 2017)) that
document AC elements with various shapes and rep-
resent their relationships in a structured way. The
graphical notations facilitate the system stakeholders’
understanding of the information for arguing the sys-
tem properties.
GSN is developed by (Kelly and McDermid,
1997). It comprises 6 principal elements, goal, con-
text, justification, assumption, strategy, and solution,
and 2 types of linkages between elements, Support-
edBy and InContextOf. It is the dominant graphic no-
tation used in engineering practice and academy.
However, GSN is not originally supported by
metamodels. Therefore, many pieces of work have
proposed AC metamodels for GSN (Denney and Pai,
2018; Hawkins et al., 2015). Meanwhile, OMG re-
leased SACM for the purpose of improving standard-
isation and interoperability. Compared with the other
proposed AC metamodels, SACM provides unique
features, such as, fine-grained modularity, controlled
terminology, and traceability from argument to evi-
dence artifacts (Wei et al., 2019).
SACM supports creation of machine-readable AC
models that facilitate the exchange of information be-
tween stakeholders. SACM also supports and unifies
GSN and CAE. SACM metamodel has five compo-
nents. A Base package defines the fundamental ele-
ments of SACM, such as element names and descrip-
tions. An Argumentation package consists of claims,
evidence citations, and inferential links among them.
The Artifact package captures the concepts used in
providing evidence for the arguments made for sys-
tem properties, and represents the evidence and con-
text files referenced. The Terminology package cap-
tures the concepts used in expressing the claims re-
garding system properties, such as expressions, and
the argumentation components. An AssuranceCase
package contains Argumentation packages, Terminol-
ogy packages and Artifact packages.
Basically, an argumentation package functions the
same as a GSN module. Its metamodel is shown
in Fig.2. The ArgumentAsset groups the argument
elements including Claims, ArtifactReferences, Ar-
gumentReasoning and AssertedRelationships (Foster
et al., 2021). ArtifactReference is the reference to the
artifact to define evidence. ArgumentReasoning is the
strategy to inference the lower-level claims. Assert-
edRelationships are the relationships between differ-
ent assets. Specifically, the AssertedInference rep-
resents the inference links between the lower-level
claims which are the source of the link to the higher-
level claims which are the target. AssertedContext
builds links from an artifact that defines context to
claims. AssertedEvidence builds links from evidence
to claims that the evidence supports. For example, a
top-level claim ‘the system operates safely.’ is sup-
ported by lower-level claims ‘the control unit meets
safety requirements’ and ‘the operators follow the op-
eration manual’ through an AssertedInference; and
the 1st lower-level claim is supported by the evidence
‘control unit test report’ and ‘formal verification re-
sults’ through an assertedInference.
2.2 Assurance Case Processes
A common AC process includes four main steps: AC
pattern design, instantiable data identification, pattern
instantiation, and evidence generation.
AC patterns are introduced by (Kelly and McDer-
mid, 1997). The patterns capture repeatedly used
structures of successful arguments in an abstract way
(Denney and Pai, 2013). Many pieces of work have
proposed the patterns for various applications, such as
the ones in (Denney and Pai, 2013; Prokhorova et al.,
2015). Depending on the properties to be argued, and
the types of systems, patterns are different.
The instantiable data is the system artifacts needed
as AC inputs, and should be organized in the for-
mats that the instantiating tool can read. We need
to identify the artifacts required for AC, then to iden-
tify the relationships between system artifacts and AC
elements in the pattern, and the inner relationships
among these artifacts themselves. With the pattern
and the instantiable data as inputs, the instantiation is
to replace the AC place holder elements in the pattern
with the concrete values from the instantiable data.
After the instantiation, the evidence for the claim
MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development
254

Figure 2: SACM Argumentation Package Metamodel (OMG, 2020).
shall be generated by verification, and so a further in-
stantiation step is required using the verification re-
sults. Following this, the AC module may be ready
and complete for certification review. For model-
based ACs, formal verification and model simulation
are suitable verification methods in terms of automa-
tion of AC process.
2.3 MBE and Epsilon
MBE is a methodology that advocates the use of mod-
els as the primary artefacts to drive system devel-
opment, to increase productivity, quality and reduce
costs (France and Rumpe, 2007). Model transfor-
mation is one of the many tools in the MBE toolkit.
Automated supports for other model management
such as model query, validation, etc., are also es-
sential. However, many of the model transformation
languages lack integration with other model manage-
ment support (Kolovos et al., 2008). Epsilon is a plat-
form for building interoperable and consistent task-
specific languages for multiple model management
tasks (Kolovos et al., 2010). Therefore, in our ap-
proach we use the Epsilon language family for AC
model generation process.
2.4 RoboChart Modelling Language
There are system modelling languages for different
applications. As our approach targets UML-like mod-
elling languages, we use RoboChart modelling lan-
guage as an example to illustrate out approach. The
reasons are that (i) it is tailored from UML for RAS
applications; (ii) it is supported by an EMF meta-
model; (iii) it has a formal semantics and model
checking support which are useful for the automation
of formal evidence generation.
RoboChart includes a profile of UML state ma-
chines and their derivatives, enriched with facilities
to define real-time properties. It uses the term ‘Con-
troller’ for software components that interface with
the hardware platform. The behaviour of the con-
troller is detailed by state machines. A machine has
local variables and constants, and consists of nodes
(i.e., states), and transitions. RoboChart has the fea-
tures of hierarchy, shared variables, real-time con-
straints, and probability support (Foster et al., 2018).
It also has a formal semantics in the process algebra
CSP (Communicating Sequential Process) (Roscoe,
2010). Therefore, it can be converted into for-
mal CSP models automatically for model checking
through FDR (Gibson-Robinson et al., 2016) refine-
ment model checker. RoboChart is supported by an
assertion Domain Specific Language (DSL) devel-
oped atop CSP that provides more sophisticated asser-
tions that can be translated automatically into CSP as-
sertions and avoid the complicated modelling in CSP.
3 AC ASSEMBLY AND
VERIFICATION APPROACH
We propose a SACM compliant framework for AC
construction and assembly integrating the pattern in-
stantiation and model query-based methods, and for
formal evidence generation. The approach is de-
Model-based Generation of Hazard-driven Arguments and Formal Verification Evidence for Assurance Cases
255

signed for the Eclipse EMF environment. We in-
troduced a conceptual framework for AC generation
and verification in (Yan, 2021) based on which we
build the detailed and complete approach in this pa-
per. We use RoboChart and its development environ-
ment RoboTool to illustrate the approach in this sec-
tion. The input of the AC process, i.e., the instantiable
system artefacts and the process output AC modules
are all processed as EMF models.
The approach includes three main activities
(Fig. 3). The first step is to process the unstructured
artefacts (e.g., hazard analysis results) into the struc-
tured EMF models using Algorithm 1 and further to
generate SACM AC models from EMF models using
Algorithm 2. This is discussed in §3.1. §3.2 is to gen-
erate AC models directly from system design models
by model query using Algorithm 3, then to assem-
bly with the output of §3.1 to obtain an integrated
AC model. In §3.3, we introduce the approach for
automatic formal verification of AC claims obtained
in §3.2. We use Algorithm 4 to automatically gen-
erate formal assertions from AC claims. In our ap-
proach, the terms used are mainly of safety property,
but the approach is applicable for different properties
with adjusting the input data and AC patterns.
3.1 AC Generation from Unstructured
Artifacts
System development processes produce different
types of artifacts (e.g., specifications, design, archi-
tecture, verification and validation reports) in various
formats such as text, models, and spreadsheets. Most
of these artifacts are unstructured and do not support
MBE. The unstructured data in this paper refers to the
data which is not backed by a metamodel. To gen-
erate model-based ACs, we first convert all these un-
structured AC inputs to a unified and structured for-
mat (i.e., EMF models) using Ecore metamodels. For
each type of artifact, we design a corresponding meta-
model and the data structuring algorithm (Algorithm
1 in Fig.3) thereof. All the metamodels shall be com-
pliant with the same metamodelling language for the
unification purpose. By implementing the algorithm,
the structure is introduced into the data based on the
metamodel.
Then, the AC pattern shall be defined according to
the system nature and property to be argued, and is
embedded into the pattern instantiation rules (Algo-
rithm 2 in Fig.3). The output of the process is a set of
SACM-compliant AC models.
In the paper, we illustrate the approach using haz-
ard analysis artifact as an example. For safety prop-
erties, the results of hazard analysis are stored in a
hazard table, usually in a form of a spreadsheet. The
spreadsheet is regarded as an unstructured format in
our work as it has no metamodel though it can be con-
sidered as ‘structured’ in other context. Abstracting
from (Agrawal et al., 2019; Denney and Pai, 2018),
we propose a generalized Ecore metamodel
1
for the
hazard table. We present Algorithm 1 ‘Data structur-
ing - Hazard table’ in the paper. Its purpose is to scan
each column row by row in the spreadsheet, create
and instantiate a class for each element, also establish
the traceability between elements in the same row and
between elements of different rows.
Algorithm 1: Data structuring-Hazard table.
1 forall r in HazardTable.rows do
2 if r.HazardID.isDefined then
3 h ← r.createH()
4 ht.h ← ht.h ∪ {h}
5 if r.CauseID.isDefined then
6 c ← r.createC()
7 h.c ← h.c ∪ {c}
8 if r.SRID.isDefined then
9 sr ← r.createSR()
10 c.sr ← c.sr ∪ {sr}
11 if r.VerificationID.isDefined then
12 vr ← r.createV R()
13 sr.vr ← sr.vr ∪ {vr}
14 vre ← r.createEv()
15 vr.ev ← vre
16 if r.ValidationID.isDefined then
17 Repeat Line 12-15 replacing
‘vr’ with ‘va’
18 else
19 if r.CauseID.isDefined then
20 Repeat Line 6-17
21 else
22 if r.SRID.isDefined then
23 Repeat Line 9-17
24 else
25 Repeat Line 12-17
In the hazard table, there are seven elements for
each row including hazard, cause, safety requirement,
verification, validation, verification evidence, and val-
idation evidence. The algorithm creates models h, c,
sr, vr, va, vre, vae correspondingly for all the ele-
ments, and builds traceability among them. Taking
the first element ‘hazard’ as an example, ‘HazardID’
(Line 2) is a header in the spreadsheet. We create a
hazard model h (Line 3) if the value of ‘HazardID’
is given, and add it to the set of table’s hazard ht.h
(Line 4). Thus, traceability is established between the
hazard table model ht and h. Then, we move to the
second element ‘CauseID’ in the spreadsheet to create
model ‘c’ for the cause, and build traceability between
1
https://github.com/uoy-fangyan/modelsward-ac-
generation.git.
MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development
256
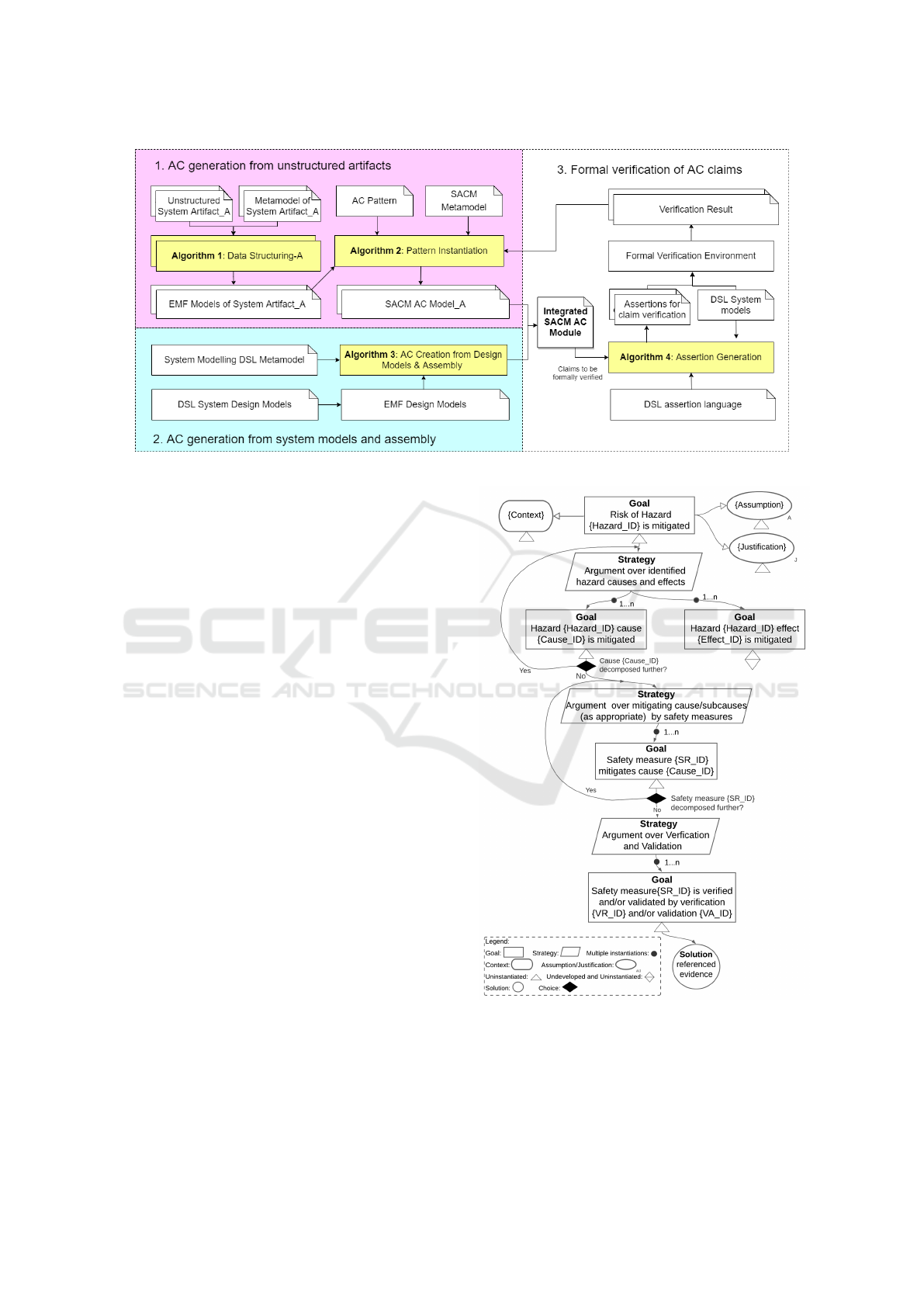
Figure 3: AC assembly and verification framework.
hazards and causes through adding c to the set of haz-
ard’s causes h.c. Also, a structure that is composed of
hazards and causes is introduced into the model. The
algorithm continues to the last element in the table.
With this algorithm, we can automatically structure
the hazard table whenever the table is updated.
Next, the AC pattern is designed for the hazard ta-
ble (Fig.4). It is represented in GSN for readability.
We constrain the AC pattern to a specific structure as
it makes AC generation more amenable to automa-
tion. The structure follows the hierarchy of the haz-
ard table. Four principles are implemented to build
the pattern as follows,
1. The elements of hazard, cause, safety require-
ment, verification, validation are the instantiation
inputs for AC claims.
2. The claims for causes and safety requirements can
be decomposed recursively. For the sake of read-
ability, Algorithm 2 presented here is constrained
to one layer of cause and safety requirement.
3. The results of verification and validation are in-
stantiation inputs for AC evidence.
4. The strategy is built between every two adjacent
levels of claims. There is no strategy between
claims and evidence. The content of strategy is
determined by the claims contents of two levels.
For example, the strategy to decompose a claim
for a hazard to a set of claims for the causes is
‘Argument over identified hazard causes’.
The pattern represents the AC structure, and the map-
ping between elements of the hazard table and instan-
tiable elements in AC. We design Algorithm 2 to em-
bed AC pattern and instantiation rules, and to comply
with SACM.
Figure 4: AC pattern in GSN notation.
In Algorithm 2 ‘Pattern Instantiation - HT’ for
generating AC from hazard table, ‘Str’ represents
strategy, ‘Inf’ represents inference which is the links
between claims, ‘Inf.src’ represents the set of source
Model-based Generation of Hazard-driven Arguments and Formal Verification Evidence for Assurance Cases
257

claims of the link, ‘Inf.tgt’ represents the target claim
of the link, ‘Ae’ represents AssertedEvidence, i.e., the
link from evidence to claim, ‘Ev’ represents evidence.
The algorithm starts from the first instantiable ele-
ment {Hazard} in AC pattern (Fig.4). Taking haz-
ard model h from Algorithm 1 as an input, a claim
model hClaim is created and instantiated (line 2). If
this hazard contains any causes, an inference link hInf
between hazard and causes is built (line 4), as well
as the strategy hStr (line 5). hClaim is also identified
as the inference’s target (line 6). Since lower-level
claims have not been created, the source claims of the
inference are not identified at this stage. Then, for
each cause of this hazard, a claim cClaim is defined
and is identified as the source of hInf (line 9). There-
after, the algorithm proceeds following the same pat-
tern for the rest of the elements in AC pattern.
Algorithm 2: Pattern Instantiation - HT.
1 forall h in ht.model do
2 hClaim ← h.createClaim
3 if ¬EMPTY(h.c) then
4 hIn f ← hClaim.createIn f
5 hStr ← hClaim.createStr
6 hIn f .tgt ← hClaim
7 forall c ∈ h.c do
8 cClaim ← c.createClaim
9 hIn f .src ← hIn f .src ∪ {cClaim}
10 if ¬EMPTY(c.sr) then
11 Repeat Line 4-9 replacing ‘c’, ‘h’
with ‘sr’, ‘c’
12 if ¬EMPTY(sr.vr) then
13 Repeat Line 4-9 replacing
‘c’, ‘h’ with ‘vr’, ‘sr’
14 if ¬EMPTY(vr.vre) then
15 vrAe ← vr.createAE
16 vrAe.tgt ← vrClaim
17 forall vre ∈ vr.vre do
18 vreEv ←
vre.createEv
19 vrAe.src ←
vrAe.src ∪ {vreEv}
20 if ¬EMPTY(sr.va) then
21 Repeat line 13-19 replacing
‘vr’ with ‘va’
3.2 AC Generation from Design Models
and Assembly
Besides the pattern instantiation method in §3.1, here
we propose to generate AC structure directly from de-
sign models without predefined AC patterns.
The design models are the models written in
certain system modelling languages (e.g., AADL,
SysML, RoboChart) which are supported by their
metamodels. According to the structure and elements
in the system modelling metamodel (e.g., states, tran-
sitions, and actions in RoboChart), we first define
the design model related claims, and then design the
query rules for generating these claims and for ob-
taining the evidence to the claims. The query rules
are implemented in Algorithm 3 of Fig.3.
To illustrate the approach, we consider a scenario
with the claim and evidence as follows,
Claim: Every state meeting Condition 1 shall have a
transition meeting Condition 2.
Evidence: A transition meeting Condition 2 exists for
each state.
If we choose to generate AC manually, a typical
way is to review the design models to manually iden-
tify the states that satisfy Condition 1 and all the tran-
sitions for each of these states that meet Condition
2. The states and the transitions will be used as in-
put for creating safety requirements and their verifica-
tion evidence respectively. The AC fragment then can
be generated by pattern instantiation following §3.1.
However, the AC arguments need to be updated man-
ually when system design changes, e.g., states have
been added or deleted.
To avoid this manual process, we apply model
querying (Gacek et al., 2014) in our approach. For the
scenario above, Algorithm 3 ‘Design model query-
st/tr’ is designed. The algorithm searches all the states
meeting condition ‘Cond1’, and create a claim for
each of these states. To obtain the evidence to claims,
all transitions of each state are checked to identify the
one meeting condition ‘Cond2’ (line 6); and the evi-
dence and an inference link to the claim are created.
This algorithm addresses the scenario that claims are
built on the constraints of states and their transitions.
There will be other types of claims involving other el-
ements in modelling languages. After query rules are
designed, they can be stored and revoked from the li-
brary for reuse. To assemble the AC fragments gener-
ated with Algorithm 2 and with Algorithm 3, we cre-
ate an identifier ‘Query’ to be inserted in the hazard
table, recognize this identifier in Algorithm 3 (line 1),
and integrate the two fragments as a complete module
(line 2 and 5).
The approach builds automatically traceability be-
tween design models and AC models, thus can avoid
the manual update of system models in the ACs and
further reduce the errors. Here we assumed the sys-
tem modelling language has the elements of the state
machine, state, and transitions for algorithm buildup.
But the idea of AC generation by model query is not
limited to a certain type of language, and can be ap-
plied to architectural languages in general.
MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development
258

Algorithm 3: Design model query-st/tr.
1 forall AC.in f ∈ {i | i.source = “Query”} do
2 inf.source.clear
3 forall System.state ∈ {s | s |= Cond1} do
4 state.createClaim&AE
5 in f .Source ← in f .Source ∪ {stateClaim}
6 forall
System.transition ∈ {tr |tr |= Cond2}
do
7 tr.createEvidence
8 state.AE.Target ← stateClaim
9 State.AE.Source ←
State.AE.Source ∪ {trEvidence}
3.3 Formal Verification of Claims
In §3.2, the evidence can be generated automatically
using the results of model querying. In this section,
we introduce an automatic approach to generate ev-
idence by verifying claims using formal verification
within RoboTool (part 3 of Fig.3). We exploit model
checking in this paper.
To perform the model checking of system prop-
erty, we need the formalized system models and the
formal assertions of the property. Both the processes
of system model formalization and assertion genera-
tion are typically manual processes and require FM
expertise. This results in two gaps in the automation
loop. To address the gap of formalization of system
models, we make use of one of the RoboChart fea-
tures. RoboChart can be converted into formal CSP
models automatically within RoboTool. And this CSP
model can be checked by FDR. Thus, we take the au-
tomatically converted CSP models as the formal mod-
els for formal verification. Therefore, We mainly ad-
dress the second gap in this paper.
The FDR assertions are written in machine-
readable CSP (CSPM). Take the property of state
reachability, for example, the assertion may be as fol-
lows,
assert not STOP [T= let
id = 0
withinSystem::VS O (id ) |\
{|State machine :: enteredV.State machine ::
SID State machine State|}
With the support of RoboChart assertion lan-
guage, the above assertion will be more concise and
easy to be created as follow,
assertion A1 reachable : State machine::State is
reachable in System.
From this example, we conclude it is feasible to
automate the assertion generation from RoboChart
models by making use of RoboChart assertion lan-
guage. Therefore, to address the gap of manual gen-
eration of formal assertions, we propose a automatic
Figure 5: Evidence generation by FDR model checking.
solution to generate RoboChart DSL assertion.
The formal evidence generation process summa-
rized in part 3 of Fig.3 is specified with RoboTool
environment as shown in Fig.5. We classify the AC
claims that can be formally verified, design the FDR
assertion templates for each class and perform model-
to-text transformation according to Algorithm 4 in
Fig.3. Note that since the assertions are generated
from AC claims, we require these AC claims and the
hazard table for deriving these claims to be written
with predefined terms and templates. Thus, the key
information can be extracted by Algorithm 4 auto-
matically. Though it requires a bit more effort to
create the constrained hazard table, it indeed lowers
the workload and the necessity of FM expertise in
terms of assertion generation and reduces the whole
workload, especially for the complex assertions. The
generated assertions then are automatically called by
FDR to output the checking results which will be fur-
ther transformed to AC evidence models. These evi-
dence models shall be integrated into the AC module
generated according to §3.1.
Algorithm 4 ‘Assertion generation - reachability’
is designed for the state reachability assertion. The
algorithm identifies all the claims that require state
reachability checking (line 2), then read the state to be
checked from the claim model (line 2), and instantiate
the assertion pattern for reachability class (line 3).
Algorithm 4: Assertion generation - reachability.
1 n ← 1
2 forall AC.assertedEvidence ∈
{ae|ae.tgt.startsWith(“Validation o f reachability”)}
do
3 createAssertion(Assertion n: l.getStmName ::
l.getStateName is reachable in
l.getStmName)
4 n ← n + 1
Model-based Generation of Hazard-driven Arguments and Formal Verification Evidence for Assurance Cases
259

4 IMPLEMENTATION AND CASE
STUDY
We implemented all the algorithms of §3, and carried
out a case study of an Autonomous Underwater Ve-
hicle (AUV) for approach evaluation. The codes and
the use case can be accessed online
2
.
4.1 System Description and Hazard
Analysis
We illustrate our approach using the AUV introduced
in (Foster et al., 2020). The AUV can be operated by
human or by system automatically. The mission of the
system is the underwater maintenance and interven-
tion tasks. The main hazard of the system is the col-
lision of AUV with different types of subsea system
components and infrastructure, which can be caused
by operator or AUV system. The local path planning
exploits machine learning techniques, but the safety
monitoring component Last Response Engine (LRE)
is developed without artificial intelligence in order to
assure that the safety component can be thoroughly
verified. Our AC is built for this LRE.
Fig. 6 shows the RoboChart state machine model
of LRE. The function of LRE is to switch the opera-
tion modeS of the system based on the safety condi-
tion of operation. There are four modes: (i) Opera-
tor Control Mode (OCM), a manual mode, (ii) Main
Operating Mode (MOM), the automatic mode in safe
condition, (iii) High Caution Mode (HCM),the au-
tomatic mode used when the collision risk is to be
lowered by reducing speed, (iv) Collision Avoidance
Mode (CAM), the emergency automatic mode used
when the collision risk is too high and need to be re-
duced by maneuver. Various transitions model the
moving of one mode to another. For example, the
LRE can move from MOM to HCM when the hor-
izontal velocity is greater than or equal to 0.1, and
the horizontal distance to a static obstacle is less then
a given constant. Moreover, the operator can com-
mand the LRE to switch modes using the events re-
qOCM/MOM/HCM. Detailed description of the sys-
tem operation can be referred in (Foster et al., 2020).
For this system, we use one hazard of LRE com-
ponent as an example to show the algorithm imple-
mentation. The process of the hazard analysis is not
the focus of our approach, and we use hazard table
as the input of AC generation. As shown in the ex-
cerpt of hazard table (Fig.7), for the safety require-
ment {SR: Operator shall obtain the control from any
2
https://github.com/uoy-fangyan/modelsward-ac-
generation.git
state in which the operator is not in control when
requesting.}, the sub-level safety requirement shall
be instantiated by the states concrete state names as
‘MOM’, ‘HCM’, and ‘CAM’ according to Fig. 6. We
discuss the details in the rest of this section.
4.2 AC Generation and Verification
We first transform the hazard table spreadsheet into
EMF models (Fig.8) using Algorithm 1 with Epsilon
Object Language (EOL). There is one to one mapping
between elements of Fig.7 and of Fig.8.
Secondly, we implement the transformation from
EMF hazard table to SACM AC according to Al-
gorithm 2 with Epsilon Transformation Language
(ETL). A fragment of output including claims for
‘SubCause’ and ‘SR’ is shown in line 36 and 50 of
Fig. 9 in the form of XML. The complete output is
available online. Thirdly, we generate the claims for
sub-level safety requirements SubSR in Fig.7 and their
evidence by querying RoboChart models according to
Algorithm 3. An AC fragment is automatically gen-
erated as follows,
Claim 1: {State MOM} shall have a transition whose
trigger is reqOCM and target is OCM.
Inference Strategy 1: Argument over V&V methods of
{Claim 1}.
Claim 1.1: {Claim 1} is verified by model query.
Evidence 1.1: {Tr t2} exists for {State MOM}.
Claim 2: {State HCM} shall have a transition whose
trigger is reqOCM and target is OCM.
Inference Strategy 2: Argument over V&V methods of
{Claim 2}.
Claim 2.1: {Claim 2} is verified by model query.
Evidence 2.1: {Tr t3} exists for {State HCM}.
Claim 3: {State CAM} shall have a transition whose
trigger is reqOCM and target is OCM.
Inference Strategy 3: Argument over V&V methods of
{Claim 3}.
Claim 3.1: {Claim 3} is verified by model query.
Evidence 3.1: {Tr t17} exists for {State CAM}.
Each of these claims uses a named transition as evi-
dence that ‘reqOCM’ is always possible. If the state
machine is later changed, for example, an extra state
is added, the process would require this new state to
fulfill this requirement.
Fourthly, there is the claim requiring that the
reachability of state OCM shall be checked by FDR
(Fig.7). The DSL assertion template for reachability
is designed in EGL, and is transformed into an asser-
tion file using EGL Co-Ordination Language (EGX).
The generated assertion is as follows,
Assertion: LRE
Beh::OCM is reachable in LRE Beh.
MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development
260

Figure 6: RoboChart model of LRE (Foster et al., 2020).
Figure 7: Excerpt of LRE hazard table spreadsheet.
Figure 8: Excerpt EMF models of hazard table.
Figure 9: AC model fragment generated from hazard table.
Here, the state name ‘OCM’ is obtained automat-
ically from the AC claim models, and the state ma-
chine name ‘LRE Beh’ from RoboChart models.
In this section, we illustrate our approach of §3
using an excerpt of the LRE use case. The complete
implementation and the case study are available on-
line. The execution of formal assertions in FDR is
currently manual and the automation is under devel-
opment. The ability to derive AC models from system
models enables the co-evolution of system design and
ACs.
5 RELATED WORK
(Denney and Pai, 2018) provide a solution and tool
for automatic generation of a complete set of ACs us-
ing the pattern instantiation method. The tool also
provides functions of AC query and review which are
convenient for AC management. But the system arti-
facts are not necessarily to be structured models thus
the work does not cover AC generation from system
models nor the ACs integration of different sources.
(Hawkins et al., 2015) use the concept of pattern
instantiation for generating GSN-based ACs. They
use model weaving (Del Fabro et al., 2006) to fa-
cilitate the relationship building at metamodel level
Model-based Generation of Hazard-driven Arguments and Formal Verification Evidence for Assurance Cases
261

between instantiable artifacts and AC elements. The
premise of the work is that both the instantiable data
and the AC pattern are structured models. The advan-
tage of the work is that instantiable models can be ex-
tracted automatically. Our approach is inspired by this
work, and we expand the instantiable data from only
system design models to cover also the unstructured
artifacts. We also provide the solution for assembly.
(Gacek et al., 2014) presents a method of AC gen-
eration by AADL model querying. The query envi-
ronment is integrated with the Open Source AADL
Tool Environment (OSATE). The claim is formalized
and verified by querying system models. The cou-
pling of ACs with system design ensures the consis-
tency between the ACs and system models when de-
sign changes. We refer to the model query concept in
our Algorithm 3. Different from this work, our model
query is not constrained to a specific development en-
vironment. This independence allows a wider scope
of applicability.
(
ˇ
Sljivo et al., 2020) proposes to generate AC from
system design pattern using MBE. This is different
from our method of generating AC directly from sys-
tem models. (Gallina and Nyberg, 2017) exploits
model query technique and AC patterns to generate
AC from system artifacts that comply with OSLC
(Open Services for Lifecycle Collaboration) (Oasis,
2021) standard. The method does not address the un-
structured artifacts nor system design models. Our
approach complements their work.
For formal verification of AC claims, (Diskin
et al., 2018) and (Gleirscher et al., 2019) both gen-
erate assertions by formalizing claims. The advan-
tage is the rigorous mathematical refinement check-
ing on the inference by formal verification. However,
the work does not address the automation of formal
verification of AC claims. (C
ˆ
arlan et al., 2020) tack-
les the consistency checking between system artifacts
and AC elements, and use model checking as one of
the claim verification methods. The automation of as-
sertion generation is not addressed.
Our approach provides an automatic solution cov-
ering AC generation and verification, and has ex-
tended the existing work, closed the gaps of AC as-
sembly and automatic formal verification. To the
best of our knowledge, our approach of model-based
AC generation, assembly and formal verification is
the first one that can generate and assemble SACM-
compliant AC from both structured and unstructured
system artifacts, and can formally verify AC claims
by automatic generation of formal assertions.
6 CONCLUSION AND FUTURE
WORK
ACs evolve along the system development lifecycle.
The automation of the AC process based on MBE re-
duces the workload and chances of errors. The stan-
dardized metamodel SACM provides a foundation for
model-based AC generation. We have developed an
approach for model-based assembly and formal veri-
fication of ACs based on EMF. The approach provides
an automatic solution that is compliant with SACM
and is applicable to system models of UML-like lan-
guages. We apply our approach to a robotic system
simply as an illustrative example. However, our tech-
niques are general enough to be applied to a wide
range of systems. Hazard analysis is a generally ap-
plied technique. So is the CSP process algebra, which
has been applied to many kinds of systems.
For AC generation, we will develop more meta-
models for different system atifacts and the transfor-
mation rules thereof. For AC generation by query-
ing design models, the method is not applicable to
all types of claims. But we will expand the types of
claims to obtain good coverage. Also, our approach
of formal verification is currently supported by FDR
model checker. Further, we will explore other FM
tools to expand the formal verification methods on
other model checkers for different properties, such as
probabilistic property, and on theorem provers to im-
prove the applicability of our approach.
ACKNOWLEDGEMENTS
The research leading to these results has received
funding from the European Union’s Horizon 2020 re-
search and innovation programme under the Marie
Skłodowska-Curie grant agreement No 812.788
(MSCA-ETN SAS). This publication reflects only the
author’s view, exempting the European Union from
any liability. Project website: http://etn-sas.eu/. Ran
Wei is funded by the the Fundamental Research Funds
for the Central Universities of China.
REFERENCES
Adelard (2017). Claims-Argument-Evidence-Adelard
LLP. https://www.adelard.com/asce/choosing-asce/
cae.html. Online; accessed 6th Sep, 2021.
Agrawal, A., Khoshmanesh, S., Vierhauser, M., Rahimi,
M., Cleland-Huang, J., and Lutz, R. (2019). Leverag-
ing Artifact Trees to Evolve and Reuse Safety Cases.
In 2019 IEEE/ACM 41st International Conference
MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development
262

on Software Engineering (ICSE), pages 1222–1233.
IEEE.
C
ˆ
arlan, C., PetriS¸or, D., Gallina, B., and Schoenhaar, H.
(2020). Checkable safety cases: Enabling automated
consistency checks between safety work products.
In 2020 IEEE International Symposium on Software
Reliability Engineering Workshops (ISSREW), pages
295–302. IEEE.
Del Fabro, M. D., B
´
ezivin, J., and Valduriez, P. (2006).
Weaving models with the eclipse amw plugin. In
Eclipse Modeling Symposium, Eclipse Summit Eu-
rope, volume 2006, pages 37–44.
Denney, E. and Pai, G. (2013). A formal basis for safety
case patterns. In International Conference on Com-
puter Safety, Reliability, and Security, pages 21–32.
Springer.
Denney, E. and Pai, G. (2018). Tool support for assurance
case development. Automated Software Engineering,
25(3):435–499.
Diskin, Z., Maibaum, T., Wassyng, A., Wynn-Williams,
S., and Lawford, M. (2018). Assurance via model
transformations and their hierarchical refinement. In
Proc. the 21th ACM/IEEE International Conference
on Model Driven Engineering Languages and Sys-
tems, pages 426–436.
Foster, S., Baxter, J., Cavalcanti, A., Miyazawa, A., and
Woodcock, J. (2018). Automating verification of state
machines with reactive designs and isabelle/utp. In
International Conference on Formal Aspects of Com-
ponent Software, pages 137–155. Springer.
Foster, S., Nemouchi, Y., Gleirscher, M., Wei, R., and Kelly,
T. (2021). Integration of formal proof into unified as-
surance cases with isabelle/sacm. Formal Aspects of
Computing, pages 1–30.
Foster, S., Nemouchi, Y., O’Halloran, C., Stephenson, K.,
and Tudor, N. (2020). Formal model-based assurance
cases in isabelle/sacm: An autonomous underwater
vehicle case study. In Proceedings of the 8th Inter-
national Conference on Formal Methods in Software
Engineering, pages 11–21.
France, R. and Rumpe, B. (2007). Model-driven devel-
opment of complex software: A research roadmap.
In Future of Software Engineering (FOSE’07), pages
37–54. IEEE.
Gacek, A., Backes, J., Cofer, D., Slind, K., and Whalen, M.
(2014). Resolute: an assurance case language for ar-
chitecture models. In ACM SIGAda Ada Letters, vol-
ume 34, pages 19–28. ACM.
Gallina, B. and Nyberg, M. (2017). Pioneering the cre-
ation of iso 26262-compliant oslc-based safety cases.
In 2017 IEEE International Symposium on Software
Reliability Engineering Workshops (ISSREW), pages
325–330. IEEE.
Gibson-Robinson, T., Armstrong, P., Boulgakov, A., and
Roscoe, A. W. (2016). FDR3: a parallel refinement
checker for CSP. International Journal on Software
Tools for Technology Transfer, 18(2):149–167.
Gleirscher, M., Foster, S., and Nemouchi, Y. (2019). Evo-
lution of formal model-based assurance cases for au-
tonomous robots. In International Conference on Soft-
ware Engineering and Formal Methods, pages 87–
104. Springer.
Hawkins, R., Habli, I., Kolovos, D., Paige, R., and Kelly,
T. (2015). Weaving an Assurance Case from Design:
A Model-Based Approach. In 2015 IEEE 16th Inter-
national Symposium on High Assurance Systems En-
gineering, pages 110–117. IEEE.
ISO (2011). ISO 26262 Road vehicles–Functional Safety,
Version 1.
Kelly, T. P. and McDermid, J. A. (1997). Safety case con-
struction and reuse using patterns. In Safe Comp 97,
pages 55–69. Springer.
Kolovos, D. D., Rose, L., Paige, R., and Garc
´
ıa-dom
´
ınguez,
A. (2010). The Epsilon book. Technical report.
Kolovos, D. S., Paige, R. F., and Polack, F. A. (2008).
The epsilon transformation language. In International
Conference on Theory and Practice of Model Trans-
formations, pages 46–60. Springer.
Miyazawa, A., Ribeiro, P., Li, W., Cavalcanti, A., Tim-
mis, J., and Woodcock, J. (2019). Robochart: mod-
elling and verification of the functional behaviour of
robotic applications. Software & Systems Modeling,
18(5):3097–3149.
Oasis (2021). Open Services for Lifecycle Collaboration.
http://open-services.net/. Online; accessed 15th Au-
gust, 2021.
OMG (2020). Structured Assurance Case Metamodel
(SACM), Version 2.1 beta.
OMG (2021). GSN Community Standard. Version 3.
Prokhorova, Y., Laibinis, L., and Troubitsyna, E. (2015).
Facilitating construction of safety cases from formal
models in Event-B. Information and Software Tech-
nology, 60:51–76.
Roscoe, A. W. (2010). Understanding concurrent systems.
Springer Science & Business Media.
ˇ
Sljivo, I., Uriagereka, G. J., Puri, S., and Gallina, B. (2020).
Guiding assurance of architectural design patterns for
critical applications. Journal of Systems Architecture,
110:101765.
Wei, R., Kelly, T. P., Dai, X., Zhao, S., and Hawkins,
R. (2019). Model based system assurance using the
structured assurance case metamodel. Journal of Sys-
tems and Software, 154:211–233.
Yan, F. (2021). Generation and verification of exe-
cutable assurance case by model-based engineering.
In 2021 IEEE International Symposium on Software
Reliability Engineering Workshops (ISSREW). IEEE.
Preprint: https://eprints.whiterose.ac.uk/179470/1.
Yan, F., Foster, S., and Habli, I. (2021). Safety case genera-
tion by model-based engineering: State of the art and
a proposal. In The Eleventh International Conference
on Performance, Safety and Robustness in Complex
Systems and Applications, pages 4–7. IARIA.
Model-based Generation of Hazard-driven Arguments and Formal Verification Evidence for Assurance Cases
263
