An Asymetric-key Cryptosystem based on Artiﬁcial Neural Network

Rafael Valencia-Ramos

1,2 a

, Luis Zhinin-Vera

1,2 b

, Gissela E. Pilliza

1,2 c

and Oscar Chang

1,2 d

School of Mathematical and Computational Sciences, Yachay Tech University, 100650, Urcuqui, Ecuador

MIND Research Group - Model Intelligent Networks Development, Urcuqui, Ecuador

Keywords:

Autoencoder, Cryptography, Cryptosystem, Encryption and Decryption Keys, Artiﬁcial Neural Networks.

Abstract:

Protect the information has always been important concerns for society, and mainly now in digital era. Cur-

rently exists different platforms to manage critical and sensitive information, ranging from bank accounts to

social media. All platforms have taken steps to guarantee that the data passing through them is protected from

hackers. An essential subject in digital world born, giving place to symmetric and asymmetric key algorithms.

Asymmetric key algorithms work by manipulating very big prime numbers, which gives a high level of secu-

rity but also takes a long time to compute. This paper offers a cryptographic system based on deep learning

techniques. The approach avoided the necessity of big prime numbers by using the synaptic weights of an au-

toencoder neural network as encryption and decryption keys. The suggested method allows for a high amount

of unpredictability in the initial and ﬁnal synaptic weights without compromising the network’s overall per-

formance. The results was shown to be resilient and difﬁcult to break in a theoretical security study with a low

computational time.

1 INTRODUCTION

Currently, technology can’t ensure 100% data secu-

rity, and it has become a big topic in academy and

industry. As the number of internet users has grown,

the data transport networks have had to strengthen

their security. The available systems are based on the

concept of cryptography. Artiﬁcial Neural networks

(ANN) helps to develop complex works in the ﬁeld

of information security, such as detection of Credit

Card Fraud (Zhinin-Vera et al., 2020) and Commu-

nication Protection with adverse neural cryptography

(Coutinho et al., 2018).

Two cryptographic keys are created in this work

using an Autoencoder. The system is trained using the

complete ASCII code of 256 characters, using random

training that requires an initialization password. The

suggested system is compared to different public-key

algorithms in terms of encryption, decryption, and

key generation times to determine its effectiveness.

The security analysis is performed to estimate the dif-

ﬁculty of breaking the system’s security.

https://orcid.org/0000-0002-1036-1817

https://orcid.org/0000-0002-6505-614X

https://orcid.org/0000-0001-6386-9254

https://orcid.org/0000-0002-4336-7545

2 RELATED WORK

According to Charniya, ANN can correctly identify a

nonlinear system model from a complicated system’s

inputs and outputs without knowing the exact con-

nection between inputs and outputs (Charniya, 2013).

By applying these ideas to the realm of cryptography,

ANN might generate high-security encryption keys

(Kinzel and Kanter, 2002).

ANNs offer a highly strong generic framework

for expressing the non-linear mapping of various in-

put variables to various output variables, according to

Volna (Volna et al., 2012) works on ANN-based en-

cryption. Jogdand proposed that ANN can be used

to generate common secret keys (Jogdand, 2011).

Kinzel and Kanter show the application of interac-

tive ANN for the exchange of keys through a pub-

lic channel (Kanter and Kinzel, 2003). Klein et al.

demonstrates the use of mutual learning ANN with

time-dependent weights that synchronize (Klein et al.,

2005).

In another approach is shown that using an autoen-

coder neural network as a data encoder and decoder

is possible (Quinga-Socasi et al., 2020). Then, new

approach creates a symmetric encryption system in

which a ANN is utilized as a data encryption system

that can encode and decode data with only a single

540

Valencia-Ramos, R., Zhinin-Vera, L., Pilliza, G. and Chang, O.

An Asymetric-key Cryptosystem based on Artiﬁcial Neural Network.

DOI: 10.5220/0010857700003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 540-547

ISBN: 978-989-758-547-0; ISSN: 2184-433X

initialization key (Quinga and Chang, 2020). Another

work shows that using a basic autoencoder architec-

ture, an asymmetric data encryption system can be de-

veloped. It also demonstrates that all of the characters

of the ASCII code can be encoded without causing

any signiﬁcant accuracy problems when encoding and

decoding each character (Valencia and Chang, 2020).

Taking the concepts established in (Quinga-Socasi

et al., 2020), (Quinga and Chang, 2020) and (Valen-

cia and Chang, 2020) this paper presents a novel tech-

nique for developing an asymmetric key system capa-

ble of enhancing security by decomposing the ANN

and using each component as a separate encryption

and decryption key.

3 METHODOLOGY

An experimental research was performed in this work

to create an asymmetric key cryptography system

based on ANN that may provide acceptable security

while executing quickly. This research was divided

into three sections: (1) Calibration of an autoencoder

neural network to randomize the training process and

create a distinct ASCII code codiﬁcation based on an

initialization password (2) The neural weights that

will serve as a public and private key will be cali-

brated. (3) A comparison of system performance and

security analysis to assess how resistant the system is

to hacker assaults.

3.1 Autoencoder Neural Network

Architecture

An autoencoder with 8 neurons in the input layer, 10

neurons in the hidden layer, and 8 neurons in the out-

put layer was used to build this system. The amount

of predeﬁned characters in the full ASCII code, the

size of the produced keys, and the scaling of plain

text were all taken into consideration while choosing

this design. The entire ASCII code was encoded in

bits, which meant that each character in the cryp-

tosystem was represented by an 8-bit character. The

neural network received each 8-bit set as input.

3.2 Randomization Algorithm

A randomization technique was used in the proposed

system to generate initial random synaptic weights

and a vector of random indices. This algorithm was

based on changing “seeds” in conjunction with the

rand() function. The changing of seeds was a crucial

step in increasing the system’s unpredictability.

3.3 Asymmetric Key Cryptography

Model

To create a public and private key, the system used an

autoencoder neural network design. These keys corre-

spond to the synaptic weights of the network (W

and

). The system uses a randomization technique that

is based on the user’s secret initialization password

and a random character string unique to this system.

In addition, before producing the ciphertext from

the plain text, the system preprocessed the informa-

tion. In the same way, a preprocess was used to create

plain text from ciphertext that was reversed from the

one used previously. A complete scheme of the sys-

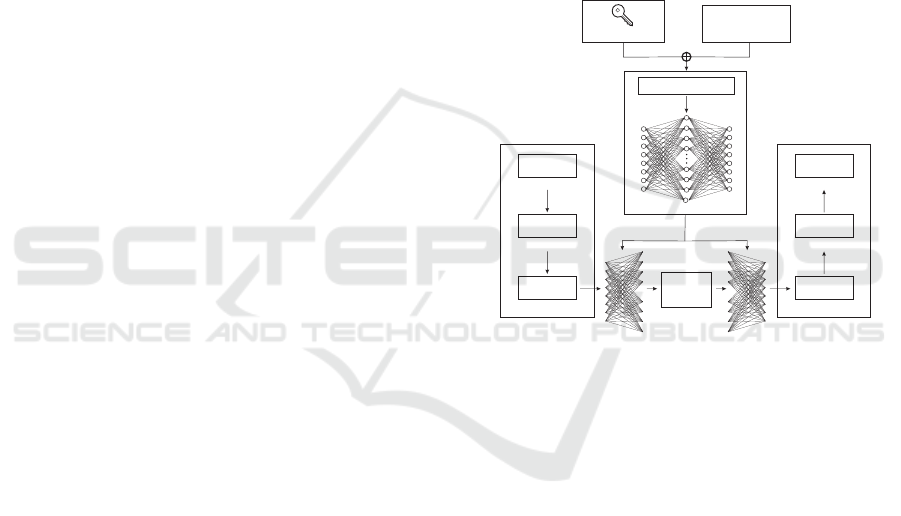
tem is presented in Figure 1.

Initialization Password

Internal Random String

“---------”

Randomization Algorithm

Training

Public Key Private Key

“Hello World”

Plain Text

01110111

Binary Message

01100010

XOR Message

0.471285 0.966985

0.116430 0.243542

0.058160 0.020261

0.9876870.987435

0.377028

Cipher Text

“Hello World”

Plain Text

01110111

Binary Message

01100010

XOR Message

Preprocessing

Reverse

Preprocessing

c10

Figure 1: The proposed cryptographic system’s scheme,

which includes the system’s initialization, the creation of

keys, and the data encryption/decryption process.

• Encryption. Plain text must be pre-processed be-

fore data encryption can be performed. First, the

original message was converted to binary text us-

ing the ASCII code. The binary text was then

split into 8-bit sets, each of which was subjected

to a series of XOR operations. After getting the

“XOR text”, it was encrypted with the public key

to acquire the ciphertext. Each 8-bit set was trans-

formed to a set of 10 ﬂoating integers, and the ci-

phertext was scaled from “XOR text”.

• Decryption. The ciphertext was split into blocks

of 10 ﬂoating integers and decrypted using the pri-

vate key and the “XOR text”. After that, a reversal

of the preprocessing was carried out. The “XOR

text” was broken down into 8-bit blocks and then

XOR techniques were used to retrieve it. The bi-

nary text was then retrieved, followed by the plain

text.

An Asymetric-key Cryptosystem based on Artiﬁcial Neural Network

541

3.4 Performance and Security

Parameters

When evaluating performance, a variety of factors

are considered. Data from asymmetric cryptographic

techniques is compared to these parameters. Secu-

rity considerations are also taken into account. Fi-

nally, a method for determining the randomization

algorithm’s efﬁciency in the production of keys is

established. The Hardware Characteristics of the

system are: Windows 10 64-bit operating system,

8Gb RAM and Intel(R) Core(TM) i7-5500U CPU

2.40GHz 2.40GHz.

3.4.1 Performance Parameters

Encryption Time is determined based on the time re-

quired by an algorithm or system to translate a plain

text into a ciphertext. Besides, Decryption Time is

determined during the translation into the plain text

from the ciphertext and Key Generation Time is the

required to generate the keys, and it is equivalent to

ANN training time.

3.4.2 Security Parameters

The parameters that will be considered are:

Accuracy: It is the number of characters successfully

retrieved, over the total of characters that the complete

ASCII code has. This value is expressed in percent-

ages and can change in training process.

Network Tolerance: It is the amount of noise that

the synaptic weights of a trained network can tolerate

before data recovery fails.

Private Key Security: It is a portion of all synap-

tic weights involved in data recovery. The synaptic

weights of an ANN are continuous values, generally

with a large number of signiﬁcant digits (SD). Equa-

tion 1 is used to determine the number of attempt nec-

essary to hack the private key.

V R

= n

(1)

Where n is the set of all possible elements that can

be used to generate the public key. In this case, n de-

pends on the number of SDand the rank correspond-

ing to the synaptic weights of a network with a high

accuracy. Besides m is a subset of n, that depends

on the number of elements in the private key (size of

Signiﬁcant Digits Determination: A random ﬂoat

value in the range [0.001, 0.1] is added and subtracted

from the public key to determine the minimum num-

ber of SD that will be used to recover the data. The

number of SD of the ﬂoat value capable of having a

high accuracy is set as the lowest quantity when the

accuracy reduces by more than 75%.

Neural Network Security. Two strings are used to

generate public and private keys. The ﬁrst is a user-

entered string, while the second is a random string

generated internally. The strings are randomized to

initialize the network’s synaptic weights and create a

chain of pseudo-ordered indexes that will be used in

training. Therefore, a hacker would have to guess the

user’s password through brute force to obtain a ANN

capable of generating equivalent keys. Equation 2 is

used to calculate the necessary time to hack.

T = (N

) × t

(2)

Where N is the total number of printable ASCII

characters, M is the length of the string entered, and

is the ANN training time.

Randomization Algorithm Efﬁciency. The initial-

ization password is crucial to the randomization algo-

rithm. If the password is changed, the keys that are

generated must be completely different. To evaluate

the algorithm’s performance in data randomization, it

is suggested that the keys created by two initialization

passwords with high similarity be compared.

4 RESULTS

The results of the proposed system’s performance

evaluation and security analysis, including random-

ization, are presented. The time needed to encrypt

and decrypt the data was compared with the results

obtained in (Maqsood et al., 2017), (Matta and Ku-

mar, 2016) and (Farah et al., 2012). To evaluate the

performance of the cryptographic system, the encryp-

tion/decryption time and the key generation time were

used.

4.1 Performance Evaluation

• Encryption and Decryption Time of

Cryptosystem.

The suggested system was run with the following

input ﬁle sizes to establish overall performance

in terms of encryption and decryption time: 200,

300, 400, 500, and 600 KB. The cryptosystem was

run ten times for each ﬁle size to provide a repre-

sentative average time. The results are shown in

Figure 2.

The results reveal that when ﬁle sizes grow larger,

the time it takes the cryptosystem to encrypt and

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

542

decrypt data grows as well. This is because the

cryptosystem resizes the data, which means the

decrypted ﬁle is larger than the encrypted ﬁle.

Figure 2: Execution time corresponding to the encryption

and decryption processes of the cryptographic system.

• Key Generation Time of the Cryptosystem.

The following initialization password lengths

(numbers of characters) were used to establish the

average time required for the cryptosystem to gen-

erate the public and private key: 4, 5, 10, 12, 14,

15. The system was run ten times for each ini-

tialization password, and the average value was

taken. In Figure 3, the average times of each

password length are shown graphically, and the

key creation time does not depend on the pass-

word length. Furthermore, it was discovered that

the size of the keys is constant and independent

of the initialization password size. Because the

time it takes to generate the keys is unrelated to

the length of the initialization password, a general

average of 27.47 seconds was calculated. Further-

more, because the password length is always the

same, it was not taken into consideration in future

calculations.

Figure 3: Time required by the cryptographic system to gen-

erate a set of keys with respect to the length of the initial-

ization password. The Public and Private Key have 1KB in

size and the average is 27.47 (s).

• Comparison between RSA, ElGamal and the

Proposed Cryptosystem.

In terms of encryption/decryption time and key

generation time, (Maqsood et al., 2017) compared

the performance of the RSA and Elgamal asym-

metric cryptographic methods. The experiments

were carried out on a 2.34 GHz Intel Pentium

CPU with 1 GB of RAM, and the algorithms

were developed in Java (Eclipse platform version:

3.3.1.1). The methods were tested with text ﬁles

ranging in size from 32 KB to 126 KB, 200 KB to

246 KB to 280 KB, and the results were measured

in seconds.

Encryption Time. Table 1 shows a comparison

of encryption timings for RSA, ElGamal, and the

proposed cryptosystem. The cryptosystem’s en-

cryption times are substantially faster than those

of RSA and ElGamal. In addition, when the ﬁle

size grows greater, the cryptosystem takes longer

to encrypt it.

Decryption Time. Table 2 compares the de-

cryption times of the RSA and ElGamal algo-

rithms, as well as the proposed cryptosystem. The

behavior was comparable to the encryption proce-

dure, where decryption times are much lower than

SRA and ElGamal’s, and the decryption time in-

creases as the ﬁle size grows. Furthermore, the de-

cryption timings of cryptosystems are very com-

parable to the encryption periods. This is because

RSA and ElGamal’s decryption relies on mathe-

matical operations between very big prime inte-

gers.

Key Size and Generation Time. Table 3 shows

the size of the keys and the time it takes to gen-

erate them. The time it takes the cryptosystem to

create a set of keys is signiﬁcantly longer than the

time it takes RSA and ElGamal to do so. The en-

cryption key’s size was added to the decryption

key’s size to calculate the overall size of the set of

keys. The proposed cryptosystem generates keys

that are much larger than those generated by RSA

and ElGamal.

• Comparison between RSA-16bits, ECC-16bits

and the Proposed Cryptosystem.

Matta et. al (Matta and Kumar, 2016) used a

steganographic technique to analyze the perfor-

mance of the RSA-16bits and ECC-16bits encryp-

tion algorithms. Despite the fact that Matta’s

study used steganography rather than encryption,

in which plain text is converted to ciphertext, it

gives important information for assessing the pro-

posed system. The key generation time and en-

cryption/decryption times for the RSA-16bits and

An Asymetric-key Cryptosystem based on Artiﬁcial Neural Network

543

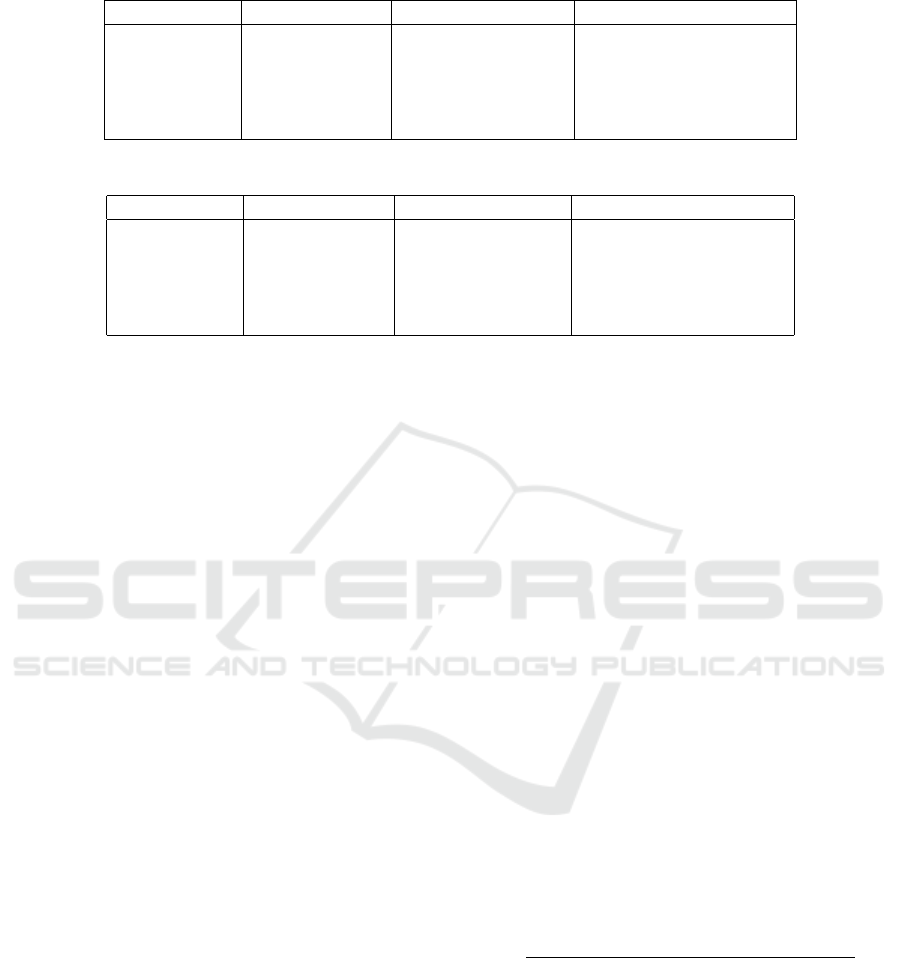
Table 1: Encryption Time comparative with Maqsood et al.

File size (KB) RSA Time (ms) ElGamal Time (ms) Cryptosystem Time (ms)

32 130 450 10

126 520 1030 31

200 740 1410 47

246 1110 1750 47

280 1390 1830 62

Table 2: Decryption Time comparative with Maqsood et al.

File size (KB) RSA Time (ms) ElGamal Time(ms) Cryptosystem Time (ms)

32 150 430 16

126 430 850 32

200 660 130 47

246 930 1300 62

280 230 1640 63

ECC-16bits algorithms were assessed individu-

ally. Matta, use the following ﬁle sizes to evaluate

RSA-16bits and ECC-16bits: 22 KB, 87 KB, and

174 KB.

Encryption Time. Data ﬁles of the same size

as those used in Matta’s comparison were uti-

lized to test the proposed cryptosystem with the

RSA-16bits and ECC-161bits algorithms (Matta

and Kumar, 2016). Table 4 shows a comparison of

the encryption times for RSA-16bits, ECC-16bits,

and the proposed cryptosystem. The cryptosys-

tem’s encryption speeds are signiﬁcantly faster

than those of RSA-16bits and ECC-16bits. This

is due to the fact that the suggested cryptosystem

is based on matrix operations, which work much

better to compute.

Decryption Time. Table 5 shows the compar-

ison of decryption times for RSA-16bits, ECC-

16bits, and the proposed cryptosystem. The

cryptosystem’s decryption times are signiﬁcantly

faster than those of RSA-16bits and ECC-16bits.

This is due to the fact that one employs ma-

trix operations while the other employs operations

and functions using extremely big prime integers.

When comparing the data given, the cryptosys-

tem’s decryption procedure takes longer than the

encryption process. This is related to the fact that

plaintext is re-dimensioned when it is encrypted.

Key Generation Time. Table 6 shows the critical

generation periods. The creation time of the public

key was added to the creation time of the private key

to get the generation time of the set of keys. In the

case of the cryptosystem, the two keys have just one

creation time. The suggested cryptosystem’s key gen-

eration time is signiﬁcantly longer than the disclosed

time for RSA-16bits, although it is signiﬁcantly less

than that of ECC-16bits.

4.2 Security Evaluation

Private Key Security Results. The number of SD

required for a cryptosystem to have high accuracy is

in the hundreds, according to the data in Table 7. This

means that the cryptosystem’s numbers must include

at least three digits. The private key has a rank of

(-2,2) and a size of W

is 80 bytes. We have the set [-

1.99, ..., 1.99], which has 399 items based on the rank

and SD. Equation 1 is used to compute the number

of attempts (a) a hacker will need to reproduce the

correct sequence of numbers that make up the private

key.

V R

399

= 399

−→ V R

399

= 1.19628 × 10

288

× a

To ﬁgure out how long it will take to complete all

of these attempts, we’ll use a hypothetical machine

that can make 1 × 10

attempts per second (s).

x =

1.19628 × 10

288

total

) × 1(s) × 1(years)

1 × 10

machine

) × 3.15 × 10

193

(s)

(3)

We can deduce from Equation 3 that it will take

3, 79 × 10

193

years to hack the private key.

Neural Network Security. The hacker needs

to know the system initialization password in order to

obtain the correct password capable of generating the

correct public and private key. We know that the net-

work’s average training time is 27.47 seconds (Figure

3). The ASCII code has a total of 223 printable char-

acters. Equation 2 then yields the following results.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

544

Table 3: Key Generation Time comparative with Maqsood et al.

Key Size (bits) Generation Time (s)

RSA 1024 0.287

ElGamal 160 0.86

Cryptosystem 16000 27.74

Table 4: Encryption Time comparative with Matta et al.

File size (KB) RSA-16. Time (ms) ECC-16. Time (ms) Cryptosystem Time (ms)

22 3782 51391 16

87 4297 93741 16

174 4265 113947 32

Table 8 shows the length of the initialization pass-

word used in proportion to the time it would take to

hack the cryptosystem in years. When the length of

the initialization password is increased, the calcula-

tion time required to hack the system using a brute

force technique grows exponentially. Table 8 shows

that all of the times are excessively long, making the

hacking procedure computationally unfeasible.

Randomization Algorithm Performance. The ini-

tialization passwords “helloworld” and “helloworle”

are used to produce keys to test the randomization al-

gorithm’s performance. The difference between the

passwords is minimal for determining the algorithm’s

efﬁcacy.

Pseudo-ordered Index Vector. The distribution of

pseudo-ordered vectors of indices produced with the

passwords “helloworld” and “helloworle” is shown in

Figure 4. The distribution of the two vectors follows

the same pattern, but they are distinguished by a trans-

lation on the x axis. The x-axis shift is due to the fact

that the initialization passwords were just one bit dif-

ferent from one another. Each point that moves away

from the “line” of linear growth represents the ran-

domness that is introduced in the process of creating

the vectors of pseudo-ordered indexes (Valencia and

Chang, 2020).

Figure 4: Pseudo-order index vector distribution with pass-

words “helloworld” and “helloworle”.

Distribution of Public and Private Key: The dif-

ference between the public and private key produced

using the password “helloworld” is shown in Figure 5.

The values that make up the public key and the private

key do not coincide at any point. In terms of conceiv-

able values that each key may make up, the private

key is “bigger” than the public key. Figure 5 shows

that the private key is made up of numbers in the

[−2.2, 1.5] range, whereas the public key is made up

of values in the approximate range of [−0.65, 0.65].

Figure 5: Public and Private key distribution with password

“helloworld”.

The difference between the keys generated using

the password “helloworle” is shown in Figure 6. The

public and private keys have a high degree of random-

ness in their distribution, and they do not coincide at

any time. The private key is “bigger” than the pub-

lic key, as seen in Figure 6. The private key is in the

[−2.5, 1.75] range, whereas the public key is approx-

imately in the [−0.60, 0.60] range.

Figure 6: Public and Private key distribution with password

“helloworle”.

Because the cryptosystem seeks to ensure a high

level of security, the public and private keys differ.

The potential values that make up the public key are

useless for security because it is publicly known. The

An Asymetric-key Cryptosystem based on Artiﬁcial Neural Network

545

Table 5: Decryption Time comparative with Matta et al.

File size (KB) RSA-16. Time (ms) ECC-16. Time (ms) Cryptosystem Time (ms)

22 4328 24187 16

87 4188 75402 31

174 4390 115137 47

Table 6: Key Generation Time comparative with Matta et al.

Public Key Private Key Total Time (s)

RSA-16bits 0.031 0.015 0.046

ECC-16bits 123.203 122.922 246.125

Cryptosystem - - 27.47

private key, on the other hand, requires a method that

makes it impossible to duplicate because it is a secret.

Public Key Comparison: The difference between

the public key created with the password “helloworld”

and the public key created with “helloworle” is seen

in Figure 7. Even if the initialization password is only

one bit different, the distributions of the public keys

are considerably different. The key corresponding

to “helloworld” is in the range [−0.61, 0.52], while

the key corresponding to “helloworle” is in the range

[−0.45, 0.45], as seen in Figure 7.

Figure 7: Comparison between public keys generated by

passwords “helloworld” and “helloworle”.

Private Key Comparison: The difference between

the private key generated by “helloworld” and the pri-

vate key generated by “helloworle” is seen in Figure

8. The distributions of private keys are signiﬁcantly

diverse from one another. The key corresponding

to “helloworld” is in the range [−2.2, 1.32], whereas

the one corresponding to “helloworle” is in the range

[−2.5, 1.8], as seen in ﬁgure 8.

Figure 8: Comparison between private keys generated by

passwords “helloworld” and “helloworle”.

The level of randomness contained in the public

and private keys when compared to one another shows

that the cryptosystem’s randomization mechanism is

working properly. Furthermore, the system has a high

level of security because to the variance between the

ranges of values that make up the keys.

5 CONCLUSIONS

The proposed cryptosystem has much faster compu-

tation times than existing asymmetric algorithms, ac-

cording to the results of the experiments. The ﬁle

sizes utilized for the purchase ranged from 32 KB

to 280 KB, depending on the method. Additionally,

the system was tested with ﬁles ranging in size from

200 KB to 600 KB, and it was found that the en-

cryption and decryption of the data was not a major

problem. In terms of key generation time, the system

takes longer to execute than traditional methods since

it takes the same amount of time to train the ANN.

The proposed autoencoder neural network design

has a large capacity for encoding all ASCII code in

a reasonable amount of time. Because this procedure

is only run once per set of keys, the average training

time was 27.47 seconds, which is acceptable. With

a single bit change in the initialization password, the

system was able to produce completely new sets of

keys. As a consequence, the high-level randomness

randomization method created for the ANN training

process yielded positive results.

The cryptographic system’s security evaluation re-

vealed that a brute force attack, whether attempting

to “reconstruct” the private key or compromising the

whole system, would take a huge amount of comput-

ing time, making hacking impossible.

Since the suggested cryptographic system is based

on ANNs, we will build it using a parallelization tech-

nique in the future, reducing training times (genera-

tion of keys). The level of randomness might be in-

creased without affecting the neural network’s perfor-

mance using this method.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

546

Table 7: Network Tolerance.

Thousandths (4 digits) Hundredths (3 digits) Tenths (2 digits)

Noise Accuracy Noise Accuracy Noise Accuracy

0,001 99,61 0,01 100,00 0,1 66,67

0,002 99,61 0,02 100,00 0,2 17,65

0,003 99,61 0,03 99,22 0,3 3,92

0,004 99,61 0,04 98,43 0,4 0,78

0,005 100,00 0,05 98,04 0,5 0,00

0,006 100,00 0,06 92,55 0,6 0,00

0,007 100,00 0,07 86,67 0,7 0,00

0,008 99,61 0,08 78,43 0,8 0,00

0,009 99,61 0,09 74,12 0,9 0,00

Table 8: Neural Network Security Results.

Initialization Password

Length

Equation Time (s) Time (years)

4 T = (223

) × 27.47(s) 67932580424 2,15E+03

5 T = (223

) × 27.47(s) 15148965434612 4,80E+05

10 T = (223

) × 27.47(s) 8,35425E+24 2,65E+17

12 T = (223

) × 27.47(s) 4,15448E+29 1,32E+22

14 T = (223

) × 27.47(s) 2,06598E+34 6,55E+26

15 T = (223

) × 27.47(s) 4,60714E+36 1,46E+29

REFERENCES

Charniya, N. N. (2013). Design of near-optimal classiﬁer

using multi-layer perceptron neural networks for in-

telligent sensors. International Journal of Modeling

and Optimization.

Coutinho, M., de Oliveira Albuquerque, R., Borges, F., Gar-

cia Villalba, L. J., and Kim, T.-H. (2018). Learning

perfectly secure cryptography to protect communica-

tions with adversarial neural cryptography. Sensors,

18(5):1306.

Farah, S., Javed, M. Y., Shamim, A., and Nawaz, T. (2012).

An experimental study on performance evaluation of

asymmetric encryption algorithms.

Jogdand, R. M. (2011). Design of an efﬁcient neural key

generation. International Journal of Artiﬁcial Intelli-

gence & Applications (IJAIA).

Kanter, I. and Kinzel, W. (2003). The theory of neural net-

works and cryptography. In The Physics of Communi-

cation, pages 631–642. World Scientiﬁc.

Kinzel, W. and Kanter, I. (2002). Interacting neural net-

works and cryptography. In Advances in solid state

physics, pages 383–391. Springer.

Klein, E., Mislovaty, R., Kanter, I., Ruttor, A., and Kinzel,

W. (2005). Synchronization of neural networks by

mutual learning and its application to cryptography.

Advances in Neural Information Processing Systems.

Maqsood, F., Ahmed, M., Ali, M. M., and Shah, M. A.

(2017). Cryptography: A comparative analysis for

modern techniques. International Journal of Ad-

vanced Computer Science and Applications, 8(6).

Matta, R. and Kumar, A. (2016). Performance comparison

for rsa and ecc in video steganography. International

Journal of Engineering Science and Computing.

Quinga, F. and Chang, O. (2020). A Deep Learning Ap-

proach for a Symmetric Key Cryptography System.

Quinga-Socasi, F., Velastegui, R., Zhinin-Vera, L.,

Valencia-Ramos, R., Ortega-Zamorano, F., and

Chang, O. (2020). Digital cryptography implemen-

tation using neurocomputational model with autoen-

coder architecture.

Valencia, R. and Chang, O. (2020). Cryptography system

implementation using neurocomputational model and

deep learning.

Volna, E., Kotyrba, M., Kocian, V., and Janosek, M. (2012).

Cryptography based on neural network. In ECMS,

pages 386–391.

Zhinin-Vera, L., Chang, O., Valencia-Ramos, R., Ve-

lastegui, R., Pilliza, G. E., and Quinga-Socasi, F.

(2020). Q-credit card fraud detector for imbalanced

classiﬁcation using reinforcement learning. pages

279–286.

An Asymetric-key Cryptosystem based on Artiﬁcial Neural Network

547