Univariate Time Series Prediction using Data Stream Mining

Algorithms and Temporal Dependence

Marcos Alberto Mochinski

, Jean Paul Barddal

and Fabrício Enembreck

Graduate Program in Informatics, PPGIa, Escola Politécnica, Pontifícia Universidade Católica do Paraná, PUCPR

Curitiba, Brazil

Keywords: Time Series Forecasting, Data Stream Mining Algorithms, Multiple Time Series, Ensemble, Feature

Engineering, Temporal Dependence.

Abstract: In this paper, we present an exploratory study conducted to evaluate the impact of temporal dependence

modeling on time series forecasting with Data Stream Mining (DSM) techniques. DSM algorithms have been

used successfully in many domains that exhibit continuous generation of non-stationary data. However, the

use of DSM in time series is rare since they usually are univariate and exhibit strong temporal dependence.

This is the main motivation for this work, such that this study mitigates such gap by presenting a univariate

time series prediction method based on AdaGrad (a DSM algorithm), Auto.Arima (a statistical method) and

features extracted from adjusted autocorrelation function (ACF) coefficients. The proposed method uses

adjusted ACF features to convert the original series observations into multivariate data, executes the fitting

process using the DSM and the statistical algorithm, and combines the AdaGrad's and Auto.Arima's forecasts

to establish the final predictions. Experiments conducted with five datasets containing 141,558 time series

resulted in up to 12.429% improvements in sMAPE (Symmetric Mean Average Percentage Error) error rates

when compared to Auto.Arima. The results depict that combining DSM with ACF features and statistical time

series methods is a suitable approach for univariate forecasting.

1 INTRODUCTION

To work with univariate time series, the information

available for the prediction must be extracted from

the series’ observations. A series can be summarized

in a set of events observed in time at a constant

frequency (Makridakis, 1976). Statistical algorithms,

such as regression algorithms, identify the temporal

dependencies between the elements of a series. Yet,

this is not a characteristic inherent to all data stream

mining (DSM) algorithms that are multivariate in

nature, i.e., to deal with univariate data they depend

on attributes (artificial or not) to improve their

learning mechanism.

In time series, the temporal dependence between

the series' observations can be identified by analyzing

the correlation between the elements of the series,

called autocorrelation. Autocorrelation expresses the

correlation between an observation of the series and

https://orcid.org/0000-0002-7118-9993

https://orcid.org/0000-0001-9928-854X

https://orcid.org/0000-0002-1418-3245

its lagged values (Hyndman, 2014). This paper

proposes the extraction of features from

autocorrelation function (ACF) and the combination

of DSM algorithms with univariate autoregressive

models in multi-series scenarios. We show that using

time dependency features improves AdaGrad's

(Duchi et al., 2011) predictions, and their

combination with Auto.Arima's (Box and Jenkins,

1976) predictions yields lower error rates.

The main motivation for this study is that the use

of DSM algorithms in univariate time series

prediction is rare, since time series usually present

strong temporal dependence and they are constituted

solely by their observed values. Although in a

previous paper (Mochinski et al., 2020), DSM has

been applied to time series forecasting, the impact of

temporal dependency modeling in this context is

unexplored so far. Thus, proposing a novel method

focusing on this scenario is challenging. In our

398

Mochinski, M., Barddal, J. and Enembreck, F.

Univariate Time Series Prediction using Data Stream Mining Algorithms and Temporal Dependence.

DOI: 10.5220/0010859600003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 398-408

ISBN: 978-989-758-547-0; ISSN: 2184-433X

approach, we opted for the use of adjusted ACF

coefficients as new features for the univariate time

series processing and we explore its applicability in

an extensive experimentation process using series of

different datasets.

First, we discuss related works on time series

forecasting and the use of temporal dependence in

different scenarios. Next, we introduce our approach

for the feature engineering process and the method

used to evaluate it, which is later analyzed in the

following section. Finally, we conclude this paper and

list future works.

2 RELATED WORK

Authors in (Žliobaitė et al., 2015) cite that temporal

dependence can also be called serial correlation or

autocorrelation and explain that in data stream

problems, an input set of multi-dimensional variables

submitted to a DSM algorithm usually contains the

information that makes it possible to process the data

classification or prediction. They discuss that the past

values of the target variable (usually the only

information available for univariate data) are not

enough for the predictive process.

According to (Stojanova, 2012), there are four

different types of autocorrelation: spatial, temporal,

spatio-temporal and network (relational)

autocorrelation. Stojanova explains that spatial

autocorrelation is defined as the correlation among

data values that considers their location proximity.

Therefore, near observations are more correlated than

distant ones. Temporal autocorrelation refers to the

correlation of a time series with its own past and

future values, and the author cites that it can be also

called lagged correlation or serial correlation, as in

(Žliobaitė et al., 2015). Spatio-temporal

autocorrelation considers spatial and temporal

correlation between observations, and network

autocorrelation expresses the interdependence

between values in different nodes of a network.

In this paper we focus on temporal

autocorrelation. Authors in (Stojanova, 2012) explain

that temporal autocorrelation is the simplest form of

autocorrelation as it focuses on a single dimension,

i.e., time. Many fields study autocorrelation. Authors

in (Nielsen et al., 2018) use autocorrelation to predict

the wave-induced motion of a marine’s vessel by

combining values of autocorrelation function and

previous measurements. Despite the fact that the

autocorrelation can express a stationary condition, the

authors use a sample of an ACF (autocorrelation

function) obtained at a recent time window to help in

the prediction of a dynamic system, considering that

the values are valid as they have not changed

significantly. The authors cite in (Nielsen et al., 2018)

that the ACF function can be seen as a direct

measurement of the memory effect of a physical

process.

Authors in (Rodrigues and Gama, 2009) use

autocorrelation coefficients in an electricity-load

streams prediction study. They identify the

correlation of historical inputs and use the most

correlated values as input to a Kalman filter system

used in combination with a multi-layered perceptron

neural network to create new predictions across

different horizons, i.e., one hour, one day, and one

week ahead load forecasts.

Authors in (Duong et al., 2018) used temporal

dependencies to detect changes in streaming data.

The authors introduce a model named Candidate

Change Point Detector (CCPD), used to model high-

order temporal dependencies and compute the

probabilities of finding change points in the stream

using time dependency information from different

points of the stream.

According to (Hyndman, 2014), autocorrelation

measures the linear relationship between lagged

values of a time series. Figure 1 presents the original

data for a time series and its ACF (autocorrelation)

function plot. The authors in (Hyndman, 2014)

explain that, in an ACF plot, the relationship r

expressed between two events

and y

t-k

can be

written as follows (1):

(1)

where T represents the length of the time series in

analysis, and

ȳ the mean of its observations. Authors

also inform that trend and seasonality can also be

evaluated from the analysis of the ACF plot: trend

data tend to have positive values that slowly decrease

as the lags increase; seasonal data, on the other hand,

will present larger values for the autocorrelation

coefficients at multiples of the seasonal frequency.

According to (Werner and Ribeiro, 2003), ACF

functions evaluate the stationarity of a series. In

general, when analysing an ACF plot, it is important

to observe the coefficients that present most

significant values (statistically different from zero).

As described previously in this paper, a time

series is defined as a set of events observed in time at

a constant frequency (Makridakis, 1976). In (Esling

and Agon, 2012), authors complement that a time

series can be defined as a set of contiguous instants of

time, and that a series can be univariate or

Univariate Time Series Prediction using Data Stream Mining Algorithms and Temporal Dependence

399

multivariate (when several series simultaneously

cover several dimensions in the same time interval).

In general, it can be said that a univariate series is one

whose observations refer to a single variable, and a

multivariate series is one that contains information

relating to more than one variable. In this work, we

present a prediction approach for multi-series

scenarios where a set of univariate time series is

available, regardless of whether these are inter-

correlated or not. Our approach is multivariate

because, at first, it converts original univariate series

observations into multivariate data using adjusted

ACF coefficients as their additional features.

Despite the exciting results of classical statistical

methods for time series forecasting, it is increasingly

common to find machine learning alternatives, or

even their combination. Modern techniques like data

stream mining (DSM) algorithms deal with big data

scenarios or situations in which it is inconceivable, or

at least difficult, to have access to the entire dataset at

once. The authors in (Bontempi et al., 2013) say that,

in the last two decades, machine learning models have

established themselves as serious competitors to

classical statistical models. This study, in turn,

proposes the combined use of a classical statistical

method and a DSM algorithm to benefit from their

characteristics.

The authors in (Bifet et al., 2018) enumerate,

among other characteristics, that a data stream mining

algorithm must process one instance at a time using a

limited amount of memory and time for processing,

and that it must be able to give a response at any time,

detecting and adapting a model to temporal changes.

Modern applications demand faster responses and

innovative techniques that adapt to the increasingly

overloaded world of information in which we live.

According to (Gama et al., 2014), learning should

take place in an incremental and adaptive fashion,

thus allowing the reaction to variations in data

behaviour (concept drifts) and the data prediction in

an increasingly precise way. It is essential that the

algorithms used in time series analysis can identify

variations of data behaviour with greater accuracy so

that the forecasting process is more precise. Thus, it

is justifiable to seek to apply data stream mining

algorithms, which allow gradual, incremental

processing of the observations, and which are highly

adaptive in time series forecasting. In this work,

statistical and DSM algorithms forecasts are

combined to improve their individual results.

AdaGrad (Duchi et al., 2011) is an example of an

adaptive data stream mining algorithm, capable of

dealing with very sparse and non-sparse data.

Figure 1: M1 series (M4 dataset). Original data and ACF

plot. Dotted lines in the ACF plot indicate the confidence

interval. We may consider the values inside this interval as

not statistically significant.

According to the authors in (Duchi et al., 2011),

AdaGrad generalizes the online learning paradigm of

specializing an algorithm to fit a particular dataset,

and automatically adjusts the learning rates for online

learning and stochastic gradient descent on a per-

feature basis.

Regarding statistical algorithms for time series

forecasting, this work focuses on the use of

Auto.Arima (Hyndman and Khandakar, 2008;

Hyndman et al., 2019), an automated implementation

of ARIMA (Box and Jenkins, 1976), a classic

statistical algorithm also known as a Box-Jenkins

model. In a problem with multiple time series, to

avoid demanding an individual analysis of each

series, a solution that automates the selection of the

best ARIMA parameters can certainly be of great help

in the process. Therefore, we seek to predict multiple

time series without the need for a meticulous analysis

of each series, thus rendering the process user-

independent.

The combined use of different algorithms is not a

novelty in time series forecasting. In competitions

like M4 (Makridakis et al., 2018a), from the 17 most

accurate results, 12 used combinations and one used

a hybrid approach integrating statistical and machine

learning methods.

Authors in (Mochinski et al., 2020) also explore

using a hybrid approach combining DSM and

statistical algorithms in univariate time series

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

400

prediction. The proposed method executes the fitting

process using a DSM algorithm and Auto.Arima, and

selects the best algorithm for the series' forecasting

based on the calculated fitting error. We think that

using a different technique can improve the feature

engineering process used by that study. Based on this

assumption, we decided to extend it by using the

temporal dependence information present on each

series for the feature engineering. For this, we

decided to explore the Temporally Augmented

concept (presented in (Žliobaitė et al., 2015) for

classification problems) and the use of ACF

coefficients as the basic information for the creation

of additional features for time series processing. To

validate our proposal, we applied it to a more diverse

set of time series, resulting in more extensive

experimentation than that observed in (Mochinski et

al., 2020). For data stream mining algorithms, an

additional issue being considered is their dependence

on multivariate input vectors capable of helping their

learning process. This is handled in our proposal by

introducing time dependence features as their input.

3 THE AA-ACF METHOD FOR

TIME SERIES FORECASTING

In this section, we describe the Auto.Arima and

AdaGrad Autocorrelation Coefficient Function (AA-

ACF) method, which is the result from an exploratory

study conducted to evaluate the combined use of

statistical and DSM methods for improved univariate

time series forecasting.

The proposed method includes the following

phases: pre-processing, training, algorithm selection

and forecasting. In the pre-processing phase, the time

series data is loaded, and the feature engineering

process is done. In the training phase, Auto.Arima

and AdaGrad are trained and assessed w.r.t. training

error. The algorithm selection phase picks the

algorithm that presented the lowest training error, and

finally, in the forecasting phase the predictions for the

time series are calculated using the algorithm selected

to each series. Our implementation was created using

the R language, which also controls the execution of

the MOA framework (Bifet et al., 2010), where

AdaGrad training and forecasting are done. Details

about each step of the proposal are given below.

The use of 288 observations (W288) and 18 lags are

explained in detail in the "AA-ACF hyperparameters"

subsection.

3.1 Pre-processing

To introduce the concept of temporal dependence on

the series attributes, coefficients obtained with the

autocorrelation function (ACF) are extracted from the

series and used in the creation of new features.

Considering the nature of DSM algorithms, which

do not analyze all data in batch mode since they work

with the most recent instances of the series, the

concept of a sliding window was used. Also, the use

of this technique allows for the adjustment of the

autocorrelation coefficients during the entire feature

engineering process, adapting them to the most recent

aspect of the series events.

In the feature engineering process, the additional

attributes associated with each observation in the

series are created based on previous events (values

from previous observations in the series), using

sliding windows of up to 288 observations (referred

in this study as W288). The window data is used to

calculate ACF coefficients that express the

relationship between an observation and the events

that precede it.

The coefficients generated for the first 18 lags

are considered as the most relevant for the purpose of

this approach in spite of their values, i.e., positive and

negative values are considered. The rationale behind

using time dependency attributes in the feature

engineering process was based on the study of

(Žliobaitė et al., 2015), which proposed the use of

temporal autocorrelation in data stream classification

problems. For classification, it suggests two

approaches: the Temporal Correction classifier in

which the predictive model is adapted to support the

concept, and the Temporally Augmented classifier,

which proposes the feature engineering process with

the advantage of not requiring modifications to the

classifier structure and, thus, allowing the use of any

algorithm, without the need to recode it.

In this paper, the Temporally Augmented concept

is adapted for regression problems of univariate

series. The goal is to create features that represent the

dependency between the input features and past

observations of each series, using them as input for

the DSM algorithms predictions. Figure 2 presents

the approach used in this study to create features

based on ACF coefficients values. The diagram

presents the creation of features for a specific time

series, and Algorithm 1 explains the process in more

detail. First, the events are read using a sliding

Univariate Time Series Prediction using Data Stream Mining Algorithms and Temporal Dependence

401

window of up to 288 registers (W288). Second, ACF

coefficients are calculated considering the events

selected in W288.

Figure 2: Feature Engineering approach diagram, based on

ACF Coefficients.

Next, the first 18 ACF coefficients are normalized

for the interval from 1 to 2 (to avoid negative or zero

values) and then multiplied for the last 18 events from

the sliding window (the most recent ones) resulting in

the ACF features (or adjusted autocorrelation

coefficients) that are added to the series. Additionally,

a feature is created based on a linear regression model

considering the W288 events. This last attribute was

created to help DSM algorithms in one-step-ahead

forecasts. It was considered necessary because of the

characteristics of the test-then-train model used by

DSM algorithms. Therefore, suggesting a more

assertive value for the next Events attribute would

help to keep DSM model calibrated, with lower error

on the prequential process.

Algorithm 1: The Feature Engineering Approach.

1: for each series in the dataset do

2: S ← series observations

// loop through each observation in the series S

// to compute its new additional features

3: for N = 1 to length(S) do

// sliding-window data (time series data type):

// select up to 288 previous events for the current

//N record in S

4: W288 ← S[N-288-1 .. N-1]

// calculate ACF coefficients for the sliding window

5: ACF_W288 ← forecast::Acf(W288, plot=FALSE)

// normalize the first 18 ACF coefficients (lags 1 to 18)

// for the range 1 to 2 to avoid negative or zero values

6: ACF_W288_norm ←

BBmisc::normalize(ACF_W288$acf[1:18],

method="range", range = c(1,2))

// select the last 18 sliding window data in reverse order

7: W288_18r ← reverse(tail(W288,18))

// multiplies normalized ACF by the last 18 values from

// the sliding window to compute the new 18 additional

// features based on ACF coefficients

8: ACF_Lag ← ACF_W288_norm * W288_18r

// create additional feature based on a linear regression

// one-step-ahead forecast considering trend and

// seasonality

9: fit ← forecast::tslm(W288 ~ trend + season)

10: fcTSLM_h1 ← forecast(fit, h=1)$mean

// new ACF_Lag1 to ACF_Lag18 and fcTSLM_h1

// features are ready to be aggregated to the original

// series data

11: S[N] ← bind(S[N], ACF_Lag1..ACF_Lag18,

fcTSLM_h1)

12: end for

// series S and its new features are stored in ARFF file

13: write series S to ARFF

14:end for

The feature engineering process creates ARFF

(Attribute-Relation File Format) files with the

following structure:

• Events (target, numeric): series observation

value.

• ACF_Lag1 to ACF_Lag18 (numeric):

features calculated based on ACF

coefficients for W288 window data,

normalized for 1 to 2 range, multiplied by

the last 18 values from the sliding window.

• fcTSLM_h1 (numeric): one-step-ahead

forecast calculated by a regression model for

W288 window (function forecast::tslm

(Hyndman et al., 2019) available for the R

language).

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

402

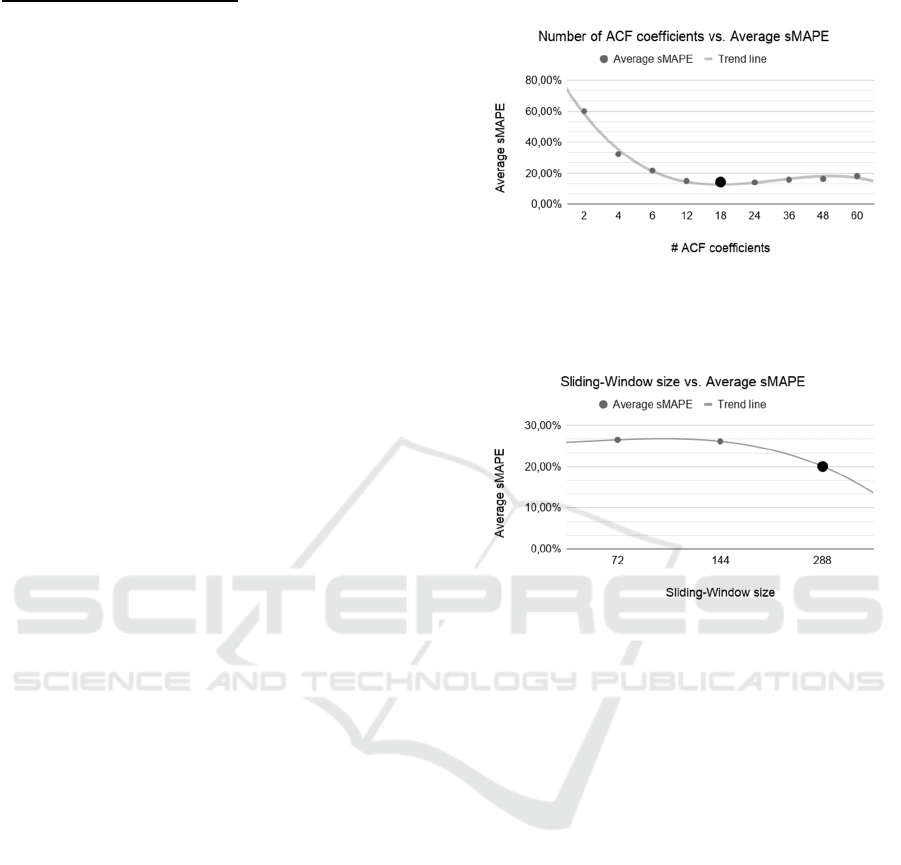
AA-ACF hyperparameters:

To establish the use of 18 lagged values and

coefficients as well as to define the size of the 288-

event sliding window, previous experiments were

done using windows from 72 to 288 events, and

selecting 2, 4, 6, 12, 18, 24, 36, 48 and 60 ACF

coefficients. The final values were selected based on

the combination that presented best results, i.e., lower

sMAPE (Armstrong, 1985) values in forecasting

tests. Experiments were done using time series from

M4 dataset, selecting up to 200 series from each

periodicity (daily, hourly, monthly, quarterly,

weekly, and yearly) of that dataset, evaluating the

parameters in up to 1200 distinct series. The trend line

presented in Figure 3 shows that as the number of

ACF coefficients increases, lower sMAPE values are

reached considering 18 coefficients.

In Figure 4 the trend line shows that lower

sMAPE values were reached using 288-observation

sliding windows.

Naturally, the hyperparameters were set

according to the results obtained from a sample of a

specific dataset, and thus, we further analyse the

impact of this choice in a larger testbed containing

more datasets in Section 5 Results.

3.2 Training

In this step, the Auto.Arima training is done using the

function forecast::auto.arima (Hyndman and

Khandakar, 2008; Hyndman et al., 2019). For model

fitting with Auto.Arima, no additional features are

required, since only the original time series are used.

Next, the training error is calculated according to

sMAPE, depicted in (2) (cf. Section 4.3 Evaluation

Protocol). AA-ACF calculates the fitting error based

on the last n series observations (or n records, NRecs)

as depicted in Figure 5. The parameter n coincides

with the prediction horizon (h) established for the

series, based on its periodicity.

For the experiments with AA-ACF the following

prediction horizons were established: daily series,

h=14; hourly series, h=48; monthly series, h=18;

quarterly series, h=8; weekly series, h=13; annual

series, h=6.

Next, ARFF files prepared with ACF features (see

Algorithm 1) are processed with AdaGrad using the

prequential mode in MOA, and the training error

(sMAPE) is calculated based on the last n records of

the series.

3.3 Algorithm Selection

Figure 3: Results of the experiments to select the number of

ACF coefficients for the AA-ACF method. Trend line

shows lower average sMAPE value for 18 ACF

coefficients.

Figure 4: Results of the experiments to select the size of the

sliding-window for the AA-ACF method. Trend line shows

lower average sMAPE value for a 288-observation sliding-

window.

Algorithm selection is performed based on the

training error (sMAPE) obtained for each algorithm

(Auto.Arima and AdaGrad) in the training phase. The

algorithm that presented the smallest error is selected

for each series forecasting.

3.4 Forecasting

AA-ACF implements three strategies to forecast a

series according to the option selected by the user.

The first strategy is called SelectionNRecs (or simply

NRecs) and consists of selecting the algorithm based

on the training error computed on the last n records of

the series and calculating the series forecasts using

the algorithm that presented smallest training error.

The second strategy (default) is called

SelectionAndFusion (or Fusion), which also consists

of selecting the algorithm given the error calculated

during the training phase. Next, if the algorithm

selected for the series is Auto.Arima, forecasting

values are calculated using this algorithm. Else, if the

Univariate Time Series Prediction using Data Stream Mining Algorithms and Temporal Dependence

403

selected algorithm is AdaGrad, the forecasts

calculated using AdaGrad will be combined with the

Figure 5: Original data from the N1738 time series (M3

dataset) and values obtained in the training and forecasting

by AdaGrad and Auto.Arima (h=forecasting horizon).

“40%” and “n” indicate portions considered in the fitting

error calculation.

Auto.Arima forecasts using a fusion process based on

the average of the forecasts of both methods.

The third strategy is called Selection40p (or 40p).

It is similar to the NRecs strategy, however, instead

of calculating the training error based on the last n

records of the series, the last 40% of the records are

considered.

For the Auto.Arima forecasting, the function

forecast::auto.arima is used to establish the fitting

model, and the function forecast::forecast to calculate

the h forecasts (h=prediction horizon) for the series

being analysed. For AdaGrad forecasting, ARFF files

prepared with ACF features (see Algorithm 1) are

used. A program in R is used to control the iterative

process of the execution of the streamer and get its

one-step-ahead forecasts. After obtaining the forecast

for one horizon, the ACF feature engineering process

is considered to prepare a file for the next prediction,

until the forecasting horizon (h) is reached. The

process is repeated from 6 to 48 times for each series

according to its periodicity.

4 EXPERIMENT

The experiment carried out in this study aimed at

validating the hypothesis that a DSM algorithm used

in combination with a statistical method presents

competitive results with those obtained by a classic

statistical method. Besides the combined use of

algorithms, the evaluated method proposes the use of

additional features that are able to represent temporal

dependency characteristics, capable of expressing or

translating the temporal profile of the series as input

to the learning process.

It is important to say that this study is part of an

extensive work that evaluated in previous phases the

use of different DSM algorithms available in MOA,

and selected AdaGrad based on its results. Regarding

statistical algorithms, ARIMA was chosen as a

classical method applicable to a wide range of series

prediction problems, and selected among other

statistical methods based on its results in earlier

studies for the feature engineering process that

evaluated its use and other statistical methods

available as functions of the forecast package

(Hyndman et al., 2019) available for R.

The forecast::auto.arima function was selected as

the statistical algorithm used in this study given its

ability to automatically select its parameters and

because of its use in metalearning methods like those

proposed in (Montero-Manso et al., 2018a; Montero-

Manso et al., 2018b), that use Auto.Arima combined

with a set of different algorithms.

This section is organized with the following

subsections: Algorithms and Tools, Datasets, and

Evaluation Protocol.

4.1 Algorithms and Tools

To perform the experiment, the following algorithms

and tools were mainly considered:

1) Statistical algorithm: forecast::auto.arima

(Hyndman and Khandakar, 2008).

2) Data stream mining algorithm: AdaGrad (Duchi

et al., 2011). Hyperparameters:

learningRate=0.01, epsilon=1e-8,

lambdaRegularization=0, lossFunction=HINGE.

3) Tools:

a) MOA (Massive Online Analysis): a

framework for data stream mining (Bifet et al.,

2010).

b) R language (R Core Team, 2018) and RStudio

(RStudio Team, 2020): programming

language R and IDE for R programming.

c) Main R packages: Metrics (Hamner and

Frasco, 2018), forecast (Hyndman and

Khandakar, 2008), and BBmisc (Bischl et al.,

2017).

4.2 Datasets

The experiments were performed using 141,558

univariate time series available in 5 different datasets

described as follows:

Dataset 1 (M3 competition, 3003 time series):

The M3 dataset is composed of 3003 time series from

the M3 competition (Makridakis and Hibon, 2000).

The dataset includes series with monthly, yearly,

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

404

quarterly, and other periodicities, with data extracted

from different domains, like Macroeconomics,

Microeconomics, Demographic data among others.

In this dataset the series are relatively short, with

lengths ranging from 14 to 126 events. Therefore, it

is a dataset that can help to evaluate the behaviour of

the AA-ACF method in short series.

Dataset 2 (M4 competition, 100,000 time

series): The M4 dataset has a set of 100,000

differently ranged time series (13 to 9,919

observations) used in the M4 competition

(Makridakis et al., 2018a). In the M4 dataset, the

series represent information from different domains

such as Microeconomic, Macroeconomic,

Demography data, among others, making it possible

to verify the applicability of the proposed method for

data of different domains, with different profiles,

some showing a higher level of data variation, while

others may have a linear trend, without major

variations in terms of seasonality and trend.

Dataset 3 (M5 competition, 30,490 time series):

The M5 dataset contains time series data from

product sales of a large supermarket chain

(Makridakis et al., 2020). In the M5 competition,

product sales data per store, in a total of 30,490 time

series, are consolidated hierarchically, grouping the

predictions by product, category, store, and state,

until completing the total of 42,840 series originally

established for the competition. Thus, for this study,

the 30,490 series that refer to the lowest level of the

hierarchy and that represent the total sales of a

product aggregated for a given store were considered.

Regarding the series, for each product/store up to

1941 observations regarding the registered sales were

available. For each series, the 14 final records were

reserved for testing, resulting in 1927 observations

for training. Although the original data includes

information about the stores, sales prices, promotions,

calendar and special dates, only basic information,

like date and observations of the series were

considered. The dataset includes daily series.

Additionally, intermittent data can be found in the

series due to absence of product sales in specific

dates.

Dataset 4 (COVID-19 data subset, 7,465 daily

univariate time series): The COVID-19 Data

Repository by the Center for Systems Science and

Engineering (CSSE) at Johns Hopkins University

(Dong et al., 2020) (available at

https://github.com/CSSEGISandData/COVID-19) is

an up-to-date information on the novel coronavirus

global spread. In the following experiments, the data

available regarding confirmed cases, deaths and

recovered cases in multiple cities around the globe

were considered. The files were retrieved on

September 16th, 2020, with daily accumulated data

for the period from January 22nd, 2020 to September

15th, 2020, with information regarding spanning 224

observations on 3,261 US and 266 non-US locations.

Dataset 5 (TSDL, Time Series Data Library,

subset with 600 time series): The TSDL dataset

(Hyndman and Yang, 2020) is composed by 648 time

series with different frequencies and information

collected from different domains like Agriculture,

Crime, Demography, Finance, Health, Industry,

Labor market, Macroeconomic, Meteorology,

Microeconomic, Production, Sales, Transport, among

other areas. For this experiment, univariate series

with the frequencies 1, 4 and 12 were selected,

considering only the 600 series with more than 20

observations.

4.3 Evaluation Protocol

sMAPE, the acronym for Symmetric Mean Average

Percentage Error, also known as symmetric MAPE, is

the primary metric used in this work and it was

earliest presented in (Armstrong, 1985). It was also

used by M4 and M3 competitions among other

metrics, so this influenced our choice for the use of it

in our experiments.

Equation (2) depicts the sMAPE computation

(Makridakis et al., 2018b), where k is the forecasting

horizon, Y

the actual values, and Ŷ

the forecasts for

a specific time t.

(2)

As baseline, the prediction error (sMAPE) values

calculated by Auto.Arima were used.

5 RESULTS

Table 1 presents the results obtained using the

proposed featuring engineering method and the

algorithms in the prediction of the series of each

dataset (1 to 5).

The gain ratio values, GR (%), presented in the

results are calculated as expressed in (3), where

sMAPE

DSM

is the forecast error calculated for the AA-

ACF strategy used, and sMAPE

auto.arima

means the

forecast error calculated for the baseline algorithm.

(3)

Univariate Time Series Prediction using Data Stream Mining Algorithms and Temporal Dependence

405

Table 1: Gain (%) obtained by AA-ACF strategies in

comparison to Auto.Arima (baseline).

Dataset h auto.arima

sMAPE

AdaGrad

Gain (%)

NRecs 40p Fusion

M3 Monthly 18 0.149 -4.476%

3.339% 3.397% 3.875%

M3 Yearly 6 0.171 -87.949% -0.991% -0.732% -0.309%

M3 Quarterly 8 0.100 -56.349% -0.437%

0.397% 0.380%

M3 Other 8 0.045 -20.850%

2.711%

-0.091%

2.078%

M4 Daily 14 0.032 -27.518% -0.449%

0.116% 1.288%

M4 Hourly 48 0.141 -93.932% -2.803% -0.931% -1.083%

M4 Monthly 18 0.135 -9.602% -0.438%

0.146% 0.499%

M4 Quarterly 8 0.104 -18.872% -1.179% -0.151%

0.384%

M4 Weekly 13 0.086 -33.158% -10.734% -0.357% -3.462%

M4 Yearly 6 0.152 -41.241% -0.730% -0.101%

0.449%

M5 Daily 14 1.369 10.164%

11.874% 11.212%

-0.461%

COVID-19

Confirmed

14 0.059 -36.991%

5.206% 4.959%

-0.088%

COVID-19

Deaths US

14 0.112

-13.173%

6.419% 5.780% 0.079%

COVID-19

Confirmed

Global

14 0.028

-142.914%

0.107%

-1.908%

0.147%

COVID-19

Deaths

Global

14 0.037 -78.619% -0.900%

0.425%

-0.101%

COVID-19

Recovered

Global

14 0.046 -80.198%

2.479% 7.736% 1.363%

TSDL Freq 1 6 0.341 -7.706%

1.077% 2.313% 5.528%

TSDL Freq 4 8 0.220 -26.330% -3.892% -3.268%

12.429%

TSDL Freq

18 0.440 -3.195%

5.823% 6.095% 8.307%

Average Gain: -40.68%

0.87% 1.84% 1.65%

Positive gain ratio values (%) highlighted in Table

1 indicate that the method reached a better prediction

than the baseline algorithm (Auto.Arima)

individually. It is possible to notice that the

combination of Auto.Arima and AdaGrad improves

the individual results of Auto.Arima in different

scenarios suggesting the importance of future studies

to improve the combined technique. For the three of

AA-ACF strategies presented in Table 1, Fusion was

capable of presenting positive gain in most of the

subsets analysed.

In additional analyses, considering the Fusion

strategy, calculating the gain values for prediction

horizons equal 1 and 6 forecasts (h=1 and h=6) for

each series in the datasets, the method AA-ACF also

presented positive gains (Table 2).

6 DISCUSSION

Considering the gain values obtained by AA-ACF

method (Table 1), it is possible to note that the

combined use of AdaGrad and Auto.Arima

algorithms can reach positive gain compared to the

baseline (Auto.Arima) in most of the datasets/subsets

Table 2: Positive Gain (%) values obtained obtained by the

AA-ACF Method (using the Fusion strategy).

h (prediction horizon) #Subsets with

positive gain

Min. Max. Average

h=Original (6 to 48) 13 0.079% 12.429% 1.650%

h=6 13 0.120% 15.110% 1.880%

h=1 13 0.214% 32.726% 2.081%

used in the experiment. The Fusion strategy could

reach positive gains in 13 of the 19 subsets evaluated.

AdaGrad used individually only presented

positive gains in one dataset (M5 daily) suggesting

that, in this case, it was possible to reach better

forecasting results than the ones calculated by

Auto.Arima. Despite the individual AdaGrad results,

we must highlight that this DSM algorithm when

combined with Auto.Arima improved the results and

helped to reach positive gains for all the 3 evaluated

AA-ACF strategies. This can be explained by the fact

that the Selection process was capable of

recommending the best algorithm to each series in

quantity enough to get positive gains that surpassed

the results presented by Auto.Arima. And this could

only be achieved because AdaGrad used individually

was also capable of getting better forecast results than

Auto.Arima in an expressive amount of series. This

suggests that the adaptive behavior of the gradient-

descent-based algorithm AdaGrad benefits from the

features created based on time series’ dependencies.

Comparing the results from the AA-ACF fusion

strategy (Table 2), it is possible to note that the

average gain is positive for all the evaluated horizons.

The original predictions were calculated for the

horizons from 6 to 48 forecasts, according to the

periodicity of each dataset/subset. Moreover, positive

results are observed even for short-term forecasts

(h=6 and h=1). Considering the original horizon

forecasts, despite the existence of negative gains in

some subsets, the positive gain equals 12.429% for

the TSDL Frequency 4 subset deserves to be

highlighted.

The results suggest that there is a potential to be

explored in the feature engineering process based on

ACF coefficients as it denotes a capability of

translating temporal dependency information to the

DSM algorithm used in the experiment.

7 CONCLUSION

In this paper, we demonstrated that the use of adjusted

autocorrelation (ACF) values helps DSM learners in

the prediction process. Most of the works based on

ACF coefficients use these values as the basis to

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

406

select lagged values that are most correlated to recent

events in a time series. In this study, however, ACF

coefficients were used to introduce time dependency

characteristics as input vectors of AdaGrad in our

method AA-ACF that combines Auto.Arima and

AdaGrad in the time series forecasting.

The results obtained using the method suggest that

positive gains can be observed in different datasets,

and for different forecasting horizons. For the 19

subsets evaluated, the average gain varied from

1.65% (for 6 to 48 forecasts) to 2.081% (when

considered forecasting horizon equals 1). The gain

values calculated for TSDL datasets (5.528% for

frequency 1 series, 12.429% for frequency 4 series,

and 8.307% for frequency 12 series) were expressive.

Besides that, the results obtained by the processing of

the 1428 series of M3 monthly dataset (3.875%) also

can be noted.

The combined use of different methods is not a

novelty. However, a combination of a statistical

algorithm and DSM methods is not evident in the

literature, especially for the prediction of series

relatively short in length.

Finally, we highlight that the experiments were

performed using time series with fixed length and

using a batch mode processing. Therefore, the support

to data streams is envisioned in future versions, as

well as tests with intermittent time series data, helping

to assess the method's applicability in other scenarios.

Additional studies regarding the algorithm selection

strategy shall be evaluated, as the analysis of the

oracle established that the best overall forecast results

can be obtained designating AdaGrad for 55,912

(39.5%) from the 141,558 analysed series. Thus,

improvements in the selection criteria having the

oracle as a goal may lead to better overall results.

ACKNOWLEDGEMENTS

This study was financed in part by the Coordenação

de Aperfeiçoamento de Pessoal de Nível Superior -

Brasil (CAPES) - Finance Code 001.

REFERENCES

Armstrong, J. (1985). Long-range forecasting: from crystal

ball to computer. Wiley, 2nd edition edition.

Bifet, A., Gavalda, R., Holmes, G., and Pfahringer, B.

(2018). Machine Learning for Data Streams with

Practical Examples in MOA. MIT Press.

Bifet, A., Holmes, G., Kirkby, R., and Pfahringer, B. (2010).

MOA: Massive Online Analysis. Technical report.

Bischl, B., Lang, M., Bossek, J., Horn, D., Richter, J., and

Surmann, D. (2017). BBmisc: Miscellaneous Helper

Functions for B. Bischl. R package version 1.11.

Bontempi, G., Ben Taieb, S., and Le Borgne, Y.-A. (2013).

Machine Learning Strategies for Time Series

Forecasting, volume 138.

Box, G. and Jenkins, G. (1976). Time series analysis:

forecasting and control. Holden-Day series in time

series analysis and digital processing. Holden-Day.

Dong, E., Du, H., and Gardner, L. (2020). An interactive

web-based dashboard to track covid-19 in real time. The

Lancet Infectious Diseases, 20(5):533–534.

Duchi, J., Hazan, E., and Singer, Y. (2011). Adaptive

subgradient methods for online learning and stochastic

optimization. J. Mach. Learn. Res., 12(null):2121–

2159.

Duong, Q.-H., Ramampiaro, H., and Nørvåg, K. (2018).

Applying temporal dependence to detect changes in

streaming data. Applied Intelligence, 48(12):4805–

4823.

Esling, P. and Agon, C. (2012). Time-series data mining.

ACM Comput. Surv., 45(1).

Gama, J., Žliobaitė, I., Bifet, A., Pechenizkiy, M., and

Bouchachia, A. (2014). A survey on concept drift

adaptation. ACM Computing Surveys, 46(4):1–37.

Hamner, B. and Frasco, M. (2018). Metrics: Evaluation

Metrics for Machine Learning. R package version

0.1.4.

Hyndman, R., Athanasopoulos, G., Bergmeir, C., Caceres,

G., Chhay, L., O’Hara-Wild, M., Petropoulos, F.,

Razbash, S., Wang, E., and Yasmeen, F. (2019).

forecast: Forecasting functions for time series and

linear models. R package version 8.9.0.9000.

Hyndman, R. and Yang, Y. (2020). tsdl: Time Series Data

Library. https://finyang.github.io/tsdl/,

https://github.com/FinYang/tsdl.

Hyndman, R. J. (2014). Forecasting: Principles and

Practice.

Hyndman, R. J. and Khandakar, Y. (2008). Automatic time

series forecasting: the forecast package for R. Journal

of Statistical Software, 26(3):1–22.

Makridakis, S. (1976). A Survey of Time Series. Technical

Report 1.

Makridakis, S. and Hibon, M. (2000). The M3-competition:

Results, conclusions and implications. International

Journal of Forecasting, 16:451–476.

Makridakis, S., Spiliotis, E., and Assimakopoulos, V.

(2018a). The M4 competition: Results, findings,

conclusion and way forward. International Journal of

Forecasting, 34(4):802 – 808.

Makridakis, S., Spiliotis, E., and Assimakopoulos, V.

(2018b). Statistical and machine learning forecasting

methods: Concerns and ways forward. PLOS ONE,

13(3):1–26.

Makridakis, S., Spiliotis, E., and Assimakopoulos, V.

(2020). The M5 accuracy competition: Results,

findings and conclusions.

Mochinski, M. A., Paul Barddal, J., and Enembreck, F.

(2020). Improving multiple time series forecasting with

data stream mining algorithms. In 2020 IEEE

Univariate Time Series Prediction using Data Stream Mining Algorithms and Temporal Dependence

407

International Conference on Systems, Man, and

Cybernetics (SMC), pages 1060–1067.

Montero-Manso, P., Athanasopoulos, G., Hyndman, R. J.,

and Talagala, T. S. (2018a). FFORMA: Feature-based

forecast model averaging. Monash Econometrics and

Business Statistics Working Papers 19/18, Monash

University, Department of Econometrics and Business

Statistics.

Montero-Manso, P., Athanasopoulos, G., Hyndman, R. J.,

and Talagala, T. S. (2018b). M4metalearning.

Nielsen, U. D., Brodtkorb, A. H., and Jensen, J. J. (2018).

Response predictions using the observed

autocorrelation function. Marine Structures, 58:31 –

52.

R Core Team (2018). R: A Language and Environment for

Statistical Computing. R Foundation for Statistical

Computing, Vienna, Austria.

Rodrigues, P. and Gama, J. (2009). A system for analysis

and prediction of electricity-load streams. Intell. Data

Anal., 13:477–496.

RStudio Team (2020). RStudio: Integrated Development

Environment for R. RStudio, PBC., Boston, MA.

Stojanova, D. (2012). Considering Autocorrelation in

Predictive Models. PhD thesis, Jozef Stefan

International Postgraduate School, Ljubljana, Slovenia.

Doctoral Dissertation.

Werner, L. and Ribeiro, J. L. (2003). Previsão de Demanda:

uma Aplicação dos Modelos Box-Jenkins na Área de

Assistência Técnica de Computadores Pessoais. Gestão

& Produção, 10.

Žliobaitė, I., Bifet, A., Read, J., Pfahringer, B., and Holmes,

G. (2015). Evaluation methods and decision theory for

classification of streaming data with temporal

dependence. Machine Learning, 98(3):455–482.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

408