Optimizing Heterogeneous Maritime Search Teams using an

Agent-based Model and Nonlinear Optimization Methods

Jarrod Grewe

and Igor Griva

Department of Computational and Data Sciences, George Mason University,

4400 University Dr Fairfax VA, U.S.A.

Department of Mathematical Sciences, George Mason University, 4400 University Dr Fairfax VA, U.S.A.

Keywords: Search Theory, Optimization, Search and Rescue, Agent-based Modeling, Search Planning.

Abstract: This paper introduces a new search planning methodology, nicknamed Pathfinder, that can optimize

heterogeneous teams of mobile and stationary searchers. Unlike previously developed search methods, the

new methodology applies an Agent-Based Model (ABM) to simulate target movement and behavior then uses

nonlinear optimization methods to find optimal search plans for complex teams of searchers. We describe

initial target location with a probability distribution influenced by evidence and environmental data. The ABM

models target movement based on environmental and behavioral factors. Then, Pathfinder suggests a search

plan that maximizes the probability of target detection and satisfies searcher requirements.

1 INTRODUCTION

Search Theory was initially developed during World

War 2 by B.O. Koopman to assist with creating

optimal search strategies to find German U-boats

(Koopman, 1946 (declassified in 1958)) Search

Theory has advanced significantly in the past 75 years

to include most elementary searcher types and target

types (see, (Stone, Royset, & Washburn, Optimal

Search for Moving Targets, 2016)) for a

comprehensive review. Historically, the Office of

Naval Research (ONR) has been a driving force in

Search Theory research in the United States. The

USCG was one of the first organizations to deploy a

computerized methodology for search and rescue

(SAR) operations called Computer-Assisted Search

Planning System (CASP) (Richardson & Discenza,

1980). This used a Monte Carlo particle method to

model targets. In 2003 the USCG started

development of the Search and Rescue Optimal

Planning System (SAROPS) (Kratzke, Stone, &

Frost, 2010) to replace CASP. SAROPS was a

significant improvement over the USCG’s CASP

system by incorporating a custom numerical search

technique to find search plans and improving the

https://orcid.org/0000-0002-9807-2410

https://orcid.org/0000-0002-2291-233X

Monte Carlo particle method used to model targets.

This methodology has been operational since January

2007.

In more recent times, more methodologies in

Search Theory were developed that accommodate

more search scenarios. One of them is the genetic

simulated annealing algorithm (GSAA). (Ai, Li, Gao,

Xu, & Shang, 2019) Another one is based on branch-

and-bound algorithms. (Sato & Royset, 2010) There

is also a new interactive heuristic-based optimization

model (Abi-Seid, Morin, & Nilo, 2019) created to

assist SAR operations in Canada. Nonlinear

optimization has been applied to search theory

research, in particular, finding hidden objects (El-

Hadidy & Alfreedi, 2020). At the same time nonlinear

optimization techniques have not yet been fully

utilized to optimize heterogeneous teams of mobile

and stationary searchers.

An important component in any search theory

methodology, that optimizes search plans to find a

mobile target, is how it models target movement.

Traditionally diffusion processes have been popular

see (Lin & Goodrich, 2010) and (Eagle, 1984).

Currently a particle method is used by SAROPS.

(Kratzke, Stone, & Frost, 2010). Some research has

been done to apply an Agent-Based Model (ABM) to

200

Grewe, J. and Griva, I.

Optimizing Heterogeneous Maritime Search Teams using an Agent-based Model and Nonlinear Optimization Methods.

DOI: 10.5220/0010869100003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 200-207

ISBN: 978-989-758-548-7; ISSN: 2184-4372

model wilderness searches (Mohibullah & Julie,

2013). In addition, some case studies have been done

to apply agent-based simulations to maritime search

operations as a way to improve verification and

validation methods. (Onggo & Karatas, 2016)

Most relevant research in adopting ABM in

maritime environments is focused on military and

security applications. This includes port security

(Harris, Dixon, Dunn D.L., & Romich, 2013) and

using UAVs for surface surveillance (Steele, 2004).

In addition, several papers have been published in

regards to force protection simulations including

(Walton, Paulo, McCarthy, & Vaidyanathn, 2005)

and (Sullivan, 2016). Finally, there has been several

papers published on the use of ABM and counter-

piracy operations (Dabrowski & Villiers, 2015) and

(Marchione, Johnson, & Wilson, 2014). A common

issue encountered by this line of research is in

verification and validation of these models. For

example, in analysing strategies to protect merchant

ships from pirate attack (Deraeve, Anderson, & Low,

2010).

In the past 20 years, Search Theory has been used

multiple times to find missing aircraft. The search for

Air France, which was lost in June 2009, was found

using Search Theory. (Stone, In Search of Air France

Flight 447, 2011) The flight recorders were recovered

in May 2011. Currently Search Theory is used every

day by the USCG to find missing persons along the

US coastlines using SAROPS.

We propose a new search planning methodology

based on an Agent-Based Model (ABM) and

nonlinear optimization techniques. Pathfinder

introduced in this paper strives to advance search

planning by focusing on 4 core areas:

1. optimizing heterogeneous teams of mobile and

stationary searchers

2. modeling target behavior

3. inherent searcher safety

4. enhance future research, training, and

appropriations

Pathfinder incorporates an ABM that can model

target movement based on behavioral factors, besides

environmental factors. This is important because the

behavior of missing targets could fall into different

scenarios such as, for example dropping an anchor or

clinging onto a buoy (Adlerstein, 2019). Therefore,

by incorporating various scenarios in the ABM,

Pathfinder can model a more realistic target

movement. The second important feature of

Pathfinder is that it employs nonlinear optimization

methods to find optimal search plans based on

modeled target movement. Furthermore, employment

of nonlinear optimization methods allows us to

optimize teams of heterogeneous searchers, including

stationary and mobile searchers together, among

other benefits, including not constraining Pathfinder

to using ladder pattern search plans and rectangular

search areas. The ladder pattern searches may include

regions of least concern (Kratzke, Stone, & Frost,

2010) and thus can be less efficient. Pathfinder finds

search paths that maximize the probability of

detection (POD) with the flexibility of adding

constraints and penalties, that help find search paths

that are realistic and easy to implement. This

flexibility of the methodology allows searchers to

focus on regions of high POD. In addition, Pathfinder

can strengthen the optimization model to address

concerns and demands of naval pilots and SAR

personnel. Another important feature of Pathfinder is

that it can accommodate searcher safety. For

example, additional modifications can guarantee that

searchers do not come within a dangerous distance

from each other. Finally, since Pathfinder can

efficiently simulate thousands of different scenarios,

it can be used for SAR research, training,

appropriations, and evaluation of new equipment and

techniques.

We organized the paper as follows. The next

section reviews a search scenario that will help

explain Pathfinder, Section 3 reviews Pathfinder,

Section 4 discusses results, Section 5 provides

concluding remarks, and Section 6 discusses how

Pathfinder could be further improved and

transformed into a new life saving application.

2 SEARCH SCENARIO

Imagine being a search manager that creates,

implements, and manages SAR operations. It is a

normal summer day at a popular beach location,

warm with clear skies. There is a strong wind due

north at 10knots. This day the currents are strong,

with a west to east flow. Then a distress signal was

received and a search operation needs to be launched.

The call is from a recreational boat with people on

board that have possibly experienced a health issue.

This boat is not far from the coastline and the caller

indicates they are heading to a pier along the

coastline. The call was interrupted and further

communication attempts were unsuccessful. We

estimate the boat is no longer being actively sailed

and may have lost power. The last known location

was estimated by triangulating the emergency radio

call. Suppose the search assets available, and modeled

Optimizing Heterogeneous Maritime Search Teams using an Agent-based Model and Nonlinear Optimization Methods

201

in Pathfinder, are short range assets like the MH-60

“Jayhawk” (Pike, n.d.) and search boats like the 47-

foot Motor Lifeboat. (MLB). (Motor Lifeboat (MLB),

n.d.). We also include a theoretical “smart buoy”

which represents a stationary searcher. We will

demonstrate the feasibility and benefits of this new

methodology by finding optimal search plans for this

search scenario.

3 DETAILED DESCRIPTION OF

PATHFINDER AND ITS

COMPONENTS

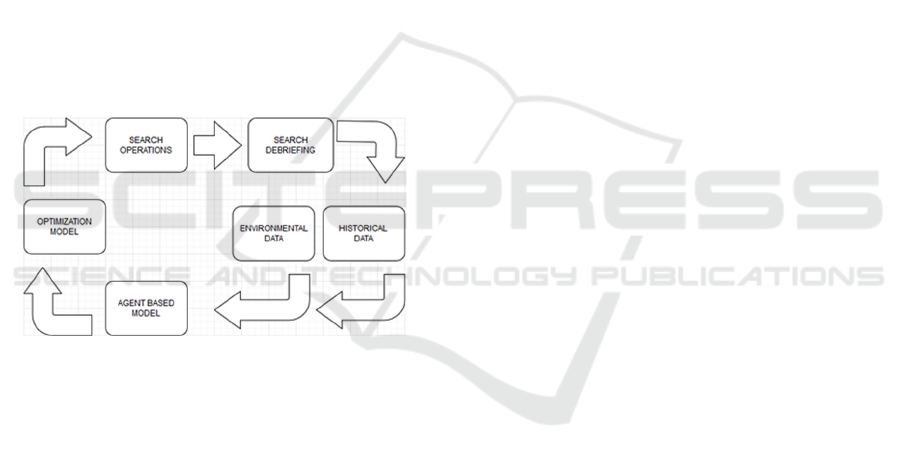
There are two principal components of Pathfinder.

The optimization model and the ABM. The ABM

simulates a large number of possible scenarios of a

target trajectory, and then sends the information to the

optimization model, which then creates optimal

search plans for the search operation. Figure 1 shows

the relationship of these components to search

operations and data.

Figure 1: The two principal components of Pathfinder,

ABM and optimization model, and their relationship with

available data and search operations.

3.1 Domain

We need to discuss a few fundamental definitions.

Pathfinder uses a two-dimensional domain to model

the search area.

𝛺∈𝑅



Searchable subdomains are constructed to limit

searchers from areas they are not allowed, such as

foreign or restricted territories. We define this area,

𝛺

𝑠

, such that

𝛺

𝑠

⊆𝛺.

In our case the searchable sub domain is the same

as the domain. In addition, the domain is a coastline

that is mostly maritime environment that is 1,000

𝑘𝑚

We define our searcher paths 𝑧

𝑡

𝑘

,𝑡1,..,𝑇 for

searcher 𝑘1,…,𝐾 and target paths 𝑢

𝑡

𝑔

,𝑡

1,…,𝑇 for target g of G targets to satisfy the

following.

𝑢

𝑔

∈𝛺

𝑧

𝑘

∈𝛺

𝑠

3.2 Prior Distribution

To describe the position of the target before the search

starts we use a initial probability distribution 𝜃𝑥,

which could be based, in particular, on a targets last

known location. To add more accuracy and

flexibility, we use regions defined as 𝑅

𝑖

⊆𝛺 with

probabilities 𝑎

𝑖

. This is useful when there are several

sources of information, evidence, and the chance of

error. These regions satisfy the probability that the

target is in the domain 𝑀.

𝑎









𝜃𝑥𝑑𝑥





𝑀𝑎𝑛𝑑 𝑎







1

(1)

For example, in our scenario, we have two

circular regions representing the last known location

at the center of the domain. A large 40% region with

a radius of 4.15 km, where there is a 40% chance the

target was in that region at 𝑡0. Then a smaller 50%

region within it with a radius of 1.65 km where there’s

is a 50% chance the target was there at 𝑡0. The rest

of the domain falls within a 10% region where there

is a 10% chance that a target is there. The 40% and

50% regions will reside in the center of the search

domain.

3.3 Agent-based Model

This prior distribution is used in an ABM to model

target movement. This model uses numerous

independent agents that are affected by

environmental factors, behavioral factors, and

hazards.

First, environmental factors are wind and currents

that are in our search area. The wind the currents in

our example will push these agents north then east.

The ABM uses equations from the USCG (USCG,

2013) to calculate leeway speed and can incorporate

the Rayleigh Method (Kratzke, Stone, & Frost, 2010)

in the future. The ABM also incorporates hazards

such as rocks and etc. that agents must navigate

around. In our example, there are no hazards to

navigate around.

There are also behavioral factors. These

behavioral factors depend on survival modes to model

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

202

target movement. When most people are lost they rely

on a survival strategy to survive or find their way

home. These include overdue, travel aid, route

finding, wandering, and staying put. In our example,

overdue, travel aide, wandering, and stay put are seen.

When a target is overdue, it is not lost at all and are

simply late getting home or their next waypoint. The

travel aide mode is when a target has some travel aids

and has the ability to eventually self-rescue. This

mode relies on the theory of “bounded rationality”

(Simon, 1982) According to this theory, rationality is

bounded due to data and mental capabilities. Thus, a

missing person’s idea of a path home is more accurate

as they approach future waypoints. Wandering is

when a target does not have travel aids and wonders

the domain. Finally, the stay put mode is when a

target decides to stay where they are. In the case of a

boat this could be implemented by using an anchor or

beaching the boat. The ABM provides us with our

estimate target paths 𝑢





𝑡1,…,𝑇 that will be used

to optimize search plans.

This is unlike current methodologies that

implement particle methods. Particle methods use

particles that move based on environmental factors

and hazards. Therefore, particle methods cannot

model intelligent agents that can make decisions.

With an ABM, the agents are intelligent and can think

and make decisions. Thus, we can model behavioral

factors. The ABM can also model targets that decide

to change survival modes and target type changes.

Therefore, an ABM can model far more target types

accurately than a particle method.

In our example the ABM is using 501 agents to

model target movement. Such a number provides

sufficient map coverage and also shows a variety of

target behaviors while being within the technical

capability of the test system.

3.4 Detection Function

Next, we model the probability that a searcher at 𝑧





will detect a target at 𝑢





at time 𝑡 . This is

implemented using a detection function, which

depends on several factors including time, distance,

visibility, and properties of the target. Some previous

methodologies use the idea of sweep widths, lateral

ranges, etc. See (Frost & Stone, 2001). In Pathfinder,

we use a modification of the inverse Nth power law

(Iida, 1993) below, because it gives us a lot of

flexibility.

𝛤𝑢





,𝑧





,∆𝑡1exp



∆𝑡











,











,





,





























,











,





,





(2)

𝑛



∗



0,𝛼



∗



0,∆𝑡0,𝑧





∈𝛺



,𝑢





∈𝛺

This function depends on time step ∆𝑡, target type

𝑢





, searcher type 𝑧





, visibility 𝑣, terrain type 𝜏𝑧





,

and the parameters 𝛼



∗



and 𝑛



∗



. For notational

simplicity we also define the probability of not

detecting a target as below:

𝛤



𝑢





,𝑧





,∆𝑡1 𝛤𝑢





,𝑧





,∆𝑡 (3)

Since our example is a marine search operation,

we used data for a missing boat (N. C. Edwards,

1981) and found some of these values.

For example, for a USCG Point Class cutter

searching for a 16-foot boat or orange life raft in a

maritime terrain, n and 𝛼 were found as 𝛼0.413

and 𝑛5.955 . Likewise, for a USCG HH-52

helicopter searching for a 16-foot boat or orange life

raft in a maritime terrain, n and 𝛼 were found as 𝛼

0.471 and 𝑛3.656.

Both of these search assets are retired by the

USCG so future data collection and analysis is

needed.

3.5 Optimization Model

The objective of the Pathfinder methodology is to

find optimal searcher paths, 𝑧

𝑡

𝑘

,𝑡1,…,𝑇, that

maximize the POD. These paths depend on target

paths from the ABM, 𝑢

𝑡

𝑔

,𝑡1,…,𝑇, and the

detection function. We call a collection of searcher

paths a search plan. This POD function is as follows:

𝐹



𝑧







1/|𝐺|𝛤𝑢





,𝑧





,∆𝑡





𝜞



𝑢





,𝑧





,∆𝑡











∆



(4)

This objective function is a modification of the

objective function found in (Ding & Castanon, 2018)

and follows the theory in (Przemieniecki, 2000) page

277.

To make the objective function produce realistic

search trajectories, we incorporate three penalty terms

for fuel, momentum, and center-of-mass. The fuel

penalty below is used to make more cost-effective

search trajectories and cut down on suboptimal

waypoints.

𝑃





𝑧







𝑃





‖𝑧





𝑧





‖













(5)

𝑤ℎ𝑒𝑟𝑒 𝑃





0 𝑓𝑜𝑟 𝑠𝑒𝑎𝑟𝑐ℎ𝑒𝑟 𝑘

Optimizing Heterogeneous Maritime Search Teams using an Agent-based Model and Nonlinear Optimization Methods

203

The following is the momentum penalty. This

penalty reduces zig-zagging and generally smooths

paths and make them easier to follow.

𝑃



𝑧







𝑀



𝑃





𝑧





2𝑧





𝑧









𝛥𝑡











(6)

𝑤ℎ𝑒𝑟𝑒 𝑀



0 𝑓𝑜𝑟 𝑠𝑒𝑎𝑟𝑐ℎ𝑒𝑟 𝑘

𝑎𝑛𝑑 𝑃





0 𝑓𝑜𝑟 𝑠𝑒𝑎𝑟𝑐ℎ𝑒𝑟 𝑘

Finally, the center-of-mass penalty eliminates

erratic search trajectory and helps the nonlinear

optimization model converge to a solution.

𝑃

𝐶𝑀

𝑧

𝑡

𝑘

 𝑃

𝑘

𝐶𝑀

‖𝑧

𝑡

𝑘

𝑎𝑣𝑔𝑢

𝑡

𝑔

‖

𝑇/𝛥𝑡

𝑡1

|𝐾|

𝑘1

(7)

𝑤ℎ𝑒𝑟𝑒 𝑃





0 𝑓𝑜𝑟 𝑠𝑒𝑎𝑟𝑐ℎ𝑒𝑟 𝑘

𝑤ℎ𝑒𝑟𝑒 𝑎𝑣𝑔𝑢





𝐺

 𝑢









With these 3 penalty terms we have the following

Pathfinder’s optimization model with the positive

weights 𝑤

𝐹

, 𝑤

𝑀

, and 𝑤

𝐶𝑀

Maximize:

𝐹



𝑧







𝑤



𝑃





𝑧







𝑤



𝑃





𝑧







𝑤



𝑃





𝑧







(8)

Subject to:

 Movement constraints on the searchers

with 𝜀



𝑠



,𝜏



𝑧









0 implying a

stationary searcher

‖

𝑧

𝑡

𝑘

𝑧

𝑡1

𝑘

‖

 𝜀



𝑠

𝑘

,𝜏



𝑧

𝑡1

𝑘





 0, 𝑓𝑜𝑟 𝑘 𝑠𝑒𝑎𝑟𝑐ℎ𝑒𝑟

 Initial locations constraints on the searchers

𝑧

𝑘

𝑍

𝑘

𝑓𝑜𝑟 𝑠𝑒𝑎𝑟𝑐ℎ𝑒𝑟 𝑘

 Final locations constraints on the searchers

𝑧

𝑇

𝑘

𝑍

𝑇

𝑘

𝑓𝑜𝑟 𝑠𝑒𝑎𝑟𝑐ℎ𝑒𝑟 𝑘

4 DISCUSSION OF RESULTS

To examine search trajectories calculated by

Pathfinder, we built a prototype to run experiments,

described in figure 1. We used NetLogo (Wilensky,

1999) for the ABM module and a nonlinear solver

MINOS (Murtagh & Saunders, 1978) and AMPL

(AMPL Optimization inc, 2021) for the Optimization

module. The computer being used is a Dell Alienware

M17 with 8GB of ram and an Intel i7-9750H

processor. We experiment with several search teams

to find optimal solutions to the search scenario

described in this paper. We were able to find optimal

solutions for several scenarios. Here we demonstrate

one of them.

The ABM performed as expected. The

environmental factors move agents that have lost

power and have not deployed an anchor, some agents

are moving to their destination when they have

power, and some of them employ an anchor if they

are in shallow water. Of the two target types in this

scenario, boat with power and a boat without power,

the model shows 3 distinct behaviors a missing boat

could employ. We can see these behaviors below.

Figure 2: visualization of target behavior including A)

agents being swept away by the current and wind B) Agents

heading to their final destination under their own power C)

agents that decided to deploy an anchor and stay put. D)

agents being blown away primarily by the wind. E) the

center-of-mass of target agents with direction.

Figure 2 also shows another important advantage

of using an ABM to model target behavior. When

searching for a missing boat, that boat may or may not

have power, it may have deployed its anchor, it may

have capsized, it may have sunk, there could be life

rafts in the water, or the passengers may be in the

water. Therefore, there are multiple target types that

the SAR operations could be looking for, with several

distinct behaviors each target could inhibit. Using the

ABM is beneficial to search operations because it can

model simultaneously all potential target types, target

behaviors, and the transition of one target type to

another. This ABM has the potential to be tuned and

optimized by employing historical data.

Using nonlinear optimization techniques,

Pathfinder can optimize a search operation with

searchers with radically different capabilities. Figure

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

204

3 is a search operation optimized with Pathfinder and

has 3 assets: a helicopter, a boat, and a “smart” buoy

that can detect targets. Also note that there is an

operations outpost from which the helicopter is

operating from. This is also an asset that can detect a

target while stationary, thus not optimized by

pathfinder but its detection abilities considered in the

model. This search plan's POD is 8.08% and shows

that this new methodology can optimize teams of

mobile and stationary searchers.

Figure 3: A helicopter (orange), boat (yellow), operations

outpost (blue), and one buoy (green) searching the domain.

Note the difference in travel distance in each searcher type.

Pathfinder utilized each searcher's performance to find an

optimal search plan. Also note how the search plans were

affected by the target center-of-mass moving to the

Northeast.

Figure 3 also demonstrates how the target

movement affects the search plans. The target center-

of-mass is moving to the Northeast and as agents

encounter the currents in the North of the map, they

immediately move East. Thus, the search plan skews

North East.

One of the important features of Pathfinder is

attaining searchers’ safety since the optimization

model can separate searchers by imposing constraints

on the search trajectories. For example, the search

plan visualized in figure 4, we use two helicopters

based near each other for a search. Pathfinder found

an optimal search plan below for which the

helicopters never crossed paths.

Figure 4: Two helicopters (yellow/orange) searching the

domain. Note that the helicopters never crossed paths.

Another benefit of employing a computational

methodology is that it can perform simulations on

new SAR assets and methods. For example,

Pathfinder can determine what would be better: a

helicopter that is 10% faster or a helicopter that has

10% better sensors? We ran a few experiments with

the prototype using the same initial search plans as

figure 3 without the boat and buoy. Pathfinder could

show, for example, that a 10% increase in speed gives

us a search plan with a POD of 5.6% and a helicopter

that is 10% better at detecting targets gives us a search

plan with a POD of 6.2%. Thus, in this search

scenario, a helicopter with 10% better sensors is more

beneficial than those that are 10% faster. Thus,

Pathfinder can find what assets are the most effective

and consider the costs of using them. These are

important questions to address (Biesecker, 2021) This

methodology could eliminate a lot of the guesswork

from appropriations and training.

5 CONCLUDING REMARKS

The obtained results have demonstrated that a

methodology based on an ABM and optimization

model is promising. This methodology can optimize

teams of mobile and stationary searchers. The natural

application of Pathfinder would be in assisting

maritime searches. Pathfinder has the potential to

improve the capabilities and functionality of current

methodologies and could also be used for land

searches. Using Pathfinder could advance both SAR

and Anti-Submarine Warfare (ASW) operations.

Even though the described results are related to the

maritime SAR operations, we believe only a few

Optimizing Heterogeneous Maritime Search Teams using an Agent-based Model and Nonlinear Optimization Methods

205

modifications are sufficient for Pathfinder to be

applied to ASW operations and land SAR operations.

For ASW planning, it may be necessary to add

constraints so that the searcher could approach targets

only from a certain direction, for example, from a

blind spot behind submarines where their propellers

are. Such constraints could be implemented.

Combining an ABM and optimization model to

find optimal search plans in a maritime domain has

achieved several goals. The ABM can model target

behavior and its effects on target movement. This is

an improvement over current methods that only

model target movement based on environmental

factors. Then heterogeneous teams of searchers can

be seamlessly optimized. The optimization model

also gives us the flexibility to change penalties and

searcher constraints based on naval aviator and SAR

personal input. Finally, using the proposed

methodology allows us to consider past search plans

(successful and failed) and compare them to optimal

search plans to refine Pathfinder’s models. Thus, we

believe Pathfinder has potential to enhance current

search methodologies.

6 FUTURE RESEARCH

There are several research directions that can refine

and improve the Pathfinder methodology.

To create quality search plans Pathfinder relies on

accurate estimation of the parameters

𝛼𝑠



,𝜏𝑧





,𝑠



,𝑣 and 𝑛𝑠



,𝜏𝑧





,𝑠



,𝑣

since they can influence accuracy of the search.

Currently, there is not enough published data to

derive these values for all target types, searcher types,

terrain types, and visual ranges. In the future, we

would like to gather these data points and then derive

the values of 𝛼 and 𝑛. One way of making the data

collection less expensive is to use Virtual Reality

(VR) to gather the data points. The cost of using VR

to simulate a helicopter searching for a boat is

significantly cheaper than renting a helicopter and

boat to do experiments.

Likewise, more research is needed to collect data

and perform analysis for the ABM. In the current

state, the ABM needed several estimations for

parameters. More research is needed to analyse these

parameters to turn the ABM. In addition, we need

more behavioural data, such as how often people in

boats without power deploy their anchor or how often

a missing kayaker will beach their kayak to conserve

energy. This data needs to be collected and analyzed

to fine tune the ABM. Machine learning techniques

could be used to analyse this data and discover how

targets make decisions.

Another important research question is, how

many agents are sufficient for an accurate target

trajectory description? The answer may depend on

computing resources. In the future, employing

parallel computing methods may change the

dynamics of answering this question. With them, tens

of thousands of agents over a multi-hour search

operation could be modeled in seconds. But even in

that case, Pathfinder’s users or search managers may

need some guidance. This line of research will

continue as Pathfinder develops.

There is room for further improvement and fine-

tuning of the optimization model. This includes

refining the penalty weights and possibly the addition

of more constraints and penalties. Collaboration with

practitioners such as naval aviators and SAR

personnel can help. We hope that such collaboration

has a significant potential to produce search paths that

are easy to implement and navigate.

Finally, we plan to add to Pathfinder's new

searcher and target types that current methodologies

cannot handle. That includes searchers that can

transport and deploy other searchers such as, for

example, USCG cutters that can transport helicopters.

Another possibility is to model active targets that may

change behavior depending on the searcher’s

movement, such as, for example, a submarine being

searched by another submarine.

ACKNOWLEDGEMENTS

The authors would like to acknowledge Institute for

Defense Analyses and the researchers who provided

invaluable knowledge in the field of Search Theory.

We would also like to acknowledge Jack Frost of the

USCG for sharing his expertise in the realm of

maritime SAR.

REFERENCES

Abi-Seid, I., Morin, M., & Nilo, O. (2019). Decision

Support for Planning Maritime Search and Rescue

Operations in Canada. PROCEEDINGS OF THE 21ST

INTERNATIONAL CONFERENCE ON ENTERPRISE

INFORMATION SYSTEMS, 328-339.

Adlerstein, D. (2019, May). Fisherman rescued, clinging to

buoy. Retrieved from Apalachicola Times:

https://www.apalachtimes.com/news/20190525/fisher

man-rescued-clinging-to-buoy

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

206

Ai, B., Li, B., Gao, S., Xu, J., & Shang, H. (2019). An

Intelligent Decision Algorithm for the Generation of

Maritime Search and Rescue Emergency Response

Plans. IEEE, 155835-155850.

AMPL Optimization inc. (2021). MINOS for AMPL.

Retrieved from AMPL:

https://ampl.com/products/solvers/solvers-we-

sell/minos/

Biesecker, C. (2021, March 2). House Panel Wants

Updated Coast Guard Fleet Analysis To Factor In New

Demands. Retrieved from Defense Daily:

www.defensedaily.com/house-panel-wants-updated-

coast-guard-fleet-analysis-factor-new-

demands/congress/

Dabrowski, J. J., & Villiers, J. P. (2015). Maritime piracy

situation modelling with dynamic Bayesian networks.

Information Fusion, 116-130.

Deraeve, J., Anderson, M., & Low, M. (2010). Maritime

counte-piracy study using agent-based simulation. 2012

Spring Simulation Multiconference (SpringSim '10),

(pp. 1-8).

Ding, H., & Castanon, D. (2018). Moving Object Search

with Multiple Agents. Miami FL: IEEE.

Eagle, J. (1984). The Optimal Search for a Moving Target

When the Search Path is Constrained. JSTOR.

El-Hadidy, M., & Alfreedi, A. (2020). Minimizing the

expected search time of finding the hidden object by

maximizing the discount effort reward search.

JOURNAL OF TAIBAH UNIVERSITY FOR SCIENCE,

479-487.

Frost, J., & Stone, L. (2001, September). Review of Search

Theory: Advances and Applications to Search and

Rescue Decision Support. Retrieved from Defense

Technical Information Center:

https://apps.dtic.mil/dtic/tr/fulltext/u2/a397065.pdf

Harris, S., Dixon, D., Dunn D.L., & Romich, A. (2013).

Simulation modeling for maritime port security.

Journal of Defense Modeling and Simulation, 193-201.

Iida, K. (1993). Inverse Nth power detection law for

washburn's lateral range curve. Journal of the

Operations Research Society of Japan , 90-101.

Koopman, B. (1946 (declassified in 1958)). Search and

Screening.

Kratzke, T., Stone, L., & Frost, J. (2010). Search and

Rescue Optimal Planning System. 2010 13th

International Conference on Information Fusion.

Edinburgh, UK .

Lin, L., & Goodrich, M. A. (2010). A Bayesian approach to

modeling lost person behaviors based on terrain

features in Wilderness Search and Rescue.

Computational and Mathematical Organization

Theory, 300-323.

Marchione, E., Johnson, S. D., & Wilson, A. (2014).

Modelling Maritime Piracy: A Spatial Approach.

Journal of Artificial Societies and Social Simulation.

Mohibullah, W., & Julie, S. J. (2013). Developing an Agent

Model of a Missing Person in the Wilderness. 2013

IEEE International Conference on Systems, Man, and

Cybernetics. Manchester, UK: IEEE Xplore.

Motor Lifeboat (MLB). (n.d.). Retrieved from

Textronsystems.com:

https://www.textronsystems.com/products/motor-

lifeboat-mlb

Murtagh, B., & Saunders, M. (1978). Large-scale linearly

constrained optimization. Mathematical Programming,

14: 41–72.

N. C. Edwards, J. T. (1981). Factors Affecting Coast Guard

SAR Unit Visual Detection Performance. Croton, CT

063: USCG R&D Center.

Onggo, B. S., & Karatas, M. (2016). Test-driven simulation

modelling: A case study using agent-based maritime

search-operation simulation. European Journal of

Operational Research, 517-531.

Pike, J. (n.d.). HH-60J Jayhawk Specification. Retrieved

from GlobalSecurity.org.

Przemieniecki, J. S. (2000). Mathematical Methods in

Defense Analysis. In J. S. Przemieniecki, Mathematical

Methods in Defense Analysis (pp. 278-279).

Washington DC: AIAA.

Richardson, H. R., & Discenza, J. (1980). The United States

Coast Guard Computer-Assisted Search Planning

System (CASP). Naval Research Logistics Quarterly,

Vol. 27, 141-157.

Sato, H., & Royset, J. O. (2010). Path Optimization for the

Resource-Constrained Searcher. Navel Research

Logistics , 422-440.

Simon, H. (1982). Models of Bounded Tationality .

Cambridge MA: MIT Press.

Steele, M. J. (2004). Agent-Based Simulation of Unmanned

Surface Vehicles: A Force in the Fleet. Monterey CA:

Naval Postgraduate School.

Stone, L. (2011). In Search of Air France Flight 447.

Informs ORMS-Today.

Stone, L., Royset, J., & Washburn, A. (2016). Optimal

Search for Moving Targets. Springer.

Sullivan, P. J. (2016). Evaluating the Effectiveness of

Waterside Security Alternatives for Force Protection of

Navy Ships and Installations Using X3D Graphics and

Agent-Based Simulation. MONTEREY CA: NAVAL

POSTGRADUATE SCHOOL.

USCG. (2013). USGS Addendum to the US National Search

and Rescue Supplement (NSS). Washington DC:

USCG.

Walton, D., Paulo, E., McCarthy, C., & Vaidyanathn, R.

(2005). Modeling force response to small boat attack

against high value commercial ships. Proceedings of

the Winter Simulation Conference . Orlando FL USA:

IEEE.

Wilensky, U. (1999). Netlogo. Retrieved from

NorthWestern: https://ccl.northwestern.edu/netlogo/

Optimizing Heterogeneous Maritime Search Teams using an Agent-based Model and Nonlinear Optimization Methods

207