Towards a Certiﬁcation of Deep Image Classiﬁers against Convolutional

Attacks

Mallek Mziou-Sallami

1,3

and Faouzi Adjed

1,2

IRT SystemX, Palaiseau, France

Expleo Group, Montigny-le-Bretonneux, France

CEA, Evry, France

Keywords:

NN Robustness, Uncertainty in AI, Perception, Abstract Interpretation.

Abstract:

Deep learning models do not achieve sufﬁcient conﬁdence, explainability and transparency levels to be inte-

grated into safety-critical systems. In the context of DNN-based image classiﬁer, robustness have been ﬁrst

studied under simple image attacks (2D rotation, brightness), and then, subsequently, under other geometrical

perturbations. In this paper, we intend to introduce a new method to certify deep image classiﬁers against

convolutional attacks. Using the abstract interpretation theory, we formulate the lower and upper bounds with

abstract intervals to support other classes of advanced attacks including image ﬁltering. We experiment the

proposed method on MNIST and CIFAR10 databases and several DNN architectures. The obtained results

show that convolutional neural networks are more robust against ﬁltering attacks. Multilayered perceptron

robustness decreases when increasing number of neurons and hidden layers. These results prove that the

complexity of DNN models improves prediction’s accuracy but often impacts robustness.

1 INTRODUCTION

Experiments showed that DNNs are overly sensitive

to small disturbances in their input data. It is well

known that one can generate adversarial examples by

applying geometrical transformation (Biggio et al.,

2013; Szegedy et al., 2013). In the other hand, to em-

bed DNN-based algorithm into safety-critical systems

such as aircraft systems or autonomous vehicles, ro-

bustness proof remains essential. Moreover, the non-

transparency nature of DNNs makes robustness ver-

iﬁcation a major challenge facing the many different

possibilities of disturbances. For example, to evalu-

ate the lightness effects, we have to verify whether if

a NN-based image classiﬁer is robust against bright-

ness shift or not. In other words, whether the classi-

ﬁcation results are invariant under afﬁne variation of

pixels intensity or not. This assumption hugely sim-

pliﬁes the reality. If we use an hypothesis closer to

the reality, a more complicated modeling have to be

considered, such as, the case where, views taken are

linked by perspective transformations in the presence

of thick fog inducing a blur on the images. The ques-

tion to be addressed therefore is how to guarantee the

robustness of DNN model? To overcome this chal-

lenge and come up with a solution, many DNN ro-

bustness veriﬁcation frameworks have been proposed

such as DeepSymbol (Li et al., 2019), ERAN (Singh

et al., 2018), DeepG (Balunovic et al., 2019), Relu-

plex (Katz et al., 2017), PLANET (Bunel et al., 2018)

and PRODeep (Li et al., 2020). The common idea

behind all these veriﬁcation tools is the prediction of

disturbed input model using an approximate neural

network behavior. In another approach, researchers

focus on robustness study during the design phase to

build more accurate models against such transforma-

tions (Xiao et al., 2018; Jaderberg et al., 2015).

It should be noted that robustness veriﬁcation is a

different approach from the empirical evaluation of

neural networks. Table [1] summarize some research

in the two approaches classiﬁed according to image’s

attacks. Despite the multitude of methods dealing

empirically with the evaluation of neural networks

(Xiao et al., 2018; Engstrom et al., 2019; Kanbak

et al., 2018; Goodfellow et al., 2009; Fawzi et al.,

2017; Alaifari et al., 2018), robustness certiﬁcation

still a remaining challenge. In this context, formal

methods are widely applied to assess the local and

global robustness of deep neural networks. Typically,

static analysis with abstract interpretation or SAT

solvers approaches are applied to neural networks

and leverages the important progress of formal

Mziou-Sallami, M. and Adjed, F.

Towards a Certiﬁcation of Deep Image Classiﬁers against Convolutional Attacks.

DOI: 10.5220/0010870400003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 419-428

ISBN: 978-989-758-547-0; ISSN: 2184-433X

419

Table 1: Summary of research work related to DNNs veriﬁcation against image’s attacks or deformations.

DNNs Certiﬁcation DNNs Evaluation

DeepG DeepPoly (Xiao et al., 2018)

Attacks References Attacks References (Engstrom et al., 2019)

Translation (Balunovic et al., 2019) Brightness,L

∞

(Singh et al., 2018; Gehr et al., 2018; Singh et al., 2019b; Singh et al., 2019a) (Kanbak et al., 2018)

Rotation 2D (Balunovic et al., 2019) FGSM (Singh et al., 2018; Gehr et al., 2018; Singh et al., 2019b; Singh et al., 2019a) (Goodfellow et al., 2009)

Scaling (Balunovic et al., 2019) Rotation 2D (Singh et al., 2019a) (Fawzi et al., 2017)

Sheering (Balunovic et al., 2019) Rotation 3D (Sallami et al., 2019) (Alaifari et al., 2018)

Vector Fields (Ruoss et al., 2020) Convolution (Sallami et al., 2019)

methods over the last decades. Such approaches

estimate bounds on the perturbation of the inputs

and formally guarantee the same DNN prediction

within these bounds. However, formal methods

over DNN for image perception system have often

been applied to simple image attacks. Existing

robustness veriﬁcation tools often consider norm

based robustness or brightness robustness. For

example, authors, in (Singh et al., 2018; Gehr et al.,

2018; Singh et al., 2019b), have introduced a neural

network certiﬁcation method based on the abstract

interpretation. Experimental results on MNIST and

CIFAR databases have proven the capability of a

such system to certify the robustness against attacks

including simple contrast, FGSM (Fast Gradient

Signed Method) noise and L

∞

attacks. Other works

have explored certiﬁcation against geometric trans-

formation such as 2D rotation (Singh et al., 2019a),

scaling (Balunovic et al., 2019) and 3D rotations

(Sallami et al., 2019). This paper is the continuity

of the earlier work proposed in (Sallami et al.,

2019). We focus on formal methods for NN-based

object recognition systems and we introduce a new

method to assess the robustness of a given NN-based

image classiﬁer under convolutional attacks. We

propose a new algorithm to compute lower and upper

bounds abstract elements that allow us to verify the

robustness of a DNN against ﬁltering attacks. To

the best of our knowledge, the proposed method is

currently the state-of-the-art system for certifying

robustness of neural networks under ﬁltering and

convolutional attacks. Fig.1 illustrates this fact by

brieﬂy describing the proposed system.

Figure 1: End-to-end DNN robustness veriﬁcation against

ﬁltering.

The following article is organized as follows: In

section 2, a brief review of veriﬁcation approaches is

given with a focus on the abstract interpretation the-

ory and its distinctive contribution to neural network

veriﬁcation. We present in Section 3 the system de-

signed to certify ﬁltering robustness. Our experimen-

tal settings and results will be given respectively in

section 4 and 5. Finally, in Section 6, we present our

conclusions and we discuss some future perspectives.

2 BACKGROUND AND RELATED

WORKS

Several techniques allowing the veriﬁcation of neural

networks are developed in the literature. The abstract

interpretation, which is one among these techniques

will be presented in more details in the next sections.

We will recall the formulation of the lower bound and

upper bound for both contrast and geometric attacks.

2.1 Abstract Interpretations for Neural

Network Certiﬁcation

Abstract interpretation is an approach to infer seman-

tic properties from computer programs and to demon-

strate their soundness (Cousot and Cousot, 1992).

Static analysis by abstract interpretation allows to au-

tomatically extract information about all possible ex-

ecution states of a computer program. It is used

for automatic debugging, compilers optimizing, code

execution and the certiﬁcation of programs against

some classes of bugs. One of the ﬁrst application

of static analysis with abstract interpretation for neu-

ral networks is implemented by Pulina and Tacchella

(Pulina and Tacchella, 2010) in 2010. However, their

work was focused on shallow NN (MLP).

Recently, several scientiﬁc contributions adapted

this method for verifying the robustness property of

larger neural networks by proposing abstract trans-

formers

for each type of activation function (Singh

et al., 2018; Gehr et al., 2018; Singh et al., 2019b;

Singh et al., 2019a). In what follows, we recall in a

synthetic way some concepts.

Let

X be a given input.

X may undergo a deforma-

tion or even an attack. In such a case, ¯x ∈

X will be

Abstract transformer is a step of abstract interpretation

construction which is a abstract set that includes all concrete

outputs corresponding to the real data

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

420

transformed into ¯x

. The original inputs perturbed by

ε are denoted by R

X,ε

. Verifying the robustness prop-

erty for R

X,ε

consists of checking the property over

the whole possible perturbation of

Let C

be the output sets with the same label L. We

denote

Y as the set of each prediction for each element

in R

X,ε

= { ¯y ∈

Y |argmax ¯y

= L} (1)

The (R

X,ε

) robustness property is veriﬁed only if

the outputs O

of R

X,ε

are included in C

. However,

in reality, we are not able to control the behavior of

hidden layers. Accordingly, we have no knowledge

about O

. The abstract interpretation is an alterna-

tive to face this defect. In fact, it allows to determine

an abstract domain thought transformers and veriﬁes

the inclusion condition in new abstract domains α

which is an abstraction of

X. We denote the output ab-

stract domain α

. The (R

X,ε

) property is checked:

• If the outputs O

of R

X,ε

are included in C

• If the outputs α

of the abstraction of R

X,ε

(α

)

are included in C

It seems necessary to deﬁne abstract transformers that

are precise for the different existing activation func-

tions. However, the sacalability is one of the major

shortcoming in the implementation of this approach.

Therefore, Singh et al. (Singh et al., 2018) proposed

an alternative solution, called DeepZ analyzer, to deal

with the scalability problem. DeepZ allows also to

certify the robustness of neural network. Another

analyzer, called DeepPoly, have been introduced by

Gerhr et al. (Gehr et al., 2018). This approach re-

lies on a novel abstract domain that merge polyhe-

dron with ﬂoating point and intervals. The approach

is denoted AI

(Gehr et al., 2018). This analyzer may

automatically prove the robustness of different neural

networks architectures, including convolutional neu-

ral networks. The test results demonstrate that AI

an-

alyzer is fully accurate and may be used to certify the

most recent defense efﬁciency for neural networks.

It is characterized by its high precision arithmetic in

ﬂoating point and it manages several activation func-

tions, including ReLU (REctiﬁed Linear Unit),TanH,

and Sigmoid. It is worth mentioning that DeepZ is

based on the abstract domains and more particularly

the zonotopes (Ghorbal et al., 2009). DeepPoly anal-

yser supports reﬁne transformation as well as modern

activation functions such as ReLU, sigmoid, TanH

and maxpool. According to authors, DeepPoly is the

most precise analyser compared to AI

and DeepZ

and manage also deep convolutional neural networks.

This method has been used to check complex pertur-

bation, including 2D rotation.

2.2 Lower and Upper Bound for

Contrast and Geometrical Attacks

In the abstract interpretation for computer science

(Henry, 2014), lower bound and upper bound are de-

ﬁned as longest execution time case. Similarly, for

, the lower and upper bounds are the limits of ac-

cepted disturbance. In the case of luminosity distur-

bance, the lower bound (LB) and the upper bound

(UB) are respectively the minimum and maximum

brightness values. We can approximate it to a bright-

ness shift. Indeed, these two values allow us to deﬁne

the abstract intervals that we need. In the case of plane

rotation, the contribution of the neighboring pixels to

the intensity of the disturbed pixel is proportional to

its distance from the initial pixel. This approximation

lets us estimate the possible LB and UB, which give

us the polytopes in which each rotated pixel is going

to end. Combined with abstract intervals, they allow

us to compute the needed abstract domain. It is rec-

ommended to add a tracing algorithm which split the

rotation interval into sub-intervals. Such procedure

validate whether the neural network is able to recog-

nize the object when it changes orientation in the im-

age.

3 PROPOSED METHOD

Image attacks have been extensively studied over the

last few years for solving real world problems in sev-

eral areas. Different attacks were explored on images

and videos as summarized by Vassaux et al. (Vassaux

et al., 2002). We recall here the three following cate-

gories of image attacks:

• Common Signal Processing: It is necessary that

the neural network recognize the object despite

common signal processing operations being ap-

plied to the input image. Among these opera-

tions, we name few: ﬁltering, re-sampling, re-

quantization, compression, color contrast and en-

hancement.

• Occlusion Attack: is deﬁned by masking some

parts of the images like cropping.

• Common Geometric Distortions: which are ge-

ometric deformation of the image, such as rota-

tion, translation and scaling.

We focus our exploration on the ﬁrst category, speciﬁ-

cally on convolutional (ﬁltering) attacks. With regard

to the geometric image distortions, the basic ones in-

clude rotation, uniform scale change, reﬂection and

shearing are studied in Sallami et al. (Sallami et al.,

Towards a Certiﬁcation of Deep Image Classiﬁers against Convolutional Attacks

421

2019), and by Balunovic et al. (Balunovic et al.,

2019) by proposing different and more precise ab-

stract domains for NN geometrical certiﬁcation.

The particularity of this work is to avoid the speci-

ﬁcity of the disturbance. As a matter of fact, the

proposed method allows the evaluation of the model

depending on the internal structural data and not by

adding an ε-perturbation. The ﬁltering attack depends

on the structural variability of the neighborhood of

each pixel encompassing all disturbances. Using the

convolution ﬁlter with different kernel size, the pro-

posed method may certify all the possible values of

the ﬁlter as illustrated in ﬁgure 2.

3.1 Filtering Attack

Filtering is a practice for enhancing images. Mathe-

matically, the ﬁltering is the result of the convolution

of a function (image) with a kernel. Suppose that we

have a ﬁlter H with d × d size applied to the image I.

For every pixel in the ﬁltered image I

will have the

following value:

(i, j) = ( f ∗h)(i, j) =

d−1

∑

n=−

d−1

∑

m=−

d−1

f (i−n, j−m)h(n, m)

(2)

In image processing ﬁeld, the resulting image de-

pends on the choice of the kernel. In fact, it can be

used for blurring, enhancement, smoothing and ﬁl-

tering, etc. For example, the Gaussian ﬁlter is used

for noising and denoising depending on the variance

of the kernel. In other words, the Gaussian distribu-

tion is approximated by a convolution kernel to build

a convolution matrix (Gedraite and Hadad, 2011). In

the real world case, the noise is applied randomly like

a fog or snow. Therefore, when the image is captured,

some pixels will be masked. Consequently, the recog-

nition of an object in the image depends strongly on

the size of the mask applied. With the convolution,

locally (pixel by pixel), we can ﬁt the weights of the

kernel to reproduce the same noise. However, it will

not be possible to create a kernel for each pixel, there-

fore we suggest to build an interval for every pixel

and to verify it formally by abstract interpretation ap-

proach. It can be seen as a 3D image with variable

voxels.

3.2 Lower and Upper Bound for

Convolutional Attacks

Our approach consists in deﬁning a lower bound (LB)

and an upper bound (UB) independently from the ap-

plied ﬁlter coefﬁcients. The pixel on the ﬁltered im-

age is estimated according to the size of the ﬁlter. The

LB and the UB of each pixel are computed using the

pixel’s neighborhood. Indeed, the value of pixel af-

ter the convolution will have the minimum value of

its neighborhood for the LB and the maximum for the

UB. i.e,

I(i, j)

d−1

∑

n=−

d−1

∑

m=−

d−1

f (i−n, j−m)

maxN (f (i, j))

(3)

I(i, j)

d−1

∑

n=−

d−1

∑

m=−

d−1

f (i−n, j−m)

minN (f (i, j))

(4)

where N ( f (i, j)) deﬁnes the neighborhood of the

pixel (i, j), f deﬁnes the original image and h is the

ﬁlter. The ﬁgure 2 illustrates an example of a se-

lection of the upper and the lower bounds. It il-

lustrates also the indicative minimum neighborhood

(

minN ( f (i, j))

) and the indicative maximum neighbor-

hood (

maxN ( f (i, j))

) by respectively the convolution

kernels up and down. The ﬁnal LB and UB corre-

spond respectively to the min and the max values be-

tween the LB and the UB images related to the mini-

mum and the maximum ﬁlter size. Algorithms 1 and

2 describe in more details the different steps, where

and p

are the horizontal and vertical position of

the pixel in the image, w and h are the ﬁlters and dim

deﬁnes its size. In algorithm 1, depending on the ﬁl-

ter size, we extract for each pixel its neighborhood,

whereas algorithm 2 computes the lower and upper

bounds of the selected neighborhood.

4 EXPERIMENTAL SETTINGS

AND RESULTS

This section is dedicated to highlight our experimen-

tal settings and results for evaluating the effectiveness

of our approach used to verify the robustness proper-

ties against the convolution attacks.

4.1 Experimentation Settings

Herein, we point out the two main settings that allow

us to carry out our experiment. The ﬁrst one is the

used datasets and the second one is the a set of the

neural networks, to evaluate, pre-trained on the two

datasets. The details of the implementation are pre-

sented in the subsection 4.2.

4.1.1 Datasets

Well known datasets, MNIST and CIFAR, are used to

evaluate the impact of ﬁlter’s size on the robustness of

the selected neural networks models.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

422

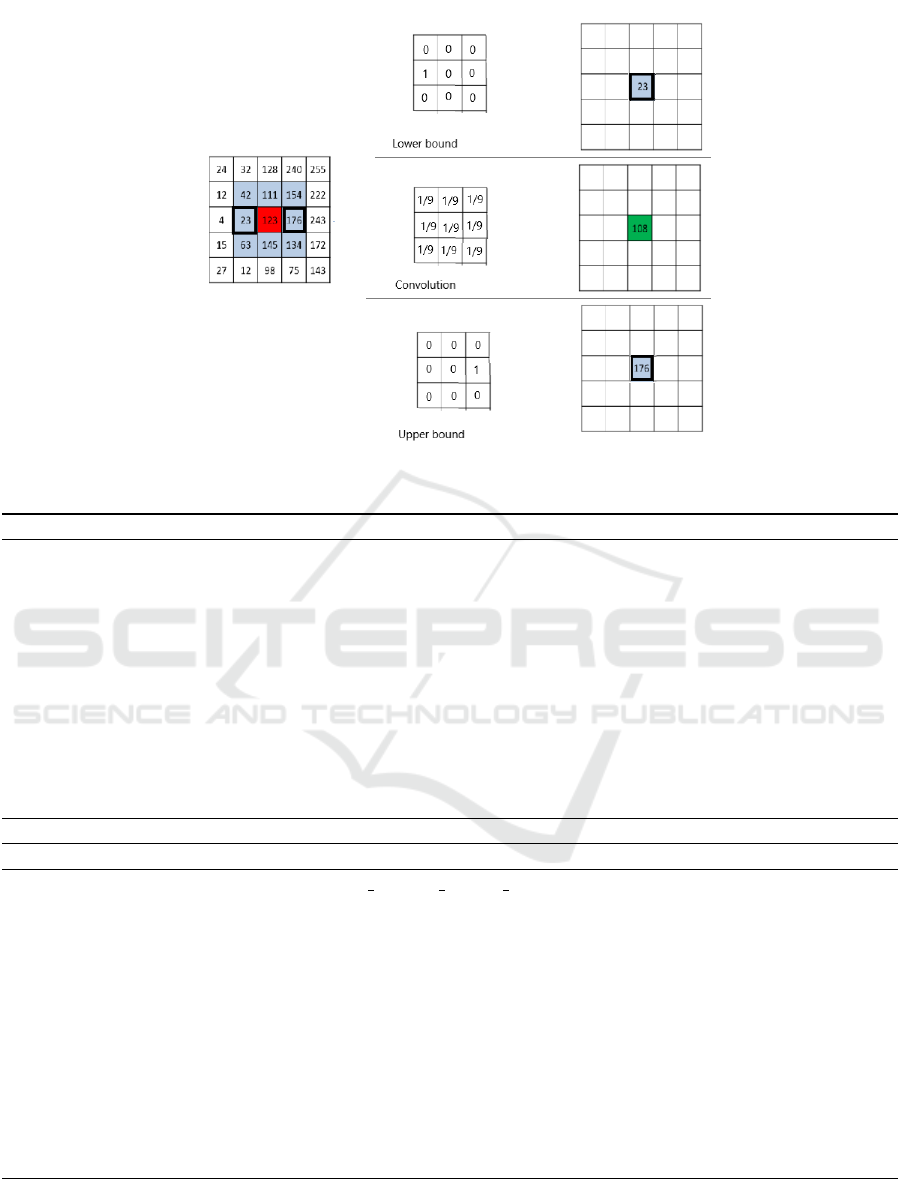
Figure 2: Lower and upper bound for convolution. The ﬁrst line convolution illustrates the lower bound kernel, the second

line convolution represents an example of convolution (Box blur), whereas the third line illustrates the upper bound kernel.

Algorithm 1: Neighbors.

1: procedure PROCEDURE NEIGHBORS

Require:Image ∈ [0, 255]

m×n

, dim ∈ [1, N]

Require:p

∈ [1, m], p

∈ [1, n]

2: Neighbors ← []

3: for t

∈ {−dim, . . . , dim}; t

∈ {−dim, . . . , dim} do

4: if



(0 < p

−t

< m) & (0 < p

−t

< n)



then

5: Neighbors ← Neighbors ∪ Image



−t

; p

−t

: p



6: end if

7: end for

8: Return Neighbors

9: end procedure

Algorithm 2: Lower and Upper Bound for convolution.

1: procedure PROCEDURE CONVOLUTION LOWER UPPER BOUND

Input: I ∈ [0, 255]

m×n

;h, w ∈ J1, T K, T size of the ﬁlter

2: I

, I

← I

3: for p

∈ {1, . . . , m}; p

∈ {1, . . . , n} do

4: L

, p

] ← min(Neighbors(I, h, p

, p

))

5: U

, p

] ← max(Neighbors(I, h, p

, p

))

6: L

, p

] ← min(Neighbors(I, w, p

, p

))

7: U

, p

] ← max(Neighbors(I, w, p

, p

))

8: I

, p

] ← min(L

, p

], L

, p

])

9: I

, p

] ← max(U

, p

],U

, p

])

10: end for

11: Return I

, I

12: end procedure

Towards a Certiﬁcation of Deep Image Classiﬁers against Convolutional Attacks

423

1. MNIST Dataset (LeCun, 1998; LeCun et al.,

1998) contains grayscale images of size 28 × 28

pixels. It consists of a handwritten digits size nor-

malized and centred in ﬁxed-size image where 50

images are selected for the evaluation.

2. CIFAR 10 dataset (Krizhevsky et al., 2009) con-

tains a color images of size 32 ×32 pixels. It con-

tains 10 different and exclusive classes where 100

images are selected for the evaluation.

The robustness criterion of the evaluation is the frac-

tion between the number of veriﬁed images (V I) un-

der the attack and the total number of well classiﬁed

ones (WCI). Then, the robustness metric R

ess

is set

to:

ess

#V I

#WCI

(5)

The equation 5 values vary between 0 and 1. The

more the results of the equation is closer to 1, the

more the combination, neural network model and ﬁl-

ter size is robust. The use of abstract interpretation

(see section 2.1) certify formally the robustness of the

given combination.

4.1.2 Evaluated Neural Networks

Four fully connected neural network models with 3, 6

and 9 layers and one convolutional are selected for the

MNIST dataset. Whereas, for CIFAR-10, four mod-

els are used: three of them are fully connected layers

with 4, 6 and 9 layers respectively and a last one con-

volutional with 3 layers. Table 2 resumes the charac-

teristic of the evaluated models giving more details,

such as the activation function used and the number

parameters estimated (#units).

4.2 Implementation

The abstract domain for convolutional attacks is im-

plemented in Python. As abstract interpretation ana-

lyzer, DeepPoly solution (see section 2.1) has been

used. This latter is based on two main libraries

ERAN and ELINA, coded in respectively Python and

C programming languages. The pre-trained models

presented in table 2 are implemented, where fully

connected layers and convolutional models are eval-

uated using MNIST and CIFAR10 datasets. The size

of the ﬁlters varies from 2 × 2 to 18 × 18 which is

equivalent to dim ∈ {1, 2, . . . , 9} in algorithm 1.

All needed libraries for the implementation are given

in the following Github https://github.com/eth-sri/eran

5 RESULTS

To investigate the efﬁcacity and scalability of our cer-

tiﬁcation method, we evaluate it on a different size

of ﬁlters. The effect of the convolution attack, based

on the size of the ﬁlter, is illustrated in the examples

given in ﬁgures 5 and 7 for MNIST dataset and ﬁg-

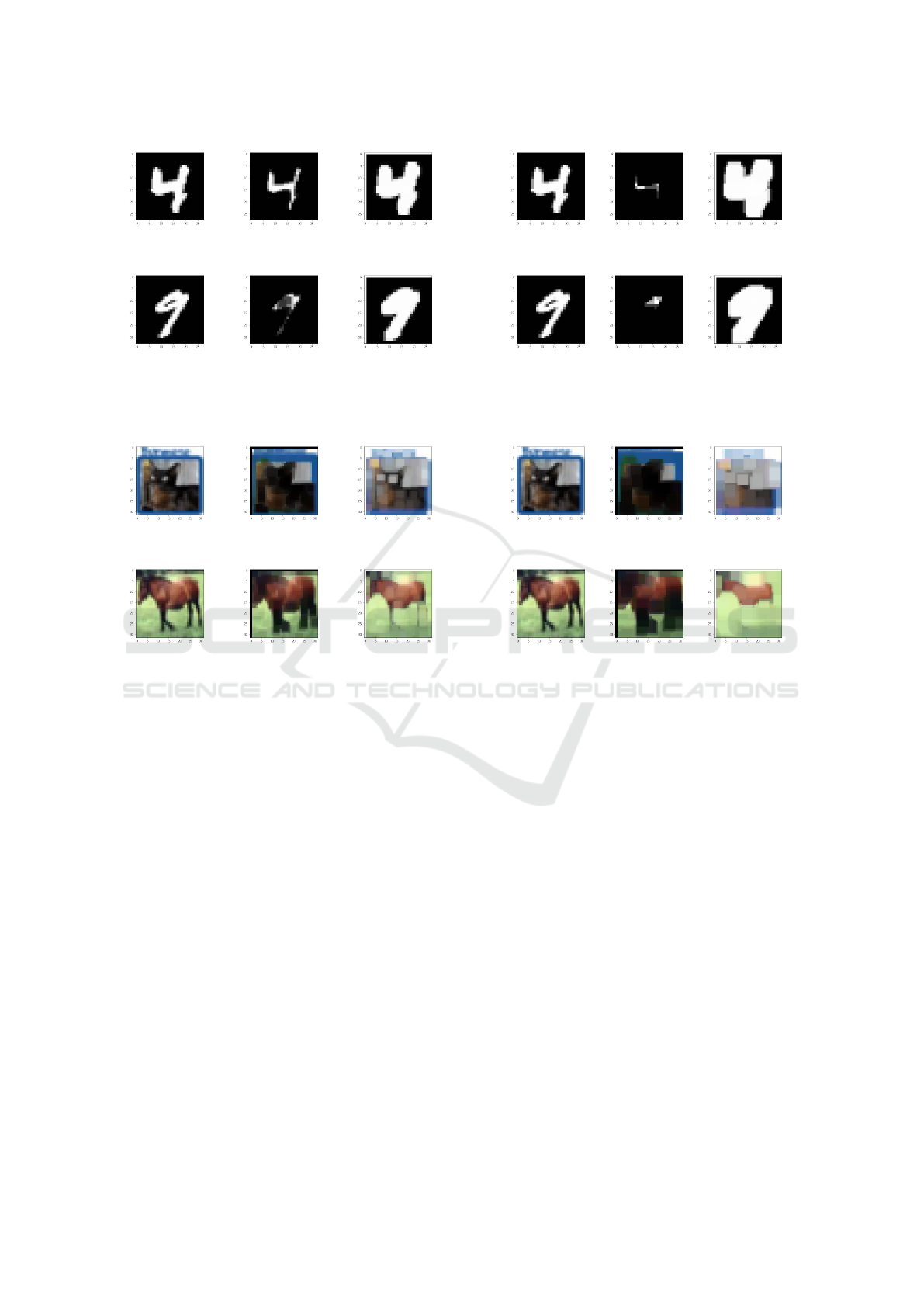
ures 6 and 8 for CIFAR10 dataset. For MNIST ex-

amples, it is obviously visible that the lower bound

attack reduces the white (clear) pixels and replace it

with dark ones, and the upper bound attack increases

the white pixels. These examples highlight the effect

of the borders and object structure in the classiﬁca-

tion. The CIFAR10 examples highlights this effect on

the RGB images making darker and clearer the image

for respectively lower and upper bounds. In RGB im-

ages, the convolution attack shows also a blurring of

the object. From the examples given in ﬁgures 7 and

8, where the size of the convolution kernel is larger,

the attacks damages further the object in the image

compared to ﬁgures 5 and 6.

The lower and upper bounds are also highlighted

attacking only one channel of the RGB images given

in CIFAR10. Figure 9 illustrates respectively the at-

tack of red, green and blue channels. The lower bound

reduces the effect of the channel and the upper one in-

creases it. This attack could simulate the failure of the

channel sensors of a camera.

As described in earlier sections, we applied our

proposed method to prove a neural network robust-

ness against ﬁltering attacks. Speciﬁcally, our anal-

ysis can prove that the MNIST network can classify

a given image of a digit correctly even if every pixel

intensity is an aggregation of its neighbors intensity.

Filtering according to x and y generate a blurry ap-

pearance on the image. So, to test the robustness of

the neural network, just consider a two dimensional

ﬁlter with a size between dim

and dim

. Figure 3

(resp 4) show an example of robustness function for

dim

∈ [0, 9], dim

∈ [0, 9] on MNIST dataset (resp

CIFAR dataset). The results of MNIST robustness,

using the equation 5, are given in the ﬁgures 3. The

results show the square ﬁlter i.e 1 in the x-axis is

equivalent to the ﬁlter 3 × 3, in other words dim1 = 1

and dim2 = 1. The y-axis graphs represents the ro-

bustness metric. For example, in ﬁgure 3 the robust-

ness of convMaxPool model is equal to 30% when

MNIST images are ﬁltered with a ﬁlter 3 × 3 (x-axis

= 1). From MNIST results, we can see that the con-

volutional layers model is more robust than fully con-

nected layers models especially for ﬁlters with size

not exceeding 13 × 13. This is expected since the

convolutional models capture shapes using the con-

volution operator. Consequently, ﬁltering has a low

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

424

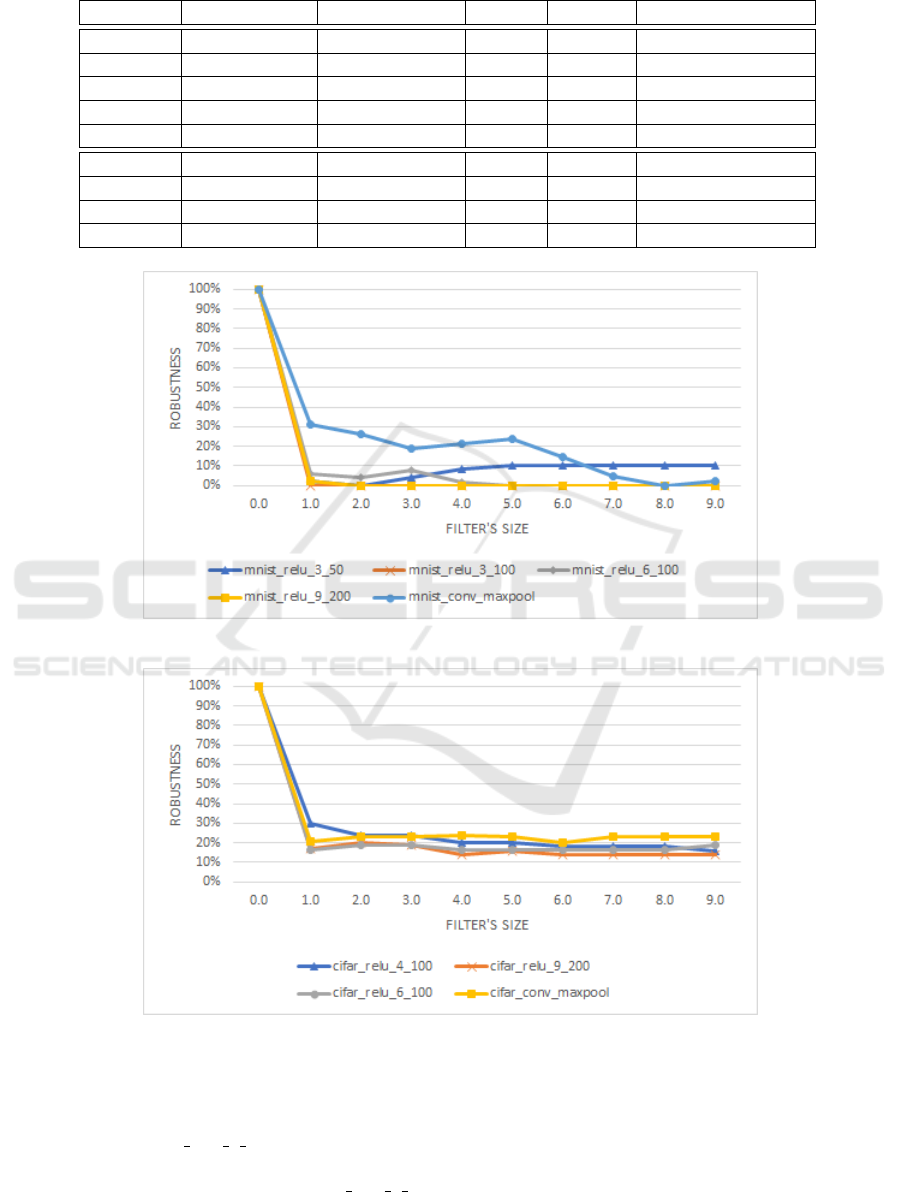
Table 2: Neural Networks used for the evaluation of convolutional attacks.

Dataset Model Type #units #Layers Activation function

MNIST 3 × 50 fully connected 110 3 ReLU

3 × 100 fully connected 210 3 ReLU

6 × 100 fully connected 510 6 ReLU

9 × 200 fully connected 1, 610 9 ReLU

convMaxPool convolutional 13,798 9 ReLU

CIFAR10 4 × 100 fully connected 140 4 ReLU

6 × 100 fully connected 610 6 ReLU

9 × 200 fully connected 1, 810 9 ReLU

convMaxPool convolutional 53,938 9 ReLU

Figure 3: MNIST robustness variation according to the ﬁler’s size.

Figure 4: CIFAR robustness variation according to the ﬁler’s size.

impact on robustness although it modiﬁes the images

content. Beyond this size (13 ×13), model robustness

decrease, same for fully connected models with the

exception of the mnist relu 3 50 model. Indeed, ﬁl-

tering the images with a large ﬁlter greatly modiﬁes

the initial information in the images. mnist relu 3 50

model did not capture details on the images during

training stage. Therefore, it is invariant with respect

to the ﬁltering operation.

Result obtained using CIFAR10 dataset, illus-

trated in ﬁgure 4, conﬁrm that multilayer perceptron

models are more sensitive to ﬁltering regardless of the

dataset. However, the robustness on CIFAR is overall

more important by comparing it with robustness on

Towards a Certiﬁcation of Deep Image Classiﬁers against Convolutional Attacks

425

(a) Real image (b) Convolu-

tion LB

tion UB

(d) Real image (e) Convolu-

tion LB

(f) Convolu-

tion UB

Figure 5: MNIST Database: Lower and Upper bounds in

Convolutional attacks (for dim1=0 and dim2=1).

(a) Real image (b) Convolu-

tion LB

tion UB

(d) Real image (e) Convolu-

tion LB

(f) Convolu-

tion UB

Figure 6: CIFAR10 Database:Lower and Upper bounds in

Convolutional attacks (for dim1=0 and dim2=1).

MNIST. This is due to several factors. First, the CI-

FAR images are larger which changes the proportion

between the ﬁlter size and the image size. Second, in

the presence of a convolution-type disturbance, part

of the information will be deleted from the initial im-

age. Cifar models may persist because images contain

more information and more texture. Such interpreta-

tion can be deduced by comparing image 5e in ﬁgure

5 with image 6e in ﬁgure 6. For this reason the NN

models which are trained on CIFAR are, overall, more

robust against convolutional attacks.

Nevertheless, all models are sensitive to convolu-

tion attacks with a maximum of 30% of robustness.

This could be interpreted as the model learns more

on the object texture than on the object structure, this

makes the model lose (dramatically) on robustness

even with a small disturbance of the structure.

(a) Real image (b) Convolu-

tion LB

tion UB

(d) Real image (e) Convolu-

tion LB

(f) Convolu-

tion UB

Figure 7: Lower and Upper bounds in Convolutional attacks

(for dim1=0 and dim2=2).

(a) Real image (b) Convolu-

tion LB

tion UB

(d) Real image (e) Convolu-

tion LB

(f) Convolu-

tion UB

Figure 8: Lower and Upper bounds in Convolutional attacks

(for dim1=0 and dim2=2).

6 CONCLUSIONS

We introduced a new method for certifying deep neu-

ral networks robustness against ﬁltering attacks. The

core idea of this work is the extension of the abstract

interpretation based certiﬁcation method, which is an

abstract domain suitable to compute the LB and the

UB in the presence of convolution. To the best of our

knowledge this is the ﬁrst study that tries to prove, by

the proposed method we showed, for the ﬁrst time,

how to prove the robustness of a neural network when

the input image is convoluted by a random kernel. We

tested our method with DeepPoly analyzer, and eval-

uated it extensively on a wide range of networks of

different sizes and different architectures. We believe

this work is a promising step towards more effective

evaluation of deep neural networks against convolu-

tional attacks such as blurring, enhancement, smooth-

ing and ﬁltering. In a future study, we propose to op-

timize our abstract domain to achieve more precision.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

426

(a) Real image (b) Convolu-

tion LB on red

channel

tion UB on red

channel

(d) Real image (e) Convolu-

tion LB on

green channel

(f) Convolu-

tion UB on

green channel

(g) Real image (h) Convolu-

tion LB on

blue channel

(i) Convolu-

tion UB on

blue channel

Figure 9: Lower and Upper bounds in Convolutional attacks

(for dim1=0 and dim2=1).

We will also consider the optimisation of neural net-

work architecture for training neural networks to be

provably robust against convolutional attacks.

REFERENCES

Alaifari, R., Alberti, G. S., and Gauksson, T. (2018). Adef:

an iterative algorithm to construct adversarial defor-

mations. arXiv preprint arXiv:1804.07729.

Balunovic, M., Baader, M., Singh, G., Gehr, T., and Vechev,

M. (2019). Certifying geometric robustness of neural

networks. In Advances in Neural Information Pro-

cessing Systems, pages 15313–15323.

Biggio, B., Corona, I., Maiorca, D., Nelson, B.,

Srndi

c, N.,

Laskov, P., Giacinto, G., and Roli, F. (2013). Eva-

sion attacks against machine learning at test time. In

Joint European conference on machine learning and

knowledge discovery in databases, pages 387–402.

Springer.

Bunel, R. R., Turkaslan, I., Torr, P., Kohli, P., and

Mudigonda, P. K. (2018). A uniﬁed view of piece-

wise linear neural network veriﬁcation. In Advances in

Neural Information Processing Systems, pages 4790–

4799.

Cousot, P. and Cousot, R. (1992). Abstract interpretation

and application to logic programs. The Journal of

Logic Programming, 13(2-3):103–179.

Engstrom, L., Tran, B., Tsipras, D., Schmidt, L., and

Madry, A. (2019). Exploring the landscape of spatial

robustness. In International Conference on Machine

Learning, pages 1802–1811. PMLR.

Fawzi, A., Moosavi-Dezfooli, S.-M., and Frossard, P.

(2017). The robustness of deep networks: A geomet-

rical perspective. IEEE Signal Processing Magazine,

34(6):50–62.

Gedraite, E. S. and Hadad, M. (2011). Investigation on the

effect of a gaussian blur in image ﬁltering and seg-

mentation. In Proceedings ELMAR-2011, pages 393–

396. IEEE.

Gehr, T., Mirman, M., Drachsler-Cohen, D., Tsankov, P.,

Chaudhuri, S., and Vechev, M. (2018). Ai2: Safety

and robustness certiﬁcation of neural networks with

abstract interpretation. In 2018 IEEE Symposium on

Security and Privacy (SP), pages 3–18. IEEE.

Ghorbal, K., Goubault, E., and Putot, S. (2009). The zono-

tope abstract domain taylor1+. In International Con-

ference on Computer Aided Veriﬁcation, pages 627–

633. Springer.

Goodfellow, I., Lee, H., Le, Q., Saxe, A., and Ng, A. (2009).

Measuring invariances in deep networks. Advances in

neural information processing systems, 22:646–654.

Henry, J. (2014). Static Analysis by Abstract Interpretation

and Decision Procedures. PhD thesis, Universit

e de

Grenoble.

Jaderberg, M., Simonyan, K., Zisserman, A., et al. (2015).

Spatial transformer networks. Advances in neural in-

formation processing systems, 28:2017–2025.

Kanbak, C., Moosavi-Dezfooli, S.-M., and Frossard, P.

(2018). Geometric robustness of deep networks: anal-

ysis and improvement. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion, pages 4441–4449.

Katz, G., Barrett, C., Dill, D. L., Julian, K., and Kochender-

fer, M. J. (2017). Reluplex: An efﬁcient smt solver for

verifying deep neural networks. In International Con-

ference on Computer Aided Veriﬁcation, pages 97–

117. Springer.

Krizhevsky, A., Hinton, G., et al. (2009). Learning multiple

layers of features from tiny images.

LeCun, Y. (1998). The mnist database of handwritten digits.

http://yann. lecun. com/exdb/mnist/.

LeCun, Y., Bottou, L., Bengio, Y., Haffner, P., et al. (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE, 86(11):2278–2324.

Li, J., Liu, J., Yang, P., Chen, L., Huang, X., and Zhang,

L. (2019). Analyzing deep neural networks with sym-

bolic propagation: towards higher precision and faster

veriﬁcation. In International Static Analysis Sympo-

sium, pages 296–319. Springer.

Li, R., Li, J., Huang, C.-C., Yang, P., Huang, X., Zhang,

L., Xue, B., and Hermanns, H. (2020). Prodeep: a

platform for robustness veriﬁcation of deep neural net-

works. In Proceedings of the 28th ACM Joint Meeting

on European Software Engineering Conference and

Symposium on the Foundations of Software Engineer-

ing, pages 1630–1634.

Pulina, L. and Tacchella, A. (2010). An abstraction-

reﬁnement approach to veriﬁcation of artiﬁcial neural

Towards a Certiﬁcation of Deep Image Classiﬁers against Convolutional Attacks

427

networks. In International Conference on Computer

Aided Veriﬁcation, pages 243–257. Springer.

Ruoss, A., Baader, M., Balunovi

c, M., and Vechev, M.

(2020). Efﬁcient certiﬁcation of spatial robustness.

arXiv preprint arXiv:2009.09318.

Sallami, M. M., Khedher, M. I., Trabelsi, A., Kerboua-

Benlarbi, S., and Bettebghor, D. (2019). Safety and

robustness of deep neural networks object recogni-

tion under generic attacks. In International Confer-

ence on Neural Information Processing, pages 274–

286. Springer.

Singh, G., Gehr, T., Mirman, M., P

uschel, M., and Vechev,

M. (2018). Fast and effective robustness certiﬁcation.

In Advances in Neural Information Processing Sys-

tems, pages 10825–10836.

Singh, G., Gehr, T., P

uschel, M., and Vechev, M. (2019a).

An abstract domain for certifying neural networks.

Proceedings of the ACM on Programming Languages,

3(POPL):41.

Singh, G., Gehr, T., P

uschel, M., and Vechev, M. T. (2019b).

Boosting robustness certiﬁcation of neural networks.

In ICLR (Poster).

Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Er-

han, D., Goodfellow, I., and Fergus, R. (2013). In-

triguing properties of neural networks. arXiv preprint

arXiv:1312.6199.

Vassaux, B., Nguyen, P., Baudry, S., Bas, P., and Chassery,

J.-M. (2002). Survey on attacks in image and video

watermarking. In Tescher, A. G., editor, Applications

of Digital Image Processing XXV, volume 4790, pages

169 – 179. International Society for Optics and Pho-

tonics, SPIE.

Xiao, C., Zhu, J.-Y., Li, B., He, W., Liu, M., and Song, D.

(2018). Spatially transformed adversarial examples.

arXiv preprint arXiv:1801.02612.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

428