Soft Adversarial Training Can Retain Natural Accuracy

Abhijith Sharma

and Apurva Narayan

Department of Computer Science, The University of British Columbia, BC, Canada

Keywords:

Adversarial Attacks, Abstract Certiﬁcation, Adversarial Training, Interpretable Artiﬁcial Intelligence.

Abstract:

Adversarial training for neural networks has been in the limelight in recent years. The advancement in neural

network architectures over the last decade has led to signiﬁcant improvement in their performance. It sparked

an interest in their deployment for real-time applications. This process initiated the need to understand the

vulnerability of these models to adversarial attacks. It is instrumental in designing models that are robust

against adversaries. Recent works have proposed novel techniques to counter the adversaries, most often

sacriﬁcing natural accuracy. Most suggest training with an adversarial version of the inputs, constantly moving

away from the original distribution. The focus of our work is to use abstract certiﬁcation to extract a subset

of inputs for (hence we call it ’soft’) adversarial training. We propose a training framework that can retain

natural accuracy without sacriﬁcing robustness in a constrained setting. Our framework speciﬁcally targets

moderately critical applications which require a reasonable balance between robustness and accuracy. The

results testify to the idea of soft adversarial training for the defense against adversarial attacks. At last, we

propose the scope of future work for further improvement of this framework.

1 INTRODUCTION

Deep Neural Networks (DNNs) have been through

tremendous advancement in recent times. Unsur-

prisingly, we have also observed a simultaneous

interest among the researchers to adopt deep learning

techniques for the models in various applications.

Especially, DNNs are being extensively utilised in

designing models for computer vision (Voulodimos

et al., 2018), (Khan et al., 2018) and natural language

processing (NLP) (Otter et al., 2020) applications.

Although there are many areas where DNNs can be

adopted apart from the two stated above, we have

settled for conventional machine learning methods

due to the lack of interpretability in DNNs. Most of

these examples can be attributed to the applications

in business contexts, where feature engineering on

top of machine learning models (Dong and Liu,

2018) is adopted to achieve the goals. Even though,

the shortcoming of lack of interpretability in DNNs

is quite evident, but we cannot take away their

credit for powerful behavior. In the past decade,

researchers have been quite involved in the process

of producing more and more powerful models. It

induced an unwavering interest among researchers

https://orcid.org/0000-0002-4592-2928

https://orcid.org/0000-0001-7203-8698

for its implementation in critical real-time systems.

Interestingly, until quite recently, we were ignorant

of the robustness aspect of DNN models. It unveiled

an unexplored space of DNN’s behavior against

adversarial attacks.

Despite the powerful capabilities of DNNs, the

lack of reliability and explainability in the technique

restricts it from playing a comprehensive role in a

real-time system. Hence, it became increasingly

necessary to understand and explain the behavior

of DNNs even in vision or NLP-based applications.

Some of the famous works of (Goodfellow et al.,

2014) and (Nguyen et al., 2015) have exposed the

vulnerability of neural networks against adversaries.

Moreover, (Papernot et al., 2016) has demonstrated

that the attacks are transferable, which implies that it

is effortless to design an attack even without the ex-

act knowledge of the model. Even though producing

a secure DNN model is an active area of research, au-

thors in (Madry et al., 2017) have shown that the idea

is achievable. Another exciting approach towards in-

terpretable artiﬁcial intelligence, focusing on devel-

oping robust models against attacks, is evident in the

work of (Gehr et al., 2018). In this work, the authors

proposed an idea of abstract approximation of possi-

ble perturbation to the inputs in the setting. The the-

Sharma, A. and Narayan, A.

Soft Adversarial Training Can Retain Natural Accuracy.

DOI: 10.5220/0010871000003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 621-628

ISBN: 978-989-758-547-0; ISSN: 2184-433X

621

ory of abstract interpretation dates back to the 1970s

(Cousot and Cousot, 1977). Although prominently

it was being used as an elegant theoretical framework

for automated analyzers, authors in (Gehr et al., 2018)

have presented a new dimension for its utilization in

analyzing neural networks. On similar lines, authors

in (Singh et al., 2019b), and (Singh et al., 2018) have

demonstrated certiﬁed veriﬁcation of model with ab-

stract symbolic regions and abstract transformers for

operations in the context of neural networks.

2 MOTIVATION

Our work combines the idea of adversarial training as

proposed in (Madry et al., 2017) and the abstract cer-

tiﬁcation. In this paper, we propose a new training

strategy by amalgamating the conventional adversar-

ial training and abstract interpretation techniques to

ﬁnd a better space of inputs for the adversarial train-

ing. Typically, in the traditional adversarial training,

we perturb every input in original data space and train

the models with the new perturbed adversarial space.

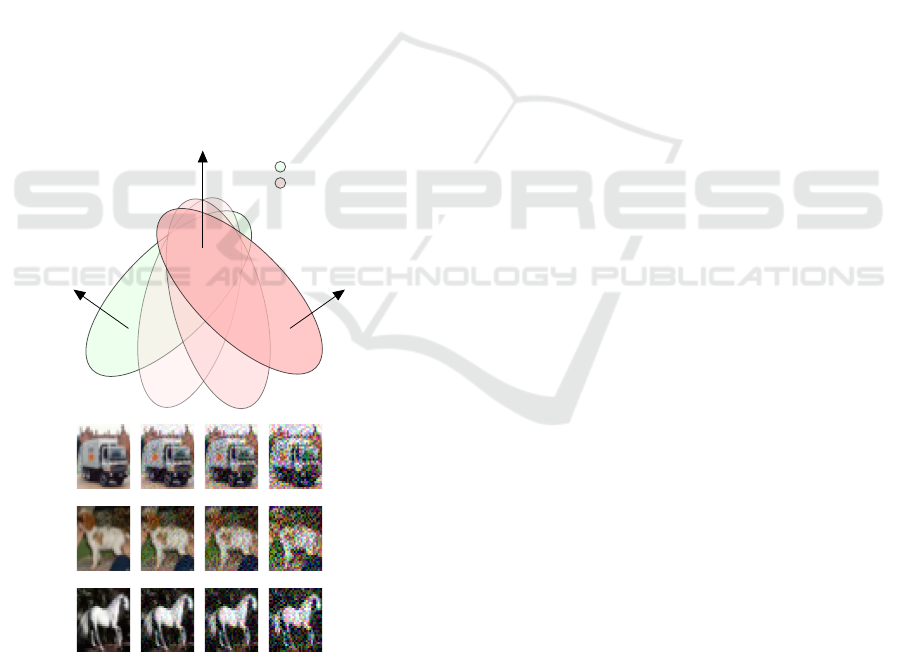
Actual Space

Adversarial Space

Good adversarial and natural accuracy

Good adversarial

bad natural

accuracy

Good natural and

bad adversarial

accuracy

Truck

Dog

Horse

Figure 1: Illustration of Input Space.

However, in this process we tend to sacriﬁce our

natural accuracy as the model is trained on a space

different from the original one. The intuition behind

our reasoning is as shown in 1. In this ﬁgure, one

can see how we move away from original distribution

during adversarial attacks. Hence, in this research we

investigate the trade off between severity of adver-

sarial attack and natural accuracy. The safety critical

applications require strong adversarial training, how-

ever, there exist applications that are not overly criti-

cal, and we aim for a decent trade-off between accu-

racy and robustness (Kamilaris and Prenafeta-Bold

2018), (You et al., 2016), (Brosnan and Sun, 2004) .

In these scenarios, we do not want to perform adver-

sarial training on the complete set of inputs. In prac-

tice, we might observe data points in input space that

may not get affected by the adversaries. Hence, in our

work, we focus on understanding each of the inputs’

behavior through an abstract interpretation-based cer-

tiﬁcation (Gehr et al., 2018) in a constrained setting.

Later, we perform an adversarial training over speciﬁc

subset of original distribution.

3 BACKGROUND

3.1 Attacks and Adversarial Training

There has been extensive work on designing adversar-

ial attacks on neural networks, each having its speci-

ﬁcity and specialty (Akhtar and Mian, 2018). Sub-

sequently, the motivation to build robust models had

led to the design of a defense mechanism for such at-

tacks (Xu et al., 2020). Most of the popular defenses

built to date are broadly inspired by the setting as pro-

posed in (Madry et al., 2017) for training against the

adversarial attack. In the problem formulation of the

defenses, we consider a robust generalization of the

optimization problem as given in 1:

min

ρ(θ);ρ(θ) = E

(x,y)∼D



max

δ∈S

L(θ, x + δ, y)



(1)

The above expression is a saddle point optimiza-

tion problem with an inner maximization problem

aiming for high loss with respect to adversarial ex-

ample x + δ, where δ is imperceptible perturbation to

the original input x. At the same time, outer mini-

mization problem tries to ﬁnd the model parameters

to reduce the overall expected loss in classiﬁcation.

Here, we incorporate adversarial attacks during the

training phase for optimizing the inner maximization

problem. One of the famous attacks is Projected Gra-

dient Descent (PGD), which is quite simple to imple-

ment and has performed exceptionally well in prac-

tice. It is derived from Fast Gradient Sign Method

(FGSM) (Goodfellow et al., 2014). It is essentially a

one-step l

∞

bounded adversary, which ﬁnds an adver-

sarial example as given in 2:

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

622

x + ε.sgn(∇

L(θ, x, y)) (2)

Predominantly, PGD is an iterative version of FGSM

with an additional projection utility to ensure the so-

lution lies within the predeﬁned bounds ε. This inher-

ent characteristic of PGD makes it more potent than

one-step-based attacks like FGSM. Each iteration in a

PGD attack is as given in equation 3:

t+1

= P

x+S

+ α.sgn(∇

L(θ, x, y))) (3)

where P

x+S

is the projection of the point on the

boundary S, and α is the step size. In recent times,

OUTER MINIMIZATION

INNER MAXIMIZATION

Original

Data

Perform

Attack

Adversarial

Data

Train ModelModel

Validate

Figure 2: Traditional training procedure.

the newer upgraded versions outperformed the idea

proposed by (Madry et al., 2017), either in efﬁciency

(Shafahi et al., 2019) or speed (Wong et al., 2020).

However, all these settings are similar in that we dis-

turb our original distribution of inputs by generating

an adversarial substitute for each of the input space

data points. Figure 2 depicts the design ﬂow of each

training epoch in conventional adversarial training.

3.2 Abstract Certiﬁcation

The response of each input to an adversarial attack

might be different. Hence, it is quite reasonable

that some inputs might be more vulnerable than the

rest. Here, we deﬁne an input as vulnerable if it vio-

lates a property over outputs called post-condition ψ

for a pre-deﬁned input property φ (l

∞

bound in case

of brightening attack). The φ, also known as pre-

condition, is deﬁned as:

Ball(x)

= {´x | kx − ´xk

∞

< ε} (4)

where x and ´x are actual and perturbed input, respec-

tively. The ψ is deﬁned as:

∀ j ∈ [0, K], o

≥ o

(5)

where K is the number of classes, k is the actual label

of the input being veriﬁed, and o

is the j

element

of the output vector. Even though authors in (Madry

et al., 2017) have shown the presence of a local max-

imum of loss value in a PGD attack, one cannot guar-

antee the absence of an adversary. In fact, it is infeasi-

ble to enumerate all possible adversaries of an input.

For example, in the MNIST data set, we have 28 × 28

= 784 total pixels for each image. Even if we consider

the binary perturbation for each pixel (0 for black,

1 for white), we will end up enumerating 2

784

total

perturbed version of a single image. Hence, abstract

interpretation of neural networks helps overcome the

shortcoming of working with a ﬁnite but signiﬁcant

number of images.

In abstract certiﬁcation, the output is formulated

using abstract transformation of symbolic regions, un-

like concrete transformers, where operations are per-

formed over concrete vectors. This certiﬁcation is car-

ried out using state-of-the-art sound, precise and scal-

able toolbox: ETH’s Robustness ANalyzer (ERAN)

(Singh et al., 2019c), which is a robustness analyzer

based on abstract interpretation for veriﬁcation of

neural network model. The elements of the abstract

certiﬁcation are explained below:

• Region Deﬁnition: This is the most important

decision in an abstract certiﬁcation. The type of

symbolic region determines the precision of the

analysis. In practice, we aim for regions that are

scalable to large networks and, at the same time,

approximates the perturbation in the best possi-

ble way. The symbolic region in ﬁgure 3 is Box.

Some examples of other regions are DeepZono

and DeepPoly, which are inspired by the geom-

etry of regular zonotope and polytope, respec-

tively, and are modiﬁed in the context of neural

networks. The DeepPoly is the most precise re-

gion but has expensive scalability.

Scalability: Box > DeepZono > DeepPoly

Precision: DeepPoly > DeepZono > Box

The trade-off between scalability and precision

exists, as deﬁnition complexity increase with pre-

cision leading to expensive time complexity.

• Region Transformation: To work with sym-

bolic regions, we deﬁne abstract operations for

the transformations of these regions in a typical

DNN. Some examples of transformations include

Soft Adversarial Training Can Retain Natural Accuracy

623

Figure 3: Illustration of abstract certiﬁcation to verify all possible perturbations. Initially, the input distribution is approxi-

mated by an box abstract region. It is then propagated through layers through suitable box transformations. # shows that the

transformations are abstract. At the last stage, it verify if all points in abstract region corresponds to the same output label.

afﬁne, ReLU, Max-pool, sigmoid, etc. In Fig-

ure 3, we observe the abstract transformations of

box region. These transformations may lose pre-

cision during the operation, and hence, it is nec-

essary to design the transformations carefully. We

aim for exactness(completeness) and soundness in

this process. However, most often, the scalable

regions lose precision and hence are incomplete

methods. As we see in Figure 3, the colored re-

gions inside the boxes are the actual region of the

presence of data points; however, the box trans-

formations lead to loss of precision at each step.

• Veriﬁcation: The goal of the ﬁnal stage is veri-

ﬁcation. In general, to have a guarantee, the out-

put shape produced after all the transformations

should satisfy the condition in 6:

∀ i ∈ I, i  φ =⇒ N (i)  ψ (6)

where I is the input space, and N (i) is the output

after passing an input through neural network N

transformations. In other words, every concrete

point inside the output region should classify to

the same label, which means the entire region has

to lie inside the space represented by postcondi-

tion ψ as shown in ﬁgure 3.

The authors in (Gehr et al., 2018), (Singh et al.,

2019b), (Singh et al., 2018) and (Singh et al., 2019a)

have shown detailed analysis of box, zonotope and

polytope regions with their abstract transformations.

Designing symbolic regions is an active area of re-

search to achieve higher precision.

4 TRAINING METHODOLOGY

In this section, we describe the training strategy. As

stated earlier, the goal is to use the subset of the orig-

inal dataset for adversarial training. The following

steps are involved in the proposed methodology:

• Select a model of choice and required dataset

• Deﬁne a pre-condition φ bounded by ε. The larger

the value of ε, the higher the risk of an attack

• Run the ERAN toolbox with the model, deﬁned

pre-condition, required symbolic region, and the

whole training dataset

• For every input in the training dataset, the tool-

box initially checks whether the input is correctly

classiﬁed or not.

• Once it is correctly classiﬁed, the toolbox veri-

ﬁes the image. Hence, the dataset is partitioned

into three subsets: incorrectly classiﬁed, correctly

classiﬁed but unveriﬁed, and correctly classiﬁed,

which are veriﬁed.

• In each training epoch, the inputs that were ver-

iﬁed and classiﬁed correctly are not touched and

are used for training using the natural method.

• In the same training epoch, we perform training

with adversarial examples from the group of in-

puts that are either incorrectly classiﬁed or cor-

rectly classiﬁed but unveriﬁed.

• The model is ﬁnally validated using the test data

Adopting the training methodology ensures that that

the veriﬁed samples are not attacked. Unlike con-

ventional adversarial training, we do not disturb the

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

624

whole input distribution. Hence, we have comparable

robust performance, i.e., adversarial accuracy, to the

conventional adversarial training using this method-

ology. However, the beauty of this methodology lies

in the lesser sacriﬁce of natural accuracy. Figure 4

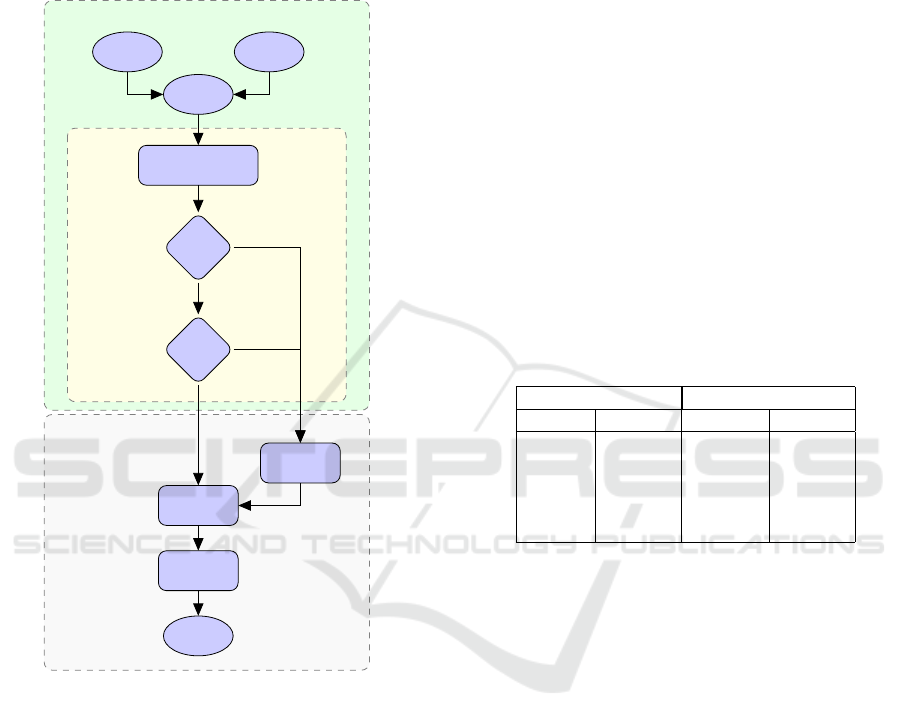
shows the ﬂow of the proposed training procedure.

ABSTRACT CERTIFICATION

ERAN

ADVERSARIAL

TRAINING

Model

Original

Data

Deﬁne

Property

Symbolic Abstraction

and Transformations

Correct?

Veriﬁed?

Perform

Attack

Custom

Dataset

Train Model

Validate

Yes

Figure 4: Our training procedure.

5 EXPERIMENTS

In order to demonstrate our reasoning, we propose the

following datasets, neural network architectures, and

other conditions (attack type, symbolic region, etc.),

establishing the environment required for the exper-

iments. The proposed training method is evaluated

using the two famous datasets

• MNIST: dataset for digit recognition (LeCun,

1998) . The dataset contains 60,000 grayscale

training images with 28 × 28 pixels. Each image

is labelled as one of the ten digits (0-9).

• CIFAR10: dataset of tiny images (Krizhevsky

et al., 2009). The data set set contains 5 batches

of 10,000 training images. Every image consists

of RGB channels each having 32 × 32 pixels,

where each image belongs to one of the 10 dif-

ferent classes (e.g, dog, cat, truck, ship etc.)

We have considered a small, simple, and similar

convolution-based architecture for both MNIST and

CIFAR10 datasets for neural network models. The

simplicity of the data sets will ensure less time to be

spent on training and will help to focus more on the

method. However, the idea is general and can be eas-

ily implemented for other data sets of interest. In or-

der to deﬁne the convolutional layer, we use a notation

p×q

, where N is the ﬁlters present in each layer and

p and q being the dimension of the kernel. Similarly,

for a fully connected layer, we use another notation

A × B, where A is the number of layers present in the

network and B is the total neurons in each layer. We

are interested in deﬁning our architectures in terms of

neurons present in them because the time complexity

of certiﬁcation largely depends on the neuron present

in the model. The proposed architecture for our pre-

liminary study is given in table 1.

Table 1: Model Architecture.

MNIST CIFAR10

Shape Neurons Shape Neurons

4×4

1 × 800 3,614 1 × 1152 4,862

1 × 100 1 × 100

1 × 10 1 × 10

For training, adversarial examples are generated by

attacking the inputs samples. In our case, we have

used a PyTorch based attack library named Torchat-

tacks (Kim, 2020). It consists of many options to

select an attack. However, we have settled for the

old famous PGD attack in our study. The results re-

fer to conventional adversarial training as ’Adversar-

ial Training’ and our methodology as ’Our Training.’

We are limiting ourselves to DeepPoly abstractions

for symbolic regions due to their high precision com-

pared to other symbolic regions.

Additionally, the toolbox has a variant of Deep-

Poly called GPUPoly for fast veriﬁcation of models

on GPU. For MNIST, we have conducted the trial

with 20 iterations of PGD attack with a step size of

0.01. The adversarial training and evaluation are car-

ried out with l

∞

bound (ε) of 0.1 for 50 epochs. Fig-

ure 5 shows the result of the trial. We observe that

for the MNIST dataset, the improvement is not con-

siderable. Also, when we tried to increase ε beyond

0.1, the subset of veriﬁed inputs was minimal to pro-

duce considerable improvement against conventional

adversarial training. Here we observed a reasonable

Soft Adversarial Training Can Retain Natural Accuracy

625

Figure 5: MNIST Trial: Epochs:50 ε:0.1 Steps:20 α : 0.01.

trade-off where increasing ε lead to meager veriﬁed

samples while reducing ε led to the insigniﬁcant dif-

ference between natural and adversarial accuracy.

For CIFAR 10, we conducted the experiments

with 15 iterations of the PGD attack. The adver-

sarial training and evaluation is carried out with l

∞

bounds (ε) of 1/255 (Figure 6a), 2/255 (Figure 6b),

4/255 (Figure 6c), 8/255 (Figure 6d) respectively for

64 epochs. We observe that the accuracy achieved

is less as we have used a primitive and small con-

volutional model. However, our experiments aim to

demonstrate the boost of natural accuracy. Although

not very signiﬁcant, we have observed around 1.5% -

2% improvement in Figure 6c and Figure 6d. Since

the accuracy achieved is lower, the veriﬁed samples

being a subset tends to be lower. Hence, using power-

ful models will improve accuracy, leading to a larger

set of veriﬁed inputs. It naturally increases the pos-

sibility of achieving signiﬁcant improvement in nat-

ural accuracy. However, unsurprisingly, the need for

computational resources and the training time also in-

creases, and this analysis will be a necessary compo-

nent of our future work. We also observe the similar

trade-off as observed with MNIST dataset; the num-

ber of veriﬁed samples becomes less as we increase

ε. Speciﬁcally, when ε is made to 10/255, we ob-

served no veriﬁed samples through abstract certiﬁca-

tion leading to the comparable performance by ’Our

Training’ and ’Adversarial Training’ in terms of nat-

ural and adversarial accuracy.

6 CONCLUSIONS

In this position paper, we have demonstrated the uti-

lization of abstract certiﬁcation for training neural

networks against adversarial attacks. The proposed

framework is practical and straightforward to boost

the natural accuracy in applications where natural ac-

(a) Epochs:64 ε:1/255 Steps:15 α : 0.001. (b) Epochs:64 ε:2/255 Steps:15 α : 0.001.

Figure 6: CIFAR10 Trial.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

626

curacy is as important as the defense against adver-

saries. The preliminary results pave the way for the

broader research that can be done in this area. The

study aimed to initially evaluate the feasibility of the

framework implementation and then understand the

scope of improvement in the performance. We have

achieved satisfactory results with the initial set of ex-

periments; however, we aim to validate this work in

future with more concrete results. Hence, we propose

some of the possible directions to extend our work:

• Train with powerful models to observe the consid-

erable improvement in accuracy

• Train with different types and variants of attacks

to understand the generalization of the method.

Also, training defense against geometric adver-

saries will be interesting as the ERAN toolbox

supports geometric certiﬁcation.

• Extending the work to real-life datasets will give

better insights into this framework. Even the sim-

plest of the models already have a good perfor-

mance on simple datasets like MNIST.

• Formulate hyper-parameter tuning to get right ε

for abstract certiﬁcation to achieve maximum im-

provement in accuracy

ACKNOWLEDGEMENT

We gratefully acknowledge the support from the ad-

vanced research computing platform: Sockeye at The

University of British Columbia for the resource allo-

cation for this study.

REFERENCES

Akhtar, N. and Mian, A. (2018). Threat of adversarial at-

tacks on deep learning in computer vision: A survey.

Ieee Access, 6:14410–14430.

Brosnan, T. and Sun, D.-W. (2004). Improving quality in-

spection of food products by computer vision—-a re-

view. Journal of food engineering, 61(1):3–16.

Cousot, P. and Cousot, R. (1977). Abstract interpretation:

a uniﬁed lattice model for static analysis of programs

by construction or approximation of ﬁxpoints. In Pro-

ceedings of the 4th ACM SIGACT-SIGPLAN sympo-

sium on Principles of programming languages, pages

238–252.

Dong, G. and Liu, H. (2018). Feature engineering for ma-

chine learning and data analytics. CRC Press.

Gehr, T., Mirman, M., Drachsler-Cohen, D., Tsankov, P.,

Chaudhuri, S., and Vechev, M. (2018). Ai2: Safety

and robustness certiﬁcation of neural networks with

abstract interpretation. In 2018 IEEE Symposium on

Security and Privacy (SP), pages 3–18. IEEE.

Goodfellow, I. J., Shlens, J., and Szegedy, C. (2014). Ex-

plaining and harnessing adversarial examples. arXiv

preprint arXiv:1412.6572.

Kamilaris, A. and Prenafeta-Bold

u, F. X. (2018). Deep

learning in agriculture: A survey. Computers and elec-

tronics in agriculture, 147:70–90.

Khan, S., Rahmani, H., Shah, S. A. A., and Bennamoun,

M. (2018). A guide to convolutional neural networks

for computer vision. Synthesis Lectures on Computer

Vision, 8(1):1–207.

Kim, H. (2020). Torchattacks: A pytorch repository for

adversarial attacks. arXiv preprint arXiv:2010.01950.

Krizhevsky, A., Hinton, G., et al. (2009). Learning multiple

layers of features from tiny images.

LeCun, Y. (1998). The mnist database of handwritten digits.

http://yann. lecun. com/exdb/mnist/.

Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and

Vladu, A. (2017). Towards deep learning mod-

els resistant to adversarial attacks. arXiv preprint

arXiv:1706.06083.

Nguyen, A., Yosinski, J., and Clune, J. (2015). Deep neural

networks are easily fooled: High conﬁdence predic-

tions for unrecognizable images. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 427–436.

Otter, D. W., Medina, J. R., and Kalita, J. K. (2020). A sur-

vey of the usages of deep learning for natural language

processing. IEEE Transactions on Neural Networks

and Learning Systems, 32(2):604–624.

Papernot, N., McDaniel, P., and Goodfellow, I. (2016).

Transferability in machine learning: from phenomena

to black-box attacks using adversarial samples. arXiv

preprint arXiv:1605.07277.

Shafahi, A., Najibi, M., Ghiasi, A., Xu, Z., Dickerson, J.,

Studer, C., Davis, L. S., Taylor, G., and Goldstein, T.

(2019). Adversarial training for free! arXiv preprint

arXiv:1904.12843.

Singh, G., Ganvir, R., P

uschel, M., and Vechev, M. (2019a).

Beyond the single neuron convex barrier for neural

network certiﬁcation.

Singh, G., Gehr, T., Mirman, M., P

uschel, M., and Vechev,

M. T. (2018). Fast and effective robustness certiﬁca-

tion. NeurIPS, 1(4):6.

Singh, G., Gehr, T., P

uschel, M., and Vechev, M. (2019b).

An abstract domain for certifying neural networks.

Proceedings of the ACM on Programming Languages,

3(POPL):1–30.

Singh, G., Mirman, M., Gehr, T., Hoffman, A., Tsankov,

P., Drachsler-Cohen, D., P

uschel, M., and Vechev, M.

(2019c). Eth robustness analyzer for neural networks

(eran).

Voulodimos, A., Doulamis, N., Doulamis, A., and Protopa-

padakis, E. (2018). Deep learning for computer vi-

sion: A brief review. Computational intelligence and

neuroscience, 2018.

Wong, E., Rice, L., and Kolter, J. Z. (2020). Fast is bet-

ter than free: Revisiting adversarial training. arXiv

preprint arXiv:2001.03994.

Xu, H., Ma, Y., Liu, H.-C., Deb, D., Liu, H., Tang, J.-L., and

Jain, A. K. (2020). Adversarial attacks and defenses in

Soft Adversarial Training Can Retain Natural Accuracy

627

images, graphs and text: A review. International Jour-

nal of Automation and Computing, 17(2):151–178.

You, Q., Jin, H., Wang, Z., Fang, C., and Luo, J. (2016). Im-

age captioning with semantic attention. In Proceed-

ings of the IEEE conference on computer vision and

pattern recognition, pages 4651–4659.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

628