Agent-based Modeling for Dynamic Hitchhiking Simulation and
Optimization
Corwin F
`
evre
a
, Hayfa Zgaya-Biau
b
, Philippe Mathieu
c
and Slim Hammadi
d
Univ. Lille, CNRS, Centrale Lille, UMR 9189 CRIStAL, F-59000 Lille, France
Keywords:
Dynamic Ridesharing, Hitchhicking, Multi-agent Systems, Optimization.
Abstract:
Although many new transportation services have emerged, hitchhiking continues to be popular, especially in
rural areas. In the last 10 years, many countries have tried to encourage and revitalize this mode of transport
for its ecological and social aspects. The objective is then to develop tools to ensure the connection of the users
as well as the optimization of their journey while respecting the dynamic and volatile character of hitchhiking.
In this perspective, we propose the Realtime Trip Avaibility Graph (ReTAG) approach. This approach consists
of a recursive algorithm to identify and filter the relevant drivers for the riders. This algorithm generates a
graph that allows the riders to establish a perception of the set of rideshares that are eligible and profitable to
their situation. We establish a multi-agent system to describe the behavior and interactions of hitchhikers and
drivers. We propose a comparative study of two hitchhiker behaviors. The first one simulating the behavior
of a real hitchhiker, i.e. without any knowledge of his environment. The second one simulating a hitchhiker
connected to an information system, and thus with knowledge of a part of the environment. We compare these
two behaviors on more or less challenging problem instances in order to have a panel of convincing results.
We conclude that the connected hitchhiker is superior to the real hitchhiker on a set of indicators such as the
waiting time and the instance resolution speed.
1 INTRODUCTION
In this article, we focus on a special case of the dy-
namic ridesharing problem: hitchhiking. This type
of ridesharing is still widely used in the world as a
travel experience or by necessity. It is characterized
by the complete absence of any prediction or reserva-
tion of a ride for the rider and, in general, by the lack
of detours by the drivers. These strong characteristics
make this mean of transport much less efficient than
other ridesharing solutions due to a lack of communi-
cation of information between users. However, it has
the advantage that it can be optimized at any time and
is independent of its scale of use, making hitchhiking
fully dynamic and generic.
The lack of driver detours prevents, in most cases,
the possibility for a rider to rideshare with a single
driver, i.e. to do a single hop ridesharing (Agatz et al.,
2011) (Herbawi and Weber, 2012b). This issue leads
to the need for a rider to transfer between different
a
https://orcid.org/0000-0003-3922-336X
b
https://orcid.org/0000-0002-7761-7725
c
https://orcid.org/0000-0003-2786-1209
d
https://orcid.org/0000-0002-5187-4870
drivers to advance in his journey, i.e to do a multi-hop
ridesharing. Multi-hop ridesharing expands the trans-
portation offer by making it possible to share trips that
would be unfeasible with a single vehicle (Coltin and
Veloso, 2014). In addition, this variant of ridesharing
reduces rider waiting time and travel time (Herbawi
and Weber, 2012a) (Xu et al., 2020).
However, the introduction of transfers involves
identifying the most optimal combination of many
possible drivers and transfer nodes. This operation
involves an increased complexity. In consequence,
different researchers proposed space reduction meth-
ods to limit the exploration of the numerous possi-
bilities. A first approach is the abstraction of space.
This abstraction can be done by dividing the space
into zones (Nourinejad and Roorda, 2016), by select-
ing pickup and delivery stations (Di Febbraro et al.,
2013) or by partitioning roads according to their im-
portance (Pelzer et al., 2015). In these papers, the ab-
straction of space is empirical and globalizing. Alter-
natively, individualizing approaches propose the use
of agents to design a limited and proper perception of
the environment to each user of a ridesharing system.
This alternative approach allows to limit the search
322
Fèvre, C., Zgaya-Biau, H., Mathieu, P. and Hammadi, S.
Agent-based Modeling for Dynamic Hitchhiking Simulation and Optimization.
DOI: 10.5220/0010876600003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 1, pages 322-329
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

space of a rider dynamically and according to his con-
straints and preferences. This perception is notably
modeled by a transfer graph in (Jeribi et al., 2011a).
This article studies ridesharing in a multi-modal con-
text (public transport, self-service car) and proposes
a graph referencing the different means of transport
accessible to the rider as well as the possible transfers
between these means of transport. We have chosen to
extend the scope of this transfer graph to the hitch-
hiking problem in our paper. Indeed, its dynamic and
generic character corresponds to the hitchhiking prob-
lem in which the optimization is continuous through-
out the rider’s journey. Moreover, the hitchhiking
framework can be naturally represented by a multi-
agent system since drivers and riders are autonomous
entities in interaction. Multi-agent systems have been
shown to be efficient for the simulation and resolu-
tion of several ridesharing variants such as taxi fleet
management (Mathieu and Nongaillard, 2018), vehi-
cle sharing services (Jeribi et al., 2011b) and rideshar-
ing optimization with professional (Xu et al., 2020) or
private drivers (Fevre et al., 2021). We therefore pro-
pose to simulate road traffic and hitchhikers as agents.
In summary, the contributions of this paper are:
(1)We formalize the hitchhiking problem using a
graph abstraction. (2)We define a multi-agent sys-
tem modeling drivers, hitchhikers and their commu-
nications. (3)We propose a comparative study of two
hitchhiker behaviors. The first one simulating the be-
havior of a real hitchhiker, i.e. without any knowl-
edge of his environment. The second one simulat-
ing a hitchhiker connected to an information system,
and thus with knowledge of a part of the environment.
(4)We develop the Realtime Trip Avaibilty Graph Ap-
proach that uses a recursive algorithm to generate a
graph of admissible solutions for a hitchhiker.
The reminder of this paper is organized as follows.
The hitchhiking problem is formulated in the section
2. Section 3 describes the suggested multi-agent ar-
chitecture. The Realtime Trip Avaibilty Graph Ap-
proach is described in section 4. Section 5 presents an
evaluation of our approach. Finally, conclusion and
prospects are addressed in section 6.
2 PROBLEM FORMULATION
2.1 Definition of an Instance of the
Dynamic Hitchhiking Problem
We consider an instance of a dynamic hitchhiking
problem as follows:
• A Road Infrastructure: represented by a graph
G = hV, Ei, roads are modeled by edges E =
{e
1
,e
2
,...,e
n
} and road intersections by nodes
V = {v
1
,v
2
,...,v
n
}.
• A Set of Riders. R, with a rider r ∈
R;r : (id,v
s
,v
l
,v
e
,wt, p) defined respectively by a
unique identifier, a departure position, a current
position, a destination position, a total waiting
time and a perception. The waiting time wt corre-
sponds to the current waiting time of the rider in
the simulation. The perception p of a rider corre-
sponds to the set of the nodes accessible through
candidate drivers. It is initialized with its starting
node.
• A Set of Drivers: D, with a driver d ∈ D; d :
(id, v
s
,v
l
,v
e
,trip,c) defined respectively by a
unique identifier, a departure position, a current
position, a destination position, a trip and a ca-
pacity. The driver’s trip is the set of the nodes that
compose the shortest path from its start node to its
end node. The capacity of a driver corresponds to
the number of seats available in his vehicle.
Such representation of the road infrastructure per-
mits us to compute the shortest path and the distance
between two nodes. It also permits us to detect com-
mon nodes in the itineraries of system users.
We are using a discrete time and space simulation.
Time evolves at constant intervals and traveling from
one node to an adjacent node requires a unit of time.
Therefore, in our simulation, time and distance are
merged and we denote the distance-time between two
nodes v
i
and v
j
: dt(v
i
,v
j
) = SPL(v
i
,v
j
), SPL being
the shortest path length between the two nodes. Each
rider and driver can travel on the graph from node
to adjacent node. Several riders and drivers may be
present on the same node. At each time step, all rid-
ers and drivers present in the system can perform an
action based on their behavior.
2.2 Formulations
To identify whether a trip sharing is possible between
a rider and a driver, we use several constraints.
The Shareability Constraint: for a driver d
j
to be
a candidate for a ridesharing with a rider r
i
, he must
pass through one of the nodes present in the percep-
tion r
i
.p of this rider.
r
i
.p ∩ d
j
.trip 6=
/
0 (1)
The Transferability Constraint: for a passenger r
i
ridesharing with a driver d
j
to transfer with another
driver d
k
at the transfer node v
trs
, the first driver d
j
must arrive before or at the same time as the second
driver d
k
at the transfer node v
trs
.
Agent-based Modeling for Dynamic Hitchhiking Simulation and Optimization
323

dt(d
j
.v
l
,v
trs
) ≤ dt(d
k
.v
l
,v
trs
) (2)
dt(d
k
.v
l
,v
trs
) − dt(d
j
.v
l
,v
trs
) ≥ 0 (3)
If the ridesharing is possible, the left-hand side result
of the Eq.3 is called the delay :
delay(d
j
,d
k
,v
trs
) = dt(d
k
.v
l
,v
trs
) − dt(d
j
.v
l
,v
trs
)
(4)
The Delay. then represents the waiting time of the
rider on the transfer node between the arrival of the
first driver and the departure of the second driver.
Concerning the delay of a driver d
j
to pick up a pas-
senger r
i
not being in a car - and thus in a stationary
state - it corresponds to the time distance between the
current node of the driver d
j
.v
l
and the current node
of the passenger r
i
.v
l
.
delay(r
i
,d
j
,r
i
.v
l
) = dt(d
j
.v
l
,r
i
.v
l
) − dt(r
i
.v
l
,r
i
.v
l
)
(5)
(6)delay(r
i
,d
j
,r
i
.v
l
) = dt(d
j
.v
l
,r
i
.v
l
)
We have shown how to establish candidate
ridesharing drivers. It is now a question of establish-
ing whether a candidate driver profits to a rider’s trip.
Indeed, one can imagine that a driver who is heading
towards the opposite direction, although satisfying the
stated constraints, is not necessarily relevant. To eval-
uate the profit of ridesharing with a driver, we use two
values: the contribution and the delay.
The Ccontribution of a Move to a node v
k
∈ d
j
.trip
to a rider’s journey is described as the difference
between the shortest path length (SPL) between the
rider’s current node r
i
.v
l
and its arrival node r
i
.v
e
and
the shortest path length between the target node v
j
and
the same arrival node r
i
.v
l
.
contrib(r
i
.v
l
,r
i
.v
e
,v
k
) = S PL(r
i
.v
l
,r
i
.v
e
) − SPL(v
k
,r
i
.v
e
)
(7)
We consider relevant a path sharing between a
rider r
i
and driver d
j
to a node v
k
if the delay does
not exceed the contribution.
contrib(r
i
.v
l
,r
i
.v
e
,v
k
) > delay(r
i
,d
j
,v
k
) (8)
contrib(r
i
.v
l
,r
i
.v
e
,v
k
) − delay(r
i
,d
j
,v
k
) > 0 (9)
The Profit of a Ridesharing: the result of the left-
hand side of Eq.9 performing the difference of the
driver’s delay over the contribution of the move to a
node in the driver’s path results in the profit.
(10)
pro f it(r
i
,d
j
,v
k
) = contrib(r
i
.v
l
,r
i
.v
e
,v
k
)
− delay(r
i
,d
j
,v
k
)
Thus, a negative or zero profit is of little inter-
est, while a positive profit allows the hitchhiker to
progress efficiently towards his destination. However,
a driver with a null or negative profit can lead a rider
to another driver who is much more interesting. It is
therefore necessary to be able to not only evaluate the
direct contribution of a driver but also the opportuni-
ties that he offers with his itinerary.
Therefore, we define the objective function of a
rider as maximizing the sum of the drivers’ profits.
max
size(D)
∑
j=0
size(d
j
.trip)
∑
k=0
pro f it(r
i
,d
j
,v
k
) (11)
3 THE SUGGESTED MULTI
AGENT ARCHITECTURE
In this section, we detail our approach based on an
individual-centered simulation and a transfer graph.
The drivers and riders present in our hitchhiking
system are autonomous and interactive. They make
their proper decisions and communicate to share in-
formation about their journey. A multi-agent system
(MAS) permits the organization of such a popula-
tion: it is composed of autonomous agents who have
their own behavior and characteristics and who inter-
act with their environment. In a MAS, the agents are
not systematically individuals on the move, they may
also be responsible for system-related tasks such as
collecting and sharing information on the user agents.
Our multi-agent system is composed of various
agents with specific functions and purposes. Driver
agents D aim to arrive at their destination as quickly
as possible and without detours. Rider agents R want
to reach their destination by ridesharing with driver
agents. In order to do so, they have to decide at each
step of the simulation what action to perform in order
to get closer to their goal.
In this article we detail two rider agent behaviors.
The first behavior is the naive hitchhiker, it reproduces
the behavior of a real hitchhiker. A hitchhiker usually
takes the first vehicle permitting him to progress on
its journey, it is not connected and does not plan its
transport. According to this idea, a naive rider agent
only consider its current node, it does not browse the
rest of the environment. If one or more drivers ap-
pear on its current node, it evaluates the contribution
of their next move. If it turns out that the next move-
ment of one of the drivers makes him move towards
its goal, then it gets into the vehicle, otherwise it does
not move and increment its waiting time.
The second behavior is called the ReTAG hitch-
hiker (Real-time Trip Availability Graph). It corre-
sponds to a hitchhiker connected to a transport ser-
vice allowing him to have information on the drivers
in the environment. He can then plan a dynamic and
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
324

optimized route. If one or more drivers appear on its
current node, the rider evaluates their profit as well as
the profit of the drivers accessible on the way via a
transfer. Moreover, it takes into account the drivers
passing through its current node in the future. Indeed,
it may be better to wait a few simulation steps for an-
other driver providing a better solution.
The need for this rider behavior to have limited
information about the environment leads us to detail
the tsa transport service agent. This agent acts like a
blackboard. It stores the current and future positions
of the drivers and associates to them the related time
delay, i.e. the number of simulation steps needed be-
fore reaching the concerned position. Thus, when a
new driver agent appears in the system, it transmits
its route to the tsa agent. The tsa agent updates at
each simulation step the blackboard by decrementing
the delays and by removing or adding drivers on each
node in a dynamic way. To establish its perception
and in order to make a decision, a ReTAG passenger
agent sends a query on its current perception, i.e the
set of nodes accessible via candidate drivers, to the
tsa agent, which return the set of admissible driver
agents, their trips and their delays. The rider agent
applies the ReTAG approach, whose algorithms are
detailed later in this paper, and updates its transfer
graph and perception. It will do this again as long
as new candidate drivers are returned as a result of
the query on its perception to the tsa agent. Finally,
it applies the objective function detailed in the section
2.2 and identifies whether it should update its position
following the optimal driver’s move or remain in the
same place and increment its waiting time. The iden-
tification of this set of nodes and associated drivers is
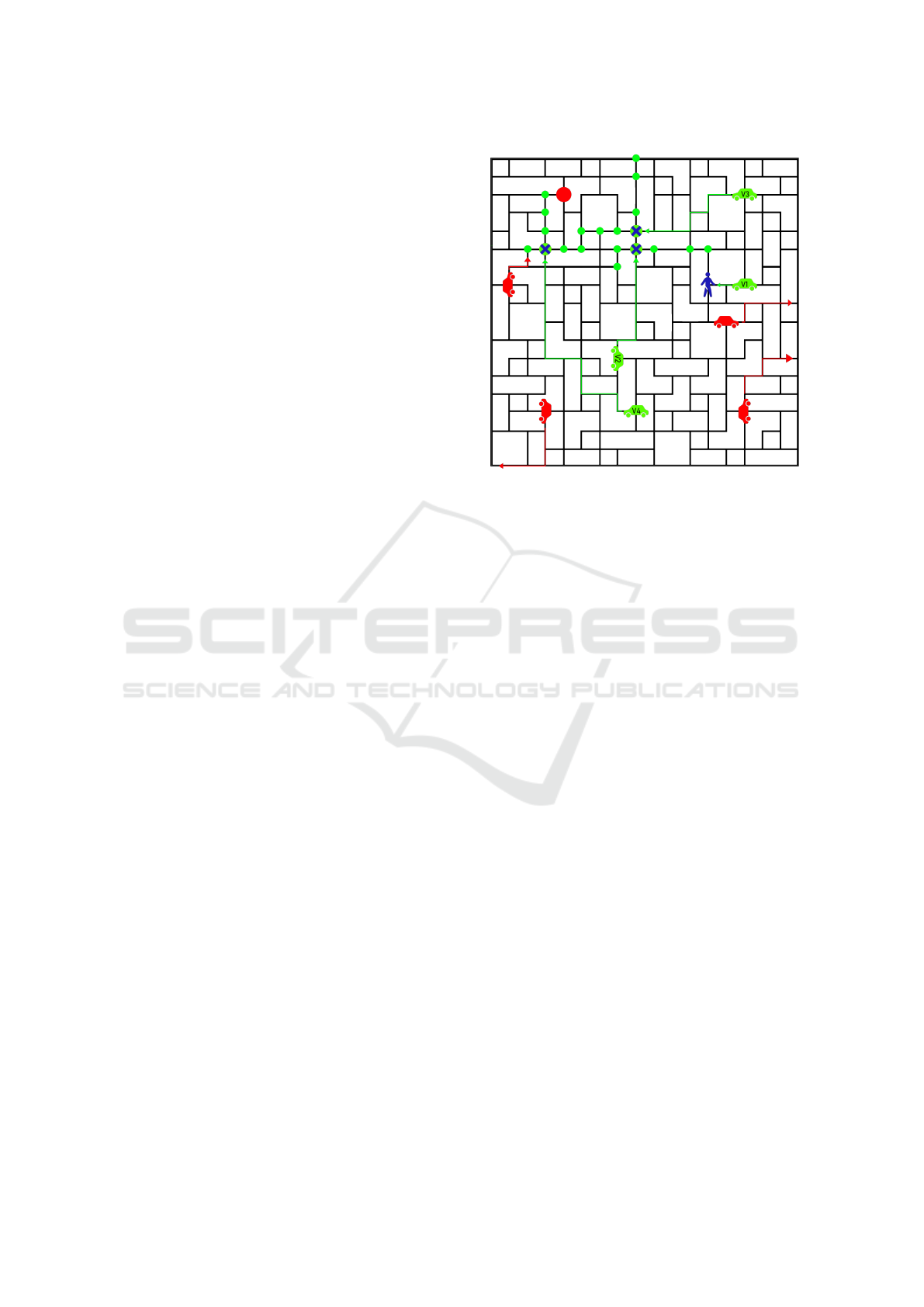
schematically shown in Fig. 1.
4 THE REAL-TIME TRIP
AVAILABILITY GRAPH
APPROACH (ReTAG)
Once the set of admissible driver agents is returned by
the tsa transport service agent, the ReTAG rider agent
builds the ReTAG graph.
4.1 Definition of the ReTAG Graph
The ReTAG graph must contain enough information
to allow the rider agent to identify the optimal solu-
tion at each simulation step, but must also be light
enough to be browsed and updated regularly and an
inexpensive way. It is therefore excluded to create
a graph including all the nodes from the response
Figure 1: Diagram of the process of identifying the set
of reachable positions (green nodes) via compatible drivers
(green cars) to the situation of a rider (blue man). The possi-
ble transfers are represented by the green nodes with a blue
cross and the arrival node is in red. The discarded drivers
(red cars) violate the constraints. There exists a path be-
tween the current position of the rider and his arrival.
to the query. We therefore define the ReTAG graph
G
rtg
= hV
rtg
,E
rtg
i overcoming this issue.
We define two types of nodes in this graph. The
first type is the transfer node, which is added to the
graph in the case of a possible transfer between sev-
eral drivers and if the travel opportunities associated
with this transfer result in a positive profit. The sec-
ond type is the profitable node. When a rider agent
is looking for the best route to his destination, there
may not yet be a ridesharing sequence that would al-
low him to fulfill his objective. In this case, his goal
is to take the path that gets him as close as possible to
his destination. It is then necessary to limit the inter-
est of a ridesharing to the position limiting the profit,
this limit is represented by the profitable node. Each
of the above mentioned nodes has an attribute: the
arrival time arrTime representing the number of sim-
ulation steps needed by a rider to reach the concerned
node. It is made of the sum between the previous and
current delays of the drivers and the previous and cur-
rent distances between each node of the graph. We
finally note that since the set of nodes of the ReTAG
graph are above all nodes of the route graph, this set
is a subset of the nodes of the route graph V
rtg
⊆ V.
The edges of the ReTAG graph contain informa-
tion about the trip between two nodes. These edges
are oriented according to the direction of the driver
agent responsible for the trip. They contain the iden-
tifier of the driver agent, the contribution of the trip
Agent-based Modeling for Dynamic Hitchhiking Simulation and Optimization
325

Figure 2: Example of a ReTAG graph built from the sce-
nario in Fig.1. The blue node and the red node are respec-
tively the departure and arrival node of the rider agent. The
green nodes and green nodes with a blue cross are respec-
tively profitable nodes and transfer nodes. The different arcs
represent the possible trips between the nodes. The infor-
mation contained on the arcs are respectively the identifier
of the driver responsible for the trip, the trip contribution
and the delay (see 2.2). The best path (at this step of the
simulation) to the arrival node is highlighted in yellow.
and the delay, i.e. the waiting time before being
picked up. It is important to mention that this model is
generic and that we could add other attributes to these
edges. An example of the information contained in
these edges is shown in Fig.2.
4.2 Generation of the ReTAG Graph
A ReTAG graph is built recursively by connecting,
step by step, the subgraphs resulting from the explo-
ration of the space drivers’ trip. For each new driver
compatible with the situation of the rider (at the de-
parture node or by a transfer and respecting the con-
straints), a sub-graph of exploration of the trip of this
driver is created. The objective is to recursively iden-
tify if a profitable path exists in the solution space.
Thus, during the recursion, if a node is identified as
profitable, the subgraph resulting from the exploration
is connected to the rest of the ReTAG graph and so on
until the set of possible solutions is covered. We note
that with this method, each driver agent or node of the
road graph G is visited and studied only once.
The generation of the ReTAG graph is based on
two algorithms. The algorithm 1 is named ICRG for
Initialization and Connection algorithm of the ReTAG
Graph. It aims at initializing the ReTAG graph with
the drivers passing through the starting node of the
rider (ICRG, L1-2). It runs the algorithm 2 on each
of these candidate drivers and connects the subgraphs
resulting from the exploration of the possible transfers
in their trip if a profitable solution is found (ICRG,
L3-8). The ICRG algorithm returns the ReTAG graph
at the end of the process (ICRG, L9).
Algorithm 1: ICRG: Initialization and Connection algo-
rithm of the ReTAG Graph.
Input: G = road infrastructure graph, r = a rider
Output: G
rtg
= the rider ReTAG graph
1: instantiate G
rtg
with rider current node (r.v
l
, arrTime = 0)
2: AD = query tsa for avaible drivers passing by rider current node r.v
l
3: for all d ∈ AD do
4: node =REDT(d,r.v
l
,delay(r, d, r.v
l
))
5: if node not None then
6: G
rtg
.addEdge(r.v
l
,
node,d.id,contrib(r.v
l
,r.v
e
,node),delay(r, d, r.v
l
))
7: end if
8: end for
9: return G
rtg
The algorithm 2 is referred as REDT for Recursive
Exploration of Drivers’ Trips algorithm. This algo-
rithm is responsible for recursively exploring drivers’
trips in search of profitable or transfer nodes. It con-
siders as parameters a driver candidate to rideshar-
ing curD, the node studied in the previous recursion
prevNode and the time accumulated during the pre-
vious recursion prevArrTime (rider travel time and
rider waiting time). These variables are essential to
check if the ridesharing constraints are not violated
and to maintain the time consistency in each explo-
ration. Thus, prevNode allows to limit the set of
nodes to consider in the driver’s trip curD. Indeed,
all the nodes prior to prevNode will represent the past
itinerary of the driver at the time of ridesharing. The
subset curD.subTrip is then created and includes all
the nodes of the driver’s trip from prevNode excluded
(REDT, L1). The variable prevArrTime initializes the
time reference in the recursion (REDT, L2).
We then initialize two variables: f irstNode and
lastNode (REDT, L3). These variables are used to
find the first and last node added to the subgraph of
the profitable and transfer nodes. Indeed, once the
path of the current driver curD has been explored, it
is necessary to initially determine if a profitable path
has been found from this driver. If so, it is necessary
to determine which node to connect to the graph of
the previous recursion. This function is filled by the
variable f irstNode. It is initialized to None so that,
if at the end of the recursion there is still no node as-
sociated with this variable, then there is no interest in
carpooling with this driver (ICRG, L5).
Concerning the lastNode, it stores the last node
added to the current subgraph during the traversal of
the nodes of the current driver curD. We are going to
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
326

Algorithm 2: REDT: Recursive Exploration algorithm of
Drivers’ Trips.
Input: curD: the current studied driver,prevNode the previous studied
node, prevArrTime: the time it takes the rider to reach the previous node
with curD
Output: f irstNode: the first node of the driver’s trip added to the Re-
TAG graph if any
1: curD.subTrip = curD.trip nodes from prevNode to the end of the trip
2: arrTime = prevArrTime
3: f irstNode = None, lastNode = None
4: for all node ∈ curD.subTrip do
5: arrTime+ = 1
6: AD = query tsa for available drivers passing by node
7: for all d ∈ AD do
8: if delay(curD,d,node) ≥ 0 then
9: # possible transfer on node between d and curD
10: newNode =REDT(d, node, delay(curD, d, node) + arrTime)
11: if newNode! = None then
12: # profitable node found through transfers
13: if node /∈ G
rtg
then
14: G
rtg
.addNode(node, ar rTime)
15: end if
16: if f irstNode == None then
17: f irstNode = nod e
18: else
19: G
rtg
.addEdge(lastNode, node, curD.id,
contrib(lastNode, r.v
e
,node), delay = 0)
20: end if
21: lastNode = node
22: G
rtg
.addEdge(node, newNode, d.id,
contrib(node,r.v
e
,newNode), delay(curD,d, node)
23: end if
24: end if
25: end for
26: end for
27: if f irstNode == None then
28: # no transfer found or no profitable node found through transfers
29: search for the most profitable node in curD.trip
30: if exists a profitable node then
31: f irstNode = most profitable node
32: end if
33: end if
34: return f irstNode
detail its utility by analyzing the algorithm 2. The
REDT algorithm traverses each node node of the sub
trip of the current driver curD.subTrip. The reference
time arrTime is then incremented by 1: a movement
from one node to another adjacent node requiring 1
simulation step. The passenger agent makes a query
to the transport service agent tsa on node to obtain the
drivers passing through this node. The result of this
query, namely the set of available drivers, is stored
in a new set AD (REDT, L4-6). For each of these
drivers, we check if the transferability constraint de-
fined in section 2.2 is respected. If so, a transfer is
possible and the algorithm performs a new recursion
on the driver d and the node node (REDT, L7-9). If
this new recursion returns a node, it is the first node
of the subgraph of this new recursion. We thus obtain
the information that the driver currently studied curD
allows the rider to reach a profitable node by means
of a transfer on the node node. The node node is then
a node of interest and is added to the subgraph of the
current recursion (REDT, L11-15).
Finally comes the linking phase between the sub-
graph resulting from the transfer with the driver d and
the subgraph of the current driver curD. First, the
transfer node node is added in the ReTAG graph. If
it is the first node added in the graph for the current
driver curD, we associate its value to f irstNode. Oth-
erwise it must be linked with an edge to the last node
added during the current recursion. This node is not
necessarily the node preceding node in the subpath of
the current driver. Indeed, we have previously speci-
fied that only profitable or transfer nodes are included
in the ReTAG graph. Some nodes of the driver’s trip
are omitted because they are not of interest to the
rider. It is therefore essential to have a variable such
as lastNode and to update it each time a node is added
(REDT, L16-21). Finally, the algorithm links by an
edge the subgraph resulting from the transfer with the
driver d with the subgraph of the current driver curD
on the transfer node node (REDT, L22).
It may happen that after having visited all the
nodes of the trip of the current driver curD, the al-
gorithm has not identified any interesting transfer for
the passenger. In this case, the algorithm looks for
the most profitable node of the driver and associates it
with the firstNode (REDT, L27-33). If no such node
exists, the driver and his path are naturally discarded
by both algorithms (ICRG, L5 and REDT, L11).
Once a rider agent has generated its ReTAG graph,
it searches for the path maximizing its profit by ap-
plying the objective function described in section 2.2.
The resolution is simplified because the rider only has
to find the path, i.e. the edge sequence, in the ReTAG
graph maximizing the sum of the differences of the
delay over the contribution.
5 EXPERIMENTS
This section details the framework of our simulation
and the results derived from it. We define the different
parameters used in the hitchhiking problem instance
and compare the naive hitchhiker with the hitchhiker
using the ReTAG approach.
5.1 Experimental Setup
Each of the two rider behaviors (naive and ReTAG)
is tested on 50 different instances and the resulting
data are averaged. An instance is composed of a route
Agent-based Modeling for Dynamic Hitchhiking Simulation and Optimization
327

graph, a set of driver agents and a set of rider agents.
For the generation of our route graph, we chose to
study a grid graph because many works use the city
of Manhattan for their experiments as (Alonso-Mora
et al., 2017) or (Tafreshian and Masoud, 2020). The
streets of this city are organized in a regular grid form
with some perturbations like parks for example. Thus,
after having generated our road graph in grid form, we
apply a perturbation to it. This perturbation consists
in randomly removing edges from the graph while
checking that the graph remains connected. The de-
parture and arrival nodes of the driver and rider agents
are randomly drawn.
We propose a simulation with a continuous gen-
eration of drivers while all the riders are generated at
the initialization of the instance and their number is
fixed beforehand.
5.2 A Simulation with a Continuous
Generation of Drivers
The simulation with a continuous generation of
drivers allows us to reproduce a real situation where
there is an incoming and outgoing flow of drivers in
the system. By varying the density of this flow we can
simulate a whole panel of road traffic and evaluate the
behaviors in situations of scarcity or abundance of the
ridesharing offer. The instance resolution ends when
all the rider agents have reached their destination.
In this simulation, we generate a road graph of 100
nodes perturbed on 30% of the edges to obtain a con-
vincing road graph. The number of rider agents gen-
erated is 100 and the density of the driver flow varies
between 25 and 225 in order to generate situations
of scarcity and abundance of ridesharing solutions for
the riders. In other words, during a simulation step
there cannot be more drivers than the defined flow
density. Each time a driver agent arrives at its des-
tination and dies, a new driver agent is generated.
The results of this simulation are presented in
Fig.3, Fig.4 and Fig.5. In these figures, the varia-
tion of the maximum number of drivers present in
the simulation for one simulation step, i.e. the max-
imum flow, is represented on the x-axis. The differ-
ent metrics studied, such as the average waiting time,
the average travel time and the number of simulation
steps are shown on the y-axis. Finally, the curves and
areas represent respectively the average values and
the standard deviation of the data resulting from the
application of the ReTAG (orange) and naive (blue)
rider behavior. These results show the efficiency of
the ReTAG passenger behavior compared to the naive
passenger behavior. Indeed, the average number of
simulation steps required for all the rider agents to
Figure 3: Number of simulation steps required to achieve
an instance according to the maximum number of drivers
and the rider behaviors: naive in blue, ReTAG in orange.
The lower the values, the better the result, as the target is to
minimize the number of steps.
Figure 4: Average travel time of rider agents according to
the maximum number of drivers and the rider behaviors:
naive in blue, ReTAG in orange.
arrive at their destination is reduced considerably as
shown in Fig.3. This reduction is more pronounced
when the flow of drivers is in a situation of scarcity,
i.e. for a maximum flow of drivers between 25 and
75 approximately. It is also in this interval that we
observe a shorter travel time for ReTAG riders than
for naive riders in the Fig.5. Once a maximum driver
flow of 150 is reached, the ReTAG passenger’s curve
stabilizes while the naive passenger’s curve continues
to decrease and consequently does better in terms of
travel time. This phenomenon can be explained by the
fact that a rider with ReTAG behavior does not only
consider the contribution of a ridesharing but also the
Figure 5: Average waiting time of riders according to the
maximum number of drivers and the rider behaviors: naive
in blue, ReTAG in orange.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
328

waiting time associated to each transfer. He therefore
favors motion over waiting, i.e., he prefers to make
detours that lengthen his trip than to stay in one place
and wait. This phenomenon is emerging and very in-
teresting because once a situation of solution abun-
dance is reached, ReTAG riders balance their travel
time against their waiting time, i.e. the components
of profit. The Fig.5 tends to confirm this justification
with an average waiting time of ReTAG passengers
lower than that of naive passengers regardless of the
maximum flow of drivers.
6 CONCLUSION
In this paper, we present a recursive algorithm named
ReTAG for solving and optimizing the hitchhiking
problem. We define the characteristics of this prob-
lem and propose an individual-centered simulation
using a multi-agent architecture to study it. A com-
parative study of two rider agent behaviors is per-
formed on more or less complex problem instances.
The first one simulating the behavior of a real hitch-
hiker, namely the naive hitchhiker, and the second one
simulating a hitchhiker connected to an information
system, namely the ReTAG hitchhicker. The results
of this study imply better performance for the ReTAG
hitchhiker and this in particular when the situation is
complex.
This study was designed as a framework for ad-
dressing the hitchhiking problem, which has been
only slightly studied in the past. It would therefore
be interesting to go deeper into the model by over-
coming the abstraction of time and space. Each edge
would then have a distance and a speed limit allowing
to calculate a realistic travel time for each trip. On the
other hand, the comparison with the slugging problem
(Ma and Wolfson, 2013), i.e. hitchhiking with meet-
ing places, can be very interesting to estimate the im-
pact of the concentration of demand and supply as a
means of connection.
REFERENCES
Agatz, N., Erera, A. L., Savelsbergh, M. W., and Wang,
X. (2011). Dynamic ride-sharing: a simulation study
in metro atlanta. Procedia - Social and Behavioral
Sciences, 17:532–550.
Alonso-Mora, J., Samaranayake, S., Wallar, A., Fraz-
zoli, E., and Rus, D. (2017). On-demand high-
capacity ride-sharing via dynamic trip-vehicle assign-
ment. Proceedings of the National Academy of Sci-
ences, 114(3):462–467.
Coltin, B. and Veloso, M. (2014). Ridesharing with pas-
senger transfers. In 2014 IEEE/RSJ International
Conference on Intelligent Robots and Systems, page
3278–3283.
Di Febbraro, A., Gattorna, E., and Sacco, N. (2013). Opti-
mization of dynamic ridesharing systems. Transporta-
tion Research Record: Journal of the Transportation
Research Board, 2359(1):44–50.
Fevre, C., Zgaya-Biau, H., Mathieu, P., and Hammadi,
S. (2021). Multi-agent systems and r-trees for dy-
namic and optimised ridesharing. In IEEE Interna-
tional Conference on Systems, Man, and Cybernetics,
page 1352–1358. in press.
Herbawi, W. and Weber, M. (2012a). Modeling the Mul-
tihop Ridematching Problem with Time Windows and
Solving It Using Genetic Algorithms, volume 1. jour-
nalAbbreviation: Proceedings - International Confer-
ence on Tools with Artificial Intelligence, ICTAI.
Herbawi, W. and Weber, M. (2012b). The ridematch-
ing problem with time windows in dynamic rideshar-
ing: A model and a genetic algorithm. 2012 IEEE
Congress on Evolutionary Computation, page 1–8.
Jeribi, K., Mejri, H., Zgaya, H., and Hammadi, S. (2011a).
Distributed graphs for solving co-modal transport
problems. In 2011 14th International IEEE Con-
ference on Intelligent Transportation Systems (ITSC),
page 1150–1155.
Jeribi, K., Mejri, H., Zgaya, H., and Hammadi, S.
(2011b). Vehicle sharing services optimization based
on multi-agent approach. IFAC Proceedings Volumes,
44(1):13040–13045.
Ma, S. and Wolfson, O. (2013). Analysis and evaluation
of the slugging form of ridesharing. In Proceedings
of the 21st ACM SIGSPATIAL International Confer-
ence on Advances in Geographic Information Systems
- SIGSPATIAL’13, page 64–73. ACM Press.
Mathieu, P. and Nongaillard, A. (2018). Effective evalua-
tion of autonomous taxi fleets. In ICAART (1), pages
297–304.
Nourinejad, M. and Roorda, M. J. (2016). Agent based
model for dynamic ridesharing. Transportation Re-
search Part C: Emerging Technologies, 64:117–132.
Pelzer, D., Xiao, J., Zehe, D., Lees, M. H., Knoll,
A. C., and Aydt, H. (2015). A partition-based match
making algorithm for dynamic ridesharing. IEEE
Transactions on Intelligent Transportation Systems,
16(5):2587–2598.
Tafreshian, A. and Masoud, N. (2020). Trip-based
graph partitioning in dynamic ridesharing. Trans-
portation Research Part C: Emerging Technologies,
114:532–553.
Xu, Y., Kulik, L., Borovica-Gajic, R., Aldwyish, A., and
Qi, J. (2020). Highly efficient and scalable multi-hop
ride-sharing. In Proceedings of the 28th International
Conference on Advances in Geographic Information
Systems, page 215–226. ACM.
Agent-based Modeling for Dynamic Hitchhiking Simulation and Optimization
329