Fair-Net: A Network Architecture for Reducing Performance Disparity

between Identiﬁable Sub-populations

Arghya Datta

1 a

and S. Joshua Swamidass

2 b

Department of Computer Science and Engineering, Washington University in Saint Louis, Saint Louis, U.S.A.

Department of Pathology and Immunology, Washington University School of Medicine in Saint Louis, Saint Louis, U.S.A.

Keywords:

Fairness, Classiﬁcation, Deep Learning, Neural Networks.

Abstract:

In real world datasets, particular groups are under-represented, much rarer than others, and machine learn-

ing classiﬁers will often preform worse on under-represented populations. This problem is aggravated across

many domains where datasets are class imbalanced, with a minority class far rarer than the majority class.

Naive approaches to handle under-representation and class imbalance include training sub-population speciﬁc

classiﬁers that handle class imbalance or training a global classiﬁer that overlooks sub-population disparities

and aims to achieve high overall accuracy by handling class imbalance. In this study, we ﬁnd that these ap-

proaches are vulnerable in class imbalanced datasets with minority sub-populations. We introduced Fair-Net,

a branched multitask neural network architecture that improves both classiﬁcation accuracy and probability

calibration across identiﬁable sub-populations in class imbalanced datasets. Fair-Nets is a straightforward

extension to the output layer and error function of a network, so can be incorporated in far more complex

architectures. Empirical studies with three real world benchmark datasets demonstrate that Fair-Net improves

classiﬁcation and calibration performance, substantially reducing performance disparity between gender and

racial sub-populations.

1 INTRODUCTION

Machine learning systems are widely used in a vari-

ety of tasks such as computer vision (LeCun et al.,

2010), natural language processing (Mikolov et al.,

2013), graphs (Matlock et al., 2019) as well as iden-

tifying causes and interventions for diseases (Datta

et al., 2020; Barnette et al., 2020; Datta et al., 2021a).

Decision-making systems, based on neural network

architectures, are widely used in many critical tasks

such as criminal justice (Zavr

snik, 2021), granting

loans (Turiel and Aste, 2020), skin cancer detec-

tion (Esteva et al., 2017) and face recognition (Mer-

ler et al., 2019). However, there have been grow-

ing concerns regarding the performance disparities

of these decision making systems across many sensi-

tive domains where there are under-represented sub-

populations in the underlying training dataset or ap-

plication domain.

Under-representation is when samples from a par-

ticular sub-population such as those based on gender

or race are rare. Under these circumstances, clas-

https://orcid.org/0000-0003-3543-3829

https://orcid.org/0000-0003-2191-0778

siﬁers tend to exhibit disparate performance, with

greater accuracy on the majority sub-populations than

the minority sub-populations. A previous case study

by Buolamwini et al. (Buolamwini and Gebru, 2018)

known as ”Gender Shades” highlighted noticeable

performance disparities in facial recognition systems

between male and female sub-populations for classiﬁ-

cation tasks. Even though these classiﬁcation systems

achieved more than 90% global classiﬁcation accu-

racy for gender detection, classiﬁcation accuracy was

much higher in light skinned individuals than dark-

skinned ones.

Numerous studies have been conducted that

highlight the problem of under-representation in

datasets (Kearns et al., 2019; Kim et al., 2019; Hardt

et al., 2016; Verma and Rubin, 2018). The prob-

lem of under-representation is even more challeng-

ing in presence of class imbalance. Class imbal-

ance occurs when samples from one class are far

more rare than the other. Classiﬁers are usually bi-

ased towards the majority class, thereby performing

poorly on the minority class. Since machine learn-

ing classiﬁers are commonly used in decision-making

systems, they should simultaneously be accurate as

Datta, A. and Swamidass, S.

Fair-Net: A Network Architecture for Reducing Performance Disparity between Identiﬁable Sub-populations.

DOI: 10.5220/0010877400003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 645-654

ISBN: 978-989-758-547-0; ISSN: 2184-433X

645

well as produce well calibrated probabilities. Pre-

dictions from a binary classiﬁer are said to be well-

calibrated if the outcomes predicted to occur with a

probability p occur p fraction of the time. Since clas-

siﬁers minimize error on training, it is often a com-

mon practise to assign high costs on misclassiﬁcations

on the minority class so as to maximize the classi-

ﬁcation performance on the minority class but over-

looking the calibration performance. Common para-

metric and non-parametric approaches such as Platt

scaling (Platt, 1999), isotonic regression (Zadrozny

and Elkan, 2002) and Bayesian binning into quan-

tiles (BBQ) (Pakdaman Naeini et al., 2015) are often

used to post-process classiﬁers’ outputs for probabil-

ity calibration. However, previous research (Huang

et al., 2020) has shown that the common paramet-

ric and non-parametric calibration techniques are of-

ten unstable on class imbalanced datasets. Even

though, a classiﬁer is trained and post-processed to

maximize classiﬁcation and calibration accuracy for

class imbalanced datasets, there may still be signiﬁ-

cant performance drops across under-represented sub-

populations present in the dataset population.

Little work has been done to develop neural net-

work architecture that jointly learns classiﬁcation

and calibration in under-represented sub-populations

while handling the skewed distribution of the mi-

nority and majority samples in class imbalanced

datasets. Recently, the Cal-Net neural network ar-

chitecture (Datta et al., 2021b) demonstrated simul-

taneous improvement in classiﬁcation and calibra-

tion performance on class imbalanced datasets. Here,

we aim to build on this architecture to improve pre-

dictive performance across multiple sub-populations

with Fair-Net: a neural network architecture that si-

multaneously optimizes classiﬁcation and calibration

performances across identiﬁable sub-populations in

the dataset population. Empirically, we ﬁnd that Fair-

Net achieves the best classiﬁcation and calibration

performances across diverse sub-populations of inter-

est.

2 RELATED WORK

Prior research works and methodologies that have

been proposed to handle class imbalance and proba-

bility calibration while improving classiﬁcation per-

formance across under-represented sub-populations

in datasets.

Previous research studies have proposed paramet-

ric and non-parametric post-processing probability

calibration techniques such as Platt scaling (Platt,

1999), isotonic regression (Zadrozny and Elkan,

2002), histogram binning (Zadrozny and Elkan, 2001)

and bayesian binning into quantiles (BBQ) (Pak-

daman Naeini et al., 2015). The post-processing cali-

bration techniques utilize a holdout validation dataset

for re-scaling the base classiﬁers’ outputs to improve

calibration performance thereby reducing the effec-

tive number of sampling for training the base classi-

ﬁer. In datasets where the number of samples is low,

this may often lead to under-trained classiﬁers.

Class imbalance is a widespread challenge in ma-

chine learning and previous studies have proposed

several strategies to mitigate this problem. Sam-

pling is a common approach to mitigate class im-

balance. Common sampling strategies include over-

sampling (Ling and Li, 1998), where samples from

the minority class is re-sampled randomly to elimi-

nate the skewness from the data distribution. Sim-

ilarly, under-sampling (Kubat and Matwin, 1997)

eliminates samples from the majority class randomly

to match the distribution of the minority class. Meth-

ods such as synthetic minority over-sampling tech-

nique (SMOTE) (Chawla et al., 2002) has been pro-

posed that removes the skewness from the imbal-

anced data distributions by generating synthetic mi-

nority class samples. Cost-sensitive learning (Domin-

gos, 1999; Elkan, 2001) and sample weighting(Ting,

1998) are commonly used to assign high weights to

samples from the minority class by modifying the ob-

jective function. Even though sampling strategies are

widely used for managing class imbalance, there are

well-known pitfalls such as overﬁtting (Holte et al.,

1989) due to over-sampling as well as information

loss (Tang et al., 2009) and inducing bias in calibra-

tion due to under-sampling (Dal Pozzolo et al., 2015).

A naive approach to address challenges in pre-

dictive modeling across sub-populations of interest

in a dataset is to train a separate classiﬁer on each

sub-population of interest while simultaneously us-

ing previously proposed strategies to handle class im-

balance. We have included this approach as a base-

line in our study. We ﬁnd that this approach per-

forms poorly in minority sub-populations where only

a small number of samples are available to train

sub-population speciﬁc classiﬁers. To overcome this

shortcoming, branched neural network architectures

can be used where each branch is trained on different

sub-populations so as to improve the predictive per-

formance for that speciﬁc sub-population. In our ab-

lation studies, we have showed that this approach does

not simultaneously achieve the best classiﬁcation and

calibration performances in minority sub-populations

in class imbalanced datasets. Previous research stud-

ies have proposed methodologies (Kearns et al., 2019;

Kim et al., 2019) to improve classiﬁcation accuracy

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

646

across sub-populations as well as various deﬁnitions

of fairness such as equalized odds and equal opportu-

nity (Hardt et al., 2016), demographic parity (Verma

and Rubin, 2018) etc. Our deﬁnition of fairness is dif-

ferent from parity based notions (Hardt et al., 2016;

Verma and Rubin, 2018). Instead, we increase fair-

ness by reducing disparity in classiﬁcation and cali-

bration performance across sub-populations. Dispar-

ity is deﬁned as the variance of performance across

identiﬁable sub-populations of interest in class imbal-

anced datasets.

3 MATERIALS & METHODS

3.1 The Fair-Net Architecture

The Fair-Net architecture expands the Cal-Net archi-

tecture, which aimed to improve calibration on imbal-

anced datasets (Datta et al., 2021b). Like the Cal-Net

architecture, the Fair-Net architecture transforms the

binary classiﬁcation problem into a multi-task prob-

lem using two outputs (Figure 1). The primary out-

put (Y ) is tuned to produce well-scaled probabilities,

whereas the secondary output (Y

) is utilized only dur-

ing the training phase to maximize the classiﬁcation

performance by upweighting samples from the minor-

ity class to be equally prevalent as samples from the

majority class.

Mirroring Cal-Net , the primary (Y ) and secondary

) outputs in Fair-Nets, computed using logistic ac-

tivation functions, are computed from a hidden layer

(H) with a single node. This structure ensures that

the neural network architecture enforces a monotonic

relationship between the primary and the secondary

outputs. Both the outputs are monotonic functions of

a single number H so they are monotonic transforma-

tions of each other.

We have introduced two broad variants of Fair-

Nets: “Fair-Net Branched” and “Fair-Net Un-

Branched”. In the ﬁrst variant, ”Fair-Net Branched”

trains a different “branch” consisting of a primary out-

put (Y ) and a secondary output (Y

), computed using a

single hidden node H, for each sub-population of in-

terest. The primary output (Y ) in a “branch” is tuned

to produce well-calibrated probabilities, whereas the

secondary output (Y

) is tuned to maximize classi-

ﬁcation performance by upweighting samples from

the minority class in the sub-population to be equally

prevalent as samples from the majority class for that

sub-population. This modiﬁcation requires six train-

able parameters in total, with three weights and three

biases for each sub-population of interest. Thus, each

branch is tuned to maximize the classiﬁcation and cal-

Figure 1: Different variants of Fair-Nets. Fair-Net Branched

trains a different branch for each sub-population, whereas

Fair-Net Un-Branched computes the total loss by summing

over losses for each sub-population of interest.

ibration performances for each sub-population of in-

terest at the cost of more trainable parameters.

In the second variant, “Fair-Net Un-Branched,” a

single “branch” consisting of a primary output (Y )

and a secondary output (Y

), computed from a single

hidden node H, is tuned to maximize the classiﬁca-

tion and calibration performance across all the sub-

populations of interest. Unlike the variant “Fair-Net

Branched”, the variant “Fair-Net Un-Branched” does

not result in additional trainable parameters for each

sub-population of interest.

3.2 Loss Components

All the variants of Fair-Nets make use of the same loss

components used by Cal-Net (Datta et al., 2021b).

The primary output, Y = {y

g,i

}, indexed by in-

stance, i, in sub-population, g, for both “Fair-Net

Branched” and “Fair-Net Un-Branched” utilize a lo-

gistic activation function. The loss component for

each sub-population, g, are computed based on this

output and the target class labels T = {t

g,i

The ﬁrst loss component, L

X,g

, is the binary cross

entropy error between Y and T for sub-population

g. The instances in the majority class for each sub-

population contribute more to the loss in class imbal-

anced datasets.

The second loss component, L

B,g

, computes the

balanced cross-entropy loss for each sub-population,

g, between T and Y

. Instances from the minor-

Fair-Net: A Network Architecture for Reducing Performance Disparity between Identiﬁable Sub-populations

647

ity class for each sub-population is upweighted to be

equally prevalent as samples from the majority class

for that sub-population. In all the variants of Fair-

Nets, the majority (negatives) class samples in sub-

population g are weighted as N

/2n

and the minor-

ity (positives) class samples are weighted as N

/2p

where N

is the number of samples in sub-population

g and p

and n

are the number of samples in the

minority (positives) and majority (negatives) classes,

respectively. This weighting scheme ensures that

for each sub-population g, the minority and majority

classes are weighed equally.

The total loss function (L) for Fair-Net Branched

and Fair-Net Un-Branched is computed as,

L =

∑

g∈G

· [L

X,g

+ L

B,g

], (1)

where G is the set of all sub-populations of interest

and λ

is a hyper-parameter that can be tuned to assign

higher mis-classiﬁcation costs for sub-population g.

In all our experiments, λ

= 1 for all sub-populations.

We also use the histogram loss from Cal-Net

(Datta et al., 2021b) on the primary output Y for gen-

erating well scaled-probabilities. In a well-calibrated

probabilistic model for binary classiﬁcation tasks, the

proportion of positive examples in each bin of a reli-

ability diagram should match the average of the pre-

dictions for the bin, which is usually close to the mid-

point of the bin. Hence, the histogram loss, L

H,g

for

each sub-population g is computed as the RMSE be-

tween the proportion positives and the midpoints of

the bin.

The total loss function (L) for Fair-Net Branched

[histogram loss] and Fair-Net Un-Branched [his-

togram loss] is computed as,

L =

∑

g∈G

· [L

X,g

+ L

B,g

+ λ

H,g

] (2)

where L

H,g

is the histogram loss for sub-population

g and λ

H,g

is a hyper-parameter that can be used to

tune L

H,g

. Other formulations of the histogram loss

may be effective, but exploring them is left for future

work. Empirical analyses show that all the loss com-

ponents are necessary to optimize classiﬁcation and

calibration across under-represented sub-populations

in class imbalanced scenarios.

3.3 Datasets

For our experiments, we used three datasets namely

(Table 1): (1) Propublica COMPAS dataset (Kirch-

ner and Angwin, 2017) (2) UCI credit card default

dataset (Yeh and hui Lien, 2009) and (3) UCI adult

census dataset (Kohavi, 1996).

• Propublica COMPAS dataset: We used a smaller

subset of the propublica COMPAS dataset (Kirch-

ner and Angwin, 2017) consisting of 6172 in-

stances with 5 features. A binary target variable

indicated if an individual would re-offend within

the next two years. We used the gender variable to

consider two sub-populations namely: Female (F)

and Not Female (NF). The imbalance ratios of the

target variable in F and NF sub-populations were

1.8 and 1.08 respectively.

• UCI credit card default dataset: The credit card

default dataset (Yeh and hui Lien, 2009) from

UCI (Dua and Graff, 2020) repository consists

of 30,000 instances with 23 features. The bi-

nary target variable indicated whether an individ-

ual would incur a default payment or not. We have

considered two sub-populations based on gender

namely: Male (M) and Female(F). The imbalance

ratios for the target variable for M and F sub-

populations are 3.14 and 3.81 respectively.

• UCI Adult Census dataset: The adult census

dataset (Kohavi, 1996) from UCI (Dua and Graff,

2020) repository consists of 48,842 instances with

14 features and a binary target variable that indi-

cated if an individual earned more than $50, 000

or not. After removing samples with missing val-

ues, 45,222 samples were used for the analyses.

We have considered 8 sub-populations based on

gender and race namely: Male (M), Female (F),

Black (B), White (W), Black Male (BM), Black

Female (BF), White Male (WM) and White Fe-

male (WF).

3.4 Training and Evaluation Protocol

We evaluated the variants of Fair-Nets and baseline

models for probability calibration performance and

classiﬁcation accuracy using a stratiﬁed train, valida-

tion and test split. For each dataset, we kept a strat-

iﬁed split of the dataset as a test set(20 − 25% of the

dataset) such that the percentages of sub-populations

and the imbalance ratios for each sub-population are

preserved across train, validation and test sets. Since

most of these datasets have a low number of samples

for the minority sub-populations, this strategy ensured

that sufﬁcient minority samples are present in all the

splits. For our experiments, we trained the variants of

Fair-Nets with a single hidden layer of 5 units with

exponential linear unit (ELU) activation and L2 regu-

larization.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

648

3.5 Baselines

As a baseline for comparison with different variants

of Fair-Nets, we trained neural network (NN) archi-

tectures with one ELU activated hidden layer consist-

ing of 10 hidden units. We used balanced cross en-

tropy loss to train these neural network architectures

such that the samples from the minority class are up-

weighted to be equally prevalent as samples from the

majority class. Balanced cross entropy loss usually

improves the classiﬁcation performance in class im-

balanced datasets (Johnson and Khoshgoftaar, 2019).

Also, we trained neural network architectures us-

ing the same architecture (one hidden layer with 10

ELU activated hidden units) for each sub-population

of interest using balanced cross-entropy losses. Fi-

nally, we trained Cal-Net architectures with one hid-

den layer consisting of 5 hidden units with ELU acti-

vation. For our case studies, all the variants of Fair-

Nets usually had less number of trainable parame-

ters than the baseline NN [balanced xent] and sub-

population speciﬁc baselines.

3.6 Assessment Metrics

We evaluate the predictive performance of Fair-

Nets and the associated baselines on different sub-

populations by reporting the maximum F-measure

and area under the receiver operating characteris-

tic (ROC AUC). Previous research work (Davis and

Goadrich, 2006) has shown that ROC AUC is often

unreliable in class imbalanced datasets. On the con-

trary, F-measure is a commonly used metric to sum-

marize classiﬁcation performance in class imbalanced

datasets. We highlight the imbalance ratio (IR), calcu-

lated as

, where n

is the number of minority (posi-

tives) samples and n

is the number of majority (nega-

tives) samples across different sub-populations of in-

terest in the datasets. In order to summarize the cal-

ibration performance of Fair-Nets and the associated

baselines, we have reported the expected calibration

error (ECE) (Pakdaman Naeini et al., 2015; K

uppers

et al., 2020) and utilized reliability diagrams (DeG-

root and Fienberg, 1983). A classiﬁer that achieves

higher F-measure and higher AUROC along with

lower ECE across different sub-populations of inter-

est is preferred.

Table 1: Class Imbalance statistics for real world datasets.

Dataset Size % +ve IR

COMPAS 6172 45.5 1.2

Credit default 30000 22.12 3.52

Census income 45222 24.78 3

4 RESULTS & DISCUSSION

4.1 Propublica COMPAS Dataset

Fair-Net variants outperformed the baselines on the

Propublica COMPAS dataset in classiﬁcation and cal-

ibration performances both on the overall population

as well as on the different sub-populations of inter-

est (Figure 2). For the F sub-population, the IR for

the target variable was 1.8 , which was higher than

that of the overall sub-population. Fair-Net variants

outperformed the baselines on the F sub-population

in predictive performance by achieving the highest

F-measure while simultaneously achieving the low-

est ECE, thereby improving the calibration perfor-

mance. Both the variants of Fair-Net Branched out-

performed the variants of Fair-Net Un-Branched in

classiﬁcation performance owing to a greater num-

ber of available trainable parameters. For both Fair-

Nets Branched and Fair-Nets Un-Branched variants,

the inclusion of the histogram loss helped in improv-

ing calibration performance by reducing ECE. This

highlights the potential beneﬁt of incorporating his-

togram loss to further improve the calibration perfor-

mance across sub-populations. Sub-population spe-

ciﬁc baseline models, trained exclusively for each

sub-population of interest, usually exhibited poor pre-

dictive performance due to the availability of a lower

number of samples in the training dataset. As empir-

ically shown, all the variants of Fair-Nets improved

predictive performance in the under-represented F

sub-population with a high IR than the overall pop-

ulation.

4.2 UCI Credit Card Default Dataset

All the variants of Fair-Nets outperformed the base-

lines in classiﬁcation and calibration performance on

the overall population while simultaneously improv-

ing predictive performances across M and F sub-

populations (Figure 2). We observed similar trends

in this case study as well where both the variants of

Fair-Net Branched outperformed the variants of Fair-

Net Un-Branched at the cost of more trainable param-

eters. Both the variants of Fair-Nets with histogram

loss outperformed the corresponding variants without

histogram loss in calibration performance by achiev-

ing lower ECE scores. All the variants of Fair-Nets

improved the predictive performance in the under-

represented M sub-population in the dataset.

Fair-Net: A Network Architecture for Reducing Performance Disparity between Identiﬁable Sub-populations

649

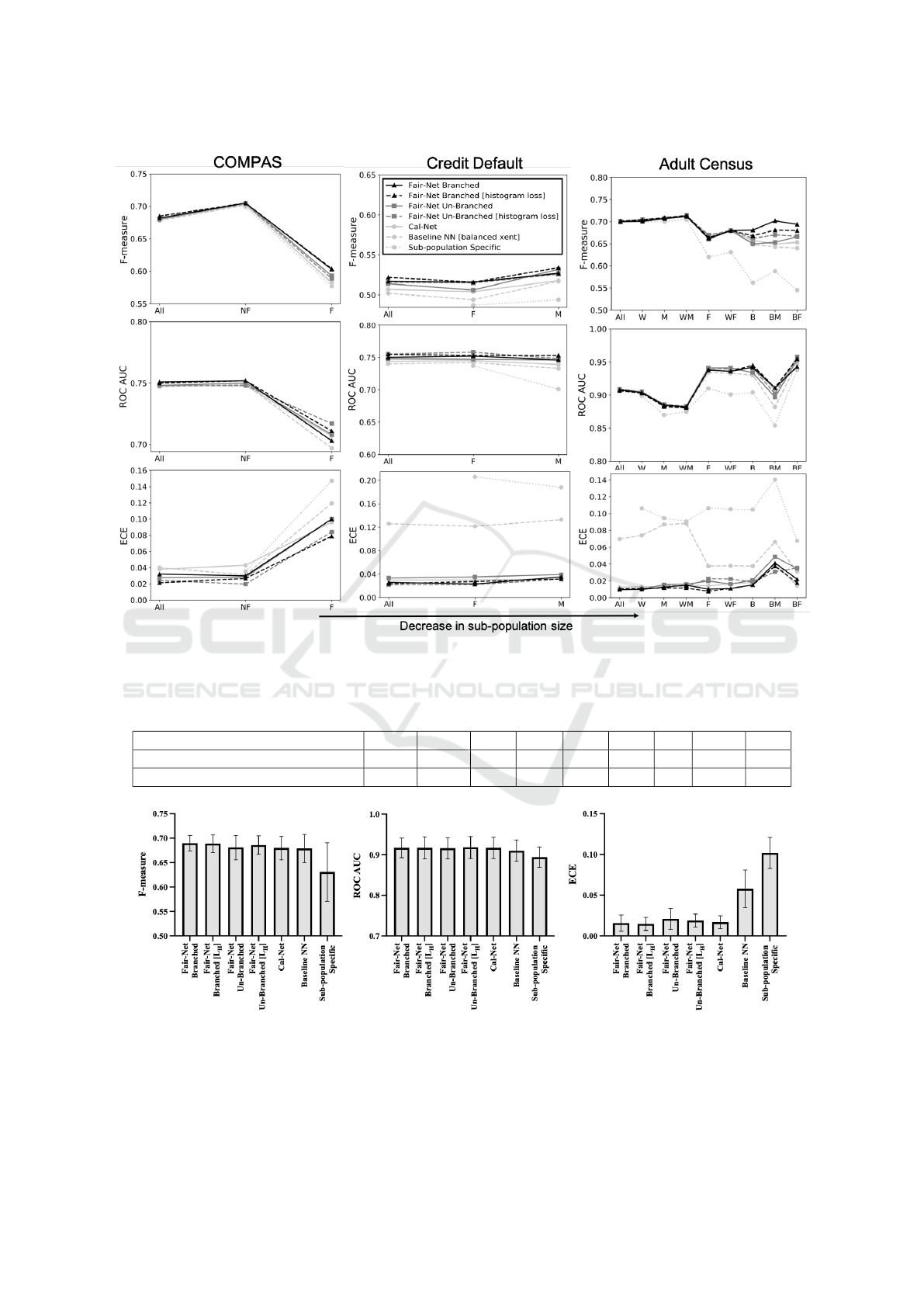
Figure 2: On the benchmark datasets, variants of Fair-Net achieved the best predictive performance in terms of F-measure,

ROC-AUC and ECE across different sub-populations of interest.

Table 2: Comparing performance of Fair-Net with published results in the literature such as Multi-accuracy (Kim et al., 2019)

on similar, but not identical, test dataset.

all W M WM F WF B BM BF

Fair-Net Branched 16.29 17.09 20.1 21.7 7.67 7.95 9.5 13.25 3.83

Multi-Accuracy (Kim et al., 2019) 14.7 15 18.3 18.3 7.2 7.3 9.4 13.9 4.5

Figure 3: Variants of Fair-Net achieved the best predictive performance (high F-measure and ROC AUC alongside low ECE)

with lowest variance across identiﬁable sub-populations of interest for the adult census dataset (Kohavi, 1996). L

refers to

the histogram loss.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

650

4.3 UCI Adult Census Dataset

Similar to the prior two case studies, variants of

Fair-Nets achieved the best classiﬁcation and calibra-

tion performance across different sub-populations in

the adult census dataset (Kohavi, 1996). Eight sub-

populations were considered in this case study: Male

(M), Female (F), Black (B), White (W), Black Male

(BM), Black Female (BF), White Male (WM) and

White Female (WF). Out of all these sub-populations,

B, BM and BF sub-populations were the most under-

represented, accounting for less than 10% of the over-

all population. Furthermore, the IR values across B,

BM and BF sub-populations are 6.8, 4.26 and 14.7

respectively. Empirical results (Figure 2) showed

that the variants of Fair-Nets outperformed the base-

lines across all the eight sub-populations as well

as on the overall population in classiﬁcation and

calibration performances. Moreover, the improve-

ments in classiﬁcation performance for the variants

of Fair-Nets were noticeable in the B, BM and BF

subpopulations, where, all the variants of Fair-Nets

outperformed the baselines by achieving higher F-

measure and ROC AUC and lower ECE. The base-

line neural network, trained using balanced cross en-

tropy loss for the overall population, achieved sim-

ilar classiﬁcation performance to Fair-Nets in the

majority sub-populations but incurred drops in F-

measure in the under-represented sub-populations

such as B, BM and BF. The sub-population spe-

ciﬁc baseline models, trained exclusively on differ-

ent sub-populations, performed poorly in the under-

represented sub-populations with high class imbal-

ances owing to a shortage in training samples. On

the contrary, branched variants of Fair-Net achieved

signiﬁcantly higher predictive performance by adding

six trainable parameters (three weight variables and

three bias variables) for each sub-population of inter-

est, whereas the un-branched variants of Fair-Nets did

not add any additional trainable parameters for differ-

ent sub-populations of interest. The branched vari-

ants of Fair-Net outperformed the un-branched vari-

ants in predictive performance due to the availabil-

ity of more trainable parameters in the neural net-

work architecture. Furthermore, the average classiﬁ-

cation and calibration performances of Fair-Net vari-

ants across different sub-populations are higher than

the baselines with low standard deviation (Figure 3).

This suggests that Fair-Nets do not incur any sub-

stantial performance drops in under-represented sub-

populations with high class imbalance ratios. Fi-

nally, the classiﬁcation error (%) across different sub-

populations for the Fair-Net variants are compara-

ble with prior published work by Kim et al. (Kim

et al., 2019). We observed that Fair-Net Branched

achieved lower classiﬁcation error (Table 2), suggest-

ing that Fair-Nets achieve the best predictive accu-

racy in the under-represented sub-populations for the

adult census dataset. However, we note that clas-

siﬁcation error(%) is a poor metric in class imbal-

anced sub-populations since a classiﬁer with low clas-

siﬁcation error (%) may not achieve high F-measure

and performs substantially worse in class imbalanced

datasets (Luque et al., 2019).

4.4 Ablation Analyses

Ablation analyses demonstrated the importance of

different components in the Fair-Net’s architecture.

We trained multi-task neural network architectures

that resembled variants of Fair-Net Branched by re-

moving (1) the primary output Y and (2) the sec-

ondary output Y

from each of the sub-population

heads in Fair-Net’s architecture to evaluate whether

the classiﬁcation and calibration performances are af-

fected. For the ablation analyses, we focused on the

adult census dataset (Kohavi, 1996) since it contains

sub-populations with a diverse range of samples and

imbalance ratios.

4.4.1 With and without Primary Output Y for

Each Sub-population

We trained a modiﬁed architecture without the pri-

mary output Y from every sub-population network

head. Thus, the Fair-Net architecture was reduced to

a branched neural network architecture, where each

branch was trained on a different sub-population us-

ing a balanced cross-entropy loss. The balanced

cross-entropy loss upweighted minority class samples

to be equally prevalent as samples from the majority

class for each sub-population. Empirical results (Fig-

ure 4) showed that this modiﬁed architecture incurred

a drop in classiﬁcation performance across minority

sub-populations such B, BM and BF. Moreover, we

observed that this architecture had poor calibration

performance (Figure 4) when compared to a standard

Fair-Net architecture with a primary output Y for each

sub-population. Post-processing this modiﬁed archi-

tecture’s outputs using parametric and non-parametric

calibration techniques may improve the calibration

performance. The standard Fair-Net Branched archi-

tecture continued to achieve the best overall classi-

ﬁcation and calibration performances across all the

sub-populations of interest.

Fair-Net: A Network Architecture for Reducing Performance Disparity between Identiﬁable Sub-populations

651

Figure 4: Ablation analyses demonstrating different com-

ponents of Fair-Net are essential to improve classiﬁcation

and calibration performances for the adult census income

dataset (Kohavi, 1996).

4.4.2 With and without Secondary Output Y

for

Each Sub-population

We trained a modiﬁed architecture after eliminat-

ing the secondary output Y

from each of the sub-

population branches. This essentially reduced the

Fair-Net architecture to a branched neural network ar-

chitecture, where a separate network head was trained

for each sub-population using non-weighted cross-

entropy loss. Hence, samples from both the majority

(negatives) and the minority (positives) classes were

weighted equally. The multi-task architecture with-

out the secondary output Y

for each sub-population

produced well calibrated probabilities. However, it

achieved the lowest classiﬁcation performance across

all the under-represented sub-populations. In the stan-

dard Fair-Net architecture, the secondary output Y

was trained using a balanced cross-entropy loss so

that samples from the minority class were upweighted

to be equally prevalent as samples from the majority

class belonging to the same sub-population thereby

improving classiﬁcation performance. We hypothe-

sized that this modiﬁed architecture without the sec-

ondary output Y

would be comparatively weaker

than the standard Fair-Net architecture in classiﬁca-

tion performance.

Empirically, we observed that there were drops in

classiﬁcation performance of this modiﬁed architec-

ture across B, BM and BF sub-populations in terms

of F-measure and ROC-AUC (Figure 4). As evident

from the distribution of these sub-populations in the

dataset, B, BM and BF had very few samples with

a high class imbalance ratio when compared to other

sub-populations. Hence, we concluded that the sec-

ondary output Y

is necessary to improve the classi-

ﬁcation performance across minority sub-populations

with high class imbalance ratios. Both the variants of

Fair-Net Branched continued to achieve the best clas-

siﬁcation and calibration performances across all the

sub-populations of interest.

4.4.3 With and without Histogram Loss (L

)

We introduced two variants of Fair-Nets that used the

histogram loss (Datta et al., 2021b). Our case studies

across COMPAS data, credit card default dataset and

adult census dataset showed that the variants of Fair-

Nets trained using histogram loss often outperformed

the corresponding variants of Fair-Nets without the

histogram loss by achieving lower ECE scores. This

suggests that optimizing on the histogram loss may

result in improved calibration performance. There

may be other formulations for the histogram loss and

fully exploring options is left for future studies.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

652

4.5 Study Limitations & Future

Directions

The proposed modeling framework requires that all

sub-populations are identiﬁable from the outset. We

explicitly identify each sub-populations in training

the model, summing over the losses for each sub-

population. Hence, our modeling framework needs

access to the features that were used to identify these

sub-populations of interest. In our study, the sec-

ondary output Y

equally weighs the minority and

the majority samples for each sub-population. How-

ever, upweighting the minority samples using a higher

weight may yield better results in class imbalanced

scenarios. In general, neural network architectures

may often exhibit poor predictive performance and

generalization due to unavailability in training data

for under-represented sub-populations (Cui et al.,

2015). As a result, variants of Fair-Net may exhibit

degraded performance in the absence of enough train-

ing data. In our case studies, we weighted each sub-

population of interest equally by setting λ

as 1 for

all g ∈ G. However, upweighting under-represented

or minority sub-populations may result in improved

predictive performance in these subpopulations and

exploring options is left for future work. Exploiting

multi-task architectures may prove to be an effective

way to improve predictive performance across these

sub-populations, as evident in our study.

5 CONCLUSION

In this work, we have introduced Fair-Net, a class

of neural network architectures that simultaneously

improved classiﬁcation and calibration performances

across diverse sub-populations of interest in class im-

balanced datasets. Empirically, we showed that the

variants of Fair-Net outperformed commonly used

neural network architectures by achieving higher F-

measure, ROC-AUC and low ECE across differ-

ent sub-populations of interest in three real world

datasets: UCI Credit card default dataset, UCI Adult

census dataset and Propublica COMPAS datasets.

Due to its simplicity, Fair-Nets can readily be incor-

porated in complex network architectures as the ﬁnal

layer to improve predictive performance across sub-

populations of interest.

ACKNOWLEDGEMENT

This research was supported by the National Library

of Medicine of the National Institutes of Health under

award numbers R01LM012222 and R01LM012482

and the National Institute of General Medical Sci-

ences under award number R01GM140635.

REFERENCES

Barnette, D. A., Schleiff, M. A., Datta, A., Flynn, N.,

Swamidass, S. J., and Miller, G. P. (2020). Meloxi-

cam methyl group determines enzyme speciﬁcity for

thiazole bioactivation compared to sudoxicam. Toxi-

col. Lett.

Buolamwini, J. and Gebru, T. (2018). Gender shades: In-

tersectional accuracy disparities in commercial gender

classiﬁcation. In Friedler, S. A. and Wilson, C., edi-

tors, Proceedings of the 1st Conference on Fairness,

Accountability and Transparency, volume 81 of Pro-

ceedings of Machine Learning Research, pages 77–

91, New York, NY, USA. PMLR.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,

W. P. (2002). Smote: Synthetic minority over-

sampling technique. J. Artif. Int. Res., 16(1):321–357.

Cui, X., Goel, V., and Kingsbury, B. (2015). Data aug-

mentation for deep neural network acoustic modeling.

IEEE/ACM Transactions on Audio, Speech, and Lan-

guage Processing, 23(9):1469–1477.

Dal Pozzolo, A., Caelen, O., and Bontempi, G. (2015).

When is undersampling effective in unbalanced clas-

siﬁcation tasks? In Appice, A., Rodrigues, P. P., San-

tos Costa, V., Soares, C., Gama, J., and Jorge, A., ed-

itors, Machine Learning and Knowledge Discovery in

Databases, pages 200–215, Cham. Springer Interna-

tional Publishing.

Datta, A., Flynn, N. R., Barnette, D. A., Woeltje, K. F.,

Miller, G. P., and Swamidass, S. J. (2021a). Ma-

chine learning liver-injuring drug interactions with

non-steroidal anti-inﬂammatory drugs (nsaids) from

a retrospective electronic health record (ehr) cohort.

PLOS Computational Biology, 17(7):1–24.

Datta, A., Flynn, N. R., and Swamidass, S. J. (2021b).

Cal-net: Jointly learning classiﬁcation and calibration

on imbalanced binary classiﬁcation tasks. In 2021

International Joint Conference on Neural Networks

(IJCNN), pages 1–8.

Datta, A., Matlock, M. K., Dang, N. L., Moulin, T., Woeltje,

K. F., Yanik, E. L., and Swamidass, S. J. (2020).

”black box” to ”conversational” machine learning:

Ondansetron reduces risk of hospital-acquired venous

thromboembolism. IEEE Journal of Biomedical and

Health Informatics, pages 1–1.

Davis, J. and Goadrich, M. (2006). The relationship be-

tween precision-recall and roc curves. In Proceed-

ings of the 23rd International Conference on Machine

Learning, ICML ’06, page 233–240, New York, NY,

USA. Association for Computing Machinery.

DeGroot, M. H. and Fienberg, S. E. (1983). The com-

parison and evaluation of forecasters. Journal of the

Royal Statistical Society. Series D (The Statistician),

32(1/2):12–22.

Domingos, P. (1999). Metacost: A general method for

making classiﬁers cost-sensitive. In Proceedings of

the Fifth ACM SIGKDD International Conference on

Fair-Net: A Network Architecture for Reducing Performance Disparity between Identiﬁable Sub-populations

653

Knowledge Discovery and Data Mining, KDD ’99,

page 155–164, New York, NY, USA. Association for

Computing Machinery.

Dua, D. and Graff, C. (2020). UCI machine learning repos-

itory.

Elkan, C. (2001). The foundations of cost-sensitive learn-

ing. In In Proceedings of the Seventeenth Inter-

national Joint Conference on Artiﬁcial Intelligence,

pages 973–978.

Esteva, A., Kuprel, B., Novoa, R. A., Ko, J., Swetter, S. M.,

Blau, H. M., and Thrun, S. (2017). Dermatologist-

level classiﬁcation of skin cancer with deep neural net-

works. Nature, 542(7639):115–118.

Hardt, M., Price, E., and Srebro, N. (2016). Equality of op-

portunity in supervised learning. In Proceedings of the

30th International Conference on Neural Information

Processing Systems, NIPS’16, page 3323–3331, Red

Hook, NY, USA. Curran Associates Inc.

Holte, R. C., Acker, L. E., and Porter, B. W. (1989). Con-

cept learning and the problem of small disjuncts. In

Proceedings of the 11th International Joint Confer-

ence on Artiﬁcial Intelligence - Volume 1, IJCAI’89,

page 813–818, San Francisco, CA, USA. Morgan

Kaufmann Publishers Inc.

Huang, L., Zhao, J., Zhu, B., Chen, H., and Broucke,

S. V. (2020). An experimental investigation of cali-

bration techniques for imbalanced data. IEEE Access,

8:127343–127352.

Johnson, J. M. and Khoshgoftaar, T. M. (2019). Survey on

deep learning with class imbalance. Journal of Big

Data, 6(1):27.

Kearns, M., Neel, S., Roth, A., and Wu, Z. (2019). An

empirical study of rich subgroup fairness for machine

learning. Proceedings of the Conference on Fairness,

Accountability, and Transparency.

Kim, M. P., Ghorbani, A., and Zou, J. Y. (2019). Multiaccu-

racy: Black-box post-processing for fairness in classi-

ﬁcation. In Conitzer, V., Hadﬁeld, G. K., and Vallor,

S., editors, Proceedings of the 2019 AAAI/ACM Con-

ference on AI, Ethics, and Society, AIES 2019, Hon-

olulu, HI, USA, January 27-28, 2019, pages 247–254.

ACM.

Kirchner, J. L. S. M. L. and Angwin, J. (2017). Compas

dataset.

Kohavi, R. (1996). Scaling up the accuracy of naive-bayes

classiﬁers: a decision-tree hybrid. Proceedings of the

Second International Conference on Knowledge Dis-

covery and Data Mining.

uppers, F., Kronenberger, J., Shantia, A., and Haselhoff,

A. (2020). Multivariate conﬁdence calibration for ob-

ject detection. In The IEEE/CVF Conference on Com-

puter Vision and Pattern Recognition (CVPR) Work-

shops.

Kubat, M. and Matwin, S. (1997). Addressing the curse

of imbalanced training sets: One-sided selection. In

ICML.

LeCun, Y., Kavukcuoglu, K., and Farabet, C. (2010). Con-

volutional networks and applications in vision. In

2010 IEEE International Symposium on Circuits and

Systems (ISCAS), pages 253–256.

Ling, C. X. and Li, C. (1998). Data mining for direct

marketing: Problems and solutions. In Proceedings

of the Fourth International Conference on Knowledge

Discovery and Data Mining, KDD’98, page 73–79.

AAAI Press.

Luque, A., Carrasco, A., Mart

ın, A., and de las Heras, A.

(2019). The impact of class imbalance in classiﬁca-

tion performance metrics based on the binary confu-

sion matrix. Pattern Recognition, 91:216–231.

Matlock, M. K., Datta, A., Dang, N. L., Jiang, K., and

Swamidass, S. J. (2019). Deep learning long-range

information in undirected graphs with wave networks.

In 2019 International Joint Conference on Neural Net-

works (IJCNN), pages 1–8.

Merler, M., Ratha, N., Feris, R. S., and Smith, J. R. (2019).

Diversity in faces. arXiv preprint arXiv:1901.10436.

Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and

Dean, J. (2013). Distributed representations of words

and phrases and their compositionality. In Burges, C.

J. C., Bottou, L., Welling, M., Ghahramani, Z., and

Weinberger, K. Q., editors, Advances in Neural In-

formation Processing Systems 26, pages 3111–3119.

Curran Associates, Inc.

Pakdaman Naeini, M., Cooper, G., and Hauskrecht, M.

(2015). Obtaining well calibrated probabilities using

bayesian binning. Proceedings of the ... AAAI Con-

ference on Artiﬁcial Intelligence. AAAI Conference on

Artiﬁcial Intelligence, 2015:2901–2907.

Platt, J. C. (1999). Probabilistic outputs for support vector

machines and comparisons to regularized likelihood

methods. In ADVANCES IN LARGE MARGIN CLAS-

SIFIERS, pages 61–74. MIT Press.

Tang, Y., Zhang, Y., Chawla, N. V., and Krasser, S. (2009).

Svms modeling for highly imbalanced classiﬁcation.

IEEE Transactions on Systems, Man, and Cybernet-

ics, Part B (Cybernetics), 39(1):281–288.

Ting, K. M. (1998). Inducing cost-sensitive trees via in-

stance weighting. In

Zytkow, J. M. and Quafafou,

M., editors, Principles of Data Mining and Knowl-

edge Discovery, pages 139–147, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Turiel, J. D. and Aste, T. (2020). Peer-to-peer loan ac-

ceptance and default prediction with artiﬁcial intelli-

gence. Royal Society Open Science, 7(6):191649.

Verma, S. and Rubin, J. (2018). Fairness deﬁnitions ex-

plained. In 2018 IEEE/ACM International Workshop

on Software Fairness (FairWare), pages 1–7.

Yeh, I.-C. and hui Lien, C. (2009). The comparisons of

data mining techniques for the predictive accuracy of

probability of default of credit card clients. Expert

Systems with Applications, 36(2, Part 1):2473–2480.

Zadrozny, B. and Elkan, C. (2001). Obtaining calibrated

probability estimates from decision trees and naive

bayesian classiﬁers. In Proceedings of the Eigh-

teenth International Conference on Machine Learn-

ing, ICML ’01, page 609–616, San Francisco, CA,

USA. Morgan Kaufmann Publishers Inc.

Zadrozny, B. and Elkan, C. (2002). Transforming classiﬁer

scores into accurate multiclass probability estimates.

In Proceedings of the Eighth ACM SIGKDD Interna-

tional Conference on Knowledge Discovery and Data

Mining, KDD ’02, page 694–699, New York, NY,

USA. Association for Computing Machinery.

Zavr

snik, A. (2021). Algorithmic justice: Algorithms and

big data in criminal justice settings. European Journal

of Criminology, 18(5):623–642.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

654