A Zero-blockage based Scheduling for Import Containers Pickup

Operations at Container Terminal Yards

Ahmed Azab

and Hiroshi Morita

Department of Information and Physical Sciences, Graduate School of Information Science and Technology,

Osaka University, Suita, Japan

{ahmed.azab, morita}@ ist.osaka-u.ac.jp

Keywords: Truck Appointment Scheduling, Container Terminals, Stacking Sequence.

Abstract: In container terminals (CTs), containers are stacked above each other due to the limited yard area space used

for storing the containers. External trucks usually submit appointment requests to pick up their import

containers from the CT. However, some containers are not on the top stack and are blocked by other containers

when trucks arrive at the terminal yard. Resolving this blockage requires relocating all containers above the

targeted container. This non-value-added operation reduces the yard crane utilization and increases the service

of external trucks. This paper studies the appointment scheduling for picking up containers, considering the

container stacking sequence in the yard. We propose a scheduling method for container pickup appointments

to avoid container blockages. An IP model is developed to minimize shifting appointment times for picking

up import containers from its preferable pickup time windows. The performance of the developed model is

investigated by solving some numerical instances. In addition, further analyses are performed to study the

effect of container blocking on appointment scheduling.

1 INTRODUCTION

The Global seaborne trade acts as the key player in

the global supply chain. According to the United

Nations Conference on Trade and Development, It

has been reported that about 80% of the global cargo

is transported by sea (UNCTAD 2020). Using

containers in cargo shipping is very cost-efficient

with added supply chain values. Containers are

transported between different parties in the supply

chain, involve manufacturers producing goods for

global use, freight forwarders, shipping lines, transfer

facilities, and finally, customers(Günther and Kim

2006). As essential nodes in the maritime supply

chain, container terminals (CTs) play an

indispensable role in the container's transportation

and cargo handling efficiency.

As a response to the container shipping growth,

container ports always strive to increase their

throughput by investing the infrastructure and

designing more efficient operations. Figure 1 shows

the growth in container terminal throughput at ports

worldwide from 2012 to 2020, with a forecast for

https://orcid.org/0000-0002-3169-0943

https://orcid.org/0000-0002-1325-8655

2021 until 2024. CTs are faced with increasing

numbers of containers to be handled at a low cost and

in a short time (Stahlbock and Voß 2008). Therefore,

CTs always try to enlarge their handling capacities

and strive to achieve higher productivity without

losing competitiveness.

Figure 1: Container throughput at ports worldwide from

2012 to 2020 with a forecast for 2021 until 2024) (source:

Statista 2021).

286

Azab, A. and Morita, H.

A Zero-blockage based Scheduling for Import Containers Pickup Operations at Container Terminal Yards.

DOI: 10.5220/0010885000003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 286-293

ISBN: 978-989-758-548-7; ISSN: 2184-4372

Typically

, CTs consist of three main areas:

Landside: In this area, export containers are

received from outside the terminal by external trucks

or trains, and import containers are picked up by the

same transportation means.

Seaside: In this area, export containers are loaded

to vessels to deliver to another CT. In contrast, import

containers are unloaded from vessels to be picked up

by road transportation or another vessel.

Yard Area: containers received from the seaside

and landside are temporarily stored in the yard.

Typically, containers are stacked above each other's

due to limited yard area space and transported

between seaside and yard using internal trucks or

automated guided vehicles. A stack is a vertical

column of containers and several stacks from a two-

dimensional bay configuration, as shown in Figure 2.

Each area inside the container terminal has

operations that interrelate with different processes

inside and outside the terminal. For instance, the

container unloading sequence from the vessels

impacts the container handling and stacking

operations at the yard area. The arrival times of the

external truck at the terminal to deliver or pick up

containers also affect the yard operations. Therefore,

decision-making in this complex system is highly

dependent, so that the integration of operational

planning is essential.

This paper focuses on managing the arrival of the

external trucks at the landside while considering the

container stacking sequence in the yard. At landside,

the external trucks arrive at the terminal at a pre-

decided time window to deliver export and (or pickup

import containers). The decided arrival times are

usually obtained from Truck Appointment System

(TAS). TAS is typically applied in a CT to control the

terminal congestion and smooth the arrival peaks

(Huynh, Smith, and Harder 2016). In addition, it is

widely implemented in many terminals to coordinate

the truck arrival process between trucking companies

and container terminals.

Once the truck's arrival time (appointment time)

is decided, trucking companies dispatch their trucks

to the terminals. At the landside gates, pre-entry

processes are performed, such as scanning the export

container, checking the container customs, and

revising the container and driver-related documents.

Once the gate operations are finished, trucks are

directed to the yard area, where containers are stored

in separate yard blocks. A yard crane is used at a

particular yard block to load the import containers to

the external trucks or unload the export container

from the truck to the container stack (See Figure 2).

If the terminal adopts TAS, the yard crane

stacks/unstacks the containers based on a prepared

plan to achieve the best operational performance

considering containers arrival or departure time, yard

block configuration, and other spatial constraints.

Figure 2: Container Bay Configuration showing the

blockage.

A typical situation in CT occurs when an external

truck is given an appointment to pick up an import

container, but this targeted container is not on the top

of the stack (see Figure 2). In this case, the yard crane

must remove (relocate) all containers above the

targeted container, resulting in more truck waiting

time and extra container movements performed by the

yard crane.

The container Relocation Problem (CRP) is

typically solved to determine the optimum relocation

sequence (de Melo da Silva et al. 2018) and resolve

the container blockage. The truck arrival information

is usually obtained from the TAS and used as an input

to the CRP. The arrival time of each truck will

determine the pickup sequence of the containers from

the yard. The truck appointment scheduling problem

is solved, usually independent from the CRP. In most

cases, TAS is designed to tackle the congestion

problems in CT regardless of some root causes of

congestion inside the terminal and long truck waiting

times. One of the hidden causes of such truck delay

issues is the time consumed for resolving container

blockage when picking up import containers from the

yard.

This paper introduces a scheduling approach for

truck appointments considering the container

blockage in the yard. Unlike the previous studies, we

consider the container stacking sequence in the yard

when deciding final truck appointments to avoid

container blockage during import container pickup

A Zero-blockage based Scheduling for Import Containers Pickup Operations at Container Terminal Yards

287

operations. Considering container stacking sequence

will enable the terminal operators to prevent or

control the blockage and resolve one of the

congestion root causes: container relocations.

The remainder of the paper is organized as

follows; section 2 discusses some related work. In

section 3, the problem description is introduced. The

proposed mathematical model is explained in section

4. Section 5 discusses the numerical experiments and

results. Conclusions and future work are discussed in

section 6.

2 RELATED WORKS

TAS and CRP are extensively studied in the literature.

In this section, some recent studies are presented. In

Zeng, Feng, and Yang ( 2019), the impact of partial

truck arrival information on the number of container

relocations in yard areas is studied. An optimization

model is developed, and five heuristic algorithms are

introduced to solve the model. Results illustrated how

the proposed algorithms could help CT operators to

reduce container rehandling. To minimize the

expected number of container relocations, Ku and

Arthanari (2016) used the departure time windows for

containers revealed by TAS. A stochastic dynamic

programming model is developed, and a heuristic

algorithm is proposed to beat the computational

complexity of the exact method. Yi, Gui, and Kim

(2018) used the real-time arrival information of the

external trucks to improve the carry-out operations of

the import containers. They showed how the expected

arrival time of the trucks obtained by GPS in drivers'

smartphones could help in reducing container

relocation operations.

Truck appointment scheduling is also studied

from the perspective of reducing terminal congestion.

Torkjazi, Huynh, and Shiri (2018) formulated a

mixed-integer nonlinear programming model to

minimize both waiting time and the cost of external

trucks. To study the effect of appointments on truck

waiting times, Yi et al. (2019) developed a

mathematical model and a heuristic algorithm to

solve the problem within a reasonable computational

time. In this context, Azab, Karam, and Eltawil

(2020) also proposed a simulation-based optimization

approach to minimize the truck congestion at terminal

gates and in yard blocks for multiple trucking

companies. Their approach illustrated the benefits of

using TAS in managing truck arrival and reducing

truck turnaround times.

Zhang, Zeng, and Yang (2019) proposed a

mathematical optimization model to minimize the

waiting time of external trucks and internal trucks

used to transport containers inside the terminal. Their

proposed queuing model reduced terminal operating

costs and provided a more accurate estimation of the

truck waiting times. More recently, Abdelmagid,

Gheith, and Eltawil (2020) proposed an IP model to

minimize the external truck delays under several

truck arrival scenarios. Their results showed that the

truck delays could be reduced while considering

service time limitation and yard capacity. For a more

comprehensive survey on TAS, interested readers can

refer to Abdelmagid, Gheith, and Eltawil (2021).

From the surveyed studies in this section and more

studies in the literature, it is noted that considering the

container stacking sequence in scheduling the truck

appointments is still undercovered. Moreover,

studying the import container operations received less

interest than export containers since the latter are

prioritized to reduce the vessel operational time than

trucking companies' operational times. So that, this

paper introduces a preliminary design of the

appointment scheduling system, which considers

container stacking orders from the container terminal

side and the preferable container pickup time from

trucking companies' side.

3 PROBLEM DESCRIPTION

For a truck to access the CT for picking up an import

container, an appointment request shall be submitted

one day before heading to the terminal. The

submitted request represents the preferred arrival

time window for the truck to pick a predefined

container. However, arriving truck at the terminal at

the desired time window can experience a long

service time since other containers may be blocking

the targeted container (

Figure 2). The blocking occurs

when the truck arrives to pick up its targeted container

before the container above it. On the other hand,

terminal operators want to avoid container blockage

as much as possible to increase the yard crane

productivity. The more blocking containers the bay

has, the more container relocations the yard crane will

perform.

Changing the arrival time of trucks such that

trucks with the topmost containers in the bay arrive

before the trucks with the bottom containers can

reduce the blockage scenarios. However, matching

truck appointment times with container stacking

sequence to prevent blocking may shift the trucks

from their preferable arrival time. This paper

proposes a new IP model to minimize shifting the

appointment from the preferable container pickup

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

288

time window while keeping container blockage under

control.

It is worth mentioning that the proposed approach

only considers the static blockage in the initial stack

configuration. The initial stack configuration

describes the stacking order of import containers in

each stack before trucks arrive at the yard. However,

considering the future relocations resulting from this

blockage is not considered, and it requires

considering the change of stack configuration as the

containers pickup is progressing. Minimizing the

number of relocations accordingly with appointment

scheduling is recently considered by Azab and Morita

(2022). The authors developed an IP model that

considered a limited tolerance for container

appointment shift while keeping relocations at a

minimum.

In this paper, the container blockage describes the

number of blocked containers in the initial stack

configuration. For example, in Figure 3, the last

highlighted stack in the initial bay configuration

(right-hand side of the figure) shows that there is a

blocking container if the trucks arrive according to

their preferred times. However, our approach

introduces a pre-processing scheduling method to

schedule the truck appointments to control the

blockage or avoid it when trucks arrive according to

the scheduled times. This can be seen on the left-hand

side of Figure 3. Assuming that attached times to the

containers (highlighted in grey) will be the actual

(newly scheduled) container pickup times. This leads

to fewer blockages in the initial stack configuration.

According to Zhu et al. (2012), the number of

blocking containers in the initial configuration of the

stacks is considered the lower bound for the total

number of containers relocations required to retrieve

all containers from the bay. This lower bound

contributes to determining the maximum number of

relocations or the upper bound (Zehendner et al.

2015). Reducing the number of blocking containers

in the initial stacks' configuration and accordingly

bay configuration can reduce the total number of

container relocations. Let 𝐿𝐵



is the number of

blocking containers (lower bound for container

relocations) at time window 𝑡 . Then the overall

minimum number of container relocations (𝐿𝐵) can

be obtained as follows:

𝐿𝐵  𝐿𝐵



𝐿𝐵



⋯ 𝐿𝐵



𝑇: Latest time window to pick up an import

container from the bay.

Reducing the number of blocking containers in

the initial bay (𝐿𝐵



) can reduce the number of future

relocations, which is our paper's primary motivation.

We make this reduction by scheduling the pickup

time of containers. This can be seen clearly in the

illustrative example in Figure 3. Now you can see

that the last highlighted stack does not contain any

blocking just by changing the pickup time of the

containers one or two time windows.

Figure 3: Illustration of the proposed appointment

scheduling approach and the resultant stack configuration.

In our approach, the planning horizon is

discretized in several time widows; each time window

is assumed to be one-hour length. Each container is

given a unique index corresponding to one truck in

the truck appointment system. Since we don't study

the dynamic version of the problem that deals with

the change of stacks configuration with time, we

solve the optimization problem of truck appointment

scheduling for containers located in each vertical

stack. This adds an advantage to our approach since

we can solve the problem for a large number of stacks

regardless of the location of this stack in the yard.

We also consider the number of trucks that can be

received at the terminal yard during a particular time

window. This is expressed as the yard capacity in the

developed mathematical model. For instance, the

number of appointment requests exceeds the yard

capacity; some trucks will be scheduled to less

congested time windows. In the proposed scheduling

A Zero-blockage based Scheduling for Import Containers Pickup Operations at Container Terminal Yards

289

approach, the number of allowed blockings is

typically assumed to be zero. This means that no

relocations will be required in the future if the trucks

arrive according to the developed schedule. However,

terminal operators shall be aware that avoiding all

blockings might require shifting many trucks away

from their preferred arrival times, leading to less

satisfaction for truckers. Therefore, we further

analyze the impact of the number of acceptable

container blockings on the appointment shifting. In

the next section, we introduce the mathematical

formulation for the described problem in this section.

4 PROBLEM FORMULATION

Indices:

𝑖

Container index.

𝑠

Stack index.

𝑡 Time window index,

𝑡∈



1,..,𝑇



Parameters:

𝑝



Preferable container pickup time of container

𝑖 located at stack 𝑠. 𝑝



∈



1,..,𝑇



ℎ



Stack 𝑠 height (number of containers in stack

𝑠).

𝑚

Number of stacks.

𝐶

Yard capacity (truck arrival quota) per time

window.

𝑇

Latest possible container pickup time

window.

k Number of allowable container blockings in

the initial stack confi

uration.

Decision Variables:

Integer variables:

𝑥



The pickup time window of the container 𝑖

located at stack 𝑠.

Derived binary variables:

𝑦



A binary variable represents the state of

container i if it has pickup time later than the

container j below it: 𝑗1,…,ℎ



1,𝑖

𝑗1,…,ℎ



. In other words, whether

container 𝑖 is blocking container

𝑗

𝑧



A binary variable represents if container 𝑖

will be picked up from the stack 𝑠 at time

window 𝑡.

Objective Function:

𝑀𝑖𝑛 

𝑥



𝑝

















(1)

Subjected to:

𝑦





1, 𝑖𝑓 𝑥



𝑥



0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒

∀

𝑗

∈



1,…ℎ



1



,𝑖∈

𝑗

1,…,ℎ





(2)

𝑦

















𝑘, ∀𝑠∈1,…,𝑚

(3)

𝑧





1, 𝑖𝑓𝑥



𝑡

0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒

,∀𝑡∈1,…,𝑇 (4)

𝑧













𝐶, ∀𝑡∈1,…,𝑇

(5)

0𝑥



𝑇,∀𝑖∈



1,…,ℎ





∀𝑠 ∈ 1,…,𝑚

(6)

The objective function (1) is to minimize the total

shift of the final appointments from the preferred

appointments. Constraint (2) defines the derived

binary variable 𝑦



. 𝑦



 1, if container 𝑖 is

blocking a container 𝑗 below it. The container

indexing 𝑖 in each stack is ascending from the bottom

to the top (See Figure 4). The model avoids/controls

container blockage by defining the constraint (3).

This constraint specifies the number of allowed

blockings in the initial stack configuration using the

parameter 𝑘. One "blocking" is counted if a container

𝑖 has a later pickup time than a container 𝑗 below it.

Figure 4 shows two illustrative examples of blocking

modeling in constraints (2) and (3). Typically, we use

𝑘 equals 0 and called constraint (3) non-blocking

constraint. The 𝑘 values are further changed to

investigate the effect of increasing the number of

allowed blockings on appointments, as explained in

section 5.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

290

Figure 4: Illustrative examples for the constraints (2) and

(3).

Practically, CTs have limited resources capacity

to accept all appointments and handle containers

demand. Constraint (4) defines the derived binary

variable 𝑧



. The variable 𝑧



is used later in

constraint (5) to determine and restrict the number of

containers picked up during a specific time window

𝑡. For modeling simplicity, constraints (2) and (4) are

formulated in such binary condition form since many

commercial solvers can handle the definition of

binary conditions without the need for "Big M"

notations. In constraint (6), picking up containers are

not allowed after the last working time window in the

terminal. This constraint also defines the discrete

domain of the decision variable 𝑥



. The domain of

the binary decision variables 𝑦



and 𝑧



inherently defined in constraints (2) and (4).

5 NUMERICAL EXPERIMENTS

AND RESULTS

A number of 10 randomly generated instances with

different sizes are synthesized to investigate the

performance of the developed model. An instance

size is determined by the number of stacks (𝑚) and

the planning horizon (𝑇). A total number of 525

stacks are solved. Practically, the maximum number

of containers in each stack is 5 or 6, where the yard

crane can move above the stacks freely without

collision. In this paper, we used the maximum height

of the container stack (ℎ



) to be five, and all stacks

are full. All containers are assumed to be picked up in

time windows (𝑝



) between 1 and 𝑇. Finally, the

number of allowable container blockings in the initial

stack configuration is assumed to be zero; constraint

(3) will be

∑∑

𝑦

















0, ∀𝑠∈1,…,𝑚.

To solve the generated instances, CPLEX Studio

IDE 12.9.0 is used. Table 1 illustrates the input

parameters of the generated instances and

computational results. The optimal objective values

that determine the total appointment shift (in time

windows) are obtained. The average appointment

shift for each container is also obtained. Results show

that all instances are solved to the optamilty in a

reasonable time; however, the solution time is long

for larger instances. It is noticed that each container

can be shifted from its preferable pickup time by an

average range from 1.4 to 2.5-time window.

Therefore, a truck may face delaying or advancing its

preferred appointment to avoid the container

blockage in the initial stack configuration.

As more illustration, instance (1) solution is

shown in Figure 5. In this instance, Figure 5 (a) shows

the submitted preferable pickup time ( 𝑝



)

corresponding to each container. In Figure 5 (b), the

decided pickup times (𝑥



) obtained by solving the IP

model are shown. It can be noted that in the stack (𝑠

2), the first container on the top of the stack is

preferred to be picked up by truck at time window 5,

and the container below it ( 𝑖2) has an earlier

preferred pick up at time window of 1. As a result, the

topmost container is shifted to be picked up in time

window 1 to avoid blocking the container below it.

Results show that every container in the first instance

will be shifted by 1.8 time windows on average from

its preferable pickup time.

Table 1: Instances and results.

Inst. m T C Optimal Obj.

value

Optimal Obj.

value /stac

Avg. shift/container CPU time sec.

1 5 10 4 45 9.0 1.8 0.33

2 10 10 6 93 9.3 1.86 9.51

3 15 10 8 119 7.9 1.58 137.19

4 20 10 12 145 7.25 1.45 55.22

5 25 10 14 183 7.32 1.46 69.06

6 30 10 17 208 6.39 1.39 59.63

7 40 10 22 288 7.2 1.44 151

8 80 16 30 921 11.5 2.3 378.89

9 100 18 32 1,261 12.61 2.5 113.03

10 200 32 40 4,470 22.35 4.47 1,195.39

A Zero-blockage based Scheduling for Import Containers Pickup Operations at Container Terminal Yards

291

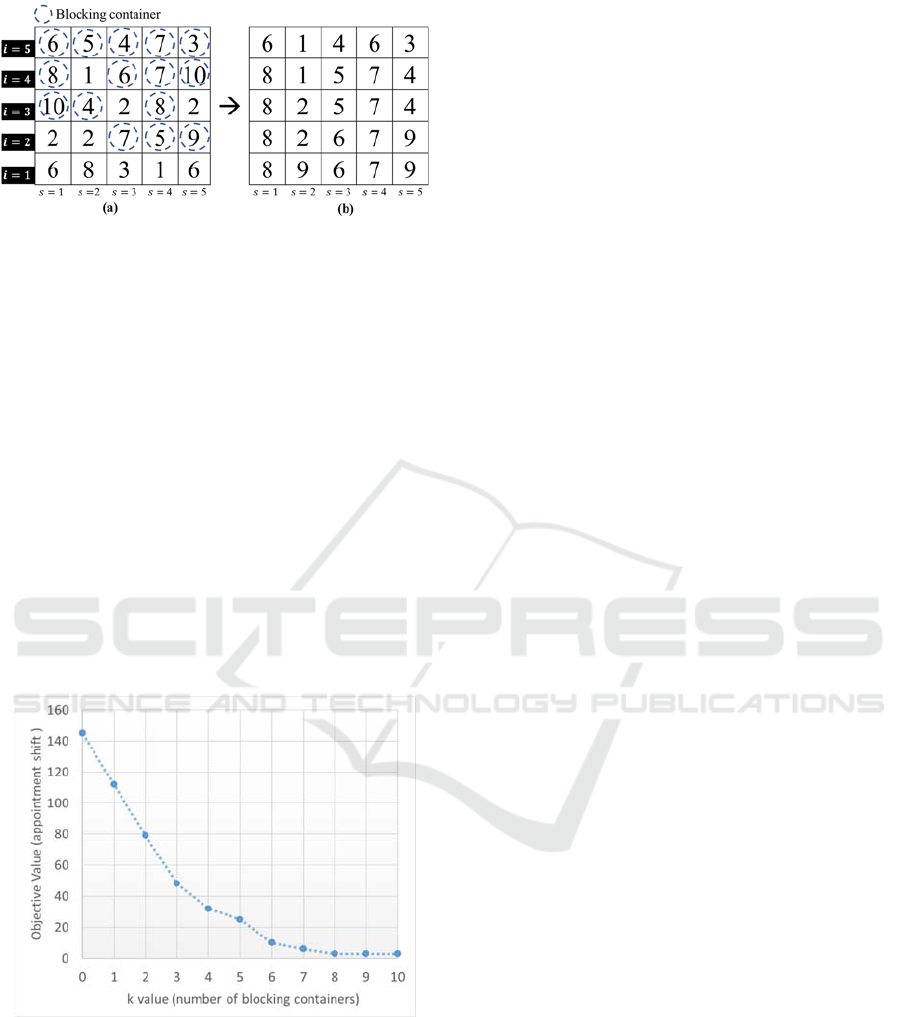
Figure 5: Instance 1 solution (a) stacks configuration with

preferable appointment times (𝑝



), (b) the same stacks

configuration with optimal appointment times (𝑥



The number of allowed blockings (𝑘) and their

impact on the objective values are also studied. We

solved instance number 4, with the 20 stacks and

planning horizon of 10 time windows length, under

different k values. Results in Figure 6 show that the

more the number of blockings is allowed, the less the

container will be shifted from their preferable pickup

time. This result is reasonable since the terminal

operator may accept more blocking containers in the

initial configuration of the stack to achieve higher

satisfaction for trucking companies. However, it's

worth mentioning that the non-blocking scenario

guarantees less service time for external trucks since

fewer non-value-added container relocations will be

avoided and hence higher productivity for yard

cranes.

Figure 6: Effect of parameter 𝑘 on objective values.

5 CONCLUSIONS AND FUTURE

WORK

This paper proposes a preliminary design for an

appointment scheduling system for picking up import

containers by external trucks in CTs considering

containers stacking sequence. Results showed that the

non-blocking could be achieved while minimizing the

appointment shifting from the desired pickup time

windows. The developed IP model also considers the

terminal capacity and appointment at the latest

available time.

This work will be extended in the future by

integrating truck appointment scheduling problems

with container relocation problems (TAS-CRP). The

primary motivation behind the integration is that most

TASs are designed to alleviate the terminal

congestion without considering the number of

relocations that may confront the container retrieval

process. Since the container stacking sequence is

almost well known at the time of appointment

submission, considering the number of relocations

and terminal congestion issues is expected to improve

the solution of both problems. The main goal is to

match truck arrival times with container stacking

sequence to minimize relocations, not only the

blocking containers in the static stacks

configurations, and maximize trucking companies'

satisfaction.

However, some issues may arise due to

integrating TAS with CRP, such as the problem of

hardness. CRP alone has been proven to be an NP-

hard problem. In this case, exact or heuristic

algorithms may be developed to solve the integrated

problem. Another issue is the uncertainty of truck

arrival times and container stacking sequence.

Considering the number of relocations and preferable

truck arrival times may not guarantee the system's

efficiency. As a result, a real-time recovery system to

recover the distrusted plans supported by reliable

response strategies might be interesting to study.

REFERENCES

Abdelmagid, Ahmed M., Mohamed S. Gheith, and Amr B.

Eltawil. 2020. “Notice of Removal: A Binary Integer

Programming Formulation and Solution for Truck

Appointment Scheduling and Reducing Truck

Turnaround Time in Container Terminals.” Pp. 149–53

in 2020 IEEE 7th International Conference on

Industrial Engineering and Applications (ICIEA).

Abdelmagid, Ahmed Mohssen, Mohamed Samir Gheith,

and Amr Bahgat Eltawil. 2021. “A Comprehensive

Review of the Truck Appointment Scheduling Models

and Directions for Future Research.” Transport

Reviews 0(0):1–25.

Azab, Ahmed, Ahmed Karam, and Amr Eltawil. 2020. “A

Simulation-Based Optimization Approach for External

Trucks Appointment Scheduling in Container

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

292

Terminals.” International Journal of Modelling and

Simulation 40(5):321–38.

Azab, Ahmed and Hiroshi Morita. 2022. “The Block

Relocation Problem with Appointment Scheduling.”

European Journal of Operational Research 297(2):680–

94.

Günther, Hans-Otto and Kap-Hwan Kim. 2006. “Container

Terminals and Terminal Operations.” OR Spectrum

28(4):437–45.

Huynh, Nathan, Daniel Smith, and Frank Harder. 2016.

“Truck Appointment Systems: Where We Are and

Where to Go from Here.” Transportation Research

Record 2548(1):1–9.

Ku, Dusan and Tiru S. Arthanari. 2016. “Container

Relocation Problem with Time Windows for Container

Departure.” European Journal of Operational Research

252(3):1031–39.

de Melo da Silva, Marcos, Güneş Erdoğan, Maria Battarra,

and Vitaly Strusevich. 2018. “The Block Retrieval

Problem.” European Journal of Operational Research

265(3):931–50.

Stahlbock, Robert and Stefan Voß. 2008. “Operations

Research at Container Terminals: A Literature Update.”

OR Spectrum 30(1):1–52.

Torkjazi, Mohammad, Nathan Huynh, and Samaneh Shiri.

2018. “Truck Appointment Systems Considering

Impact to Drayage Truck Tours.” Transportation

Research Part E: Logistics and Transportation Review

116:208–28.

UNCTAD. 2020. “Shipping in Times of the Covid-19

Pandemic.”

Yi, Sanghyuk, Lin Gui, and Kap Hwan Kim. 2018.

“Improving Carry-Out Operations of Inbound

Containers Using Real-Time Information on Truck

Arrival Times.” Pp. 457–63 in Advances in Production

Management Systems. Production Management for

Data-Driven, Intelligent, Collaborative, and

Sustainable Manufacturing, edited by I. Moon, G. M.

Lee, J. Park, D. Kiritsis, and G. von Cieminski. Cham:

Springer International Publishing.

Yi, Sanghyuk, Bernd Scholz-Reiter, Taehoon Kim, and

Kap Hwan Kim. 2019. “Scheduling Appointments for

Container Truck Arrivals Considering Their Effects on

Congestion.” Flexible Services and Manufacturing

Journal 31(3):730–62.

Zehendner, Elisabeth, Marco Caserta, Dominique Feillet,

Silvia Schwarze, and Stefan Voß. 2015. “An Improved

Mathematical Formulation for the Blocks Relocation

Problem.” European Journal of Operational Research

245(2):415–22.

Zeng, Qingcheng, Yuanjun Feng, and Zhongzhen Yang.

2019. “Integrated Optimization of Pickup Sequence and

Container Rehandling Based on Partial Truck Arrival

Information.” Computers & Industrial Engineering

127:366–82.

Zhang, Xiaoju, Qingcheng Zeng, and Zhongzhen Yang.

2019. “Optimization of Truck Appointments in

Container Terminals.” Maritime Economics &

Logistics 21(1):125–45.

Zhu, Wenbin, Hu Qin, Andrew Lim, and Huidong Zhang.

2012. “Iterative Deepening A* Algorithms for the

Container Relocation Problem.” IEEE Transactions on

Automation Science and Engineering 9(4):710–22.

A Zero-blockage based Scheduling for Import Containers Pickup Operations at Container Terminal Yards

293