Multi-objective Risk Analysis for Crowd Evacuation
Guidance using Multiple Visual Signs
Akira Tsurushima
a
Intelligent Systems Laboratory, SECOM CO., LTD., Mitaka, Tokyo, Japan
Keywords:
Evolutionary Multi-objective Optimization, Black-box Optimization, Visual Evacuation Signage Assignment
Problem, Average Value at Risk, NSGA-II.
Abstract:
Efficient crowd evacuation guidance is crucial but challenging owing to the randomness involved in evacuation
situations and to the unpredictable human behaviors, e.g., herd behavior among evacuees. Many researchers
have found that visual evacuation signage is useful for this purpose, and, thus, evacuation guidance systems
employing visual signage have been developed. A proper arrangement of visual signs on the premises is
necessary to obtain the most out of these attempts; however, several factors make this task challenging, such as
multiple conflicting objectives in the evacuations and randomness and uncertainties in the situation. This study
formulates the visual evacuation signage assignment problem as a stochastic multi-objective optimization
problem and explores the efficient layouts of multiple visual signs on the premises. We consider two objectives
for the efficient layout of visual signs, namely, maximizing the number of evacuees selecting the correct exit
and minimizing the total evacuation time. The average value at risk is employed to deal with the risks involved
in noisy objective functions, while the expected values of these objectives are optimized. Pareto-optimal
solutions satisfying both the expected values and the risk measures were explored in cases with one, two and
five evacuation signs using the NSGA-II algorithm.
1 INTRODUCTION
Numerous researchers have found that cognitive fac-
tors during evacuations are crucial because they of-
ten make individual behaviors uncertain and some-
times lead to unexpected crowd behaviors (Haghani,
2020b; Haghani, 2020a). Herd behavior, i.e., the ten-
dency of an individual to follow other people’s be-
haviors or decisions, is one of those still unclear, al-
beit well-studied, cognitive factors in crowd evacu-
ations (Haghani et al., 2016; Sieben et al., 2017).
One difficulty caused by herd behaviors in evacua-
tions is the large variances of the results, which make
the consequences of the evacuation protocol designs
unpredictable. This is especially true if the evac-
uation process involves some evacuation decisions,
such as selections of the evacuation routes or exits,
or choices of evacuation actions (Haghani and Sarvi,
2016; Lovreglio et al., 2014). Unsymmetry in exit
choices in crowd evacuations is a well-known exam-
ple of unpredictable crowd evacuation behavior (Hel-
bing et al., 2000; Ji et al., 2017; Tsurushima, 2019;
Tsurushima, 2020; Tsurushima, 2021a).
a
https://orcid.org/0000-0003-2711-297X
Recently, evacuation protocols employing visual
signs or signage systems to achieve efficient evac-
uations have been designed and developed (Galea
et al., 2014; Zhou et al., 2019). The proper arrange-
ment of visual signs within the premises is crucial
in these attempts; simulations and optimization tech-
niques are often employed to explore the efficient
positions of visual signs (Cisek and Kapalka, 2014;
Dubey et al., 2020). However, several properties of
the problem make this task challenging, e.g., large de-
cision spaces, computationally expensive evaluation
methods, noisy objective functions, lack of efficient
search methods, and multiple conflicting objectives.
These factors result in high computational costs that
are often unaffordable for most architectural projects.
Tsurushima addressed these issues in the visual
signage arrangement problem for crowd evacuations
and formulated it as a stochastic multi-objective op-
timization problem, namely, the visual evacuation
signage assignment problem (VESAP) (Tsurushima,
2021c). Tsurushima analyzed an instance of the
VESAP in which evacuees must choose one of two
exits— the correct (safe) exit and the incorrect one —
to flee from the environment. The problem has two
Tsurushima, A.
Multi-objective Risk Analysis for Crowd Evacuation Guidance using Multiple Visual Signs.
DOI: 10.5220/0010886400003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 1, pages 71-82
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
71

objective functions: the number of evacuees select-
ing the correct exit f
1
(to be maximized) and the total
evacuation time of the crowd f
2
(to be minimized).
Objective f
2
is crucial because the single objective
problem with f
1
will lead to an optimal solution: a
position in front of the incorrect exit. In this solu-
tion, many evacuees move to the incorrect exit first
and then change to the correct one, leading to an un-
necessarily long travel distance, which also leads to a
long evacuation time.
Tsurushima considered the VESAP as the mean
risk model and analyzed it in terms of the Pareto-
efficiencies and risks associated with the solutions.
However, in his analysis, he only considered a single
visual sign assignment case that might be considered
unrealistic in practice. He also assumed a discrete
decision space and conducted brute-force approaches
for all the candidate positions of assigning the visual
sign to analyze the Pareto-optimal solutions, which
might be inapplicable to practical problems, owing to
the computational cost.
In this study, we analyzed the VESAP in cases
with multiple visual signs. The combinatorial prop-
erty of the problem leads to a large decision space
and costly computations, making the brute-force ap-
proach inapplicable. Assuming a continuous search
space, we applied multiple objective optimization
techniques to explore the Pareto-frontiers and em-
ployed the average value at risk to estimate the risks
involved in the solutions.
2 MOTIVATING EXAMPLE AND
BASIC CONCEPT
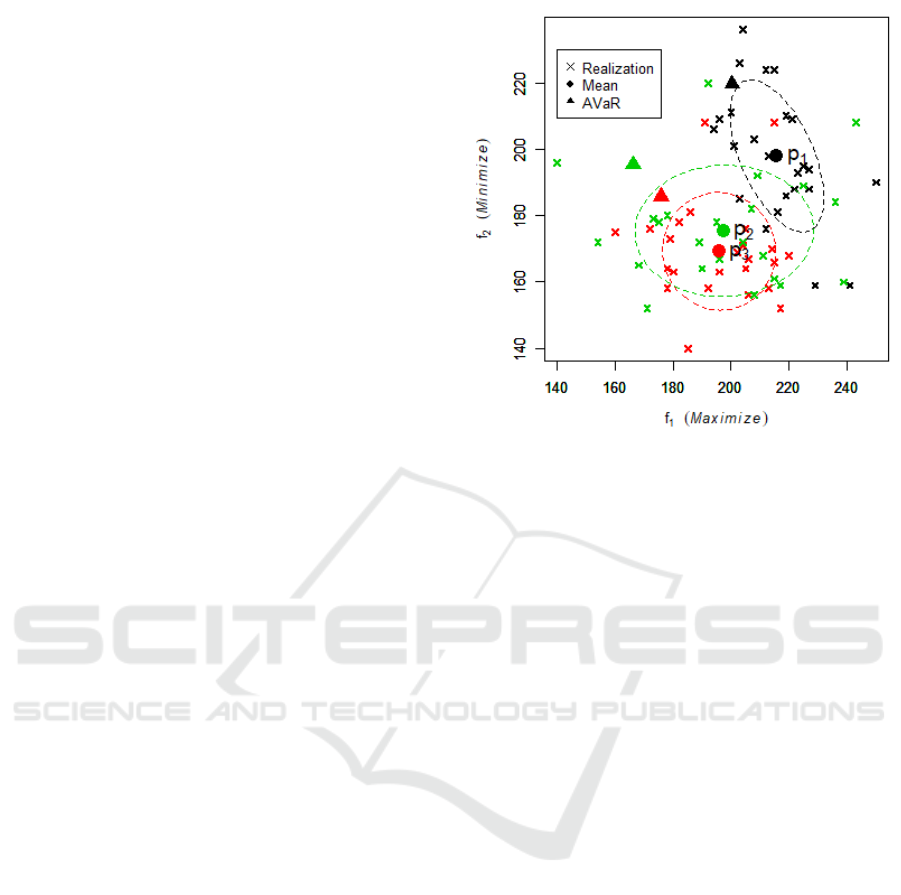
Figure 1 shows the means of three example solutions,
p
1
, p
2
, and p
3
, of the VESAP on the objective space
of f
1
and f
2
, indicated in black, green, and red, re-
spectively. Because f
1
is to be maximized and f
2
is to be minimized, the solutions close to the lower-
right corner are preferable, whereas those close to
the upper-left corner are not. Twenty-four simula-
tions were conducted for each solution, and the objec-
tive values of each Realization were plotted as ‘×’ on
the objective space. Realizations of each solution are
broadly distributed over the objective space, owing to
the effects of herd behaviors and to the random prop-
erties of the problem. This makes it difficultto specify
the coordinates of the points that properly represent
the outcomes of the solutions on the objective space.
One possible way to represent the solutions is to use
the expected values of the objective functions (
¯
f
1
,
¯
f
2
)
by explicit sampling, which are shown in small filled
circles in Fig. 1. This approach has been employed to
Figure 1: Motivating example.
solve many stochastic optimization problems; how-
ever, it disregards the risk or uncertainty involved in
the problem, i.e., solutions with large and small vari-
ances are indistinguishable.
Most human decision makers tend to avoid risks,
meaning that they have concave utility functions.
People prefer random variables with a small variance
to those with a large one if the expected values are
equal. Thus, the quantities to be maximized are not
the expected values, but rather are their expected util-
ities. However, in general, estimating people’s utility
functions is difficult or sometimes impossible.
In Fig. 1, the expected values of the objective
functions of p
2
and p
3
are close to each other for
both f
1
and f
2
; thus, two solutions are almost indis-
tinguishable if we only consider the expected values.
The ellipses in Fig. 1 illustrate the 50% probability el-
lipses of three solutions, i.e., the ranges where 50% of
those Realizations will fall within. In the figure, the
probability ellipse of p
2
is larger than that of p
3
and
almost includes the ellipse of p
3
. This implies that the
outcomes of p
2
are more unpredictable than those of
p
3
, even though the expected values are almost equal;
human decision makers usually prefer p
3
to p
2
be-
cause most people are averse to risk and dislike unpre-
dictability. Because risks are major factors in evacu-
ation problems, the risk attitude of decision makers
is crucial and should be considered in the evacuation
protocol analysis. Some numerical risk measures that
properly represent risks in the solutions would be de-
sirable.
The average value at risk (AVaR), which is a
widely used risk measure in many fields, includ-
ing economics and finance, is currently considered
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
72

Figure 2: S
1
: e
+
and e
−
are indicated in blue and red, re-
spectively. The intersections of the dashed lines indicate the
candidate positions.
a coherent risk measure that is consistent with the
maximum expected utility principle and second-order
stochastic dominance (Gutjahr and Pichler, 2016;
Ogryczak and Ruszczynski, 2002). The AVaR also
satisfies several desired properties, including mono-
tonicity, positive homogeneity, subadditivity, and
translation invariance. It is defined on the basis of
the value at risk (VaR), which is another risk measure
employed prior to the AVaR (Rachec et al., 2008).
Definition 1 (Value at Risk: VaR). The value at risk
of the random outcome X at level α(0 < α ≤ 1) is the
α−quantile
†
of the random variable X, i.e.,
VaR
α
(X) = F
−1
X
(α).
Definition 2 (Average Value at Risk: AVaR). The
AVaR of the random outcome X at level α(0 < α ≤ 1)
is defined
†
as
AVaR
α
(X) =
1
α
Z
α
0
VaR
p
(X)dp (1)
= E[X|X ≤ VaR
α
(X)]. (2)
The triangles in Fig. 1 depict the coordinates of
(AVaR
0.3
( f
1
), AVaR
0.3
( f
2
)) of p
1
, p
2
, and p
3
in black,
red, and green, respectively.
In Fig. 1, it is difficult or impossible to set the
order of the expected values of p
1
, p
2
, and p
3
(three filled circles) without using someone’s subjec-
tive preferences because one may have a better value
for one objective function than those of the others
while having a worse value for another objectivefunc-
tion. Solutions like these are called Pareto-optimal
in multi-objective optimizations (Gutjahr and Pichler,
2016).
Definition 3 (Pareto-optimal). A solution x is said to
be non-dominated, Pareto-efficient, or Pareto-optimal
if no solution y 6= x dominates x. A solution y is said
to dominate x if a solution y satisfies the following:
‡
†
In the financial field, VaR is usually defined as the neg-
ative α-quantile of the random variable X because X is the
return value, which can be negative or positive but not the
outcome itself. However, we use this definition (outcome)
for simplicity.
‡
We assumed f
i
to be maximized.
Figure 3: S
2
: e
+
and e
−
are indicated in blue and red, re-
spectively. The intersections of the dashed lines indicate the
candidate positions.
1. ∀h : f
h
(y) ≥ f
j
(x)
2. ∃g : f
g
(y) > f
g
(x).
If x is a Pareto-optimal solution, the image of x,
f(x), is called the Pareto-optimal point and the set of
Pareto-optimal points on the objective space is called
the Pareto-frontier.
In our example, p
2
and p
3
are Pareto-optimal
points with respect to the expected values; however,
p
2
is dominated by p
3
with respect to the risks be-
cause p
3
has better values for both AVaR
0.3
( f
1
) and
AVaR
0.3
( f
2
) than those of p
2
. By considering AVaRs,
we may conclude that p
3
is a better solution than
p
2
because p
3
has smaller risks than those of p
2
,
even though the expected values of the two are almost
equivalent.
3 VISUAL EVACUATION
SIGNAGE ASSIGNMENT
PROBLEM
In the VESAP, 300 agents A = {a
1
, . . . , a
300
} are ran-
domly distributed on the two-dimensional Euclidian
space S ∈ R
2
; S has two exits: the correct exit e
+
and
the incorrect exit e
−
for the agents to flee from the
space. The correct exit is assumed to lead the agents
to safe evacuations; thus, the aim of the problem is
to maximize the number of agents who select e
+
. In
addition, another objective, the total evacuation time,
is introduced to the VESAP because a single objec-
tive problem with f
1
will lead to a solution that has
an unnecessarily long evacuation time, which is a se-
rious problem in most evacuation situations. These
objectives were evaluated through multi-agent sim-
ulations; the outcomes of the simulation were con-
taminated with noise owing to the randomness and
herd behaviors of the agents. Therefore, Tsurushima
(2021b) formulated the VESAP as a stochastic multi-
objective problem. In this paper, we adopt a simpli-
fied version of the formulation as follows:
Multi-objective Risk Analysis for Crowd Evacuation Guidance using Multiple Visual Signs
73

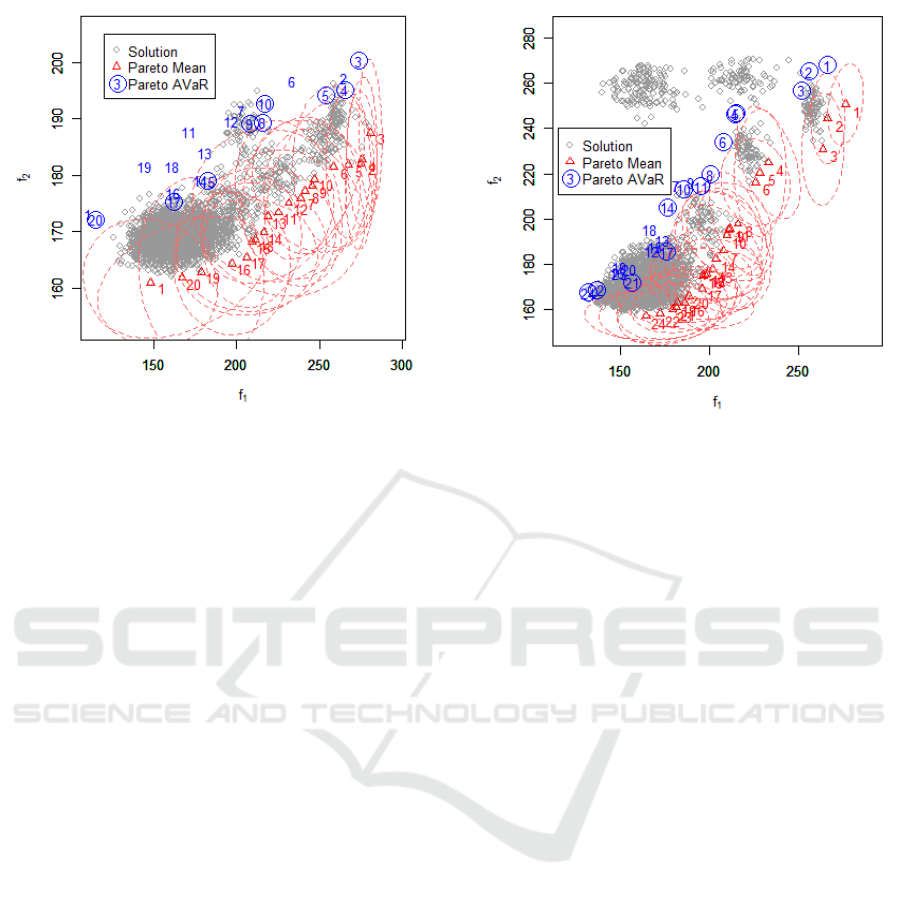
Figure 4: Case study for S
1
.
max f
1
(k, ω) (3)
max − f
2
(k, ω) (4)
s.t. k ∈ K , |k| ≤ L, ω ∈ Ω.
Here, k = {(x, y),. ..} represents a set of visual sign
coordinates on S, K represents the solution space, L
is the maximum number of visual signs assigned to
S, ω is a stochastic scenario, and Ω is the sample
space. The functions f
1
and f
2
are the two objec-
tive functions of the VESAP referring to the number
of agents selecting the correct exit and the total evac-
uation time, respectively. Because we want to min-
imize the total evacuation time, − f
2
is maximized.
In this study, we examined two example spaces with
different arrangements of exits, S
1
and S
2
, as shown
in Figs. 2 and 3, respectively. Both S
1
and S
2
are
x ∈ [− 65, 65], y ∈ [−21, 21] units with different lay-
outs of e
+
(the blue exit) and e
−
(the red exit).
Moreover, in this study, we analyzed the VESAP
in cases with L ≥ 2 signs, whereas Tsurushima
(2021b) only examined L = 1. The evacuation deci-
sion model (Tsurushima, 2019), which represents the
herd behavior of evacuees, was incorporated into each
agent; however, the social force model (Helbing et al.,
2000) was not employed owing to the computational
cost. We also assumed that the visual field of an agent
is a fan shape with a radius of 10 units and an angle
of 20
◦
(Tsurushima, 2021b; Tsurushima, 2021d).
4 TWO VISUAL SIGNS: A CASE
STUDY
In this section, the VESAP in the case with two visual
signs (|k| = 2) is examined. We assumed the candi-
Figure 5: Case study for S
2
date positions of the visual signs as x = { −64, −56,
−48, −40, −32, −24, −16, −8, 0, 8, 16, 24, 32, 40,
48, 56, 64} and y = {−18, −9, 0, 9,18}; a total of 85
candidate positions were introduced on S. We con-
ducted 24 simulation runs for each assignment of the
visual signs using a combination of two out of 85 can-
didate positions (3570 combinations) for S
1
and S
2
.
Figures 4 and 5 show the results of the simulations
for S
1
and S
2
, respectively. Because we want to max-
imize f
1
and minimize f
2
, the lower-right corner of
the figure is the best position and the upper-left one
is the worst position of these spaces. The gray small
circles show the means of f
1
and f
2
for all solutions
(3570 combinations of the candidate positions), and
the red triangles with numbers indicate the Pareto-
optimum of those solutions. The blue numbers depict
the AVaRs of f
1
and f
2
associated with the Pareto-
optimal solutions; the blue numbers with a blue circle
indicate that these points are the Pareto-optimal for
the AVaR.
5 METHOD
In Section 4, we assumed 85 candidate positions and
assigned visual signs to any of two positions. We ex-
amined a total of 3570 (
85
C
2
) feasible combinations
through simulations. A total of 24 simulations were
conducted for each feasible solution to estimate the
means of f
1
and f
2
. Thus, 85,680 simulation trials
were performed to obtain the Pareto-optima. How-
ever, this type of brute-force approach is unrealistic
and inapplicable in general cases due to the high com-
putational cost; for example, 2,370,480 simulations
will be required with three visual signs. An efficient
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
74

Figure 6: Landscapes of S
1
. The left figure shows f
1
, and the right figure shows f
2
.
Figure 7: Landscapes of S
2
. The left and right figures show f
1
and f
2
, respectively.
Figure 8: Case study and NSGA (S
1
and S
2
).
method to obtain the Pareto-optima is required for the
VESAP.
A black-box optimization technique is useful for
this purpose. The evolutionary multi-objective op-
timization (EMO) algorithm is one such technique
that is also applicable for multi-objectiveoptimization
problems with noisy objective functions. The EMO
algorithm is a multi-point search meta-heuristic that
holds a set of candidate solutions and gradually con-
verges them to Pareto-frontiers. One advantage of this
technique is the ease of implementing it to a parallel
algorithm because a set of candidate solutions are mu-
tually independent. In particular, parallel simulations
can be applied to evaluate these solutions.
Figure 9: Pareto-optima obtained by NSGA-II and 100 sim-
ulations (S
1
and S
2
).
Theoretically, the VESAP has four objective func-
tions: the expected values and AVaRs of f
1
and f
2
, re-
spectively. However, multi-objective problems with
many objectives lead to a large number of Pareto-
Multi-objective Risk Analysis for Crowd Evacuation Guidance using Multiple Visual Signs
75

Figure 10: Four representative solutions satisfying the
Pareto-optimal for both the expected values and AVaRs for
the two-sign case in S
1
Figure 11: Four representative solutions satisfying the
Pareto-optimal for both the expected values and AVaRs for
the two-sign case in S
2
optima and are difficult to address. We conducted
simulations by assigning a single evacuation sign for
each 85 candidate position to examine the landscapes
of objective functions f
1
and f
2
. The simulations
were repeated 250 times, and the mean values of f
1
and f
2
were estimated. Figures 6 and 7 show the land-
scapes of both objectives for S
1
and S
2
, respectively.
The left figure depicts the landscape of f
1
, and the
right figure depicts the landscape of f
2
. These figures
illustrate that all of the four landscapes were found to
be smooth, flat, and not complex. We expect that the
problem will be handled by most optimization algo-
rithms.
Tsurushima (2021c) analyzed the correlations be-
tween the expected values and the AVaRs, and found
that these two are highly correlated for both f
1
and
f
2
(Observation 8 in (Tsurushima, 2021c)). This ob-
servation suggests that VESAP can be reduced to a
bi-objective optimization problem, which is easier to
handle than the four-objective problem, with the ex-
pected values of f
1
and f
2
. Because the expected
values and AVaRs are highly correlated, AVaRs of f
1
and f
2
may be treated after the expected values of the
Pareto-optima of f
1
and f
2
were obtained.
NSGA-II (Deb et al., 2002) is one of the most
representative and widely applied evolutionary algo-
rithms for solving multi-objective optimization prob-
lems. The fast non-dominated sort algorithm in
NSGA-II can efficiently generate a series of ranked
non-dominated frontiers with O(MN
2
) computational
complexity. Here, N is the population size, and M
is the number of objectives. Crowding distances are
also used in NSGA-II to keep individuals in a pop-
ulation diverse to represent the entire Pareto-frontier
properly. NSGA-II is known as a good algorithm for
a problem with a relatively small number of objective
functions.
In this study, we formulated VESAP as a bi-
objectiveoptimization problem with the expected val-
ues of f
1
and f
2
as the objective functions. Then,
we employed the NSGA-II algorithm to obtain a set
of Pareto-optimal solutions for a bi-objective prob-
lem. Because the outcome of a solution is evaluated
through a simulation, numerous simulation trials are
required to estimate the expected values. Determin-
ing the number of simulations to estimate an expected
value is debatable because the solutions will be un-
trusted if the number is small, whereas it is accurate
but computationally expensive if the number is large.
We conducted 24 simulations, similar to that in Sec-
tion 4, to estimate the expected values for each solu-
tion in the NSGA-II search procedure. Thus, to obtain
a set of Pareto-optima, we required a total of 24NG
simulations in a single NSGA-II run with N popula-
tion size and G generations.
However, the number 24 might be quite small to
explore a Pareto-optimum that is precise to repre-
sent the true Pareto-frontiers. Therefore, we adopted
a two-phase approach. First, we explored a set of
Pareto-optima using NSGA-II with a small number
(N=24) of simulations. Second, 100 simulation runs
were reconducted for the Pareto-optima obtained in
the first phase to calculate more accurate expected
values and AVaRs. Note that some Pareto-optima ob-
tained in the first phase might degenerate in the sec-
ond phase.
In this study, NetLogo 6.0.2 (Wilensky, 1999) was
used to implement the crowd evacuation simulator by
using the evacuation decision model. The entire pro-
cedure was implemented in R x64 3.5.1 with the fol-
lowing libraries: nsga2R for the NSGA-II algorithm,
parallel for the parallel execution of the simulations
and RNetLogo for the connection between R and Net-
Logo. Simulations and optimizations were executed
on a machine with an Intel Core i7-6700 CPU.
6 PERFORMANCE ANALYSIS
6.1 Case Study and NSGA-II
First, we attempted to explore the Pareto-optimal so-
lutions for the case with two visual evacuation signs
like in Section 4. The coordinates of the visual signs
were chosen as continuous decision Variables, x ∈
[−65, 65] and y ∈ [−21, 21], and the NSGA-II algo-
rithm with 36 populations and 50 generations was ap-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
76

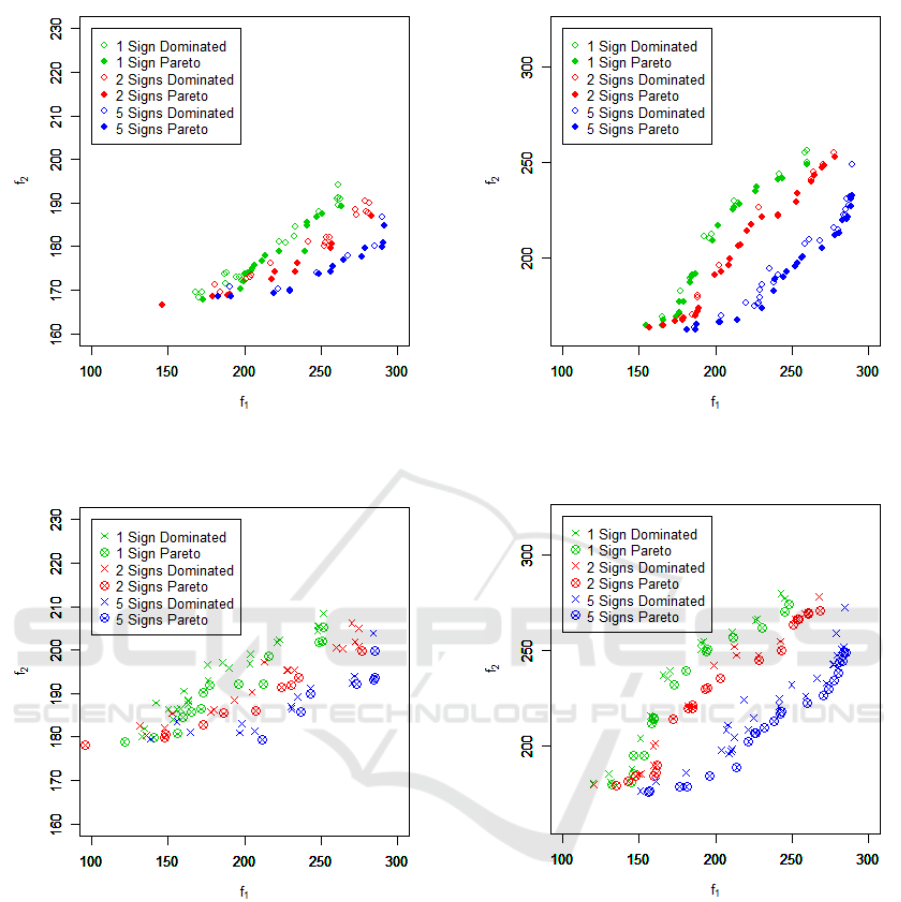
Figure 12: Expected value of the Pareto-frontier for S
1
. The
one-, two-, and five-sign cases are depicted in green, red,
and blue, respectively.
Figure 13: AVaR of the Pareto-frontier for S
1
. The one-
, two-, and five-sign cases are depicted in green, red, and
blue, respectively.
plied to explore the Pareto-optima. Because 24 simu-
lations were repeated to estimate the expected values
of f
1
and f
2
for each solution, a total of 43,200 sim-
ulations were performed to obtain the Pareto-optimal
solutions.
Figure 8 shows the results of NSGA-II with the
results obtained in the case study presented in Sec-
tion 4 for S
1
and S
2
. The red triangles show the
Pareto-optima obtained by the brute-force approach
in Section 4; the blue open and filled circles represent
the dominated and the Pareto-optimal solutions ob-
tained by NSGA-II, respectively. NSGA-II explored
Figure 14: Expected value of the Pareto-frontier for S
2
. The
one-, two-, and five-sign cases are depicted in green, red,
and blue, respectively.
Figure 15: AVaR of the Pareto-frontier for S
2
. The one-
, two-, and five-sign cases are depicted in green, red, and
blue, respectively.
22 and 36 Pareto-optimal solutions for S
1
and S
2
, re-
spectively. These figures show that the Pareto-optima
obtained by NSGA-II almost overlap with those ob-
tained by the brute-force approach, even though the
former only requires 43,200 simulations, whereas the
latter requires 85,680 simulations. This shows that
NSGA-II can explore Pareto-optima reasonably good
enough with lower computational cost.
Multi-objective Risk Analysis for Crowd Evacuation Guidance using Multiple Visual Signs
77

Table 1: Four representative solutions satisfying the Pareto-
optimal for both the expected values and the AVaRs in the
two-sign case.
Solution
¯
f
1
¯
f
2
AVaR( f
1
) AVaR( f
2
)
S
1
1 274.67 186.63 267.07 201.33
2 257.40 180.92 236.40 192.80
3 217.98 173.04 197.37 186.50
4 173.97 167.38 124.63 178.93
S
2
1 276.43 249.65 267.93 273.40
2 220.80 210.91 202.23 237.73
3 203.74 190.28 180.63 213.77
4 175.62 166.07 147.10 179.50
6.2 Validation Simulation
We then reconducted 100 simulation runs for the
Pareto-optima obtained by NSGA-II to evaluate
the expected values and AVaRs accurately. Fig-
ure 9 shows the Pareto-optimal solutions obtained by
NSGA-II and the results of 100 simulations recon-
ducted for the validation purpose. The black filled
circles show the Pareto-optima obtained by NSGA-II,
and the red filled and open circles show the Pareto-
optimal and the dominated solutions obtained by 100
simulations, respectively. The AVaRs at level 0.3 of
these Pareto-optima are also indicated by the red ‘×’
in the figure. In both figures, the red filled circles
are located in the upper-left area of the black filled
circles, suggesting that NSGA-II with 24 simulation
trials will produce Pareto-optima that are more op-
timized than the real ones. The numbers of Pareto-
optima for S
1
and S
2
decreased to 12 and 19, respec-
tively, in this analysis (red filled circles in Fig. 9).
Among these, 8 and 14 solutions in S
1
and S
2
, re-
spectively, satisfy the Pareto-efficiency for both the
expected values and the AVaRs. Four representative
solutions for S
1
and S
2
are presented in Table 1 and
illustrated in Figs. 10 and 11, respectively.
6.3 Number of Visual Signs
We also conducted the same analysis for the cases
with one, two, and five visual signs to illustrate the
effect of the number of visual signs. In the one- and
two-sign cases, the population size and the genera-
tions in NSGA-II were set to 48 and 50, respectively.
In the five-sign case, both the population size and the
generations were set to 100. The one-sign case can
be considered as a baseline. The one-, two-, and five-
sign cases are shown in green, red, and blue, respec-
tively, in Fig. 12 for S
1
and in Fig. 14 for S
2
, respec-
tively. The Pareto-frontiers in blue, red, and green are
arranged in the order close to the lower right corner,
showing that the best result was obtained by the five-
Table 2: Summary of the analysis in Section 6 for S
1
and
S
2
. The column labels represent the following: S, number
of signs; Pops, population size in NSGA-II; Pareto, number
of expected values of the Pareto-optima found in NSGA-II;
EP, number of expected values of the Pareto-optima; AP,
number of AVaRs of the Pareto-optima; EP&AP, number of
expected values and AVaRs of the Pareto-optima. EP, AP,
and EP&AP are the results of 100 simulations reconducted
on the basis of the Pareto-optima found in NSGA-II (the
column labeled Pareto).
S Pops Pareto EP AP EP&AP
1 48 37 17 14 10
S
1
2 48 28 11 10 8
5 100 20 13 7 6
1 48 34 22 16 15
S
2
2 48 36 26 21 18
5 100 49 24 22 18
Table 3: Four representative solutions satisfying the Pareto-
optimal for both the expected values and the AVaRs in the
five-sign case.
Solution
¯
f
1
¯
f
2
AVaR( f
1
) AVaR( f
2
)
S
1
1 291.73 184.73 285.53 199.77
2 265.12 176.99 243.37 189.97
3 256.74 174.23 236.87 185.83
4 229.66 169.82 211.50 179.40
S
2
1 288.80 230.47 283.87 248.60
2 270.09 204.85 260.40 222.33
3 230.21 173.12 214.00 188.53
4 187.04 162.09 155.87 175.37
sign case and the worst result by the one-sign case.
The AVaRs corresponding to the expected values
of the Pareto-optima are presented in Figs. 13 and 15
for S
1
and S
2
, respectively. These AVaRs are not nec-
essarily Pareto-optimal, even though the correspond-
ing expected values are. The solutions satisfying the
Pareto-optimal for both the expected values and the
AVaRs are depicted by ‘⊗’ in Figs. 13 and 15. These
solutions are considered to be some of the best solu-
tions to the VESAP because they are Pareto-optima
for the expected values and have small risks. The re-
sults of the analysis are summarized in Table 2.
Four representative solutions with five signs for
S
1
and S
2
are presented in Table 3 and illustrated in
Figs. 16 and 17, respectively.
6.4 Illustrative Example
Figures 18 and 19 show two example solutions, P1
and P2, obtained by the VESAP with two visual signs
for S
1
in the objective and decision spaces, respec-
tively; Table 4 summarizes these solutions. These ex-
ample solutions highlight the advantage of the AVaR.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
78

Figure 16: Four representative solutions satisfying the
Pareto-optimal for both the expected values and the AVaRs
for the five-sign case in S
1
.
Figure 17: Four representative solutions satisfying the
Pareto-optimal for both the expected values and the AVaRs
for the five-sign case in S
2
.
Table 4: Two example solutions: P1 and P2. The column
‘PO’ indicates yes if the solution is Pareto-optimal for the
AVaR; no otherwise. A cell with a blue background shows
a better value.
¯
f
1
¯
f
2
AVaR( f
1
) AVaR( f
2
) PO
P1 257.40 180.92 236.40 192.80 yes
P2
258.30 181.79 224.33 196.60 no
In Fig. 18, the expected values, AVaR
0.3
s, and Real-
izations of f
1
and f
2
are depicted by the filled circles,
triangles, and ‘×,’ respectively. Both P1 and P2 are
Pareto-optimal for the expected values; whereas P1
is a Pareto-optimum, P2 is dominated by P1 for the
AVaRs (see the blue cells in Table 4). The two dashed
ellipses illustrate the 50% probability ellipses of P1
and P2, which reveals that P2 has more risks than
those of P1, whereas the expected values of the two
are almost equivalent. This is because the probability
ellipse of P1 is included in that of P2. The Realiza-
tions of P2 distributed more broadly than those of P1
in Fig. 18, which implies that P2 has a greater chance
of producing unexpectedly bad outcomes if we adopt
it as a solution.
Moreover, the p-values of the Wilcoxon rank sum
test for the statistically significant differences be-
tween P1 and P2 for
¯
f
1
,
¯
f
2
, AVaR( f
1
), and AVaR( f
2
)
were 0.50, 0.68, 0.00, and 0.53, respectively.
Figure 19 depicts P1 and P2 on the decision space.
The figure illustrates that these two solutions are simi-
lar, almost sharing one position (-31, -17) and with the
other positions also being close. This example high-
lights the advantage of the AVaR in that a subtle dif-
ference in the decision space will produce a solution
that can reduce the risks significantly.
Figure 18: Two example solutions: P1 and P2.
Figure 19: Two example solutions: P1 and P2.
7 RELATED WORKS
Numerous studies have been conducted on multi-
objective optimizations, and, currently, many re-
searchers in this field havedeveloped methods that are
based on EMO algorithm, which holds a set of solu-
tions, and iteratively approximating them to a Pareto-
frontier is intriguing and promising. Some repre-
sentative EMO algorithms besides NSGA-II include
MOEA/D (Zhang and Li, 2007), MSOPS (Hughes,
2005), and NSGA-III (Deb and Jain, 2014). Other
approaches promising to solve real-world multi-
objective optimization problems with cost-efficient
ways are CMA-ES (Hansen and Ostermeier, 1996)
and MOTPE (Ozaki et al., 2020).
Numerous works have been conducted to tackle
fitness functions contaminated with noise in the
EMO. Siegmund et al. (2015) proposed dynamic
resampling strategies based on evolutionary genera-
tions, Pareto-rankings, and distances to the reference
point to mitigate noisy environments(Siegmund et al.,
2015). Implicit sampling techniques that use a large
population size as a substitute for explicit sampling
were proposed in (Tan et al., 2001). Sano and Kita
Multi-objective Risk Analysis for Crowd Evacuation Guidance using Multiple Visual Signs
79

(2002) proposed a method that has a history of search
results to reduce the fitness evaluations (Sano and
Kita, 2002). Goh and Tan (2007) adopted an exper-
imental learning-directed perturbation strategy for a
noise-tolerant search strategy (Goh and Tan, 2007).
Probabilistic dominance was proposed for a robust
selection operation against noise in evolutionary op-
timizations (Fieldsend and Everson, 2005). All of
these approaches addressed the issues of how to ob-
tain quality solutions with lower cost; the risks be-
tween the real and the expected outcomes, which we
addressed in this study, were not considered.
Saadatseresht et al. (2009) formulated a crowd
evacuation guidance problem as a multi-objective op-
timization problem and solved it using NSGA-II to
develop evacuation plans (Saadatseresht et al., 2009).
Dubey et al. (2020) developed an interactive design
support system (AUTOSIGN) to develop an optimal
signage system with multiple objectives; the random
weight genetic algorithm (MO-RWGA) was applied
to handle these objectives in this system (Dubey et al.,
2020). Li et al. (2010) developed a method to achieve
optimal evacuation route assignments with three ob-
jectives, and NSGA-II was employed to solve the
problem (Li et al., 2010). However, none of these
approaches considered the risks or uncertainties in-
volved in the problem in the solution procedure.
Furthermore, Le´on et al. (2020) analyzed a
stochastic multi-objective problem using the AVaR,
assuming the risk aversion of the decision makers
(Le´on et al., 2020).
8 DISCUSSION
In this study, we analyzed the VESAP with mul-
tiple visual evacuation signs from the viewpoint of
the expected outcomes and risks involved in the so-
lutions. We formulated the VESAP as a stochastic
multi-objective optimization problem with two objec-
tive functions: maximizing the number of agents se-
lecting the correct exit ( f
1
) and minimizing the total
evacuation time (f
2
). NSGA-II, a multiple objective
evolutionary optimization algorithm, was applied to
explore the Pareto-optimal solutions, and the Pareto-
frontiers of the two objective functions were obtained
for the cases with one, two, and five visual signs for
two exit layouts (S
1
and S
2
). To save computational
efforts, we first explored Pareto-optima with a rela-
tively small sampling size (N=24) and then recon-
ducted 100 simulations on the basis of the Pareto-
optima obtained by the first trial to produce more ac-
curate results. Solutions satisfying the Pareto-optimal
for both the expected values and the AVaRs were ob-
tained in all cases (one, two, and five signs; two lay-
outs: S
1
and S
2
).
Figure 8 shows that NSGA-II can explore Pareto-
frontiers reasonably close enough to those obtained
by brute-force approaches. However, NSGA-II with
a small sample size will lead to somewhat inaccurate
solutions whose outcomes are estimated optimisti-
cally (Fig. 9). This indicates that reconducting sim-
ulation with a large sample size may be necessary.
Simulations with a different number of visual
signs (Figs. 10, 11, 16, and 17) revealed that having
many visual signs always led to better solutions. This
is especially true if both the objective values were dis-
tant to the extreme point (minimum or maximum).
Figure 12–15 show that the difference between the
two Pareto-frontiers with a small and a large num-
ber of visual signs is significant at the middle of the
Pareto-front. If more visual signs are introduced, bet-
ter solutions would be obtained, whereas the problem
with many signs requires massive computational re-
sources. The tradeoff between computational cost and
solution quality would be of interest.
We are aware that our research has some limita-
tions and open problems. Some may consider our
results inaccurate, owing to the insufficient compu-
tational resources. Had we conducted more simula-
tion runs or incorporated the social force model in the
simulations, we could have obtained more accurate
results. Some approaches that can generate Pareto-
optimal solutions with lower costs, as discussed in
Section 7, might be adopted for this purpose. We
also assumed that the two objective functions are
independent and employed a logical conjunction of
two AVaRs (AVaR( f
1
) ∧ AVaR( f
2
)) to test the Pareto-
efficiency. This might be inappropriate if two objec-
tives are negatively correlated. In such cases, one
objective will produce a better outcome, whereas the
other will have a worse value; both objectives produc-
ing worse outcomes simultaneously will hardly occur
though. The logical conjunction of two AVaRs that
may overestimate the risks is not likely to realize; a
different approach is required to deal with this issue.
However, we reserve these problems for future works.
9 CONCLUSION
In this study, we analyzed the VESAP in cases with
multiple visual evacuation signs. The NSGA-II algo-
rithm was applied to explore the Pareto-optimal solu-
tions efficiently with a relatively small number of sim-
ulation trials. The VESAPs in cases with one, two and
five visual evacuation signs were investigated, and the
solutions satisfying the Pareto-efficiency for both the
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
80

expected values and the AVaRs were obtained for two
different exit layouts.
ACKNOWLEDGMENTS
The author is grateful to Mr. Kei Marukawa
for helpful discussions and comments on the
manuscript. The author would like to thank Editage
(www.editage.com) for English language editing.
REFERENCES
Cisek, M. and Kapalka, M. (2014). Evacuation route assess-
ment model for optimization of evacuation in build-
ings with active dynamic signage system. Transporta-
tion Research Procedia, 2:541–549. The Conference
on Pedestrian and Evacuation Dynamics 2014 (PED
2014), 22-24 October 2014, Delft, The Netherlands.
Deb, K. and Jain, H. (2014). An evolutionary many-
objective optimization algorithm using reference-
point-based nondominated sorting approach, Part I:
Solving problems with box constraints. IEEE Trans-
actions on Evolutionary Computation, 18(4):577–
601.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).
A fast and elitist multiobjective genetic algorithm:
Nsga-ii. IEEE Transactions on Evolutionary Compu-
tation, 6(2):182–197.
Dubey, R. K., Khoo, W. P., Morad, M. G., H¨olscher, C., and
Kapadia, M. (2020). AUTOSIGN: A multi-criteria
optimization approach to computer aided design of
signage layouts in complex buildings. Computers &
Graphics, 88:13–23.
Fieldsend, J. and Everson, R. (2005). Multi-objective opti-
misation in the presence of uncertainty. In 2005 IEEE
Congress on Evolutionary Computation, IEEE CEC
2005. Proceedings, volume 1, pages 243–250.
Galea, R. E., Xie, H., and Lawrence, J. P. (2014). Experi-
mental and survey studies on the effectiveness of dy-
namic signage systems. Fire Safety Science, 11:1129–
1143.
Goh, C. K. and Tan, K. C. (2007). An investigation on
noisy environments in evolutionary multiobjective op-
timization. IEEE Transactions on Evolutionary Com-
putation, 11(3):354–381.
Gutjahr, W. J. and Pichler, A. (2016). Stochas-
tic multi-objective optimization: a survey on non-
scalarizing methods. Annals of Operations Research,
236(2):475–499.
Haghani, M. (2020a). Empirical methods in pedestrian,
crowd and evacuation dynamics: Part I. experimen-
tal methods and emerging topics. Safety Science,
129:104743.
Haghani, M. (2020b). Empirical methods in pedestrian,
crowd and evacuation dynamics: Part II. field methods
and controversial topics. Safety Science, 129:104760.
Haghani, M. and Sarvi, M. (2016). Human exit choice
in crowd built environments: investigating underlying
behavioural differences between normal egress and
emergency evacuations. Fire Safety Journal, 85:1–9.
Haghani, M., Sarvi, M., Shahhoseini, Z., and Bolts,
M. (2016). How simple hypothetical-choice ex-
periments can be utilized to learn humans’ naviga-
tional escape decisions in emergencies. PLOS ONE,
11(11):e0166908.
Hansen, N. and Ostermeier, A. (1996). Adapting arbitrary
normal mutation distributions in evolution strategies:
the covariance matrix adaptation. In Proceedings of
IEEE International Conference on Evolutionary Com-
putation, pages 312–317.
Helbing, D., Farkas, I., and Vicsek, T. (2000). Simu-
lating dynamical features of escape panic. Nature,
407(28):487–490.
Hughes, E. (2005). Evolutionary many-objective optimi-
sation: many once or one many? In 2005 IEEE
Congress on Evolutionary Computation, volume 1,
pages 222–227 Vol.1.
Ji, Q., Xin, C., Tang, S., and Huang, J. (2017). Symmetry
associated with symmetry break: revisiting ants and
humans escaping from multiple-exit rooms. Physica
A.
Le´on, J., Puerto, J., and Vitoriano, B. (2020). A risk-
aversion approach for the multiobjective stochastic
programming problem. Mathematics, 8(11).
Li, Q., Fang, Z., Li, Q., and Zong, X. (2010). Multiobjective
evacuation route assignment model based on genetic
algorithm. In 2010 18th International Conference on
Geoinformatics, pages 1–5.
Lovreglio, R., Fonzone, A., dell’Olio, L., and Ibeas, A.
(2014). The role of herding behaviour in exit choice
during evacuation. Procedia - Social and Behavioral
Sciences, 160:390–399.
Ogryczak, W. and Ruszczynski, A. (2002). Dual stochas-
tic dominance and related mean-risk models. SIAM
Journal on Optimization, 13(1):60–78.
Ozaki, Y., Tanigaki, Y., Watanabe, S., and Onishi, M.
(2020). Multiobjective tree-structured parzen estima-
tor for computationally expensive optimization prob-
lems. In Proceedings of the 2020 Genetic and Evolu-
tionary Computation Conference, GECCO ’20, page
533–541, New York, NY, USA. Association for Com-
puting Machinery.
Rachec, S. T., Stoyanov, S. V., and Fabozzi, F. J. (2008). Ad-
vanced stochastic Models, Risk Assessment, and Port-
folio Optimization: The Ideal Risk, Uncertainty, and
Performance Measures. Wiley.
Saadatseresht, M., Mansourian, A., and Taleai, M. (2009).
Evacuation planing using multiobjective evolutionary
optimization approach. European Journal of Opera-
tional Research, 198:305–314.
Sano, Y. and Kita, H. (2002). Optimization of noisy fitness
functions by means of genetic algorithms using his-
tory of search with test of estimation. In Proceedings
of the 2002 Congress on Evolutionary Computation.
CEC’02 (Cat. No.02TH8600), volume 1, pages 360–
365 vol.1.
Multi-objective Risk Analysis for Crowd Evacuation Guidance using Multiple Visual Signs
81

Sieben, A., Schumann, J., and Seyfried, A. (2017).
Collective phenomena in crowds—where pedestrian
dynamics need social psychology. PLOS ONE,
12(6):e0177328.
Siegmund, F., Ng, A., and Deb, K. (2015). Hybrid dynamic
resampling for guided evolutionary multi-objective
optimization. volume 9018.
Tan, K., Lee, T., and Khor, E. (2001). Evolutionary algo-
rithms with dynamic population size and local explo-
ration for multiobjective optimization. IEEE Transac-
tions on Evolutionary Computation, 5(6):565–588.
Tsurushima, A. (2019). Modeling herd behavior caused
by evacuation decision making using response thresh-
old. In Davidsson, P. and Verhagen, H., editors,
Multi-Agent-Based Simulation XIX. MABS2018. LNAI
11463, pages 138–152. Springer.
Tsurushima, A. (2020). Validation of evacuation decision
model: An attempt to reproduce human evacuation
behaviors during the great east japan earthquake. In
In Proceedings of the 12th International Conference
on Agents and Artificial Intelligence (ICAART 2020) -
Volume 1, pages 17–27.
Tsurushima, A. (2021a). Herd behavior is sufficient to re-
produce human evacuation decisions during the great
east japan earthquake. In Rocha, A., Steels, L., and
Van den Herik, J., editors, Agents and Artificial In-
telligence. ICAART 2020. Lecture Notes in Computer
Science, volume 12613, pages 3–25. Springer.
Tsurushima, A. (2021b). Reproducing evacuation behav-
iors of evacuees during the Great East Japan Earth-
quake using the evacuation decision model with re-
alistic settings. In Proceedings of the 13th Inter-
national Conference on Agents and Artificial Intelli-
gence (ICAART 2021) - Volume 1, pages 17–27. IN-
STICC, SciTePress.
Tsurushima, A. (2021c). Scochastic multi-objective deci-
sion analysis for crowd evacuation guidance using a
single visual signage. In 2021 IEEE International
Conference on Systems, Man, and Cybernetics (SMC),
pages 360–367.
Tsurushima, A. (2021d). Simulation analysis of tunnel
vision effect in crowd evacuation. In Rutkowski,
L., Scherer, R., Korytkowski, M., Pedryca, W.,
Tadeusiewicz, R., and Zurada, J. M., editors, Artificial
Intelligence and Soft Computing. ICAISC 2021. Lec-
ture Notes in Computer Science, volume 12854, pages
506–518. Springer.
Wilensky, U. (1999). NetLogo. Center for Connected
Learning and Computer-Based Modeling, Northwest-
ern University, Evanston, IL.
Zhang, Q. and Li, H. (2007). MOEA/D: A multiob-
jective evolutionary algorithm based on decomposi-
tion. IEEE Transactions on Evolutionary Computa-
tion, 11(6):712–731.
Zhou, M., Dong, H., Ioannou, P. A., Zhao, Y., and Wang,
F. (2019). Guided crowd evacuation: approaches and
challenges. IEEE/CAA Journal of Automatica Sinica,
6(5):1081–1094.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
82