Refined co-SVD Recommender Algorithm: Data Processing and
Performance Metrics
Jia Ming Low
1 a
, Ian K. T. Tan
2 b
and Chern Hong Lim
1 c
1
School of IT, Monash University Malaysia, Bandar Sunway, 47500 Subang Jaya, Selangor, Malaysia
2
MACS, Heriot-Watt University Malaysia, Precinct 5, 62200 Putrajaya, Malaysia
Keywords:
Recommender System, Reproducibility, Matrix Co-factorization, Top-N Recommendation.
Abstract:
A resurgence of research interest in recommender systems can be attributed to the widely publicized Netflix
competition with the grand prize of USD 1 million. The competition enabled the promising collaborative
filtering algorithms to come to prominence due to the availability of a large dataset and from it, the growth
in the use of matrix factorization. There have been many recommender system projects centered around use
of matrix factorization, with the co-SVD approach being one of the most promising. However, the field is
chaotic using different benchmarks and evaluation metrics. Not only the performance metrics reported are
not consistent, but it is difficult to reproduce existing research when details of the data processing and hyper-
parameters lack clarity. This paper is to address these shortcomings and provide researchers in this field with
a current baseline through the provision of detailed implementation of the co-SVD approach. To facilitate
progress for future researchers, it will also provide results from an up-to-date dataset using pertinent evaluation
metrics such as the top-N recommendations and the normalized discounted cumulative gain measures.
1 INTRODUCTION
The matrix factorization approach and the applica-
tion of various deep learning algorithms are the cur-
rent favored approaches by recommender systems re-
searchers (Low et al., 2019). Matrix factorization
came to prominence due to the Netflix competition
with a grand prize of USD 1,000,000. This was won
by Robert Bell and Chris Volinsky, whose algorithm
ignite the subsequent immediate work in this field in
utilizing the matrix factorization algorithm.
It was quickly noted that the matrix factorization
algorithm suffers from an over-fitting issue, due to
the sparsity of the data in the matrix. This was the
main challenge that was being attempted by the re-
searchers in this field and it became more apparent as
the newer datasets grew in size. The richness of the
rating entries is therefore crucial to the performance
of recommender systems. When the system has mil-
lions of items, users are unlikely to have rated every
item. Hence the rating matrix will be constructed with
many empty entries. The sparse matrix will cause the
a
https://orcid.org/0000-0002-0422-9991
b
https://orcid.org/0000-0003-1474-8717
c
https://orcid.org/0000-0003-4754-6724
recommender systems to produce inaccurate recom-
mendations.
To reduce the sparsity of the matrix, Luo et al.
(2019) proposed the co-SVD method, a state of
the art matrix factorization algorithm based recom-
mender system. The proposed method is a matrix
co-factorization that utilizes short text descriptions of
items (tag) and related time information to mitigate
the over-fitting issue caused by the highly sparse rat-
ing matrix. We reviewed the published article and dis-
covered several limitations in the reproduction. The
identified issues are as follows.
1. Complete implementation details were not avail-
able, leading to reproducible limitations.
2. It reported objective relevance using precision, re-
call and F
1
scores, whereas for recommender sys-
tem, the recommended items should be based on
the likelihood that they will meet the users’ inter-
est, which is inherently subjective Herlocker et al.
(2004).
1.1 Reproducible Research
A systematic analysis of publications (Dacrema et al.,
2019) discovered that there is a state of discontinu-
ance happening for research work on recommender
668
Low, J., Tan, I. and Lim, C.
Refined co-SVD Recommender Algorithm: Data Processing and Performance Metrics.
DOI: 10.5220/0010887500003122
In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 668-674
ISBN: 978-989-758-549-4; ISSN: 2184-4313
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

systems. The lack of information regarding the imple-
mentation of the algorithm, and the evaluation proce-
dure has hindered the progress of recommender sys-
tems research as it is difficult for the research com-
munity to continue or replicate the proposed research
works.
Similarly to the current co-SVD work by Luo et al.
(2019), there are missing details of the work for the
research community to build upon. In the absence of
source code for the work by Luo et al. (2019), the de-
scriptions in the published article were insufficient to
reproduce the co-SVD work accurately. The missing
details include:
1. The exact filtering rules for the tag records to re-
produce the same number of tags,
2. The hyper-parameters setting, and
3. The seed number for the data splitting in order to
reproduce the results.
1.2 Appropriate Evaluation Metric for
Recommender Systems
Root Mean Square Error (RMSE) and Mean Abso-
lute Error (MAE) are the 2 main measurements used
for the work by Luo et al. (2019). They are used
to measure the deviation from the predicted ratings
and the actual ratings given by the users. These mea-
sures can be complemented by a classification model,
which will provide a more direct association with the
purpose of a recommender system.
Objective measures of precision, recall and F
1
scores were also applied by Luo et al. (2019) to evalu-
ate the co-SVD. However, specific measurement met-
rics for recommender systems, such as the top-N rec-
ommendation evaluation as used in research works
(Maheshwari and Majumdar, 2018; Hu et al., 2018;
Lee et al., 2019) should be reported.
1.3 Reproducible Research Summary
To summarize, details of the reproducible research are
as follows:
1. Reproduce the co-SVD implementation with mi-
nor result differences against the original work,
2. Conduct additional evaluations, using the top-
N recommendations, including using the newer
dataset released by MovieLens
1
,
3. Publish the source code of this implementation to
contribute to the recommender systems commu-
nity for research continuation.
1
MovieLens Dataset https://grouplens.org/datasets/
movielens
The rest of this paper is structured as follows; in
Section 2, the procedures of reproducing co-SVD are
elaborated, in Section 3, the evaluation of the repro-
duced co-SVD are discussed and we conclude in Sec-
tion 4.
2 REPRODUCING THE co-SVD
METHOD
In reproducing the work by Luo et al. (2019), several
challenges were encountered.
1. Data Pre-processing
Applying the same data pre-processing proce-
dures described by Luo et al. (2019) on the same
dataset, resulted in a difference in the number of
tags.
2. Hyper-parameters
The hyper-parameters such as the learning rate
and seed number for dataset splitting, were not
provided nor clearly explained in Luo et al.
(2019). Without access to these settings, results
consistent with the published article cannot be re-
produced accurately and pose a challenge to vali-
date the implementation.
The next subsections will elaborate and discuss
the reproducible issues and their corresponding solu-
tions, starting with a description of the datasets.
2.1 Evaluation Datasets
Two MovieLens datasets were applied in the work by
Luo et al. (2019); a small dataset and a larger dataset.
The small dataset is the MovieLens 100K dataset (ml-
100K (2016))
2
released in the year 2016. This dataset
contains 100,004 ratings and 1296 tag records across
9125 movies. It was collected from 671 users between
January 9, 2015, and October 16, 2016. However,
this dataset is no longer available on the GroupLens
official website. The dataset was downloaded from
the Internet Archive online library.
The large dataset is the MovieLens 10M dataset
(ml-10M) that was released in the year 2009. This
dataset contains 10,000,054 ratings and 95,580 tag
records across 10,681 movies. It was collected from
71,567 users of MovieLens.
For both of the datasets, the users were selected
randomly, with the condition that the users have rated
at least 20 movies. The values of the users’ ratings are
between the range of 0.5 and 5.
2
MovieLens 100K dataset 2016 https://bit.ly/2ULNV5i
Refined co-SVD Recommender Algorithm: Data Processing and Performance Metrics
669

As a newer version of the MovieLens 100K
dataset (ml-100K (2018))
3
has been published, we
also reported the results using this newer dataset. This
is to assess the stability of the co-SVD results and
also to provide continuation for the work. This ml-
100K (2018) dataset was published in 2018, it con-
tains 100,836 ratings and 3683 tag records across
9742 movies that were collected from 610 users. The
dataset was collected between March 29, 1996, and
September 24, 2018.
Table 1: Details of datasets used.
Attributes
ml-100K
(2016)
ml-100K
(2018)
ml-10M
No of Users 671 610 71,567
No of Movies 9125 9739 10,681
No of Ratings 100,004 100,836 10,000,054
No of Tags 1296 3683 95,564
Completeness (Ratings) 1.63e
−2
1.70e
−2
1.31e
−2
Completeness (Tags) 2.11e
−2
6.20e
−4
1.25e
−4
The rating scale of all the MovieLens datasets is
from 0 to 5. Summary of the three datasets used for
our evaluation is tabulated in Table 1.
2.2 Data Pre-processing
The datasets were pre-processed where the discontin-
uous numbering of user id, movie id and tag id
were re-ordered and re-mapped to the lower ranges
(re-indexed) in order not to affect the dataset repre-
sentation.
The other data pre-processing was to filter tags
with less than 5 occurrences, which was proposed by
Vig et al. (2012), although they used 10 instead of 5.
Despite applying the same filtering rules, we
could not match the recorded remaining tag records
as stated by Luo et al. (2019). The differences of the
post-processed datasets are as shown in Tables 2 and
3.
Table 2: Comparison of ml-100K(2016) dataset between
original work and reproduction.
Attributes
Original
Reproduced
with Filter
Reproduced
without Filter
No of Users 671 671 671
No of Movies 9125 9125 9125
No of Ratings 100,004 100,004 100,004
No of Tags 1056 598 1296
Completeness (Ratings) 1.63e
−2
1.63e
−2
1.63e
−2
Completeness (Tags) 1.72e
−4
9.76e
−5
2.11e
−2
In order to replicate as closely as possible to the
figures recorded by Luo et al. (2019), several assump-
tions and additional methods were applied to both
datasets. The methods are listed as follow:
Step I: Convert tags (text) to lowercase
Step II: Remove punctuations and whitespaces
3
MovieLens 100K dataset 2018 https://bit.ly/2xNMzhp
Table 3: Comparison of ml-10M dataset between original
work and reproduction.
Attributes
Original
Reproduced
with Filter
Reproduced
without Filter
No of Users 71,552 71,268 71,567
No of Movies 10,681 10,681 10,681
No of Ratings 10,000,054 10,000,054 10,000,054
No of Tags 91,450 75,385 95,564
Completeness (Ratings) 1.31e
−2
1.31e
−2
1.31e
−2
Completeness (Tags) 1.20e
−4
9.9e
−5
1.25e
−4
Step III: Cross-reference with larger dataset (Lat-
est complete MovieLens dataset
4
)
A complete list of the tags was derived from
the 27M MovieLens dataset instead of the ml-100K
(2016) and ml-10M datasets. Although this narrowed
the gap, there is still a significant gap.
To achieve a closer match to the figures stated in
(Luo et al., 2019), the tag filtering threshold was re-
vised. Various thresholds were used and re-applied
to both datasets and the results for the number of
remaining tags are depicted in Figures 1 and 2 for
the ml-100K(2016) and ml-10m datasets respectively.
Even with regressive testing using different thresh-
olds, it was decided that by removing the threshold,
it would result in the closest match to the number of
tags. Hence, we proceeded with no threshold setting.
Figure 1: The number of remaining tag records of ml-
100K(2016) dataset by different thresholds.
2.3 Model Development
The co-SVD implementation was reproduced from
the algorithms provided by Luo et al. (2019) using the
Python programming language (version 3.7). It uti-
lizes Suprise
5
, a Python library with common algo-
rithms used for recommender systems. This enables
the standardization of the models used for evaluation.
The format of the input to the model was not
clearly discussed in the published work. To gener-
4
Full Latest MovieLens Dataset https://bit.ly/2xNMzhp
5
Surprise Python package http://surpriselib.com/
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
670

Figure 2: The number of remaining tag records of ml-10M
dataset by different thresholds.
ate the user-tag matrix and movie-tag matrix, the rat-
ings data and tags data were assumed to be merged.
Both datasets were merged by using the user ID
and movie ID with an outer join. Also, the merged
datasets were utilized for the model training later.
The source code of the reproduced co-SVD is pub-
lished on a GitHub
6
repository to facilitate future re-
search and development for researchers and practi-
tioners.
2.4 Hyper-parameters Tuning
For the model, the settings of the hyper-parameters
are crucial to generate consistent results. However,
some hyper-parameters, such as learning rate and the
seed number for data splitting, were not provided nor
clearly explained in the original publication. In or-
der to reproduce similar results as reported by Luo
et al. (2019), hyper-parameters tuning is required.
”Grid Search” (also known as Brute-force Search)
(Chicco, 2017) was applied to find the optimal hyper-
parameters of the reproduced model.
In order to achieve the lowest RMSE, the learning
rate of the model was set as 0.0028 and 65 iterations
(epoch) were used for each execution iteration. The
regularization weights of co-SVD stated by Luo et al.
(2019) was followed. With the same setting, the re-
sults of other evaluation metrics are optimal.
3 EVALUATION
The next few sub-sections will elaborate on the setup
of the experiments, the extensive verification proce-
dures, description of the measurements metrics and
the baseline methods.
6
GitHub Repository https://git.io/JY8hg
3.1 Dataset
Three datasets (as shown in Table 1) were used
for this evaluation. They are 100K MovieLens
dataset year 2016 (ml-100K (2016)), 100K Movie-
Lens dataset year 2018 (ml-100K(2018)) and 10M
MovieLens dataset (ml-10M).
3.2 Performance Metrics
3.2.1 Precision and Recall
In addition to the RMSE and MAE, precision and re-
call measures were used for evaluating the model per-
formance by Luo et al. (2019). Some data transfor-
mation steps are required for measuring precision and
recall. The actual and predicted ratings need to be
transformed into binary labels (high rating as 1, low
ratings as 0). A threshold was set for classifying the
ratings and 3.5 was adopted as the threshold by Luo
et al. (2019). The ratings that are greater or equal to
3.5 will be labelled as “high rating”. Otherwise, they
will be labelled as “low rating”.
However, the precision and recall based on the
threshold to rate high and low were not applied in
our work. We omitted this evaluation because we
deemed this setting of the threshold to be unsuitable.
To measure the precision and recall, the separation
(the threshold setting) of the high and low rated items
was defined and it was done across the board with-
out taking into account the individual user’s rating
scale. We deemed this as inappropriate as each user
will have their own personal rating scales. This is in
concurrence with Herlocker et al. (2004), where it was
stated that an item rated with 3 on a 5-point scale may
be considered as a high rating by a user, but another
user may or may not agree with it.
Instead of using a fixed threshold for all users, in-
dividual thresholds were computed using the top-N
recommendations approach. To generate top-N rec-
ommendations, the predicted ratings were ranked and
the highest N ranked items will be the selected rec-
ommendations.
For the purpose of computing the precision and
recall, the thresholds to determine whether the ratings
are relevant (high rating) or irrelevant (low rating) is
determined individually by computing the means of
the ratings given by the users. If the rating of the item
is greater than or equal to the threshold, then the item
is considered relevant to the user, otherwise irrelevant.
Based on the predicted top-N recommendations,
the precision and recall rates determine the algorithm
performance on making relevant recommendations.
The value of N is typically set as 5. The number is
Refined co-SVD Recommender Algorithm: Data Processing and Performance Metrics
671

low as users are generally interested and will rate only
a few items. This setting is most effective for top-N
recommendations as discussed in the work proposed
by Steck (2010).
For a user u, the precision rate for top-5 recom-
mendations is denoted as Precision
u
@5; the recall
rate is denoted as Recall
u
@5. The Precision
u
@N and
Recall
u
@N can be computed by the equations given
in Equation 1.
Precision
u
@N =
|Rel
u
∩ Rec
u
|
|Rec
u
|
Recall
u
@N =
|Rel
u
∩ Rec
u
|
|Rel
u
|
(1)
where Rel
u
represents a set of items that is relevant to
the user u (e.g., a set of items rated by user u); Rec
u
represents a set of N items that are recommended to
the user u.
An overall average Precision
u
@N and
Recall
u
@N were calculated across the users base.
They were denoted as Precision@5 and Recall@5
for top-5 recommendations.
3.2.2 Normalized Discounted Cumulative Gain
In addition to using Precision@5 and Recall@5, the
normalized discounted cumulative gain (nDCG) mea-
sure (J
¨
arvelin and Kek
¨
al
¨
ainen, 2002) was also re-
ported.
nDCG is to examine the performance according to
the ranked positions of the recommended items. Let
y
k
represents the availability of the rating (r
u,i
k
) for
user-item pairs (u, i
k
) that the item is the k
th
items in
the recommended items set Rec
u
. If i
k
/∈ Rel
u
, then y
k
will be set as 0. The equation for nDCG@N is given
in Equation 2:
nDCG@N =
DCG
u
@N
IDCG
u
@N
DCG
u
@N =
N
∑
k=1
2
y
k
− 1
log
2
(k + 1)
(2)
where IDCG
u
@N represents the ideal DCG
u
@N that
the y
k
for every item i
k
appeared in recommended
item list will be set as 1.
3.3 Baseline Methods
Three baseline matrix factorization algorithms were
selected for the performance comparison with our re-
produced co-SVD. SVD (Koren et al., 2009), SVD++
(Koren, 2008) and NMF (Luo et al., 2014) were se-
lected.
Luo et al. (2019) compared the co-SVD with
SVD. The same comparisons were evaluated in our
work as the results reported for SVD were very close
to that of the co-SVD implementation. We have also
included SVD++ and NMF as alternative approaches
to the improvement of SVD and hence will be a suit-
able comparison vis-
`
a-vis co-SVD.
Hyper-parameters optimization was done for all
the models with “Grid Search”. The Surprise pack-
age do provide the functionality to perform the “Grid
Search”. 10-fold cross-validation was applied to se-
lect the appropriate values of the hyper-parameters.
The settings for the baseline methods are tabulated in
Table 4.
Table 4: Optimized hyper-parameters of baseline methods.
Model Epochs Learning Rate Regularization Weight (reg)
SVD 60 0.008 0.091
SVD++ 45 0.0012 0.0012
NMF 40 0.001
reg(users): 0.19
reg(items): 0.08
reg(users’ bias): 0.001
reg(items’ bias): 0.001
3.4 Experimental Setup
The reproduced co-SVD was evaluated with 10-
fold cross-validation for each different factor size F,
where F indicates the size of the dimension of the la-
tent features. Neither the learning rate nor the epoch
were stated by Luo et al. (2019) and through the Grid
Search function provided by the Python Surprise
package, the learning rate of 0.0028 and 65 iterations
(epoch) were used for each execution iteration. The
regularization weights of co-SVD stated by Luo et al.
(2019) was followed. To ensure that the results can
be reproduced in future, the seed number for the data
splitting of cross-validation is set as 123.
3.5 Experimental Results
The RMSE and MAE results generated from cross-
validation are shown in Table 5 and 6. The means
are measured from the results obtained from cross-
validation. The co-SVD was reproduced with mini-
mal differences in terms of RMSE and MAE. The per-
formance of reproduced co-SVD on 100K MovieLens
(ml-100K (2016)) dataset is similar to that reported by
Luo et al. (2019) with differences of less than 0.005.
Also, the reproduced co-SVD performed slightly bet-
ter when dealing with 10M MovieLens dataset (ml-
10M).
Since the co-SVD was reproduced with minimal
difference, the model was tested further with the top-
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
672

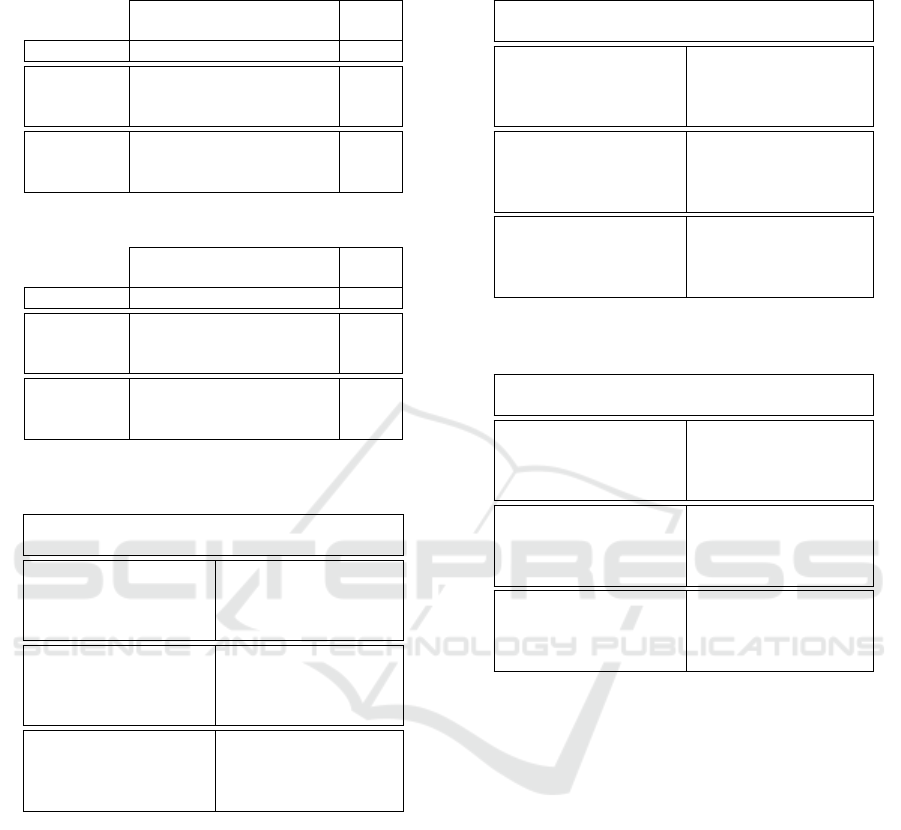
Table 5: RMSE and MAE performance on ml-100K (2016)
dataset.
Reproduced
co-SVD
co-SVD
Luo et al. (2019)
Metrics F Mean Results Diff.
RMSE
40 0.8813 0.8804 0.0009
30 0.8817 0.8818 0.0001
20 0.8832 0.8818 0.0014
MAE
40 0.6759 0.6721 0.0038
30 0.6763 0.6731 0.0032
20 0.6773 0.6731 0.0042
Table 6: RMSE and MAE performance on ml-10M dataset.
Reproduced
co-SVD
co-SVD
Luo et al. (2019)
Metrics F Mean Results Diff.
RMSE
40 0.7834 0.7890 0.0056
30 0.7842 0.7899 0.0057
20 0.7866 0.7917 0.0051
MAE
40 0.6012 0.6054 0.0042
30 0.6019 0.6061 0.0042
20 0.6039 0.6076 0.0038
Table 7: Precision@5, Recall@5 and nDCG@5 perfor-
mance on ml-100K (2016) dataset.
Metrics Model Number of Factors(F)
F=40 F=30 F=20
Precision@5
(Re)co-SVD 0.5975 0.5947 0.5887
SVD 0.5988 0.5971 0.6008
SVD++ 0.5819 0.5806 0.5766
NMF 0.5744 0.5748 0.5640
Recall@5
(Re)co-SVD 0.4166 0.4154 0.4126
SVD 0.4215 0.4188 0.4210
SVD++ 0.4078 0.4063 0.4041
NMF 0.3984 0.3890 0.3744
nDCG@5
(Re)co-SVD 0.8320 0.8320 0.8309
SVD 0.8365 0.8358 0.8350
SVD++ 0.8303 0.8307 0.8298
NMF 0.8216 0.8207 0.8202
N recommendation evaluation. The top-5 recommen-
dations were generated for each baseline method and
the reproduced co-SVD model with the three datasets
mentioned in Section 3.1. Those recommendations
were evaluated based on Precision@5, Recall@5 and
nDCG@5 score. The results of each dataset are in Ta-
ble 7, 8 and 9. The best results among the comparison
were bold and colored.
3.6 Discussion
Based on the results shown in Table 7 and 8, SVD
performed marginally better than co-SVD in terms
of both Precision@5 and Recall@5 metrics. Even
with careful tweaking of the evaluation parameters,
the co-SVD cannot outperform SVD. However, both
Table 8: Precision@5, Recall@5 and nDCG@5 perfor-
mance on ml-100K (2018) dataset.
Metrics Model Number of Factors(F)
F=40 F=30 F=20
Precision@5
(Re)co-SVD 0.5839 0.5846 0.5835
SVD 0.5930 0.5899 0.5935
SVD++ 0.5711 0.5678 0.5651
NMF 0.5661 0.5593 0.5534
Recall@5
(Re)co-SVD 0.4046 0.4058 0.4039
SVD 0.4115 0.4099 0.4105
SVD++ 0.3954 0.3942 0.3923
NMF 0.3915 0.3831 0.3694
nDCG@5
(Re)co-SVD 0.8253 0.8257 0.8236
SVD 0.8318 0.8280 0.8269
SVD++ 0.8220 0.8222 0.8235
NMF 0.8153 0.8134 0.8118
Table 9: Precision@5, Recall@5 and nDCG@5 perfor-
mance on ml-10m dataset.
Metrics Model Number of Factors(F)
F=40 F=30 F=20
Precision@5
(Re)co-SVD 0.6541 0.6531 0.6515
SVD 0.6297 0.6297 0.6289
SVD++ 0.6657 0.6664 0.6655
NMF 0.5888 0.5828 0.5720
Recall@5
(Re)co-SVD 0.4714 0.4708 0.4708
SVD 0.4553 0.4553 0.4548
SVD++ 0.4868 0.4879 0.4882
NMF 0.4224 0.4116 0.3938
nDCG@5
(Re)co-SVD 0.8739 0.8735 0.8723
SVD 0.8621 0.8621 0.8616
SVD++ 0.8702 0.8710 0.8713
NMF 0.8379 0.8377 0.8370
results shown in Table 7 and 8 were generated with
smaller datasets (ml-100K year 2016 & 2018) where
they have lesser tag records and could not represent
users preferences well.
The larger dataset (ml-10M), with more tag
records, was therefore used for the model’s eval-
uation. The results are shown in Table 9, where
SVD++ outperforms other models in terms of both
Precision@5 and Recall@5 metrics.
SVD++ has better performance because of the im-
plicit feedback derived from the rating matrix. The
implicit feedback indicates that a user rated an item,
regardless of the rating value. It reflects the users’
options among the items and enriched the users’ pref-
erence of the model. However, the tag application of
a user on an item does not imply the user’s preference
for the item. The users could just apply the tag on the
item without taking into consideration of their own
interest of the item. The tag is just treated as a better
descriptor of the item.
Although the co-SVD method was outperformed
by SVD++, even with the richer tag records, it does
Refined co-SVD Recommender Algorithm: Data Processing and Performance Metrics
673

achieve a better nDCG@5 score than all the other
baseline methods (Table 9). It is likely to be due to
the richer tag records that enhanced the rating predic-
tions and improve the quality of the ranking of the
items produced.
4 CONCLUSION AND FUTURE
WORKS
We have successfully reproduced and implemented
the co-SVD algorithm. In our work, we have also
eliminated an immaterial step (tags filtering) in the
data processing, provided detailed hyper-parameters,
and reported results using suitable performance met-
rics, including updated dataset results.
Even with the elimination of the number of tag
records selection threshold, the reproduction was able
to produce results that had minimal differences with
the work published by Luo et al. (2019). With the
evaluation using the latest dataset (ml-100K (2018)),
the performance of co-SVD was consistent compared
to the results generated with ml-100K (2016). To
achieve this, the hyper-parameters of the reproduced
co-SVD was selected through the ”Grid Search” as
stated in Section 3.4.
With the reproduced co-SVD, the model eval-
uation was extended with top-N recommendations.
Overall, the co-SVD does not outperform other base-
line models in terms of Precision@5 and Recall@5,
but it achieved the highest nDCG@5 score among
the baseline models. Overall, SVD++ performed bet-
ter than co-SVD in top-5 recommendation evaluation.
For the continuity of the research, the source code of
this experiment was published on GitHub for others
to replicate or enhance.
For future works, we will proceed to evaluate co-
SVD with extreme situation, such as cold-start prob-
lem. Since implicit feedback contributed well to
the recommendations prediction, we will continue re-
search in this direction.
REFERENCES
Chicco, D. (2017). Ten quick tips for machine learning in
computational biology. BioData Mining, 10(1):35.
Dacrema, M. F., Cremonesi, P., and Jannach, D. (2019).
Are we really making much progress? a worrying
analysis of recent neural recommendation approaches.
In Proceedings of the 13th ACM Conference on Rec-
ommender Systems, RecSys ’19, page 101–109, New
York, NY, USA. Association for Computing Machin-
ery.
Herlocker, J. L., Konstan, J. A., Terveen, L. G., and Riedl,
J. T. (2004). Evaluating collaborative filtering recom-
mender systems. ACM Trans. Inf. Syst., 22(1):5–53.
Hu, B., Shi, C., Zhao, W. X., and Yu, P. S. (2018). Leverag-
ing meta-path based context for top- n recommenda-
tion with a neural co-attention model. In Proceedings
of the 24th ACM SIGKDD International Conference
on Knowledge Discovery & Data Mining, KDD ’18,
page 1531–1540, New York, NY, USA. Association
for Computing Machinery.
J
¨
arvelin, K. and Kek
¨
al
¨
ainen, J. (2002). Cumulated gain-
based evaluation of ir techniques. ACM Trans. Inf.
Syst., 20(4):422–446.
Koren, Y. (2008). Factorization meets the neighborhood:
A multifaceted collaborative filtering model. In Pro-
ceedings of the 14th ACM SIGKDD International
Conference on Knowledge Discovery and Data Min-
ing, KDD ’08, page 426–434, New York, NY, USA.
Association for Computing Machinery.
Koren, Y., Bell, R., and Volinsky, C. (2009). Matrix factor-
ization techniques for recommender systems. Com-
puter, 42(8):30–37.
Lee, J., Hwang, W., Parc, J., Lee, Y., Kim, S., and Lee,
D. (2019). l-injection: Toward effective collaborative
filtering using uninteresting items. IEEE Transactions
on Knowledge and Data Engineering, 31(1):3–16.
Low, J. M., Tan, I. K. T., and Ting, C. Y. (2019). Re-
cent developments in recommender systems. In
Chamchong, R. and Wong, K. W., editors, Multi-
disciplinary Trends in Artificial Intelligence, pages
38–51, Cham. Springer International Publishing.
Luo, L., Xie, H., Rao, Y., and Wang, F. L. (2019). Per-
sonalized recommendation by matrix co-factorization
with tags and time information. Expert Systems with
Applications, 119:311 – 321.
Luo, X., Zhou, M., Xia, Y., and Zhu, Q. (2014). An
efficient non-negative matrix-factorization-based ap-
proach to collaborative filtering for recommender sys-
tems. IEEE Transactions on Industrial Informatics,
10(2):1273–1284.
Maheshwari, S. and Majumdar, A. (2018). Hierarchical au-
toencoder for collaborative filtering. In 2018 Interna-
tional Joint Conference on Neural Networks (IJCNN),
pages 1–7.
Steck, H. (2010). Training and testing of recommender sys-
tems on data missing not at random. In Proceedings
of the 16th ACM SIGKDD International Conference
on Knowledge Discovery and Data Mining, KDD ’10,
page 713–722, New York, NY, USA. Association for
Computing Machinery.
Vig, J., Sen, S., and Riedl, J. (2012). The tag genome: En-
coding community knowledge to support novel inter-
action. ACM Trans. Interact. Intell. Syst., 2(3).
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
674