On the Use of Allen’s Interval Algebra in the Coordination of Resource

Consumption by Transactional Business Processes

Zakaria Maamar

1 a

, Fadwa Yahya

2,3 b

and Lassaad Ben Ammar

2,3 c

Zayed University, Dubai, U.A.E.

Prince Sattam Bin Abdulaziz University, Al kharj, K.S.A.

University of Sfax, Sfax, Tunisia

Keywords:

Allen’s Interval Algebra, Business Process, Coordination, Resource, Transaction.

Abstract:

This paper presents an approach to coordinate the consumption of resources by transactional business pro-

cesses. Resources are associated with consumption properties known as unlimited, limited, limited-but-

extensible, shareable, and non-shareable restricting their availabilities at consumption-time. And, processes

are associated with transactional properties known as pivot, retriable, and compensatable restricting their ex-

ecution outcomes in term of either success or failure. To consider the intrinsic characteristics of both con-

sumption properties and transactional properties when coordinating resource consumption by processes, the

approach adopts Allen’s interval algebra through different time-interval relations like before, overlaps, and

during to set up the coordination, which should lead to a free-of-conﬂict consumption. A system demonstrat-

ing the technical doability of the approach based on a case study about loan application business-process and

a real dataset is presented in the paper, as well.

1 INTRODUCTION

It is known that all organizations, whether private or

public, multinational or local, etc., rely on Business

Processes (BP) to achieve their goals, sustain their

competitiveness, improve their performance, etc. Ac-

cording to Weske, a BP “is a set of activities that

are performed in coordination in an organizational

and technical environment. These activities jointly

realize a business goal” (Weske, 2012). A BP has

a process model that is designed using dedicated

languages like Business Process Model and Nota-

tion (BPMN) (OMG, ) and then, executed on top of a

Business Process Management System (BPMS). Prior

to executing BPs, their owners could have a “say” on

the expected outcomes. For instance, an owner insists

that her BP must succeed regardless of technical ob-

stacles, another accepts that her BP could fail, while

another approves the undoing of her BP despite the

successful execution. All these options from which

BPs’ owners can select are framed thanks to a set of

transactional properties referred to as pivot, retriable,

https://orcid.org/0000-0003-4462-8337

https://orcid.org/0000-0003-4661-1344

https://orcid.org/0000-0002-4698-3693

and compensatable (Little, 2003).

On top of identifying who does what, where,

when, and why, a BP’s process model also identi-

ﬁes the necessary resources that a BP is expected to

consume at run-time. These resources are of differ-

ent types including human capital, software, hard-

ware, and money. Contrarily to what some disciplines

assume that resources (whether logical or physical)

are abundant, we argue the opposite. It is common

that resources are limited (e.g., 2 hours to complete a

transaction), limited-but-extensible (e.g., 2-week va-

lidity for an access permit that can be renewed for an-

other week), and not-shareable (e.g., a delivery truck

is booked between 8am and 9am). In a previous

work, we captured resources’ characteristics with a

set of consumption properties referred to as unlim-

ited, limited, limited-but-extensible, shareable, and

non-shareable (Maamar et al., 2016). In this paper,

we examine from a temporal perspective the impact

of consumption properties on transactional properties

by raising questions like could a limited resource ac-

commodate a retriable BP knowing that this resource

could become unavailable after a certain number of

necessary execution retrials of this BP? And, could a

limited-but-extensible resource accommodate a com-

pensatable BP knowing that extending this resource

Maamar, Z., Yahya, F. and Ben Ammar, L.

On the Use of Allen’s Interval Algebra in the Coordination of Resource Consumption by Transactional Business Processes.

DOI: 10.5220/0010887600003176

In Proceedings of the 17th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2022), pages 15-25

ISBN: 978-989-758-568-5; ISSN: 2184-4895

would be required to support the undoing of this BP?

To address these questions, we proceed as follows.

First, we blend time with consumption properties al-

lowing to deﬁne a resource’s availability-time inter-

val. Second, we blend time with transactional proper-

ties allowing to deﬁne a BP’s consumption-time in-

terval. Finally, we resort to Allen’s interval alge-

bra, (Allen, 1983), to examine the potential relations

between availability-time interval and consumption-

time interval. The choice of this algebra is motivated

by its exhaustive coverage of the possible relations

between time intervals along with the possibility of

reasoning over these relations. Examples of Allen’s

time relations include equals, overlaps, starts, and

during. Our objective is to recommend the actions to

take when a BP’s consumption-time interval overlaps

with a resource’s availability-time interval, when a

BP’s consumption-time interval is during a resource’s

availability-time interval, when a BP’s consumption-

time interval and a resource’s availability-time inter-

val start or ﬁnish at the same time, etc. In a nut-

shell, could a BP consume a resource considering

both the BP’s temporal-transactional properties and

the resource’s temporal-consumption properties?

Our contributions are, but not limited to, (i) tem-

poral analysis of consumption and transactional prop-

erties, (ii) illustration of how resources’ availability

times are adjusted to accommodate BPs’ transactional

properties, (iii) identiﬁcation of Allen’s relevant time

relations between consumption-time and availability-

time intervals, and (iv) development of a system al-

lowing the reasoning over the identiﬁed Allen’s rele-

vant time relations. The rest of this paper is organized

as follows. Section 2 is an overview of consumption

properties, transactional properties, and Allen’s inter-

val algebra and presents some related works. Sec-

tion 3 suggests a case study. Section 4 discusses

the temporal coordination of processes consuming re-

sources. Implementation details and concluding re-

marks are included in Sections 5 and 6, respectively.

2 BACKGROUND

We discuss consumption properties of resources,

transactional properties of tasks, and Allen’s interval

algebra, and then, present some related works.

2.1 Resources’ Consumption Properties

In compliance with our previous work on social co-

ordination of BPs (Maamar et al., 2016), the con-

sumption properties of a resource (R ) could be un-

limited (u), shareable (s), limited (l), limited-but-

extensible (lx), and non-shareable (ns). A resource

is limited when its consumption is restricted to an

agreed-upon period of time (capability, too, but not

considered). A resource is limited-but-extensible

when its consumption continues to happen after ex-

tending the (initial) agreed-upon period of time. Fi-

nally, a resource is non-shareable when its concur-

rent consumption needs to be coordinated (e.g., one

at a time). A resource is by default unlimited and/or

shareable. The consumption cycles (cc) of the 5 prop-

erties are captured into Fig. 1. However, only 2 are

listed below due to lack of space.

R .cc

: not-made-available

start

−→ made available

waiting−to−be−bound

−→ not-consumed

consumption−approval

−→

consumed

no−longer−use f ul

−→ withdrawn.

R .cc

: not-made-available

start

−→ made available

waiting−to−be−bound

−→ not-consumed

consumption−approval

−→

consumed

consumption−update

−→ done

renewable−approval

−→

made available. The transition from done to made

available allows a resource to be regenerated for an-

other cycle of consumption.

2.2 Tasks’ Transactional Properties

The following deﬁnitions of transactional properties

of a BP’s tasks are reported in the literature, for in-

stance (Frank and Ulslev Pedersen, 2012) and (Little,

2003). A task (T ) is pivot (p) when the outcomes

of its successful execution remain unchanged forever

and cannot be semantically undone. Should this ex-

ecution fail, then it would not be retried. A task is

compensatable (c) when the outcomes of its success-

ful execution can be semantically undone. Like pivot,

should this execution fail, then it would not be retried.

Finally, a task is retriable (r ) when its successful exe-

cution is guaranteed to happen after several ﬁnite ac-

tivations. It happens that a task is both compensat-

able and retriable. The transactional cycles (tc) of the

3 properties are listed below:

T .tc

: not-activated

start

−→ activated

commitment

−→ done

or T .tc

: not-activated

start

−→ activated

f ailure

−→ failed.

T .tc

: not-activated

start

−→ activated 0[

f ailure

−→ failed

retrial

−→ activated]*

commitment

−→ done.

T .tc

: not-activated

start

−→ activated

commitment

−→ done,

T .tc

: not-activated

start

−→ activated

f ailure

−→ failed, or

T .tc

: not-activated

start

−→ activated

commitment

−→ done

compensation

−→ compensated.

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

start

Locked

lock

consumption

approval

Unlocked

release

Not made

available

renewable approval

Made available

waiting

to be bound

Not consumed

consumption

update

consumption

rejection

Withdrawn

Done

consumption

completion

no-longer

useful

consumption update

consumption

approval

Consumed

Legend

Final state

Initial state

Figure 1: Representation of a resource’s consumption cycles (from (Maamar et al., 2016)).

2.3 Allen’s Interval Algebra

Table 1 presents some potential relations (in fact,

there exist 13) between time intervals, i.e., pairs of

endpoints, allowing to support multiple forms of tem-

poral reasoning in terms of what to do when 2 time

intervals start/end together, when a time interval falls

into another time interval, etc. (Allen, 1983).

2.4 Related Work

Resource allocation to tasks has been dealt with using

various techniques such as data mining, probabilis-

tic allocation, and even manual allocation. Recently,

process mining is also used to allocate resources to

tasks. In this section, we restrict ourselves to works

that adopt time-centric techniques and process mining

techniques to address resource allocation concern.

In (Michael et al., 2015), Michael et al. propose

a process mining-based framework for resource al-

location. The framework recommends resources at

the sub-process level instead of task-level by con-

sidering criteria and historical information extracted

from event logs. To this end, the framework uses the

best position algorithm to combine different criteria.

In (Renuka et al., 2016), Sindhgatta et al. propose

an approach for making decisions about resource al-

location to tasks. The approach uses event log to ex-

tract information about the process context and per-

formance from past executions. These information

are analyzed using data mining techniques to dis-

cover past resource allocation decisions. The knowl-

edge about past decisions are used by the approach

to improve resource allocations in new process in-

stances. In (Weidong et al., 2016), Zhao et al. con-

sider resource allocation to tasks as a multi-criteria

decision problem. They propose an entropy-based

clustering ensemble approach for allocating resources

to BPs. Recommending resources to tasks depends

on tasks’ requirements and preference patterns es-

tablished based on past executions. In addition, the

authors adopt a heuristic technique to support dy-

namic resource allocation in the context of multi-

ple process instances running concurrently. In a re-

cent work (Zhao et al., 2020), the same authors ad-

dress the problem of human resource allocation using

team faultlines. They describe resources’ character-

istics from demographic and past execution perspec-

tives. They also use clustering to identify and measure

team faultlines with multiple subgroups of resources

and different characteristics. On top of the identi-

ﬁed team faultlines, Zhao et al. adopt neural network

for the allocation human resources to tasks. In (Ra-

nia Ben et al., 2020), Ben Halima et al. propose an

approach that ensures time-aware allocation of cloud

resources to BPs. The approach prevents violating

time constraints on the processes while minimizing

the deployment cost of these processes. First, the ap-

proach uses timed automata for a formal veriﬁcation

of the matching between BPs’ temporal constraints

and cloud resources’ time availabilities. Then, linear

programming is used to optimize costs. In (Alessan-

dro et al., 2020), Stefanini et al. suggest a process

mining-based approach to support the planning of re-

sources in healthcare services. The approach allows a

semi-automatic extraction and evaluation of the tasks,

service times, and resource consumption for speciﬁc

medical conditions from the event logs. Indeed, the

approach estimates the expected resource consump-

tion for a pre-deﬁned period. In (Delcoucq et al.,

2020), Delcoucq et al. consider that process mining

techniques are mainly used to address control-ﬂow re-

lated problems like BP’s performance or compliance.

However, limited works exist on using these tech-

niques to address resource allocation. Our proposal is

a step in this direction as we adopt Allen’s interval al-

gebra to assign availability intervals to resources and

consumption intervals to tasks. We also adopt process

mining to allocate resources to tasks based on their re-

spective availability and consumption intervals.

On the Use of Allen’s Interval Algebra in the Coordination of Resource Consumption by Transactional Business Processes

Table 1: Representation of some Allen’s time-interval relations.

x y

time

x

y

x

y

x

y

time

x before y x equals y x meets y x overlaps y

3 CASE STUDY

To illustrate task-resource coordination from a time

perspective, we adapt the case study of loan-

application BP that was used in the context of

BPI challenge 2017 (van Dongen, 2017).

The process model of the loan-application BP be-

gins when a customer submits an online application

that a credit staff checks for completeness. Should

any documentation be missing, the staff would con-

tact the customer prior to processing the application

further. Otherwise, the staff would do some addi-

tional work like assessing the customer’s eligibility

based on the requested amount, income, and history.

Should the customer be eligible, the staff would pre-

pare a proposal that the customer has to either accept

or reject according to a deadline. After this deadline

and in the absence of a response, the application is

automatically cancelled. Otherwise, the staff would

ﬁnalize the necessary paperwork by seeking the man-

ager’s approval. Finally, the customer would be in-

formed of the approval concluding the whole process.

For our needs, we split the loan-application BP

into 3 parts, review application, prepare proposal, and

make decision, that are subject to temporal constraints

that, if not met, would terminate the application. To

complete the review-application part, the customer

has to submit any missing documentation during a

certain time period. This period can be extended ac-

cording to how far the credit staff is from her monthly

target of loan applications to process.

To complete the prepare-proposal part, the credit

staff checks the customer’s eligibility, waits for some

additional details like credit score that the central

bank provisions, and ﬁnally prepares the proposal.

All this needs to happen within 15 days from the sub-

mission date as instructed by the central bank.

To complete the make-decision part, the staff must

receive the customer’s response to the proposal and

seek the manager’s approval before the 15 days limit.

Otherwise, the application is cancelled.

Based on the description above, we identify some

concerns that task/resource coordination is expected

to address. Firstly, ensuring resource availability im-

pacts the outcomes of some tasks. For instance, the

customer’s response to the bank’s proposal must be

received while the credit staff is on duty and within

the 15 days limit. Should the staff be off duty, then

analysing the response should be allocated to a differ-

ent staff while satisfying this limit as well. Secondly,

extending resource availability permits to accommo-

date the execution of more tasks instead of cancelling

them. For instance, securing customers’ approvals

about any potential delays would help the bank re-

main compliant with the 15 days limit. Finally, pro-

viding an efﬁcient resource allocation plan would im-

prove the process performance.

4 COORDINATION OF TASKS

CONSUMING RESOURCES

This section details our approach for coordinat-

ing task/resource consumption from a time perspec-

tive (Fig. 2). The approach goes through 3 stages

though the ﬁrst 2 happen concurrently. In the ﬁrst

stage, the approach blends time with consumption

properties allowing to deﬁne the availability-time in-

terval of a resource (Section 4.1). In the second stage,

the approach blends time with transactional proper-

ties allowing to deﬁne the consumption-time interval

of a task (Section 4.2). Finally, the approach exam-

ines the overlap between availability-time interval and

consumption-time interval according to Allen’s inter-

val algebra (Section 4.3). This overlap corresponds

to the coordination that should take place when tasks

consume resources. The approach also mines pro-

cesses by analysing logs to guide task and resource

coordination. More details about Fig. 2’s modules,

repositories, and operations are given in Section 5.

4.1 Time/Consumption Properties

Blend

To decide when a task (T

) would con-

sume (con

i{ j=1...}

, one-to-many times) a re-

source (R

), we proceed as follows. First, we

associate the effective consumption with a time

interval, T

con

i j

, y

con

i j

], that will be deﬁned at

run-time (Section 4.3). Second, we associate unlim-

ited, limited, limited-but-extensible properties with

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

Providers Designers

R-Definition module

initiate

produce

T-Definition module

initiate

produce

1

d

1

d

input

Consumption

properties

input

Transactional

properties

Resource's consumption cycle

....

state 

j

state 

1

state 

2

Task's transactional cycle

....

state 

j

state 

1

state 

2

initiate

inject

R-Injection module

2

d

inject

T-Injection module

2

d

initiate

Timed

resources

Timed

tasks

notify

Design time

Run time

Legend

i

Chronology of

operations

Repository

input

Resources

input

Tasks

input

Allen's

relations

Coordination module

1

r

Coordinated

tasks-resources

Log

input

Execution module

2

r

update

BPMS

Figure 2: Approach for coordinating tasks consuming resources from a time perspective.

3 intervals deﬁning a resource’s availability time,

[b, e[, R

[b, e], R

[b, e 0[+δ]∗], where b, e, δ, and

0[. . . ]∗ stand for begin-time, end-time, extra-time

and 0-to-many times. Third, we associate shareable

and non-shareable properties with tolerating the con-

current consumption (con

, con

, . . . ) of a resource

by separate tasks (T

, T

, . . . ) during the availability

time of this resource, e.g., ((T

con

, e

con

] ⊆

[b, e]) ∧ (T

con

, e

con

] ⊆ R

[b, e]) ∧ . . . )

where i, j ∈ 1..N, N is the number of tasks, and

n, n

∈ N

∗

. Finally, we ensure that an unlimited

resource accommodates any task’s multiple con-

sumption requests. Using Table 2 that refers to

1,2,3

and their different resource consumption such

as T

’s con

and T

’s con

31,32,33,34

, we discuss

the impact of limited and limited-but-extensible

properties on a resource’s availability-time interval.

1. Limited property means that a resource’s avail-

ability time, R

[b, e], set at design-time, re-

mains the same at run-time despite the addi-

tional resource consumption coming from the

same tasks (after their ﬁrst consumption). A

task requesting to consume a limited resource

is conﬁrmed iff the task’s ﬁrst consumption-

time falls into the resource’s availability time

(e.g., T

con

, e

con

] ⊂ R

[b, e] in Table 2 (a)

where b

con

> b and e

con

< e) and, then, any ex-

tra consumption times must fall into the resource’s

Could be repeated but not indeﬁnitely.

same availability time (e.g., T

con

, e

con

] ⊆

[b, e] in Table 2 (a) where b

con

= e

con

and

con

= e).

2. Limited-but-extensible property means that a

resource’s availability time, R

[b, e], set at design-

time, can be adjusted at run-time, R

[b, e 0[+δ]∗],

so, that, additional resource consumption

coming from the same tasks (after their ﬁrst

consumption) are accommodated. A task re-

questing to use a limited-but-extensible resource

is conﬁrmed iff the task’s ﬁrst consumption-

time falls into the resource’s availability

time (e.g., T

con

, e

con

] ⊂ R

[b, e] in

Table 2 (b) where b

con

> b and e

con

< e)

and, then, any extra consumption times still

fall into either the resource’s same availability

time (e.g., T

con

, e

con

] ⊂ R

[b, e] in Ta-

ble 2 (b) where b

con

= e

con

and e

con

< e)

or the resource’s extended availability time

(e.g., T

con

, e

con

] ⊂ R

[e, e + δ] in Ta-

ble 2 (b) where b

con

= e

con

and e

con

< e + δ).

In the 2 cases above, we assume that any addi-

tional resource consumption happens immediately af-

ter the end of the previous resource consumption,

i.e., b

con

i j

= e

con

i j+1

. Another option is to have a

gap (γ) between the 2 consumption, i.e., b

con

i j

con

i j+1

+γ, but this is not considered further and does

not impact the whole coordination approach.

On the Use of Allen’s Interval Algebra in the Coordination of Resource Consumption by Transactional Business Processes

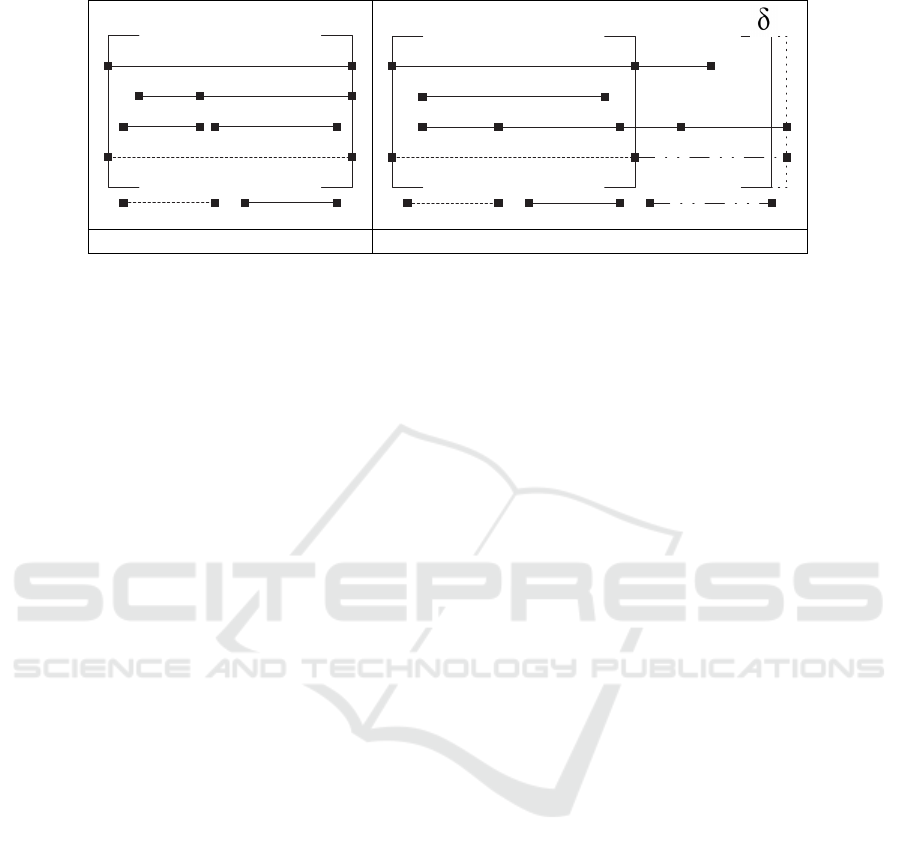
Table 2: Representation of a resource’s availability-time intervals during consumption.

b e

con 

11

con 

21

con 

31

con 

41

availability

time

consumption

time

con 

22

b e

con 

11

con 

21

con 

12

con 

31

con 

32

con 

33

con 

34

availability

time

consumption

time

extended

availability time

(a) limited resource (b) limited-but-extensible resource

4.2 Time/Transactional Properties

Blend

In Section 4.1, we refer to T

con

i j

, y

con

i j

] as a task’s

effective consumption-time interval with regard to a

resource. This interval will be deﬁned based on a

task’s expected consumption-time interval, T

[et, l t],

where et and lt are earliest time and latest time, re-

spectively. While the expected consumption time is

set at design-time, the effective consumption time will

be set at run-time as per Section 4.3 and will happen

anytime between the earliest time and latest time. We

discuss below how we foresee the impact of a task’s

transactional properties on a resource’s availability-

time intervals.

1. Pivot: a resource’s availability-time interval ac-

commodates the execution of a task whether this

execution leads to success or failure.

2. Compensatable: a resource’s availability-time in-

terval accommodates the execution of a task

whether this execution leads to success or fail-

ure. Prior to undoing the execution outcomes after

success (assuming an undoing decision has been

made), there will be a need to check whether the

resource’s remaining availability time accommo-

dates the undoing. Should the accommodation

be not possible, extra availability time would be

requested subject to checking the resource’s con-

sumption property.

3. Retriable: a resource’s availability-time interval

accommodates the execution of a task along with

an agreed-upon number of retrials, if deemed nec-

essary, that are all expected to lead to success.

Should this number of retrials still lead to failure,

extra availability time would be requested sub-

ject to both checking the resource’s consumption

property and ensuring that the extra number of re-

trials (that are expected to lead to success) do not

go over a threshold.

4.3 Task/Resource Time-connection

To deﬁne the effective consumption-time interval of a

resource by a task, we examine potential overlaps be-

tween the task’s expected consumption-time interval

and resource’s availability-time interval. We resort

to Allen’s interval algebra to identify these overlaps,

i.e., T

con

, e

con

] where n is the consumption

number. In the following, T H , R

(b|e), and T

(et|lt)

correspond to threshold during retriable execution,

lower|upper values of a resource’s availability-time

interval, and lower|upper values of a task’s excepted

consumption-time interval, respectively. Due to lack

of space, equals and overlaps relations are detailed

and during relation is summarized.

Consumption-time Interval Equals Availability-

time Interval. Since the expected consumption-time

interval and availability-time interval are the same,

the following would happen considering both the re-

source’s consumption property and the task’s transac-

tional property:

1. limited: the effective consumption-time interval,

con

, e

con

], falls into the availability-time

interval in a way that b

con

≥ R

(b) and e

con

≤

(e).

- pivot: T

execution happens during

con

, e

con

- compensatable: T

execution happens during

con

, e

con

]. Should there be an undoing

of this execution’s outcomes, then the remain-

ing availability time would accommodate the

undoing, T

con

, e

con

] and b

con

= e

con

subject to verifying that R

(e) − e

con

> 0.

Should the veriﬁcation fail, then the compen-

sation would be canceled. Despite the can-

cellation, T

execution is still compliant with

the requirements of a compensatable property

(i.e., done is a ﬁnal state).

- retriable: T

execution and potential agreed-

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

upon retrials happen during T

con

, e

con

Should there be extra retrials to ensure success-

ful execution, then the remaining availability

time would accommodate these extra retrials,

con

, e

con

] and b

con

= e

con

i(n−1)

, subject

to verifying that R

(e) − e

con

i(n−1)

> 0 where

1 < n < T H . Should the veriﬁcation fail, then

the retrials would be stopped making T

execu-

tion uncompliant with the requirements of a re-

triable property (i.e., failed is not a ﬁnal state).

2. limited-but-extensible: the effective

consumption-time interval, T

con

, e

con

falls into the availability-time interval in a way

that b

con

≥ R

(b) and e

con

≤ R

(e).

- pivot: T

execution happens during

con

, e

con

- compensatable: T

execution happens during

con

, e

con

]. Should there be an un-

doing of this execution’s outcomes, then the

remaining availability time would accommo-

date the undoing, T

con

, e

con

] and b

con

, subject to verifying that R

(e) − e

con

0. Should the veriﬁcation fail, then the re-

source’s availability time would be extended,

(e) + δ, in a way that T

con

, e

con

] ⊆

con

, e + δ], b

con

= e

con

, and e

con

≤

(e) + δ. Whether the extension happens

or not, T

execution is still compliant with

the requirements of a compensatable property

(i.e., both done and canceled are ﬁnal states).

- retriable: T

execution and potential agreed-

upon retrials happen during T

con

, e

con

Should there be extra retrials to ensure suc-

cessful execution, then the remaining avail-

ability time would accommodate these ex-

tra retrials, T

con

, e

con

] and b

con

i(n−1)

, subject to verifying that R

(e) −

con

i(n−1)

> 0 where 1 < n < T H . Should

the veriﬁcation fail, then the resource’s avail-

ability time would be extended a certain

number of times, R

(e) + 1[δ]∗, in a way

that T

con

, e

con

] ⊆ R

con

i(n−1)

, e + 1[δ]∗],

con

= e

con

i(n−1)

, e

con

≤ R

(e) + δ, and 1 <

n < T H . Thanks to the extension, T

execu-

tion is still compliant with the requirements of

a retriable property (i.e., done is a ﬁnal state).

Consumption-time Interval Overlaps Availability-

time Interval. Since the expected consumption-time

interval and availability-time interval have some time

in common, the lower value of the task’s expected

consumption-time interval is adjusted in a way that it

matches the lower value of the resource’s availability-

time interval, i.e., T

= [R

(b), lt]. After this adjust-

ment, the following would happen considering both

the resource’s consumption property and the task’s

transactional property:

1. limited: the effective consumption-time inter-

val, T

con

, e

con

], falls into a part of the

availability-time interval in a way that b

con

≥

(b) and e

con

< R

(e). The remaining part of

the availability-time interval, that corresponds to

con

, (R

(e) − e

con

)], could be used to accom-

modate additional consumption (Table 2-(a)).

- pivot: T

execution happens during

con

, e

con

- compensatable: T

execution happens during

con

, e

con

]. Should there be an undoing

of this execution’s outcomes, then the remain-

ing availability time would accommodate the

undoing, T

con

, e

con

] and b

con

= e

con

subject to verifying that R

(e) − e

con

> 0.

Should the veriﬁcation fail, then the compen-

sation would be canceled. Despite the can-

cellation, T

execution is still compliant with

the requirements of a compensatable property

(i.e., done is a ﬁnal state).

- retriable: T

execution and potential agreed-

upon retrials happen during T

con

, e

con

Should there be extra retrials to ensure suc-

cessful execution, then the remaining availabil-

ity time would accommodate these extra re-

trials, T

con

, e

con

] and b

con

= e

con

i(n−1)

subject to verifying that R

(e) − e

con

i(n−1)

> 0

where 1 < n < T H . Should the veriﬁcation

fail, then the extra retrials would be stopped

making T

execution uncompliant with the re-

quirements of a retriable property (i.e., failed is

not a ﬁnal state).

2. limited-but-extensible: the effective

consumption-time interval, T

con

, e

con

falls into a part of the availability-time interval in

a way that b

con

≥ R

(b) and e

con

< R

(e). The

remaining part of the availability-time interval,

that corresponds to [e

con

, (R

(e) − e

con

)], could

be used to accommodate additional consumption

before considering to extend this availability-time

interval (Table 2-(b)).

- pivot: T

execution happens during

con

, e

con

- compensatable: T

execution happens during

con

, e

con

]. Should there be an un-

On the Use of Allen’s Interval Algebra in the Coordination of Resource Consumption by Transactional Business Processes

doing of this execution’s outcomes, then the

remaining availability time would accommo-

date the undoing, T

con

, e

con

] and b

con

, subject to verifying that R

(e) − e

con

0. Should the veriﬁcation fail, then the re-

source’s availability time would be extended,

(e) + δ, in a way that T

con

, e

con

] ⊆

con

, e + δ], b

con

= e

con

, and e

con

≤

(e) + δ. Whether the extension happens

or not, T

execution is still compliant with

the requirements of a compensatable property

(i.e., both done and canceled are ﬁnal states).

- retriable: T

execution and potential agreed-

upon retrials happen during T

con

, e

con

Should there be extra retrials to ensure suc-

cessful execution, then the remaining avail-

ability time would accommodate these ex-

tra retrials, T

con

, e

con

] and b

con

i(n−1)

, subject to verifying that R

(e) −

con

i(n−1)

> 0 where 1 < n < T H . Should

the veriﬁcation fail, then the resource’s avail-

ability time would be extended a certain

number of times, R

(e) + 1[δ]∗, in a way

that T

con

, e

con

] ⊆ R

con

i(n−1)

, e + 1[δ]∗],

con

= e

con

i(n−1)

, e

con

≤ R

(e) + δ, and 1 <

n < T H . Thanks to the extension, T

execu-

tion is still compliant with the requirements of

a retriable property (i.e., done is a ﬁnal state).

Availability-time Interval Overlaps Consumption-

time Interval. Although “availability-time interval

overlaps consumption-time interval” looks similar to

“consumption-time interval overlaps availability-time

interval”, there are 2 adjustments that need to take

place considering the fact that availability-time in-

terval and expected consumption-time interval have

some time in common. The ﬁrst adjustment con-

sists of matching the lower value of the resource’s

availability-time interval with the lower value of the

task’s expected consumption-time interval, i.e., R

, e] and b

= T

(et). The second adjustment is con-

ditional since it applies to limited-but-extensible re-

sources

, only, and consists of matching the highest

value of the resource’s availability-time interval with

the highest value of the task’s expected consumption-

time interval, i.e., R

= [b

, e

] and e

= T

(l t). Ex-

tending from the beginning permits to offer a com-

plete coverage of tasks’ expected consumption-time

intervals instead of waiting for these tasks’ extension

requests. As a result of the second adjustment, the

Considering limited resources could be an option. But,

this would require reducing a task’s expected consumption-

time interval, which might not be practical in real-life.

analysis of “availability-time overlaps consumption-

time” becomes similar to “availability-time equals

consumption-time” after dropping limited resources

from the analysis.

Availability-time Interval during Consumption-

time Interval. 2 adjustments need to happen as fol-

lows. The ﬁrst adjustment consists of adjusting the

lower value of the task’s expected consumption-time

to match the lower value of the resource’s availability-

time interval, i.e., T

= [R

(b), lt]. The second ad-

justment is applicable only if the resource is limited-

but-extensible. This consists of extending the re-

source availability-time interval so, that, its highest

value matches the highest value of the task’s expected

consumption-time interval, i.e., R

= [b, e

] and e

(lt). As a result of these adjustments, the analy-

sis of “availability-time interval during consumption-

time interval” becomes similar to “availability-time

interval equals consumption-time interval”.

5 IMPLEMENTATION

To demonstrate the technical doability of our ap-

proach for coordinating the consumption of resources

by processes from a time perspective, we deployed

an in-house testbed that uses BPI-Challenge-2017’s

real dataset (van Dongen, 2017). The dataset is

about a credit application system’s execution traces

and is available in eXtensible Event Stream (XES). In

conjunction with this dataset, we developed several

Python programs and performed several experiments.

5.1 Dataset Preprocessing

Necessary steps for preprocessing BPI-Challenge-

2017’s dataset are detailed below:

• Data transformation from XES into pandas

DataFrame

format aims at tapping into pandas

library’s predeﬁned routines which we applied to

the next preprocessing steps. DataFrame is suit-

able for manipulating data and building prediction

models.

• Data reduction/sampling downsized the dataset to

make it manageable. We applied sampling to

extract a representative set, 30%, of the original

dataset. This number was chosen for performance

purposes, given the dataset’s initial size and time

spent considering other data volumes.

• Feature selection considered a subset of the fea-

tures describing relevant data. The objective is

pandas.pydata.org/docs/reference/api/pandas.

DataFrame.html.

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

to obtain a concise representation of the available

data in the reduced dataset such as org:resource,

lifecycle:transition, and time:timestamp. Fea-

ture selection also permits to drop irrelevant

data such as case:LoanGoal, MonthlyCost, and

case:RequestedAmount that could slowdown our

system or affect the inaccuracy of the results.

• Feature creation generated new features that aim

at capturing the most important data in a dataset

much more efﬁciently than the original dataset.

We used 2 techniques, feature extraction and fea-

ture construction. In the former technique, we ex-

tracted the resource’s availability time, R

[b, e],

from the time:timestamp feature in the dataset.

For each resource R

, b and e refer, respectively,

to the lowest and highest values per date of the

time part in the time:timestamp feature. In the lat-

ter technique, we performed a deep analysis of the

reduced dataset to deﬁne the consumption-time

interval of the resource, T

con

i j

, y

con

i j

]. For

each task, we computed the time between its in-

stances and their successors. The average time is

then considered as the consumption-time interval

for that task.

Once a resource’s availability-time interval and

consumption-time interval are deﬁned, we worked

on task/resource time-connection as per Sec-

tion 4.3. In addition, the analysis of the dataset

and several papers on the BPI challenge 2017 al-

lowed us to work on the consumption property of

each resource and transactional property of each

task. For instance, we noticed that the execution

of some tasks was suspended when the resource

availability-time ended. Hence, we assigned lim-

ited property to this resource. As for the trans-

actional property, we associated compensatable

property with make offer task since 3% of offers

were canceled or refused after their successful ex-

ecution according to (Bolt, 2017). Finally, we

added the consumption and transactional proper-

ties to the preprocessed dataset.

5.2 Task/Resource Recommendations

To enact task/resource coordination, we resorted

to process mining that is known for addressing

BP decision-making problems and providing recom-

mendations to improve future BP executions. In this

context, a good number of recommendations tech-

niques are reported in the literature. We opted for De-

cision Trees (DT)

known for easiness, performance,

and ability to visually communicate choices. We cre-

scikit-learn.org/stable/modules/tree.html.

ated a prediction model following 2 stages, ofﬂine and

online, allowing to build and process the required pre-

diction model.

Ofﬂine Stage. We built a prediction model by refer-

ring to an open-source Python library called Sklearn

It supports a variety of built-in prediction models

(e.g., DT, KNN, and SVM). Building a prediction

model with Sklearn usually starts with preparing the

dataset in the most suitable format as per Section 5.1

that is Pandas DataFrame in our case. Then, the target

of the prediction model must be deﬁned. This latter is

about the recommendation of the actions to take when

a resource is assigned to a task (e.g., adjusting the

resource-availability time or consumption-time inter-

val). Finally, the set of variables that may affect the

recommendations such as resource’s availability-time

and consumption-time are deﬁned.

In terms of technical details, we, ﬁrst, selected

the DT model and then, set its parameters namely,

attribute selection criterion (Entropy or Gini index)

and maximum depth of the tree. These parameters

are critical to the accuracy of the results and are usu-

ally set manually after several trials to ﬁnd the best

results. Afterwards, we ﬁtted the DT model into the

speciﬁed data. We had to split the reduced dataset

into training dataset and test dataset using Sklearn’s

TRAIN TEST SPLIT

built-in function. Finally, we

evaluated the accuracy of our model by comparing the

result of the prediction to the real data included in the

test dataset as per Section5.3.

Online Stage. The objective here is to recommend

actions to take when a resource is assigned to a task in

the new executions. Obviously, recommendations are

determined using the prediction model built during

the ofﬂine stage. We carried out some experiments to

predict the actions to perform for each task-resource

with respect to some new simulated BP instances. We

checked how accurate our prediction model is. Dur-

ing the experiments, we considered 30 simulated in-

stances of the BP. The accuracy of results are dis-

cussed next.

5.3 Discussions of the Results

To appreciate our DT-based prediction model’s rec-

ommendations, we also adopted the k-Nearest Neigh-

bors (KNN) as another technique for developing pre-

diction models. As for the DT prediction model, the

experiments showed encouraging results during either

the ofﬂine stage or the online stage. In this context,

scikit-learn.org/stable/index.html.

scikit-learn.org/stable/modules/generated/sklearn.

model selection.train test split.html.

On the Use of Allen’s Interval Algebra in the Coordination of Resource Consumption by Transactional Business Processes

Test dataset Simulated dataset

Datasets used during the experiments

Accuracy

KNN

Figure 3: Accuracy of DT versus KNN.

we used Accuracy as a performance measure (Equa-

tion 1).

Accuracy =

TrueObservations

TotalObservations

(1)

First, we computed Accuracy after applying the

DT prediction model to the test dataset as per the of-

ﬂine stage. We obtained 93% Accur acy, which we

treated as an acceptable value. Then, we computed

Accuracy again after applying our prediction model

during the online stage to the simulated instances. We

obtained 89% Accuracy that also proves the high per-

formance of our DT prediction model. Last but not

least, we used KNN prediction model. Similarly to

the DT prediction model, we used our preprocessed

dataset to build the KNN prediction model and, then,

we applied it to the simulated instances. The objec-

tive is to compare the results obtained using both tech-

niques (DT and KNN). The results show an Accuracy

of 87% and 76% when the KNN prediction model

is applied to the test dataset and the simulated in-

stances. These results are in line with those of the

DT and proves its performance. Fig. 3 illustrates the

comparison between the Accuracy values obtained by

DT and KNN prediction models using both the test

dataset and the simulated instances.

6 CONCLUSION

This paper presented an approach for coordinating

the consumption of resources by business processes.

The coordination took place from a time perspective

thanks to speciﬁc relations deﬁned by Allen’s interval

algebra. Examples of relations included equals, over-

laps, starts, and ﬁnishes. The coordination also con-

sidered both the consumption properties of resources

(unlimited, limited, limited-but-extensible, shareable,

and non-shareable) and the transactional properties

of business processes (pivot, retriable, and compen-

satable). Since resources and processes were associ-

ated with availability-time intervals and consumption-

time intervals, respectively, different types of reason-

ing took place leading sometimes to adjusting some

time intervals and/or allowing some re-executions. A

system demonstrating the technical doability of the

approach based on a case study about loan applica-

tion business-process was implemented. We built a

decision-tree prediction model using a real dataset

from the BPI Challenge 2017. The evaluation of this

prediction model proved its performance. In addition,

to consolidate these results, we carried out a second

experiment using KNN whose results were in line

with those of DT and have proven its performance.

In term of future work we would like to examine the

remaining Allen’s time relations, the scalability of the

system when a large number of processes are under-

execution, and ﬁnally, the impact of resource failure

on process execution.

REFERENCES

Alessandro, S., Davide, A., Elisabetta, B., Riccardo, D.,

and Valeria, M. (2020). A Data-driven Methodology

for Supporting Resource Planning of Health Services.

Socio-Economic Planning Sciences, 70.

Allen, J. (1983). Maintaining Knowledge about Temporal

Intervals. CACM, 26(11).

Bolt, A. (September 2017). BPI Challenge 2017 Pro-

cess Variability Analysis over Offers. https:

//www.win.tue.nl/bpi/lib/exe/fetch.php?media=2017:

bpi2017 paper 22.pdf,visitedMay

∼

2021.

Delcoucq, L., Lecron, F., Fortemps, P., and van der Aalst,

W. M. (2020). Resource-centric Process Mining:

Clustering using Local Process Models. In Proceed-

ings of SAC’2020, online.

Frank, L. and Ulslev Pedersen, R. (2012). Integrated Dis-

tributed/Mobile Logistics Management. TLDKS, 5.

Little, M. (2003). Transactions and Web Services. CACM,

46(10).

Maamar, Z., Faci, N., Sakr, S., Boukhebouze, M., and Bar-

nawi, A. (2016). Network-based Social Coordination

of Business Processes. IS, 58.

Michael, A., Eric, R., Jorge, M., and Marcos, S. (2015).

A Framework for Recommending Resource Alloca-

tion based on Process Mining. In Proceedings of

BPM’2015 Workshops, Innsbruck, Austria.

OMG. Business Process Model and Notation.

www.omg.org/spec/BPMN/2.0.2.

Rania Ben, H., Kallel, K., Gaaloul, W., Maamar, Z., and

Jmaiel, M. (2020). Toward a Correct and Optimal

Time-aware Cloud Resource Allocation to Business

Processes. FGCS, 112.

Renuka, S., Aditya, G., and Hoa Khanh, D. (2016).

Context-aware Analysis of Past Process Executions to

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

Aid Resource Allocation Decisions. In Proceedings

of CAiSE’2016, Ljubljana, Slovenia.

van Dongen, B. (2017). BPI Challenge 2017. data.4tu.nl/

articles/dataset/BPI Challenge 2017/12696884.

Weidong, Z., Haitao, L., Weihui, D., and Jian, M. (2016).

An Entropy-based Clustering Ensemble Method to

Support Resource Allocation in Business Process

Management. KIS, 48(2).

Weske, M. (2012). Business Process Management Archi-

tectures. In Business Process Management. Springer.

Zhao, W., Pu, S., and Jiang, D. (2020). A Human Resource

Allocation Method for Business Processes using Team

Faultlines. Applied Intelligence, 50(9).

On the Use of Allen’s Interval Algebra in the Coordination of Resource Consumption by Transactional Business Processes