Robust Traffic Signal Timing Control using Multiagent Twin Delayed
Deep Deterministic Policy Gradients
Priya Shanmugasundaram
1a
and Shalabh Bhatnagar
2b
1
Department of Electrical and Electronics Engineering, Shiv Nadar University, NH-91, Tehsil Dadri,
Gautam Buddha Nagar, Uttar Pradesh, India
2
Department of Computer Science and Automation and the Robert Bosch Centre for Cyber Physical Systems,
Indian Institute of Science, Bangalore, India
Keywords: Vehicular Traffic Control, Traffic Signal Control, Multi-agent Reinforcement Learning, Deep Reinforcement
Learning.
Abstract: Traffic congestion is an omnipresent and serious problem that impacts people around the world on a daily
basis. It requires solutions that can adapt to the changing traffic environments and reduce traffic congestion
not only across local intersections but also across the global road network. Traditional traffic control strategies
suffer from being too simplistic and moreover, they cannot scale to real-world dynamics. Multiagent
reinforcement learning is being widely researched to develop intelligent transportation systems where the
different intersections on a road network co-operate to ease vehicle delay and traffic congestion. Most of the
literature on using Multiagent reinforcement learning methods for traffic signal control is focussed on
applying multi-agent Q learning and discrete-action based control methods. In this paper, we propose traffic
signal control using Multiagent Twin Delayed Deep Deterministic Policy Gradients (MATD3). The proposed
control strategy is evaluated by exposing it to different time-varying traffic flows on simulation of road
networks created on the traffic simulation platform SUMO. We observe that our method is robust to the
different kinds of traffic flows and consistently outperforms the state-of-the-art counterparts by significantly
reducing the average vehicle delay and queue length.
1 INTRODUCTION
As population and urbanization increased over the
years, it has caused a steady increase in the volume of
vehicles on the road. This has given rise to increased
traffic congestion across urban traffic networks.
Traffic congestion is the root cause of various social
and economic problems like increased pollution,
increased fuel or energy consumption and increased
travel times. It is of crucial importance to develop
improvements over existing traffic signal control
technology and infrastructure to deal with this
growing traffic demand and to efficiently mitigate
traffic congestion and its ill effects. We aim to use
data-driven methods, which sample sensor data from
traffic networks to perceive the current state of the
traffic and use it to dynamically learn an optimal
a
https://orcid.org/0000-0002-9452-3798
b
https://orcid.org/0000-0001-7644-3914
strategy for controlling the traffic flow by taking
appropriate actions.
Traffic signal control is a complex problem that
requires solutions that can dynamically cater and
adapt to the changing traffic conditions. Traditional
rule-based control strategies like fixed timing traffic
signal control, use historical data to determine a
signal plan under the assumption that traffic flows
will always remain similar to the referred historical
demand data. Since they do not account for lift or
drops that deviate from the user data, these methods
result in sub-optimal traffic flows and increased
traffic congestion. Adaptive traffic signal control
strategies that decide the signal timings by using
algorithms on real-time traffic information like
UTOPIA (Mauro & Taranto, 1990), SCATS (Lowrie,
1990) and RHODES (Head, Mirchandanai, & Shelby,
1998) have been adopted in various cities and
Shanmugasundaram, P. and Bhatnagar, S.
Robust Traffic Signal Timing Control using Multiagent Twin Delayed Deep Deterministic Policy Gradients.
DOI: 10.5220/0010889300003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 2, pages 477-485
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
477

countries. However, these methods are modelled to
respond to long-term changes in traffic flows and
suffer under dynamic fluctuations. These systems
also need the environment to be modelled extensively
by domain experts and need manual intervention from
time to time. To design intelligent systems that do not
require the environment to be extensively modelled
and learn with minimal manual intervention,
reinforcement learning is being studied extensively.
Reinforcement Learning is the learning paradigm
whereby learning for an agent happens dynamically
through trial-and-error methods that the agent adopts
during the course of its interactions with the
environment. The agent learns optimal behaviour by
performing actions that maximize the cumulative
future rewards. State-action value function 𝑄(𝑠

,𝑎

)
is defined as the expected cumulative reward that can
be obtained when performing the action, 𝑎
𝑡
in state 𝑠
𝑡
and following the optimal policy subsequently. For
example, in 𝑄-Learning (Watkins & Dayan, 1992),
the state-action value estimate is maximised
iteratively to learn optimal behaviour by minimizing
the cost 𝐽
𝑄
as shown below:
𝑦

= 𝑟

+ 𝛾𝑚𝑎𝑥

𝑄
(
𝑠

,𝑎
)
,
(1)
𝐽

= 𝐸 [𝑦

−𝑄
(
𝑠

,𝑎

)
]

.
(2)
With the advent of Deep Learning, reinforcement
learning tasks that required processing unstructured
data, dealing with high dimensional vector spaces and
increased computational needs became easier and
tractable. However, a significant challenge in deep
reinforcement learning methods is that the agents
cannot learn to coordinate and share information
with each other to optimize a collective objective.
Multiagent Deep Reinforcement Learning uses
Deep Reinforcement Learning techniques to control
multiple agents present in the environment and enable
them to cooperate or compete so as to achieve a
collective objective. Since traffic networks have
many intersections that are dependent on each other,
it is crucial to exploit multiagent deep reinforcement
learning techniques to enable the different
intersections in the network to work collectively
towards reducing traffic congestion. There have been
significant contributions in applying multiagent
reinforcement learning to traffic signal control in the
past, see for instance (Prabhuchandran, Hemanth
Kumar, & Bhatnagar, 2014) where the authors have
used Multiagent 𝑄−Learning to efficiently learn
traffic control. In (T Chu, 2019), multiagent
advantage actor-critic has been used to enable phase
selection for traffic control. In (Ge , 2019), the
authors model cooperative traffic signal control using
Deep 𝑄 learning and transfer learning. However,
most applications to traffic signal control have been
focussed on using multiagent 𝑄− learning and
discrete-action settings. Other prior work in this area,
see for instance, (Prashanth & Bhatnagar, 2011),
(Prashant & Bhatnagar, 2012) used centralized
control strategies for a common decision maker again
assuming a discrete set of available actions. In this
paper, we propose a traffic signal control strategy in
continuous action settings using Multi-agent Twin
Delayed Deep Deterministic Policy Gradients
(MATD3) (Ackermann, Gabler, Osa, & Sugiyama,
2019).
The main contributions in this paper are as
follows:
1) We develop a co-operative multiagent deep
reinforcement learning framework that
undertakes and ameliorates traffic
congestion.
2) To the best of our knowledge, this is the first
work that uses multiagent twin delayed deep
deterministic policy gradients for traffic
signal control.
3) We use target policy smoothing, delayed
target policy updates and double critics to
enhance learning stability.
4) We observe that the reward obtained
while following our method is much
higher than independent control methods,
which tells us that cooperation is better
than independent behavior.
5) We observe that our framework performs
significantly better than state of the art
traffic control methods by effectively
reducing the vehicle delay and queue lengths
across different traffic flows.
The different sections of the paper have been
arranged as follows: We present our problem
formulation in section 2. In this section, the MDP
formulation and the proposed solution method are
presented. In section 3, we elaborate on the results
obtained from our experiments. Finally in section 4,
we will conclude our paper by suggesting possible
future directions.
2 PROBLEM FORMULATION
A road network 𝑅
(
𝑛,𝑙
)
is defined where 𝑛 denotes a
collection of 𝑀 different intersections on the road
network given as {𝑛
𝑖
}
𝑖=1,2,..,𝑀
and 𝑙 is the set of
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
478

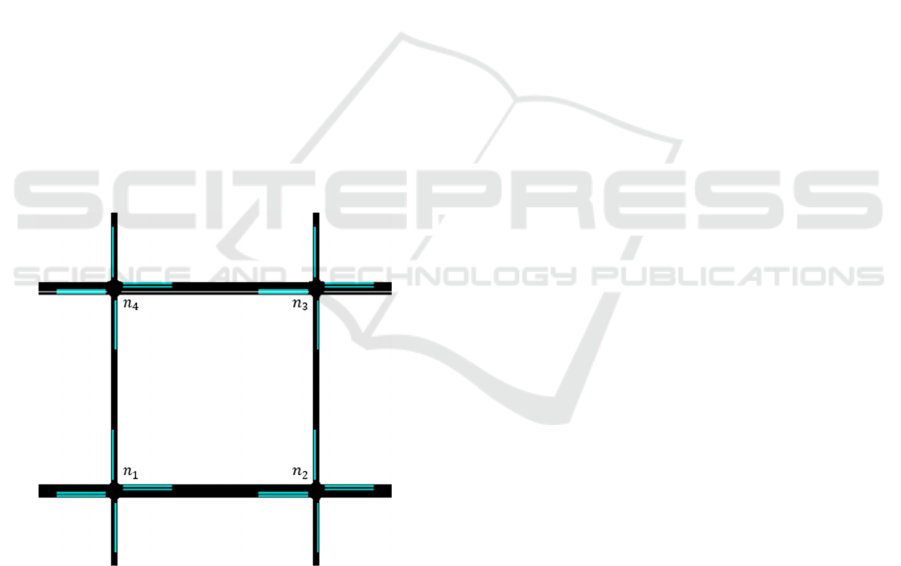
incoming lanes 𝑙
𝑗𝑘
coming from the intersection 𝑗 to
an intersection 𝑘. It is assumed here that j and k are
one-hop neighbouring junctions. The subset 𝑙
𝑛
𝑖
is the
set of incoming lanes coming to 𝑛
𝑖
given by
{𝑙
𝑗𝑛
𝑖
}
𝑗=1,2,..,𝑀, 𝑗𝑛
𝑖
. Each intersection has a traffic light
that executes phases, which are a combination of red
and green traffic signals that go green or red
simultaneously for a finite duration. Phase 𝑝 from a
set of possible phases 𝑃
𝑛
𝑖
for an intersection 𝑛
𝑖
, is
executed in a round robin manner for a phase duration
𝑑. The phase duration for the green phases 𝑑
𝑔
, is
learnt by our method, while the duration for the
yellow phases 𝑑
𝑦
, remains fixed. There are induction
loop detectors and lane area detectors on the
incoming lanes in the road network, which provide
traffic related information like queue length 𝑞
𝑙
𝑛
𝑖
and
vehicle delay 𝑤
𝑙
𝑛
𝑖
. The queue length 𝑞
𝑙
𝑛
𝑖
can be
defined as the number of vehicles that are present in
the incoming lanes for the intersection 𝑛
𝑖
and have a
speed of less than 0.1m/s. The vehicle delay 𝑤
𝑙
𝑛
𝑖
can
be defined as the delay faced by the vehicle located at
the end of the queue in incoming lanes 𝑙
𝑛
𝑖
.
Figure 1: A simulated 2x2 Road Network 𝑅.
Reinforcement learning systems can be modelled
as Markov Decision Processes (MDP) (Bellman,
1957), (Puterman, 1994), (Bertsekas, 2012), using the
tuple (𝑆,𝐴,𝑅,𝑇) where 𝑆 denotes the state space, 𝐴
denotes the action space, 𝑅 denotes the reward
function and 𝑇 denotes the transition probability
function, respectively. At time 𝑡, the agent observes
the state 𝑠
𝑡
∈𝑆 of the environment and takes an
action 𝑎
𝑡
∈𝐴. This action decides on the amount of
green light to allocate to the next phase at that instant
and causes the agent to transition into a new state 𝑠
𝑡+1
and thereby receive a reward 𝑟
𝑡
, that then acts as a
feedback signal on the action 𝑎
𝑡
. Since our
framework uses model free algorithms, we will
ignore the transition kernel T because even though
state transitions indeed occur through
T, it is assumed
unknown to the agent who only has access to online
data in the form of state, action, reward and next state
tuples. Now, we represent the traffic signal control
problem as an MDP where the agents are the traffic
lights present on the intersections and define the state
space, action space and reward function used in our
solution.
State Space Definition:
Choosing the correct state representation to use for an
agent is dependent on the kind of control problem and
is key to efficient learning. There are many frequently
used state definitions in literature for traffic signal
control like DTSE (Genders & Razavi, 2016), camera
images (Liang, Du, Wang, & Han, 2018) and traffic
parameters like queue length (Abdulhai, Pringle, &
Grigoris J., 2003). We have used the tuple of vehicle
delay and queue length at the different incoming lanes
at an intersection to define the state of our agent.
Since there are multiple agents in the road network,
each agent observes a local state 𝑜
𝑡
which is a subset
of the global state 𝑠
𝑡
of the road network. The
observation for the agent corresponding to the traffic
light at an intersection 𝑛
𝑖
at time t, i.e., 𝑜
𝑡,𝑛
𝑖
is
defined as,
𝑜
,

:={𝑞
,


,𝑤
,


},
(3)
where 𝑞
𝑡,𝑙
𝑛
𝑖
and 𝑤
𝑡,𝑙
𝑛
𝑖
refer to queue length 𝑞
𝑙
𝑛
𝑖
and
vehicle delay 𝑤
𝑙
𝑛
𝑖
at time instant 𝑡. This state
information can be collected from SUMO at runtime
and fed to our algorithm using TRACI, a python API.
Action Space Definition:
As with regular junctions, we assume the various
phases at any junction to go green in a round-robin
manner. The decision to be made by each agent is the
amount of green time to assign to any phase during a
cycle. We thus define the actions to be the green
phase duration 𝑑
𝑔
to be executed at an intersection
when a green phase is enabled by the round-robin
Robust Traffic Signal Timing Control using Multiagent Twin Delayed Deep Deterministic Policy Gradients
479

phase controller. The phase duration 𝑑
𝑔
is allowed to
lie in the interval (𝑑
𝑔
𝑚𝑖𝑛
,𝑑
𝑔
𝑚𝑎𝑥
), where the upper and
lower bounds 𝑑
𝑔
𝑚𝑎𝑥
and 𝑑
𝑔
𝑚𝑖𝑛
are suitably chosen. The
precise value of 𝑑
𝑔
to be used is obtained from the
actor network output 𝑎 as follows:
𝑚𝑖𝑑∶=
𝑑


− 𝑑


2
+𝑑


,
(4)
𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙∶=𝑑


−𝑚𝑖𝑑,
(5)
𝑑

:=
(
𝑚𝑖𝑑
)
+𝑎∗
(
𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙
)
.
(6)
A fixed 𝑑
𝑦
is executed to ensure a smooth transition
into green phase from red phase and to avoid any
unexpected incidents.
Reward Function Definition:
The reward is the most important ingredient in a
reinforcement learning problem and it needs to be
chosen in a way that it can easily achieve the goal of
the optimization problem. Our objective here is to
reduce traffic congestion and there are several widely
used reward functions to achieve this in related
works, like the delta in delay or queue length from
last timestep (Li, Lv, & Wang, 2016), throughput in
the lane and other linear combinations of traffic
parameters like waiting time, density, etc. We use the
following as our definition of the single stage reward:
𝑞
,

:=  𝑞
,
,


,

,
(7)
𝑤
,

:=  𝑤
,
,


,

,
(8)
𝑟

:= −(𝑞
,


+ 𝑐∗𝑤
,


).
(9)
where, 𝑞
,

and 𝑤
,

denote the cumulative queue
size and cumulative vehicle delay faced due to the set
of incoming lanes 𝑙


at intersection 𝑛

. Also, c = 0.3
is a weight parameter used for the waiting time that
indicates the relative importance of vehicle delay with
respect to the queue length. As our goal is to
minimize traffic congestion, the linear combination of
queue length and vehicle delay in the traffic network
is modelled as a negative function of these parameters
Thus, maximizing the objective function defined in
terms of the single-stage rewards defined as in (9)
would amount to minimizing an analogous objective
function defined via costs that are in turn defined by
taking the negative of the rewards.
MATD3 for Traffic Signal Control:
Traffic flows in a road network 𝑅, are controlled by
the traffic lights present at the different intersections.
The control actions taken by a single traffic light at an
intersection 𝑛
𝑖
not only affects the traffic congestion
around it but also has a widespread effect across the
network. Thus, it is of crucial importance to learn a
control strategy that is robust to the actions taken by
the other agents and improves the traffic congestion
both locally and globally in the road network. Single
agent reinforcement learning methods do not scale
efficiently when the action spaces and state spaces
expand to higher dimensions. Multiagent
reinforcement learning methods are an apt choice for
our solution as they can learn a global objective by
coordinating with other agents and can scale
efficiently to high dimensional state and action
spaces.
The road network 𝑅 can be defined using a
multiagent setting like in Figure 2 with the 𝑀 traffic
lights as the agents present in the environment, at time
𝑡. The agents see a local state 𝑜
𝑡,𝑖
from the collection
𝑜
𝑡
=(𝑜
𝑡,1
,𝑜
𝑡,2
,…,𝑜
𝑡,𝑀
) and perform actions 𝑎
𝑡
=
( 𝑎
𝑡,1
,𝑎
𝑡,2
,…,𝑎
𝑡,𝑀
). These actions cause the
environment to change and the agents receive a
reward 𝑟
𝑡
=(𝑟
𝑡,1
,𝑟
𝑡,2
,…,𝑟
𝑡,𝑀
) and observe the next
local state 𝑜
(
𝑡+1
)
,𝑖
from the collection 𝑜

=
𝑜
(

)
,
,𝑜
(

)
,
,…,𝑜
(

)
,
. The rewards act as
feedback signals about the actions 𝑎
𝑡,𝑖
taken by the
agent 𝑖 in achieving the global control objective.
Multiagent Twin Delayed Deep Deterministic
Policy Gradient is a multiagent actor-critic based
algorithm, which uses the feedback from critic (state-
action value function) to improve the actor (policy).
Overestimation bias is a common problem in
reinforcement learning methods where the state-
action value function is maximised to learn the
optimal policy. This causes the learned policy to
become overoptimistic and unstable. Multiagent
Deep Deterministic Policy Gradient (MADDPG)
suffers from this maximisation bias as it maximises
the estimate of a target critic and uses it to learn the
optimal policy. MATD3 mitigates the bias by
learning two critics and uses the minimum of their
estimates to learn the optimal policy.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
480

Figure 2: Multiagent reinforcement learning setting.
Since, it now becomes an underestimation bias it
does not propagate through the algorithm and results
in stable learning. The critics are learnt by minimizing
the cost function 𝐽


as below:
𝑦


=𝑟

+ 𝛾 𝑚𝑖𝑛
,
𝑄
,

(
𝑥,𝑎

,..,𝑎

)
,
(10)
𝐽


= 𝐸𝑦


−𝑄

(
𝑥,𝑎

,…,𝑎

)


. (11)
Each agent learns two centralized critics that use the
actions of all the agents in the network and predict a
state-action value function that describes how good
the action of its agent was, given its knowledge about
the actions of all the other agents. The actor uses the
state-value function as feedback on its predictions and
thus implicitly learns to model the behaviour of other
agents in the network, as in (Ackermann et al., 2019).
∇


𝐽
(
𝜇

)
=𝐸 ∇


𝜇

(
𝑎

|𝑜

)
∇


𝑄
,
(𝑥,𝑎

,..,𝑎

).
(12)
During the execution phase, the actors act
independently as they have modelled the behaviour of
other agents in the training phase. This enables
centralized training and decentralized execution,
thereby circumventing challenges that arise due to
partial observability of agents.
MATD3 learns a deterministic actor 𝜇, which
maps a state to a particular action rather than a
probability distribution over actions. Ornstein-
Uhlenbeck noise is used to encourage exploration for
deterministic policy. Overfitting of state-action value
estimate is common in actor-critic methods like
MADDPG, which work with deterministic policies.
This causes the policy to exhibit high variance even
for similar actions. MATD3 uses a regularization
method which smooths out the target policy 𝜇
′
by
fitting an appropriately clipped Gaussian noise 𝐺
with zero mean and a small standard deviation 𝜎 on
the actions like in (14), so that the variance across
similar actions can be minimized.
𝜖~𝑐𝑙𝑖𝑝(𝐺
(
0,𝜎
)
,−𝑐,𝑐)
(13)
𝑎

=𝜇′(𝑜
,
)+ 𝜖
(14)
Negative effects tend to multiply in actor-critic
methods due to the feedback loop that exists between
the actor and critic modules. The instability of one
can affect the other resulting in sub-optimal overall
performance. Thus, in MATD3, the actor network
updates are delayed so that the critic can achieve
reasonable reduction in residual error before the actor
network is updated. It also uses other common
methods like target networks and experience replay
buffers to ensure stable learning. It uses two online
critics 𝑄
1
, 𝑄
2
and corresponding target critics
𝑄
1
′
,𝑄
2
′
. The weights of the target actor 𝜇
′
and the
target critics 𝑄
1
′, 𝑄
2
′, slowly follow the weights of
their online counterparts as follows,
𝜃

=𝜏𝜃

+(1−𝜏)𝜃

(15)
𝜃

=𝜏𝜃

+(1−𝜏)𝜃

(16)
𝜃

=𝜏𝜃

+(1−𝜏)𝜃

(17)
MATD3 improves the shortcomings of MADDPG by
using techniques explained above like double
centralized critics to minimize overestimation bias,
target policy smoothing to reduce variance in
deterministic policies and delayed policy updates to
ensure stable learning updates. Thus, have chosen it
to solve the traffic signal control problem at hand.
Deep Neural Network Architecture:
In this section, we shed light on the deep neural
networks that were used in the different algorithms
considered in this paper. Each traffic light agent 𝑖 for
the road network requires six neural networks, one
deterministic online actor, two centralized online
critics and their corresponding target networks. The
compute resource usage is maintained at a reasonable
level as costly operations involving backpropagation
are incurred only for the online networks.
The deterministic actor network takes the current
observation of agent 𝑖 as input and returns the action
𝑎
𝑖
to be taken. The actor network has 4 x 400 hidden
dense layers with ReLU activation. The output unit
produces a Tanh activation to bound the continuous
action generated within safe limits. The action 𝑎

is
then converted into the corresponding green phase
duration 𝑑

using (6).
The critic networks take the current observation
𝑜
𝑖
and the concatenated actions of all the agents in the
Robust Traffic Signal Timing Control using Multiagent Twin Delayed Deep Deterministic Policy Gradients
481

road network as input and return a state-action value
for the input pair. The critic network has 3 x 400
hidden dense layers with ReLU activation. The output
unit had linear activation and returned the centralised
critic value. We used Adam optimizer (Kingma & Ba,
2014), a discount factor 𝛾=0.99, learning rates 𝛼=
0.001 and 𝜏 = 0.003. We train the online network
once every three steps along with the target networks
for target policy smoothing. We train the neural
networks for around 2000 episodes. Experience
Replay buffer 𝐷 which stores tuples of past
experience has size 𝐵 = 50000. The old samples are
removed and new samples are stored in their place as
the buffer becomes full. Mini Batches of size 𝑆 = 120
are randomly sampled from the replay buffer and
used in the training process.
Algorithm 1: Multiagent Twin Delayed Deep
Deterministic Policy Gradients (MATD3).
for episode = 1 to E do
Initialize empty experience replay buffer
𝐷 and network parameters
Reset the environment, OU Noise 𝑁

and
obtain initial observation 𝒐
𝟎
for t = 1 to max_episode_length do
Select action 𝑎

~ 𝜇

(
𝑜

)
+ 𝑁

Convert 𝑎

to 𝑑


Execute actions (𝑑


,𝑑


,…,𝑑


) and
observe 𝑟
,
, 𝑜
,
Store
(
𝑜

,𝑎

,…,𝑎

,𝑟

,…,𝑟

,𝑜

)
in 𝐷
𝑜

= 𝑜

for agent 𝑖 = 1 to 𝑀 do
Sample a random mini-batch of 𝑆
samples (𝑜


,𝑎

,𝑟

,𝑜


) from 𝐷
Set 𝑦

= 𝑟


+
𝛾 𝑚𝑖𝑛
,
𝑄
,


𝑜


,𝑎

,…,𝑎


Minimize critic loss for both 𝑗=1,2
ℒ 𝜃

 =


∑
(𝑄
,

(
𝑜


,𝑎

,..𝑎

)
−

𝑦

)

if 𝑡 % 𝑑 = 0 then
Update policy 𝜇

with gradient
∇

,
=


∑
∇

𝜇

𝑜
,



∗

∇


𝑄
,
(
𝑜


,𝑎

,..𝑎

)

Update target network parameters as
𝜃

,
= 𝜏𝜃

,
+ (1 − 𝜏)𝜃

,

𝜃

,
= 𝜏𝜃

,
+ (1 − 𝜏)𝜃

,

𝜃



= 𝜏𝜃


+ (1 − 𝜏)𝜃



3 RESULTS AND DISCUSSIONS
In this section, we present results about the
performance of our proposed control strategy and
examine them for insights and improvement areas.
First, we verify the ability of our proposed strategy in
learning to alleviate traffic congestion. We also look
at how our strategy impacts traffic parameters like
average delay faced by the vehicles and the average
queue length. Second, we evaluate the performance
of our control strategy in comparison to strategies that
belong to different levels of control complexity as
follows:
1) Non-Adaptive control – Describes the class
of control strategies that are static and
predefined. We compare the performance of
our method opposed to Fixed Duration (FD)
control where the phases are executed in a
round robin manner for a fixed green phase
duration dg = 8𝑠;
2) Independent control – Control strategies that
belong to this class act independently
without co-operation according to their local
state and optimize their individual reward
functions. We choose IDQN (Tampuu,
Matiisen, & Vicente, 2017), a widely used
independent control strategy and compare its
performance with the performance of our
method; and
3) Co-operative control – This set contains
state-of-the-art control strategies that are
capable of cooperating with the different
agents in the network and optimize
individual performance in a way to achieve
a global control objective. We have chosen
MADDPG (Lowe, Wu, Tamar, & Abbeel,
2017) which is a very robust multiagent
control strategy and compare its
performance with our proposed strategy.
We compare our method’s performance against the
aforementioned algorithms over two different time-
varying traffic flows, namely Major-Minor flows and
Weibull Flows. We assess the robustness of our
control strategy adapting to the different kinds of
traffic flows.
3.1 Simulation Settings
A 2 x 2 road network 𝑅 with four intersections
denoted as
{
𝑛

,𝑛

,𝑛

,𝑛

}
was simulated on SUMO.
The network has horizontal arms that have two lanes
and the vertical arms that have a single lane. The
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
482

length of the arms is 450𝑚, with a maximum allowed
speed of 11𝑚/𝑠 on the horizontal arms and 07𝑚/𝑠
on the vertical arms. We have four agents in our road
network, as there are four intersections and each
intersection has a traffic light.
Phases can be defined as a combination of the red
and green traffic lights that can be shown for the
different movements in an intersection like moving
straight, turning left or right, etc. The possible phases
that can be executed are stored in arrays separately for
the different intersections. When a phase changes
from red to green for a particular link, we execute a
yellow signal duration 𝑑
𝑦
=2𝑠 to avoid any crashes
or unexpected incidents. The green duration is fixed
at 𝑑
𝑔
=8𝑠 for FD controls. This duration was picked
as a benchmark as it provided reasonable
performance on our use case across the different
traffic flows. The different phases are executed in a
round robin manner in the intersections. The green
duration 𝑑
𝑔
∈(5,25) for the different intersections.
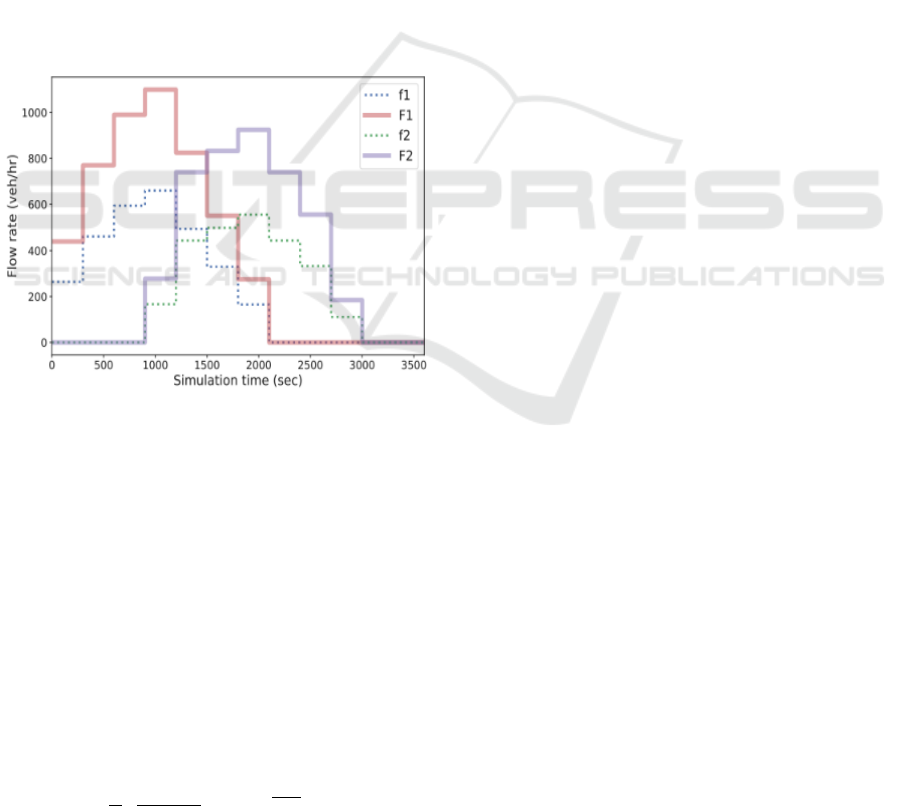
Figure 3: Major-Minor Traffic Flows.
Two different traffic flows have been used to
generate vehicles in the network and to analyse the
robustness of our framework. Firstly, we use Minor-
Major Flows (T Chu, 2019), in which time-displaced
and alternating high density (major) flows 𝐹
1
, 𝐹
2
are
generated on the horizontal arms and lower density
(minor) flows 𝑓
1
, 𝑓
2
are generated on the vertical
arms as shown above in Figure 3.
The arrival of vehicles at intersections is a
stochastic process. To generate vehicles in our traffic
flow simulation, the time interval between the
successive arrival of vehicles was modelled as
Weibull Distributions as follows,
𝑓
(
𝑡
)
=
𝛾
𝛼

(
𝑡− 𝜇
)
𝛼


𝑒


 



(18)
This probability distribution was chosen as it is a
good fit for a wide range of traffic flows (Riccardo &
Massimiliano, 2012). The parameters α, γ and μ
describe the scale, shape and location respectively. In
our case, we have used the standard one-parameter
Weibull Distribution where 𝛾 = 2. Based on the
arrival timing, we spawn the vehicles and assign
routes randomly at the start of every episode.
3.2 Training Results
The phases are executed in a round-robin cycle and
the green phase durations are controlled by the
different candidates we are comparing. In FD
algorithm, the green phase duration is fixed at 𝑑

=
8𝑠. This was picked as a benchmark as it provided
reasonable performance on our use case across the
different traffic flows. In the IDQN algorithm, the
continuous action space of phase duration has been
discretized and each of the integer durations
between 𝑑
𝑔
𝑚𝑖𝑛
and 𝑑
𝑔
𝑚𝑎𝑥
are its actions. In MATD3
and MADDPG algorithms, the action space is
continuous and the actions are the green phase
durations.
From Figs. 4 & 5 below, it can be seen that the
proposed control strategy is able to successfully learn
iteratively over episodes by performing actions that
increase its reward. It is important to note that during
the initial stages of learning, our strategy has lower
average reward than the FD control and MADDPG
algorithms. However, as learning continues, the
average reward of our control strategy exhibits a
strong rate of increase over episodes and settles after
learning for 1,000 episodes. As FD control is static, it
does not improve the congestion over episodes. It can
be seen that MADDPG learns at a significantly
slower pace than our strategy, as it settles after
learning for 1,600 episodes. IDQN suffers to learn
over episodes as it cannot scale to address high
dimensional discrete action spaces and does not co-
ordinate with other agents in the network. As its
performance deteriorates over episodes across the
different kinds of traffic flows, it has been excluded
from the Vehicle Delay and Queue Length
comparisons. The average reward of our strategy
improves over MADDPG by 8% and 10% for the
Major-Minor and Weibull traffic flows respectively.
It also shows a significant improvement over FD
control by 22% and 35% for the Major-Minor and
Weibull traffic flows respectively. The efficiency of
our framework in mitigating traffic congestion can be
inferred from the average episodic vehicle delay in
Figs. 6 & 7. The vehicle delay in the initial phases
Robust Traffic Signal Timing Control using Multiagent Twin Delayed Deep Deterministic Policy Gradients
483

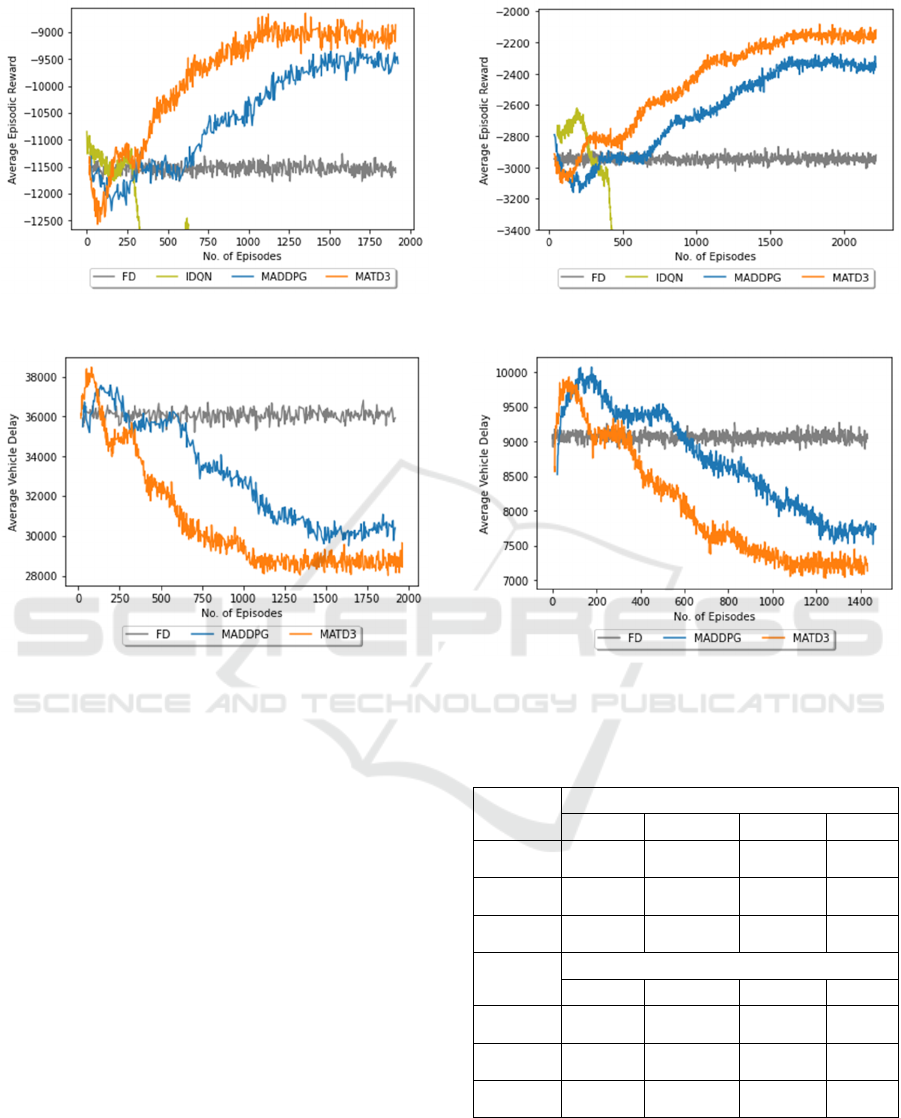
Figure 4: Average Episodic Reward (Major-Minor Flows).
Figure 6: Average Episodic Vehicle Delay (veh) on Major-
Minor Flows.
was significantly higher than FD control, however as
learning progressed, our control strategy effectively
minimized it over the episodes by adapting
incrementally. As our control strategy learns to adapt
to the traffic conditions quickly, we can see that the
average vehicle delay also reduces quickly compared
to MADDPG. The average vehicle delays were
reduced by 7% compared to MADDPG across the
different traffic flows. The vehicle delays were
reduced by 24% and 28% compared to FD control for
the Major-Minor flows and Weibull Flows
respectively.
The final performance metrics of all the
algorithms have been summarized in Table 1. These
values denote the values of Average Episodic
Reward, Average Vehicle Delay and Average Queue
Length after the learning stabilises.
We can see that our control strategy shows
significant improvement over MADDPG and FD
control strategies as explained above and shown in
Table 1.
Figure 5: Average Episodic Reward (Weibull Flows).
Figure 7: Average Episodic Vehicle Delay (veh) on Weibull
Flows.
Table 1: Average Performance Metrics separated by TSC
Algorithm and Flows.
Metrics
Major-Minor Flows
FD IDQN MADDPG MATD3
Average
Reward
-11532 -23939 -9790 -9214
Average
Delay
36043 -- 30126 28233
Average
Queue
719 -- 752 744
Metrics
Weibull Flows
FD IDQN MADDPG MATD3
Average
Reward
-2928 -17342 -2393 -2176
Average
Delay
9064 -- 7871 7012
Average
Queue
209 -- 109 102
Thus, we can conclude that the proposed strategy is
1) learning dynamically to alleviate traffic
congestion; 2) surpassing all the different algorithms
of varied control complexities that were used as
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
484

comparison; and 3) robust to different kinds of time-
varying traffic flows.
4 CONCLUSIONS
In this paper, we proposed co-operative traffic signal
control using Multiagent Twin Delayed Deep
Deterministic Policy Gradients (MATD3). Our
method establishes traffic signal duration control in a
road network where the traffic lights at each
intersection learn cooperatively to reduce traffic
congestion. We have shown that our method
outperforms existing reinforcement learning traffic
control strategies like Multiagent Deep Deterministic
Policy Gradients (MADDPG), Independent Deep Q
Networks (IDQN) and the traditional traffic signal
control method Fixed Duration control (FD) across
different time varying traffic flows. More
experiments over larger networks are being
conducted using our algorithm with comparisons on
different kinds of traffic flows. We are also studying
the scalability of our solution to larger networks.
ACKNOWLEDGEMENTS
The work of the second author was supported through
the J. C. Bose Fellowship, a grant from the
Department of Science and Technology, Government
of India, and the Robert Bosch Centre for Cyber
Physical Systems, Indian Institute of Science,
Bangalore.
REFERENCES
Abdulhai, B., Pringle, R., & Grigoris J., K. (2003).
Reinforcement learning for true adaptive traffic signal
control. Journal of Transportation Engineering, 278-
285.
Ackermann, J., Gabler, V., Osa, T., & Sugiyama, M.
(2019). Reducing overestimation bias in multi-agent
domains using double centralized critics. arXiv preprint
arXiv:1910.01465. arXiv .
Bellman, R. (1957). A Markovian Decision Process.
Journal of Mathematics and Mechanics, 679-684.
Bertsekas, D. (2012). Dynamic Programming and Optimal
Control. Athena Scientific, Boston.
Ge , H. (2019). Cooperative deep Q-learning with Q-value
transfer for multi-intersection signal control. IEEE
Access 7, 40797-40809.
Genders, W., & Razavi, S. (2016). Using a deep
reinforcement learning agent for traffic signal control.
arXiv preprint arXiv:1611.01142.
Head, K., Mirchandanai, P., & Shelby, S. (1998). The
RHODES prototype: a description and some results.
USA: Transportation Research Board.
Kingma, D., & Ba, J. (2014). Adam: A method for
stochastic optimization. arXiv preprint
arXiv:1412.6980.
Li, L., Lv, Y., & Wang, F. (2016). Traffic signal timing via
deep reinforcement learning. Traffic signal timing via
deep reinforcement learning, IEEE/CAA Journal of
Automatica Sinica.
Liang, X., Du, X., Wang, G., & Han, Z. (2018). Deep
Reinforcement Learning for Traffic Light Control in
Vehicular Networks. ArXiv abs/1803.11115.
Lowe, R., Wu, Y., Tamar, A., & Abbeel, P. &. (2017).
Multi-agent actor-critic for mixed cooperative-
competitive environments. arXiv preprint
arXiv:1706.02275.
Lowrie, P. (1990). Scats, sydney co-ordinated adaptive
traffic system: A traffic responsive method of
controlling urban traffic.
Mauro, V., & Taranto, C. (1990). UTOPIA. IFAC
Proceedings Volumes, 23(2), 245-252.
Prabhuchandran, K., Hemanth Kumar, A., & Bhatnagar, S.
(2014). Multi-agent reinforcement learning for traffic
signal control. 17th Interna-tional IEEE Conference on
Intelligent Transportation Systems (ITSC) (pp. 2539-
2534). Qingdao: IEEE.
Prashant, L., & Bhatnagar, S. (2012). Threshold tuning
using stochastic optimization for graded signal control.
IEEE Transactions on Vehicular Technology, 3865-
3880.
Prashanth, L., & Bhatnagar, S. (2011). Reinforcement
Learning with Function Approximation for Traffic
Signal Control. IEEE Transactions on Intelligent
Transportation Systems, 12(2):412-421.
Puterman, M. (1994). Markov Decision Processes. Wiley,
New York.
Riccardo, R., & Massimiliano, G. (2012). An empirical
analysis of vehicle time headways on rural two-lane
two-way roads. Procedia-Social and Behavioral
Sciences, 865-874.
T Chu, T. (2019). Multi-agent deep reinforcement learning
forlarge-scale traffic signal control.
IEEE Transactions
on Intelligent Transportation Systems.
Tampuu, A., Matiisen, T., & Vicente, R. (2017). Multiagent
cooperation and competition with deep reinforcement
learning. PloS one.
Watkins, C., & Dayan, P. (1992). Q Learning. Machine
Learning, 279-292.
Robust Traffic Signal Timing Control using Multiagent Twin Delayed Deep Deterministic Policy Gradients
485