Improving Usual Naive Bayes Classiﬁer Performances with Neural Naive

Bayes based Models

Elie Azeraf

1,2 a

, Emmanuel Monfrini

2 b

and Wojciech Pieczynski

2 c

Watson Department, IBM GBS, Avenue de l’Europe, Bois-Colombes, France

SAMOVAR, CNRS, Telecom SudParis, Institut Polytechnique de Paris, Evry, France

Keywords:

Naive Bayes, Bayes Classiﬁer, Neural Naive Bayes, Pooled Markov Chain, Neural Pooled Markov Chain.

Abstract:

Naive Bayes is a popular probabilistic model appreciated for its simplicity and interpretability. However, the

usual form of the related classiﬁer suffers from two signiﬁcant problems. First, as caring about the observa-

tions’ law, it cannot consider complex features. Moreover, it considers the conditional independence of the

observations given the hidden variable. This paper introduces the original Neural Naive Bayes, modeling the

classiﬁer’s parameters induced from the Naive Bayes with neural network functions. This method allows for

correcting the ﬁrst default. We also introduce new Neural Pooled Markov Chain models, alleviating the con-

ditional independence assumption. We empirically study the beneﬁts of these models for Sentiment Analysis,

dividing the error rate of the usual classiﬁer by 4.5 on the IMDB dataset with the FastText embedding, and

achieving an equivalent F

as RoBERTa on TweetEval emotion dataset, while being more than a thousand

times faster for inference.

1 INTRODUCTION

We consider the hidden random variable X, tak-

ing its values in the discrete ﬁnite set Λ

{λ

, ..., λ

}, and the observed random variables

1:T

= (Y

, ..., Y

), ∀t, Y

∈ Ω

. The Naive Bayes is a

probabilistic model considering these variables. This

probabilistic model is deﬁned with the following joint

law:

p(X, Y

1:T

) = p(X)

∏

t=1

p(Y

|X). (1)

It can be represented in Figure 1. It is especially ap-

preciated for its simplicity, its interpretability, and it is

one of the most famous probabilistic graphical models

(Koller and Friedman, 2009; Wainwright and Jordan,

2008).

The Bayes classiﬁer (Devroye et al., 2013; Duda

et al., 2006; Fukunaga, 2013) of the Maximum A

Posteriori (MAP) can be written as follows, with the

realization y

1:T

of Y

1:T

(we use the shortcut notation

p(X = x) = p(x):

φ(y

1:T

) = arg max

∈Λ

p(X = λ

1:T

) (2)

https://orcid.org/0000-0003-3595-0826

https://orcid.org/0000-0002-7648-2515

https://orcid.org/0000-0002-1371-2627

Figure 1: Probabilistic oriented graph of the Naive Bayes.

Therefore, the MAP classiﬁer induced from the

Naive Bayes is based on the posterior law, ∀λ

∈

, p(X = λ

1:T

), usually written as follows:

p(X = λ

1:T

) =

p(X = λ

, y

1:T

)

∑

∈Λ

p(X = λ

, y

1:T

)

p(X = λ

)

∏

t=1

p(Y

|X = λ

)

∑

∈Λ

p(X = λ

)

∏

t=1

p(Y

|X = λ

)

π(i)

∏

t=1

(t)

)

∑

∈Λ

π( j)

∏

t=1

(t)

)

with, ∀λ

∈ Λ

, y ∈ Ω

, t ∈ {1, ..., T }:

Azeraf, E., Monfrini, E. and Pieczynski, W.

Improving Usual Naive Bayes Classiﬁer Performances with Neural Naive Bayes based Models.

DOI: 10.5220/0010890400003122

In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 315-322

ISBN: 978-989-758-549-4; ISSN: 2184-4313

315

• π(i) = p(X = λ

);

• b

(t)

(y) = p(Y

= y|X = λ

Thus, the classiﬁer is:

1:T

) = arg max

∈Λ







π(i)

∏

t=1

(t)

)

∑

∈Λ

π( j)

∏

t=1

(t)

)







(3)

We consider for all this paper the stationary case

for all models, i.e., the different parameters are not

depending on time t. Thus, for the Naive Bayes, we

set b

(t)

(y) = b

(y).

The classiﬁer induced from the Naive Bayes for

classiﬁcation with supervised learning always uses

the form (3), depending on the parameters π and b

(Jurafsky and Martin, 2009; Ng and Jordan, 2002;

Metsis et al., 2006; Liu et al., 2013). It is applied

in many applications, such as Sentiment Analysis or

Text Classiﬁcation (Jurafsky and Martin, 2009; Kim

et al., 2006; McCallum et al., 1998).

However, it is is mainly criticized for two major

drawbacks (Ng and Jordan, 2002; Sutton and McCal-

lum, 2006). First, through the parameter b, it cares

about the observations’ law. It implies that one can-

not consider complex features with the usual Naive

Bayes classiﬁer. Indeed, assuming that Y

∈ R

, and

modeling b by a Gaussian law, the number of param-

eters to learn is equal to:

|{z}

for the mean

d(d + 1)

| {z }

for the covariance matrix

If it is tractable for relatively small values of d, it

quickly becomes intractable when d increases. For

example, with Natural Language Processing (NLP),

it is common to convert words to numerical vectors of

size 300 (Pennington et al., 2014), 784 (Devlin et al.,

2019), or even 4096 (Akbik et al., 2018), which be-

comes impossible to estimate. This process is called

word embedding and is mandatory to achieve rele-

vant results. One can suppose the independence be-

tween the different components, also called features,

of Y

, resulting in estimating only d parameters for

the covariance matrix, but this process achieves poor

results. We select the Gaussian law as an example,

but this problem happens for every law. This “fea-

ture problem” is even more signiﬁcant when the fea-

tures belong to a discrete space, and approximation

methods remain limited (Brants, 2000; Azeraf et al.,

2021b).

Another main drawback of the Naive Bayes con-

cerns the conditional independence assumption of the

observed random variables. It implies not considering

the order of the different observations with the classi-

ﬁer induced from the stationary Naive Bayes model.

In this paper, inspired by the writing of the clas-

siﬁer in (Azeraf et al., 2021a) and the Hidden Neu-

ral Markov Chain in (Azeraf et al., 2021c), we pro-

pose the Neural Naive Bayes. This model consists in

deﬁning the classiﬁer induced from the Naive Bayes

written in a discriminative manner with neural net-

works functions (LeCun et al., 2015; Ian Goodfellow

and Courville, 2016). This neural model corrects the

ﬁrst default of the usual Naive Bayes classiﬁer, as it

can consider complex features of observations. More-

over, we propose the Neural Pooled Markov Chains,

which are neural models assuming a conditional de-

pendence of the observations given the hidden ran-

dom variables, modeling them as a Markov chain.

Therefore, they also correct the second drawback of

the usual Naive Bayes classiﬁer. Finally, we empiri-

cally study these different innovations’ contributions

to the Sentiment Analysis task.

This paper is organized as follows. In the next

section, we present the classiﬁer of the Naive Bayes

written discriminatively, i.e., which does not use the

observations’ law, the Pooled Markov Chain (Pooled

MC) and Pooled Markov Chain of order 2 (Pooled

MC2) models and their classiﬁers. The third section

presents a different way to compute the classiﬁers,

estimating parameters with neural network functions.

Then, we empirically evaluate the contributions of our

neural models applied to Sentiment Analysis. Conclu-

sion and perspectives lie at the end of the paper.

To summarize our contributions, we present (i)

three original neural models based on probabilistic

models, and (ii) we show their efﬁciency compared

with the usual form of the Naive Bayes classiﬁer for

Sentiment Analysis.

2 NAIVE BAYES AND POOLED

MARKOV CHAINS

2.1 The Classiﬁer Induced from the

Naive Bayes Written

Discriminatively

A classiﬁer is considered “written generatively” if its

form uses some p(Y

), with A, B non-empty sub-

sets of the observed and hidden variable sets. If it

is not written generatively, a classiﬁer is written dis-

criminatively. These notions rejoin the usual ones

about generative and discriminative classiﬁers (Ng

and Jordan, 2002; Jebara, 2012). For example, (3)

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

316

Figure 2: Probabilistic oriented graph of the Pooled Markov

Chain.

is the classiﬁer induced from the Naive Bayes written

generatively, as its form uses b

) = p(Y

= y

(Azeraf et al., 2021a) presents how to write the

classiﬁer induced from the Naive Bayes written dis-

criminatively:

1:T

) = arg max

∈Λ

norm

π(i)

1−T

∏

t=1

(i)

(4)

with, ∀λ

∈ Λ

, t ∈ {1, ..., T }, y ∈ Ω

(i) = p(X = λ

= y),

and the norm function deﬁned as, ∀x ∈ R

norm : R → R, x

→

∑

j=1

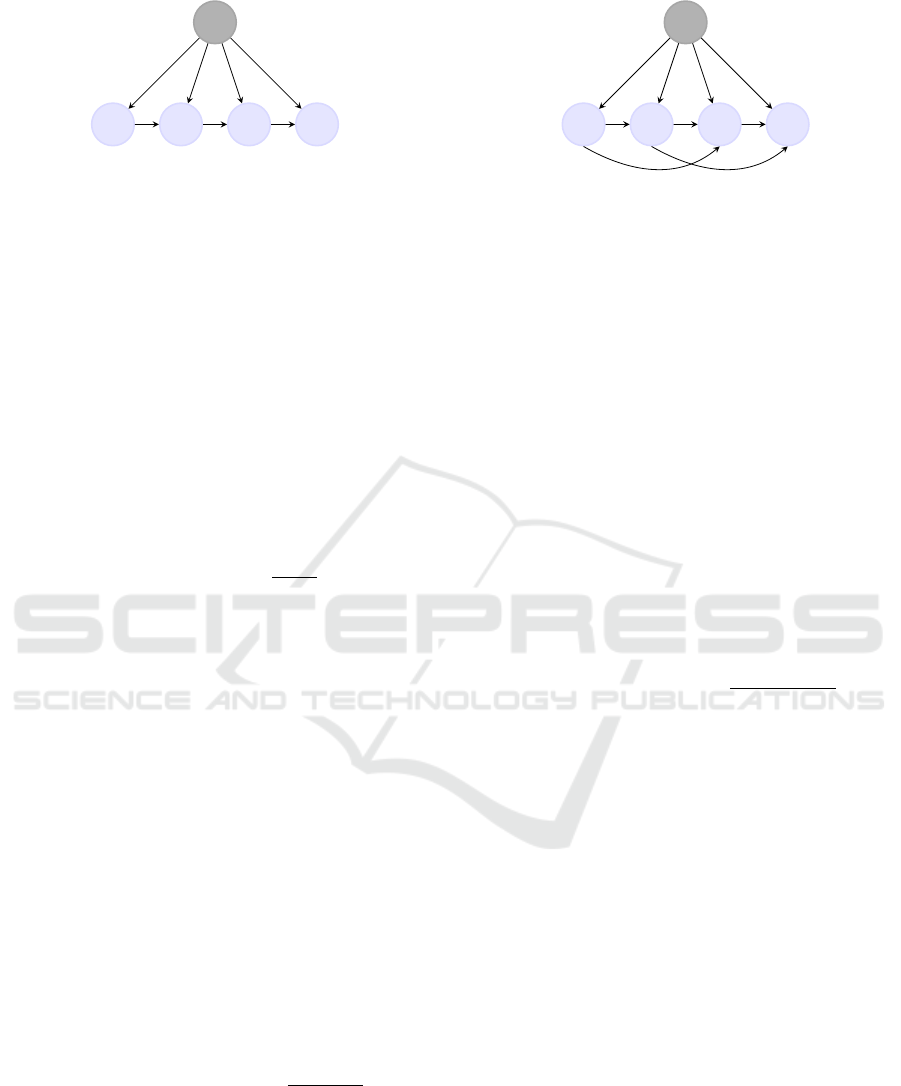
2.2 Pooled Markov Chain

We introduce the Pooled Markov Chain model, con-

sidering the same random variables as the Naive

Bayes. It is deﬁned with the following joint law:

p(X, Y

1:T

) = p(X)p(Y

|X)

T −1

∏

t=1

p(Y

t+1

|X, Y

) (5)

This model generalizes the Naive Bayes, insofar as

the latter is a special case of it, supposing that the ob-

served random variables follow a Markov chain given

the hidden variable, while the Naive Bayes supposes

the conditional independence. It is represented in Fig-

ure 2.

The classiﬁer induced from the Pooled MC writ-

ten discriminatively is deﬁned as:

1:T

) =

arg max

∈Λ

norm

MC,1

(i)

T −1

∏

t=1

MC,2

t+1

(i)

MC,1

(i)

(6)

with the following parameter of the stationary Pooled

MC, ∀λ

∈ Λ

, y

∈ Ω

• L

MC,1

(i) = p(X = λ

= y

);

• L

MC,2

(i) = p(X = λ

= y

, Y

t+1

= y

The proof is given in the appendix.

Figure 3: Probabilistic oriented graph of the Pooled Markov

Chain of order 2.

2.3 Pooled Markov Chain of Order 2

The Pooled Markov Chain of order 2, represented in

Figure 3 is deﬁned with the joint law:

p(X, Y

1:T

) = p(X)p(Y

|X)p(Y

|X, Y

)

T −2

∏

t=1

p(Y

t+2

|X, Y

, Y

t+1

)

(7)

This probabilistic model generalizes the two others,

considering the observations follow a Markov chain

of order 2 given the hidden variable.

The classiﬁer induced from the Pooled MC2 writ-

ten discriminatively is deﬁned as:

MC2

1:T

) =

arg max

∈Λ

norm

MC2,1

(i)

T −1

∏

t=1

MC2,2

t+1

t+2

(i)

MC2,1

t+1

(i)

(8)

with the following parameter of the stationary Pooled

MC2, ∀λ

∈ Λ

, y

∈ Ω

• L

MC2,1

(i) = p(X = λ

= y

, Y

t+1

= y

);

• L

MC2,2

(i) = p(X = λ

= y

, Y

t+1

= y

, Y

t+2

The proof is also given in the appendix.

3 NEURAL NAIVE BAYES BASED

MODELS

3.1 Neural Naive Bayes

We consider the classiﬁer induced from the Naive

Bayes written discriminatively (4). We assume the

functions π and L, allowing to deﬁne this classiﬁers,

are strictly positive, and Ω

= R

, d ∈ N

∗

. (4) can be

written as follows:

1:T

) = arg max

∈Λ

norm

π(i)

1−T

∏

t=1

(i)

Improving Usual Naive Bayes Classiﬁer Performances with Neural Naive Bayes based Models

317

= arg max

∈Λ

norm

π(i)

∏

t=1

(i)

π(i)

= arg max

∈Λ

softmax

log(π(i)) +

∑

t=1

log



(i)

π(i)



(9)

with the softmax function deﬁned as, ∀x ∈ R

softmax : R → R, x

→

exp(x

)

∑

j=1

exp(x

)

Moreover, we suppose, ∀i ∈ {1, ..., N}, that the in-

ﬂuence of log(π(i)) is negligible in (9), which is true

if the classes of X have the same probability, or if T

is big enough.

We set NN

a neural network function with y

input and the output of size N. We deﬁne it as follows:

)

= log



(i)

π(i)



with NN

)

the i-th component of the vector

Therefore, (4) is approximated with:

1:T

) ≈ arg max

∈Λ

sotfmax

∑

t=1

)

(10)

As (10) is the classiﬁer induced from the Naive Bayes

parametrized with neural networks, we call this appli-

cation the Neural Naive Bayes.

3.2 Neural Pooled Markov Chains

We consider the Pooled MC model, and we assume

the same hypothesis as above about the parameter

functions. The classiﬁer of the Pooled MC (6) can

be written:

1:T

) = arg max

∈Λ

softmax

log



MC,1

(i)



T −1

∑

t=1

log

MC,2

t+1

(i)

MC,1

(i)

(11)

As above, we suppose that log



MC,1

(i)



is neg-

ligible. We deﬁne a neural network function, NN

with the concatenation of y

and y

t+1

as input, and an

output of size N. It is used to model:

, y

t+1

)

= log

MC,2

t+1

(i)

MC,1

(i)

Therefore, (11) is approximated as follows:

1:T

) ≈ arg max

∈Λ

sotfmax

T −1

∑

t=1

, y

t+1

)

(12)

We called (12) the Neural Poooled Markov Chain

(Neural Pooled MC) function.

In the same idea, the Neural Pooled Markov Chain

of order 2 (Neural Pooled MC2) is deﬁned with:

MC2

1:T

) ≈arg max

∈Λ

sotfmax

T −2

∑

t=1

MC2

, y

t+1

, y

t+2

)

(13)

with NN

MC2

a neural function having the concatena-

tion of y

, y

t+1

, and y

t+2

as input, and an output of size

To go further, ∀k ∈ N

∗

, we introduce the Neu-

ral Pooled Markov Chain of order k (Neural Pooled

MC(k)):

MCk

1:T

) ≈ arg max

∈Λ

sotfmax

T −k

∑

t=1

MCk

, y

t+1

, ..., y

t+k

)

(14)

with NN

MCk

a neural function having the concatena-

tion of y

to y

t+k

as input, and an output of size N.

4 APPLICATION TO SENTIMENT

ANALYSIS

Sentiment Analysis is an NLP task consisting of pre-

dicting the sentiment of a given text. In this sec-

tion, we are going to apply the usual classiﬁer in-

duced from the Naive Bayes (3), the Neural Naive

Bayes (10), the Neural Pooled MC (12), and the Neu-

ral Pooled MC2 (13) for Sentiment Analysis. The goal

is to observe the improvement brought by our new

classiﬁers compared to the usual one usually.

We use two different embedding methods: Fast-

Text (Bojanowski et al., 2017) and ExtVec (Komninos

and Manandhar, 2016), allowing to convert each word

in a given sentence to a vector of size 300. Therefore,

Ω

= R

300

in this use-case.

Every parameter of neural models,

, NN

MC2

, is a feedforward neural

network with the adapted input size, a hidden layer of

size 64 followed by a ReLU (Nair and Hinton, 2010)

activation function, and an output layer of size N, the

latter depending on the dataset.

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

318

Table 1: Accuracy errors of the usual classiﬁer induced from the Naive Bayes and our proposed neural models on IMDB

dataset with FastText and ExtVec embeddings.

Usual Naive Bayes Neural Naive Bayes Neural Pooled MC Neural Pooled MC2

FastText 49.49% 12.46% ± 0.19 11.37% ± 0.24 11.01% ± 0.05

ExtVec 46.64% 13.40% ± 0.34 12.68% ± 0.17 12.34% ± 0.14

Table 2: Accuracy errors of the usual classiﬁer induced from the Naive Bayes and our proposed neural models on SST-2

dataset with FastText and ExtVec embeddings.

Usual Naive Bayes Neural Naive Bayes Neural Pooled MC Neural Pooled MC2

FastText 48.00% 15.32% ± 0.20 14.50% ± 0.17 14.10% ± 0.26

ExtVec 49.80% 17.22% ± 0.22 16.14% ± 0.29 15.88% ± 0.14

Table 3: F

scores of the usual classiﬁer induced from the Naive Bayes and our proposed neural models on TweetEval dataset

with FastText and ExtVec embeddings.

Usual Naive Bayes Neural Naive Bayes Neural Pooled MC Neural Pooled MC2

FastText 17.68 71.15 ± 0.16 71.32 ± 0.20 72.00 ± 0.28

ExtVec 15.68 68.17 ± 0.37 69.07 ± 0.46 69.28 ± 0.45

Table 4: F

scores of the usual classiﬁer induced from the Naive Bayes and our proposed neural models on Financial Phrase-

bank dataset with FastText and ExtVec embeddings.

Usual Naive Bayes Neural Naive Bayes Neural Pooled MC Neural Pooled MC2

FastText 31.83 ± 0.99 82.87 ± 0.53 84.61 ± 0.91 86.02 ± 0.49

ExtVec 34.48 ± 1.39 82.60 ± 0.58 85.01 ± 0.77 85.14 ± 1.06

4.1 Dataset Description

We use four datasets for our experiments:

• the IMDB dataset (Maas et al., 2011), com-

posed of movie reviews, with a train set of 25000

texts and a test set of the same size, with Λ

{Positive, Negative}.

• the SST-2 dataset (Socher et al., 2013) from

GLUE (Wang et al., 2019), also composed of

movie reviews, with a train set of 67349 texts, a

test set of 1821 texts, and a validation set of 872

texts, with Λ

= {Positive, Negative};

• the TweetEval emotion dataset (Barbieri et al.,

2020; Mohammad et al., 2018), composed with

Twitter data, with a train set of 3257 texts, a test

set of 1421 texts, and a validation set of 374 texts,

with Λ

= {Anger, Joy, Optimism, Sadness};

• the Financial Phrasebank (FPB) dataset (Malo

et al., 2014), which consists in English sen-

tences from ﬁnancial news. We select the

“All agree” data of 2264 sentences with Λ

{Positive, Neutral, Negative}. We set aside 453

randomly for test set. To avoid biases, we do a

different draw at every experiment.

All these datasets are freely available with the datasets

library (Lhoest et al., 2021).

4.2 Parameter Learning and

Implementation Details

On the one hand, the parameter π and b from (3) are

learned with maximum likelihood estimation. For π,

it consists of estimating it by counting the frequencies

of the different patterns:

π(i) =

∑

with N

the number of times X = λ

in the training set.

We model b with a gaussian law. As the estimation

of the covariance matrix of size 300 × 300 for each

class is intractable and result in computational prob-

lems when used, we select the vector’s mean as the

observation of each word. It estimates a mean and a

variance of size 1 for each class. Therefore, for each

∈ Λ

, b

∼ N (µ

, σ

), with µ

and σ

estimated by

maximum likelihood.

On the other hand, parameters NN

, NN

, and

MC2

are estimated with stochastic gradient descent

algorithm using Adam (Kingma and Ba, 2014) opti-

mizer with back-propagation (Rumelhart et al., 1986;

LeCun et al., 1989) and Cosine Annealing gradient

method (Loshchilov and Hutter, 2016). We minimize

the Cross-Entropy loss function with a learning rate

of 0.001 and a mini-batch size of 64 - selected af-

ter a K-fold cross-validation step. For the IMDB and

Improving Usual Naive Bayes Classiﬁer Performances with Neural Naive Bayes based Models

319

FPB datasets, where the validation set is not directly

given, we construct it with 20% of the train set, drawn

randomly. For each experiment, we train our model

for 5 epochs (except for TwetEval, which requires 15

epochs, and FPB, requiring 25 epochs), and we keep

the one achieving the best score on the validation set

for testing. As it is a stochastic algorithm, every ex-

periment with a Neural Naive Bayes based model is

realized ﬁve times, and we report the mean and the

95% conﬁdence interval. Every experiment is real-

ized 10 times for FPB, even for the usual classiﬁer,

due to the test set drawing.

About the implementation details, all the codes

are written in python. We use the Flair (Akbik et al.,

2019) library for the word embedding methods, and

PyTorch (Paszke et al., 2019) for neural functions and

training. All experiments are realized with a CPU

having 16Go RAM.

4.3 Results

We apply the usual classiﬁer induced from Naive

Bayes, the Neural Naive Bayes, the Neural Pooled

MC, and the Neural Pooled MC2 to the four datasets.

The accuracy errors are available in Table 1 and 2 for

IMDB and SST-2, and the F

scores in Table 3 and 4

for TweetEval and FPB.

As expected, one can observe important improve-

ments with the neural models related to the usual

classiﬁer induced from the Naive Bayes. Indeed,

for example, with FastText embedding on the IMDB

dataset, this error is divided by about 4.5 with the

Neural Pooled MC2. It conﬁrms the importance of

considering complex features.

As one can observe in Table 1, 2, 3, and 4, increas-

ing the Markov chain’s order allows to improve re-

sults. It shows the effect of alleviating the conditional

independence condition. This observation is expected

as the model becomes more complex and extended.

Indeed, for each k ∈ N, the Pooled Markov Chain

of order k is a particular case of the Pooled Markov

Chain of order k + 1. To observe the limits of this

case, we also apply the Neural Pooled MC(k), with

k ∈ {3, 5, 7, 10}. All these models achieve slightly

equivalent results as the Neural Pooled MC2, with-

out signiﬁcant improvements, showing the empirical

limits of this method.

Moreover, we can compare our models’ results

with other popular ones. First, we precise that our

models are lights, as training and inference time are

very fast: about 5 minutes to train a model and about

1.5 milliseconds for inference. Therefore, we com-

pare our results only with models reputed as “light”

and not heavy models as the ones based on Trans-

former (Vaswani et al., 2017), or LSTM-CRF (Akbik

et al., 2018). These light models present the beneﬁt

of being easy to serve for industrial purposes. Thus,

about IMDB, our models are largely better than SVM

with TF-IDF, Convolutional Neural Networks (Tang

et al., 2015), or even the classic FastText algorithm for

text classiﬁcation (Joulin et al., 2017), which achieve

accuracy errors of 59.5%, 62.5%, and 54.8%, respec-

tively. About TweetEval, our models achieves bet-

ter results than the BiLSTM (66.0), FastText (65.2),

SVM (64.7), and even equivalent result as RoBERTa

(Barbieri et al., 2020; Liu et al., 2019) (72.0), the lat-

ter being an heavy model based on the Transform-

ers, requiring about 2 seconds for inference. We

can make the same observation for FPB, with LSTM

(0.74), LSTM with ELMO (0.77), and other models

available in (Araci, 2019). These results show our

proposed models’ interest regarding the other popu-

lar ones. Therefore, they are a great alternative con-

sidering the training and inference time/performances

threshold.

5 CONCLUSION AND

PERSPECTIVES

This paper presents the original Neural Naive Bayes

and Neural Pooled Markov Chain models. These

models signiﬁcantly improve the usual Naive Bayes

classiﬁer’s performances, considering complex obser-

vations’ features without constraints, modeling their

parameters with Neural Network functions, and al-

leviating the conditional independence hypothesis.

They allow to achieve great performances and sim-

plicity, and present an original way to deﬁne the clas-

siﬁer induced from probabilistic models with neural

network functions.

Moreover, these new neural models can be viewed

as original pooling methods for textual data. Indeed,

starting from word embedding methods, a usual way

for text embedding consists of summing the embed-

ding of the words of the text. Our methods, which

beneﬁt from being computationally light, propose a

new way to do this document embedding process and

can be included in any neural architecture. Therefore,

going further in this direction can be a promising per-

spective.

REFERENCES

Akbik, A., Bergmann, T., Blythe, D., Rasul, K., Schweter,

S., and Vollgraf, R. (2019). FLAIR: An Easy-To-Use

Framework for State-Of-The-Art NLP. In Proceed-

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

320

ings of the 2019 Conference of the North American

Chapter of the Association for Computational Lin-

guistics (Demonstrations), pages 54–59.

Akbik, A., Blythe, D., and Vollgraf, R. (2018). Contex-

tual String Embeddings for Sequence Labeling. In

Proceedings of the 27th International Conference on

Computational Linguistics, pages 1638–1649.

Araci, D. (2019). FinBERT: Financial Sentiment Analysis

with Pre-Trained Language Models. arXiv preprint

arXiv:1908.10063.

Azeraf, E., Monfrini, E., and Pieczynski, W. (2021a). Us-

ing the Naive Bayes as a Discriminative Model. In

Proceedings of the 13th International Conference on

Machine Learning and Computing, pages 106–110.

Azeraf, E., Monfrini, E., Vignon, E., and Pieczynski, W.

(2021b). Highly Fast Text Segmentation With Pair-

wise Markov Chains. In 6th IEEE Congress on Infor-

mation Science and Technology, pages 361–366.

Azeraf, E., Monfrini, E., Vignon, E., and Pieczynski, W.

(2021c). Introducing the Hidden Neural Markov

Chain Framework. In Proceedings of the 13th Inter-

national Conference on Agents and Artiﬁcial Intelli-

gence - Volume 2, pages 1013–1020.

Barbieri, F., Camacho-Collados, J., Espinosa-Anke, L., and

Neves, L. (2020). TweetEval: Uniﬁed Benchmark and

Comparative Evaluation for Tweet Classiﬁcation. In

Proceedings of Findings of EMNLP.

Bojanowski, P., Grave, E., Joulin, A., and Mikolov, T.

(2017). Enriching Word Vectors with Subword Infor-

mation. Transactions of the Association for Computa-

tional Linguistics, 5:135–146.

Brants, T. (2000). TnT: a Statistical Part-of-Speech Tag-

ger. In Proceedings of the 6th Conference on Applied

Natural Language Processing, pages 224–231.

Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K.

(2019). BERT: Pre-training of Deep Bidirectional

Transformers for Language Understanding. In Pro-

ceedings of the 2019 Conference of the North Amer-

ican Chapter of the Association for Computational

Linguistics: Human Language Technologies, Volume

1 (Long and Short Papers), pages 4171–4186.

Devroye, L., Gy

orﬁ, L., and Lugosi, G. (2013). A Prob-

abilistic Theory of Pattern Recognition, volume 31.

Springer Science & Business Media.

Duda, R. O., Hart, P. E., et al. (2006). Pattern Classiﬁcation.

John Wiley & Sons.

Fukunaga, K. (2013). Introduction to Statistical Pattern

Recognition. Elsevier.

Ian Goodfellow, Y. B. and Courville, A. (2016). Deep

Learning. MIT Press.

Jebara, T. (2012). Machine Learning: Discriminative and

Generative. Springer Science & Business Media.

Joulin, A., Grave, E., Bojanowski, P., and Mikolov, T.

(2017). Bag of Tricks for Efﬁcient Text Classiﬁca-

tion. In Proceedings of the 15th Conference of the Eu-

ropean Chapter of the Association for Computational

Linguistics: Volume 2, Short Papers, pages 427–431,

Valencia, Spain.

Jurafsky, D. and Martin, J. H. (2009). Speech and Lan-

guage Processing: An Introduction to Natural Lan-

guage Processing, Speech Recognition, and Compu-

tational Linguistics, 2nd Edition. Prentice-Hall.

Kim, S.-B., Han, K.-S., Rim, H.-C., and Myaeng, S. H.

(2006). Some Effective Techniques for Naive Bayes

Text Classiﬁcation. IEEE Transactions on Knowledge

and Data Engineering, 18(11):1457–1466.

Kingma, D. P. and Ba, J. (2014). Adam: A

Method for Stochastic Optimization. arXiv preprint

arXiv:1412.6980.

Koller, D. and Friedman, N. (2009). Probabilistic Graphi-

cal Models: Principles and Techniques. MIT press.

Komninos, A. and Manandhar, S. (2016). Dependency

Based Embeddings for Sentence Classiﬁcation Tasks.

In Proceedings of the 2016 conference of the North

American Chapter of the Association for Computa-

tional Linguistics: Human Language Technologies,

pages 1490–1500.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learn-

ing. Nature, 521(7553):436–444.

LeCun, Y., Boser, B., Denker, J. S., Henderson, D., Howard,

R. E., Hubbard, W., and Jackel, L. D. (1989). Back-

propagation Applied to Handwritten Zip Code Recog-

nition. Neural computation, 1(4):541–551.

Lhoest, Q., Villanova del Moral, A., Jernite, Y., Thakur,

A., von Platen, P., Patil, S., Chaumond, J., Drame,

M., Plu, J., Tunstall, L., Davison, J.,

sko, M., Chh-

ablani, G., Malik, B., Brandeis, S., Le Scao, T., Sanh,

V., Xu, C., Patry, N., McMillan-Major, A., Schmid,

P., Gugger, S., Delangue, C., Matussi

ere, T., Debut,

L., Bekman, S., Cistac, P., Goehringer, T., Mustar, V.,

Lagunas, F., Rush, A., and Wolf, T. (2021). Datasets:

A Community Library for Natural Language Process-

ing. In Proceedings of the 2021 Conference on Empir-

ical Methods in Natural Language Processing: Sys-

tem Demonstrations.

Liu, B., Blasch, E., Chen, Y., Shen, D., and Chen, G. (2013).

Scalable Sentiment Classiﬁcation for Big Data Anal-

ysis using Naive Bayes Classiﬁer. In IEEE Interna-

tional Conference on Big Data, pages 99–104.

Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D.,

Levy, O., Lewis, M., Zettlemoyer, L., and Stoyanov,

V. (2019). Roberta: A Robustly Optimized BERT Pre-

training Approach. arXiv preprint arXiv:1907.11692.

Loshchilov, I. and Hutter, F. (2016). SGDR: Stochastic

Gradient Descent with Warm Restarts. arXiv preprint

arXiv:1608.03983.

Maas, A. L., Daly, R. E., Pham, P. T., Huang, D., Ng, A. Y.,

and Potts, C. (2011). Learning Word Vectors for Sen-

timent Analysis. In Proceedings of the 49th Annual

Meeting of the Association for Computational Lin-

guistics: Human Language Technologies, pages 142–

150, Portland, Oregon, USA. Association for Compu-

tational Linguistics.

Malo, P., Sinha, A., Korhonen, P., Wallenius, J., and Takala,

P. (2014). Good Debt or Bad Debt: Detecting Se-

mantic Orientations in Economic Texts. Journal of the

Association for Information Science and Technology,

65(4):782–796.

McCallum, A., Nigam, K., et al. (1998). A Comparison of

Event Models for Naive Bayes Text Classiﬁcation. In

Improving Usual Naive Bayes Classiﬁer Performances with Neural Naive Bayes based Models

321

AAAI-98 Workshop on Learning for Text Categoriza-

tion, volume 752 (1), pages 41–48.

Metsis, V., Androutsopoulos, I., and Paliouras, G. (2006).

Spam Filtering with Naive Bayes - which Naive

Bayes? In CEAS, volume 17, pages 28–69.

Mohammad, S., Bravo-Marquez, F., Salameh, M., and Kir-

itchenko, S. (2018). Semeval-2018 task 1: Affect in

tweets. In Proceedings of the 12th international work-

shop on semantic evaluation, pages 1–17.

Nair, V. and Hinton, G. E. (2010). Rectiﬁed Linear Units

Improve Restricted Boltzmann Machines. In Proceed-

ings of the Internation Conference on Machine Learn-

ing.

Ng, A. Y. and Jordan, M. I. (2002). On Discriminative vs.

Generative Classiﬁers: A Comparison of Logistic Re-

gression and Naive Bayes. In Advances in Neural In-

formation Processing Systems, pages 841–848.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., et al. (2019). Pytorch: An Imperative

Style, High-Performance Deep Learning Library. Ad-

vances in Neural Information Processing Systems,

32:8026–8037.

Pennington, J., Socher, R., and Manning, C. D. (2014).

Glove: Global Vectors for Word Representation.

In Proceedings of the 2014 Conference on Empiri-

cal Methods in Natural Language Processing, pages

1532–1543.

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986).

Learning Representations by Back-Propagating Er-

rors. nature, 323(6088):533–536.

Socher, R., Perelygin, A., Wu, J., Chuang, J., Manning,

C. D., Ng, A. Y., and Potts, C. (2013). Recursive

Deep Models for Semantic Compositionality over a

Sentiment Treebank. In Proceedings of the 2013 Con-

ference on Empirical Methods in Natural Language

Processing, pages 1631–1642.

Sutton, C. and McCallum, A. (2006). An Introduction to

Conditional Random Fields for Relational Learning.

Introduction to Statistical Relational Learning, 2:93–

128.

Tang, D., Qin, B., and Liu, T. (2015). Document Modeling

with Gated Recurrent Neural Network for Sentiment

Classiﬁcation. In Proceedings of the 2015 Conference

on Empirical Methods in Natural Language Process-

ing, pages 1422–1432.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, L. u., and Polosukhin, I.

(2017). Attention is all you need. In Advances in

Neural Information Processing Systems, volume 30.

Curran Associates, Inc.

Wainwright, M. J. and Jordan, M. I. (2008). Graphical

Models, Exponential Families, and Variational Infer-

ence. Now Publishers Inc.

Wang, A., Singh, A., Michael, J., Hill, F., Levy, O., and

Bowman, S. R. (2019). GLUE: A Multi-Task Bench-

mark and Analysis Platform for Natural Language

Understanding. In In the Proceedings of International

Conference on Learning Representations.

APPENDIX

Proof of the Classiﬁer Induced from the

Pooled MC Written Discriminatively

The joint law of the Pooled MC is given with (5). For

all λ

∈ Λ

and the realization Y

1:T

= y

1:T

, it can be

written:

p(X = λ

, y

1:T

)

= p(X = λ

)p(y

|X = λ

)

T −1

∏

t=1

p(y

t+1

|X = λ

, y

)

= p(X = λ

)

p(X = λ

, y

)

p(X = λ

)

T −1

∏

t=1

p(X = λ

, y

t+1

)

p(X = λ

, y

)

= p(y

)

T −1

∏

t=1

p(y

t+1

MC,1

(i)

T −1

∏

t=1

MC,2

t+1

(i)

MC,1

(i)

Therefore, the posterior law of the Pooled MC can

be written using the Bayes rule, allowing to deﬁne the

Bayes classiﬁer with the MAP criterion of the Pooled

MC as (6).

Proof of the Classiﬁer Induced from the

Pooled MC2 Written Discriminatively

The joint law of the Pooled MC2 is given with (7).

For all λ

∈ Λ

and the realization Y

1:T

= y

1:T

, it can

be written:

p(X = λ

, y

1:T

)

= p(X = λ

)p(y

|X = λ

)p(y

|X = λ

, y

)

T −2

∏

t=1

p(y

t+2

|X = λ

, y

t+1

)

= p(X = λ

)

p(X = λ

, y

)

p(X = λ

)

p(X = λ

, y

)

p(X = λ

, y

)

T −2

∏

t=1

p(X = λ

, y

t+1

, y

t+2

)

p(X = λ

, y

t+1

)

= p(y

, y

)

T −2

∏

t=1

p(y

t+2

, y

t+1

)

× L

MC2,1

(i)

T −2

∏

t=1

MC2,2

t+1

t+2

(i)

MC,1

t+1

(i)

Therefore, the posterior law of the Pooled MC2

can be written using the Bayes rule, allowing to de-

ﬁne the Bayes classiﬁer with the MAP criterion of the

Pooled MC2 as (8).

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

322