Cognitive Planning in Motivational Interviewing

Emiliano Lorini

, Nicolas Sabouret

, Brian Ravenet

, Jorge Fernandez

and C

eline Clavel

IRIT-CNRS, Toulouse University, France

Universit

e Paris-Saclay, CNRS, Laboratoire Interdisciplinaire des Sciences du Num

erique, Orsay, France

Keywords:

Artiﬁcial Intelligence, Automated Planning, Motivational Interviewing, Human-computer Interaction, Health

Coaching.

Abstract:

This paper presents a cognitive planning model that implements the principles of motivational interviewing, a

counseling method used to guide people in adopting behavior changes. This planning system is part of a wider

dialogical architecture of artiﬁcial counseling agent. We present the formal model and planning problem. We

show how it can be used to plan for dialogue in the architecture. We illustrate its functionalities on a simple

example.

1 INTRODUCTION

Motivational Interviewing. Motivational inter-

viewing (for short MI) is a counseling method used

in clinical psychology for eliciting behavior change

(Lundahl and Burke, 2009). One crucial aspect of

MI consists in exploring the participant’s subjectivity

through open questions to identify her desires and

personal values (e.g., conformity, independence,

carefulness, etc.) (Miller and Rollnick, 2012). This

exploration allows the participant to become aware

of the inconsistency between her desires or personal

values (e.g., being in good health), and her current

behavior (e.g., not doing enough physical activity).

However, MI does not necessarily try to induce

beliefs about positive aspects of the behavior change

(e.g., most people are already aware that reasonable

physical activity is good for health and would like

to practice a sport regularly). It rather helps the

participant to identify the reasons why she did not

convert her mere desires (e.g., I would like to practice

a sport) into intentions (e.g., I commit to do sport

regularly) and reassures her that these limitations can

be overcome. To this aim, the counselor rephrases the

ideas expressed by the participant so as to provoke

reﬂections about the connection between her beliefs,

desires and intentions.

Several automated MI systems have been pro-

posed in recent times (da Silva et al., 2018; Kanaoka

and Mutlu, 2015; Lisetti et al., 2013; Olafsson et al.,

2019; Schulman et al., 2011). However, all these sys-

tems use predeﬁned dialogue trees to conduct the MI.

In this paper, we propose a model based on cognitive

planning for driving MI in a human-agent interaction

system.

Cognitive Planning. Classical planning in artiﬁcial

intelligence (AI) is the general problem of ﬁnding a

sequence of actions (or operations) aimed at achiev-

ing a certain goal (Ghallab et al., 2004). It has been

shown that classical planning can be expressed in

the propositional logic setting whereby the goal to

be achieved is represented by a propositional formula

(Bylander, 1994). In recent times, epistemic planning

was proposed as a generalization of classical planning

in which the goal to be achieved can be epistemic,

i.e., the goal of inducing a certain agent to believe or

to know something (Bolander and Andersen, 2011;

owe et al., 2011). The standard languages for epis-

temic planning are epistemic logic (EL) (Halpern and

Moses, 1992) and its dynamic extension, the so-called

dynamic epistemic logic (DEL) (van Ditmarsch et al.,

2007). A variety of epistemic logic languages and

fragments of DEL with different levels of expressivity

and complexity have been introduced to formally rep-

resent the epistemic planning problem and efﬁciently

automate it (see, e.g., (Muise et al., 2015; Muise

et al., 2021; Kominis and Geffner, 2015; Cooper et al.,

2016; Cooper et al., 2021)).

In a recent paper (Fernandez et al., 2021), cogni-

tive planning was introduced as a further generaliza-

tion of epistemic planning. In cognitive planning, it

is not only some knowledge or belief state of a target

agent that is to be achieved, but more generally a cog-

508

Lorini, E., Sabouret, N., Ravenet, B., Fernandez, J. and Clavel, C.

Cognitive Planning in Motivational Interviewing.

DOI: 10.5220/0010895400003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 508-517

ISBN: 978-989-758-547-0; ISSN: 2184-433X

nitive state. The latter could involve not only knowl-

edge and beliefs, but also desires, intentions and,

more generally, motivations. The cognitive planning

(CP) approach is well-suited for modeling interaction

whereby an agent tries to trigger attitude change in

another agent through the execution of a sequence

of speech acts. CP takes into consideration resource

boundedness and limited rationality of the interlocu-

tor agent. This makes CP a very well-suited model for

implementing motivational interviewing in human-

machine interaction (HMI) applications in which an

artiﬁcial agent is expected to interact with a human

— who is by deﬁnition resource-bounded — through

dialogue and to induce her to behave in a certain way.

Motivational interviewing is composed of several

stages: prior to having the participant change her in-

tentions, one has to make her aware of the inconsis-

tencies between her desires and her actual behavior.

The artiﬁcial agent has both (i) a model of the hu-

man’s overall cognitive state, including her beliefs

and intentions, and (ii) a goal towards the human’s

mental attitudes, e.g., the goal of making the human

aware of the inconsistency between her desires and

her actual behavior. Given (i) and (ii), it tries to

ﬁnd a sequence of speech acts aimed at modifying

the human’s cognitive state thereby guaranteeing the

achievement of its goal.

Outline. The aim of this paper is to explain how

to situate the cognitive planning module in a gen-

eral architecture of an artiﬁcial agent which is ex-

pected to interact with a human user through dialogue

and to motivate her to behave in a certain way or to

change/adopt a certain style of life through motiva-

tional interviewing methods. In Section 2, we provide

a birds-eye view of the architecture. In Section 3, we

present the formal framework on which the cognitive

planning approach is built. In Section 4, a variety of

cognitive planning problems are formalized. Section

5 is devoted to describe the belief revision module of

the architecture. Finally, in Section 6, the cognitive

planning problem is instantiated in a concrete exam-

ple of motivational interviewing between an artiﬁcial

agent and a human.

2 GENERAL ARCHITECTURE

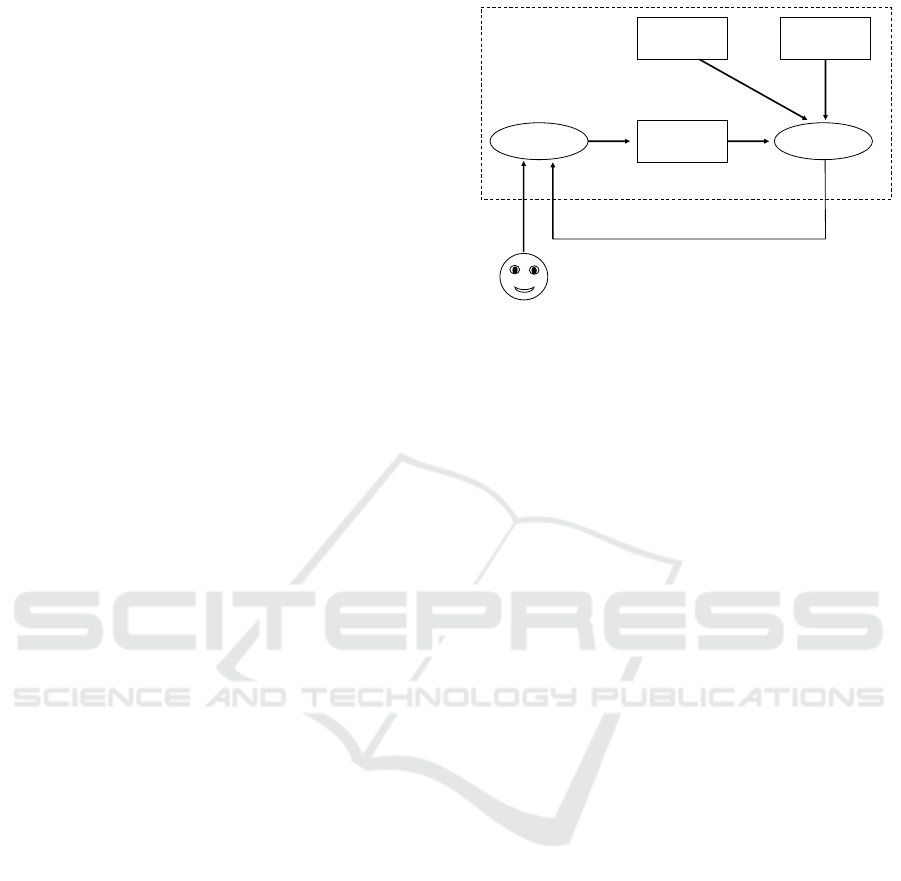
The general architecture of the system is detailed in

Figure 1.

Data Structures. The artiﬁcial planning agent, that

for simplicity we call the machine, is endowed with

three kinds of data structure: its belief base, the goal

Belief base

revision

Planning

Goal

Speech act

repertoire

Act

Machine

Human

Figure 1: General architecture.

to be achieved and the repertoire of speech acts (or

communicative actions) it can perform. We assume

the machine’s action repertoire includes two types of

speech act: assertions and questions. The machine

can have persuading goals, aimed at changing the hu-

man’s beliefs, or inﬂuencing goals, aimed at inducing

the human to form a certain intention or to behave

in a certain way. The machine’s belief base includes

both information about the environment and informa-

tion about the human’s overall cognitive state and its

way of functioning. In other words, the machine has

a theory of the human’s mind. The machine’s belief

base evolves during its dialogue with the human.

Interrogative and Informative Phase. The inter-

action between the machine and the human is struc-

tured in two phases the interrogative (or exploratory)

phase and the informative phase. In the interroga-

tive phase the machine gathers information about the

human’s cognitive state. This includes information

about the human’s beliefs, desires and preferences.

The interrogative phase is identiﬁed with a sequence

of questions by the machine to the human. The in-

formative phase is the core of the inﬂuence process.

In this phase, the machine performs a sequence of

assertions aimed at modifying the human’s cognitive

state (her beliefs and/or intentions). The interrogative

phase is propaedeutic to the informative phase. In-

deed, for the machine to be able to lead the human to

change her behavior, it must have information about

the human’s cognitive state. Such an information is

acquired during the interrogative phase. In this work,

we assume that the two phases are uniﬁed at the plan-

ning level: the machine includes in its plan not only

the assertions but also also the questions. In particu-

lar, the machine has to ﬁnd a sequence of questions

followed by a sequence of assertions such that, for

some possible answer by the human, the composition

of the two sequences guarantees that the persuading

Cognitive Planning in Motivational Interviewing

509

or inﬂuencing goal will be achieved. It is reasonable

to assume that the machine ﬁrst tries to ﬁnd a plan

with only assertions. (why asking questions to the

human if what the machine knows about the human’s

cognitive state is already sufﬁcient to persuade or in-

ﬂuence her). However, in most cases, the machine

has uncertainty and lacks information about the hu-

man’s cognitive state so that it must ask questions to

the human before trying to induce her attitude change.

In Section 6, we will show how some aspects of the

motivational interviewing (MI) methodology can be

naturally captured in the two phases of the cognitive

planning approach.

Execution of the Plan. After having selected a

plan, the machine executes it. The machine can ei-

ther execute the entire plan or execute it one piece

after the other by waiting the reply of the human be-

fore executing the next piece. We assume that how

the plan is executed depends on the application un-

der consideration and on the type of speech act in the

plan to be executed. It is reasonable to suppose that

when executing the interrogative part of the plan, the

machine asks a single question at each step and waits

the answer by the human before moving to the next

question. After each question by the machine, the

human gives an answer and the machine expands or

revises, when necessary, its belief base accordingly.

Indeed, the information provided by the human in re-

sponse to the machine’s question can enrich the ma-

chine’s belief base with new facts about the environ-

ment (objective facts) or about the human’s cognitive

state (mental facts) or make the machine’s belief base

inconsistent. In the latter case, the machine must re-

vise its belief base after having incorporated the new

information.

3 FORMAL FRAMEWORK

In this section, we present the epistemic language on

which the cognitive planning approach is based. The

language is a two-agent fragment of the multi-agent

epistemic language presented in (Lorini, 2020). The

language distinguishes explicit from implicit belief:

an agent’s belief of explicit type is a piece of infor-

mation contained in the agent’s belief base, while a

belief of implicit type corresponds to a piece of infor-

mation that is derivable from the agent’s belief base.

Assume a countably inﬁnite set of atomic proposi-

tions Atm and a ﬁnite set of agents Agt = {h, m}, with

h denoting the human and m the machine. The lan-

guage is deﬁned in two steps. First, the language L

is deﬁned by the following grammar in BNF:

α ::= p | ¬α | α

∧ α

| 4

α,

where p ranges over Atm and i ranges over Agt. L

the language for representing agents’ explicit beliefs.

The formula 4

α is read “agent i explicitly believes

that α”. Then, the language L extends the language

by a modal operator of implicit belief and a dy-

namic operator for belief expansion for the machine.

It is deﬁned by the following grammar:

ϕ ::= α | ¬ϕ | ϕ

∧ ϕ

| 

α | [+

α]ϕ,

where α ranges over L

. The formula 

α is read

“agent m implicitly believes that α”. The formula

α]ϕ is read “ϕ holds after agent m has privately

expanded its belief base with α”. The other Boolean

constructions >, ⊥, →, ∨ and ↔ are deﬁned in the

standard way.

In L, both agent h and agent m have explicit be-

liefs but only agent m has implicit beliefs, and more-

over the latter are restricted to L

formulas of type

α. So there are no nested implicit beliefs for agent m.

Agent m is assumed to be the unique artiﬁcial agent in

the system which is endowed with unbounded reason-

ing and planning capabilities. The cognitive planning

problem will be modeled from agent m’s perspective.

The interpretation of language L exploits the no-

tion of belief base. While the notions of possible

state (or world) and epistemic alternative are primi-

tive in the standard semantics for epistemic logic (Fa-

gin et al., 1995), they are deﬁned from the primitive

concept of belief base in our semantics. In particular,

a state is a composite object including a description

of both the agents’ belief bases and the environment.

Deﬁnition 1 (State). A state is a tuple B =

, B

, V) where: for every i ∈ Agt, B

⊆ L

is agent

i’s belief base; V ⊆ Atm is the actual environment.

The set of all states is noted S.

Note that an agent’s belief base B

can be inﬁ-

nite. The sublanguage L

(Atm, Agt) is interpreted

w.r.t. states, as follows:

Deﬁnition 2 (Satisfaction). Let B = (B

, B

, V) ∈ S.

Then:

B |= p ⇐⇒ p ∈ V,

B |= ¬α ⇐⇒ B 6|= α,

B |= α

∧ α

⇐⇒ B |= α

and B |= α

B |= 4

α ⇐⇒ α ∈ B

Observe in particular the set-theoretic interpreta-

tion of the explicit belief operator: agent i explicitly

believes that α if and only if α is included in its belief

base.

This is similar to the way states are modeled in the

interpreted system semantics for multi-agent systems (Lo-

muscio et al., 2017).

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

510

A model is deﬁned to be a state supplemented with

a set of states, called context. The latter includes all

states that are compatible with the common ground

(Stalnaker, 2002), i.e., the body of information that

the agents commonly believe to be the case.

Deﬁnition 3 (Model). A model is a pair (B, Cxt),

where B ∈ S and Cxt ⊆ S. The class of all models

is noted M.

Note that we do not impose that B ∈ Cxt. When

Cxt = S then (B, Cxt) is said to be complete, since S

is conceivable as the complete (or universal) context

which contains all possible states. We compute agent

m’s set of epistemic alternatives from the agent m’s

belief base, as follows.

Deﬁnition 4 (Epistemic Alternatives). R

is the bi-

nary relation on the set S such that, for all B =

, B

, V), B

= (B

, B

, V

) ∈ S:

if and only if ∀α ∈ B

: B

|= α.

means that B

is an epistemic alternative

for agent m at B. So m’s set of epistemic alternatives

at B includes exactly those states that satisfy all m’s

explicit beliefs.

Deﬁnition 5 extends Deﬁnition 2 to the full lan-

guage L. Its formulas are interpreted with respect to

models as follows. (We omit Boolean cases that are

deﬁned in the usual way.)

Deﬁnition 5 (Satisfaction). Let B = (B

, B

, V) ∈ S

and (B, Cxt) ∈ M. Then:

(B, Cxt) |= α ⇐⇒ B |= α,

(B, Cxt) |= 

ϕ ⇐⇒ ∀B

∈ Cxt, if BR

then (B

, Cxt) |= ϕ,

(B, Cxt) |= [+

α]ϕ ⇐⇒ (B

, Cxt) |= ϕ,

with B

= (B

, B

, V

), V

= V,

= B

∪ {α} and B

= B

According to the previous deﬁnition, agent m im-

plicitly believes that ϕ if and only if, ϕ is true at all

states in the context that m considers possible. More-

over, the private expansion of m’s belief base by α

simply consists in agent m adding the information α

to its belief base, while agent h keeps her belief base

unchanged.

A formula ϕ ∈ L is said to be valid in the class

M, noted |=

ϕ, if and only if (B, Cxt) |= ϕ for ev-

ery (B, Cxt) ∈ M; it is said to be satisﬁable in M if

and only if ¬ϕ is not valid in M. Finally, given a ﬁ-

nite Σ ⊂ L

, we say that ϕ is a logical consequence

of Σ in the class M, noted Σ |=

ϕ, if and only if,

for every (B, Cxt) ∈ M such that Cxt ⊆ S(Σ) we have

(B, Cxt) |= ϕ, with S(Σ) = {B ∈ S : ∀α ∈ Σ, B |= α}.

In (Fernandez et al., 2021), it is proved that the satisﬁ-

ability checking problem and the logical consequence

problem so deﬁned are, respectively, NP-complete

and co-NP-complete.

4 PLANNING PROBLEMS

The cognitive planning problem is speciﬁed in the

context of the language L. It consists in ﬁnding a se-

quence of questions or informative actions for agent

m which guarantees that it believes that its goal α

is satisﬁed. As we emphasized above, agent m is as-

sumed to be an artiﬁcial agent which interacts with

the resource-bounded human agent h.

Informative Actions. Let Act

= {+

α : α ∈ L

}

be agent m’s set of belief expansion operations (or in-

formative actions) and let elements of Act

be noted

ε, ε

, . . . Speech acts of type ‘assertion’ are formalized

as follows:

assert(m,h,α)

def

= +

α.

The event assert(m,h,α) captures the speech act

“agent m asserts to agent h that α”. The latter is

assumed to coincide with the perlocutionary effect

(Searle, 1969, Sect. 6.2) of the speaker learning that

the hearer has learnt that the speaker believes that α.

We distinguish simple assertions from convincing ac-

tions:

convince(m,h,α)

def

= +

α.

The event convince(m,h,α) captures the action

“agent m convinces agent h that α”. We have

assert(m,h,α) = convince(m,h,4

α). We assume

‘to assert’ and ‘to convince’ correspond to differ-

ent utterances. While ‘to assert’ corresponds to the

speaker’s utterances of the form “I think that α is

true!” and “In my opinion, α is true!”, ‘to convince’

corresponds to the speaker’s utterances of the form “α

is true!” and “it is the case that α!”.

The previous abbreviations and, more generally,

the idea of describing speech acts of a communica-

tive plan performed by agent m with m’s private be-

lief expansion operations is justiﬁed by the fact that

we model cognitive planning from the perspective of

the planning agent m. Therefore, we only need to rep-

resent the effects of actions on agent m’s beliefs.

We implicitly assume that, by default, m believes that

h trusts its sincerity, so that h will believe that m believes

what it says.

Cognitive Planning in Motivational Interviewing

511

Questions. We consider binary questions by the

machine m to the human h of the form ?

m,h

α.

The

set of binary questions is noted Que

. Intuitively,

m,h

α is the utterance performed by agent m to agent

h of the form “Do you think that α is true?”. Let el-

ements of Que

be noted λ, λ

, . . . Each question is

associated with its set of possible answers. The an-

swer function A : Que

−→ 2

Act

is used to map each

binary question to its set of possible answers and is

deﬁned as follows:



m,h





α, +

¬4



Answers to binary questions are noted ρ, ρ

, . . . The

operation +

α captures agent h’s positive answer

to agent m’s binary question ?

m,h

α (“I think that α is

true!”), while +

¬4

α captures agent h’s negative

answer (“I don’t think that α is true!”). Note that if

agent h answers negatively to the consecutive ques-

tions ?

m,h

α and ?

m,h

¬α, then she expresses her un-

certainty about the truth value of α .

We assume that the positive answer is the default

answer to a question. Indeed, when agent m asks

question ?

m,h

α, it wants to verify whether agent h en-

dorses the belief that α and presupposes that agent h

will answer positively to the question. In this perspec-

tive, the speaker expects a conﬁrmation by the inter-

locutor. Thus, for notational convenience, we write

da(?

m,h

α) to denote the default answer +

α to

the question ?

m,h

α.

The following abbreviation deﬁnes a dynamic op-

erator capturing the necessary effects of agent m’s

question:

[λ]ϕ

def

ρ∈A(λ)

[ρ]ϕ,

with λ ∈ Que

. Note that, unlike the basic belief

expansion operator [+

α], the operator [λ] is non-

deterministic, as it represents the consequences of all

possible answers to question λ. In fact, while the for-

mula [+

α]¬ϕ ∨ [+

α]ϕ is valid in the class M, the

formula [λ]¬ϕ ∨ [λ]ϕ is not.

Executability Preconditions. The set of events in-

cludes both informative actions and questions, and is

deﬁned as follows: Evt

= Act

∪ Que

. Elements

of Evt

are noted γ, γ

, . . . They have executability

preconditions that are speciﬁed by the following func-

tion: P : Evt

−→ L. We assume that an event γ can

take place if its executability precondition P (γ) holds.

We use the executability precondition function P

to deﬁne the following operator of possible occur-

In speech act theory, binary (yes-no) questions are usu-

ally distinguished from open questions.

rence of an event:

hhγiiϕ

def

= P (γ) ∧ [γ]ϕ,

with γ ∈ Evt. The abbreviation hhγiiϕ has to be read

“the event γ can take place and ϕ necessarily holds

after its occurrence”.

Informative and Interrogative Planning Problems.

We conclude this section with a formal speciﬁcation

of two planning problems, informative planning and

interrogative planning.

Deﬁnition 6 (Informative Planning Problem). An in-

formative planning problem is a tuple hΣ, Op

inf

, α

where:

• Σ ⊂ L

is a ﬁnite set of agent m’s available infor-

mation,

• Op

inf

⊂ Act

is a ﬁnite set of agent m’s informa-

tive actions,

• α

∈ L

is agent m’s goal.

Informally speaking, an informative planning

problem is the problem of ﬁnding an executable se-

quence of informative actions which guarantees that,

at the end of the sequence, the planning agent m be-

lieves that its goal α

is achieved. Typically, α

a persuading or inﬂuencing goal, i.e., the goal of af-

fecting agent’s h cognitive state (including her beliefs

and intentions) in a certain way. A solution plan to

an informative planning problem hΣ, Op

inf

, α

i is a

sequence of informative actions ε

, . . . , ε

from Op

inf

for some k such that Σ |=

hhε

ii. . . hhε

ii

In an interrogative planning problem, the machine

can perform both informative actions and questions.

This problem is speciﬁed in the following deﬁnition.

Deﬁnition 7 (Interrogative Planning Problem).

An interrogative planning problem is a tuple

hΣ, Op

inf

, Op

quest

, α

i where:

• Σ ⊂ L

is a ﬁnite set of agent m’s available infor-

mation,

• Op

inf

⊂ Act

is a ﬁnite set of agent m’s informa-

tive actions,

• Op

quest

⊂ Que

is a ﬁnite set of agent m’s ques-

tions,

• α

∈ L

is agent m’s goal.

Intuitively, an interrogative planning problem is

the problem of ﬁnding a sequence of questions as a

means of understanding the interlocutor’s cognitive

state and, consequently, of being able to identify the

inconsistencies that she must be made aware of, via a

sequence of informative actions. In other words, the

sequence of questions serves the purpose of “explor-

ing” the interlocutor’s cognitive state and of building

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

512

a representation of it in order to being able to ﬁnd a

plan to reach the motivational interviewing (MI) goal.

A strong solution plan to an interrogative planning

problem hΣ, Op

inf

, Op

quest

, α

i is a sequence of ques-

tions λ

, . . . , λ

from Op

quest

such that

Σ |=

hhλ

ii. . . hhλ

ii>,

and ∀ρ

∈ A(λ

), . . . , ∀ρ

∈ A(λ

), ∃τ

, . . . , τ

∈

inf

such that

Σ |=

[ρ

]. . . [ρ

]hhτ

ii. . . hhτ

ii

A weak solution plan to an interrogative planning

problem hΣ, Op

inf

, Op

quest

, α

i is a sequence of ques-

tions λ

, . . . , λ

from Op

quest

such that

Σ |=

hhλ

ii. . . hhλ

ii>,

and ∃τ

, . . . , τ

∈ Op

inf

such that

Σ |=

[da(λ

)]. . . [da(λ

)]hhτ

ii. . . hhτ

ii

It is easy to verify that checking existence of a weak

solution for an interrogative planning problem (EWS-

INT problem) is reducible to checking existence of

a solution for an informative planning problem (ES-

INF problem). In (Fernandez et al., 2021) it was

proved that the ES-INF problem is in NP

= Σ

Thus, we get the following complexity upper bound

for the EWS-INT problem.

Theorem 1. The EWS-INT problem is in NP

= Σ

Checking existence of a strong solution for an in-

terrogative planning problem (ESS-INT problem) is

not comparable to the ES-INF problem or the EWS-

INT problem. Indeed, it requires to take all possible

answers to the questions and their possible ramiﬁca-

tions into account. The EWS-INT problem considers

a single sequence of answers (the sequence of default

answers) instead.

5 BELIEF REVISION MODULE

In this section, we describe the belief revision module

of the architecture we sketched in Section 2. As we

emphasized above, such a module is necessary for up-

dating the machine’s belief base after the human has

replied to its questions.

Let L

PROP

be the propositional language built

from the following set of atomic formulas:

Atm

= Atm ∪ {p

: 4

α ∈ L

Moreover, let tr

PROP

be the following translation

from the language L

deﬁned in Section 3 to L

PROP

(p) =p,

PROP

(¬α) =¬tr

PROP

(α),

PROP

(α

∧ α

) =tr

PROP

(α

) ∧ tr

PROP

(α

PROP

α) =p

For each ﬁnite X ⊆ L

, we deﬁne tr

PROP

(X) =

{tr

PROP

(α) : α ∈ X}. Moreover, we say that X

is propositionally consistent if and only if ⊥ 6∈



PROP

(X)



, where Cn is the classical deduc-

tive closure operator over the propositional language

PROP

. Clearly, the latter is equivalent to saying that

α∈X

PROP

(α) is satisﬁable in propositional logic.

Let Σ

core

, Σ

mut

⊆ L

denote, respectively, the core

(or, immutable) information in agent m’s belief base

and the volatile (or, mutable) information in agent m’s

belief base. Agent m’s core beliefs are stable and do

not change under belief revision. On the contrary,

volatile beliefs can change due to a belief revision op-

eration . Moreover, let Σ

input

⊆ L

be agent m’s in-

put information set. We deﬁne Σ

base

= Σ

core

∪ Σ

mut

The revision of (Σ

core

, Σ

mut

) by input Σ

input

, noted

Rev(Σ

core

, Σ

mut

, Σ

input

), is formally deﬁned as follows:

1. if Σ

core

∪ Σ

input

is not propositionally consistent

then Rev(Σ

core

, Σ

mut

, Σ

input

) = (Σ

core

, Σ

mut

2. otherwise, Rev(Σ

core

, Σ

mut

, Σ

input

) = (Σ

core

, Σ

mut

with Σ

core

= Σ

core

and

mut

X∈MCS(Σ

core

,Σ

mut

,Σ

input

)

where X ∈ MCS(Σ

core

, Σ

mut

, Σ

input

) if and only if:

• X ⊆ Σ

mut

∪ Σ

input

• Σ

input

⊆ X ,

• X ∪ Σ

core

is propositionally consistent, and

• there is no X

⊆ Σ

mut

∪Σ

input

such that X ⊂ X

and

∪ Σ

core

is propositionally consistent.

The revision function Rev has the following effects on

agent m’s beliefs: (i) the core belief base is not modi-

ﬁed, while (ii) the input Σ

input

is added to the mutable

belief base only if it is consistent with the core beliefs.

If the latter is the case, then the updated mutable be-

lief base is equal to the intersection of the subsets of

the mutable belief base which are maximally consis-

tent with respect to the core belief base and which

include the input Σ

input

This guarantees that belief

Note that the revision function Rev does not expand

agent m’s core belief set Σ

core

with the input information

set Σ

input

. It would be interesting to introduce a function

appr

: L

−→ {0, 1} which speciﬁes for every formula α in

whether the information α is completely apprehensible

by agent m (i.e., f

appr

(α) = 1) or not (i.e., f

appr

(α) = 0).

Speciﬁcally, f

appr

(α) = 1 means that if agent m learns that

α is true then, as a consequence, it will ﬁrmly believe that

α is true thereby adding α not only to its set of muta-

ble beliefs but also to its set of core beliefs. The func-

tion f

appr

would allow us to deﬁne a variant of belief re-

vision according to which if Σ

core

∪ Σ

input

is proposition-

ally consistent, then the core belief set Σ

core

is expanded

by all formulas α in Σ

input

such that f

appr

(α) = 1, that is,

core

= Σ

core

∪ {α ∈ Σ

input

: f

appr

(α) = 1}.

Cognitive Planning in Motivational Interviewing

513

revision satisﬁes minimal change. The function Rev

is a screened revision operator as deﬁned in (Makin-

son, 1997). The latter was recently generalized to the

multi-agent case (Lorini and Schwarzentruber, 2021).

Let Rev(Σ

core

, Σ

mut

, Σ

input

) = (Σ

core

, Σ

mut

For notational convenience, we write

Rev

core

(Σ

core

, Σ

mut

, Σ

input

) to denote Σ

core

and

Rev

mut

(Σ

core

, Σ

mut

, Σ

input

) to denote Σ

mut

. Note

that, if Σ

base

is propositionally consistent, then

Rev

core

(Σ

core

, Σ

mut

, Σ

input

) ∪ Rev

mut

(Σ

core

, Σ

mut

, Σ

input

)

is propositionally consistent too.

6 EXAMPLE

In this section, we illustrate the use of the cogni-

tive planning and belief revision module of the archi-

tecture with the aid of a human-machine interaction

(HMI) scenario. We assume m is a virtual coach-

ing agent which has to motivate the human agent h

to practice a physical activity. We suppose agent m

complies with the general principles of the theory of

motivational interviewing (MI) to ﬁnd a persuasive

strategy aimed at changing the human’s attitude.

One of the central cornerstones of MI is the postu-

late that for eliciting behavior change in a person, she

has to become aware of the inconsistency between her

current behavior and her desires. In other words, she

has to recognize the fact that her current behavior will

prevent her from obtaining what she likes.

Let us assume the disjoint sets CondAtm, DesAtm

and ActAtm are subsets of the set of atomic proposi-

tions Atm. Elements of CondAtm are atoms specify-

ing conditions, while elements of DesAtm are atoms

specifying desirable properties, that is, properties that

agent h may wish to achieve (i.e., agent h’s possi-

ble desiderata). Finally, atoms in ActAtm are used to

describe agent h’s behavior. Speciﬁcally, we deﬁne

ActAtm = {does(h,a) : a ∈ Act}, where Act is a ﬁnite

a set of action names. The atom does(h,a) has to be

read “agent h behaves in conformity with the require-

ment a” or, simply, “agent h does action a”.

The sets of literals from CondAtm, DesAtm and

ActAtm are deﬁned in the usual way as follows:

DesLit = DesAtm ∪ {¬p : p ∈ DesAtm},

CondLit = CondAtm ∪ {¬p : p ∈ CondAtm},

ActLit = ActAtm ∪ {¬p : p ∈ ActAtm},

Lit = DesLit ∪ CondLit ∪ ActLit.

We deﬁne LitSet = 2

Lit

and LitSet

= LitSet \ {

0}.

We moreover assume that the set of atomic propo-

sitions Atm includes one atom des(h, l) for each l ∈

DesLit standing for “agent h desires l to be true”.

For the sake of illustration, we suppose that Act =

{ps} where ps is the action (or requirement) “to prac-

tice regularly a sport or physical activity”. There-

fore, ActAtm = {does(h,ps)}. Moreover, DesAtm =

{dr, pw, lw, at, gh, st} and CondAtm = {ow, sl, co},

with the atoms having the following intuitive mean-

ing: dr: “agent h has dietary restrictions”; pw: “agent

h puts on weight”; lw: “agent h loses weight”; at:

“agent h is attractive”; gh: “agent h is in good health”;

st: “agent h is stressed”; ow: “agent h has an ofﬁce

work”; sl: “agent h has a sedentary life style”; co:

“agent h is a commuter and spends quite some time in

the trafﬁc everyday”.

The following abbreviation captures a simple no-

tion of necessity for X ∈ LitSet and l ∈ Lit:

nec(X, l)

def

∈X

→ l.

nec(X, l) has to be read “the facts in X will not be true

unless l is true” or more shortly “l is necessary for X”.

Agent m’s initial knowledge about agent h’s cog-

nitive state is speciﬁed by the following six abbrevia-

tions:

def

l∈Lit

nec({l}, l),

def

l∈Lit



nec(

0, l) ↔ 4



def

l∈Lit,X ,X

∈LitSet:X

⊆X



nec(X, l) →



∈X

→ 4

nec(X \X

, l)





def

l∈Lit,X ,X

∈LitSet:X⊆X



nec(X, l) →

nec(X

, l)



def

l∈Lit





des(h, l) ↔ 4

des(h, l)



∧



¬des(h, l) ↔ 4

¬des(h, l)





def

a∈Act





does(h, a) ↔ 4

does(h, a)



∧



¬does(h, a) ↔ 4

¬does(h, a)





Hypotheses α

-α

are general properties about agent

h’s conception of necessity. According to α

, agent

h believes that every fact is necessary for itself while,

according to α

, agent h believes a fact is true regard-

less of the circumstances if and only if she believes

that it is true. According to α

, if agent h believes

that l is necessary for the facts in X being true and

believes every fact in X

⊆ X, then she believes that l

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

514

is necessary for the facts in the remaining set X \ X

being true. According to α

, if X ⊆ X

and agent h be-

lieves that l is necessary for X then she believes that

l is necessary for X

as well. Hypotheses α

and α

capture agent h’s introspection over her desires (hy-

phothesis α

) and agent h’s perfect knowledge about

her actions and inactions (hyphothesis α

We moreover suppose that agent m has the follow-

ing information in its belief base capturing the neces-

sity relations between conditions, desirable properties

and actions:

def

= nec



{¬dr, ¬pw, sl}, does(h,ps)



∧

nec



{at, ¬dr}, does(h,ps)



∧

nec



{sl, gh}, does(h,ps)



∧

nec



{gh}, ¬st



∧

nec



{co, ow}, sl



For example, nec



{¬dr, ¬pw, sl}, does(h,ps)



means that practicing regularly a sport is necessary

for not having dietary restrictions and not putting

weight, while having a sedentary work style (i.e., a

person cannot pretend to not put weight and not have

dietary restrictions without practicing a sport, if she

has a sedentary work style).

The following abbreviation deﬁnes the concept of

agent h’s awareness of the inconsistency between the

actual state of affairs α and her desires:

AwareIncon(h, α)

def

X∈LitSet



∈X

des(h, l

)∧

nec(X, ¬α)∧ 4



According to the previous deﬁnition, agent h is aware

of the inconsistency between the actual state of affairs

α and her desires, noted AwareIncon(h, α), if she be-

lieves that the satisfaction of her desires is jeopardized

by the fact that α is true. More precisely, (i) agent h

believes that she will not achieve her desires unless α

is false and (ii) she believes that α is actually true.

We suppose that the pieces of information

, . . . , α

constitute agent m’s initial core belief base,

that is, Σ

core

= {α

, . . . , α

}. Moreover, we suppose

that agent m’s initial mutable belief base is empty,

that is, Σ

mut

0. We consider the planning problem

in which agent m tries to motivate agent h to practice

regularly a sport. To this aim, agent m tries to achieve

the following goal:

def

= ¬does(h,ps) → AwareIncon



h, ¬does(h,ps)



In other words, agent m tries to make it the case that

if agent h does not practice a sport, then she becomes

aware of the inconsistency between her actual desires

and the fact that she does not practice a sport.

Let X ⊆ DesLit, X

⊆ CondLit and

l ∈ ActLit ∪ CondLit. We assume agent m’s

action convince



m,h,nec(X ∪ X

, l)



to be con-

cretely realized through the utterance “since

condition X

holds, you will not satisfy your

desires X unless l is true!”. For example,

convince



m,h,nec(X ∪ X

, does(h,ps))



corresponds

to the utterance “since condition X

holds, you will

not satisfy your desires X unless you do action

ps!”, while convince



m,h,nec(X ∪ X

, ¬does(h,ps))



corresponds to the utterance “since condition X

holds, you will not satisfy your desires X unless you

refrain from doing action ps!”. For notational conve-

nience, we abbreviate convince



m,h,nec(X ∪ X

, l)



by !

m,h

(X,X

,l). We assume the following repertoires

of informative and interrogative actions for agent m:

inf



m,h

(X,X

,l) : X ⊆ DesLit, X

⊆ CondLit

and l ∈ ActLit ∪ CondLit



quest



m,h

des(h, l) : l ∈ DesLit



∪



m,h

l : l ∈ ActLit ∪ CondLit



with the following executability preconditions for

their elements:



m,h

(X,X

,l)



=



nec(X ∪X

, l)∧

∈X

des(h, l

) ∧

∈X



m,h

des(h, l)





m,h



= >.

In other words, a question is always executable.

Moreover, agent m can perform the action

m,h

(X,X

,l) — i.e., “since condition X

holds,

you will not satisfy your desires X unless l is true!”

— only if (i) it believes that agent h desires every

fact in X to be true, (ii) it believes that agent h

believes every fact in X

, and (iii) it believes that l is

necessary for X when X

holds. Thus, by performing

the speech act !

m,h

(X,X

,l), agent m informs agent h

that, in view of the fact that condition X

holds, l is

necessary for the satisfaction of her desires X, since

it presupposes that agent h has indeed such desires

and believes that the condition holds.

We suppose that at every step k of the interac-

tion with agent h, agent m tries to ﬁnd a solution for

the informative planning problem hΣ

base

, Op

inf

, α

If it can ﬁnd it, it proceeds with its execution and

then interaction stops. Otherwise, it tries to ﬁnd a

weak solution for the interrogative planning problem

hΣ

base

, Op

inf

, Op

quest

, α

i. If it cannot ﬁnd it, the

interaction stops. Otherwise, it executes the corre-

sponding sequence of questions and revises its be-

lief base according to agent h’s set of responses

Resp

. Then, it moves to step k + 1. We suppose

Cognitive Planning in Motivational Interviewing

515

that Σ

core

= Σ

core

, Σ

mut

= Σ

mut

, Op

inf

= Op

inf

and

quest

= Op

quest

. Moreover,

k+1

core

=Rev

core

(Σ

core

, Σ

mut

, Resp

k+1

mut

=Rev

mut

(Σ

core

, Σ

mut

, Resp

k+1

inf

=Op

inf

k+1

quest

=Op

quest

\ Selected(Op

quest

where Selected(Op

quest

) is the set of questions in-

cluded in the interrogative plan selected at step k. We

remove them because we want to avoid that agent m

keeps asking the same question indeﬁnitely.

Let us illustrate an example of interaction. At step

0, agent m cannot ﬁnd a solution for the informative

planning problem. Thus, it decides to go with ques-

tions. It ﬁnds ?

m,h

does(h,ps) as solution for the in-

terrogative planning problem. We suppose agent h’s

response to agent m’s question is +

¬4

does(h,ps).

At step 1, again agent m cannot ﬁnd a solution for the

informative planning problem. Thus, it moves to the

interrogative planning problem and ﬁnds the follow-

ing sequence of questions as a weak solution:

m,h

des(h, gh), ?

m,h

co, ?

m,h

ow.

Agent m executes the interrogative plan. We suppose

agent h’s set of responses to agent m’s questions at

step 1 is



des(h, gh), +

co, +



Thus, at step 2, agent m can ﬁnd a solution for

the informative planning problem. The solution is the

following sequence of assertive speech acts of length

m,h

(

0,{co, ow},sl), !

m,h



{gh},{sl},does(h,ps)



Agent m executes the informative plan. The previous

interaction between agent m and agent h is illustrated

in Figure 2 in which every speech act is associated

with its corresponding utterance.

7 CONCLUSION

Let’s take stock. We have presented a model of cog-

nitive planning and shown that it can elegantly for-

malize some principles of the motivational interview-

ing (MI) methodology, a counseling method used in

clinical psychology for eliciting attitude and behavior

change in humans.

Directions of future work are manifold. An im-

portant strategy of MI consists in helping the partici-

pant to overcome the obstacles that prevent her from

converting her mere desires into intentions and then

into effective behavior. Some of these obstacles are of

cognitive nature. For example, the participant could

Speaker Utterance Speech act

m Do you practice ?

m,h

does(h,ps)

a sport regularly?

h I don’t +

¬4

does(h,ps)

m Do you wish ?

m,h

des(h, gh)

to be in good health?

h Yes +

des(h, gh)

m Do you spend quite ?

m,h

some time in the trafﬁc

everyday as a commuter?

h Yes +

m Do you have ?

m,h

an ofﬁce work?

h Yes +

m You spend quite some !

m,h

(

0,{co, ow},sl)

time in the trafﬁc

everyday as a

commuter and you have

an ofﬁce work. Therefore,

your life style is sedentary!

m Your life style is sedentary. !

m,h



{gh},{sl},

Therefore, you will not does(h,ps)



satisfy your desire to be

in good health unless you

practice a sport regularly!

Figure 2: Human-machine dialogue.

hesitate whether to start to practice a sport regularly

since she fears that practicing a sport increases the

risk of getting injured. In this situation, the coun-

selor can try to reassure the participant that her fear

is unfounded. More generally, it can try to make the

participant to revise her beliefs that a certain action

has negative consequences. Another cognitive ob-

stacle could be the participant’s belief that she does

not have the right capabilities and potential to change

her behaviour. The counselor can again try to make

the participant revise her belief by providing counter-

evidence. We plan to extend our analysis to these as-

pects of MI that we were neglected in the paper.

In future work, we also plan to experimentally val-

idate our approach to MI based on cognitive planning.

To this aim, we plan to implement the scenario de-

scribed in Section 6 and to evaluate the performance

of the artiﬁcial agent in its interaction with the human.

The work presented in this paper is part of a larger

project which is devoted to development of an artiﬁ-

cial agent with persuasive capabilities which can pro-

mote positive behavior change in the human. The

next step of our investigation is to endow the artiﬁ-

cial agent with multimodal communicative capabil-

ities which go beyond verbal behavior. As shown

in (Potdevin et al., 2021), non-verbal behavior in

communication including facial expressions is funda-

mental for increasing the machine’s believability and

trustworthiness thereby making the human more will-

ing to believe what the machine says.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

516

ACKNOWLEDGEMENTS

Support from the ANR project CoPains “Cognitive

Planning in Persuasive Multimodal Communication”

(grant number ANR-18-CE33-0012) is gratefully ac-

knowledged.

REFERENCES

Bolander, T. and Andersen, M. B. (2011). Epistemic plan-

ning for single- and multi-agent systems. Journal of

Applied Non-Classical Logics, 21(1):9–34.

Bylander, T. (1994). The computational complexity of

propositional STRIPS planning. Artiﬁcial Intelli-

gence, 69(1-2):165–204.

Cooper, M. C., Herzig, A., Maffre, F., Maris, F., Perrotin,

E., and R

egnier, P. (2021). A lightweight epistemic

logic and its application to planning. Artiﬁcial Intelli-

gence, 298.

Cooper, M. C., Herzig, A., Maffre, F., Maris, F., and

egnier, P. (2016). Simple epistemic planning: gen-

eralised gossiping. In Proceedings of the 22nd Eu-

ropean Conference on Artiﬁcial Intelligence (ECAI

2016), pages 1563–1564.

da Silva, J. G. G., Kavanagh, D. J., Belpaeme, T., Taylor,

L., Beeson, K., Andrade, J., et al. (2018). Experiences

of a motivational interview delivered by a robot: qual-

itative study. Journal of medical Internet research,

20(5):e7737.

Fagin, R., Halpern, J., Moses, Y., and Vardi, M. (1995).

Reasoning about Knowledge. MIT Press, Cambridge.

Fernandez, J., Longin, D., Lorini, E., and Maris, F. (2021).

A simple framework for cognitive planning. In Pro-

ceedings of the Thirty-Fifth AAAI Conference on Ar-

tiﬁcial Intelligence (AAAI-2021), pages 6331–6339.

AAAI Press.

Ghallab, M., Nau, D., and Traverso, P. (2004). Automated

planning: theory and practice. Morgan Kaufmann.

Halpern, J. Y. and Moses, Y. (1992). A guide to complete-

ness and complexity for modal logics of knowledge

and belief. Artiﬁcial Intelligence, 54(3):319–379.

Kanaoka, T. and Mutlu, B. (2015). Designing a motiva-

tional agent for behavior change in physical activity.

In Proceedings of the 33rd Annual ACM Conference

Extended Abstracts on Human Factors in Computing

Systems, pages 1445–1450.

Kominis, F. and Geffner, H. (2015). Beliefs in multiagent

planning: from one agent to many. In ICAPS 2015,

pages 147–155. AAAI Press.

Lisetti, C., Amini, R., Yasavur, U., and Rishe, N. (2013). I

can help you change! an empathic virtual agent deliv-

ers behavior change health interventions. ACM Trans-

actions on Management Information Systems (TMIS),

4(4):1–28.

Lomuscio, A., Qu, H., and Raimondi, F. (2017). MCMAS:

an open-source model checker for the veriﬁcation of

multi-agent systems. International Journal on Soft-

ware Tools for Technology Transfer, 19:9–30.

Lorini, E. (2020). Rethinking epistemic logic with belief

bases. Artiﬁcial Intelligence, 282.

Lorini, E. and Schwarzentruber, F. (2021). Multi-agent be-

lief base revision. In Proceedings of the 30th Interna-

tional Joint Conference on Artiﬁcial Intelligence (IJ-

CAI 2021). ijcai.org.

owe, B., Pacuit, E., and Witzel, A. (2011). DEL planning

and some tractable cases. In Proceedings of the 3rd In-

ternational International Workshop on Logic, Ratio-

nality and Interaction (LORI 2011), pages 179–192.

Springer Berlin Heidelberg.

Lundahl, B. and Burke, B. L. (2009). The effectiveness and

applicability of motivational interviewing: A practice-

friendly review of four meta-analyses. Journal of clin-

ical psychology, 65(11):1232–1245.

Makinson, D. (1997). Screened revision. Theoria, 63:14–

23.

Miller, W. R. and Rollnick, S. (2012). Motivational inter-

viewing: Helping people change. Guilford press.

Muise, C., Belle, V., Felli, P., McIlraith, S. A., Miller,

T., Pearce, A. R., , and Sonenberg, L. (2021). Efﬁ-

cient multi-agent epistemic planning: Teaching plan-

ners about nested belief. Artiﬁcial Intelligence, 302.

Muise, C., Belle, V., Felli, P., McIlraith, S. A., Miller, T.,

Pearce, A. R., and Sonenberg, L. (2015). Planning

over multi-agent epistemic states: A classical plan-

ning approach. In AAAI 2015, pages 3327–3334.

AAAI Press.

Olafsson, S., O’Leary, T., and Bickmore, T. (2019). Co-

erced change-talk with conversational agents pro-

motes conﬁdence in behavior change. In Proceedings

of the 13th EAI International Conference on Perva-

sive Computing Technologies for Healthcare, pages

31–40.

Potdevin, D., Clavel, C., and Sabouret, N. (2021). Virtual

intimacy in human-embodied conversational agent in-

teractions: the inﬂuence of multimodality on its per-

ception. Journal on Multimodal User Interfaces,

15(1):25–43.

Schulman, D., Bickmore, T., and Sidner, C. (2011). An in-

telligent conversational agent for promoting long-term

health behavior change using motivational interview-

ing. In 2011 AAAI Spring Symposium Series.

Searle, J. (1969). Speech acts: An essay in the philosophy of

language. Cambridge University Press, Cambridge.

Stalnaker, R. (2002). Common ground. Linguistics and

Philosophy, 25(5-6):701–721.

van Ditmarsch, H. P., van der Hoek, W., and Kooi, B.

(2007). Dynamic Epistemic Logic. Kluwer Academic

Publishers.

Cognitive Planning in Motivational Interviewing

517