Task Handover Negotiation Protocol for Planned Suspension based on

Estimated Chances of Negotiations in Multi-agent Patrolling

Sota Tsuiki, Keisuke Yoneda and Toshiharu Sugawara

Department of Computer Science and Communication Engineering, Waseda University, Tokyo169855, Japan

Keywords:

Multi-agent Patrolling Problem, Negotiation, Task Delegation, Coordination, Periodic Inspection, Scheduled

Suspension, Timed Patrol.

Abstract:

We propose a negotiation method that mitigates performance degradation in the multi-agent cooperative pa-

trolling problem not only during planned suspensions for periodic inspection and replacement, but also during

the transition period to the suspension. Recent developments in machine and information technologies have

led to the expectation of using multiple intelligent agents to control robots. In particular, cooperation between

multiple agents is necessary to process tasks that require complex and diverse capabilities or encompass a large

environment. Because robots are machines, they need to be regularly inspected and replaced with new ones

to prevent unexpected failures and prolong their lifespans. However, suspending agents for such inspections

may cause a rapid performance degradation that cannot be neglected in some applications. Such suspensions

are usually planned, and the transition period is known in advance, that is, we know which agents will be

suspended and when. Our proposed negotiation method allows agents that are scheduled for suspension to

hand over important tasks that should not be neglected to other agents. This mitigates the performance degra-

dation during both the transition and suspension periods. The experimental results show that the performance

degradation can be signiﬁcantly reduced compared to existing methods, especially for security surveillance

applications.

1 INTRODUCTION

With the recent development of AI technology, there

is a demand for applications that use networked

agents, such as intelligent sensors and autonomous

robots, to perform dangerous tasks that are impossi-

ble for humans to perform or sophisticated and com-

plex tasks on behalf of humans. In particular, the use

of multiple cooperative agents is expected in large

environments and high-complexity tasks. A prob-

lem that abstracts such tasks is the multi-agent co-

operative patrolling problem (MACPP). In this prob-

lem, agents patrol a particular environment simulta-

neously, and cooperate with and complement one an-

other to accomplish, for example, security surveil-

lance (Chen et al., 2015), environmental monitoring

(Rezazadeh and Kia, 2019; Zhou et al., 2020), and

cleaning/sweeping in warehouses and public spaces

(Altshuler et al., 2011; Wagner et al., 2008; Li et al.,

2021).

However, because the agents autonomously deter-

mine appropriate actions from their own perspectives,

https://orcid.org/0000-0002-9271-4507

cooperation and coordination between the agents are

necessary not only for each individual agent to ac-

complish its work, but also to avoid actions such as

collisions that can prevent other agents from work-

ing as well as to ensure overall efﬁciency by elimi-

nating overlapping redundant work with other agents.

However, it is not easy to design and implement co-

operative behavior in advance because many factors,

such as the temporal and spatial constraints and capa-

bilities of all the agents, must be considered. How-

ever, these factors are difﬁcult to understand fully in

the design phase. Therefore, an autonomous learning

method strategy for efﬁcient cooperative behavior be-

tween multiple agents is required in which the capa-

bilities of each individual agent and the other agents,

the characteristics of the environment, and the learned

behaviors of other cooperative agents are considered.

Moreover, if the agents are self-driving robots or ma-

chines, it is probable that they will stop for periodic

inspections over relatively long cycles that alternate

between agents , as well stop over relatively short cy-

cles, such as for recharging. Performance degrada-

tion during these suspension periods, especially for

Tsuiki, S., Yoneda, K. and Sugawara, T.

Task Handover Negotiation Protocol for Planned Suspension based on Estimated Chances of Negotiations in Multi-agent Patrolling.

DOI: 10.5220/0010896900003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 1, pages 83-93

ISBN: 978-989-758-547-0; ISSN: 2184-433X

a longer cycles that require longer suspension time,

must be reduced as much as possible.

There have been several studies on MACPP based

on two major approaches for cooperation and coor-

dination between agents. In the ﬁrst approach, the

agents divide the environment into areas of responsi-

bility by themselves explicitly and assign each area

to one or a few agents (Ahmadi and Stone, 2006;

Elor and Bruckstein, 2009; Kato and Sugawara, 2013;

Zhou et al., 2019). For example, Elor and Bruckstein

(Elor and Bruckstein, 2009) proposed an area parti-

tioning method to balance the sizes of subareas allo-

cated to individual agents based on the balloon pres-

sure model. However, if a few agents leave the sys-

tem for inspection, the assignments will need to be

recalculated from scratch, and the results for the en-

vironmental characteristics learned by the individual

agents may become useless.

In the second approach, the agents autonomously

select patrol strategies and algorithms according to

the environment and the behaviors of the other agents

without an explicit division of the environment (Kalra

et al., 2005; Elmaliach et al., 2007; Sampaio et al.,

2010; Yoneda et al., 2015; Sugiyama et al., 2019;

Othmani-Guibourg et al., 2017; Othmani-Guibourg

et al., 2018). For example, Yoneda et al. proposed

the adaptive meta-target decision strategy (AMTDS)

in which each agent autonomously decides on an ap-

propriate patrol strategy using reinforcement learning

while learning the frequency of visit requests for each

location in the environment (Yoneda et al., 2015).

Sugiyama et al. proposed AMTDS with learning of

event probabilities to enhance divisional cooperation

(AMTDS/EDC), which is an extension of AMTDS

through the addition of a dynamic and lightweight

negotiation method to balance the workloads of the

agents (Sugiyama et al., 2019). We chose the sec-

ond approach in the present study because it is more

appropriate for addressing the periodic suspension of

agents. However, we found that when the number of

agents suddenly becomes lower because of periodic

suspensions, there is a temporary but considerable

decrease in the total performance. The performance

degradation cannot be neglected in some critical ap-

plications, such as security patrols, to avoid security

gaps.

To address this issue, Tsuiki et al. proposed

a method called AMTDS with task handover for

scheduled suspension (AMTDS/TH) to mitigate the

overall performance degradation when some agents

are suspended for inspection (Tsuiki et al., 2021).

In this approach, the negotiation protocol used in

AMTDS/EDC is extended and used when agents are

in close proximity to one another because of the lim-

itations of Wi-Fi communications. Because the tran-

sition period for the next suspension of some agents

is known in advance, that is, which agents will be

stopped and when, the agents that are scheduled for

suspension can gradually delegate or hand over some

of their tasks to other agents to reduce the perfor-

mance degradation. It was shown that this method can

mitigate the temporary but signiﬁcant performance

degradation due to the planned suspension. However,

the number of tasks that are delegated to other agents

before the suspension is ﬁxed and cannot be ﬂexibly

changed. It is also difﬁcult to determine the appropri-

ate number of tasks to hand over. This led to a large

decrease in efﬁciency before suspension that canceled

out the performance improvement during the suspen-

sion period.

Therefore, in this study, we integrate a novelnego-

tiation method with conventional AMTDS/TH to es-

timate the number of tasks that should be delegated

to other agents during the transition period. The de-

crease in performance is thereby mitigated not only

during the planned suspension period but also dur-

ing the preceding transition period. We then con-

ducted experiments for the two MACPP applications

of cleaning/sweeping and security surveillance, and

evaluated the proposed method by comparing its per-

formance with those of the previous AMTDS/TH

method and other conventional methods.

2 RELATED WORK

Many studies to enable cooperative and coordinated

behavior between multiple agents to execute an

MACPP instance efﬁciently and effectivelyhave been

conducted. As mentioned in the previous section,

there are two major approaches for agent coordina-

tion in MACPPs. The ﬁrst approach involves the di-

vision of the environment into distinct subareas that

one or a few agents are in charge of autonomously so

that the agents can work cooperatively with high ef-

ﬁciency while avoiding conﬂicts and redundant work

(Ahmadi and Stone, 2006; Elor and Bruckstein, 2009;

Kato and Sugawara, 2013; Zhou et al., 2019; Xie

et al., 2020). For example, Ahmadi and Stone pro-

posed a method to partition the areas of responsibility

through negotiations in an environment in which the

frequency of events is possibly non-uniform, as in our

case, and the agents should visit the locations with

different frequencies. Hence, the area is partitioned

by the agents to balance their visiting frequency (Ah-

madi and Stone, 2006). Elor and Bruckstein pro-

posed a method to divide the environment into areas

of responsibility for individual agents by equalizing

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

their expansion force. This method was inspired by

the pressure model of a balloon (Elor and Bruckstein,

2009).

The second approach is to autonomously decide

on an appropriate patrol strategy based on the sur-

rounding environment and the state of the agents

without explicitly dividing the environment in ad-

vance (Kalra et al., 2005; Elmaliach et al., 2007; Sam-

paio et al., 2010; Yoneda et al., 2015; Sugiyama et al.,

2019). For example, Elmaliach et al. proposed a

method in which the patrol paths in the environment

are generated and assigned to individual agents (El-

maliach et al., 2007). Sugiyama et al. proposed a

negotiation protocol to balance the workload between

agents by exchanging information about the locations

that should be visited frequently (Sugiyama et al.,

2019). We chose the second approach because ef-

ﬁciency may be negatively impacted in the ﬁrst ap-

proach when no agents are assigned to certain ar-

eas. However, even in the second approach, the previ-

ous studies have not considered temporal suspension.

Planned suspensions can result in signiﬁcant perfor-

mance degradation. In particular, Sugiyama et al. re-

ported that sudden stoppages considerable reduce ef-

ﬁciency (Sugiyama et al., 2019).

Some recent studies have used learning algorithms

to enable multiple agents to patrol an environment

in a cooperative manner (Zhou et al., 2019; Xie

et al., 2020). For example, Zhou et al. formulated

the patrolling problem as a Bayes-adaptive transition-

decoupled partially observable Markov decision pro-

cess and introduced a decentralized online learning

algorithm using the Monte Carlo tree search method

(Zhou et al., 2019). Xie et al. used particle swarm

optimization (PSO) to ﬁnd reasonable patrol paths

by partitioning the environment (Xie et al., 2020).

Othmani-Guibourg et al. proposed the learning of

distributed multi-agent patrol strategies using a long

short-term memory (LSTM) network which is embed-

ded in each agent and trained using data generated in

a simulated environment. The network then navigates

the agent in the environment to be patrolled by deter-

mining its next movement (Othmani-Guibourg et al.,

2018). However, these studies also did not consider

the signiﬁcant deterioration that results when peri-

odic suspensions cause sudden changes in the envi-

ronment, which includes the other agents.

There are a number of studies on planned suspen-

sion/stoppages in multi-agent frameworks. Panteleev

et al. and Ghita et al. proposed methods to produce

plans for the periodic maintenance/inspection and re-

pair of technical equipment using a multi-agent sim-

ulation environment (Panteleev et al., 2014; Ghita

et al., 2018). These studies differ from ours in that

their aim is to develop work plans that account for

planned leaves to reduce the workload of staff manag-

ing technical equipment. In other research ﬁelds, for

example, Gavranis and Kozanidis developed an algo-

rithm for the ﬂight maintenance problem (FMP prob-

lem) (Gavranis and Kozanidis, 2015). Seif and An-

drew extended this algorithm to solve the operation

and maintenance planning problem, which is a gener-

alized version of the FMP problem (Seif and Andrew,

2018). Moradi and Shadrokh proposed a robust trust-

based scheduling system that uses a heuristic algo-

rithm for efﬁcient resource allocation to ensure the re-

liability of the system for scheduling maintenance ac-

tivities during planned shutdowns with unknown ac-

tivity durations (Moradi and Shadrokh, 2019). How-

ever, to the best of our knowledge, these methods re-

quire centralized control, and there is no study so far

on methods for autonomous agents to prepare for the

planned suspension by themselves.

3 MACPP MODEL

The MACPP model and issues addressed in this study

are the same as those in the conventional studies

(Sugiyama et al., 2019; Tsuiki et al., 2021), and are

described in detail below.

3.1 Environment

The environment patrolled by the agents is repre-

sented by a graph, G = (V,E), embedded in a two-

dimensional Euclidean space, where V = {v

,... , v

}

is the set of nodes corresponding to locations in the

environment, and E is the set of edges e

i, j

connect-

ing nodes v

and v

in V. An agent, an event, and

an obstacle can exist at node v ∈ V. Note that the

events in this study can vary depending on the appli-

cation; for example, in a security surveillance appli-

cation, the number of events in a location corresponds

to the alert level at the location, and the accumula-

tion of events represents an increase in the alert level.

In other examples, an event in a cleaning application

corresponds to the accumulation of a piece of dirt at

a location and the task is to vacuum the accumulated

dirt up; in an egg collection application, an event is

the laying of an egg on a certain area of the ground

in a free-range farm, and the task is to collect the laid

eggs (Li et al., 2021).

The length of all the edges can be assumed to be

one without the loss of generality by adding dummy

nodes as needed. Let d(v

) be the shortest distance

between v

and v

(i.e., the minimum number of edges

between two nodes), and m(v

) be the Euclidean

Task Handover Negotiation Protocol for Planned Suspension based on Estimated Chances of Negotiations in Multi-agent Patrolling

distance. We introduce a discrete time with the unit

of a time step and assume that an agent can move to a

neighboring node and process the tasks on the current

node in a time step.

For a node ∀v ∈ V, we denote the event occurrence

probability at v as p(v) (0 ≤ p(v) ≤ 1) at every time

step. At time step t, the numberof accumulatedevents

(v) on node v is updated as

(v) =







t−1

(v) + 1 (if an event occurs)

t−1

(v) (otherwise, i.e., with

probability 1− p(v)).

When an agent arrives at v, all events on v are pro-

cessed and eliminated by executing the corresponding

tasks, and L

(v) is set to 0.

3.2 Agents and Their Behaviors

Let A = {1, .. ., n} be a set of n agents. Agent i ∈ A has

a ﬁnite capacity battery and must return to its charg-

ing base before the battery level reaches zero. Agent

i assigns an importance p

(v) to each node ∀v ∈ V.

(v) is the predicted probability of event occurrence

inferred from the number of events executed by the

agent itself (0 ≤ p

(v) ≤ 1). Note that because p

(v)

is the probability predicted by each individual agent,

it can differ between agents, even for the same node

v. The calculation of p

(v) is described in Section 3.3.

Although i cannot directly access the value of

L(v), it can estimate the number of events EL

(v) ac-

cumulated at node v at time t using the predicted p

(v)

through

(v) = p

(v) × (t − t

vis

where t

vis

is the time when node v is most recently

visited by an agent, and t

vis

is assumed to be shared

with all the agents.

The agent i decides its actions as follows: First, it

determines the next target node v

tar

through a target

decision strategy (TDS), generates a path to v

tar

using

the path generation strategy, and moves to it along the

path. When i arrives at v

tar

, it determines the next

target node and thereafter repeats the cycle of path

generation and movement described above. How-

ever, i returns to the charging base when its remain-

ing battery capacity is low. Agent i uses the AMTDS

(Yoneda et al., 2015) to select its TDS. AMTDS is

a meta-strategic method for selecting an appropriate

TDS from a set of basic TDSs by Q-learning based on

(v) and the expected rewards based on the number

of events executed per time step . In the experiments

below, the TDSs are the four simple basic strategies

of random selection, probabilistic greedy selection,

prioritization of unvisited interval sections, and bal-

anced neighbor-preferential selection.

After the next target node v

tar

is determined, the

agent uses gradual path generation (GPG) (Yoneda

et al., 2015) to generate a path. i generates the short-

est path to v

tar

using a simple path-ﬁnding algorithm

(such as A*-search). If there is a node that has a high

value of EL

(v) in the vicinity of the generated short-

est path, i adds a detour to that node to the path. The

details of the four TDSs, the GPG, and the method of

returning to the charging base are beyond the scope

of this paper; please refer to (Yoneda et al., 2015) for

more details.

3.3 Learning and Exchange of

Importance Values of Nodes

The importance values of the nodes and the negotia-

tion to delegate tasks/nodes, which were introduced in

AMTDS/EDC (Sugiyama et al., 2019), are the central

concepts in our proposed method. The importance

value of node ∀v is initialized as p

(v) = 0. When

agent i executes the task in node v at time t, p

(v) is

updated regardless of the number of events accumu-

lated in v as

(v) = (1− α)p

(v) + α

t − t

vis

where α (0 < α ≤ 1) is the learning rate for the im-

portance value.

To further promote load balancing and coordi-

nation between the agents and increase robustness

against environmental changes, the agents exchange

importance values through negotiation among them-

selves. This means that i delegates to or is dele-

gated to by other agents so that the agents in the sys-

tem can patrol intensively. When m(v

) < d

for

i, j ∈ A, where the parameter d

(> 0) speciﬁes the

communication range between the agents, i and j are

in communication range and can negotiate with each

other. Moreover, to suppress excessive communica-

tion, we introduce the minimum communication in-

terval B(> 0) between i and j, that is, i and j store

the last time they negotiated with each other, T

i, j

lst

, and

do not negotiate with each other until T

i, j

lst

+ B.

Agent i has its responsible node set V

⊂ V, which

is the set of N

(> 0) nodes with the highest impor-

tance values. The initial values are set to V

= V

and N

= |V|. V

and N

are updated when i re-

turns to the charging base. The agents use two types

of negotiation (negotiation for balancing task work-

loads and negotiation for exchanging responsibility)

between themselves to update p

(v), V

, and N

. For

more details on the two types of negotiations and

how p

(v), V

, and N

are updated, please refer to

(Sugiyama et al., 2019).

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

3.4 Evaluation Metrics

We evaluate the system using two types of metrics de-

pending on the expected applications. The ﬁrst is the

total number of time steps in which the events are left

unprocessed. For example, in a cleaning or egg col-

lection application, the number of unprocessed events

(pieces of dirt not sucked up by the vacuum cleaner or

uncollected eggs) remaining in the environment and

the amount of time they are left unprocessed should

be minimized. D

between time t

and t

< t

) is

deﬁned as

∑

v∈V

∑

t=t

(v).

A smaller value of D

indicates a more efﬁcient pa-

trol.

The second metric is the maximum number of un-

processed events for all the nodes. For example, in

a timed security patrol, no single point should be left

unmonitored. Therefore, all agents must maintain the

maximum number of unprocessed events (i.e., time

left unmonitored) across all nodes so that the pre-

deﬁned alert level is not exceeded . This metric U

between time t

and t

< t

) is deﬁned as

= max

v∈V,t

≤t≤t

(v).

A smaller value of U

also indicates a more efﬁcient

patrol. Hereafter, for the sake of simplicity, D

and

are denoted as D(s) and U(s), respectively, and

and t

are omitted if their values are obvious. Our

goal is to maintain D(s) and U(s) low even when a

number of agents are stopped for scheduled suspen-

sions.

4 PROPOSED METHOD

In this study, we propose an extension of AMTDS/TH

(Tsuiki et al., 2021) called AMTDS with task han-

dover for scheduled suspension based on the esti-

mated chance of encounters (AMTDS/THE) to re-

duce performance degradation during the periods of

task handover and planned suspension. Speciﬁcally,

because agents can only negotiate between them-

selves when they encounter each other, that is, when

their distance is shorter than d

, the agents memorize

the number of times that they have negotiated from

the (re)start time. The agents that are scheduling their

planned suspension estimate the number of possible

negotiation opportunities until the suspension using

these data and determine the number of nodes that

should be delegated to other agents during the tran-

sition period. This reduces the efﬁciency loss not

only during the planned suspension but also during

the transition period before the planned suspension.

4.1 Estimation of Encounters until

Planned Suspension

To estimate the number of possible negotiations until

the planned suspension time, agent i counts the num-

ber of encounters for negotiation N

(t) between the

current time t and the most recent start time or re-

turn time from inspection. Note that the agents do

not negotiate with one another until B time steps have

passed since the last negotiation. The agents also do

not consider the content or quantity of the negotiation

or the agents that they have negotiated with.

The next planned suspension S for periodic in-

spection or replacement is given in advance as a tuple

S = (A

, T

, D

), where A

(⊂ A) is the set of

agents that will be suspended from the start time of

the suspension T

to the return time from the suspen-

sion T

. Parameter D

is the length of the transition

period; thus, the scheduled suspension is announced

to all agents at T

− D

. When S is announced at t,

agent i estimates the number of opportunities for ne-

gotiation N

(t) until T

(t) = N

(t) ×

− t

t − T

|A| − 1

where T

is the time at which i initializes N

(t) and

starts to count it. Therefore, T

−t is the time remain-

ing until the planned suspension is reached. Note that

(t) is an estimated value and therefore usually dif-

fers from those of other agents which may be working

in different areas.

4.2 Negotiation for Handover during

Transition Period

When both agents i and j are in A

or in A \ A

they negotiate with each other by using the negotia-

tion protocol proposed in (Sugiyama et al., 2019) to

enhance workload balance and activity coordination

among agents. Otherwise, when i ∈ A

and j ∈ A\A

they perform a negotiation for unidirectional task del-

egation to increase the number of nodes that j is re-

sponsible for by transferring some of the importance

values from i to j. This implies that i indirectly dele-

gates some tasks in its important nodes to j.

First, agent i ∈ A

selects the top e

(> 0) nodes

with the highest importance values from V

. Then,

the selected nodes are transferred from i to j at a

ﬁxed ratio of p

(v). The importance values of the se-

Task Handover Negotiation Protocol for Planned Suspension based on Estimated Chances of Negotiations in Multi-agent Patrolling

Figure 1: Experimental environment.

lected nodes for i and j are updated using the follow-

ing equations:

(v) ← p

(v) + p

(v) × δ

(v) ← p

(v) × (1− δ

where δ

(0 < δ

< 1) is the ratio of importance value

passed. This means that agent i does not completely

forget the delegated nodes, but rather induces j to ex-

pand its work scope. Thus, j may not visit these nodes

frequently, and i will also visit the nodes that it has

delegated.

The number of nodes e

that agent i transfers to

another agent is determined using N

(t) by the fol-

lowing formula:

max(1, N

(t))

, (1)

where N

> 0 is the upper limit of the nodes to be

delegated and is updated in both i and j as

← N

− e

← min(|V|, N

+ e

The max in the denominator in Eq. (1) prevents divi-

sion by zero. Note that after the importance values are

updated, the sets of responsible nodes, V

and V

, are

updated when i and j return to their charging bases.

5 EXPERIMENTS

5.1 Experimental Setting

We conducted experiments to compare the pro-

posed AMTDS/THE method with the conventional

AMTDS/EDC and AMTDS/TH methods to demon-

strate that AMTDS/THE can mitigate performance

degradation both due to the task handover from the

suspended agents during the transition period and due

to the suspension of the agents for inspection. In this

experiment, we used D(s) for the cleaning applica-

tion and U(s) for the timed security patrol applica-

tion and introduced different lengths of the transition

period leading up to the suspension to show that the

proposed method is effective in various applications

of the MACPP.

To allow for a simple comparison with conven-

tional methods, the experimental environment was

the same as that used in (Sugiyama et al., 2019) and

(Tsuiki et al., 2021). This environment G = (V, E) is a

two-dimensional 101× 101 grid structure comprising

six rooms and a central corridor, as shown in Fig. 1.

The node v ∈ V is located on the coordinates (x

where −50 ≤ x

≤ 50. The black lines indicate the

walls. For node ∀v ∈ V in the environment, the event

occurrence probability of node p(v) in Fig. 1 is set as

follows:

p(v) =







−3

(if v is in a red region)

−4

(if v is in an orange region)

−6

(otherwise, i.e., in a while region)

based on the colors of the nodes. Events are more

likely to occur in the nodes with deeper colors.

The number of agents is 20 (|A| = 20), and the

charging base v

base

of all the agents is placed at (0,0),

the center of the environment. It is also possible to

place a charging base at a different location for each

agent. Agent i leaves v

base

when its battery is full, pa-

trols the environment according to its own strategy,

and returns to v

base

before its battery level reaches

zero. The agents perform this action cycle repeat-

edly. We set the battery capacity of each agent to 900,

and assume that the battery decreases by one per time

step. Therefore, the battery is exhausted in 900 time

steps. The time required to increase the charge in the

battery by one unit is 3 time steps. This means that it

takes 2700 time steps for the battery capacity to reach

full capacity from a totally discharged state. For this

reason, we set the data collection interval t

− t

for

the evaluation indices D(s) and U(s) to 3600, because

the maximum number of time steps in the charge and

movement cycle is 3600. The values for the battery

were set with reference to an actual cleaning robot.

The length of each experimental run was set to

3,500,000 time steps. The experimental results shown

below are the average values of 20 runs. A set com-

prising half of the agents from A was randomly se-

lected in each trial and denoted as A

. We deﬁne

It was assumed that one time step corresponds to ap-

proximately 4 seconds, the moving speed is approximately

0.25 m/s, the maximum continuous operational time is ap-

proximately 1 hour, and the maximum charging time is ap-

proximately 3 hours.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

Table 1: Experimental parameters.

Description Parameter Value

Number of agents |A| 20

Communication range d

Minimum communication interval B 10800

Ratio of importance values passed δ

0.5

Data collection interval t

− t

3600

Learning rate for importance value α 0.1

Figure 2: Variation of D(s) over time.

= A\ A

. We set two planned suspensions, S

and

, in each run by assuming that the next inspections

are scheduled for a few days or weeks and performed

two experiments with different suspension schedules.

Recall that the planned suspension is represented by

, T

, D

). In Experiment 1 (Exp. 1), the

planned suspensions are represented as

= (A

, 1, 000, 000, 1, 500, 000, 500, 000),

= (A

, 2, 500, 000, 3, 000, 000, 500, 000),

and in Experiment 2 (Exp. 2) as

= (A

, 1, 000, 000, 1, 500, 000, D

= (A

, 2, 500, 000, 3, 000, 000, D

where we set D

= 100, 000 and 20, 000. As men-

tioned above, 3600 time steps correspond to approx-

imately four hours in our simulated environment;

therefore, the transition periods of D

= 500, 000,

100, 000, and 20, 000 correspond to approximately

three weeks, 4.5 days, and one day, respectively. The

number of agents to be suspended in each planned

suspension was 10, which is half of the total num-

ber of agents. Although it is unlikely that half of the

agents will be stopped in actual operations, the exper-

iments were performed with extreme settings to con-

ﬁrm the effectiveness of the proposed method.

5.2 Performance Comparison

We plot the results for the evaluation metric D(s)

for the cleaning-type application and U(s) for the se-

Figure 3: Variation of U(s) over time.

curity patrol for the proposed AMTDS/THE method

and the conventional AMTDS/EDC and AMTDS/TH

methods in Fig. 2 and Fig. 3. The following two ob-

servations can be made from the ﬁgures:

First, compared to the conventional AMTDS/EDC

method, in which task delegation is not performed

before the planned suspension, the large perfor-

mance degradation during the planned suspension,

especially the sharp and signiﬁcant deterioration of

U(s), are reduced in the proposed AMTDS/THE

and AMTDS/TH methods. Comparing between

AMTDS/THE and AMTDS/EDC, the peak value of

U(s) in AMTDS/THE was reduced by approximately

76.5% compared to AMTDS/EDC during the ﬁrst

planned suspension and by approximately 61.4% dur-

ing the second suspension. For the cleaning prob-

lem, the sum of D(s) was improved by approximately

14.3% for the ﬁrst suspension and by approximately

5.68% for the second. Note that there was no sig-

niﬁcant difference in performance degradation during

the planned suspension between AMTDS/THE and

AMTDS/TH, as shown in Figs. 2 and 3, respectively.

This is because agents scheduled for planned suspen-

sion could effectivelydelegate a portion of their nodes

to agents not scheduled for the next planned suspen-

sion; thus, they continued to cover the entire area,

which prevented a large performance deterioration.

Second, these ﬁgures also show that the perfor-

mance degradation during the transition period until

the planned suspension was signiﬁcantly reduced in

Task Handover Negotiation Protocol for Planned Suspension based on Estimated Chances of Negotiations in Multi-agent Patrolling

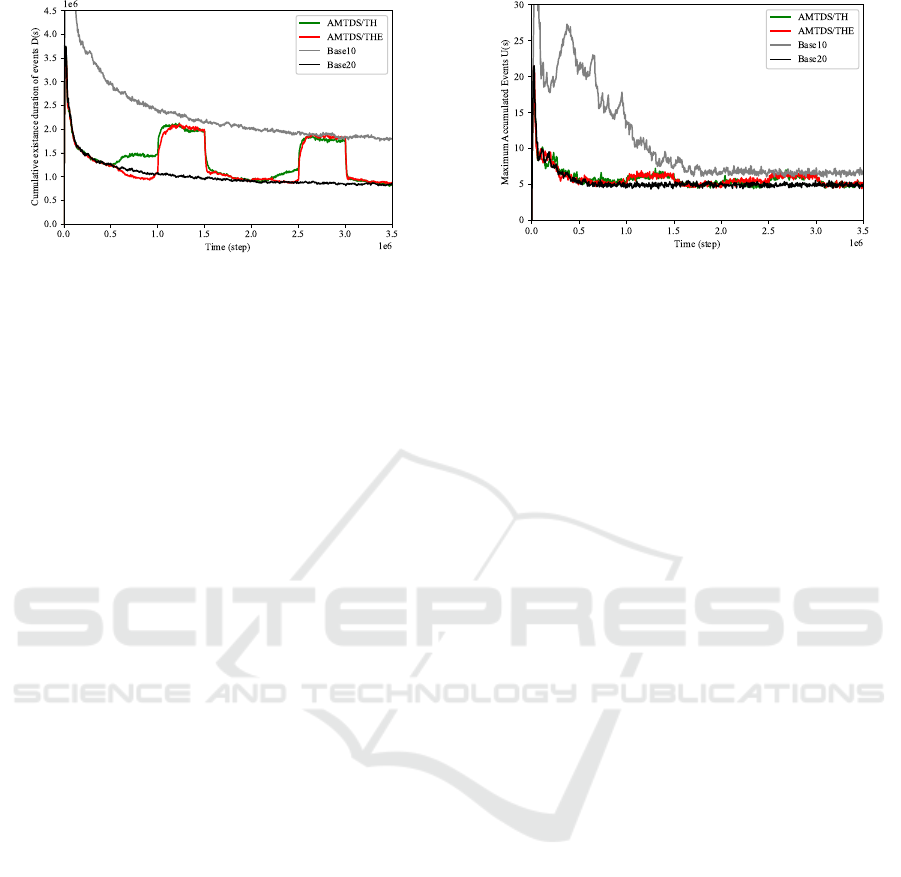
Figure 4: Performance comparison (D(s)).

AMTDS/THE compared to AMTDS/TH, especially

for D(s), although AMTDS/TH also delegated nodes

during the transition period. A detailed numerical

analysis showed that AMTDS/THE reduced the to-

tal D(s) during the transition period by approximately

26.0% for the ﬁrst transition period and by approxi-

mately 9.00% for the second transition period com-

pared to AMTDS/TH. Comparing the performance

of AMTDS/TH and AMTDS/EDC, the efﬁciency im-

provement during the planned suspension obtained

with AMTDS/TH was offset by the efﬁciency loss

during the transition period. Meanwhile, there was

no signiﬁcant difference in U(s) during the transition

period between AMTDS/THE and AMTDS/TH, and

neither method caused a signiﬁcant decrease in efﬁ-

ciency.

In general, the workload of the agents during the

transition period is likely to become unbalanced and

result in degraded performance because of task han-

dover for delegation. In AMTDS/THE, this negative

effect was prevented because the important nodes that

were deemed necessary to be always covered were

gradually and evenlyhanded overusing the accurately

estimated number of negotiation opportunities until

the beginning of the suspension period. In contrast,

because the number of negotiation opportunities were

not accurately estimated in AMTDS/TH, a large num-

ber of nodes were delegated at an early stage. There-

fore, the agents that were delegated many nodes could

not process all of them . This caused the efﬁciency to

be degraded before the suspension.

5.3 Performance Analysis

Although the sudden loss of efﬁciency due to the

planned suspension was found to be mitigated in

AMTDS/THE, we would like to verify whether the

resulting efﬁciency was adequate. Because there were

only 10 running agents during the planned suspen-

sion period, we compared the efﬁciency with that of

the case in which the MACPP instances were ex-

Figure 5: Performance comparison (U(s)).

ecuted with 10 agents from the beginning without

planned suspensions. We also examined the efﬁ-

ciency when all 20 agents were running at all times

with no planned suspension. The results are shown

in Figs. 4 and 5. Note that the labels “Base10” and

“Base20” in these ﬁgures represent the results for the

cases of 10 agents and 20 agents, respectively.

These ﬁgures show some interesting results. First,

in the performance results during the two planned sus-

pensions, both of the metrics, D(s) and U(s), were as

low as or lower than the case of 10 agents with no

planned suspensions at all (i.e., “Base10”). This in-

dicates that the proposed method not only mitigated

performance degradation during the planned suspen-

sions, but prevented it completely. Second, the values

of D(s) and U(s) were greatly improved compared to

the Base10 case when AMTDS/THE or AMTDS/TH

was adopted, especially during the ﬁrst planned sus-

pension period. This may be because it took more

time for the agents to learn, especially forU(s), when

there were only 10 agents compared to when there

were 20 agents, because there were fewer opportuni-

ties for interactions between the agents for learning.

Hence, the learning stabilized faster when the number

of agents was 20. It is therefore better to run a large

number of agents (e.g., 20) in the earlier stages and

then to reduce the number of agents using the pro-

posed method to speed up the learning convergence,

even when the ﬁnal number of agents is 10.

Furthermore, the metric D(s) during the transition

period of the ﬁrst planned suspension (Fig. 4) indi-

cates that AMTDS/THE exhibited better efﬁciency

than the case in which 20 agents worked constantly

(“Base20”). We can see from the curve for Base20 in

Fig. 4 that the learning had not yet converged, even

during the transition period of the ﬁrst planned sus-

pension. We believe that the joint work at the impor-

tant nodes was increased through information sharing

in the proposed AMTDS/THE when the agents in-

formed other agents of the important nodes they had

learned so far, albeit unilaterally.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5

Time (step)

×10

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

4.5

Events That Are Left Neglected D(s)

×10

AMTDS/THE (D

= 20000)

AMTDS/THE (D

= 100000)

AMTDS/THE (D

= 500000)

Figure 6: D(s) at different transition periods (D

5.4 Effect of Transition Period Length

In Exp. 2, we veriﬁed whether AMTDS/THE was

effective even when the transition period until the

next planned suspension was shortened by setting

= 100, 000 or 20, 000. Because we set B =

10800, the number of opportunities for negotiations

between each pair of agents was at most 8–10 when

= 100, 000 and 1-3 when D

= 20, 000; how-

ever, considering the contingency of encounters, the

actual opportunities for negotiation were lower than

these numbers. The results for D(s) obtained using

AMTDS/THE are plotted in Fig. 6, along with the re-

sults when D

= 500, 000 in Exp. 1. Note that we do

not show the results for U(s) because the results were

the same as those when D

= 500, 000.

Figure 6 indicates that even when the transition

periods were shortened to D

= 100, 000 and 20, 000

time steps, the performance degradation during the

transition period and the planned suspension was

still reduced in AMTDS/THE. Although there was a

very slight decrease in efﬁciency (i.e., D(s) has in-

creased) during the suspension period, the decrease

was negligible. Meanwhile, when the transition pe-

riod was 500,000, the learning was accelerated in

AMTDS/THE, but D

= 100, 000 and 20, 000 were

too short to positively affect the learning efﬁciency.

If B is set to a smaller value, the agents will have

more opportunities for negotiation, and the learning

efﬁciency will be improved even if the transition pe-

riod is short. However, this involves a trade-off in that

it also increases unnecessary communication. This is-

sue will be the subject of future research.

5.5 Discussion

To determine if the nodes were actually delegated, we

investigated the number of events that were processed

by agents in A

and A

over time. The results for

a randomly selected experimental run of Exp. 1 are

(a) Agents in A

(b) Agents in A

Figure 7: Number of events observed by agents.

plotted in Fig. 7). Note that the agents in A

stopped

during the ﬁrst suspension period (Fig. 7a), and the

agents in A

stopped in the second one (Fig. 7b).

The ﬁgure indicates that, even during the transition

period, agents that were going to be suspended in

the next suspension period processed a considerable

number of events, although their workload gradu-

ally decreased. Immediately after they stopped, the

events to be processed were quickly transferred to

other agents. We can also see that the agents that re-

turned from suspension quickly increased the amount

of task processed by using the learning results before

the suspension, and at the same time, the agents that

have not been suspended reduced their workload.

As mentioned before, we believe that this was

made possible by the sharing of important nodes with

other agents through the proposed negotiation method

in which the agents did not transfer the nodes with

events for processing directly but only transferred the

ratio δ

of their importance values. We set δ

= 0.5 in

our experiments. If agent i directly transfers the loca-

tions, the agent j that is receiving them may already

be overloaded or some of the received locations may

be far from the area usually covered by j; hence, it

is often not easy for j to complement i for such dele-

gated nodes.

Task Handover Negotiation Protocol for Planned Suspension based on Estimated Chances of Negotiations in Multi-agent Patrolling

Table 2: Ratio of difference between the actual and esti-

mated number of negotiations (%).

Method Mean Max Min

AMTDS/TH 91.6 92.0 91.2

AMTDS/THE 7.7 15.2 1.7

In contrast, because δ

= 0.5, agent i did not com-

pletely forget the locations it has delegated but revis-

ited them at certain intervals, albeit at a lower fre-

quency in AMTDS/THE. If a large number of events

remained, i would then understand that the delegated

agent j was in a situation in which it could not work

adequately; therefore, i increased its importance value

again. These nodes were then delegated by i to other

agents during subsequent negotiations. Through the

repeated occurrence of this process, the overloaded

conditions were reduced and inappropriate delega-

tions remedied. This led to an improvement in efﬁ-

ciency before the planned suspension.

Finally, we investigated whether the agents in

AMTDS/THE could estimate the number of future

negotiation opportunities until the next suspension pe-

riod. We calculated the ratio of the difference be-

tween the estimated and actual numbers of negotia-

tion opportunities in AMTDS/TH and AMTDS/THE.

The mean maximum and minimum ratios of the dif-

ferences are listed in Table 2. The results show that

the agents in AMTDS/THE could estimate the num-

ber of negotiation opportunities accurately, but the

agents in AMTDS/TH could not and underestimated.

In general, it is not easy to estimate the number of

future negotiation opportunities owing to contingen-

cies. The number of future negotiation opportunities

is also affected by the value of B, which may pre-

vent agents from negotiating with one another. Thus,

it seems that AMTDS/TH was designed to promote

active node delegation by estimating a smaller num-

ber of opportunities for negotiation. However, this

resulted in considerable performance degradation in

the transition period owing to some agents becoming

overloaded because of overly hasty delegation.

6 CONCLUSION

In this paper, we proposed a method called

AMTDS/THE to mitigate the temporary but rapid per-

formance degradation caused by planned suspension

in the MACPP. In AMTDS/THE, the agents to be sus-

pended delegate an important part of their tasks/nodes

to other agents during the transition period to pre-

pare for suspension and prevent performance degra-

dation during the planned suspension period, espe-

cially in the security patrol problem. Furthermore,

AMTDS/THE can also prevent performance degrada-

tion during the transition period. This improvement

is attributed to the introduction of a mechanism for

agents to accurately estimate the number of remain-

ing opportunities for negotiation with other agents un-

til the next planned suspension. The mechanism also

enables agents to decide on the number of nodes to be

delegated based on the number of estimated opportu-

nities.

In actual applications, it is necessary to shorten the

transition period before the planned suspension. For

this reason, we would like to improve the method so

that the agents can autonomously decide the timing of

the planned suspension.

ACKNOWLEDGEMENTS

This work was partly supported by JSPS KAKENHI

Grant Numbers 17KT0044 and 20H04245.

REFERENCES

Ahmadi, M. and Stone, P. (2006). A multi-robot system for

continuous area sweeping tasks. In Proceedings 2006

IEEE International Conference on Robotics and Au-

tomation, 2006. ICRA 2006., pages 1724–1729. IEEE.

Altshuler, Y., Yanovski, V., Wagner, I. A., and Bruckstein,

A. M. (2011). Multi-agent cooperative cleaning of

expanding domains. The International Journal of

Robotics Research, 30(8):1037–1071.

Chen, S., Wu, F., Shen, L., Chen, J., and Ramchurn, S. D.

(2015). Multi-agent patrolling under uncertainty and

threats. PLOS ONE, 10(6):1–19.

Elmaliach, Y., Agmon, N., and Kaminka, G. A. (2007).

Multi-robot area patrol under frequency constraints.

In Proceedings 2007 IEEE International Conference

on Robotics and Automation, pages 385–390.

Elor, Y. and Bruckstein, A. M. (2009). Multi-a(ge)nt graph

patrolling and partitioning. In 2009 IEEE/WIC/ACM

International Joint Conference on Web Intelligence

and Intelligent Agent Technology, volume 2, pages

52–57.

Gavranis, A. and Kozanidis, G. (2015). An exact solu-

tion algorithm for maximizing the ﬂeet availability of

a unit of aircraft subject to ﬂight and maintenance

requirements. European Journal of Operational Re-

search, 242(2):631–643.

Ghita, B., Agn`es, L., and Xavier, D. (2018). Scheduling

of production and maintenance activities using multi-

agent systems. In 2018 IEEE 23rd International Con-

ference on Emerging Technologies and Factory Au-

tomation (ETFA), volume 1, pages 508–515. IEEE.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

Kalra, N., Ferguson, D., and Stentz, A. (2005). Hoplites: A

market-based framework for planned tight coordina-

tion in multirobot teams. In Proceedings of the 2005

IEEE International Conference on Robotics and Au-

tomation, pages 1170–1177.

Kato, C. and Sugawara, T. (2013). Decentralized area par-

titioning for a cooperative cleaning task. In Boella,

G., Elkind, E., Savarimuthu, B. T. R., Dignum, F.,

and Purvis, M. K., editors, PRIMA 2013: Principles

and Practice of Multi-Agent Systems, pages 470–477,

Berlin, Heidelberg. Springer Berlin Heidelberg.

Li, G., Chesser, G. D., Huang, Y., Zhao, Y., and Purswell,

J. L. (2021). Development and optimization of a deep-

learning-based egg-collecting robot. Transactions of

the American Society of Agricultural and Biological

Engineers, 64(5):1659–1669.

Moradi, H. and Shadrokh, S. (2019). A robust reliability-

based scheduling for the maintenance activities dur-

ing planned shutdown under uncertainty of activ-

ity duration. Computers & Chemical Engineering,

130:106562.

Othmani-Guibourg, M., El Fallah-Seghrouchni, A., and

Farges, J.-L. (2018). Path generation with LSTM re-

current neural networks in the context of the multi-

agent patrolling. In 2018 IEEE 30th International

Conference on Tools with Artiﬁcial Intelligence (IC-

TAI), pages 430–437.

Othmani-Guibourg, M., Fallah-Seghrouchni, A. E., Farges,

J.-L., and Potop-Butucaru, M. (2017). Multi-agent pa-

trolling in dynamic environments. In 2017 IEEE In-

ternational Conference on Agents (ICA), pages 72–77.

Panteleev, V., Kizim, A., Kamaev, V., and Shabalina, O.

(2014). Developing a model of multi-agent system of

a process of a tech inspection and equipment repair. In

Joint Conference on Knowledge-Based Software En-

gineering, pages 457–465. Springer.

Rezazadeh, N. and Kia, S. S. (2019). A sub-modular re-

ceding horizon approach to persistent monitoring for

a group of mobile agents over an urban area. IFAC-

PapersOnLine, 52(20):217–222. 8th IFAC Workshop

on Distributed Estimation and Control in Networked

Systems NECSYS 2019.

Sampaio, P. A., Ramalho, G., and Tedesco, P. (2010). The

gravitational strategy for the timed patrolling. In 2010

22nd IEEE International Conference on Tools with

Artiﬁcial Intelligence, volume 1, pages 113–120.

Seif, J. and Andrew, J. Y. (2018). An extensive operations

and maintenance planning problem with an efﬁcient

solution method. Computers & Operations Research,

95:151–162.

Sugiyama, A., Sea, V., and Sugawara, T. (2019). Emer-

gence of divisional cooperation with negotiation and

re-learning and evaluation of ﬂexibility in continuous

cooperative patrol problem. Knowledge and Informa-

tion Systems, 60(3):1587–1609.

Tsuiki, S., Yoneda, K., and Sugawara, T. (2021). Reduc-

ing efﬁciency degradation due to scheduled agent sus-

pensions by task handover in multi-agent cooperative

patrol problems. In The International FLAIRS Con-

ference Proceedings, volume 34.

Wagner, I. A., Altshuler, Y., Yanovski, V., and Bruckstein,

A. M. (2008). Cooperative cleaners: A study in ant

robotics. The International Journal of Robotics Re-

search, 27(1):127–151.

Xie, J., Zhou, R., Luo, J., Peng, Y., Liu, Y., Xie, S., and Pu,

H. (2020). Hybrid partition-based patrolling scheme

for maritime area patrol with multiple cooperative un-

manned surface vehicles. Journal of Marine Science

and Engineering, 8(11).

Yoneda, K., Sugiyama, A., Kato, C., and Sugawara, T.

(2015). Learning and relearning of target deci-

sion strategies in continuous coordinated cleaning

tasks with shallow coordination1. Web Intelligence,

13(4):279–294.

Zhou, X., Wang, W., Wang, T., Lei, Y., and Zhong, F.

(2019). Bayesian reinforcement learning for multi-

robot decentralized patrolling in uncertain environ-

ments. IEEE Transactions on Vehicular Technology,

68(12):11691–11703.

Zhou, X., Wang, W., Wang, T., Li, M., and Zhong, F.

(2020). Online planning for multiagent situational in-

formation gathering in the Markov environment. IEEE

Systems Journal, 14(2):1798–1809.

Task Handover Negotiation Protocol for Planned Suspension based on Estimated Chances of Negotiations in Multi-agent Patrolling