Incentivisation of Outsourced Network Testing: View from Platform

Perspective

Sultan Alasmari

, Weichao Wang

and Yu Wang

College of Computing and Informatics, University of North Carolina Charlotte, NC, U.S.A.

Department of Computer and Information Sciences, Temple University, PA, U.S.A.

Keywords:

Incentivisation of Network Testers, Outsourced Network Testing.

Abstract:

With the development of Security as a Service (SAAS), many companies outsource their network security

functionality to security service providers. To guarantee the execution and quality of such services, a third

party can help the end customer verify the enforcement of the security service level agreement (SSLA). Since

individual testers often lack the capability and trustworthiness to attract many customers, a platform is needed

to bridge the gap between the customers and the testers. In this paper, we investigate the incentivisation of

outsourced network testing from the platform perspective. We ﬁrst deﬁne the problem of cost/beneﬁt model

of the platform and identify the restriction factors. We describe multiple testing task assignment scenarios and

prove that they are NP problems. Next we design heuristic algorithms for the problem. Our simulation results

examine the performance of the heuristic approaches.

1 INTRODUCTION

With fast development and wide adoption of Secu-

rity as a Service (SaaS) (Hawedi et al., 2018), more

and more corporations start to depend on third party

companies to protect their networks. However, the se-

curity services must be veriﬁed periodically to make

sure that the service provider does not violate any

of the service level agreements (SLA) (de Carvalho

et al., 2017).

While the requirement on periodic veriﬁcation

sounds reasonable, it is quite hard to enforce in real

life if the company depends on one or two nodes to

conduct such test since their identities can be easily

recognized and remembered by the service provider.

In (Alasmari et al., 2020), the authors propose an ap-

proach similar to the crowd-sensing system: a plat-

form serves as the middleman to connect the cus-

tomers who need their security properties to be tested

and the nodes who can conduct such tests for them.

The authors investigate the expected properties of the

outsourced veriﬁcation services and the mechanisms

to prevent either testers or customers from cheating.

While the approach in (Alasmari et al., 2020)

presents an overview of the platform, it lacks the dis-

cussion on an important problem: incentive models

for the platform and network testers to participate in

the veriﬁcation procedure. Note that to conduct net-

work testing, a tester often needs to send out some

packets that will be considered ‘suspicious’ or even

‘malicious’ under some cases. For example, to assess

whether or not the network security service provider

will react promptly enough to identify some malicious

payload, the tester may need to send out some packets

that match to the malware signature. These packets,

however, may be labeled by the tester’s internet ser-

vice provider (ISP) and cause negative consequence

(e.g. limiting the network bandwidth of the tester).

Therefore, a cost-beneﬁt model must be established

and analyzed before such a platform can be deployed.

To solve this problem, in this paper we will es-

tablish a cost-beneﬁt model from the platform point

of view. We will ﬁrst classify the network testing

trafﬁc based on the probability that they will be la-

beled as suspicious by ISP. We will then establish a

model for the problem as a linear programming prob-

lem. We analyze the complexity of the problem and

prove that it is NP hard. We will then design heuris-

tic algorithms to solve the incentive model under dif-

ferent situations. Finally, we apply the algorithm to

multiple cost/beneﬁt scenarios of outsourced network

testing and evaluate its performance.

Our paper has the following unique contributions.

First, we establish an incentive model for outsourced

network security testing. In our model the testers try

to maximize their proﬁt while staying under the radar

Alasmari, S., Wang, W. and Wang, Y.

Incentivisation of Outsourced Network Testing: View from Platform Perspective.

DOI: 10.5220/0010897300003120

In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 499-506

ISBN: 978-989-758-553-1; ISSN: 2184-4356

499

of network security monitors. Second, we model the

problem as a linear programming problem and show

that it is equivalent to variations of the knapsack prob-

lem. We then design heuristic algorithms to solve the

problem. Third, we apply our algorithms to multiple

network testing scenarios and show that the outputs

of the algorithms can explain the potential policies of

the platform very well.

The remainder of the paper is organized as fol-

lows. In Section 2, we describe related work. In Sec-

tion 3, we ﬁrst discuss the differences between our

incentive problem and several problems that also de-

mand incentive models. We then use a linear pro-

gramming model to characterize the problem and

prove that it is an NP problem. We present several

heuristic algorithms to solve it. Section 4 presents the

quantitative evaluation results. Finally, Section 5 con-

cludes the paper.

2 RELATED WORK

In this part, we will describe the state-of-the-art re-

search in several directions from which we can ben-

eﬁt. We are especially interested in the outsourced

security services, their enforcement, and incentive

models in other domains that we can refer to. For

Security-as-a-Service (SaaS), researchers have con-

ducted a lot of efforts to use Service Level Agreement

(SLA) to deﬁne the criteria of evaluation. For exam-

ple, the EU researchers built the framework SPECS

(Rak et al., 2013) and the project MUSA (Rios et al.,

2016) that allowed users to prepare, negotiate, imple-

ment, and remediate security SLAs. The efforts in

(Casola et al., 2020) try to embed security into the

system from the design phase. In (Hawedi et al.,

2018), the authors designed a different approach.

They embed a lightweight IDS system at the cloud

provider and allow the tenants to conﬁgure their own

rules in the IDS for their VM. This approach provides

a certain level of ﬂexibility to users who have security

expertise.

There are efforts in which the security provider

allows end customers to participate in the conﬁgu-

ration of security measures. For example, in (Ca-

sola et al., 2017), end users can propose security ob-

jectives and the provider will determine and allocate

resources to satisfy the needs. Example approaches

are built to measure parameters for network security

(Wonjiga et al., 2019a) and data integrity (Wonjiga

et al., 2019b). A similar approach is to standardize the

interfaces to the network security functions (NSF) in

network function virtualization environments (Hyun

et al., 2018). The deﬁnition and enforcement of secu-

rity SLAs also beneﬁt from the advances in the new

techniques such as AI and smart contract. For exam-

ple, in (Wonjiga et al., 2019b), researchers applied

blockchain to data integrity protection so that both

end users and cloud providers can verify the results.

Incentive models have been widely used to pro-

mote participation in the activities such as crowd-

sourcing, crowdsensing (Khan et al., 2019), and next

generation wireless networks. Compared to these

models, our application scenario has some unique

properties. Sending out ‘suspicious trafﬁc’ to con-

duct network security tests may lead to identiﬁcation

and disconnection by ISP, thus leading to long term

negative impacts. The only scenarios we can ﬁnd

that share the properties are the ﬁnancial incentives

for clinical trials of treatment for infectious diseases

(Paul et al., 2021). Here the volunteers will receive

cash rewards for being contacting with infectious dis-

eases and testing new medicines. They trade the short

term incentives for the potential of long term diseases.

3 INCENTIVISATION OF

OUTSOURCED NETWORK

TESTING

In this section, we will present the details of the in-

centive model the platform can use to attract more

nodes to participate in the network security services

as testers. We will ﬁrst discuss the assumed scenarios

and the functionality of different parties in the sys-

tem. We will then present the cost and payment from

both the platform’s and tester’s point of view. The in-

centivization model will then be formally deﬁned as

a linear programming problem with constraints. Our

analysis will show that the problem is NP hard and

heuristic approaches must be designed.

3.1 System Assumptions

Figure 1 shows the application scenario. We assume

that an end user u uses the network security services

provided by s. u wants to use a third party to verify

whether or not s is satisfying the security service level

agreement (SSLA). Therefore, it resolves to the net-

work security service testing platform P. To simplify

the scenario, we assume that u carefully crafts a group

of packets and asks P to conduct the test. To prevent s

from recognizing the source address of P and the test-

ing trafﬁc, P can recruit a group of testers to conduct

the test. The test results can then be shared with u.

From the platform perspective, the overall opera-

tions must be proﬁtable to make the business sustain-

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

500

Figure 1: Application scenarios of the proposed approach.

able. For example, P will charge service fees from the

user u and have to pay the testers correspondingly.

Note that different testers may charge different fees

to P because of the network service cost and security

setup. While it is not necessarily true for P to make

a proﬁt on every request, in the long term it needs to

make sure that ($income - $cost) is positive.

Different from the crowd-sensing or crowd-

sourcing scenarios (Khan et al., 2019; Zhao et al.,

2021) in which the participants use valuable resources

such as time and battery power to accomplish tasks,

the costs of network testers are usually caused by

other factors. For example, many ISPs will moni-

tor the network trafﬁc for potential attack detection.

Once a malicious or suspicious node is detected, the

ISP may restrict its network bandwidth or sometimes

directly disable the services. From this point of view,

the testers are risking their network availability to par-

ticipate in the services.

Because of the complexity of the ISP network

monitoring and restriction policies, in this paper we

adopt the model presented in (Desai, 2012). Here we

classify the testing packets into three categories based

on their sensitivity to security policies: low, middle,

and high (our model could support more ﬁne grained

classiﬁcation). For each node i, within a time period,

the node can send out at most R

i,low

, R

i,mid

, and R

i,hi

packets at the low, medium, and high sensitivity lev-

els, respectively, if it wants to avoid any restrictions

by the ISP. Therefore, P must consider such restric-

tions when assigning tasks to the tester. Table 1 sum-

marizes the symbols we use in this paper.

3.2 Working Procedure and the Cost

Model

In this section, we will describe the working pro-

cedure of the platform and establish the cost model

so that we can analyze the complexity of the overall

problem.

Step 1: User u

will submit a network testing request

to platform P that consists of (H

high, M

middle,

and L

low) sensitivity packets. The user agrees to

pay (H

∗BP

+ M

∗BP

+ L

∗BP

) to the platform;

Step 2: Platform P will assign the testing request to

one or multiple testers. Note that different criteria

and restrictions may need to be considered during this

procedure. Here the platform needs to consider both

its base price charge upon the user u

and the price

that it needs to pay to the tester to balance the book;

Step 3: The network testing will be conducted. Once

the testing operations are accomplished, each party

will pay the fee as the agreed amount. This request is

complete.

3.2.1 Task Assignment Method 1

In this task assignment method, we assume that each

testing request needs to be assigned to a single tester.

Therefore, we can formally deﬁne the problem as:

maximize:

|G|

∑

i=1

|J|

∑

j=1

i, j

∗ (BP

− P

j,h

∗ (BP

− P

j,m

) + L

∗ (BP

− P

j,l

))

subject to:

|G|

∑

i=1

i, j

∗ H

≤ R

j,h

, X

i, j

∈ {0, 1}, j = 1 to |J|

|G|

∑

i=1

i, j

∗ M

≤ R

j,m

, X

i, j

∈ {0, 1}, j = 1 to |J|

|G|

∑

i=1

i, j

∗ L

≤ R

j,l

, X

i, j

∈ {0, 1}, j = 1 to |J|

|J|

∑

j=1

i, j

= 1, i = 1 to |G|

Here the objective is to maximize the proﬁt of the

platform by assigning the testing requests to testers.

While P has uniform price rules for different types of

testing trafﬁc, each tester could charge different prices

for the same type of packets since they need to con-

sider the network costs. The proﬁt P collects is deter-

mined by the difference between the two prices and

the number of packets. At the same time, since a test-

ing request can be assigned to only one tester, the total

numbers of high, middle, and low sensitivity packets

assigned to each tester must be within its limits. Here

i, j

represents whether or not the requests G

is as-

signed to tester j. The last constraint shows that each

task is assigned to only one tester.

Complexity Analysis

From the deﬁnition of the problem, we can see that it

is related to the knapsack problem. Here each tester’s

packet limits are the knapsacks’ capacity while the

testing requests are the items. We have proven the

following theorem.

Theorem 1: Assignment method 1 is an NP-complete

problem.

Proof: A special case of this problem is equivalent to

the subset knapsack problem. 

Incentivisation of Outsourced Network Testing: View from Platform Perspective

501

Table 1: Symbols used in the paper.

P platform that provides testing services

jth tester that conducts testing services

ith user that demands testing services

, BP

base price P charges for each high, mid, and low sensitivity packet

, M

, L

) ith network testing request with H

high, M

middle, and L

low packets

j,l

, P

j,m

, and P

j,h

price tester j charges for sending a low, middle and high sensitivity packet

j,l

, R

j,m

, and R

j,h

the limits of low, middle, and high sensitivity packet tester j can send out

i, j

whether or not we assign request G

to tester j

i, j,H

# of high sensitivity packets of G

assigned to T

(same for mid and low)

G the set of network testing requests

J the set of network testers

3.2.2 Task Assignment Method 2

In this task assignment method, we assume that a

testing request can be assigned to multiple testers to

jointly accomplish the task. Note that the whole re-

quest must be satisﬁed. In other words, we will not

serve only a part of the request. Under this case,

the assignment procedure could become more com-

plicated since we can draw the packet capacity from

different sources. As long as the remaining capacity

of high, middle, and low sensitivity packets is enough

for the request, we can satisfy the request.

From the ﬁrst sight, it seems that this problem can

be solved with a greedy algorithm, e.g., always assign

the request to the tester that charges the lowest price

for a category of the packets. The greedy approach,

however, may leave a part of the testing capacity un-

usable, thus leading to a low proﬁt for P.

Below we show the formal deﬁnition of the prob-

lem. Here we can assign a request to multiple testers

as long as all of the testing packets are covered. Y

i, j,H

represents the number of high sensitivity packets of

request G

that are assigned to tester T

. Another

restriction is the total number of high (middle, or

low) sensitivity packets that are assigned to a tester

is within her limit.

maximize:

|G|

∑

i=1

|J|

∑

j=1

i, j,H

∗ (BP

− P

j,h

) +Y

i, j,M

∗

(BP

− P

j,m

) +Y

i, j,L

∗ (BP

− P

j,l

))

subject to:

|G|

∑

i=1

i, j,H

≤ R

j,h

, j = 1 to |J|

|G|

∑

i=1

i, j,M

≤ R

j,m

, j = 1 to |J|

|G|

∑

i=1

i, j,L

≤ R

j,l

, j = 1 to |J|

|J|

∑

j=1

i, j,H

= H

, i = 1 to |G|

|J|

∑

j=1

i, j,M

= M

, i = 1 to |G|

|J|

∑

j=1

i, j,L

= L

, i = 1 to |G|

Complexity Analysis

Since now a single testing request can be assigned to

multiple testers, it is different from the scenario that

we discussed in Section 3.2.1. Now the testing capac-

ity of different nodes can actually be merged together

to form a large pool. Please note that since each tester

may have different capacities in high, middle, and low

sensitivity packets, their sums are also different. At

the same time, each tester has its own price policy of

the testing packets.

Since the testing capacity can be merged to form a

large pool, we have a variant of the multi-dimensional

knapsack problem (Laabadi et al., 2018). Here the

proﬁt of satisfying a single testing request is not a

constant since each tester has its own price policy. We

have proven that this variant is still an NP-hard prob-

lem.

Theorem 2: Assignment method 2 is an NP-hard

problem.

Proof: A special case of this problem is equivalent to

the general multidimensional knapsack problem. 

3.3 Heuristic Algorithms

In this section we will discuss some heuristic algo-

rithms for the task assignment problem. Depending

on whether or not a testing request can be assigned

to multiple testers, we investigate two different ap-

proaches.

The ﬁrst heuristic algorithm we present is a

variation of the Primal Effective Capacity Heuristic

(PECH) mechanism for the general MDKP (Akcay

et al., 2007) problem. Speciﬁcally, it is a greedy al-

gorithm for the Task Assignment Method 1. Here

we assume that a task must be assigned to a single

tester. Since each tester adopts its own price model,

the proﬁt that P can collect from accomplishing the

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

502

task depends on the assigned tester. Since the plat-

form needs to select one task from all the unassigned

network testing requests, the selection method could

directly impact the ﬁnal result. Several examples of

the selection criteria include: (1) ﬁrst come ﬁrst serve;

(2) ﬁt as many requests as possible to the testing ca-

pacity; or (3) randomly choose a task.

Another criteria of tester assignment is the packet

capacity usage of different categories. Since we as-

sign a whole request to one tester, we try to use the

packet capacities in a balanced way to avoid the sit-

uations in which a certain type of packet capacity is

used up while for other types a plenty of capacity is

remained. Under this case, we will assign a request

to a tester that will create the least imbalance in its

remaining capacities after satisfying the request. Be-

low we provide an example. Assume that we have

two testers T

and T

who have used their capacities

from high to low as follows: T

(71%, 68%, 72%) and

(66%, 69%, 67%). The imbalance is deﬁned as the

largest difference between capacity usage in different

categories. So the imbalance of T

is 72% − 68% =

4%, and for T

is 3%. Now assume that a request

contains only high sensitivity packets. Because of the

difference in capacities of testers, it will use 2% of

’s capacity or 3% of T

’s capacity. Therefore, if we

assign it to T

, the new imbalance value will be ((71%

+ 2%) - 68% = 5%). While for T

the new value is

(69% - 67% = 2%). Therefore, to reduce imbalance

at testers after assignment, we will give the task to T

The Task Assignment Method 2 is a little bit dif-

ferent since we can assign the packets to multiple

testers. Therefore, a greedy algorithm will try to

assign each single testing packet to the tester who

charges the lowest price. Once that tester’s capac-

ity is reached, we can move on to the next cheapest

tester. Note that this approach tries to maximize the

proﬁt from the current request for the platform. If

the ﬁrst-come-ﬁrst-serve method is always adopted,

it is possible that a certain type of packet capacity is

used up ﬁrst, thus preventing us from admitting new

requests. For example, if all testing capacity of the

middle level sensitivity packets is used up, we will

not be able to admit any request that contains middle

sensitivity packets since we do not allow a request to

be partially satisﬁed.

To prevent this scenario from happening, we can

manage the remaining capacity of different types of

packets and try to maintain a balance. For example,

during the request assignment procedure we can set

up a threshold of the imbalance value between the re-

maining capacities of different categories. We will

not accept any request that will break the threshold.

Below we provide an example. Assume that we set

the imbalance threshold at 5%. Before admitting a

request, the capacity usage are 45% (low), 42% (mid-

dle), and 47% (high), respectively. Now if a task re-

quests 1% of middle sensitivity packet capacity and

2% of high, we will not admit it since the ending ca-

pacity usage will be 43% (middle) and 49% (high)

which will exceed the imbalance threshold 5%.

4 QUANTITATIVE RESULTS

In this part, we will present some quantitative results

of the proposed approaches. The experiments focus

on the achieved proﬁt of different approaches, and the

practicability of the task assignment models.

4.1 Achievable Proﬁts

Based on the discussion in previous sessions, we can

see that the task assignment problem is an NP prob-

lem. Therefore, in this section, we will compare the

maximum proﬁt under some scenarios to the achiev-

able proﬁt of the heuristic approaches. Restricted

by the search space size and required computation

power, we will experiment with some small scale

questions.

We assume that the prices that the platform

charges for each high, middle, and low sensitivity

packet are $12, $10, and $8, respectively. For each

tester, the capacities of high, middle, and low sensitiv-

ity packets follow uniform distribution in the ranges

of (900, 1100), (1800, 2200), (900, 1100), respec-

tively. The size of the network test requests also fol-

lows uniform distribution around the expected values.

They are divided into two groups. The ﬁrst group

have the sizes that range from 20% to 90% of the

testers’ capacities, while the second group range from

10% to 45%. The charging prices of the testers uni-

formly distribute between 92% to 100% of the plat-

form prices. To calculate the maximum proﬁt of the

assignment, we search for all possible combinations.

In this group of experiments, we consider three

task assignment mechanisms: ﬁrst come ﬁrst serve

(FCFS), random assignment, and exclusive search

(maximum proﬁt). Here the FCFS mechanism will try

to satisfy the tasks based on their arriving order. The

random assignment mechanism picks from the pool

of unsatisﬁed tasks and assign it to the tester that will

generate the highest proﬁt. In Figure 2, we show the

ratio between the proﬁts of the heuristic mechanisms

and the maximum proﬁt.

From the ﬁgure, we can see that the size of the

network testing requests has an large impact on the

achievable proﬁt. For example, when the sizes of

Incentivisation of Outsourced Network Testing: View from Platform Perspective

503

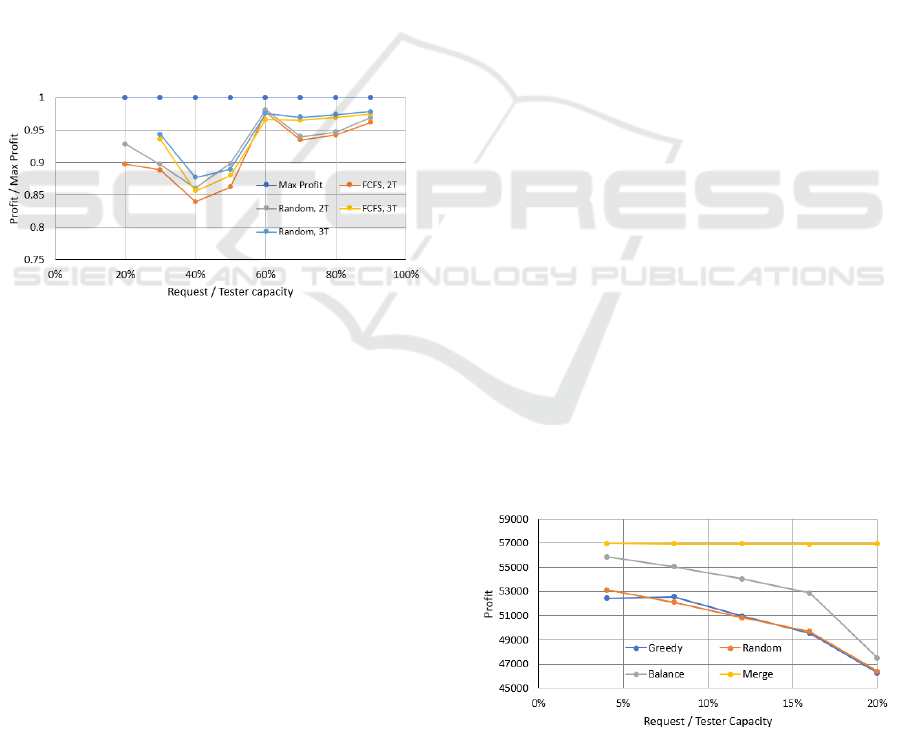
the requests are comparable to the capacities of the

testers (60% to 90%), very frequently we can ﬁt only

one or two requests into the tester’s capacity. There-

fore, the difference between the maximum proﬁt and

the achievable proﬁts of the heuristic mechanisms is

not large. As the size of the requests decreases (40%

and 50%), we can assign multiple requests to a tester.

Therefore, the selection of requests and testers could

impact the proﬁt a lot since a poorly designed as-

signment mechanism can often use low percentage of

the capacity, thus causing increased differences be-

tween the maximum proﬁt and achievable proﬁts of

the heuristic methods. When the size of the requests

further decreases, we can ﬁt many requests into the

capacity of a single tester, and the percentage usage

goes up again. From this point of view, after the plat-

form learns the distribution of the request sizes, they

can recruit testers with favorable capacity sizes that

can help the platform to increase its proﬁt. From an-

other aspect, we can see that the FCFS and Random

assignment mechanisms demonstrate similar perfor-

mance.

Figure 2: Ratio between the maximum proﬁt and proﬁt of

different mechanisms.

4.2 Comparison of Heuristic

Approaches

In the second group of experiments, we will compare

multiple heuristic approaches. Speciﬁcally, we study

4 heuristic mechanisms: (1) FCFS/Greedy: in this

mechanism, the platform adopts the ﬁrst-come-ﬁrst-

serve policy. A single request must be assigned to

one tester who can generate the largest proﬁt through

accomplishing the request. (2) Random/Greedy: in

this method, we assume that all request information

is available to the platform. We will then randomly

pick a request from the pool and assign it to a tester

who can generate the largest proﬁt. We will continue

this procedure until all testers use up their capacities,

or all requests are satisﬁed. From this point of view, it

is similar to FCFS but we choose requests randomly

instead of based on the arriving order.

The third mechanism that we experiment with is

called “balanced capacity usage”. In this method, we

try to assign a request to a tester to minimize the dif-

ference between the used capacity in high, middle,

and low sensitivity packets at the tester. Speciﬁcally,

for all tester T

, we try to achieve min (max capacity

usage di f f erence). The objective is to use the capac-

ities in a balanced way so that we can assign more

requests to a single tester.

Last but not least, in the ‘merged’ mechanism, we

allow a request to be assigned to multiple testers and

each accomplishes only a part of the task. In this

method, the capacities of the high, middle, and low

sensitivity packets of different testers are merged into

their own pools. For each request, we will choose

the tester who charges the lowest price to the cor-

responding packet type. Since different testers may

charge different prices, we may assign the high sensi-

tivity packets to one tester and the middle sensitivity

packets to another tester. In this way, we can usually

achieve higher proﬁt since we will use the tester ca-

pacities more effectively.

In this group of experiments, we assume that the

platform recruits 50 testers and there are 1500 re-

quests submitted by end users. The meanings of the

parameters are similar to those discussed in Section

4.1. Since we do not have the maximum proﬁt value,

in the following ﬁgures we will illustrate the absolute

proﬁt (in $).

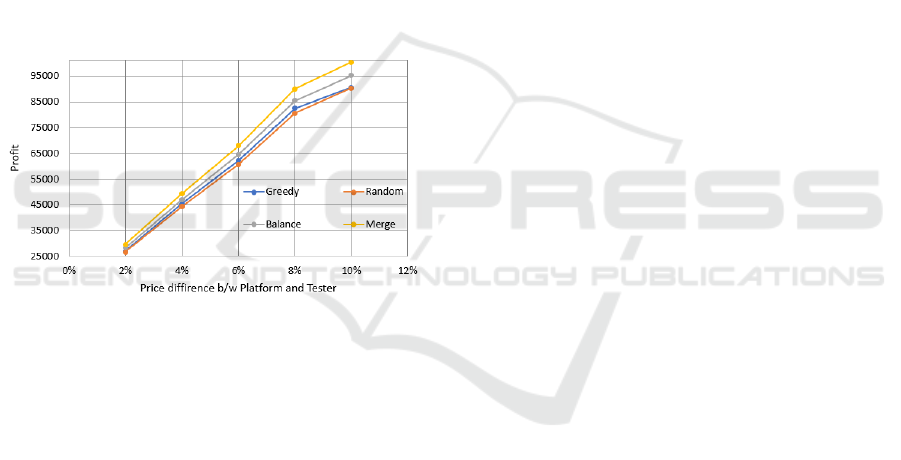
Figure 3 shows the quantitative results. On the X-

axis, we have the ratio between the size of the network

testing requests and the tester capacity. On the Y-axis,

we have the proﬁt value. We have several observa-

tions in the ﬁgure. First, for the ‘merged’ mechanism,

since we put all the capacities of the testers into the

pools of their own categories, we can continue to sat-

isfy requests until at least one of the categories can no

longer ﬁt any request. Therefore, we can see that the

proﬁt of the ‘merged’ mechanism is not largely im-

pacted by the request size. On the contrary, for the

other three mechanisms, their proﬁt will slowly de-

crease as the size of the requests increases.

Figure 3: Relationship between the achieved proﬁt and the

size of testing requests.

Compared to ‘FCFS/Greedy’ and ‘Ran-

dom/Greedy’, the ‘Balanced’ mechanism tries

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

504

to use the capacity in different categories in a strate-

gic manner so that we can avoid the scenario that

one category is exhausted while a large portion of

capacities of other categories are still unused. From

the ﬁgure, we can see that the ‘Balanced’ mechanism

generates higher proﬁt than the other two methods.

As the size of the requests increases, more capacity

at the testers could not be used. Therefore, the

overall proﬁt will decrease. Similar to the reason

we discussed in Section 4.1, the ‘FCFS/Greedy’ and

‘Random/Greedy’ mechanisms do not demonstrate

noticeable differences.

In Figure 4, we study how the price model of the

testers impacts the proﬁt of the platform. Speciﬁcally,

we adjust the average price difference between the

testers and the platform. In the X-direction, the aver-

age price difference increases from 2% to 10% of the

platform price. On the Y-direction we show the proﬁt.

From the ﬁgure we can see that as the price difference

changes, the proﬁt increases almost linearly.

Figure 4: Relationship between the achieved proﬁt and the

prices at testers.

4.3 Future Extensions

In this part, we will discuss potential extensions to our

approach.

Impacts of Price Model

This paper can be viewed as our exploration of the

practicability of the outsourced network testing ser-

vices. Speciﬁcally, we want to see how various fac-

tors impact the sustainability and proﬁt of the plat-

form. To simplify the discussion and simulation, we

assume a uniform distribution of the price difference

between the testers and platform and the prices do not

change. In real life, both platform and testers could

adopt more complicated price model. For example,

they can dynamically adjust the price based on the

number of requests, the number of testers, and the

remaining capacity. From this point of view, maxi-

mization of the platform proﬁt will become a more

challenging question.

Privacy of Security Policies

Another concern of the outsourced network testing is

the leakage of the network security policies of the end

customers. Based on the construction and contents of

the network testing packets, a tester may derive out

the network security policies that the end user adopts.

Therefore, should a tester turn malicious, it has the

capability to design attacks based on the knowledge

of the policies. To defend against such attacks, a po-

tential mechanism is to distribute the testing trafﬁc to

multiple testers so that each party holds only a portion

of the knowledge. The end user could also embed de-

ceitful trafﬁc into the request. Subsequent research is

needed in this direction.

5 CONCLUSION

In this paper we investigate the problem of outsourced

network test. Speciﬁcally, we focus on the working

model of the platform and the possible mechanisms

of task assignment. Our analysis shows that the task

assignment problem is an NP problem and we need

to design heuristic algorithms to assist the platform to

generate higher proﬁt. We conduct simulation to in-

vestigate the maximum proﬁt and the achievable prof-

its of different approaches. Our simulation shows that

maintaining a balance between the remaining testing

capacities of different categories will increase proﬁt

of the platform.

When we put the research problem in a larger

view, the goal is to allow the platform to run the net-

work testing services in a sustainable way. Therefore,

it needs to attract enough number of end users as well

as network testers to the platform. At the same time,

it needs to protect the privacy of the end users. Dif-

ferent from the service level agreements that focus on

resource usage such as CPU cycles, outsourcing of se-

curity related SLAs deserves more careful execution

since a balance between safety and effectiveness of

the approach must be maintained.

REFERENCES

Akcay, Y., Li, H., and Xu, S. (2007). Greedy algorithm

for the general multidimensional knapsack problem.

In Annals of Operations Research, volume 150, pages

17–29.

Alasmari, S., Wang, W., and Wang, Y. (2020). Proof of

network security services: Enforcement of security sla

through outsourced network testing. In International

Conference on Communication and Network Security

(ICCNS), pages 52–59.

Incentivisation of Outsourced Network Testing: View from Platform Perspective

505

Casola, V., De Benedictis, A., Eras¸cu, M., Modic, J., and

Rak, M. (2017). Automatically enforcing security slas

in the cloud. IEEE Transactions on Services Comput-

ing, 10(5):741–755.

Casola, V., De Benedictis, A., Rak, M., and Villano, U.

(2020). A novel security-by-design methodology:

Modeling and assessing security by slas with a quan-

titative approach. Journal of Systems and Software,

163:110537.

de Carvalho, C., de Andrade, R., de Castro, M., Coutinho,

E., and Agoulmine, N. (2017). State of the art and

challenges of security sla for cloud computing. Com-

puters & Electrical Engineering, 59:141–152.

Desai, V. R. (2012). Techniques for detection of malicious

packet drops in networks. Master’s thesis, University

of Massachusetts Amherst.

Hawedi, M., Talhi, C., and Boucheneb, H. (2018). Security

as a service for public cloud tenants(saas). Procedia

Computer Science, 130:1025–1030.

Hyun, S., Kim, J., Kim, H., Jeong, J., Hares, S., Dunbar,

L., and Farrel, A. (2018). Interface to network secu-

rity functions for cloud-based security services. IEEE

Communications Magazine, 56(1):171–178.

Khan, F., Ur Rehman, A., Zheng, J., Jan, M. A., and

Alam, M. (2019). Mobile crowdsensing: A survey on

privacy-preservation, task management, assignment

models, and incentives mechanisms. Future Gener-

ation Computer Systems, 100:456–472.

Laabadi, S., Naimi, M., El Amri, H., and Achchab, B.

(2018). The 0/1 multidimensional knapsack problem

and its variants: A survey of practical models and

heuristic approaches. American Journal of Operations

Research, (8):395–439.

Paul, M., Harbarth, S., Huttner, A., Thwaites, G., Theuret-

zbacher, U., Bonten, M., and Leibovici, L. (2021).

Investigator-initiated randomized controlled trials in

infectious diseases: Better value for money for regis-

tration trials of new antimicrobials. Clinical Infectious

Diseases, 72(7):1259––1264.

Rak, M., Suri, N., Luna, J., Petcu, D., Casola, V., and Vil-

lano, U. (2013). Security as a service using an sla-

based approach via specs. In Proceedings of IEEE

International Conference on Cloud Computing Tech-

nology and Science, (CloudComp), pages 1––6.

Rios, E., Mallouli, W., Rak, M., Casola, V., and Ortiz, A. M.

(2016). Sla-driven monitoring of multi-cloud applica-

tion components using the musa framework. In IEEE

International Conference on Distributed Computing

Systems Workshops (ICDCSW), pages 55–60.

Wonjiga, A. T., Rilling, L., and Morin, C. (2019a). Deﬁn-

ing security monitoring slas in iaas clouds: the exam-

ple of a network ids. Research Report RR-9263, Inria

Rennes Bretagne Atlantique, pages 1–37.

Wonjiga, A. T., Rilling, L., and Morin, C. (2019b). Security

monitoring sla veriﬁcation in clouds: the case of data

integrity. Research Report RR-9267, Inria Rennes -

Bretagne Atlantique, pages 1–29.

Zhao, B., Tang, S., Liu, X., and Zhang, X. (2021). Pace:

Privacy-preserving and quality-aware incentive mech-

anism for mobile crowdsensing. IEEE Transactions

on Mobile Computing, 20(5):1924–1939.

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

506