Quantifying Multimodality in World Models
Andreas Sedlmeier, Michael K
¨
olle, Robert M
¨
uller, Leo Baudrexel and Claudia Linnhoff-Popien
LMU Munich, Munich, Germany
Keywords:
Uncertainty, Multimodality, World Models, Model-based Deep Reinforcement Learning, Mixture-density
Networks.
Abstract:
Model-based Deep Reinforcement Learning (RL) assumes the availability of a model of an environment’s
underlying transition dynamics. This model can be used to predict future effects of an agent’s possible actions.
When no such model is available, it is possible to learn an approximation of the real environment, e.g. by
using generative neural networks, sometimes also called World Models. As most real-world environments are
stochastic in nature and the transition dynamics are oftentimes multimodal, it is important to use a modelling
technique that is able to reflect this multimodal uncertainty. In order to safely deploy such learning systems in
the real world, especially in an industrial context, it is paramount to consider these uncertainties. In this work,
we analyze existing and propose new metrics for the detection and quantification of multimodal uncertainty
in RL based World Models. The correct modelling & detection of uncertain future states lays the foundation
for handling critical situations in a safe way, which is a prerequisite for deploying RL systems in real-world
settings.
1 INTRODUCTION
While model-free reinforcement learning (RL) has
produced a continuous stream of impressive results
over the last years (Mnih et al., 2015) (Vinyals et al.,
2019), interest in model-based reinforcement learn-
ing has only recently experienced a resurgence (Silver
et al., 2018) (Schrittwieser et al., 2020). Although at
first, approaches like World Models (Ha and Schmid-
huber, 2018) might seem more complex, they also
promise to tackle some important aspects like sample-
efficiency, that still hinder wide deployment of RL
in the real world. Besides the potential benefits, it
is still necessary to consider non-functional aspects
when developing model-based RL systems. Most im-
portant might be guaranteeing reliable behaviour in
uncertain conditions. Especially considering indus-
trial systems, such uncertainty could lead to potential
safety risks when wrong predictions of the learning
system lead to the execution of harmful actions. Con-
sequenly, considering and in the case of model-based
RL, correct modelling of the present uncertainty is of
utmost importance in order to build reliable systems.
Existing work in this area has mostly focused on
differentiating between aleatoric and epistemic un-
certainty, and the question of which kind is relevant
to certain tasks (Kendall and Gal, 2017) (Osband
et al., 2018). The work at hand focuses on the un-
certainty’s aspect of multimodality. Considering the
goal of learning a model for model-based RL, this
kind of uncertainty arises whenever the distribution
of the stochastic transition dynamics of the underly-
ing Markov decision process (MDP) is multimodal.
On one hand, using a modelling technique which is
not able to reflect this multimodality would lead to
a suboptimal model. On the other hand, assuming a
modelling technique which is able to correctly reflect
this multimodality, being able to detect the presence
of states with multimodal transition dynamics would
be of great value. If one is able to detect these uncer-
tain dynamics, it becomes possible to guarantee ro-
bustness, for example by switching to a safe policy or
handing control over to a human supervisor (Amodei
et al., 2016). In this work, we analyze existing and
propose new metrics for the detection and quantifica-
tion of multimodal uncertainty in World Model archi-
tectures. We begin, by introducing basic preliminaries
in the next section, followed by related-work in sec-
tion 3. Section 4 explains the basic concepts underly-
ing the quantification of multimodality and introduces
existing and new metrics which will be used for eval-
uation. We explain our experimental setup in section
5, followed by evaluation results in section 6 and a
conclusion in section 7.
Sedlmeier, A., Kölle, M., Müller, R., Baudrexel, L. and Linnhoff-Popien, C.
Quantifying Multimodality in World Models.
DOI: 10.5220/0010898500003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 1, pages 367-374
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
367

2 PRELIMINARIES
In this section we discuss the necessary preliminaries
our work builds upon. We start with a brief introduc-
tion to reinforcement learning (RL) and World Mod-
els (Ha and Schmidhuber, 2018), a model-based RL
architecture that our work makes heavy use of. Next,
we introduce Mixture Density Networks and review
uncertainty and multimodality.
2.1 Model-based RL & World Models
In RL, an agent interacts with its environment to max-
imize reward. The environment is formally specified
in terms of a Markov decision process (MDP). An
MDP is a tuple (S, A, P, R, γ) where S is the set of states
and A the set of actions Let s
t
∈ S and a
t
∈ A be the
state and action at timestep t, then P(s
t+1
|s
t
, a
t
) de-
notes the transition function, i.e., the dynamics of the
environment, R : S × A → R the reward function and
γ ∈ (0, 1) is the discount factor. The goal is then to
find a policy π
∗
: S → A which maximizes the follow-
ing objective:
π
∗
= argmax
π
E
π

∞
∑
t=0
γ
k
R(a
t
, s
t
)

γ is needed to make the infinite sum converge and
by further decreasing γ one favors short time reward.
Model-free and model-based RL can be differenti-
ated by the question of whether the agent has ac-
cess to or learns a model of P and R. In the case
of model-free RL, the agent can only interact directly
with the environment via policy π and receive s
t
and
r
t
= R(a
t
, s
t
). In model-based RL by contrast, the
agent can plan by using the model to query possible
future consequences of it’s actions. In both cases, in-
teracting with the environment produces trajectories
of the form (s
t
, a
t
, r
t
, s
t+1
, a
t+1
, r
t+1
. . . ).
World Models are a special case of model-based
RL introcued in (Ha and Schmidhuber, 2018). In this
architecture, no pre-supplied model is available and
instead, the agent aims to learn a compressed spa-
tial and temporal representation of the environment.
Results show that a model learned this way can lead
to improved sample efficiency in optimizing the RL
policy. Architectural details of the World Model ar-
chitecture will be introduced in more depth in section
5.2.2.
2.2 Mixture Density Networks
The idea of Mixture Density Networks (MDNs) was
introduced in (Bishop, 1994). Summarized suc-
cinctly, the goal of their development was being able
to solve a supervised learning task which has a non-
Gaussian distribution. Such cases often arise with
so called inverse problems, where the distribution is
multimodal. Bishop presents the MDN as a flexible
mixture model framework which can model arbitrary
conditional densities. In the case of using gaussian
components, the conditional distribution p(y|x) is cal-
culated as:
p(y|x) =
K
∑
k=1
π
k
(x)N (y|µ
k
(x), σ
2
k
(x)) (1)
with k being the amount of mixture components,
π
k
(x) the mixture coefficients and N normal distri-
butions with means µ
k
(x) and variances σ
2
k
(x). With
the exception of k which has to be defined as a hyper-
parameter, these parameters of the mixture model can
then be learned using any kind of neural network.
2.3 Uncertainty and Multimodality
In the field of machine learning, it is common to dif-
ferentiate between two types of uncertainty. First,
aleatoric uncertainty, which describes uncertainty in-
herent in the data, for example, due to measurement
inaccuracy. The other is epistemic uncertainty, which
can be described as uncertainty regarding the parame-
ters or structure of the model. This kind of uncertainty
can be reduced by more data, whereas aleatoric uncer-
tainty is irreducible.
As a special kind of aleatoric uncertainty, multi-
modality refers to the shape of the aleatoric uncer-
tainty’s distribution. If the distribution has a sin-
gle mode, it is called unimodal, if it has at least
two modes, it is called multimodal. In the field
of RL and MDPs, such multimodal uncertainty can,
among others, be present if the state transition func-
tion P(s
t+1
|s
t
, a
t
) is stochastic in nature.
3 RELATED WORK
3.1 Bump Hunting
In the research field of statistics, the search for mul-
timodality is sometimes called Bump Hunting. Here,
methods for low-dimensional data exist that try to de-
tect the presence of multiple local maxima. The Pa-
tient Rule Induction Method (PRIM) (Friedman and
Fisher, 1999) is a method frequently used in this field.
Given a dataset, PRIM reduces the search range iter-
atively until a subrange with comparatively high val-
ues is found. If data is two- or multi-dimensional,
PRIM may not be able to distinguish two different
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
368

modes from each other (Polonik and Wang, 2010).
As our work aims to detect multimodality in high di-
mensional, possibly image based data, these classical
methods are not applicable.
3.2 Uncertainty-based OOD Detection
A slightly different line of work is concerned with
detecting untrained, out-of-distribution (OOD) situa-
tions in RL. That research is related to the work at
hand, as the goal is to achieve this by developing mul-
tiple methods for quantifying an RL agent’s uncer-
tainty. PEOC (Sedlmeier et al., 2020b) for example
uses the policy entropy of an RL agent trained us-
ing policy-gradient methods, to detect increased epis-
temic uncertainty in untrained situations. UBOOD
(Sedlmeier et al., 2020a) by contrast is applicable to
value-based RL settings and is based on the reducibil-
ity of an agent’s epistemic uncertainty in it’s Q-Value
function. Although the methods differentiate between
aleatoric and epistemic uncertainty to detect OOD sit-
uations, multimodality is not a focus.
4 QUANTIFYING
MULTIMODALITY
As explained in the introduction, being able to detect
multimodality is an important first step towards build-
ing reliable & safe learning systems. Consequently,
in this section, we focus on the question of how to
quantify multimodality. We begin in subsection 4.1
by analyzing the case of a simple 1-dimensional re-
gression case, modelled using an MDN. Section 4.2
then follows up by introducing the more complex case
of detecting multimodal state-transitions in a high-
dimensional World Model setting.
4.1 Multimodality in Mixture Density
Networks
We explain the following ideas using a simple syn-
thetic dataset. It is inspired by (Bishop, 1994) and is
generated by inverting a noisy sine wave
1
. From the
perspective of the work at hand, it is interesting as it
contains both areas of unimodality as well as multi-
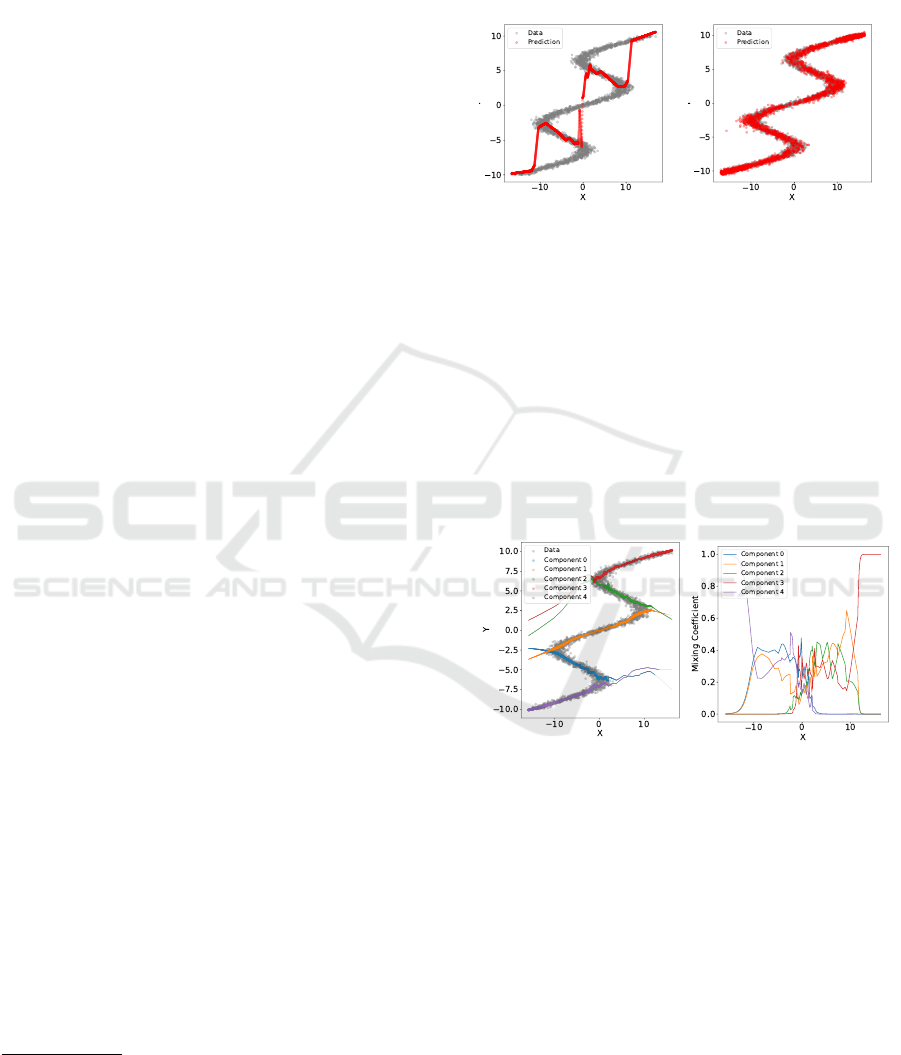
modality. Figure 1 shows the failure of a simple deep
neural network using MSE as the loss function, to cor-
rectly model the function f (x) = y. This is due to the
1
Data is generated using: f (x) = x + 7 ∗ sin (0, 7 ∗ x) and
then adding noise from a standard normal distribution. The
inverse problem is obtained by exchanging the roles of x
and y.
fact, that the network tries to reduce the mean-squared
error while only being able to make point predictions.
The predictions generated by a 5 component MDN
(red dots in Figure 1b) by contrast correctly approxi-
mate the target function.
(a) Deep NN - MSE. (b) MDN.
Figure 1: Predictions of (a) a simple deep neural network
using MSE as the loss function, and (b) a MDN with k = 5
components, trained on the inverse sine wave dataset.
When looking at the activations of the mixing co-
efficients of the trained MDN when predicting on this
dataset, it possible to analyse how this is achieved.
Each color in Figure 2 represents a single compo-
nent of the mixture model. Line width is calculated
by multiplying the component’s mixing coefficient π
with it’s standard deviation. Visualized this way, it
becomes apparent that different components focus on
different areas of the dataset.
(a) Mean prediction.
(b) Mixing coefficients.
Figure 2: MDN with k = 5 components, fitted on the in-
verse sine wave dataset. Line width in (a) is calculated by
multiplying the component’s mixing coefficient π with it’s
standard deviation.
Regarding the quantification of multimodality,
Figure 2b gives a first hint. Here, the mixing coef-
ficients π(x) of all components are visualized. It be-
comes apparent, that in areas of increasing unimodal-
ity with −10 > x > 10, a single component dominates.
In areas of multimodality, multiple components con-
tribute.
Quantifying Multimodality in World Models
369

4.2 Quantifying Multimodality in
World Models
While a visual analysis of the multimodality was pos-
sible in the simple 1D regression case presented in the
previous section, such an approach is no longer pos-
sible when using high dimensional input data. World
models, as one of the most prominent representatives
of model based RL, are most often based on input data
in the form of high dimensional images. In the work
of (Ha and Schmidhuber, 2018) for example, input
tensors have a size of 64x64x3 = 12288 dimensions.
Using any kind of classical multimodality detection
technique from the related statistics literature directly
on the input data is impossible in these dimensionali-
ties. Further more, the focus of our work is more com-
plex than simply analyzing state inputs. Instead, we
focus primarily on quantifying multimodality in order
to detect multimodal state-transitions. Consequently,
any multimodality quantification and detection which
aims to do this, needs to be applied later on, in the so
called Memory Model of the World Model pipeline.
Here, future states are predicted and multimodal tran-
sitions can possibly be detected. The exact process
and integration point of the developed multimodality
metrics will be described in section 5.2.3.
4.3 Multimodality Metrics
This section presents and discusses the different mul-
timodality metrics that will be evaluated: Two exist-
ing ones, SEMD and JSD, as well as two newly de-
veloped ones, we call MCE and WAKLD.
Mixing Coefficient Entropy
A first, simple approach we propose is to compute the
Shannon Entropy H(X) = −
∑
n
i=1
p(x
i
)log p(x
i
) of an
MDNs mixture coefficients for multimodality quan-
tification. We call the resulting metric Mixing Coeffi-
cient Entropy (MCE). It is constructed as follows:
We interpret the k mixing coefficients of a MDN
as the categories of a multinomial distribution of size
k, where each mixing coefficient’s activation corre-
sponds to a category’s probability: π
i
(x) = p
i
.
This is valid, as the mixing coefficients of a MDN
must satisfy the constraint
k
∑
i=1
π
i
(x) = 1, 0 ≤ π
i
(x) ≤ 1
according to definition (Bishop, 1994). It is then pos-
sible to compute the entropy of this distribution. In
order to be able to compare entropy values of MDNs
with different amount k of components, it is helpful
to normalize this value:
MCE(p
1
, p
2
, . . . , p
k
) =
H(π)
H
max
= −
k
∑
i=1
π
i
(x)log π
i
(x)
logk
,
with p
i
= π
i
(x). This restricts the possible values to
the range [0, 1].
It is important to note possible failure cases when
using the entropy of a MDN’s mixing coefficients as
a multimodality metric. Consider the extreme case of
a 2-component MDN, where both components model
the same distribution, e.g. when using Gaussian com-
ponents, they have the same µ and σ. This would self-
evidently produce a unimodal predictive distribution,
even when both component’s mixing coefficients are
> 0. The computed MCE in this case would also be
> 0 and wrongly signal multimodality.
Weighted Average Kullback-Leibler Divergence
(WAKLD)
In order to overcome this limitation, we designed a
new metric with the explicit goal of incorporating the
mixture components’ individual distributions. We call
this metric Weighted Average Kullback-Leibler Diver-
gence (WAKLD). It is constructed by calculating for
every component, the weighted Kullback-Leibler Di-
vergence (KLD) to every other component. By sum-
ming these up and weighing by the initial component,
a score for the complete mixture distribution is calcu-
lated.
WAKLD(p
1
, p
2
, . . . , p
k
) =
k
∑
i=1
π
i
k
∑
j=1
π
j
D
KL
(p
i
||p
j
)
!
Strongly multimodal MDNs produce large
WAKLD values, while unimodal MDNs possess a
small WAKLD value. Expressed informally, the
intuition behind the ”double-weighing” is that e.g.,
a divergence to a component with low mixing-
coefficient (π
j
) should have a low impact on the
metric, as well as all divergences of a compo-
nent with low mixing-coefficient (π
i
) to any other
component, irrespective of their mixing-coefficient.
Self Earth Mover’s Distance (SEMD)
The authors of (Makansi et al., 2019) propose a metric
for quantifying multimodality in MDNs based on the
Earth-Mover’s-Distance (EMD). EMD is also known
as the Wasserstein metric and informally describes the
amount of work needed to transform one distribution
into another. The authors apply this to MDNs with
arbitrary amount of components, by computing the
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
370

EMDs between the component with the largest mix-
ing coefficient (primary mode) and all other compo-
nents. This in effect computes the EMD to convert the
multimodal mixture into a unimodal distribution de-
fined by the primary mode. A large SEMD value con-
sequently indicates strong multimodality, while small
SEMD indicates unimodality.
Jensen-Shannon Divergence (JSD)
The Jensen-Shannon Divergence (JSD) is another
information-theoretic divergence measure, based on
the Shannon Entropy. First introduced by (Lin, 1991),
it constitutes a symmetrization of the Kullback-
Leibler Divergence and can be understood as the total
KL divergence to the average distribution
p+q
2
. It can
be extended to more than two, individually weighted
distributions:
D
JS
(p
1
, p
2
, . . . , p
n
) = H
n
∑
i=1
π
i
p
i
!
−
n
∑
i=1
π
i
H(p
i
),
with p
i
being a distribution and π
i
the respective
weight.
5 EXPERIMENTAL SETUP
We now explain the experimental setup used to
evaluate the toy example based on the inverse sine
wave function, as well as the environment, network-
architecture and evaluation pipeline used for the
world model experiment.
5.1 Inverse Sine Wave
Section 4 introduced a simple toy problem, for ana-
lyzing MDN behaviour: The inverse sine wave. We
generate a dataset containing 3000 linearly spaced
points in the interval [−10, 10] using the function
f (x) = (x + 7 ∗ sin (0, 7 ∗ x)) and then adding noise
from a standard normal distribution. By exchanging
the roles of x and y, the inverse problem is obtained.
We fit this dataset using a simple fully-connected,
3-Layer MDN with k = 5, i.e. 5 mixture components.
All neurons use ReLU as the activation function, with
the exception of the output neurons. Here, no activa-
tion function is used on the µ neurons. To enforce
positivity of the neurons outputting a component’s
variance, We follow the work of (Brando, 2017) and
compute the output as σ(x) = ELU(1, x) + 1 + 1e
−7
.
This way, increased numerical stability is achieved,
compared to using the simple exponential function, as
suggested by (Bishop, 1994). Training is performed
over 1000 episodes by minimizing the negative log-
likelihood. As fitting an MDN is inherently stochastic
in nature, due to e.g. the random initialization of neu-
ral network weights and random data batching, we re-
peat this process for 50 separate runs. Based on these
fitted networks, we then evaluate the four multimodal-
ity metrics introduced in subsection 4.3.
5.2 World Model
The following section presents the experimental setup
used to evaluate the multimodality metrics presented
in subsection 4.3 in a high-dimensional world model
setting. The goal here is to differentiate multimodal
state-transitions from unimodal ones.
5.2.1 Environment
Currently, there are no existing environments for
benchmarking multimodality in deep RL. Therefore,
we chose to use an established RL benchmarking en-
vironment with no inherent stochasticity, i.e. only
unimodal state-transitions: Coinrun (Cobbe et al.,
2019), a simple 2D platformer. Multimodality can
then be artificially introduced via action masking,
as will be explained in more depth in subsubsec-
tion 5.2.3. It is important to note here that the en-
vironment’s state and transition dynamics only rep-
resent the foundation, based on which a generative
model is learned, according to the world model ar-
chitecture. This basic setup allows us to generate a
benchmark data-set with known ground-truth (multi-
modal/unimodal) state-transitions. The exact pipeline
that realizes this will be explained in section 5.2.3.
5.2.2 Algorithms and Network Architectures
Our network architecture consists of the first two
parts that make up the World Model as described in
(Ha and Schmidhuber, 2018). The Vision Model,
which reduces a high-dimensional observation to
a low-dimensional latent vector and the Memory
Model, which makes predictions about future encod-
ings based on past information. We omit the third
part, the controller, as optimizing a RL policy is not
the focus of our work. We use a convolutional VAE
for the Vision Model that compresses each 2D-frame
from the game to a smaller latent representation z.
The Memory Model uses a MDRNN to predict the
latent vector z that the Vision Model produces by tak-
ing the conditional probability p(z
t−+1
|a
t
, z
t
, h
t
). a
t
denotes the action while h
t
denotes the hidden state
of the RNN at time t.
For the Vision Model, a Convolutional VAE (Fig.
3) is used. The input takes a 64 × 64 RGB-frame and
Quantifying Multimodality in World Models
371

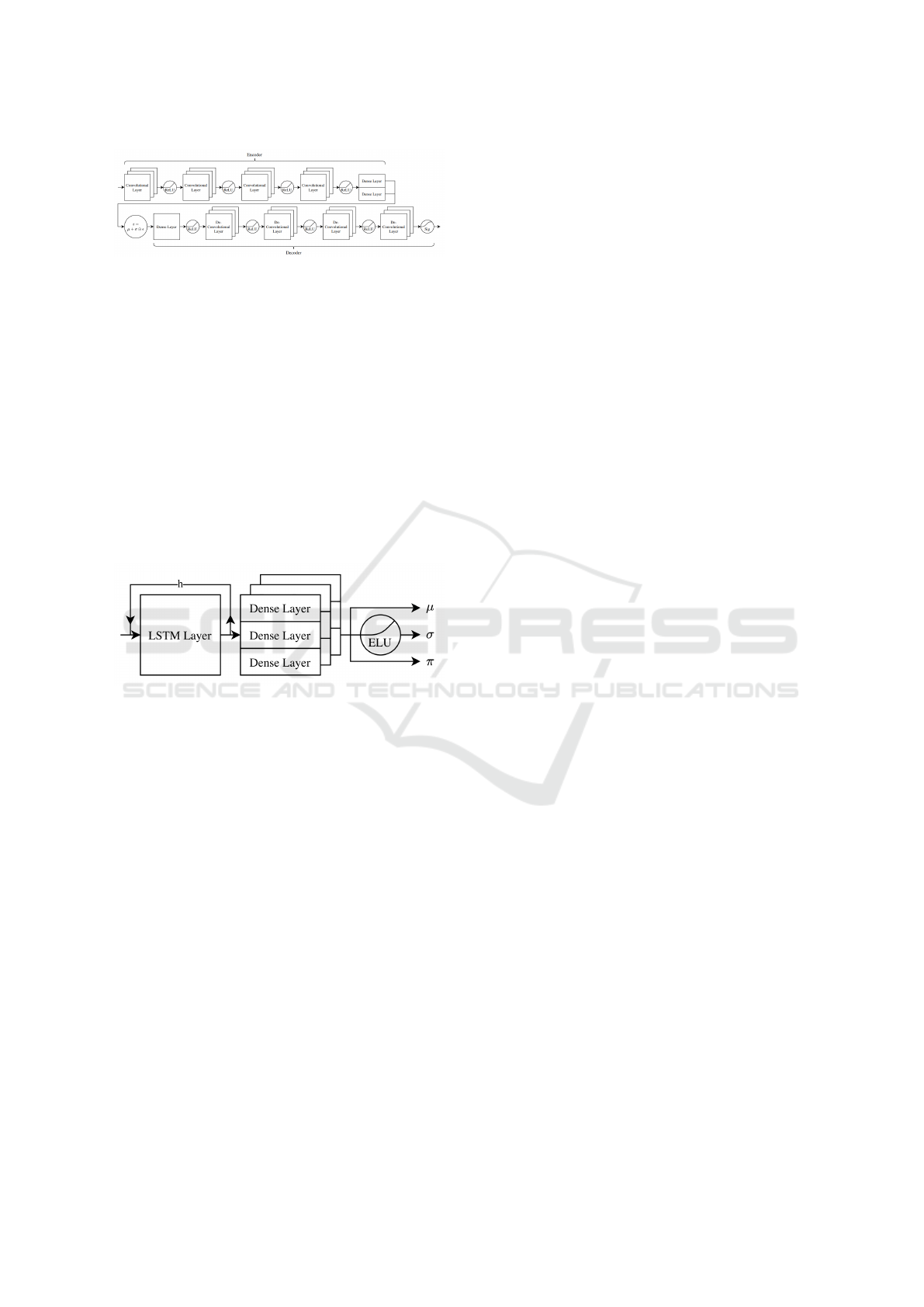
Figure 3: Architecture of the CNN-VAE.
transforms it in to a 64 dimensional latent vector z.
The encoder part consists of four convolutional
layers, each with a ReLU as activation function. The
parameters µ and σ are each calculated from a dense
layer. Using reparameterization, we get the latent rep-
resentation z = µ +σ  ε. The decoder starts with one
dense layer, followed by four deconvolutional lay-
ers, also with ReLU as activation functions, ending
with a Sigmoid layer. We used a Huber-Loss (Hu-
ber, 1992) with β = 1 to calculate reconstruction er-
ror of the cost function, as it is less sensitive to out-
liers than MSE-Loss. For regularization, Kullback-
Leibler-Divergence is used. We train this VAE over
100 epochs with the Adam optimizer, a learning rate
of 1e
−
3 and batch size 100.
Figure 4: Architecture of the MDRNN.
The Memory Model uses a MDRNN, consisting
of one LSTM layer and three stacked dense layers to
model the parameters of the mixing distribution (Fig-
ure 4). It takes an input-sequence of 20 latent vec-
tors with a dimension of 64. We trained the MDRNN
for 100 epochs using the negative log likelihood and
Huber-Loss with the Adam optimizer, a learning rate
of 1e
−
3 and batch size of 20.
5.2.3 Evaluation Pipeline
Inspired by (Ha and Schmidhuber, 2018), we use a
random policy to gather observations as input of a
VAE. The dataset consists of 1e5 64×64 RGB-frames
generated from selecting random actions [left, right,
jump, do nothing]. However, we chose the probabil-
ities of the actions to be not equally distributed [.15,
.32, .30, .50]. This results in movement towards the
goal and avoids jumping repeatedly, which takes 20
timesteps each. Using the input data as described
above, we train a VAE to encode the frames into a
64 dimensional latent space. Using the trained VAE,
another dataset is created in which a single data point
is a sequence of 20 encoded observations with cor-
responding actions and the immediate following ob-
servation. However, the encoded observations are not
stored as latent representation z, but instead as param-
eters µ and σ from the encoder. They are dynamically
reparameterized during the MDRNN training, to pre-
vent overfitting to concrete z values.
The resulting latent dataset is used to train an
MDRNN to predict the subsequent state for each se-
quence of latent observations and actions. These state
transitions are unimodal, but by omitting or masking
actions they can be made multimodal. The reason
for this is that for a given state, the subsequent state
is deterministically defined if the action which the
agent performs is known. For example, if the agent
chooses the action ”right”, the environment will be
shifted a fixed number of of pixels to the left. How-
ever, if the action is unknown, the subsequent state
cannot be predicted unambiguously, producing mul-
timodality. Since the dimensionality of the action
space is four, there are also four possible different
subsequent states. To maintain the size of the input
for the MDRNN, the actions are not simply omit-
ted, but replaced by an invalid action. We call this
process masking. To obtain both unimodal and mul-
timodal state transitions, actions are masked for the
first 50% of the time steps. For the second half, the
randomly chosen valid actions are used. This way, a
benchmarking dataset with known ground-truth (uni-
modal/multimodal) is created. Based on this dataset,
the 4 multimodality metrics presented in section 4 are
evaluated. We further evaluate how the metrics be-
have for a varying amount k of mixture components.
To do this, 13 separate MDRNNs with an amount of
mixture components varying between 2 and 50 are
constructed. In order to factor in the stochasticity of
MDRNN training, the complete training process is re-
peated 10 times, resulting in a total of 130 individual
models.
6 EVALUATION RESULTS
The following section first presents the evaluation re-
sults using the inverse sine wave dataset, followed by
the world model based experiment.
6.1 Inverse Sine Wave
Figure 5 shows the evaluation results of applying the
4 multimodality metrics introduced in section 4 to
MDNs trained on the inverse sine wave dataset. In
order to reduce stochastic effects present when train-
ing MDNs, average values of 50 runs are shown.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
372

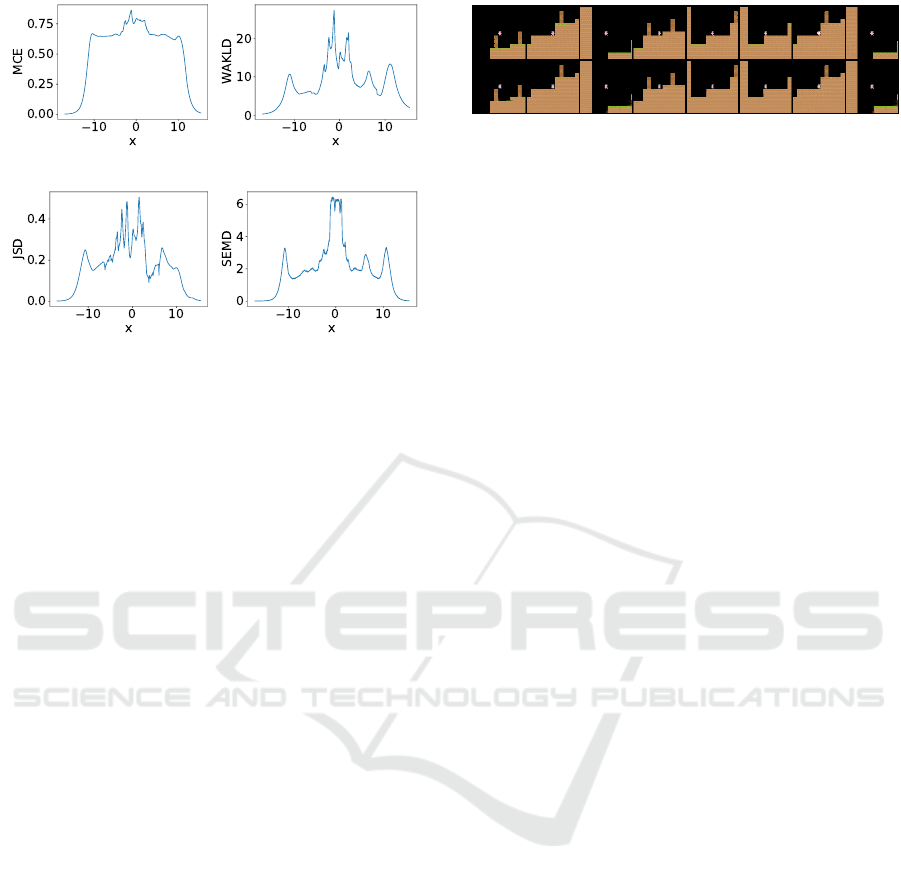
(a) MCE. (b) WAKLD.
(c) JSD. (d) SEMD.
Figure 5: MCE, WAKLD, JSD and SEMD metrics applied
to 5 component MDNs trained on the inverse sine wave
dataset. All values shown are averages of 50 runs.
What is apparent at a first glance, is that all 4
metrics behave similarly in the unimodal data range
(−10 > x > 10 ). As described in section 4, ana-
lyzing the mixing coefficients in these areas showed
that a single component is predominantely respon-
sible for predicting the values. This unimodality is
correctly reflected in all metrics by values converg-
ing towards 0. Rising values in the intermediate area
(−10 < x < 10 ) correctly reflect increasing multi-
modality, peaking around x = 0, where 3 maximally
separated modes of the inverse sine wave are present.
After having established the basic feasability of
the approach, we now evaluate whether the metrics’
behaviour transfers to the more complex case of pre-
dicting multimodal state-transitions in world models.
6.2 World Model
The first step of the evaluation pipeline was the train-
ing of the world model’s VAE. Using the 1e5 samples
generated via a random policy, the VAE converged af-
ter 100 epochs and was able to successfully compress
and reconstruct the state input. Figure 6 shows ex-
amples of the 64x64x3 sized original coinrun states
in the first row, followed by their respective VAE re-
construction in the second row. Using this VAE, 13
separate MDRNNs with between 2 and 50 mixture
components were constructed. Training was then re-
peated 10 times, resulting in a total of 130 individual
models.
Figure 7 shows a comparison of the 4 multimodal-
ity metrics when applied to state-transitions with
masked actions, i.e. multimodality (red curve) and
non-masked actions, i.e. unimodality (blue curve).
Figure 6: Example of 8, 64x64x3 coinrun input states
(first row) and their respective VAE reconstructions (sec-
ond row).
All values shown are averages of 10 evaluation runs.
At a first glance, it is already apparent that all 4 met-
rics MCE, WAKLD, JSD and SEMD show the ex-
pected behaviour: Lower metric values in the case of
unimodality and higher values in the case of multi-
modality. Note here, that it is not possible to com-
pare the absolute values between the different metrics.
What is of interest, from the perspective of building
a reliable multimodality detector, is the distance be-
tween unimodal values and multimodal values of a
single metric. If there is no overlap, and reported val-
ues of multimodal data are consistently above values
of unimodal data, a reliable differentiation is possi-
ble. For the WAKLD and JSD metrics, the distance
of unimodal and multimodal values increases along
the number k of mixture components (X-Axis), with
only minor drops. The MCE and SEMD metrics are
not as consistent when using a low component count.
Here, the reported multimodality values (red curves
in Figure 7) fluctuate strongly for component counts
of k < 10. In the case of the MCE metric, further in-
creasing the number of components does not increase
the multimodality value as much, when compoared to
the other metrics. This results in a more or less con-
stant distance between the unimodal and multimodal
curve for k > 10.
Concerning the overlap of unimodal and multi-
modal metric values, the MCE and JSD metrics per-
form best. Here, no overlap of the curves is present
for any number of components used. The WAKLD
and SEMD metrics do not perform as well here. For
WAKLD, the multimodal values only rise above the
unimodal ones for a component count k > 6. For
SEMD, the metric behaviour is strongly fluctuating,
and multimodal values only reliably lie above the uni-
modal ones for a component count k > 5. In the cases
where the curves overlap, it would not be possible to
reliably differentiate multimodality from unimodal-
ity. The consequence of this is that it would not be
possible to construct a reliable multimodality detec-
tor based on a combination of MDN networks of this
size and SEMD or WAKLD for multimodality quan-
tification. Overall, it is apparent that using a larger
component count leads to a more reliable differentia-
tion for all evaluated metrics.
Quantifying Multimodality in World Models
373

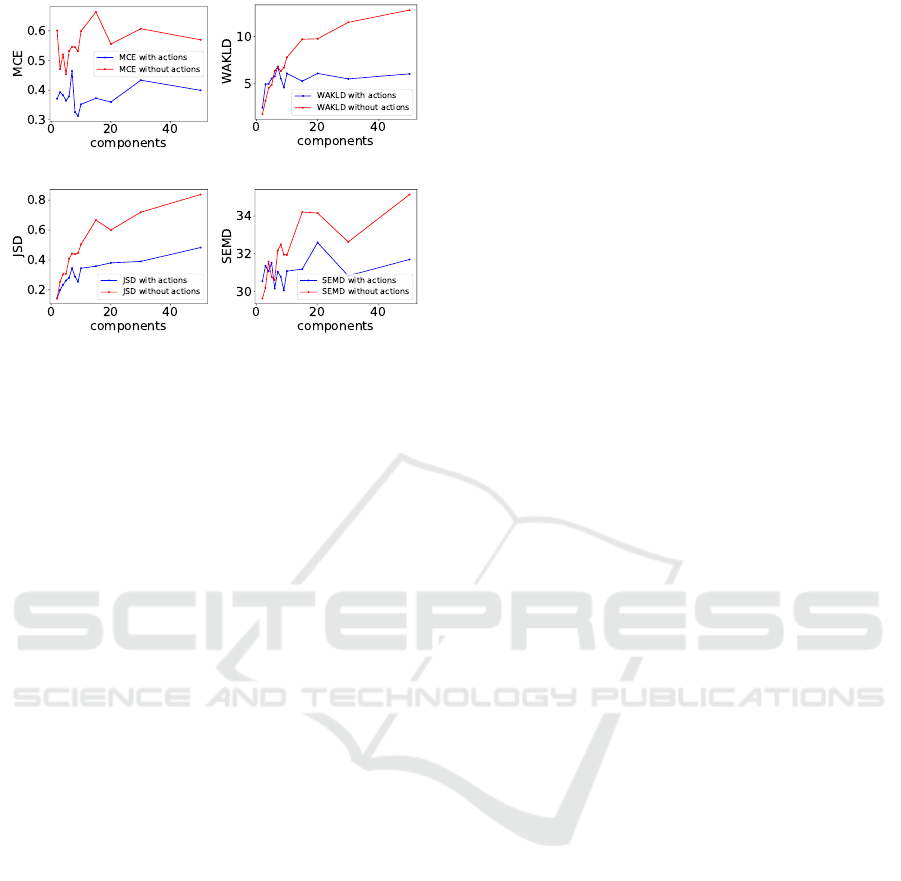
(a) MCE.
(b) WAKLD.
(c) JSD. (d) SEMD.
Figure 7: Comparison of the multimodal uncertainty met-
rics. Blue curves show computed values on the unimodal
data, while red curves show values of the multimodal data.
All values are averages of 10 evaluation runs.
7 DISCUSSION
In this work, we presented a first approach for tack-
ling the challenge of detecting multimodality in world
models. As model based reinforcement learning in-
creasingly gains practical relevance, not least through
the development of methods like world models, ap-
proaches and metrics like the ones evaluated in this
work, become of high relevance for the development
of reliable and safe RL systems. Our evaluation re-
sults showed that it is possible to detect multimodal
state-transitions and differentiate them from unimodal
ones, by applying multimodality metrics on the MDN
network of a world model architecture. The metrics
we newly introduced in this work, MCE and WAKLD
both performed well, allowing for a reliable differen-
tiation when using a mixture component count k > 6.
Using the symmetric divergence measure JSD turned
out to produce the most consistent differentiation be-
tween unimodal and multimodal data for any num-
ber of components used. On the other hand, the ap-
plication of SEMD, which is based on the Wasser-
stein metric, needs extra care, as in cases where a low
amount of mixture components is used, the reported
values fluctuated strongly. As a consequence, no reli-
able multimodality detection would be possible here.
As a next step, we plan to use the developed ap-
proach and metrics to construct a complete multi-
modal state-transition one-class classificator. It would
also be interesting to further develop variants of the
Wasserstein based SEMD as well as the WAKLD
metric, with the goal of improving the metrics for
MDNs with low component count.
REFERENCES
Amodei, D., Olah, C., Steinhardt, J., et al. (2016).
Concrete problems in ai safety. arXiv preprint
arXiv:1606.06565.
Bishop, C. (1994). Mixture density networks. Workingpa-
per, Aston University.
Brando, A. (2017). Mixture density networks (mdn) for
distribution and uncertainty estimation. Report of the
Master’s Thesis: Mixture Density Networks for distri-
bution and uncertainty estimation.
Cobbe, K., Hesse, C., Hilton, J., and Schulman, J. (2019).
Leveraging procedural generation to benchmark rein-
forcement learning. arXiv preprint arXiv:1912.01588.
Friedman, J. and Fisher, N. (1999). Bump hunting in high-
dimensional data. Statistics and Computing, 9.
Ha, D. and Schmidhuber, J. (2018). World models. CoRR,
abs/1803.10122.
Huber, P. J. (1992). Robust estimation of a location param-
eter. In Breakthroughs in statistics. Springer.
Kendall, A. and Gal, Y. (2017). What uncertainties do we
need in bayesian deep learning for computer vision?
arXiv preprint arXiv:1703.04977.
Lin, J. (1991). Divergence measures based on the shannon
entropy. IEEE Transactions on Information Theory,
37(1).
Makansi, O., Ilg, E., C¸ ic¸ek,
¨
O., and Brox, T. (2019). Over-
coming limitations of mixture density networks: A
sampling and fitting framework for multimodal future
prediction. CoRR, abs/1906.03631.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, et al.
(2015). Human-level control through deep reinforce-
ment learning. nature, 518(7540).
Osband, I., Aslanides, J., and Cassirer, A. (2018). Ran-
domized prior functions for deep reinforcement learn-
ing. In Advances in Neural Information Processing
Systems, volume 31. Curran Associates, Inc.
Polonik, W. and Wang, Z. (2010). Prim analysis. J. Multi-
var. Anal., 101.
Schrittwieser, J., Antonoglou, I., Hubert, T., et al. (2020).
Mastering atari, go, chess and shogi by planning with
a learned model. Nature, 588(7839).
Sedlmeier, A., Gabor, T., Phan, T., et al. (2020a).
Uncertainty-based out-of-distribution classification in
deep reinforcement learning. In Proceedings of the
12th International Conference on Agents and Artifi-
cial Intelligence - Volume 2: ICAART,. SciTePress.
Sedlmeier, A., M
¨
uller, R., Illium, S., and Linnhoff-Popien,
C. (2020b). Policy entropy for out-of-distribution
classification. In Artificial Neural Networks and Ma-
chine Learning – ICANN 2020, Cham.
Silver, D., Hubert, T., Schrittwieser, J., et al. (2018). A
general reinforcement learning algorithm that mas-
ters chess, shogi, and go through self-play. Science,
362(6419).
Vinyals, O., Babuschkin, I., Czarnecki, W. M., et al. (2019).
Grandmaster level in starcraft ii using multi-agent re-
inforcement learning. Nature, 575(7782).
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
374