Usage of Stacked Long Short-Term Memory for Recognition of 3D

Analytic Geometry Elements

Anca-Elena Iordan

Department of Computer Science, Technical University of Cluj-Napoca, Baritiu 26-28, Cluj-Napoca, Romania

Keywords:

Knowledge Acquisition, Supervised Learning, Stacked LSTM, Geometry.

Abstract:

For accomplish automatic solving, the capacity to comprehend problems of 3D analytic geometry formulated

in natural language is a laborious and stimulating open research theme. For this reason, this research work

attempts the achievement of a parser compounded of two important parts: the parsing module and the learning

module. The accomplishment of the parsing module requires the design of a method for engendering the series

of actions required to acquire the UCCA graph corresponding with a phrase from a 3D analytic geometry

problem. In order to design the learning module, is used a recurrent neural network of the Stacked Long

Short-Term Memory category, thereby being realized an automatic parsing system. To achieve this goal, the

proposed novel solution is accomplished through the usage of Python programming language.

1 INTRODUCTION

Currently there are several software used for the auto-

matic solution of geometry problems (Botana et al.,

2015; Iordan et al., 2010), but they accept the hy-

pothesis and the conclusion in a speciﬁc format. Im-

proving them would mean that the automatic solution

would start from the statement of the geometry prob-

lem in natural language.

Most systems in the Natural Language Text Pro-

cessing (Nadkarni et al., 2011; Viani et al., 2021) ca-

tegory take text expressed in natural language and aim

to transform it into a structured format. Parsing accu-

racy has been strongly inﬂuenced by statistical parsers

(Bose et al., 2020; Du et al., 2020).

Due to the many methods of expression in natural

language and the complexity of vocabulary, it is prac-

tically impossible to develop a deterministic parsing

system (Borsotti et al., 2021). For this reason, proba-

bilities are used in the design of parsers to predict

translation steps. Machine learning algorithms (Cz-

ibula et al., 2013) have had a strong inﬂuence in the

development of statistical parsing systems.

Statistical methods need the most accurate predic-

tion of probability distributions, and, by using ma-

chine learning algorithms (Balyan et al., 2020; Jain

et al., 2021), it is learned from the training data set,

thus increasing the accuracy of predictions.

https://orcid.org/0000-0001-9853-7102

The most important semantic representations are

AMR and UCCA. Abstract Meaning Representation,

abbreviated AMR (Banarescu et al., 2013), is a repre-

sentation of natural language text that uses a structure

with labeled graph to store information. A common

feature between AMR and syntactic representations is

that the vertices in the AMR graph do not contain all

the words from the sentence. The edges between the

nodes are labeled and are used to identify the relation-

ships between concepts.

Universal Conceptual Cognitive Annotation, ab-

breviated UCCA (Hershcovich et al., 2017), is a new

approach that seeks to abstract syntactic constraints

in order to obtain a grammatical representation, us-

ing oriented acyclic graphs (Chen and Huo, 2021) for

information storage. Through this representation the

text expressed in natural language is transformed into

a structured and uniform form, thus allowing easier

processing of information.

UCCA graphs contain units that encapsulate

meaning in terminal vertices, being seen as a co-

llection of scenes. Each word in the input phrase is

mapped to a terminal vertex, and the rest of the ver-

tices in the graph are used to identify the dependen-

cies between them. The relationships between the el-

ements of the graph are marked by edge labels so that

the edge label indicates the role of the destination ver-

tex in the formation of the parent vertex semantics.

Iordan, A.

Usage of Stacked Long Short-Term Memory for Recognition of 3D Analytic Geometry Elements.

DOI: 10.5220/0010898900003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 745-752

ISBN: 978-989-758-547-0; ISSN: 2184-433X

745

2 PARSING SYSTEM

OBJECTIVES

The main objective of this research work is to develop

a transition-based parser (Yang and Deng, 2020) that,

for a 3D analytic geometry problem expressed in nat-

ural language (English language), provides the appro-

priate UCCA graph representation with the highest

possible predictive accuracy. To achieve this goal, the

following steps will be followed:

• Data extraction - The ﬁrst step in parsing is to ex-

tract the relevant information from the dataset in-

stances and store it in the data structures that will

be used in the following steps.

• Generating of the actions sequence - It involves

the development of an algorithm capable of gen-

erating the sequence of actions to be applied to

obtain the representation of UCCA graph as input

data.

• Evaluating the correctness of the strategy for gen-

erating the sequence of actions - Correctness as-

sessment metrics will be generated for action se-

quence generation strategies.

• Development of a pattern for parsing - To allow

automatic parsing of sentences it is necessary to

form a pattern by applying a learning procedure.

• Pattern evaluation - In order to be able to evalu-

ate the performance of the obtained model, it is

necessary to use some metrics to evaluate the cor-

rectness of the predictions, such as accuracy, loss

and f1 score.

Based on the aforementioned functionalities, the

following use cases of the parser have been identiﬁed:

• Generating action sequences and associated met-

rics for a dataset - It illustrates the correctness of

the algorithm for generating the sequence of ac-

tions for a certain dataset.

• Obtaining performance metrics associated with

predicting of a test instance parsing.

• Prediction of a UCCA graph representation for a

test instance.

• Pattern training with another dataset - Due to the

fact that new datasets can be annotated in the fu-

ture, the pattern can be retrained, obtaining both

performance metrics for training and testing.

3 RELATED WORKS

Understanding of 3D analytic geometry problems de-

scribed in natural language is a signiﬁcant stage of

several automatic solvers (Seo et al., 2015; Wang and

Su, 2015). Developing automated solutions to 3D an-

alytic geometry problems is a complicated research

problem because it is a base technology in build-

ing intelligent education systems that guide learning

(Aleven et al., 2016). Using a new neural network de-

sign, in paper (Jayasinghe and Ranathunga, 2020) it

was introduced a two-step memory network used in

process of deep semantic parsing.

Other approach, presented in (Gan et al., 2019),

uses a supervised learning model based on relation

extraction for comprehension of geometry problems.

The purpose was to create a cluster of relations to em-

blematize the given geometry problem. Supervised

investigations into the collection of tested problems

presented that the suggested model obtains geometric

relationships at raised F1 scores. In paper (Quaresma

et al., 2020) was presented an adaptive ﬁltering tech-

nique for extracting geometric information.

The research work (Iordan, 2021) it is proposed

the addition of a new feature to an existing transition-

based AMR parser that constructs AMR graphs from

statement of geometry problems described in English

language. The new feature consists in explicit embed-

ding of the coreference detection into the parser.

As it results from these mentioned works, research

for understanding 3D analytic geometry problems has

made remarkable progress, but it is still an open re-

search problem.

4 DETAILED ANALYSIS OF

PROPOSED SOLUTION

The UCCA parser (Hershcovich et al., 2017)

overview may give the impression that the function-

ality of the system is trivial, but the problem of trans-

lating the text into another representation is a com-

plex one. If the parsing system is viewed as a black

box, it can be said that it receives as input data a

phrase from a 3D analytic geometry (Casillas-Perez

et al., 2021) problem expressed in English language

and forms the corresponding UCCA graph. A fea-

ture that increases the complexity of parsing is the fact

that the 3D analytic geometry problem (Iordan et al.,

2009) received at the input is not limited to a single

sentence, its size being variable. Another challenge

is the treatment of coreferences, both those explicitly

mentioned in the text and those implicit that are de-

duced from the context. Fig. 1 contains an example

of a UCCA graph containing an explicit coreference

(Kottur et al., 2018). The coreference is found at the

terminal node containing the word “ellipsoid” and in-

dicates that both scenes in the sentence have “ellip-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

746

soid” as the subject.

The proposed solution contains 2 main compo-

nents: the component responsible for parsing and the

training component of the pattern. The responsibil-

ity of the parsing component is to generate the corre-

sponding UCCA graph for a sentence belonging to the

statement of a given geometry problem given as the

input. In order to be able to perform parsing automat-

ically, by generating the sequence of actions needed

to get from an initial state to a ﬁnal state, the learning

component is required.

4.1 Parsing Component

For the development of the parsing procedure, the

syntactic parsing systems based on transitions and the

state-of-the-art parser for the representation of UCCA

graph, called TUPA (Hershcovich and Arviv, 2019),

were used as inspiration.

Figure 1: UCCA graph.

The similarity between the features of UCCA

graphs and syntactic trees allows the use of certain

common strategies between the two representations.

Unlike syntactic trees, UCCA representation can con-

tain cycles due to coreference relationships. The cur-

rent state of the solution includes the treatment of both

primary and remote relations.

The primary relations in the graph store the se-

mantic information, and through a secondary relation

the dependence between two vertices is represented,

created by a coreference from the input text. Two

types of coreferences can be found in the input data:

explicit, these being mentioned in the text, and im-

plicit ones that are not mentioned in the text and must

be deduced from the context.

4.2 Learning Component

To turn the system into an automatic parser requires

a learning procedure capable of generating the se-

quence of actions needed to get from an initial state

to a ﬁnal state with the highest possible accuracy. The

proposed learning algorithm is a supervised one, pro-

viding for the training data and the correct solution.

Conceptually, the learning component receives

as input a triplet with structure (geometry-problem,

action-sequence, UCCA-graph) and uses a recurrent

neural network to develop a pattern capable of per-

forming parsing with high action prediction accuracy.

The concepts used in the learning procedure are:

• The training set consists of the triplet of form

(geometry-problem, action-sequence, UCCA

graph), where action-sequence represents the

sequence of actions necessary to reach the UCCA

graph performance metrics associated with

predicting of a test instance parsing.

• The validation set consists of a triplet with the

same structure as the training set but is used to

evaluate the pattern from one epoch to another.

• The testing set consists of a triplet with the same

structure as the training set but is used to evaluate

the pattern performance.

• The loss function whose value associated with a

pair of shares indicates the correctness of the pre-

diction. The goal of the learning algorithm is to

minimize the loss by pattern updating.

• Weights are the parameters that initiate a speciﬁc

model and represent the values that are updated

during the learning process to minimize the value

of the loss.

4.3 Functional Description of the

Modules

In addition to the parsing component and the learning

component, several modules are required to achieve

the functionality of the proposed parsing system.

Usage of Stacked Long Short-Term Memory for Recognition of 3D Analytic Geometry Elements

747

Also, you can see the differences between the steps

taken to perform the training and testing of the parser,

respectively. The training steps represent the path to

follow to generate a pattern capable of parsing new

texts, while the test steps show the path followed to

test the performance of the pattern generated by the

training steps. The data extraction module links the

external and internal representation of the data, be-

ing responsible for extracting the information from

the data collection ﬁles. The action sequence genera-

tion module generates actions for all instances of the

dataset.

The training module uses the dataset and the infor-

mation generated in the previous components creates

a model by training the recurrent neural network. The

evaluation module is responsible for evaluating the

model by comparing the predicted graphs with those

provided and using performance metrics.

4.4 Pattern Training

Pattern training was performed using a Stacked Long

Short-Term Memory recurrent neural network. The

main feature of LSTM networks is their ability to

treat the gradient vanishing problem that accompanies

recurrent neural networks (Poon et al., 2019; Mus-

calagiu et al., 2015). LSTM cells (Laghrissi et al.,

2021) used in architecture are specializations of the

recurrent normal RNN cells. At each step, RNN cells

read input vectors a

and form a hidden state b

The state b

is obtained by applying a non-linear

sigmoid function to the input vector a

concatenated

with the hidden state of the previous step b

j-1

. Al-

though RNN cells can manage long-term dependen-

cies, their training is difﬁcult due to the exponential

increase in error. This increase is caused by the re-

peated application of a non-linear function to the data.

LSTM cells address this problem by introducing

a new dj memory state that is constructed by linearly

combining the previous state with the input signal. In

this way, LSTM cells process the input data through

three multiplicative gates, which control the propor-

tion in which the current input is transmitted to the

storage state and which proportion of the previous

j-1

storage state is forgotten. The value of the hidden

state b

is composed of the third gate by applying a

non-linear function to the value contained by the stor-

age state d

. Using this architecture, the global state

of the parser is formed using three stack-type LSTM

cells (Liu et al., 2020): one for the buffer, one for the

stack, and one for the actions list.

The parser is initiated by entering the phrase in the

buffer so that the ﬁrst word from the phrase is the ﬁrst

element in the buffer, the stack containing only the

root node and the list of applied actions is empty. At

each step, the parser state is formed by combining the

state of the LSTM cells and is used to predict the next

action, which updates the state of the cells.

The parsing process is complete when the stack

contains only the root node, the buffer is empty, and

the list of applied actions contains the history of the

applied transitions to get from the initial state to this

ﬁnal state. The parser state at a given time j is given

by the following formula:

= max(0, w



, y

, z



+ t) (1)

where w represents the weight matrix learned through

the training process, y

is the LSTM encoding of the

buffer, x

is the LSTM encoding of the stack, z

is the

LSTM encoding of the actions list, and t is the bias.

The state thus obtained is then used to calculate the

probability for each action at time j:

p(c

) =

exp(f

· s

+ h

)

∑

′

∈M

exp(f

· s

+ h

′

)

(2)

where f

represents the encoding for action c, h

the bias term associated with action c, and M is the

set of actions valid for the current state of the stack

and buffer.

5 DETAILED DESIGN AND

IMPLEMENTATION

Due to the fact that the main purpose is data process-

ing and not user interaction, the system architecture

is pipeline type. The detailed system architecture,

shown in Fig. 2, allows the visualization of the fact

that each component either modiﬁes the input data or

adds additional information to them, information that

was obtained by processing the input data. By choos-

ing this type of architecture the following characteris-

tics are obtained:

• Flexibility - Due to the fact that each componentis

isolated, the internal details can be modiﬁed with-

out inﬂuencing the other components.

• Extensibility - New features can be easily added

by changing the sequence of processing steps.

The Python programming language (Awar et al.,

2021) is used to implement the parser. Among the

libraries associated with this language, TensorFlow

(Jha et al., 2021) is used to implement the recur-

rent neural network, and MathPlotLib (Hunt, 2019)

to generate graphs based on the results obtained after

training.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

748

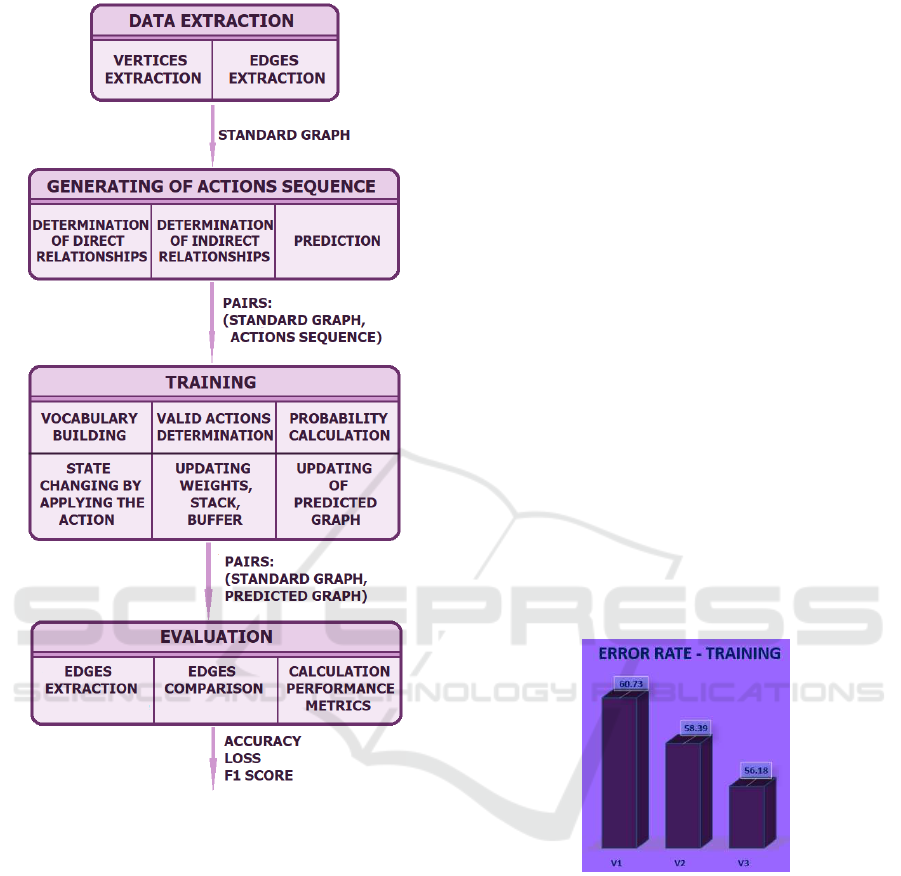
Figure 2: Detailed architecture of the parser.

6 PARSER VALIDATION

6.1 Validation of the Parsing Procedure

The parsing component aims to obtain the sequence

of actions necessary for the formation of the UCCA

graph associated with a sentence from the statement

of a problem of 3D analytic geometry. During the pro-

cess of generating the sequence of actions, the UCCA

graph is also generatedso that it can be compared later

with the standard graph of that phrase. The degree

of similarity between the two graphs (standard and

predicted) indicates the correctness of the generated

sequence of actions. Due to the fact, that the action

sequences generated by this pattern are subsequently

used to train the model, only the correct parsing were

considered, which built a graph identical to the stan-

dard one.

The process of developing the algorithm for gen-

erating the sequence of actions was composed of sev-

eral stages, and the results presented below are associ-

ated with them, dealing with the following 3 variants:

• V1 - The algorithm contains the general rules for

applying the transitions, not treating the default

coreferences or link vertices.

• V2 - To the ﬁrst variant is added the identiﬁca-

tion and treatment of the default coreferences, the

connection vertices not being treated.

• V3 - The algorithm contains both the management

of the link vertices and the treatment of the default

coreferences.

In Fig. 3 is illustrated the evolution of the perfor-

mance of the actions sequence generation mode de-

pending on the variant of the algorithm following the

application of these variants on the training data. It

can be seen the treatment of coreferences and link ver-

tices (V3) brings an improvement of 4.55% relative

to the initial variant (V1). Analogically, Fig. 4 con-

tains the evolution of the mode performance using the

testing dataset. For this set, the treatment of corefer-

ences and link vertices induces a 9.58% improvement

in performance relative to the ﬁrst variant.

Figure 3: Error rate associated with the development steps

of the algorithm for generation of the actions sequence for

the training set.

6.2 Validation of the Learning

Procedure

Within the learning component are used those in-

stances from the data set for which the sequence of

actions was generated that leads to the exact obtain-

ing of the desired graph (score f1 equal to 1) both for

training and for testing. The performance of the train-

ing procedure can be followed by the evolution of ac-

curacy and loss. Due to the fact that during the train-

ing the applied actions are the standard ones (with

Usage of Stacked Long Short-Term Memory for Recognition of 3D Analytic Geometry Elements

749

Figure 4: Error rate associated with the development steps

of the algorithm for generation of the actions sequence for

the testing set.

score f1 equal to 1), the score f1 cannot be consid-

ered a representative metric.

The notations used to identify the different tech-

niques involved are described in Table 1. By training

the T1, T2 and T3 models, the effect of the number of

cell levels on the performance was monitored, and the

T1, T4, T5 and T6 models follow the effect of chang-

ing the coding size.

Fig. 5 illustrates the accuracy and Fig. 6 illustrates

the loss for the 6 techniques in the case of the train-

ing process. The analysis of the results for the ﬁrst

3 patterns shows that the loss undergoes an increase

directly proportional to the number of levels of the

cells. At the same time, the accuracy of the train-

ing decreases for models that have a higher number of

levels. Instead, changing the coding dimension of the

elements for the last three patterns brings improve-

ments in both accuracy and loss.

Fig. 7 and Fig. 8 illustrate the performance of the

patterns on the testing set. The metrics used in this

situation are accuracy and f1 score. Some patterns

have higher prediction accuracy, but the f1 score is

limited. These patterns (T2, T3) teach the prediction

of actions sequences that do not form correct UCCA

graphs. Both the accuracy and the f1 score are im-

proved by increasing the coding size of the elements

(T4, T5, T6), the amount of information stored being

higher.

TUPA (Hershcovich and Arviv, 2019) being the

state-of-the-art parsing system for UCCA representa-

tion, the use of the f1 score as the main model evalua-

tion metric, the comparison between the parsing sys-

tems can be made. The f1 score obtained by TUPA is

62.92%, and the score of the best model developed in

this situation is 47.39%, the performance obtained be-

ing high. The result of a parsing is strongly inﬂuenced

by each precise action.

Fig. 9 illustrates the evolutions of accuracy and

Fig. 10 illustrates the evolutions of loss over the 20

training epochs. It can be seen that the loss contin-

Figure 5: Accuracy for training process.

Figure 6: Loss for training processs.

Figure 7: Accuracy for testing process.

Figure 8: F1 score for testing process.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

750

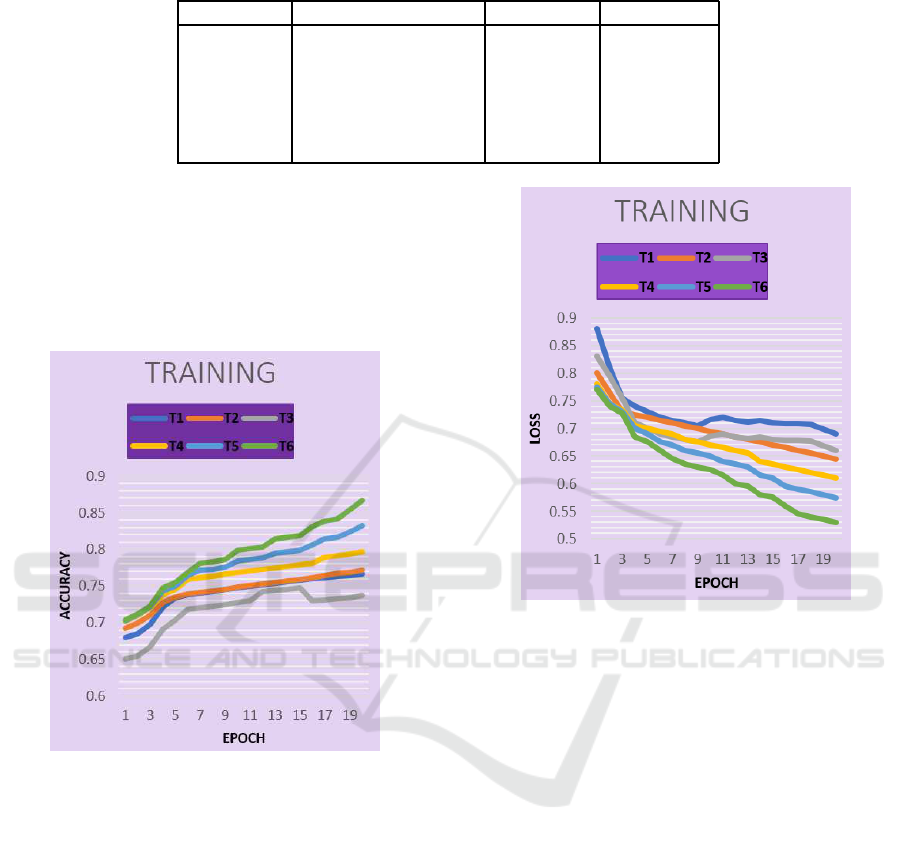
Table 1: Training Patterns.

Techniques Cells Number LSTM Levels/Cell Coding size

T1 2 1 80

T2 2 3 80

T3 2 5 80

T4 2 1 100

T5 2 1 200

T6 2 1 300

ues to decrease until the last epoch, and the accuracy

of the patterns increases from one epoch to another,

suggesting that the model improves. Thus, it is possi-

ble that the extension of the training dataset will help

to achieve a higher performance of the system, as it

would also increase the number of states learned by

it.

Figure 9: Accuracy evolution for training case.

7 CONCLUSIONS

The objective of this research work was to develop a

parsing system composed of two major components:

the parsing component and the learning component.

A parser based on transitions was deﬁned for the pars-

ing component. The development of this component

involved the construction of an algorithm for generat-

ing the actions sequence necessary to obtain a UCCA

graph. The algorithm was developed in three major

stages: identifying the general rules, treating the link

vertices, and treating the default coreferences, each

step reducing the error rate of the algorithm.

At the same time, a learning procedure based on

Stacked Long Short-Term Memory recurrent neural

networks was proposed, thus building an automatic

Figure 10: Loss evolution for training case.

parsing system. For this component it was necessary

to build the network architecture, identify the neces-

sary recurrent cells and choose the features used for

learning. The evolution of the pattern performance

according to the characteristics of the cells was fol-

lowed.

REFERENCES

Aleven, V., Roll, I., McLaren, B., and Koedinger, K. (2016).

Help helps, but only so much: Research on help with

intelligent tutoring systems. International Journal of

Artiﬁcial Intelligence in Education, 26(1):205–223.

Awar, N., Zhu, S., Biros, G., and Gligoric, M. (2021). A

performance portability framework for python. In

Proceedings of International Conference on Super-

computing, pages 467–478.

Balyan, R., McCarthy, K., and McNamara, D. (2020). Ap-

plying natural language processing and hierarchical

machine learning approaches to text difﬁculty classiﬁ-

cation. International Journal of Artiﬁcial Intelligence

in Education, 30(3):337–370.

Banarescu, L., Bonial, C., Cai, S., Georgescu, M., Grif-

ﬁtt, K., Hermjakob, U., Knight, K., Koehn, P., Palmer,

M., and Schneider, N. (2013). Abstract meaning rep-

Usage of Stacked Long Short-Term Memory for Recognition of 3D Analytic Geometry Elements

751

resentation for sembanking. In Proceedings of 7th

Linguistic Annotation Workshop and Interoperability

with Discourse, pages 178–186.

Borsotti, A., Breveglieri, L., Reghizzi, S. C., and Morzenti,

A. (2021). A deterministic parsing algorithm for

ambiguous regular expressions. Acta Informatica,

58(3):195–229.

Bose, R., Vashishtha, S., and Allen, J. (2020). Improving

semantic parsing using statistical word sense disam-

biguation. In Proceedings of 34th AAAI Conference

on Artiﬁcial Intelligence, pages 13757–13758.

Botana, F., Hohenwarter, M., Janicic, P., Kovacs, Z., Petro-

vic, I., Recio, T., and Weitzhofer, S. (2015). Auto-

mated theorem proving in geogebra: Current achieve-

ments. Journal of Automated Reasonig, 55(1):39–59.

Casillas-Perez, D., Pizarro, D., Fuentes-Jimenez, D., Mazo,

M., and Bartoli, A. (2021). The isowarp: The

template-based visual geometry of isometric sur-

faces. International Journal of Computer Vision,

129(7):2194–2222.

Chen, Y. and Huo, Y. (2021). Limitation of acyclic ori-

ented graphs matching as cell tracking accuracy mea-

sure when evaluating mitosis. Progress in Biomedical

Optics and Imaging, 21.

Czibula, G., Czibula, I., and Gaceanu, R. (2013). Intelli-

gent data structures selection using neural networks.

Knowledge and Information Systems, 34(1):171–192.

Du, J., Yu, P., and Li., X. (2020). Machine’s statistical pars-

ing and human’s cognitive preference for garden path

sentences. Advances in Intelligent Systems and Com-

puting, 1152:264–271.

Gan, W., Yu, X., and Wang, M. (2019). Automatic under-

standing and formalization of plane geometry proving

problems in natural language: A supervised approach.

International Journal on Artiﬁcial Intelligence Tools,

28.

Hershcovich, D., Abend, O., and Rapport, A. (2017).

A transition-based directed acyclic graph parser for

ucca. In Proceedings of Annual Meeting of the As-

sociation for Computational Linguistics, pages 1127–

1138.

Hershcovich, D. and Arviv, O. (2019). Tupa at mrp 2019: A

multi-task baseline system. In Proceedings of Confer-

ence on Computational Natural Language Learning,

pages 28–39.

Hunt, J. (2019). Introduction to matplotlib. Advanced Guide

to Python 3 Programming, 5:35–42.

Iordan, A., Panoiu, M., Baciu, I., and Cuntan, C. (2010).

Modelling using uml diagrams of an intelligent sys-

tem for the automatic demonstration of geometry the-

orems. Wseas Transactions on Computers, 9(9):949–

959.

Iordan, A., Panoiu, M., Muscalagiu, I., , and Rob, R. (2009).

Realization of an interactive informatical system for

the quadric surfaces study. In Proceedings of 13th

International Conference on Computers, pages 205–

210.

Iordan, A. E. (2021). Automatic comprehension of geom-

etry problems using amr parser. In Proceedings of

33rd International Conference on Software Engineer-

ing and Knowledge Engineering, pages 628–631.

Jain, S., Jain, A., and Singh, S. (2021). Building a ma-

chine learning model for unstructured text classiﬁca-

tion: Towards hybrid approach. Advances in Intelli-

gent Systems and Computing, 1187:447–454.

Jayasinghe, I. and Ranathunga, S. (2020). Two-step mem-

ory networks for deep semantic parsing of geometry

word problems. Lecture Notes in Computer Science,

12011:676–685.

Jha, A., Ruwali, A., Prakash, K., and Kanagachidambare-

san, G. (2021). Tensorﬂow basics. EAI/Springer Inno-

vations in Communication and Computing, 11:5–13.

Kottur, S., Mourra, J., Parikh, D., Batra, D., and Rohrbach,

M. (2018). Visual coreference resolution in visual di-

alog using neural module networks. Lecture Notes in

Computer Science, 11219:160–178.

Laghrissi, F., Douzi, S., Douzi, K., and Hssina, B. (2021).

Intrusion detection systems using long short-term

memory (lstm). Journal of Big Data, 8(1).

Liu, Y., Li, G., , and Zhang, X. (2020). Semi-markov crf

model based on stacked neural bi-lstm for sequence

labeling. In Proceedings of IEEE 3rd International

Conference of Safe Production and Informatization,

pages 19–23.

Muscalagiu, I., Popa, H., and Negru, V. (2015). Improving

the performances of asynchronous search algorithms

in scale-free networks using the nogood processor

technique. Computing and Informatics, 34(1):254–

274.

Nadkarni, P., Ohno-Machado, L., and Chapman, W. (2011).

Natural language processing: an introduction. Journal

of the American Informatics Association, 18(5):544–

551.

Poon, H. K., Yap, W. S., Tee, Y. K., Lee, W. K., and Goi, B.

(2019). Hierarchical gated recurrent network with ad-

versarial and virtual adversarial training on text clas-

siﬁcation. Neural Networks, 119:299–312.

Quaresma, P., Santos, V., Graziani, P., and Baeta, N. (2020).

Taxonomies of geometric problems. Journal of Sym-

bolic Computation, 97:31–55.

Seo, M., Hajishirzi, H., Farhadi, A., Etzioni, O., and Mal-

colm, C. (2015). Solving geometry problems: Com-

bining text and diagram interpretation. In Proceedings

of Empirical Methods in Natural Language Process-

ing, pages 1466–14768.

Viani, N., Botelle, R., Kerwin, J., Yin, L., Patel, R., Stew-

art, R., and Velupillai, S. (2021). A natural language

processing approach for identifying temporal disease

onset information from mental healthcare text. Scien-

tiﬁc Reports, 11(1).

Wang, K. and Su, Z. (2015). Automated geometry theorem

proving for human readable proofs. In Proceedings

of International Conference on Artiﬁcial Intelligence,

pages 1193–1199.

Yang, K. and Deng, J. (2020). Strongly incremental con-

stituency parsing with graph neural networks. Ad-

vances in Neural Information Processing Systems, 20.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

752