Post Quantum Cryptography Analysis of TLS Tunneling on a

Constrained Device

Jon Barton, William J. Buchanan

, Nikolaos Pitropakis

, Sarwar Sayeed

and Will Abramson

Blockpass ID Lab, School of Computing, Edinburgh Napier University, Edinburgh, U.K.

Keywords:

Post Quantum Cryptography, Cryptography, IoT, R-PI.

Abstract:

Advances in quantum computing make Shor’s algorithm for factorising numbers ever more tractable. This

threatens the security of any cryptographic system which often relies on the difﬁculty of factorisation. It also

threatens methods based on discrete logarithms, such as with the Difﬁe-Hellman key exchange method. For a

cryptographic system to remain secure against a quantum adversary, we need to build methods based on a hard

mathematical problem, which are not susceptible to Shor’s algorithm and create Post Quantum Cryptography

(PQC). While high-powered computing devices may be able to run these new methods, we need to investigate

how well these methods run on limited powered devices. This paper outlines an evaluation framework for

PQC within constrained devices, and contributes to the area by providing benchmarks of the front-running

algorithms on a popular single-board low-power device. It also introduces a set of ﬁve notions which can be

considered to determine the robustness of particular algorithms.

1 INTRODUCTION

Public key (asymmetric) encryption methods are

fundamental to the security of many digital sys-

tems. While symmetric methods, such as AES and

ChaCha20, provide conﬁdentiality, it is public key

methods that often provide digital signing and key ne-

gotiation. The three most widely used methods are

RSA, Elliptic Curve and ElGamal. The robustness of

cryptography depends on strong mathematical calcu-

lations that are impractical to achieve without the legit

cryptographic key. A difﬁcult calculation may take

years for powerful systems to achieve. Peter Shor,

though, deﬁned a quantum algorithm for integer fac-

torization that runs in polynomial time (Shor, 2003).

With the advent of quantum computers, most of the

existing public key methods will be cracked within

a reasonable time limit (Buchanan and Woodward,

2017). There are several methods deﬁned for quan-

tum robust cryptography including:

• Lattice-based Cryptography. This classiﬁcation

shows great potential and is leading to new cryp-

tography methods, such as for fully homomorphic

encryption, and code obfuscation.

https://orcid.org/0000-0003-0809-3523

https://orcid.org/0000-0002-3392-9970

https://orcid.org/0000-0002-9164-7672

• Code-based Cryptography. This classiﬁcation

was created in 1978 with the McEliece cryptosys-

tem (McEliece, 1978) but has barely been used in

real applications.

• Multivariate Polynomial Cryptography. This

classiﬁcation involves the difﬁculty of solving

systems of multivariate polynomials over ﬁnite

ﬁelds. Unfortunately, many of the methods that

have been proposed have already been broken

(Buchanan and Woodward, 2017).

• Hash-based Signatures. This classiﬁcation in-

volves creating random private keys and then

hashing these into hash trees. The drawback is

that a signer needs to keep a track of all of the

messages that have been signed, and that there is

a limit to the number of signatures that can be pro-

duced.

The National Institute of Standards and Technology

(NIST) runs PQC Standardization competition to im-

prove the standards to incorporate PQC. It expects to

issue the standardization papers by 2024. This pa-

per focuses on the coverage of the important meth-

ods that could be used within PQC, and in their eval-

uation around the TLS handshaking process. It in-

cludes measurements of seven key exchange methods

and ﬁve signature methods. The benchmarking tests

are performed within the ARMv8 64-bit architecture

Barton, J., Buchanan, W., Pitropakis, N., Sayeed, S. and Abramson, W.

Post Quantum Cryptography Analysis of TLS Tunneling on a Constrained Device.

DOI: 10.5220/0010903000003120

In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 551-561

ISBN: 978-989-758-553-1; ISSN: 2184-4356

551

(aarch64), speciﬁcally a Raspberry Pi 3B+ running

openSUSE, and the open-source C-library liboqs was

used to provide statistically meaningful (n > 30) sam-

ples.

The main contributions of this paper can be sum-

marised, as follows:

• It brieﬂy analyses the notable methods that are es-

sential within the Post Quantum Cryptography.

• It provides a comparison of different KEM works

to measure the key exchange. Besides, this pa-

per provides a comparison of various signature ap-

proaches.

• It also introduces a set of ﬁve notions, which can

be leveraged to determine the robustness of a par-

ticular algorithm.

2 METHODOLOGY

2.1 Open Quantum Safe Project

The Open Quantum Safe project (OQS,

https://openquantumsafe.org/) is an open-source

project aimed at making it easier to test new post-

quantum algorithms (Stebila and Mosca, 2017).

Part of that provision is a C-library liboqs which

is available from Github (https://github.com/open-

quantum-safe/liboqs). The library has some

post-quantum algorithms in place.

2.1.1 Coverage

The stated aim of the OQS project team is to pro-

vide implementations of every algorithm in the NIST

round 2 competition. Tables 1 and 2 show which ones

are in the latest master branch of liboqs, at the time

of writing. Each cipher comes with parameter sets,

which vary according to the NIST security level that

is intended.

Within the last round (Round 3), NIST have de-

ﬁned the following for standardization for public-

key encryption and key exchange: Classic McEliece;

CRYSTALS-KYBER (Lattice); NTRU (Lattice); and

SABER (Lattice). For digital signatures, the ﬁnal-

ists are: CRYSTALS-Dilithium (Lattice); FALCON

(Lattice); and Rainbow (Oil and Vinegar). These are

deﬁned as the ﬁnalists, and a winner will be chosen

from these, but because CRYSTALS-Kyber, NTRU,

and Saber are lattice methods, NIST only wants one

winner from a lattice technique. So it has drawn up

a list for an alternative of: BIKE; FrodoKEM; HQC;

NTRU Prime; and SIKE for KEMs. For digital sig-

natures, CRYSTALS-Dilithium and FALCON are lat-

tice methods, so an alternative list includes: GeMSS;

Picnic; and SPHINCS+. NIST thus wants to guard

against lattice methods being cracked in the future,

and thus would like an alternative method as a backup.

2.1.2 OQS Benchmarks

liboqs has built-in benchmarking functions for both

key encapsulation and signatures. For each cipher,

these perform key operations for a set interval (de-

fault 3 s) and then provide the arithmetic mean and

standard deviation for the time and the CPU clock cy-

cles.

2.2 TLS 1.3

TLS 1.3 reduces latency as it comprises only one

round trip, whereas TLS 1.2 consists of three rounds.

The key encapsulation and signature schemes come

together in the TLS protocol. To see how, we brieﬂy

outline the latest version, 1.3.

2.2.1 Protocol Outline

When a client initiates a connection to a server, there

are three main things that they wish to establish. First,

how are they to continue to communicate in secret;

which cipher are they going to use? Second, what is

the secret that is to be used? Third, is the server whom

it claims to be?

One feature of TLS 1.3 is that it uses an HMAC-

based key derivation function (HKDF) to generate the

keys from seeds. For TLS 1.3 we need the cipher,

together with the hash function, the key exchange

mechanism, and the signature scheme for authentica-

tion. RSA-based key exchanges were removed from

TLS 1.3 due to security concerns. The danger is that

where encrypted trafﬁc has been stored, a successful

attempt to break the RSA scheme used, in the future,

would allow that trafﬁc to be decrypted.

2.2.2 TLS Benchmarks

There is a branch of the OpenSSL project into which

liboqs has been integrated. This allows us to measure

the time for a TLS handshake, as follows. Two con-

strained devices are linked on a simple network. One

acts as a server (OpenSSL s server), the other as the

client (OpenSSL s client). For a given set of parame-

ters, the client establishes a connection to the server,

and then terminates. This is performed 50 times in a

row, and measured with the ‘perf’ command, yielding

a good approximation of the mean time to perform the

TLS handshake.

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

552

Table 1: NIST Round 2: Key Exchange By Type.

Underlying Variant Protocol In liboqs?

Lattice

LWE

Crystals-Kyber 

FrodoKEM 

LAC ×

Saber 

Three Bears ×

RLWE

NewHope 

Round5 ×

NTRU

NTRU 

Prime NTRU ×

Code-Based

Goppa

Classic McEliece ×

NTS-KEM ×

Moderate Density Parity-Check BIKE 

Hamming Quasi-Cyclic HQC ×

Low Density Parity-Check LEDACrypt ×

Low Rank Parity Check Rollo ×

Ideal and Gabidulin RQC ×

Isogeny Supersingular SIKE 

Table 2: NIST Round 2: Signature By Type.

Underlying Variant Protocol In liboqs?

Lattice

LWE Crystals-Dilithium 

RLWE qTESLA 

NTRU Falcon ×

Hash-based

Stateless SPHINCS+ 

Zero-Knowledge Picnic 

Multivariate

UOV

LUOV ×

Rainbow 

HFEv- GeMSS ×

Pure MQ MQDSS 

There are two dimensions under investigation.

One is the impact of using different cipher suites to

sign and verify the certiﬁcates. For this, the key ex-

change mechanism is held constant. The other is the

impact of varying the cipher suite used to perform the

key exchange. For this, the signing cipher is held

constant. The relevant data from the output of perf

are stripped out and normalised using simple bespoke

scripts before being presented.

2.3 The PQC/IoT Laboratory

2.3.1 Hardware

The hardware in the laboratory is as follows.

• The constrained devices are the Raspberry Pi 3B+

with a 1.2 GHz quad core ARMv8 (A53) 64-bit

processor, 1 GB RAM and 32 GB storage.

• Where needed, a simple standalone network is

created using a home-based router (TPLink TD-

W9970) as a switch. The wired network LAN

provision is 4 x 10/100 Mbps. In a real-life,

IoT scenarios are likely to use low power wire-

less communication technologies, such as Zig-

Bee, BLE, LoRa, SigFox, and so on.

• Access to the devices is over SSH from a laptop.

• The desktop machine for compiling aarch64 code

is an iMac with 3 GHz Intel i5, with 6 cores.

2.3.2 Software

• In order to save time, a cross-compiler for

ARMv8 is built and run on a more powerful desk-

top machine, running macOS 10.14.5. The cross-

compiler (Crosstool-NG) is built with gcc 8.3.0.

The aarch64 code is also compiled with gcc 8.3.0.

• liboqs and OpenSSL with liboqs, are compiled for

the ARMv8 (aarch64).

• liboqs requires a 64-bit operating system. The de-

fault operating system for a Raspberry Pi is Rasp-

bian, which is currently 32-bit only. We choose

OpenSUSE (Leap 15.0, JeOS) since it appears to

be the best maintained of the 64-bit Linux-based

systems for the ARMv8 available.

3 RESULTS

In this paper, we present our results and compare

them, where possible, with other benchmarks from

the literature. First, we look at the key exchange

mechanisms. That is followed by the results for the

signature schemes. We then look at the TLS hand-

shake which combines both exchange mechanisms

and signatures. Finally, we offer some considerations

Post Quantum Cryptography Analysis of TLS Tunneling on a Constrained Device

553

Post Quantum Cryptography Analysis of TLS

Tunneling On a Constrained Device

Jon Barton, William J Buchanan, Nikolaos Pitropakis, Sarwar Sayeed, Will Abramson

Blockpass ID Lab, School of Computing, Edinburgh Napier University, Edinburgh, UK.

0 0.5 1 1.5

NewHope

1024-CCA

Kyber

768

Saber

1.84

1.32

0.84

1.53

1.08

0.76

1.04

0.89

0.65

Time (ms)

Keygen

Encaps

Decaps

Figure 1: KEM Meantimes: Top Performing Algorithms at

Level 3.

Post Quantum Cryptography Analysis of TLS

Tunneling On a Constrained Device

Jon Barton, William J Buchanan, Nikolaos Pitropakis, Sarwar Sayeed, Will Abramson

Blockpass ID Lab, School of Computing, Edinburgh Napier University, Edinburgh, UK.

0 20 40 60 80 100 120

BIKE

1-L3

Frodo

976-AES

Frodo

976-SHAKE

NTRU-HPS

4096-821

127

87.6

61.8

30.3

87.7

62.2

8.84

24.5

46.7

119

Time (ms)

Keygen

Encaps

Decaps

Fig. 1. KEM Meantimes: 2nd Division Algorithms at Level 3

Figure 2: KEM Meantimes: 2nd Division Algorithms at

Level 3.

Post Quantum Cryptography Analysis of TLS

Tunneling On a Constrained Device

Jon Barton, William J Buchanan, Nikolaos Pitropakis, Sarwar Sayeed, Will Abramson

Blockpass ID Lab, School of Computing, Edinburgh Napier University, Edinburgh, UK.

0 1,000 2,000 3,000

SIKE-p610

3,320

3,300

1,790

Time (ms)

Keygen

Encaps

Decaps

Fig. 1. KEM Meantimes: 3rd Division Algorithm at Level 3

Figure 3: KEM Meantimes: 3rd Division Algorithm at

Level 3.

which aim to help with choosing a reliable crypto-

graphic algorithm.

3.1 Key Exchange Mechanisms

To gain an appreciation for the different systems,

we chart the public and private key sizes in Ta-

ble 3. These are gleaned from the second round sub-

missions for: Crystals-Kyber (Avanzi et al., 2019),

FrodoKEM (Alkim et al., 2019), SABER (D’Anvers

et al., 2019), NewHope (Poppelmann et al., 2019),

NTRU (Chen et al., 2019a), BIKE (Aragon et al.,

2019) and SIKE (Jao et al., 2019).

In order that the numbers are not overwhelming,

we restrict the view in several ways. First, we choose

the parameter set which has been provided for achiev-

ing level three security, which is equivalent to break-

ing AES-256, or alternatively 128 bits of quantum se-

curity. Second, where IND-CPA and IND-CCA ver-

sions are speciﬁed, we restrict the view to IND-CCA.

Third, we pick the ﬁrst BIKE model as representative

of that family of three implementations. Lastly, we

only list those which currently have a representation

in liboqs. These restrictions overlook many subtleties,

but nevertheless yield insight.

With respect to speed, the candidates fall into

three divisions, with lattice-based solutions being the

front-runners. In the ﬁrst division are Saber, Ky-

ber and NewHope. Saber has both a reasonable key

size and is performing its operations sub-millisecond.

The second division is made up of Frodo, NTRU and

code-based BIKE. Finally, SIKE is in a division of its

own; whilst having a reasonable key size, it is taking

over 3 full seconds for encapsulating or decapsulat-

ing. These divisions are compared in Figures 1, 2 and

3.1.1 Comparison with Other Work

Table 4 shows the results from three other papers

to measure the key exchange for post-quantum algo-

rithms. The listed speed is the speed of an encapsula-

tion followed by a decapsulation. The table presents

the best attempt to provide a like-for-like comparison

between the various works. The main point is that the

benchmarking is conducted under differing assump-

tions. A brief outline of the works illustrates the dif-

ferences.

Seo et al. (Seo et al., 2019) implement a

highly optimised version of SIKE, written in assem-

bly for the aarch64 instruction set, and tested on an

ARMv8 (A53) running 64-bit code at 1.536 GHz. For

SIKEp610 (NIST level 3), the reported clock cycles

(crudely) equate to 303 ms. An et al. (An et al., 2018)

measure the performance of the protocols then avail-

able in liboqs: Frodo, BCNS, NewHope, MSrln, Ky-

ber, NTRU, McBits, IQC and SIDH. The tests are on

an Intel i7-5500 at 2.4 GHz, two cores, with 16 GB

RAM. For Kyber and Frodo, they use non-standard

parameter sets for which the post-quantum security

level is unclear.

Malina et al. (Malina et al., 2018) test six key

exchange mechanisms; NewHope, NTRU, BCNS,

Frodo, McBits and SIDH. To do this they tweaked

liboqs to run in 32-bits, and then ran tests on (a)

an Android 6 device with Qualcomm Snapdragon

801 (4 cores) at 2.5 GHz with 2 GB RAM, and (b)

a Raspberry Pi 2, running Raspbian Strech Lite, on

an ARMv7 at 1.2 GHz, with 1 GB RAM. Karmakar

et al. (Karmakar et al., 2018) implement an optimised

Saber on an ARM Cortex-M4, with an assumed clock

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

554

Table 3: Key Exchange Submitted Public and Private Key Length (Bytes).

Underlying Variant: Protocol Parameter Set Private Public

Lattice

LWE: Saber SABER-KEM 2,304 992

LWE: Crystals-Kyber Kyber-768 2,400 1,184

LWE: FrodoKEM FrodoKEM-976 31,296 15,632

RLWE: NewHope NewHope1024 3,680 1,824

NTRU: NTRU ntruhps4096821 1,592 1,230

Code-Based MDPC: BIKE BIKE-1-CCA 6,592 6,205

Isogeny Supersingular: SIKE SIKEp610 524 462

Table 4: Comparison with Other KEM Work.

Cipher Bench Security Constrained? Speed

Level (ms)

Saber (Karmakar et al., 2018) —  18.84

Saber (Kannwischer et al., 2019) 185  98.60

Saber This Work 185  1.60

Kyber (An et al., 2018) — × 0.38

Kyber (Kannwischer et al., 2019) 164  93.39

Kyber This Work 164  2.40

NewHope (An et al., 2018) 233 × 0.23

NewHope (Malina et al., 2018) 206  2.36

NewHope (Kannwischer et al., 2019) 233  159.61

NewHope This Work 233  3.38

NTRU (An et al., 2018) — × 2.06

NTRU (Malina et al., 2018) 128  12.88

NTRU (Kannwischer et al., 2019) 128  94.69

NTRU This Work 128  32.82

Frodo (An et al., 2018) — × 9.38

Frodo (Malina et al., 2018) 130  702.12

Frodo This Work 150  175.30

SIKE (Seo et al., 2019) 192  303.00

SIKE (Kannwischer et al., 2019) 192  279,866.01

SIKE This Work 192  6,620.41

of 168 MHz. Kannwischer et al. (Kannwischer et al.,

2019) from July 2019 present a benchmarking frame-

work pqm4. They consistently benched 10 key encap-

sulation and ﬁve signature schemes on a 32-bit ARM

Cortex-M4 running at 24 MHz, with 196 kB of RAM.

Frodo-976 takes too much resource to run in this en-

vironment.

There are several other related works which are

not suitable for inclusion in Table 4, since they are

even more disparate than those included.

• (Czypek et al., 2012) looks at MQ-based systems

on an AtxMega128a1 microprocessor, running at

32 MHz, with 8 kB RAM and 128 kB storage.

• (Johansson and Strahl, 2016) compares the speed

of an RLWE cipher against classical ciphers,

when used for the key exchange during TLS hand-

shakes. Benchmarks are from an ARM Cortex-A7

running at 700 MHz with 1 GB of RAM and stor-

age of over 1 GB. They classify the classical se-

curity level at 128 bit.

• (Suomalainen et al., 2018) uses the ABSO-

LUT (Vatjus-Anttila et al., 2013) tool to test

Frodo and NewHope on simulated (a) Raspberry

Pi 2, with Broadcom BCM2836 at 900 MHz quad-

core 32-bit ARM Cortex-A7 processor with 1 GB

RAM, and (b) Raspberry Pi 3, with Broadcom

BCM2837 at 1.2 GHz quad-core 64-bit ARM

Cortex-A53, also with 1 GB RAM.

• (Crockett et al., 2019) provides extensive obser-

vations on the integration of post-quantum algo-

rithms into TLS and SSH.

Post Quantum Cryptography Analysis of TLS Tunneling on a Constrained Device

555

3.2 Signatures

For the different signature schemes, we chart the pub-

lic and private key sizes together with the signature

size, in Table 5. These are taken from the sec-

ond round submissions for: Dilithium (Ducas et al.,

2019), qTESLA (Bindel et al., 2019), MQDSS (Chen

et al., 2019c), Rainbow (Chen et al., 2019b) and

SPHINCS+ (Aumasson et al., 2019). As for key ex-

changes, we restrict the view to those parameter sets

which aim for security at NIST level 3, and only list

those which currently have a representation in liboqs.

Figures 4, 5, 6 and 7 show how they line up against

each other. There are some items which should be

taken into account with these comparisons.

QTESLA. There is a version of qTESLA which is

probably secure, but it is not yet implemented in li-

boqs and has not been tested here.

SPHINCS+. SPHINCS+ presents three sets of pa-

rameters of various sorts. First, since it is hash-based

it needs a hash function. There are three options:

Haraka, SHA256 and SHAKE256. Second, they pro-

duce a set of parameters optimized for small signa-

tures (‘s’ for small) and fast processing (‘f’ for fast).

For a given NIST level, there are therefore 12 dif-

ferent sets of parameters. We take SHA256 to be rep-

resentative.

Rainbow. The ‘compressed’ version can take the

private signature down to 64 bytes (512 bits).

Post Quantum Cryptography Analysis of TLS

Tunneling On a Constrained Device

Jon Barton, William J Buchanan, Nikolaos Pitropakis, Sarwar Sayeed, Will Abramson

Blockpass ID Lab, School of Computing, Edinburgh Napier University, Edinburgh, UK.

0 5 10 15 20 25

qTESLA

III (size)

qTESLA

III (speed)

DILITHIUM

1.24

1.25

2.14

10.8

5.38

6.76

25.1

14.5

1.84

Time (ms)

Keypair

Sign

Verify

Fig. 1. Signature Meantimes: Lattice-based at Level 3

Figure 4: Signature Meantimes: Lattice-based at Level 3.

3.2.1 Comparison with Other Work

Table 6 shows a comparison between the benchmarks

from (Kannwischer et al., 2019) and the results pre-

sented here. The speed is the total speed of a sign/ver-

ify pair.

3.3 TLS 1.3 Handshake

In our tests, varying the signature algorithm made no

difference to the size of the handshake (2041 B read,

391 B written), nor to the (wall-clock) speed of the

handshake (mean time of 0.05 s). This may be be-

cause the two PQC signature algorithms available,

Dilithium and qTESLA, are both lattice-based. One

area for further work is to examine this area in more

detail, when further algorithms are available. The

importance of the security of the signature algorithm

should not be underestimated; it ensures the authenti-

cation of the counterparty.

Table 7 shows how the size and speed of the TLS

1.3 handshake varies with the key exchange. This

shows that, as we expect from the results above, that

Saber, Crystal and NewHope are light and fast; BIKE,

Frodo and NTRU are comparable. While the hand-

shake for SIKE is the smallest of all, it takes orders of

magnitude longer.

3.3.1 Comparison with Other Work

Table 8 shows two other attempts from the literature

to measure post-quantum key exchange in TLS hand-

shakes. The same caveats apply as for the compar-

isons in Table 4.

(Bos et al., 2015). implements a RLWE cipher-

suite in OpenSSL (v1.0.1f) and benchmarks interac-

tions with an Apache webserver. The parameters they

choose aim for 128-bit security, which matches the

rationale chosen here. They provide results for re-

trieving a 1 byte payload, which is comparable with

completing a TLS handshake. One difference is that

they code with TLS 1.2, which is less efﬁcient than

TLS 1.3. The largest difference is that their devices

are not constrained: the ‘client’ machine is based

on an Intel i5 with 4 cores running at 2.7 GHz; the

‘server’ machine is an Intel Duo with 2 cores running

at 2.33 GHz.

(Bos et al., 2016). benchmarks connections to

a TLS-protected webserver for Frodo, BCNS,

NewHope and NTRU. These were run on a Google

Cloud VM (n1-standard-4), with 4 virtual CPUs at

2.6 GHz, with 15 GB of RAM. The clients were simi-

larly speciﬁed (n1-standard-32). The parameters were

aimed at 128 bits of security. Some testing was also

done on a BeagleBone Black, with an AM335x ARM

Cortex-A8 running at 1 GHz. The BeagleBone was

not running a TLS client, and there is no available

comparison on that front with this work.

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

556

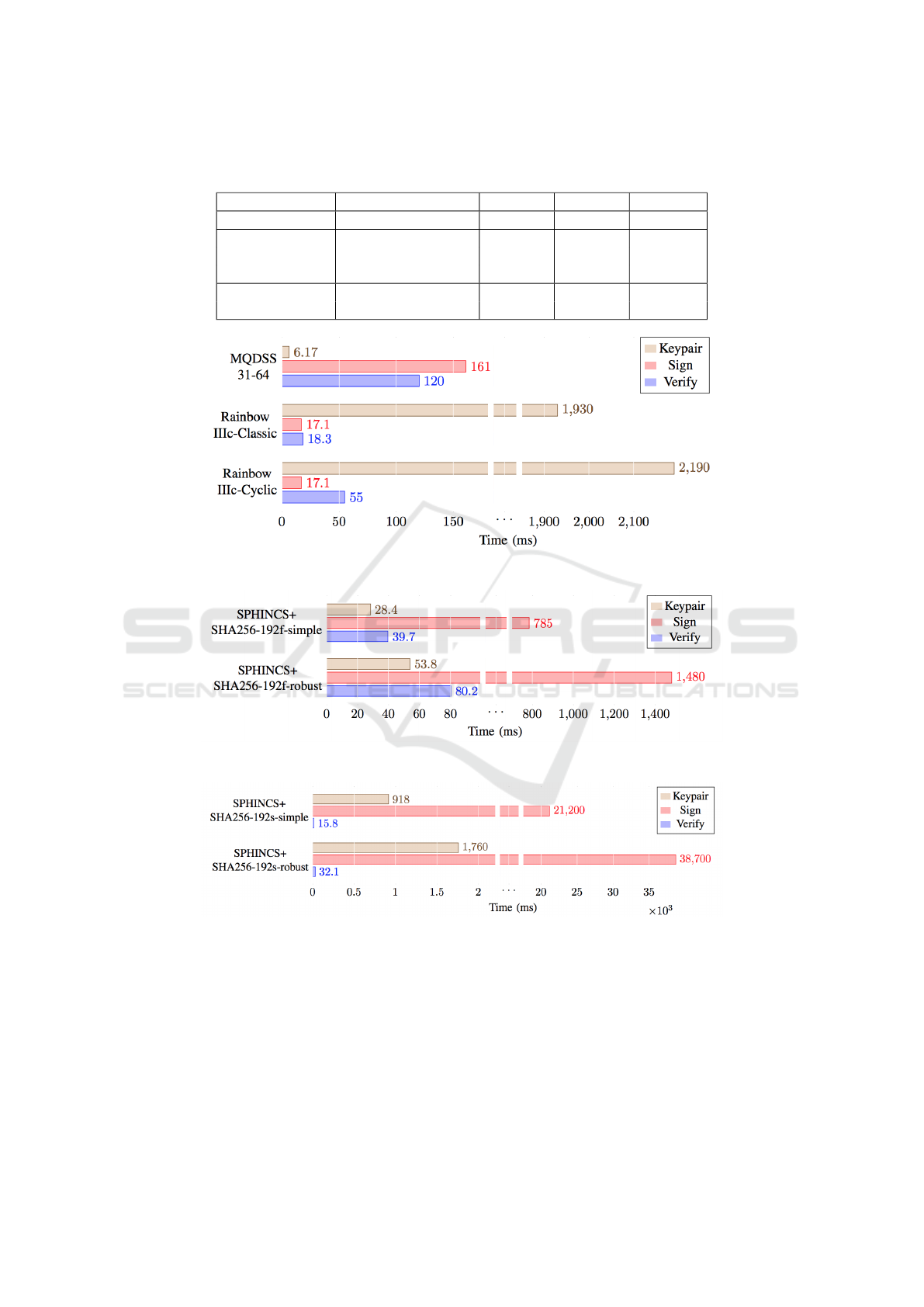
Table 5: Signature Schemes: Key and Signature Lengths (Bytes).

Underlying Parameter Set Private Public Signature

Lattice (LWE) Dilithium IV 96 1,760 3,366

Lattice (RLWE) qTESLA-III 2,368 3,104 2,848

MQDSS-31-64 24 64 43,728

Rainbow-IIIc 511.4 kB 710.6 kB 156

Rainbow-IIIc-cyclic 511.4 kB 206.7 kB 156

Hash-based

SPHINCS+-192s 96 48 17,064

SPHINCS+-192f 96 48 35,664

Figure 5: Signature Meantines: MQ-based at Level 3.

Figure 6: Signature Meantimes: SPHINCS+ ‘f’ at Level 3.

Figure 7: Signature Meantimes: SPHINCS+ SHA256 ‘s’ at Level 3.

3.4 Choosing an Algorithm

The purpose of the encryption is an important consid-

eration. Suppose the target is to verify a system up-

date for an IoT device. Then the signing will be done

by the system issuing the update; assume this is not

itself IoT. In that case the SPHINCS+ suite might be

a viable choice. The IoT device only needs to verify

the signature, which we have shown it can do sub-

second (at level 3). That may well be fast enough

for relatively infrequent system updates. On the other

hand, SIKE (SIKE-p610) would be inappropriate for

involvement in the key exchanges of TLS since the

encapsulation followed by decapsulation would add

over six seconds to the handshake. So whether an

algorithm is ‘fast enough’ will depend on the use to

which it is being put. Similar considerations will ap-

ply to the public/private key size.

Post Quantum Cryptography Analysis of TLS Tunneling on a Constrained Device

557

Table 6: Comparison with Other Signature Work.

Cipher Bench Speed (ms)

Dilithium IV

(Kannwischer et al., 2019) 485.10

This Work 0.01

qTESLA-III

(Kannwischer et al., 2019) 354.06

This Work 2.70

SPHINCS+-SHA256-192

f-sim (Kannwischer et al., 2019) 30,116.29

f-sim This Work 824,908.31

f-rob (Kannwischer et al., 2019) 57,169.86

f-rob This Work 1,558,082.26

s-sim (Kannwischer et al., 2019) 793,925.00

s-sim This Work 21,187,279.39

s-rob (Kannwischer et al., 2019) 1,433,837.19

s-rob This Work 38,682,673.41

Table 7: TLS Handshake Proﬁles by KEM.

Handshake (Bytes) Speed

Protocol Parameter Set Read Write Total (ms)

Crystals-Kyber Kyber-768 3,897 1,543 5,440 89.82

FrodoKEM FrodoKEM-976 18,553 15,991 34,544 295.81

Saber SABER-KEM 3,897 1,351 5,248 87.69

NewHope NewHope1024 5,017 2,183 7,200 88.12

NTRU ntruhps4096821 4,039 1,589 5,628 241.34

BIKE BIKE-1-CCA 7,773 5,323 13,096 199.66

SIKE SIKEp610 3,295 821 4,116 8,580.58

Table 8: Comparison with Other TLS Work.

Cipher Bench Security Level Constrained? Handshake (Bytes) Speed (ms)

NewHope (Bos et al., 2016) 206 × 5,514 13.10

RLWE (Bos et al., 2015) 82 × 10,479 54.00

NewHope This Work 233  7,200 88.12

NTRU (Bos et al., 2016) 128 × 3,691 19.90

NTRU This Work 128  5,628 241.34

Frodo (Bos et al., 2016) 130 × 24,228 20.70

Frodo This Work 150  34,554 295.81

Of the NIST key exchange ﬁnalists, there are three

main security levels (1, 3 and 5), and the key sizes for

each method is deﬁned in Table 9 (Buchanan, 2021).

It can be seen that McEliece requires relatively large

private keys, and fairly large public keys. The lattice

methods (Kyber, SABER and NTRU) offer a good

balance for key sizes and ciphertext compared with

McEliece. With digital signatures, as shown in Table

10, shows that SPHINCS+ supports the smallest key

sizes, and the largest digital signature size. The lattice

methods, again, offer a good compromise, and where

the Oil and Vinegar method (Rainbow) has fairly large

key sizes, but the smallest digital signature size.

Table 11 summarises the important elements in-

volved for the key considerations for post-quantum

cryptography. An important element is how venera-

ble the underlying mathematical problem, and where

the more cryptanalysis it has survived, the better. An-

other important element is that the method must be

NP-hard, and have a related proof with a problem-

reduction. With QROM (quantum random oracle

model)-secure, we have a proof of security in the

QROM, along with ROM (random oracle model))-

secure. The existence of such proof does not entail

security against a classical adversary, but it is taken to

be a good heuristic. ((Ducas et al., 2019, 6) conjec-

tures that whilst the theoretical details differ, security

in the ROM and security in the QROM will converge

to indicate the same level of security in practice.)

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

558

Table 9: Key sizes and ciphertext for Key exchange methods.

Method Public key (B) Private key (B) Ciphertext (B)

Kyber512 800 1,632 768

Kyber738 1,184 2,400 1,088

Kyber1024 1,568 3,168 1,568

LightSABER 672 1,568 736

SABER 992 2,304 1,088

FireSABER 1,312 3,040 1,472

McEliece348864 261,120 6,452 128

McEliece460896 524,160 13,568 188

McEliece6688128 1,044,992 13,892 240

McEliece6960119 1,047,319 13,948 226

McEliece8192128 1,357,824 14,120 240

NTRUhps2048509 699 935 699

NTRUhps2048677 930 1,234 930

NTRUhps4096821 1,230 1,590 1,230

Table 10: Key sizes and signature size for Digital Signature methods.

Method Public key (B) Private key (B) Signature (B)

Crystals Dilithium 2 1,312 2,528 2,420

Crystals Dilithium 3 1,952 4,000 3,293

Crystals Dilithium 5 2,592 4,864 4,595

Falcon 512 (Lattice) 897 1,281 690

Falcon 1024 1,793 2,305 1,330

Rainbow Level Ia 161,600 103,648 66

Rainbow Level IIIa 861,400 611,300 164

Rainbow Level Vc 1,885,400 1,375,700 204

SPHINCS+ SHA256-128 32 64 17,088

SPHINCS+ SHA256-192 48 96 35,664

SPHINCS+ SHA256-256 64 128 49,856

4 CONCLUSIONS

In terms of KEM performance, SABER is the clear

winner, executing its basic operations in under a mil-

lisecond; the TLS handshake in under 90 ms. At the

other end, SIKE’s performance makes it an unlikely

choice; the empty TLS handshake taking over 8 s. It

is true that there is at least one ﬁnely-tuned version

written in assembly which performs better.

REFERENCES

Ajtai, M. (1996). Generating Hard Instances of Lattice

Problems. Stoc.

Alkim, E., Bos, J. W., Ducas, L., Longa, P., Mironov,

I., Naehrig, M., Nikolaenko, V., Peikert, C., Raghu-

nathan, A., and Stebila, D. (2019). FrodoKEM: Learn-

ing with Errors Key Encapsulation Algorithm Speci-

ﬁcations and Supporting Documentation. Technical

report.

An, H., Lee, J., and Kim, K. (2018). Performance Evalua-

tion of liboqs in Open Quantum Safe Project ( Part I ).

pages 1–7.

Aragon, N., Barreto, P. S. L. M., Bettaieb, S., Bidoux,

L., Blazy, O., Deneuville, J.-C., Gaborit, P., Gueron,

S., Guneysu, T., Melchor, C. A., Misoczki, R., Per-

sichetti, E., Sendrier, N., Tillich, J.-P., Vasseur, V., and

Zemor, G. (2019). BIKE: Bit Flipping Key Encapsu-

lation. Technical report.

Aumasson, J.-P., Bernstein, D. J., Dobraunig, C.,

Eichlseder, M., Fluhrer, S., Gazdag, S.-L., Hulsing,

A., Kampanakis, P., Kolbl, S., Lange, T., Lauridsen,

M. M., Mendel, F., Niederhagen, R., Rechberger, C.,

Rijneveld, J., and Schwabe, P. (2019). SPHINCS+.

Technical report.

Avanzi, R., Bos, J., Ducas, L., Kiltz, E., Lepoint, T., Lyuba-

shevsky, V., Schanck, J., Schwabe, P., Seiler, G., and

Damien, S. (2019). CRYSTALS-Kyber. Technical re-

port.

Berlekamp, E. R., McEliece, R. J., and van Tilborg, H. C. A.

(1978). On the Inherent Intractability of Certain Cod-

ing Problems. IEEE Transactions on Information The-

Post Quantum Cryptography Analysis of TLS Tunneling on a Constrained Device

559

Table 11: Considerations for Certainty about Security.

Scheme Underlying Venerability (yrs) NP-hard Problem-Reduction ROM-secure QROM-secure

Saber Lattice: LWE 14



Kyber Lattice: LWE 14



Frodo Lattice: LWE 14



NewHope Lattice: RLWE 9



NTRU Lattice: NTRU 23



BIKE Code: MDPC 41



SIKE Supersingular 5

× 



Dilithium Lattice: LWE 14



qTESLA Lattice: RLWE 9



MQDSS

MQ 31



Rainbow

MQ: UOV 20



SPHINCS+ Hash: Haraka 4

— — — —

SPHINCS+ Hash: SHA256 18

— — — —

SPHINCS+ Hash: SHAKE256 7

— — — —

Notes:

a 2005 (Regev, 2009) is a revision of the original.

b 2010 (Lyubashevsky et al., 2010).

c 1996 (Ajtai, 1996).

d 1978 (McEliece, 1978) (Misoczki et al., 2013).

e 2014 (De Feo et al., 2014).

f 1988 (Matsumoto and Imai, 1988).

g 1999 (Kipnis et al., 1999).

h SPHINCS+ is no more secure than the hash it uses (Butin, 2017,

41). Haraka dates from 2015 (K

olbl et al., 2017); SHA256 from

2001 (NIST, 2002); SHAKE256 from 2012 (see (NIST, 2015)). The

notions of NP-hardness, or security in ROM do not apply directly to

hashes.

i SVP and variants have been proved NP-hard (Micciancio and Gold-

wasser, 2002). However, the systems rely on approximations which

have not (Peikert, 2016), hence no Problem Reduction.

j RLWE is NP-hard (Peikert, 2016); however, as for (i), the systems rely

on approximation problems which have not.

k The NTRU problem is not reducible to a lattice problem (Peikert, 2016,

14). However, RLWE is at least as hard as NTRU and if RLWE is hard,

then NTRU can be made secure (Peikert, 2016, 14).

l (Berlekamp et al., 1978)

m (Garey and Johnson, 1979)

n (Aragon et al., 2019, 60-1)

o (Chen et al., 2016)

p (Chen et al., 2019b, 43)

q (D’Anvers et al., 2019, 12-3)

r (Avanzi et al., 2019, 19-20)

s (Alkim et al., 2019, 31-5)

t (Poppelmann et al., 2019, 28-29)

u (Chen et al., 2019a, 30)

v (Jao et al., 2019, 41-2)

w (Ducas et al., 2019, 5-6)

x (Bindel et al., 2019, 47-8)

y (Chen et al., 2019b, 43)

ory.

Bindel, N., Akleylek, S., Alkim, E., Barreto, P. S. L. M.,

Buchmann, J., Eaton, E., Gutoski, G., Kramer, J.,

Longa, P., Polat, H., Ricardini, J. E., and Zanon, G.

(2019). qTESLA 2nd Round Submission. Technical

report.

Bos, J., Costello, C., Ducas, L., Mironov, I., Naehrig,

M., Nikolaenko, V., Raghunathan, A., and Stebila, D.

(2016). Frodo: Take off the ring! Practical, Quantum-

Secure Key Exchange from LWE. CCS’16.

Bos, J. W., Costello, C., Naehrig, M., and Stebila, D.

(2015). Post-quantum key exchange for the TLS pro-

tocol from the ring learning with errors problem. In

Proceedings - IEEE Symposium on Security and Pri-

vacy.

Buchanan, W. (2021). Ntru (nth degree truncated polyno-

mial ring) - key encapsulation mechanism (kem).

Buchanan, W. and Woodward, A. (2017). Will quantum

computers be the end of public key encryption? Jour-

nal of Cyber Security Technology, 1(1):1–22.

Butin, D. (2017). Hash-based signatures: State of play.

IEEE Security and Privacy.

Chen, C., Danba, O., Hoffstein, J., H

ulsing, A., Rijneveld,

J., Schanck, J. M., Schwabe, P., Whyte, W., and

Zhang, Z. (2019a). NTRU Round 2. Technical report.

Chen, M.-S., Ding, J., Petzoldt, A., Schmidt, D., and Yang,

B.-Y. (2019b). Rainbow: Round 2 Submission. Tech-

nical report.

Chen, M. S., H

ulsing, A., Rijneveld, J., Samardjiska, S., and

Schwabe, P. (2016). From 5-pass MQ-based identiﬁ-

cation to MQ-based signatures. In Lecture Notes in

Computer Science (including subseries Lecture Notes

in Artiﬁcial Intelligence and Lecture Notes in Bioin-

formatics).

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

560

Chen, M.-S., Hulsing, A., Rijneveld, J., Samardjiska, S.,

and Schwabe, P. (2019c). MQDSS 2nd Round Sub-

mission. Technical report.

Crockett, E., Paquin, C., and Stebila, D. (2019). Prototyping

post-quantum and hybrid key exchange and authenti-

cation in TLS and SSH.

Czypek, P., Heyse, S., and Thomae, E. (2012). Efﬁcient

implementations of MQPKS on constrained devices.

In Lecture Notes in Computer Science (including sub-

series Lecture Notes in Artiﬁcial Intelligence and Lec-

ture Notes in Bioinformatics).

D’Anvers, J.-P., Karmakar, A., Roy, S. S., and Vercauteren,

F. (2019). SABER: Mod-LWR based KEM (Round 2

Submission). Technical report.

De Feo, L., Jao, D., and Pl

ut, J. (2014). Towards quantum-

resistant cryptosystems from supersingular elliptic

curve isogenies. Journal of Mathematical Cryptology.

Ducas, L., Ducas, L., Kiltz, E., Lepoint, T., Lyubashevsky,

V., Schwabe, P., Seiler, G., and Damien, S. (2019).

CRYSTALS-Dilithium. Technical report.

Garey, M. R. and Johnson, D. S. (1979). A Guide to the

Theory of NP-Completeness.

Jao, D., Azarderakhsh, R., Campagna, M., Costello, C.,

Feo, L. D., Hess, B., Jalali, A., Koziel, B., LaMac-

chia, B., Naehrig, M., Pereira, G., Soukharev, V., and

Urbanik, D. (2019). Supersingular Isogeny Key En-

capsulation. Technical report.

Johansson, R. and Strahl, T. (2016). Post-quantum Secure

Communication on a Low Performance IoT Platform.

PhD thesis, Lund.

Kannwischer, M. J., Rijneveld, J., Schwabe, P., and Stof-

felen, K. (2019). pqm4: Testing and Benchmarking

NIST PQC on ARM Cortex-M4. Technical report.

Karmakar, A., Mera, J. M. B., Roy, S. S., and Verbauwhede,

I. (2018). Saber on ARM: CCA-secure module lattice-

based key encapsulation on ARM. IACR Transactions

on Cryptographic Hardware and Embedded Systems,

(3):243–266.

Kipnis, A., Patarin, J., and Goubin, L. (1999). Unbalanced

Oil and Vinegar Signature Schemes.

olbl, S., Lauridsen, M. M., Mendel, F., and Rechberger,

C. (2017). Haraka v2 – Efﬁcient Short-Input Hashing

for Post-Quantum Applications. IACR Transactions

on Symmetric Cryptology.

Lyubashevsky, V., Peikert, C., and Regev, O. (2010). On

ideal lattices and learning with errors over rings. In

Lecture Notes in Computer Science (including sub-

series Lecture Notes in Artiﬁcial Intelligence and Lec-

ture Notes in Bioinformatics).

Malina, L., Popelova, L., Dzurenda, P., Hajny, J., and

Martinasek, Z. (2018). On Feasibility of Post-

Quantum Cryptography on Small Devices. IFAC-

PapersOnLine, 51(6):462–467.

Matsumoto, T. and Imai, H. (1988). Public quadratic

polynomial-tuples for efﬁcient signature-veriﬁcation

and message-encryption. In Lecture Notes in Com-

puter Science (including subseries Lecture Notes in

Artiﬁcial Intelligence and Lecture Notes in Bioinfor-

matics).

McEliece, R. J. (1978). A Public-Key Cryptosystem Based

On Algebraic Coding Theory.

Micciancio, D. and Goldwasser, S. (2002). Complexity

of Lattice Problems: A Cryptographic Perspective.

Kluwer.

Misoczki, R., Tillich, J. P., Sendrier, N., and Barreto,

P. S. (2013). MDPC-McEliece: New McEliece vari-

ants from Moderate Density Parity-Check codes. In

IEEE International Symposium on Information The-

ory - Proceedings.

NIST (2002). FIPS 180-2: Announcing the Secure Hash

Standard. FIPS.

NIST (2015). Secure Hash Standard (SHS) (FIPS PUB 180-

4). Federal Information Processing Standards Publi-

cation.

Peikert, C. (2016). A decade of lattice cryptography. Foun-

dations and Trends in Theoretical Computer Science,

10(4):283–424.

Poppelmann, T., Alkim, E., Avanzi, R., Bos, J., Ducas, L.,

de la Piedra, A., Schwabe, P., Stebila, D., Albrecht,

M. R., Orsini, E., Osheter, V., Paterson, K. G., Peer,

G., and Smart, N. P. (2019). NewHope Speciﬁcation.

Technical report.

Regev, O. (2009). On lattices, learning with errors, random

linear codes, and cryptography. Journal of the ACM.

Seo, H., Jalali, A., and Azarderakhsh, R. (2019). Optimized

SIKE Round 2 on 64-bit ARM. Technical report.

Shor, P. W. (2003). Polynomial-Time Algorithms for Prime

Factorization and Discrete Logarithms on a Quantum

Computer. SIAM Journal on Computing, 26(5):1484–

1509.

Stebila, D. and Mosca, M. (2017). Post-Quantum Key Ex-

change for the Internet and the Open Quantum Safe

Project. Lecture Notes in Computer Science (includ-

ing subseries Lecture Notes in Artiﬁcial Intelligence

and Lecture Notes in Bioinformatics), pages 14–37.

Suomalainen, J., Kotelba, A., Kreku, J., and Lehtonen, S.

(2018). Evaluating the Efﬁciency of Physical and

Cryptographic Security Solutions for Quantum Im-

mune IoT. Cryptography.

Vatjus-Anttila, J., Kreku, J., Korpi, J., Khan, S., Saasta-

moinen, J., and Tiensyrj

a, K. (2013). Early-phase per-

formance exploration of embedded systems with AB-

SOLUT framework. Journal of Systems Architecture.

Post Quantum Cryptography Analysis of TLS Tunneling on a Constrained Device

561