Graph Convolutional Networks for Turn-Based Strategy Games

Wanxiang Li, Houkuan He, Chu-Hsuan Hsueh and Kokolo Ikeda

School of Information Science, Japan Advanced Institute of Science and Technology, Nomi, Ishikawa, Japan

Keywords:

Turn-Based Strategy (TBS) Game, Graph Convolutional Neural Networks, Minimax Tree Search.

Abstract:

In this paper, we research Turn-Based Strategy (TBS) games that allow players to move multiple pieces in

one turn and have multiple initial states. Compared to a game like Chess, which allows only one piece to

move per turn and has a single initial state, it is difﬁcult to create a strong computer player for such a group

of TBS games. Deep learning methods such as AlphaZero and DQN are often used to create strong computer

players. Convolutional neural networks (CNNs) are used to output policies and/or values, and input states

are represented as “image”-like data. For TBS games, we consider that the relationships among units are

more important than their absolute positions, and we attempt to represent the input states as “graphs”. In

addition, we adopt graph convolutional neural networks (GCNs) as the suitable networks when inputs are

graphs. In this research, we use a TBS game platform TUBSTAP as our test game and propose to (1) represent

TUBSTAP game states as graphs, (2) employ GCNs as value network to predict the game result (win/loss/tie)

by supervised learning, (3) compare the prediction accuracy of GCNs and CNNs, and (4) compare the playing

strength of GCNs and CNNs when the learned value network is incorporated into a tree search. Experimental

results show that the combination of graph input and GCN improves the accuracy of predicting game results

and the strength of playing TUBSTAP.

1 INTRODUCTION

Turn-Based Strategy (TBS) games are a popular game

genre where players take turns to perform actions.

Classical board games such as Chess and Go are a

special case of TBS games that players usually oper-

ate one unit in each turn (for example, moving a piece

in Chess or putting a stone in Go). Under a broader

deﬁnition, many TBS games allow players to oper-

ate multiple units in each turn (i.e., whether and how

to move each unit). Many TBS games allow play-

ers to play multiple units in one turn. In addition,

many TBS games offer various initial states, for ex-

ample, pieces(units)’ initial positions may be differ-

ent in each play. This is different from Chess and

Go, which have only one initial state. As the num-

ber and placement of pieces(units) changes, players

need to think ﬂexibly about their strategies. For exam-

ple, Fire Emblem (Nintendo, 2019), Battle for Wes-

noth (White, 2003) and Nintendo Wars (Nintendo,

1988) are famous TBS games with such rules.

To make the discussions clearer, TBS games in the

rest of this paper exclude classical board games. For

classical board games, state-of-the-art AI players are

strong enough as humans’ opponents. Particularly,

AlphaGo defeated top professional Go players Ke Jie

and Lee Sedol (Silver et al., 2017), and the successor

AlphaZero also achieved superhuman levels in Chess

and Shogi (Silver et al., 2018). In contrast, AI players

for TBS games are still weak, mainly because of the

massive number of move combinations in each turn,

coming from the fact that a player can move many

units in any order in one turn.

In this research, we employ an academic TBS

game platform called TUBSTAP (Fujiki et al., 2015),

in which several types of units exist, and each type

has different attack damage on other types. The maps

also contain different terrains (for example, plain, for-

est, and sea), which inﬂuence the mobility of units

and damage. Despite the simpliﬁed rules of TUB-

STAP, it is challenging to create strong AI players

that can deal with many different situations well. A

well-known method for creating evaluation functions

of game states is to learn from game records, such as

AlphaZero (Silver et al., 2018). The goal of our re-

search is to ﬁnd out what kind of network can be used

to create a better state evaluation function for TUB-

STAP.

In the case of AlphaZero, the state evaluation

function is called a value network, and its input, i.e.,

552

Li, W., He, H., Hsueh, C. and Ikeda, K.

Graph Convolutional Networks for Turn-Based Strategy Games.

DOI: 10.5220/0010904200003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 552-561

ISBN: 978-989-758-547-0; ISSN: 2184-433X

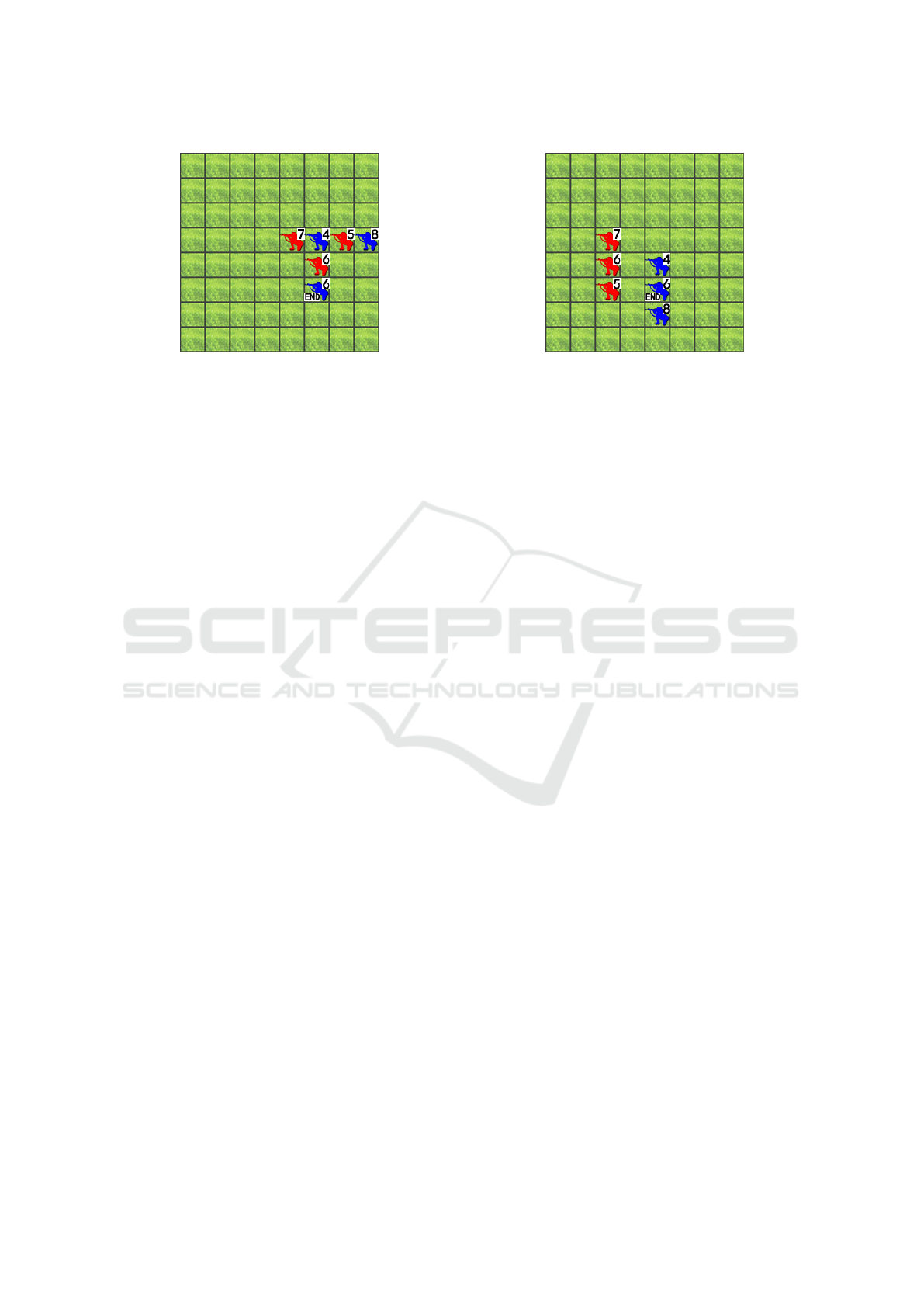
Figure 1: Game state 1.

the board, is represented as an “image” (for example,

19×19 planes representing black and white stones for

Go). And value networks are based on convolutional

neural networks (CNN) (Silver et al., 2018). Even

though TBS maps are also image-like, image input

may not be the best approach since the relationships

between units are more important for decision mak-

ing. Instead of image-like representation, we think

it is promising to treat the states as graphs in order

to adequately represent the relationships. So we pro-

pose to represent game states by graphs. Each node

is for one unit in this graph, and each directed edge

indicates that one unit can attack another. In addi-

tion, graph convolutional neural networks (GCN) has

been proposed to deal with graph-based data better

than CNN (Wu et al., 2020), so we employ GCN to

evaluate state values.

There are several potential advantages of graph

representation to image representation. Firstly, essen-

tially similar unit arrangements have the same repre-

sentation even the relative distance between two units

is not the same. Such an advantage can make the

learning efﬁcient. Secondly, learning does not depend

much on the size of the map or the terrain but most on

the relationships between units. Therefore, the trained

value network which employs graph representation is

expected to be more reusable/applicable than the case

of image representation.

In our experiments, we conﬁrm that our proposed

method increases the accuracy of the state evaluation

and thus the playing strength. At ﬁrst, we employ su-

pervised learning to train value networks that evaluate

game states and test them by prediction accuracy. The

input of networks is the game state, and the output is

game results (win/loss/tie). We collected the training

and test data (states and game results) by Monte Carlo

tree search (MCTS) (Browne et al., 2012) player vs.

MCTS player. We compare image input with graph

input, and CNN with GCN. The best estimation accu-

racy is obtained with the combination of graph input

and GCN. We then combine the value networks into

Figure 2: Game state 2.

minimax search to make the TBS game player. The

GCN player obtains the highest winning ratio among

all tested players.

In the rest of this paper, Section 2 brieﬂy intro-

duces TUBSTAP and GCN. Section 3 presents the

graph representation of TUBSTAP states, how to train

value networks, and how to do minimax searches with

the value networks. Section 4 shows the experiment

results, and Section 5 makes concluding remarks and

introduces our future work.

2 BACKGROUND

In this Section, we will explain the background of this

research. In Section 2.1, we will introduce the ex-

periment platform TUBSTAP. In Section 2.2, we will

explain the graph convolutional networks (GCN).

2.1 TBS Game and Research Platform:

TUBSTAP

In this paper, we focus on TBS games that allow play-

ers to move multiple pieces in one turn and have mul-

tiple initial states. There are many such TBS games,

and their features make them differently challenging

from Chess and Go.

TUBSTAP is a two-player complete informa-

tion TBS game platform developed for academic re-

search (Fujiki et al., 2015). It is a TBS game that

do not contain internal politics elements (for exam-

ple, gaining resources and using resource to create

units, or upgrading units to improve their ability).

TUBSTAP is a convenient platform, where some re-

searchers have introduced and tested their algorithms

on it (Fujiki et al., 2015; Sato and Ikeda, 2016;

Kimura and Ikeda, 2020; Pipan, 2021). We consider

that TUBSTAP has rules of moderate complexity and

is suitable for comparing different methods, explained

as follows. Too-simple rule will make it difﬁcult to

Graph Convolutional Networks for Turn-Based Strategy Games

553

Table 1: The characteristic of different units.

attack

Mobility Shooting Range

Fighter Attacker Panzer Cannon anti-aiR Infantry

F 55 65 0 0 0 0 9 1

A 0 0 105 105 85 115 7 1

P 0 0 55 70 75 75 6 1

C 0 0 60 75 65 90 5 2-3

R 70 70 15 50 45 115 6 1

I 0 0 5 10 3 55 3 1

propose new methods because it is easy to create a

strong player using existing methods. Too-complex

rule will make it difﬁcult to compare methods purely

because various elements of the rules need to be ad-

dressed to create a strong computer player. Hence we

consider using TUBSTAP as our test environment.

Figure 1 and Figure 2 show examples of this game

platform. TUBSTAP’s rule is based on Advance Wars

Days of Ruin (Nintendo, 1988). One player owns the

red units and the other player the blue units. The hit

point (HP) of each unit is shown on the top-right of the

unit. Different types of units have different character-

istics, such as attack ability, which will be explained

soon later. Victory condition of the game is to destroy

all enemy’s units or to have the sum of HP higher than

that of enemy after some certain turns.

There are 6 types of units in TUBSTAP game:

Fighter, Attacker, Panzer, Cannon, Anti-air and In-

fantry. Their characteristics such as attack power,

mobility, and shooting ranges are shown in Table 1.

We can ﬁnd some predator-prey relationships; for ex-

ample, Fighter(F) exploits Attacker(A), A exploits

Panzer(P), P exploits anti-aiR(R), and R exploits F.

The mobility decides how far a unit can move. For ex-

ample, Infantries have the mobility of 3. When mov-

ing on the plain terrain (moving cost 1), Infantries can

move at most three grids counted by Manhattan dis-

tances. And a unit cannot move through enemy units.

The shooting range decides how far a unit can attack.

Because of the differences between the units, how to

use them cleverly is the core issue that players need

to consider and is also the most interesting part of the

game.

As for the battle system, the damage of an attack

action is determined by the attacker’s attack power,

the attacker’s HP, the defender’s HP, and a terrain fac-

tor, as shown in Eq. 1 The terrain factor will be ex-

plained in Appendix.

70 + (Attack ×AT Kunit

sHP)

100 + (DEFunit

sHP ×TerrainFactor)

(1)

When attacking neighbor units, after the attacker’s

damage has been applied to the defender, a counterat-

tack is launched. For example, an Infantry with 10 HP

attacks another Infantry with 10 HP on the Plain; the

attack will give (70+(55×10)/100+(10 ×1)) = 5.6

damage. And the counter-attack will give (70 +(55×

4.4)/100 + (10 ×1)) = 1.2 damage

Some researchers have employed TUBSTAP in

their research on TBS games. Fujiki et al. intro-

duced a depth-limited Monte-Carlo tree search and

tested their method on TUBSTAP (Fujiki et al., 2015).

Sato and Ikeda proposed forward-pruning techniques

to minimax search variants and evaluated them on

TUBSTAP (Sato and Ikeda, 2016). Kimura and Ikeda

used an AlphaZero-like method on the TBS game and

introduced their method on TUBSTAP, and their main

idea is to use the network multiple times. Their selec-

tion unit is in the input layer, as opposed to the usual

implementation where the unit selection is in the out-

put layer. Their main purpose is to reduce the com-

plexity of the output layer and improve learning efﬁ-

ciency (Kimura and Ikeda, 2020). Pipan implemented

three MCTS-based game-playing agents in his modi-

ﬁed TUBSTAP and compared their performance; the

main purpose is to apply and understand how MCTS

variations work with hidden information (for exam-

ple, fog-of-war) in TBS game (Pipan, 2021). In our

case, the main purpose is to ﬁnd out what kind of net-

work can be used to create a better board evaluation

function for TUBSTAP.

2.2 Graph Convolutional Network

AlphaZero uses CNN to build the value network to

evaluate the state of the game of Go (Silver et al.,

2018). CNN is being used not only for games, but

also in other ﬁelds, such as image recognition (Le-

Cun et al., 2015). Usually, CNN deals with the

image or image-like data well; however, many data

in the real world are represented by graphs, such

as social networks (Meqdad et al., 2020), informa-

tion networks (Xiong et al., 2021), and knowledge

The example rounds off the HP to one decimal place;

we used ﬂoat-type to calculate the HP in our program,

which is different from the original TUBSTAP calculation

method that rounds off to integers.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

554

graphs (Yang et al., 2020). CNN may not be suit-

able to deal with graph data. Kipf and Welling (Kipf

and Welling, 2016) proposed graph convolutional net-

works (GCN) to deal with graph data in neural net-

works “directly”. Unlike CNN, the graph convo-

lution’s process is similar to matrix dot calculation,

which would not change the size of the input graph.

GCN model can make use of the graph struc-

ture (and of features extracted from the graph struc-

ture at later layers) (Kipf and Welling, 2016). GCN

has been successfully employed in some applications

where the input is essentially one or some graphs.

For example, DeepMind used GCN to boost the ac-

curacy of the Google maps estimated time of ar-

rival (Derrow-Pinion et al., 2021). Their method suc-

ceeded in reducing the estimation error by about half

in cities such as Berlin, Sydney, Tokyo and Washing-

ton DC (Derrow-Pinion et al., 2021).

3 APPROACHES

In this Section, we will introduce the purposed meth-

ods. In Section 3.1, we will introduce how we repre-

sent the game state as graph. In Section 3.2, we will

introduce the training method on state evaluation. In

Section 3.3, we will introduce minimax search with

GCN.

3.1 Graph Representation for Game

State

There are many possible ways to represent a stage of

TUBSTAP. One way is to represent TUBSTAP game

states as image-like data, which uses several matri-

ces to represent the units’ position, HP, attack, color

(side), type and other information separately. For sim-

plicity of discussions, we will explain using the HP

matrix as an example. The matrix representations of

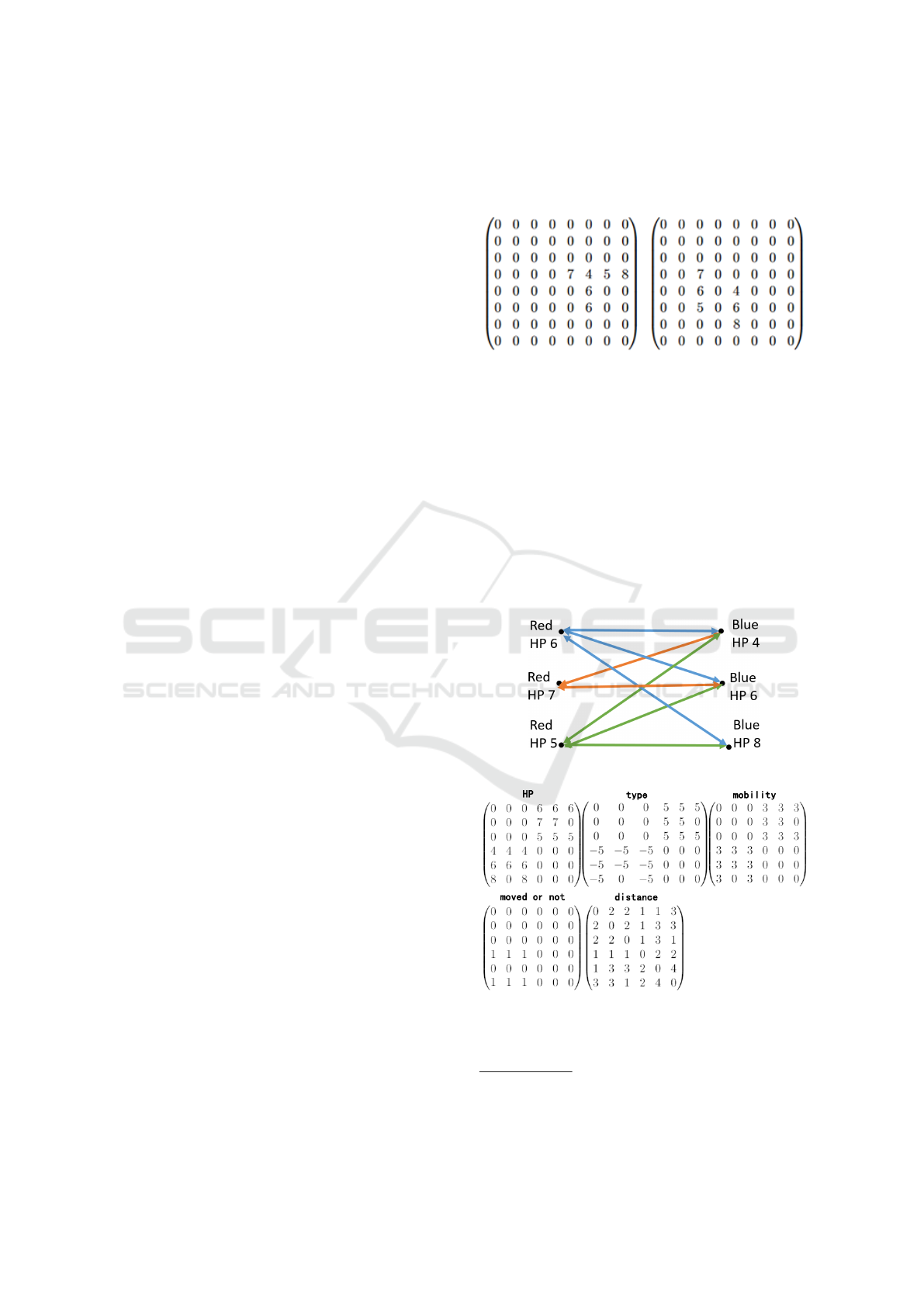
the HP information of the state in Figure 1 is shown

in the left of Figure 3, and state in Figure 2 is shown

in the right Figure 3. Each element in the matrices is

the HP of the unit on the corresponding grid.

As we can tell from the ﬁgure, the two matrices

are entirely different, i.e., image representation will

treat these two states as different states. However,

all units’ relationships (which units can attack which

units) are essentially similar; for example, both the

red units with 6 HP in Figure 1 and 2 can move and

then attack all the blue units. Using image represen-

tation may cause training inefﬁciently. Besides, the

image representation requires different sizes of net-

work inputs when the map size is changed. It is hard

to apply a trained network directly to a map of a dif-

ferent size

. It is usually necessary to prepare a new

network of that size and train it again.

Figure 3: HP matrix of game states 1(left) and 2(right).

To solve these problems, we propose to represent

a TUBSTAP state as a graph. Each node in this graph

represents one unit in the current map. A directed

edge from node-X to node-Y means that unit X can

attack unit Y. The absolute placement provides a rich

amount of information, but we believe that consider-

ing whether units can attack each other is often suf-

ﬁcient to estimate the goodness of a state. By repre-

senting many similar states with similar evaluation in

the same graph, learning is expected to be more efﬁ-

cient. If we consider the two examples before, their

representation of graphs is like Figure 4.

Figure 4: Graph for game state in Figure 1.

Figure 5: Graph representation for game state in Figure 1.

For the two game states in Figure 1 and Figure 2,

the units’ relationships (can attack another) are essen-

As CNN cannot be applied directly to larger maps, our

idea (GCN, shown next) cannot be applied directly to maps

with more units than it was trained.

Graph Convolutional Networks for Turn-Based Strategy Games

555

tially similar, so they can be represented by the simi-

lar graph. Adjacency matrices are one way to repre-

sent a graph, and GCN usually expects one or more

adjacency matrices to be input. Figure 5 shows the

adjacency matrix of HP information for the graph in

Figure 4. Each directed edge is weighted by the HP of

the attacking unit, indicated by the parent node. Natu-

rally, the size of the adjacency matrix depends on the

number of ALIVE units, but we ﬁx it to x ×x, where x

is the number of total units in the initial states. So it is

also possible to apply our graph presentation to maps

with different sizes. And we can reuse the trained net-

work for these different maps.

In addition to the HP matrix, several matrices are

input to the value network. The type, mobility ma-

trix are adjacency matrices but have different edge

weights to represent different information. The other

two matrices represent whether moved or not and the

distance information. The example of different matri-

ces are shown in Figure 5; it should be noted that the

blue unit with 6 HP has already been moved.

1. type: similar to the HP matrices, we ﬁll the posi-

tion with unit type number, and type numbers are

positive for red player, negative for blue player.

2. mobility: similar to the HP matrices, we ﬁll the

matrix with units mobility.

3. whether moved or not: if we we have n units for

each side, if Red i-th unit can move, then in i-th

row, (i,n +1) to (i,2n) are ﬁlled with 1; if Blue j-

th unit can move, then in j-th row, ( j,1) to ( j, n)

are ﬁlled with 1; with this information, the net-

work can determine the current turn player.

4. distance: if we have n units for each side, in this

matrix, for each i-th row, (i,1) to (i, 2n) are ﬁlled

with the distance between the i-th unit and all

units no matter they can attack each other or not.

We use the Manhattan distance between two units

i and j, i.e.,



−x



−y



where x

and x

are the row coordinates of i and j, y

and y

are

the column coordinates.

With the adjacency matrix’s help, we can ame-

liorate the input data of the neural network to make

one representation correspond to the different unit ar-

rangements and different map sizes. To sum it up,

we will convert the game state into a graph structure

representation, use an adjacency matrix to represent

it, and ﬁnally send it to the neural network to learn

features.

3.2 Supervised Learning on State

Evaluation

Kimura et al. tried AlphaZero-like learning to train

the value network for the TBS game (Kimura and

Ikeda, 2020), but AlphaZero learning is more com-

plex than pure supervised learning because game

records are created simultaneously, and policy net-

work is also trained. Since the output representation

of the policy network is another issue that greatly

affects the performance, we decided to separate it

and use simple supervised learning to train value net-

works. We prepare training data as follows. We ran-

domly generated various opening situations, let exist-

ing AI players play from these opening situations, and

collected the initial/intermediate states and results. As

for why using different opening situations, in TBS

games, opening situations are often designed by the

game designers and differ much. We want to train

a good value network that can handle several kinds

of opening situations, so the variety of opening situa-

tions is important.

For each state in a game record, we label the value

as the ﬁnal result (win/loss/tie) of that game from the

view of the player to move. In more detail, if Red

player wins a game, we label 1 for all Red turn states

and -1 for all Blue turn states and vice versa. And

if the game ends as a tie, we will mark all states to

0. By learning state-outcome pairs in this way, we

expect the neural network to be able to estimate the

value (how advantageous the player is) of the given

game state.

3.3 Minimax Search with GCN

The minimax algorithm is a classical tree search al-

gorithm for zero-sum two-player games, one player is

called the maximizer, and the other player is a mini-

mizer. If we assign an evaluation score to game state,s

one player tries to choose a game state with the max-

imum score, while the other chooses a state with the

minimum score (Russell and Norvig, 2010). The ideal

way of minimax tree search is searching the game

state until wins/losses/ties are obtained, but it is infea-

sible for most cases. Thus, evaluating states by some

function is practical.

Different from classical board games, players in

TUBSTAP (and other TBS games) can operate mul-

tiple units in one turn. If one “action” includes all

unit’s moves, the number of possible actions is con-

siderably large. Taking three Infantries versus three

Infantries (situation in Figure 2) without consider-

ing unit interaction as an example, each player has

roughly (3!)×25 ×25 ×25 = 93,750 moves per turn,

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

556

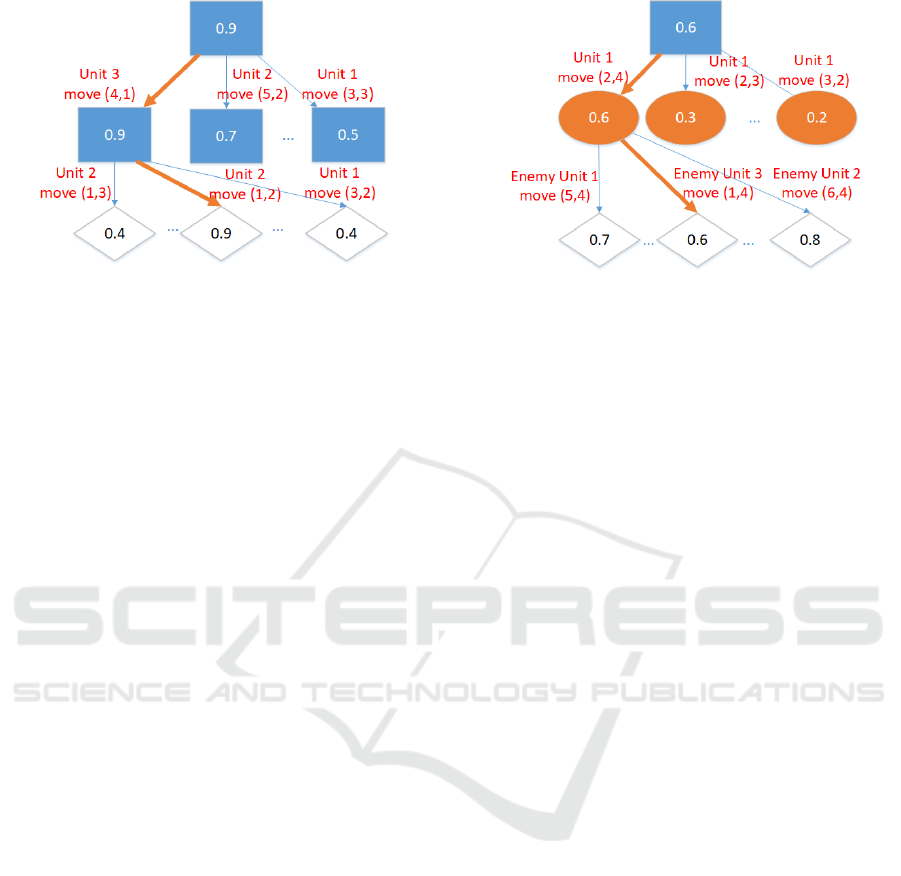
Figure 6: An example of MAX-MAX search with principal

variation (orange bold arrow).

where 3! is for the different order of moving three In-

fantries and 25 for possible movements of an Infantry.

When doing a minimax search considering only two

turns, about 93, 750

= 8, 789,062,500 states will be

evaluated, which is extremely costly.

Therefore, we break down one turn-action into

several unit operations and modify the minimax

search a little (Muto and Nishino, 2016). As long

as it is the player’s turn, the tree nodes are MAX-

nodes; similarly, when it is the opponent’s turn, the

tree nodes are MIN-nodes. Taking the same example

of three Infantries, assume to look ahead for two oper-

ations (depth 2). When 0 or 1 unit has been moved in

that turn, a MAX-MAX search is executed, which is

shown in Figure 6. When two units have been moved,

a MAX-MIN search is executed because after the ﬁrst

move, all three units complete their moves then the

opponent’s turn begins, which is shown in Figure 7.

The depth-2 search may not be promising in strength,

but we can get an affordable search cost and a sim-

ple way to compare different value networks’ abili-

ties. When doing such a unit-based search, the leaf

node is not necessarily at the beginning of the turn

but after some units have moved. To allow the value

networks to evaluate such intermediate states, we in-

clude “whether moved or not” in the input (described

in Section 3.1) and also include the intermediate states

in the training data(described in Section 3.2).

4 EXPERIMENT AND ANALYSIS

In this Section, we present the results of our evalu-

ation experiments. The purpose of our experiments

is to compare graph representation with image-like

representation, and to compare GCN with CNN. Sec-

tion 4.1 introduces the maps used for training and

evaluation. Section 4.2 describes the settings and re-

sults of supervised learning of the value network. Sec-

Figure 7: An example of MAX-MIN search with principal

variation (orange bold arrow).

tion 4.3 shows the results when the trained network is

combined with Minmax tree search.

4.1 Map Generation

In TBS games, a complete game (or story) often con-

sists of multiple scenes that happen in different maps

with various sizes, terrains, and units’ types, num-

bers, and locations. In our experiments, the TUB-

STAP games consisted of one single 8 × 8 map, and

the terrain was ﬁxed to plains only, but various pat-

terns of units were used for learning and evaluation.

The generated maps can be divided into three main

categories: random maps, symmetric maps, and local-

search maps.

The victory conditions are the same for all cate-

gories. The player who destroys all of his/her oppo-

nent’s units wins. If the HP of any unit of both sides

is not reduced for 20 turns, the game is judged as a

tie.

Random Map. A random map contains three Red

Infantries and three Blue Infantries. Their positions

and HPs were randomly determined. The HP of the

initial player ranges from 1 to 10, where the HP of

the second player ranges from 1 to 9. Maps are often

unfair because of the randomness of their placement,

rather than the impact of different HP ranges. It is

usually easy to predict the outcome of such an unfair

map.

Symmetric Map. Symmetric unit arrangement at

the beginning of a game are often used in traditional

turn-based board games such as Chess and Shogi, so

we also consider this kind of maps. A symmetric map

has two Infantries and one Panzer for each side. The

Infantries’ HP is ﬁxed to 10, and the Panzers’ HP is

ﬁxed to 5. We ﬁrstly randomly decide positions for

the red side units in the upper half of the game map.

Graph Convolutional Networks for Turn-Based Strategy Games

557

Table 3: The network layers.

Network name layer 1 layer 2 layer 3 layer 4 weight number

CNN

cnn 32 ×3 ×3 cnn 64 ×2 ×2 FC 512 FC 512 174,721

CNN

cnn 32 ×3 ×3 cnn 64 ×2 ×2 FC 256 FC 512 76,705

GCN 4 gcn 16 ×6 ×6 gcn 4 ×6 ×6 FC 144 FC 512 76,433

GCN 32 gcn 16 ×6 ×6 gcn 32 ×6 ×6 FC 1152 FC 512 596,225

Figure 8: An example of symmetric maps.

Then we set the blue side units rotationally symmet-

rically at the lower right of the game map. The sym-

metric maps may be still unfair because of an initial

player advantage or disadvantage. The example of a

symmetric map is shown in Figure 8.

Local-search Map. A local-search map contains

two Infantries and one Panzer for each side. At ﬁrst,

the units’ position is randomly set, and the Infantries’

HP is 10, the Panzers’ Hp is 5. We then employ two

MCTS players with 6400 rollouts to play this map

against each other. If one player wins, we decrease

one unit’s HP by 1 for the winning side or increase

one unit’s HP by 1 for the losing side. Until there is

a tie or the winning side changes, we save the map

as a local-search map. We expect such maps to be

relatively fair for the two players. The example of a

local-search map is shown in Figure 9.

4.2 Supervised Learning for Value

Network

In this experiment, we are going to train value net-

works and test their prediction accuracy. We led

MCTS players play against each other, then collected

the result (win/loss/tie). All states were labeled by

1/-1/0 for win/loss/tie, as mentioned in Section 3.2.

We collected 83,060 (state, result) pairs for training

from 200 random map games, 274 symmetric map

games, and 1,900 local-search map games. We also

collected 3,859 pairs for testing from another 15 ran-

dom maps, another 25 symmetric maps, and another

Figure 9: An example of local-search maps (red ﬁrst move).

80 local-search maps. The number of states for each

label in training data and test data is shown in Table 2.

Table 2: The number of states for each label.

win loss tie total

Training data 34,863 19,768 28,429 83,060

Test data 1,783 1,186 890 3,859

The collected (state, result) pairs are used for su-

pervised learning, where the state is input to net-

works, and networks output the result. Different net-

work structures and weight numbers may cause dif-

ferent prediction abilities. We designed four net-

works shown in Table 3, CNN’s structure is based

on Le-Net (Kayed et al., 2020). And in this table

gcn n ×m ×k means n-dimensional graph convolu-

tion layer with m ×k kernel; cnn n ×m ×k means

n-dimensional convolution layer with m ×k kernel;

FC n means a fully-connected layer containing n neu-

rons. All output layers consist of one node, which

expresses [-1, 1], representing the input state’s good-

ness.

The network would output the continuous value

in ﬂoat type. In order to calculate the prediction accu-

racy, we converted the output value into three labels

(win/loss/tie) in this experiment. We set the label as

“win” when the output value is higher than 0.5, and

set the label as “loss” when the output value is lower

than -0.5; otherwise, we set the label as “tie”. We will

compare the output label with the true label and get

the prediction accuracy.

We compared GCN 4, GCN 32 with CNNs. The

result in Figure 10 shows that the CNN’s prediction

accuracy was signiﬁcantly better when using graph

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

558

Table 4: The results in prediction accuracy for GCNs and CNNs.

Overall Random map Symmetric map Local-search map

CNN

58.2% 74.5% 61.1% 56.8%

CNN

71.5% 81.1% 75.9% 70.6%

GCN 4 77.5% 85.3% 81.2% 76.7%

GCN 32 78.2% 85.4% 81.2% 77.5%

Table 5: Results of game matches between 4 players on symmetric maps. The winning ratios, win-loss-tie counts and avg.

thinking times in the initial maps.

vs GCN player CNN

player CNN

player MCTS-200 player avg. thinking time

GCN player -

55.5%

(199-144-157)

78.2%

(349-67-84)

64.6%

(304-158-38)

1.42s

CNN

player 44.5% -

71.0%

(298-88-114)

42.7%

(196-269-35)

1.78s

CNN

player 21.8% 29.0% -

20.2%

(95-393-12)

1.89s

MCTS-200 player 35.4% 57.3% 79.8% - 5.34s

input (71.5%) than image input (58.2%). And GCN 4

showed better accuracy (77.5%) than CNN

(71.5%)

even though they have similar numbers of weights.

And GCN 32 is a much richer network than GCN 4,

but the improvement in accuracy was about 0.8%. Ta-

ble 4 also shows the evaluation results when applying

individual map groups to test each value network. The

tendency for graph input and GCN to outperform im-

age input and CNN is the same for each map group.

And as expected, when tested on unfair maps, it is

easier for networks to predict the game results.

Figure 10: Accuracy transition of supervised learning for

predicting win/loss/tie.

From the result, we can say that, CNN’s prediction

accuracy is signiﬁcantly improved with graph input,

and GCN shows better prediction performance than

CNN. Our approach improved the value networks’

prediction accuracy.

4.3 AI Players for TUBSTAP

Since we showed the superiority of graph input and

GCN in terms of learning accurate value networks,

next we evaluated the strength of the computer player

when the value network was combined with tree

search. We prepared four players as follows:

1. GCN player: Depth-2 minimax search with the

GCN 4 value network.

2. CNN

player: Depth-2 minimax search with the

CNN

value network, which use graph represen-

tation as input.

3. CNN

player: Depth-2 minimax search with the

CNN

value network, which use image represen-

tation as input.

4. MCTS-200 player: MCTS with 200 rollouts.

There are six possible combinations of players.

For each combination, 250 symmetric maps and 250

local-search maps were given. Each map was played

twice for fairness, where the two players alternately

played as the ﬁrst player. For symmetric maps, we

generated the map for each game. And for local-

search maps, we prepared 250 newly created maps

and shared by all combinations. The results of the

four players playing against each other are shown in

Table 5 and Table 6, denoted by winning ratio (win-

loss-tie), where a tie was counted as a half win. Wins

and losses are from the views of the players in the ﬁrst

column. The average computation time to decide the

next move in the initial maps (when both sides had all

three units) is also shown for reference.

In symmetric maps, from the result, we can ﬁnd

that the CNN

player was stronger than the CNN

player. GCN player’s superiority is not obvious when

Graph Convolutional Networks for Turn-Based Strategy Games

559

Table 6: Results of game matches between 4 players on local-search maps. The winning ratios, win-loss-tie counts and avg.

thinking time in the initial maps.

vs GCN player CNN

player CNN

player MCTS-200 player avg. thinking time

GCN player -

59.4%

(213-119-168)

78.3%

(356-73-71)

64.0%

(315-175-10)

3.64s

CNN

player 40.6% -

72.9%

(306-77-117)

39.6%

(182-286-32)

3.98s

CNN

player 21.7% 27.1% -

18.9%

(93-404-3)

4.15s

MCTS-200 player 36.0% 60.4% 81.1% - 5.54s

the opponent is a CNN

player but still gets an over-

half winning ratio. Even though the result of direct

matching on GCN player and CNN

player was not

clear, when playing against other players, GCN player

performed better, and the differences were clear. So

we can say that GCN player had the best playing

strength in these three players. The result is similar to

prediction accuracy, where GCN is better than CNN

and CNN

is better than CNN

In local-search maps, results were similar to sym-

metric maps. The graph input improved CNN’s play-

ing strength, and GCN player showed the best perfor-

mance in game playing. With the results from these

two kinds of maps, we can say that our graph repre-

sentation improved the CNN’s playing strength, and

GCN showed its advantage over CNN in our experi-

ment.

4.3.1 Experiment on Different Map Size

As we mentioned in Section 3.1, it is also possi-

ble to apply our proposed methods to maps with

different sizes. We tested the GCN player against

the MCTS-200 player in larger (10 ×10) symmetric

map. 250 maps were newly generated, and each map

was played twice, where the two players alternately

played as the ﬁrst player. In these 500 games, the

GCN player won 296 games, lost 89 games, and tied

115 games. The average thinking time in initial board

for the GCN player was 1.65s, and the average think-

ing time for the MCTS-200 player was 5.76s. The

results showed that our proposed methods could work

well even in the untrained larger map size.

5 CONCLUSION AND FUTURE

WORK

This paper studied TBS games through an academic

platform TUBSTAP. We proposed to use graphs to

represent game states and employed CNNs or GCNs

to learn state evaluations (i.e., value networks) by su-

pervised learning. We further combined the value net-

works into a modiﬁed minimax search that one edge

represents one action of one unit. The experimen-

tal results showed that graph representation improved

the prediction ability for CNN, and GCN obtained the

best prediction accuracy. When incorporating trained

networks into the minimax search with depth 2, the

GCN player obtained the highest winning ratio among

all tested players.

There are many experiments and implementations

to be done in the near future. First, since only a lim-

ited variety of unit types and terrains were used in

this paper, it would be valuable to investigate the per-

formance of GCN on more complex maps. The next

issue is that a minimax search with a depth of 2 is not

enough, but it is also difﬁcult to search any deeper.

The reason is many possible moves, including bad

ones, and prioritization using a policy network would

be effective. Hence, thirdly, it would be promising to

use graph input and GCN for AlphaZero-like learn-

ing, which learns value and policy simultaneously

while playing against itself.

REFERENCES

Browne, C. B., Powley, E., Whitehouse, D., Lucas, S. M.,

Cowling, P. I., Rohlfshagen, P., Tavener, S., Perez,

D., Samothrakis, S., and Colton, S. (2012). A survey

of monte carlo tree search methods. IEEE Transac-

tions on Computational Intelligence and AI in games,

4(1):1–43.

Derrow-Pinion, A., She, J., Wong, D., Lange, O., Hes-

ter, T., Perez, L., Nunkesser, M., Lee, S., Guo, X.,

Wiltshire, B., et al. (2021). Eta prediction with

graph neural networks in google maps. arXiv preprint

arXiv:2108.11482.

Fujiki, T., Ikeda, K., and Viennot, S. (2015). A platform

for turn-based strategy games, with a comparison of

monte-carlo algorithms. In 2015 IEEE Conference on

Computational Intelligence and Games (CIG), pages

407–414. IEEE.

Kayed, M., Anter, A., and Mohamed, H. (2020). Classi-

ﬁcation of garments from fashion mnist dataset using

cnn lenet-5 architecture. In 2020 International Con-

ference on Innovative Trends in Communication and

Computer Engineering (ITCE), pages 238–243. IEEE.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

560

Table 7: The terrain factors and moving cost in TUBSTAP.

Plain Fortress Mountain Forest Sea Road

terrain factor for F,A 0 0 0 0 0 0

terrain factor for P,C,R,I 1 4 4 3 0 0

moving cost for F,A 1 1 1 1 1 1

moving cost for P,C,R 1 1 - 2 - 1

moving cost for I 1 1 2 1 - 1

Kimura, T. and Ikeda, K. (2020). High-performance al-

gorithms using deep learning in turn-based strategy

games. In ICAART (2), pages 555–562.

Kipf, T. N. and Welling, M. (2016). Semi-supervised clas-

siﬁcation with graph convolutional networks. arXiv

preprint arXiv:1609.02907.

Kocsis, L. and Szepesv

ari, C. (2006). Bandit based monte-

carlo planning. In European conference on machine

learning, pages 282–293. Springer.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-

ing. nature, 521(7553):436–444.

Meqdad, M. N., Al-Akam, R., and Kadry, S. (2020).

New prediction method for data spreading in so-

cial networks based on machine learning algorithm.

TELKOMNIKA, 18(6):3331–3338.

Muto, K. and Nishino, J. (2016). Fuzzy evaluation of

macroscopic situation for turn based strategic games.

In 2016 Joint 8th International Conference on Soft

Computing and Intelligent Systems (SCIS) and 17th

International Symposium on Advanced Intelligent

Systems (ISIS), pages 1–4. IEEE.

Nintendo (1988). Wars (series). https://en.wikipedia.org/

wiki/Wars\ (series). accessed 2021-11-08.

Nintendo (2019). Nintendo switch ﬁre emblem: Three

houses. https://www.nintendo.com/games/detail/ﬁre-

emblem-three-houses-switch. accessed 2021-11-08.

Pipan, C. M. (2021). Application of the monte-carlo tree

search to multi-action turn-based games with hidden

information. Theses and Dissertations. 4906.

Russell, S. and Norvig, P. (2010). Artiﬁcial Intelligence: A

Modern Approach, pages 163 – 167. Prentice Hall, 3

edition.

Sato, N. and Ikeda, K. (2016). Three types of forward

pruning techniques to apply the alpha beta algorithm

to turn-based strategy games. In 2016 IEEE Con-

ference on Computational Intelligence and Games

(CIG), pages 1–8. IEEE.

Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai,

M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D.,

Graepel, T., et al. (2018). A general reinforcement

learning algorithm that masters chess, shogi, and go

through self-play. Science, 362(6419):1140–1144.

Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I.,

Huang, A., Guez, A., Hubert, T., Baker, L., Lai, M.,

Bolton, A., et al. (2017). Mastering the game of go

without human knowledge. nature, 550(7676):354–

359.

White, D. (2003). Battle for wesnoth. https://en.wikipedia.

org/wiki/The\ Battle\ for\ Wesnoth. accessed 2021-

11-08.

Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., and Philip,

S. Y. (2020). A comprehensive survey on graph neural

networks. IEEE transactions on neural networks and

learning systems, 32(1):4–24.

Xiong, Y., Zhang, Y., Kong, X., Chen, H., and Zhu, Y.

(2021). Graphinception: Convolutional neural net-

works for collective classiﬁcation in heterogeneous in-

formation networks. IEEE Transactions on Knowl-

edge and Data Engineering, 33(5):1960–1972.

Yang, J., Zhou, W., Wei, L., Lin, J., Han, J., and Hu, S.

(2020). Re-gcn: Relation enhanced graph convolu-

tional network for entity alignment in heterogeneous

knowledge graphs. In International Conference on

Database Systems for Advanced Applications, pages

432–447. Springer.

APPENDIX

In this appendix, the detailed setting is described,

which is a bit far from the central issue of this pa-

per. The following two paragraphs introduce the ter-

rain factor of TUBSTAP and the implementation of

the MCTS player used in the experiments.

In TUBSTAP maps, there are different terrains, as

listed in Table 7. In our experiments, only the plain

terrain was employed. Two sets of rules relating to

terrains are the terrain factor and the moving cost. The

terrain factor is one of the elements deciding the dam-

age of an attack, as shown in Eq. 1 in Section 2.1. A

higher terrain factor means that it is better for defense.

The moving cost, along with the mobility of a unit,

decides how far the unit can go. With a higher mov-

ing cost, a unit takes more moves to travel the same

distance.

The MCTS players in this research are MCTS

with upper conﬁdence bound (UCB) (Kocsis and

Szepesv

ari, 2006). Where the coefﬁcient for UCB is

√

2. It contains four steps, selection, expansion, sim-

ulation, and backpropagation. In the selection step,

we use the UCB to choose which node to expand. In

the expand step, the selected node would be fully ex-

panded, which means all valid child nodes would be

created. In the simulation step, we employ a random

player, and the simulation ends till the game end. In

the backpropagation step, nodes’ value is updated by

the result in the simulation.

Graph Convolutional Networks for Turn-Based Strategy Games

561