
A Fast and Cost-effective Design for FPGA-based Fuzzy Rainbow
Tradeoffs
Leonardo Veronese
1,2
, Francesco Palmarini
1,2
, Riccardo Focardi
1,2 a
and Flaminia L. Luccio
1,2 b
1
DAIS, Ca’ Foscari University, via Torino 155, Venice, Italy
2
10Sec S.r.l., via delle Industrie 13, Venice, Italy
Keywords:
Rainbow Tables, Cryptanalysis, Time/memory Tradeoff, FPGA.
Abstract:
Time/memory tradeoffs are general techniques used in cryptanalysis that aim at reducing the computational
effort in exchange for a higher memory usage. Among these techniques, one of the most modern algorithms is
the fuzzy-rainbow tradeoff, which has notably been used in 2010 to attack the GSM A5/1 cipher. Most of the
existing analyses of tradeoff algorithms only take into account the main-memory model, which does not reflect
the hierarchical (external) storage model of real world systems. Moreover, to the best of our knowledge, there
are no publicly available implementations or designs that show the performance level that can be achieved
with modern off-the-shelf hardware. In this paper, we propose a reference hardware and software design for
the cryptanalysis of ciphers and one-way functions based on FPGAs, SSDs and the fuzzy rainbow tradeoff
algorithm. We evaluate the performance of our design by extending an existing analytical model to account
for the actual storage hierarchy, and we estimate an attack time for DES and A5/1 ciphers of less than one
second, demonstrating that these ciphers can be cracked in real-time with a budget under 6000e.
1 INTRODUCTION
Time/memory tradeoffs are general techniques used
in cryptanalysis to represent a middle ground between
exhaustive search and table lookup, the first requir-
ing only computation time, the second only memory
space. The focus of these techniques is to provide
a faster way, compared to exhaustive search, to in-
vert one-way functions multiple times, but without
the need to store the whole search space in memory.
They consist, first of a precomputation phase that is
executed only once, and in which the stored data is
created, and then of an online phase, in which the
actual inversion is performed. Time/memory trade-
offs can be used in all the applications that can be
reduced to one-way functions. Examples are crypto-
graphic hash functions often used in password stor-
age, and also block ciphers in the chosen-plaintext
scenario and stream ciphers in the known-plaintext
scenario. These techniques are probabilistic: success
is not guaranteed and the success rate depends on the
time and memory allocated for cryptanalysis.
The most recent technique in the literature is the
a
https://orcid.org/0000-0003-0101-0692
b
https://orcid.org/0000-0002-5409-5039
fuzzy-rainbow tradeoff which has been used by Nohl
to attack the GSM A5/1 stream cipher in (Nohl,
2010b), and has been studied in detail in (Kim and
Hong, 2013; Kim and Hong, 2014). Most of the theo-
retical analyses of time/memory tradeoffs are carried
out in the main memory model. This means that the
storage is treated as a single level of fast memory, as
if the theoretical machine had an infinite amount of
RAM. This allows for general analyses that are not in-
fluenced by the specific implementation or platform.
However, the difference with the real setting often
brings challenges to the developer, since it is difficult
to obtain practical results comparable to the theoret-
ical ones, especially in case of high performance re-
quirements. Indeed, practical implementations have
a limited amount of main memory, and may use dif-
ferent external media to store the large precomputa-
tion tables. Each media, ranging from optical DVDs,
to mechanical hard drives, and to modern solid state
hard drives (SSDs), has a different performance that
has to be taken into account, since data have to be
loaded to RAM for processing. This typically re-
quires to modify the algorithms in order to have a
more localized access to the precomputation tables,
avoiding to transfer the same data multiple times.
In this paper, we propose a reference hardware
Veronese, L., Palmarini, F., Focardi, R. and Luccio, F.
A Fast and Cost-effective Design for FPGA-based Fuzzy Rainbow Tradeoffs.
DOI: 10.5220/0010904300003120
In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 165-176
ISBN: 978-989-758-553-1; ISSN: 2184-4356
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
165

and software design for time/memory tradeoff, espe-
cially suited for stream ciphers, based on the fuzzy-
rainbow tradeoff algorithm. The proposed off-the-
shelf hardware setup features fast SSDs as a storage
medium, and FPGA-based accelerator cards as com-
putation units. FPGAs are used to substantially accel-
erate both the precomputation phase and the online
phase. Given the complexity and variety of FPGA de-
signs, we focus on the software-side management of
the FPGA devices, specifying the interface, the com-
munication method and the black-box behavior. We
explain the issues that can be faced during the devel-
opment of an high performance time/memory tradeoff
system and illustrate our solutions, which aim at min-
imizing latency and data dependencies. It is worth
noticing that the techniques developed in our archi-
tecture are general and could be reemployed in other
settings, to improve the performance of highly con-
current and pipelined systems.
Based on (Kim and Hong, 2013), we provide an
analytical method that can be used to find the optimal
parameters for an instantiation of the fuzzy-rainbow
tradeoff and, most importantly, can be used to esti-
mate the performance of a system that follows the
proposed design in the external memory model, hence
giving accurate estimates of online and precomputa-
tion times, confirmed by a proof-of-concept imple-
mentation. We also provide a software tool that can
be used to compute the optimal parameters and to esti-
mate the performance of a given tradeoff instantiation
(Veronese et al., 2021).
Finally, we apply our design and model to esti-
mate the performance of the attack on two well known
ciphers: DES and A5/1. The results show that these
ciphers can be attacked in real-time, with a online
time of less than a second, a very high precision of
99% and a budget under 6000e. Interestingly, this
online time is one order of magnitude faster than pre-
vious solutions.
1.1 Related Work
GPUs and FPGAs are valuable tools used to acceler-
ate computation since they provide higher parallelism
levels with respect to CPUs. Both have been used
in the literature for cryptanalysis and time/memory
tradeoffs. FPGAs in particular have been used since
2002 for time/memory tradeoffs but only to acceler-
ate the precomputation step (Quisquater et al., 2002;
Quisquater and Standaert, 2005). An FPGA-based
cryptanalysis machine called COPACOBANA that
can perform exhaustive searches and time/memory
tradeoffs has been developed by Kumar et al. in 2006
(Kumar et al., 2006; G
¨
uneysu et al., 2008) and, in the
same year, Mentens et al. proposed a hardware design
for a key search machine based on the rainbow trade-
off and FPGA (Mentens et al., 2006). However, both
these works date back to fifteen years ago, and they
do not provide enough information about the usage of
the FPGA hardware in the online phase.
To the best of our knowledge, there are no pub-
licly available implementations or software designs
for time/memory tradeoff that can provide high per-
formance using current technology and off-the-shelf
hardware. The most recent public implementation is
the already mentioned project by Nohl (Nohl, 2010b;
Nohl and Paget, 2009), and the extensions of (Kalen-
deri et al., 2012; Lu et al., 2015), which are not gen-
eral since they focuses only on the A5/1 cipher. We
will show that our proposal outperforms these attacks
both in terms of time and accuracy (cf. Section 5).
Kim et al. analyzed the performance of a rainbow
tradeoff variant that is widely used in practice, within
the external memory model (Kim et al., 2013). Their
precomputation phase of the algorithm was identical
to the one described by (Oechslin, 2003), but they
proposed a variant of the algorithm for the online part
that uses smaller sub-tables so that they comfortably
fit in RAM. The authors of (Haghighi and Dakhi-
lalian, 2014) applied the same exact reasoning to the
fuzzy-rainbow tradeoff, and in (Kim and Hong, 2013;
Kim and Hong, 2014) authors provided an accurate
complexity analysis of the fuzzy-rainbow tradeoff (cf.
Section 2.3).
Our work extends the one of (Kim and Hong,
2013) by taking into account the number of inver-
sion targets, i.e., the plaintext/ciphertext pairs avail-
able to the attacker. This makes it possible to analyze
time/memory/data tradeoffs, in which having multi-
ple inversion targets improves the attack in terms of
time, memory and precision. Moreover, we describe
a novel approach for maximizing the performance of
tradeoff attacks within the external memory model by
introducing an improved hardware and software ar-
chitecture.
1.2 Structure of the Paper
In Section 2, we present the background notions; in
Section 3, we discuss the model and requirements; in
Section 4, we present the reference design; in Sec-
tion 5, we provide experimental results on DES and
A5/1 ciphers, and in Section 6 we give some conclud-
ing remarks.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
166

x
0
1
f
−→
f
−→ . . .
f
−→ x
t
1
.
.
.
.
.
.
x
0
m
f
−→
f
−→ . . .
f
−→ x
t
m
m
t
Figure 1: A Hellman table covering m ·t values.
2 BACKGROUND
In this section, we recall some notions used in the rest
of the paper, i.e., one-way functions, brute-force at-
tacks, time/memory tradeoff techniques, and FPGAs.
Readers already familiar with them can safely skip the
section.
2.1 One-way Functions
We focus on the general problem of inverting one-way
functions, i.e., functions that are infeasible to invert.
Formally:
Definition 2.1. A function S : X → Z is one-way if:
1. given x it is efficient to compute S(x) = z;
2. given z it is infeasible to compute x such that
S(x) = z.
One-way functions are quite common in cryptogra-
phy. Passwords are processed by one-way (hash)
functions before they are stored, so that attacks leak-
ing a password file do not directly leak the passwords.
Ciphers can also be considered as one-way functions,
usually in a so-called chosen-plaintext attack sce-
nario: suppose that the attacker can choose the plain-
text; then, given a key it is efficient to compute the
ciphertext but not the other way around. In these ex-
amples, inverting the one-way function reveals the
secret, i.e., the password or the cryptographic key,
meaning that the security of the mechanism is actu-
ally based on the one-way property of Definition 2.1.
One-way functions may be subject to brute-force at-
tacks that try all the possible values in the function
domain until a given hash is found.
2.2 Time/Memory Tradeoffs
When brute-force attacks become infeasible, it is pos-
sible to resort to time/memory tradeoffs which re-
duce the computational effort in exchange for a higher
memory usage. They consist of two phases: in the
precomputation phase, the attacker performs a num-
ber of random applications of the function under at-
tack, saving these results in a table; in the online
phase, the attacker uses the precomputed table in or-
der to speed up the search. Intuitively, the online time
can be reduced by increasing the size of the table,
from which the name time/memory tradeoff.
The original idea works as follows (Hellman,
1980). We consider a one-way function S : X → Z,
and a reduction function R : Z → X, so that f (x) =
R(S(x)) is still a one way function whose output can
be given as input to S. In particular, notice that R
takes a value z ∈ Z and returns a value x ∈ X. During
the precomputation phase, m random starting points
x
0
1
, . . . , x
0
m
are processed using f for t times, i.e., x
t
i
=
f
t
(x
i
) giving m endpoints x
t
1
, . . . , x
t
m
. Only the m pairs
(x
0
i
, x
t
i
) of starting points and endpoints are stored in
the table. Since f has been iterated t times one table
covers m·t values (see Figure 1). The same process is
iterated t times using a different reduction function R
so to produce t different tables, covering m ·t
2
values.
In the online phase, these tables are searched in
order to invert S. The target value z is processed with
R and then searched among the endpoints. If a match
is found with x
t
i
in a certain table, the chain is recom-
puted from the starting point x
1
i
so to recover x
t−1
i
=
f
t−1
(x
i
). This value is such that f (x
t−1
i
) = R(z) mean-
ing that S(x
t−1
i
) = z, i.e., the one-way function has
been inverted. If no match is found, it is enough to
process R(z) under f and repeat the search among the
endpoints. In case of success the chain will be recom-
puted using f
t−2
, and so on. Intuitively, the target
value is processed through f for at most t times un-
til a match with the endpoints is found. The match
allows for computing the preimage by simply recom-
puting the corresponding chain.
The memory requirement to store t tables with m
starting points is M = m · t entries. The precompu-
tation cost is m · t steps for each of the t tables, i.e.,
N = m ·t
2
. In the online phase the function f is ap-
plied at most t times for every of the t tables giving
an online cost of T = t
2
steps. Combining all these
equations we obtain the Hellman tradeoff curve:
T M
2
= N
2
(1)
A particular point in the tradeoff curve shown in
(Hellman, 1980) is T = M = N
2
3
. Thus, any arbitrary
one-way function with a domain of size N, can be in-
verted in N
2
3
steps and using N
2
3
entries. For example,
breaking the standard 56-bit DES is equivalent to an
exhaustive search of about 38 bits, using precomputed
tables of about 2
38
entries.
A Fast and Cost-effective Design for FPGA-based Fuzzy Rainbow Tradeoffs
167
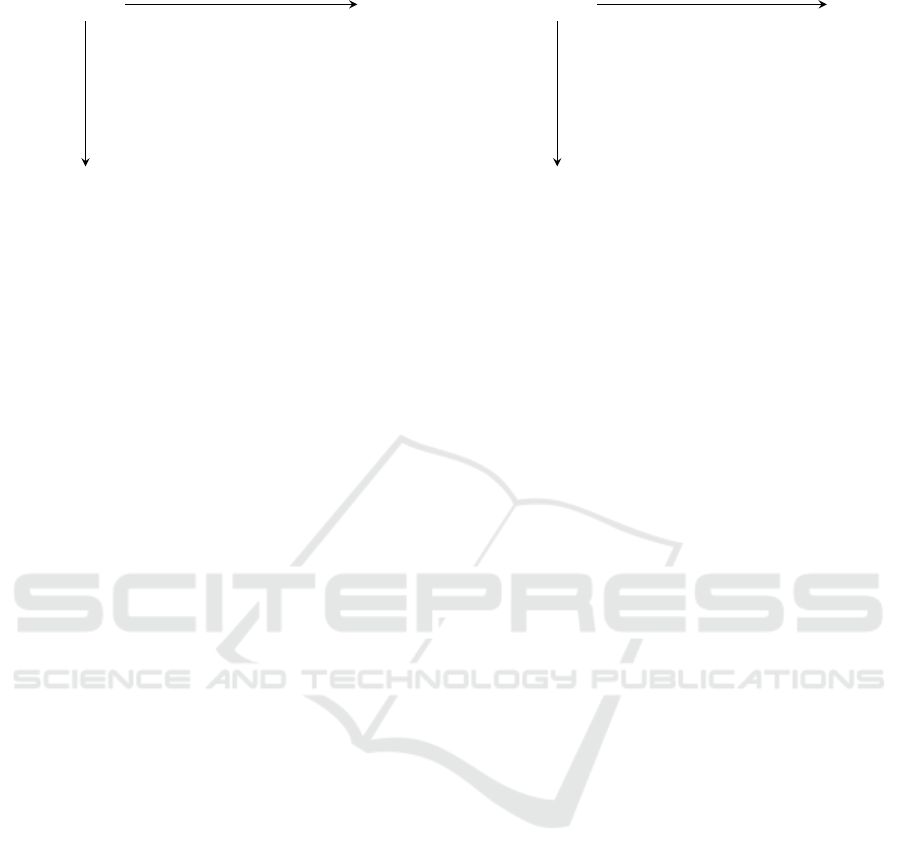
x
0
1
f
−→
f
−→ . . .
f
−→ DP
1
.
.
.
.
.
.
x
0
m
f
−→
f
−→ . . .
f
−→ DP
m
m
∼ t
Figure 2: A table in which all endpoints are distinguished
points (DP) covering m ·t values, on average.
2.3 Fuzzy Rainbow Tables
In 1982, Rivest suggested an improvement of Hell-
man’s technique that aimed at decreasing the search
time, by reducing the number of memory accesses
(Robling Denning, 1982, p.100). He suggested that
each endpoint should satisfy some easily tested syn-
tactic property, e.g., start with a fixed number of ze-
ros. This property is expected to be true after t iter-
ations of the one-way function, in order to maintain
the average number of values covered by a single ta-
ble equal to m ·t. The points that satisfy this particu-
lar property are called distinguished points (DP). This
variant is illustrated in Figure 2. The main advantage
is that during the online search phase f is repeatedly
applied until a distinguished point is reached which
is then searched in the table, i.e., only one expensive
disk operation needs to be performed per online chain.
The number of function evaluation remains t
2
as in
(Hellman, 1980), but the number of disk accesses are
reduced from t
2
to t.
In 2003 Oechslin proposed a new optimization
of the time/memory tradeoff, called rainbow tables,
which mitigates the problem of merging chains be-
longing to the same table (Oechslin, 2003). In the
original scheme a collision between two chains of the
same table resulted in a merge, with this optimization
chains can collide without merging. The idea is to
use different reduction functions, one for each of the t
points of the chain (cf. Figure 3). In this way, a merge
of chains happens only if the collision is at the same
position. Otherwise, the chains will continue with a
different reduction function, diverging. The success
probability of rainbow tables is comparable to the one
of classical tables, as t of them of size m · t have ap-
proximately the same coverage of a single rainbow
table of size m · t
2
. In both cases, the covered values
are m · t
2
with t different reduction functions. How-
ever, the total number of table lookups is reduced by
a factor t with respect to the Hellman method. More-
over, merges of chains are detectable and chains can-
not have loops.
The fuzzy rainbow table tradeoff, introduced in
x
0
1
f
1
−→
f
2
−→ . . .
f
t
−→ x
t
1
.
.
.
.
.
.
x
0
m
f
1
−→
f
2
−→ . . .
f
t
−→ x
t
m
m
t
Figure 3: A rainbow table covering m · t values.
(Barkan, 2006), uses the notion of distinguished
points in the rainbow table setting so, in a sense,
mixes the two previously presented extensions, sum-
ming up their advantages. A chain is composed as
follows:
SP
f
1
−→ ◦···◦
f
1
−→ DP
f
2
−→ ◦···◦
f
2
−→ DP
f
3
−→ ◦. . .
. . .
f
s−1
−−→ DP
f
s
−→ ◦··· ◦
f
s
−→ DP = EP
Every colored one-way function is iterated until a dis-
tinguished point is found. Then, the iterations contin-
ues under the next color, and so on. If s colors are
used, the average chain length is s · t where log
2
t is
the order of the distinguish property, i.e., log
2
t fixed
bits (cf. Figure 4).
2.4 Field-programmable Gate Arrays
An FPGA is an integrated circuit composed by sev-
eral logic blocks of circuitry that can be configured
and composed by the user to perform the desired
functions. FPGAs can be purchased as chips to be
integrated in a board design, integrated in develop-
ment boards or as Programmable Acceleration Cards
(PACs). Nowadays, all the major cloud providers give
the possibility to deploy online FPGA computing re-
sources, for example Microsoft Azure provides Arria
10 GX1150 or Intel Stratix V.
FPGAs behave just like hardware circuits, and are
generally much more efficient than CPUs and GPUs
in specialized computing tasks: although they run at
a lower clock speed they can execute more computa-
tions per clock. For example, a circuit used to execute
a stream cipher could require just a few clock cycles
with an FPGA, compared to several thousands with a
GPU. Moreover, FPGAs offer an extreme parallelism
that allows for implementing an elevated number of
specialized computing units in the same device. De-
pending on the dimension on the algorithm, it might
be possible to easily reach hundreds of units for a sin-
gle FPGA.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
168

x
0
1
f
1
−→ . . .
f
1
−→ DP
1
1
f
2
−→ . . .
f
2
−→ DP
2
1
f
3
−→ . . . . . .
f
s−1
−−→ DP
s−1
1
f
s
−→ . . .
f
s
−→ DP
s
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
x
0
m
f
1
−→ . . .
f
1
−→ DP
1
m
f
2
−→ . . .
f
2
−→ DP
2
m
f
3
−→ . . . . . .
f
s−1
−−→ DP
s−1
m
f
s
−→ . . .
f
s
−→ DP
s
m
m
∼ t · s
Figure 4: A fuzzy rainbow table with s colors, covering m · t ·s values.
3 MODEL AND REQUIREMENTS
The proposed method is very general and works for
any pseudo-random one-way function. We use the
fuzzy rainbow time/memory tradeoff which optimizes
the initial tradeoff proposed by Hellman (cf. Sec-
tion 2). It is important to notice that the possibility
for the attacker to retrieve multiple inversion targets
for the same key increases the success rate and allows
the size of the tables to be decreased. Thus, the pro-
posed method is, in fact, a time/memory/data tradeoff,
with the data part represented by the number of avail-
able inversion targets.
3.1 Computing Optimal Parameters
We use the model of (Kim and Hong, 2013) for the
choice of the algorithm parameters and for the per-
formance evaluation, suitably extended so to take into
consideration the number of inversion targets. In par-
ticular, we are interested in computing the point with
the lowest online time which fulfills the memory re-
strictions. In other words, we prioritize online time,
as precomputation time is executed only once.
In the following, we write M to denote the num-
ber of entries of the tables, N to denote the number
of precomputation steps, and T to denote the num-
ber of online steps (cf. Section 2.2). Intuitively, the
presence of more inversion targets exponentially de-
creases the probability of failure, making it possible to
reduce the table size. We incorporate this change in
the model of (Kim and Hong, 2013) obtaining a rela-
tion between the precomputation coefficient F
pc
, i.e.,
the precomputation cost over the search space size N,
versus F
tc,s
, i.e., the tradeoff coefficient for the fuzzy
rainbow table such that T M
2
= F
tc,s
N
2
. This allows
us to draw the curve F
pc
versus F
tc,s
as exemplified in
Figure 5. We are interested in the points of the curve
closest to the left side as they represent lower precom-
putation costs, and those closest to the minimum, as
they correspond to better online efficiency.
Once a point in this curve has been chosen the
Figure 5: The F
pc
vs F
tc,s
curve.
time/memory tradeoff is available, in the form
T M
2
= F
tc,s
N
2
(2)
The restrictions that the choice of the point (F
pc
, F
tc,s
)
entails is that the precomputation cost will be F
pc
N
and the online resources will be constrained by Equa-
tion 2. The developer selects an M parameter that sat-
isfies the actual memory constraints and, once a set of
parameters for the tradeoff is found, it is possible to
compute the optimal number of colors s.
We developed a software tool which implements
our updated model, (Veronese et al., 2021). The tool
can be used both to compute the optimal parameter set
for a given hardware and attack constraints, as well as
to estimate the precomputation time and online per-
formance. Furthermore, the tool can be used for re-
producing and validating the results presented in this
work (cf. Section 5).
4 REFERENCE DESIGN
We propose the first reference hardware and software
design for the cryptanalysis of ciphers and one-way
functions based on FPGAs, SSDs and the fuzzy rain-
bow tradeoff algorithm. Since the target performance
level should be close to the limitation imposed by the
hardware, the proposed reference design has under-
gone different revisions to overcome several problems
A Fast and Cost-effective Design for FPGA-based Fuzzy Rainbow Tradeoffs
169

that occurred during the development of the proof-of-
concept implementation (cf. Section 5). In particu-
lar, we found that in order to achieve the ultra-low
latency that modern PCI-e SSD drives can provide,
non-trivial software design practices must be adopted
by the developer. Thus, along with the design, we
provide guidelines for achieving the best possible per-
formance from modern off-the-shelf hardware. It is
worth noticing that the techniques developed in our
architecture are general and could be reemployed in
other settings, to improve the performance of highly
concurrent and pipelined systems.
In the following sections, we discuss in detail all
the relevant aspects of the proposed reference design:
in Section 4.1 and 4.2 we illustrate storage optimiza-
tion and precomputation, in Section 4.3 we provide an
overview of the reference design for the online phase
that we detail in Section 4.4 and 4.5.
Finally, in the next sections we denote by m the
number of entries of each table, t the length of the
chains, l the number of tables and s the number of
colors.
4.1 Storage Optimization
The storage complexity M in the tradeoff curve
(Equation 2) represents the total number of entries in
the tables. To analyze the real physical storage re-
quirements, the actual size in bits must be considered,
and it is thus very important to exploit compression
techniques. We resort to well established methods
which are extensively discussed in the literature and
are summarized below.
Since each table contains m entries and assum-
ing that the one-way function behaves as a pseudo-
random function, it is possible to generate the starting
points sequentially, and to store in each table only the
increasing offset in log
2
m bits. The common base can
be stored either in the filename or in a metadata file.
The endpoints size can be reduced as well. The first
method is used if endpoints satisfy the distinguished
point property (cf. Section 2.3): all the bits that can
be reconstructed from the property can be removed
without any loss of information. The second method,
called index file, is similar to the one applied to start-
ing points and consists in storing only offsets from a
base reference for each file. For example, once the
l tables are sorted with respect to the endpoints, each
table can be further split into n tables to remove log
2
n
bits from the endpoints. The last technique, called
endpoint truncation, unlike the previous ones, per-
forms lossy compression. For a given r, a number of
bits can be removed with a truncated matching prob-
ability of
1
r
, thus retaining log
2
r bits. This implies
extra invocations of the one way function in the on-
line phase. As stated in (Kim and Hong, 2013), the
sweet-spot for endpoint truncation is when the trun-
cated endpoints contain more than log
2
m bits, in this
way the extra invocations of the one-way function are
negligible.
4.2 Precomputation
Tables are created according to the parameters chosen
following the method we introduce in Section 3.1, and
computed with (Veronese et al., 2021). The cost of the
precomputation step versus the online phase is com-
puted according to the point chosen on the F
pc
versus
F
tc,s
curve. In particular, the precomputation cost will
be F
p
inv
= F
pc
N. This value represents the number of
invocations of the target function f for the precompu-
tation step. The following equations can be used to
estimate the required time. They ignore the disk write
time, since it is negligible with respect to the compu-
tation time. The encryption rate ER
FPGA
of the FPGA
is the number of applications of the one way function
that can be performed per second:
ER
FPGA
=
freq · cores
clocks
(3)
where freq is the maximum clock frequency that can
be achieved by the FPGA design, cores is the number
of parallel computing units, and clocks are the number
of clock cycles needed for one execution of the one
way function. In fact, FPGAs have a deterministic
behavior that allows for computing the exact number
of clock cycles for a given computation and thus the
exact throughput of the device. The time required by
the FPGA computation is thus:
T
FPGA
=
F
p
inv
ER
FPGA
=
F
p
inv
freq · cores
· clocks (4)
For each of the l tables a set of reduction functions
should be chosen. We suggest the use of s constants
for each table and of the XOR operator, which can be
efficiently implemented in FPGAs. Constants can be
easily computed in the programmable logic from shift
registers starting from an initial constant for every ta-
ble, which must be properly stored. Starting from se-
quential starting points, FPGAs create intermediate,
independent files which are subsequently sorted by
endpoint. This task is parallelized in order to exploit
the full potential of the FPGA. These intermediate ta-
bles contain only endpoints, as the starting points are
sequential, while the file metadata contain the base
number for the starting points, the table number, and
the starting constant for s. Once the intermediate ta-
bles are created they should be sorted by endpoint.
Depending on the size of the endpoints and on m, i.e.,
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
170

the number of chains for each table, the sorting phase
may have a significant impact on the overall precom-
putation time. We recommend to perform the sorting
operation entirely in RAM, applying truncation and
distinguished point property compression while load-
ing the intermediate file to memory. In this way, sort-
ing can be easily done in parallel with table creation,
with no impact on the overall precomputation time.
4.3 Overview of the Online Phase
Figure 6 provides a general overview of the whole
system for the online phase: for each FPGA device
there are two threads, Device Manager Write and De-
vice Manager Read, which are responsible for the in-
teraction with the device pipes. Communication with
device mangers is done through three main queues,
FPGA Wr ite Queue, FPGA Write Queue 2 and FPGA
Read Queue. These are used, as the name suggests,
respectively for sending and receiving data. Writing is
handled via two queues to avoid a warm-up situation
at the start of execution. Specifically, the first write
queue is used during the first step, for jobs that create
all online endpoints, and the second is used during the
second step, for jobs that recompute the stored chains.
The thread called Create-all EPs, referred to earlier as
the first step, can be replicated as needed to mitigate
the warm-up situation as well.
Once endpoints are generated, they can be found
in the FPGA Read Queue and they are fetched by the
Disk Request Generators. These threads, which are
half the number of Disk Uring Event Loops, look up
the table index corresponding to each job and send
read requests to the corresponding Disk Uring Event
Loop. Within the disk event loop, a function is called
to retrieve the events. This function is responsible to
search the fetched disk block page and, in case of a
match, to send the FPGA the corresponding starting
points for recomputation, in order to test if a preim-
age can be found. These components can be dupli-
cated, having for instance two event loops for each
disk. Notice that, each event loop corresponds to only
one disk, and the requests generator is responsible for
sending the job to the corresponding event loop based
on the job table id. The task of processing the FPGA
output relative to a found preimage can be directly
performed by the Device Manager Read. If a preim-
age is found the chain can be sent to a Win Queue.
The threads that recover the key, fetch jobs from the
Win Queue and in case of a valid result they can out-
put the value and stop the global execution.
Algorithm 1: Fuzzy rainbow tradeoff online
search.
procedure RTSingleSearch(target, table)
for cur-start-color ← (s − 1) to 0 do
cur-target-ep ← get-ep-from-color(table,
target, cur-start-color);
truncated-target-ep ←
truncation(cur-target-ep);
range ← binary-search-range(table,
truncated-target-ep);
if range then
foreach sp ∈ range do
preimage ←
find-preimage(sp,target);
if preimage then
return Found, preimage;
end
end
end
end
return Not Found;
4.4 Communication with the FPGA
Devices
Given the high performance requirements for the on-
line phase, the communication with the FPGA de-
vices is crucial to avoid bottlenecks. In the proposed
reference design, every FPGA device has a dedicated
thread for input and a dedicated thread for output
that perform the read/write system calls to mini-
mize the I/O latency. A job queue is associated to
each thread in the form of multi-producer→single-
consumer for the thread that writes to the device, and
single-producer→multi-consumer for the thread that
reads from the device. The use of a fast, thread-
safe multi-producer→multi-consumer queue is sug-
gested to allow for balancing the load across mul-
tiple FPGA devices with minor code edits and, in
our experiments, it has negligible performance penal-
ties with respect to multiple single-producer→single-
consumer queues. In order to reduce the inter-
component communication latency it is vital that the
entire queue size is preallocated and a polling mech-
anism is adopted for waiting for new data from the
queue. We have experimented with various libraries
and the only one giving satisfactory results was the
Atomic Queue Library (Egorushkin, 2019).
4.5 Online Search
Algorithm 1 represents the fuzzy rainbow tradeoff
online search on a single table and without paral-
lelization. In particular, get-ep-from-color is the func-
tion that computes an endpoint given a starting point
A Fast and Cost-effective Design for FPGA-based Fuzzy Rainbow Tradeoffs
171

FPGA
Write
Queue
FPGA
Read
Queue
Device Manager
Write
Device Manager
Read
FPGA
Device Manager
Write
Device Manager
Read
FPGA
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Request
Generator
Disk Request
Generator
Disk Request
Generator
Disk Request
Generator
Disk Request
Generator
Disk Request
Generator
Disk Request
Generator
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Uring
Event Loop
Disk Request
Generator
FPGA
Write
Queue 2
Create-all
EPs
Create-all
EPs
Create-all
EPs
Create-all
EPs
Win Queue
Input Data
Output
Win preimge and
key recovery
worker
Win preimge and
key recovery
worker
Figure 6: Overview of the reference design for the online phase.
and a starting color (online chain generation); trun-
cation is the function that performs endpoint trun-
cation; binary-search-range is the function that per-
forms the binary search on the table and returns the
range of starting points with endpoint equal to the tar-
get; find-preimage is the function that recomputes the
stored chain and searches for a preimage that gen-
erates the target. The FPGA is responsible for of-
floading the computation of the get-ep-from-color and
find-preimage functions. Each specialized unit in the
FPGA is capable of independently computing those
functions. The device operate in a asynchronous way
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
172

so that a new offloading job issued by the host does
not block the execution of other units.
The simplest approach is to try to parallelize Al-
gorithm 1 by creating l threads, one for each table,
and if required, to create multiple threads for each
table according to the number of searches. This ap-
proach falls short because it does not have enough
parallelization to keep the FPGA device fed. We ex-
perimented improvements with coroutines but they
were not fast enough to fully exploit the FPGA per-
formance. The winning strategy consisted in drasti-
cally changing the design, trying to decouple all the
components as much as possible. The idea is to view
the algorithm horizontally instead of vertically, and
hence group all the computation steps between the in-
teractions with the device into different components.
The first step consists of a thread that sends to the
device all the different online chains, with different
lengths, to be computed. Intuitively, this corresponds
to the get-ep-from-color function in Algorithm 1 for
every table, every color and every search. Then, there
is a number of worker threads that perform the search
on the tables, receiving the endpoints from the de-
vice queue and sending to the device the stored chain
starting points that needs to be recomputed in case of
a match. Finally, there is a number of workers that
receive the output from the device and that test if a
preimage was found.
This design solved the issues faced with the thread
and coroutines approach but revealed that the major
bottleneck of the search was disk access. We thus de-
veloped a technique to significantly reduce it. It con-
sists of creating an index of endpoints, stored in main
memory, for each table, that points to file blocks that
can be read independently. This divides the search
into two phases: the first phase consists of a binary
search on the index which always returns either the
lowest value of the index closest to the target, or the
actual position of the target on the index is executed;
the second phase consists of the reading of the block
corresponding to the index and a search on the loaded
block of the file. If the block size is chosen accurately,
this method allows for performing a single disk access
for each search.
Another crucial problem that limits performance
is the synchronicity of disk access. The Linux op-
erating system provides some ways to perform asyn-
chronous disk access, supported by code libraries.
The most popular are async aio and liburing. In
our experiments, liburing was the one that per-
formed best, but for maximum performance the de-
veloper should probably write its own library that uses
directly io uring operating system capabilities.
5 EXPERIMENTAL RESULTS
We have implemented a proof-of-concept system, ac-
cording to the design and guidelines of Section 4. The
implementation is generic but we tuned it to an indus-
trial case study related to a proprietary stream cipher
that we cannot describe due to a non disclosure agree-
ment. The performance of the real system was very
close to the one predicted by the model of Section 3,
with a 95% accuracy. The complexity of the attack
was the same as for DES, and for A5/1 when suffi-
cient data is available. Having a proof-of-concept im-
plementation of the proposed design is important in
order to confirm that the estimated, theoretical perfor-
mance is reachable in practice and there is no penalty
due to limitations imposed by the hardware. As an ex-
ample, adding more SSD units would not scale indefi-
nitely since the number of physical PCI-e lanes avail-
able are limited and, at some point, the total system
memory bandwidth typically becomes the bottleneck.
In principle, once the system works for a particu-
lar cipher, it can be reused for another one by updating
the FPGA implementation. In particular, we discuss
how the very same system would perform when ap-
plied to DES and A5/1, The results show that these ci-
phers can be attacked in real-time, with a online time
of less than a second, a very high precision of 99%
and a budget under 6000e. Interestingly, this online
time is one order of magnitude faster than previous
solutions.
5.1 Hardware and Software
Components
We used an AMD Threadripper platform, the 1920x
processor with 64 GB of RAM, 8 2TB NVME SSDs
(Samsung 970 EVO Plus), and 2 Intel Arria 10
GX1150 FPGA PCI-e cards having a total hardware
cost of around 6000e. For best performance we used
all the replication of the software components shown
in Figure 6. In particular we had four Device Man-
agers, two for Write and two for Read, two Win preim-
age and key recovery threads, two disk groups having
8 Disk Uring Event Loops, one per disk, and 4 Disk
Request Generators, for a total of 8 Disk Request
Generators and 16 Disk Uring Event Loops (cf. Sec-
tion 4.5). We estimated a system IOPS of 2400000,
retrieved through FIO benchmark, but we had to ap-
ply a 0.7 correction coefficient obtaining an actual
system IOPS of 2400000 · 0.7 = 1680000. This co-
efficient was retrieved during development and is due
to both the efficiency of io uring and queue imple-
mentations and general system performance, as well
as data dependencies.
A Fast and Cost-effective Design for FPGA-based Fuzzy Rainbow Tradeoffs
173

The communication interface between the host
and the FPGA was based on Xillybus, a commercial
product by Xillibus Inc., Haifa, Israel. Educational
and evaluation licenses are granted free of charge.
The Linux driver is open-source under GPLv2 and
is part of the official kernel sources. The driver ex-
poses a convenient interface using device files such as
/dev/xillybus*. These communication pipes can
be accessed using standard system calls for opening,
reading, writing and closing files and they work with-
out a user library or specific language bindings.
The FPGAs had an operating frequency of
115MHz and, for our particular industrial case study,
we could perform one encryption every 4 clock cy-
cles, parallelized in 1664 cores. The encryption rate
can be computed using Equation 3 as follows:
ER
FPGA
=
freq · cores
clocks
=
115000000 · 1664
4
≈ 2
35.48
The best encryption rates for DES and A5/1 FPGA
implementations reported in the literature are respec-
tively 2
36
and 2
35.93
, using COPACOBANA, which
are slightly higher than our value of 2
35.48
. COPA-
COBANA FPGAs have a much lower number of in-
ternal basic blocks, and employ an older intercon-
nect architecture and manufacturing process. With
respect to the full 120-FPGAs COPACOBANA, a
system equipped with only 2 Arria 10 GX1150 can
achieve comparable performance. As such, we ar-
gue that we could easily achieve the 2
35.48
encryp-
tion rate for DES and A5/1 as well. Indeed, for a
given design, the updated internal architecture of Ar-
ria 10 typically allows for improved logic density, i.e.,
more computing units per device, and higher oper-
ating clock frequencies. Further improvements can
be very likely obtained by optimizing the logic de-
sign, for instance by carefully balancing the level of
unrolling and pipelining for the specific FPGA archi-
tecture. As such, with reasonable confidence we can
employ the same encryption rate for the performance
estimations in the following paragraphs.
5.2 Estimating the Online Time
The online time is composed of both FPGA compu-
tation time and disk access time. Our tool (Veronese
et al., 2021) computes the number of function f in-
vocations F
o
inv
and the actual FPGA computation time
can be computed through Equation 4. The tool also
computes the number of lookups for the online phase.
With the proposed disk access method each lookup
requires only one disk access. Moreover, according
to our experiments we found that the limiting perfor-
mance factor is the number of input/output operations
per second (IOPS) rather than bandwidth, due to the
Table 1: Parameters and estimated performance for DES.
Parameter Value
m number of chains per table 2
27.25
t DP chain length 2
11
s number of colors 100
l number of tables 2
13.59
r truncation parameter 2
42
ε endpoint size (bits) 36
Measure Value
Available inversion data 1
Success rate 99%
Single table entry size 64 bits
Total table size 15.75 TB
Precomputation cost (F
p
inv
) 2
58.49
Precomputation FPGA time 97.73 days
f iterations for online search 2
33.69
f iterations for false alarms 2
32.90
f iterations for truncation alarms 2
22.09
Total expected f iterations (F
o
inv
) 2
34.35
Total online time FPGA 0.46 s
Total expected lookups 2
18.20
Total expected lookup time 0.18 s
Online time (T
o
) lower b. 0.46s
Online time (T
o
) upper b. 0.64s
small size of the file blocks. We can thus compute
the disk time simply as: T
Disk
=
lookups
IOPS
. The online
time T
o
is then estimated as: max(T
Disk
, T
FPGA
) ≤
T
o
≤ (T
Disk
+ T
FPGA
). Intuitively, the maximum be-
tween T
Disk
and T
FPGA
is a lower bound, achieved
with a well-configured machine with high parallelism
and low latency, while T
Disk
+ T
FPGA
represents the
worst-case, sequential scenario in which FPGA and
disk times sums up.
5.3 Attacking the DES Cipher
DES is a block cipher with a 56-bit key that can be
exhaustively searched in 12.8 days (G
¨
uneysu et al.,
2008). Given the relatively small key size we aim at a
99% success rate with one inversion target and a value
of M compatible with the 16TB of SSD capacity. We
then compute the parameters and estimate the perfor-
mance using (Veronese et al., 2021), as discussed in
Section 3.1. The output of the tool, reported in Ta-
ble 1, highlights the number of function invocations
for the successful online search and for resolving the
alarms, both when a candidate is found on disk but
the corresponding preimage is incorrect, and because
of the use of truncation. These values contribute to
the total expected number of f iterations F
o
inv
.
Notice that, the precomputation phase is expected
to take 97.73 days to complete, which is still doable,
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
174
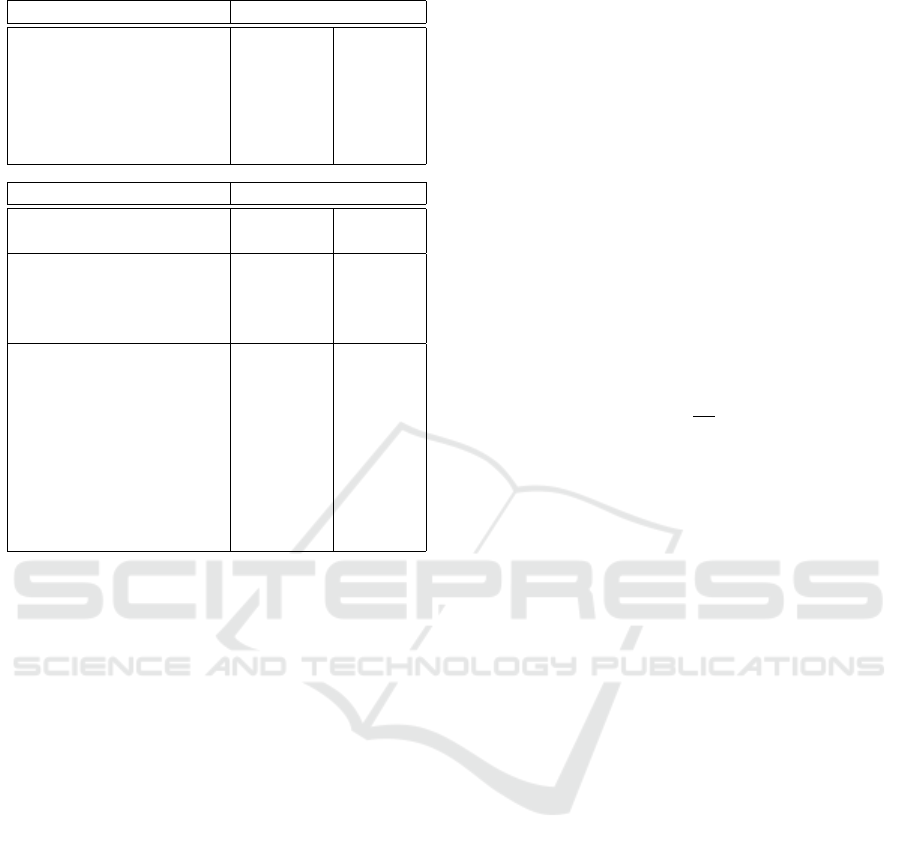
Table 2: Parameters and estimated performance for A5/1.
Parameter Value
m num. of chains per table 2
34.66
2
36.73
t DP chain length 2
11
2
10
s number of colors 53 55
l number of tables 2
6.18
2
4.11
r truncation parameter 2
38
2
39
ε endpoint size (bits) 29 27
Measure Value
Available inversion data 51 204
Success rate 90% 99%
Single table entry size 64 bits 64 bits
Total size 15.75 TB 15.75 TB
Precomputation cost (F
p
inv
) 2
57.29
2
56.29
Precomputation FPGA time 108.85 days 54.63 days
f iter. for online search 2
2
33.01
2
32.02
f iter. for false alarms 2
31.96
2
30.99
f iter. for trunc. alarms 2
26.60
2
25.90
Total exp. f iter. (F
o
inv
) 2
33.59
2
32.61
Total online time FPGA 0.69 s 0.35 s
Total expected lookups 2
17.55
2
17.55
Total expected lookup time 0.11 s 0.11 s
Online time (T
o
) lower b. 0.69s 0.35s
Online time (T
o
) upper b. 0.81s 0.46s
considering also that this step is only performed once.
The total precomputation time also includes the time
required for sorting and compressing the tables as this
operation can be executed in parallel with the table
creation phase. Interestingly, online time is around
half a second, which means DES can be cracked in
real time with our proposed architecture. The most
recent tradeoff attack on DES in the literature is de-
scribed in (G
¨
uneysu et al., 2008). We improve on
it in various respects: (i) we significantly raise the
success rate from 80% to 99%; (ii) we give an ac-
curate estimate of the online time thanks to our opti-
mized design, while (G
¨
uneysu et al., 2008) only com-
putes the number of required online steps, admitting
the existence of communication bottlenecks in COPA-
COBANA that, presumably, prevented authors to im-
plement the online search. Indeed, one of the goals
of our proposal was to reduce communication latency
and data dependencies, allowing us to implement the
online search very efficiently.
5.4 Attacking the A5/1 Cipher
A5/1 is a synchronous stream cipher used in the GSM
communication protocol. It has a 64 bit internal state.
In (Nohl, 2010a; Nohl, 2010b; Lu et al., 2015), the
authors proposed a technique called key space shrink-
ing based on a peculiar property of the cipher: after
the 100 initial clockings, only about 16% of the pos-
sible states are reachable; moreover, clocking back
100 times a valid state gives, on average, 13 ancestors.
Thus, in the online attack, once a preimage is found,
instead of directly recovering the key, it is clocked for-
ward 100 times in order to obtain the internal state that
generates the matched output, and then clocked back-
ward 100 times in order to find all the possible ances-
tors of that state, which are on average 13. This tech-
nique reduces the size of the tables, but has a penalty
in terms of computation cost: in the precomputation
phase every state-to-keystream calculation requires an
additional 100 clocks over the 64 needed to gener-
ate the output; in the online phase every found preim-
age needs to be clocked forward 100 times then back-
wards 100 times instead of only backwards. In order
to estimate the parameters and the performance of our
reference design with this optimization we reduce the
size of the key space to 2
61.36
= 2
64
· 0.16 and the en-
cryption rate by a factor of
164
64
= 2.5625.
In Table 2 we report the parameters and the es-
timates for the optimized attack. The two columns
describe the 90% success rate with 51 inversion data
(one known frame) scenario and 99% success rate
with 204 inversion data (4 known frames) scenario
respectively, with all the available 15.75TB of SSD
space. Notice that, similarly to DES, the online time
is less than a second for both scenarios.
These estimates are far better, in terms of perfor-
mance and success rate, than the most remarkable in
the literature: (Nohl, 2010b) requires 8 known frames
and has a 90% success rate with about 5s online time,
(Lu et al., 2015) requires 4 known frames and has
a 34% success rate with 1TB tables and a predicted
56% success rate with 2TB tables with 9s online time.
In terms of hardware cost our solution is comparable
to both the cited attacks, but probably requires less
energy when in operation, as demonstrated by (Kalen-
deri et al., 2012) when comparing FPGAs and GPUs
for the precomputation phase of a time/memory trade-
off attack on A5/1.
6 CONCLUSION
In this paper, we have proposed a reference hard-
ware and software design for the cryptanalysis of ci-
phers and one-way functions, based on FPGAs, SSDs
and the fuzzy rainbow trade-off algorithm. The sys-
tem has been designed using off-the-shelf affordable
hardware with the idea of realizing an extremely opti-
mized cost-effective solution that can be pushed to its
limits. In this way, we have provided a reference de-
sign and implementation that can be used to estimate
A Fast and Cost-effective Design for FPGA-based Fuzzy Rainbow Tradeoffs
175

the scalability of modern time/memory trade-off tech-
niques on real cryptographic functions.
We have empirically evaluated the performance of
our design and model on a proof-of-concept imple-
mentation, and we have estimated the performance
of attacking two well known ciphers: DES and A5/1.
Our design outperforms previous ones in the literature
by achieving a cracking time under one second with
a 99% accuracy and a 6000e budget, demonstrating
that these two ciphers can be cracked in real time.
Our experience confirms that there is a gap be-
tween the theoretical treatment of time/memory trade-
off algorithms and their practical implementations.
Given the large dimension of the precomputed tables,
it is very important to have a precise external mem-
ory model that allows both to estimate the cost of the
various components and also to parallelize and mod-
ularize the system in the correct way. We have imple-
mented a software tool that can be used to compute
the tradeoff parameters and estimate the performance
of the final system using the external memory model
(Veronese et al., 2021). We hope that our design prin-
ciples and solutions might be useful for the develop-
ment of similar projects in the future.
Finally, we plan to concretely validate the esti-
mated performance figures of DES and A5/1 ciphers
with an actual VHDL design and benchmarking.
ACKNOWLEDGEMENTS
This work has been partially supported by the POR
FESR project SAFE PLACE: “Sistemi IoT per ambi-
enti di vita salubri e sicuri”.
REFERENCES
Barkan, P. (2006). Cryptanalysis of Ciphers and Protocols.
PhD thesis, Israel Institute of Technology.
Egorushkin, M. (2019). Atomic queue. https://github.com/
max0x7ba/atomic queue.
G
¨
uneysu, T., Kasper, T., Novotn
´
y, M., Paar, C., and Rupp,
A. (2008). Cryptanalysis with copacobana. IEEE
Transactions on Computers, 57(11):1498–1513.
Haghighi, M. and Dakhilalian, M. (2014). A practical time
complexity analysis of fuzzy rainbow tradeoff. In
2014 11th International ISC Conference on Informa-
tion Security and Cryptology, pages 39–43.
Hellman, M. E. (1980). A cryptanalytic time-memory trade-
off. IEEE Trans. Inf. Theory, 26(4):401–406.
Kalenderi, M., Pnevmatikatos, D., Papaefstathiou, I., and
Manifavas, C. (2012). Breaking the GSM A5/1 cryp-
tography algorithm with rainbow tables and high-end
FPGAs. In 22nd International Conference on Field
Programmable Logic and Applications (FPL), pages
747–753.
Kim, B.-I. and Hong, J. (2013). Analysis of the non-perfect
table fuzzy rainbow tradeoff. In Boyd, C. and Simp-
son, L., editors, 18th Australasian Conference on In-
formation Security and Privacy, volume 7959, pages
347–362, Berlin, Heidelberg. Springer.
Kim, B.-I. and Hong, J. (2014). Analysis of the perfect table
fuzzy rainbow tradeoff. Journal of Applied Mathemat-
ics, 2014:765394.
Kim, J. W., Hong, J., and Park, K. (2013). Analysis of the
rainbow tradeoff algorithm used in practice. Cryptol-
ogy ePrint Archive, Report 2013/591. https://eprint.
iacr.org/2013/591.
Kumar, S., Paar, C., Pelzl, J., Pfeiffer, G., and Schimm-
ler, M. (2006). Breaking ciphers with copacobana
–a cost-optimized parallel code breaker. In Goubin,
L. and Matsui, M., editors, Cryptographic Hardware
and Embedded Systems (CHES 2006), pages 101–118.
Springer Berlin Heidelberg.
Lu, J., Li, Z., and Henricksen, M. (2015). Time–
Memory Trade-Off Attack on the GSM A5/1 Stream
Cipher Using Commodity GPGPU. In Malkin, T.,
Kolesnikov, V., Lewko, A. B., and Polychronakis, M.,
editors, Applied Cryptography and Network Security,
pages 350–369, Cham. Springer International Pub-
lishing.
Mentens, N., Batina, L., Preneel, B., and Verbauwhede, I.
(2006). Time-Memory Trade-Off Attack on FPGA
Platforms: UNIX Password Cracking. In Bertels, K.,
Cardoso, J. M. P., and Vassiliadis, S., editors, Recon-
figurable Computing: Architectures and Applications,
pages 323–334. Springer Berlin Heidelberg.
Nohl, K. (2010a). A5/1 decrypt - Back clock-
ing. https://opensource.srlabs.de/projects/a51-
decrypt/wiki/Backclocking.
Nohl, K. (2010b). Attacking phone privacy. Black Hat Lec-
ture Notes USA, page 1–6.
Nohl, K. and Paget, C. (2009). Gsm: Srsly. In 26th Chaos
Communication Congress, volume 8, pages 11–17.
Oechslin, P. (2003). Making a faster cryptanalytic time-
memory trade-off. In Boneh, D., editor, Ad-
vances in Cryptology (CRYPTO 2003), pages 617–
630. Springer Berlin Heidelberg.
Quisquater, J.-J. and Standaert, F.-X. (2005). Exhaus-
tive key search of the des: Updates and refine-
ments. Special-purpose Hardware for Attacking Cryp-
tographic Systems (SHARCS’05).
Quisquater, J.-J., Standaert, F.-X., Rouvroy, G., David, J.-
P., and Legat, J.-D. (2002). A Cryptanalytic Time-
Memory Tradeoff: First FPGA Implementation. In
Field-Programmable Logic and Applications, Recon-
figurable Computing (FL’02), pages 780–789.
Robling Denning, D. E. (1982). Cryptography and Data
Security. Addison-Wesley Longman Publishing Co.,
Inc., USA.
Veronese, L., Palmarini, F., Focardi, R., and Luccio, F. L.
(2021). Parameter calculator and performance evalu-
ator tool. https://github.com/secgroup/fuzzy-rainbow.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
176
