Completion of User Preference based on CP-nets in Automated

Negotiation

Jianlong Cai, Jieyu Zhan

∗

and Yuncheng Jiang

Guangzhou Key Laboratory of Big Data and Intelligent Education, School of Computer Science,

South China Normal University, Guangzhou, China

Keywords:

CP-nets, Automated Negotiation, Preference Completion, Incomplete Information.

Abstract:

Automated negotiation is a process in which autonomous agents negotiate with the opponents to achieve

some speciﬁc purposes for their users, such as maximising the users’ beneﬁts. CP-net is one of the most

important representations of user preferences in automated negotiation due to its ability and ﬂexibility to

express interdependent relationship among issues. In order to be able to negotiate better on behalf of users,

a negotiating agent needs to fully understand its user’s preferences, so that it can adopt suitable negotiation

strategies and obtain ideal negotiation results. However, the preference information provided to the negotiating

agents by the users is often incomplete. Hence, based on partial preference information provided, this paper

proposes a module in negotiation framework to complete user total preferences that are represented by CP-nets.

The experimental results show the validity of CP-nets structure learning algorithm in the proposed module and

conﬁrm that the module can help users achieve better agreements in negotiation.

1 INTRODUCTION

Negotiation is a behavioral activity for both parties

to solve problems, which is ubiquitous in human life.

With the rapid development of computer technology,

people have begun to be interested in automated nego-

tiation (Jennings et al., 2001; Kumar and Mastorakis,

2009), that is, a negotiating agent can help or repre-

sent human users to negotiate with other agents or

human opponents. Because of the characteristics of

intelligence and efﬁciency, negotiating agents have

begun to be widely employed in supply chain, e-

commerce and other ﬁelds (Tsimpoukis et al., 2018;

Sanchez-Anguix et al., 2021).

Modelling preferences is a necessary condition for

any step of decision analysis in the ﬁeld of automated

negotiation. Therefore, different kinds of represen-

tations of user preference have been proposed in the

previous studies (Lafage and Lang, 2000; Boutilier

et al., 2004; Amor et al., 2016). However, most of the

studies ignore the situation of incomplete user prefer-

ences. In practical negotiation situations, the assump-

tion of complete user preference is often difﬁcult to

meet due to many reasons. Firstly, users may not be

willing to spend much time to describe the utilities of

all outcomes when the issues are interdependent and

∗

Corresponding author

the outcome space of negotiation is huge. Secondly,

perhaps due to the lack of information, users cannot

give clear preferences to all outcomes of negotiation.

Thirdly, some users may only provide partial prefer-

ence information for privacy reasons. Therefore, it is

very necessary to study how to reason and complete

user preference in negotiation scenarios with incom-

plete user preference information.

Although there are many kinds of preference rep-

resentations studied in the ﬁeld of automated nego-

tiation, in this paper we focus on the one based on

Conditional preference networks (CP-nets) by consid-

ering the following advantages. Firstly, CP-nets can

represent qualitative preferences and tolerates partial

ordering, which is suitable in some scenarios where it

is difﬁcult for the user to assess their preferences in a

quantitative form. Secondly, CP-nets allow represen-

tation of conditional preferences, which can express

interdependent relationship among issues in reality.

Finally, due to the mass of outcome space, it can be

indecisive for users to provide complete information

about their preferences of outcomes one by one, while

CP-nets provide a relatively convenient and intuitive

way to represent preferences.

This paper focuses on automated negotiation with

incomplete user preference information. The contri-

bution of this paper is twofold. Firstly, we extend au-

Cai, J., Zhan, J. and Jiang, Y.

Completion of User Preference based on CP-nets in Automated Negotiation.

DOI: 10.5220/0010909200003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 1, pages 383-390

ISBN: 978-989-758-547-0; ISSN: 2184-433X

383

tomated negotiation frameworks by proposing a mod-

ule for reasoning and completing user preferences

represented by CP-nets. Secondly, we propose an al-

gorithm to learn structures of corresponding CP-nets

from partial pairwise comparisons provided by users.

The rest of the paper is organized as follows. Sec-

tion 2 reviews related work. Section 3 presents back-

ground knowledge on automated negotiation and CP-

nets. Section 4 describes the methods for user prefer-

ence modelling and completion; Section 5 discusses

the experimental setup and analyses the results. Fi-

nally, Section 6 concludes the paper with future work.

2 RELATED WORK

In this section, we will discuss related work about

both negotiations with incomplete information and

learning CP-nets. Incomplete information in auto-

mated negotiations have been studied in many differ-

ent forms, most of which focus on the uncertainty of

opponent model including preferences modelling and

strategies. Compared with opponent modelling, the

research on user modelling with incomplete informa-

tion is relatively less. (Baarslag and Gerding, 2015)

put forward a method to solve the problem of pref-

erence elicitation in negotiation. Using the idea of

greed, they proposed an optimization algorithm with

a time complexity of O(nlogn). Further than the orig-

inal algorithm, the following research (Baarslag and

Kaisers, 2017) supported the situation of stochastic

utility information. (Haddawy et al., 2003) proposed

a method for eliciting user preference models. The

method is based on the Knowledge Based Artiﬁcial

Neural Network (KBANN) pioneered by (Towell and

Shavlik, 1994). When domain knowledge is avail-

able, even in the form of weak and inaccurate hy-

potheses, much less data is required to construct an

accurate user preference model. However, the method

for user preference elicitation in (Haddawy et al.,

2003) is seen as a kind of supervised learning methods

that is not genuinely suitable for using in automated

negotiation scenarios.

The preference representation used in most auto-

mated negotiation frameworks is represented as lin-

ear additive utility functions (Baarslag, 2016), which

is simple and intuitive to compute. However, in prac-

tical situations, there is likely to be interdependence

among the issues of negotiation. CP-nets allow rep-

resentation of conditional preferences, which is more

intuitive to be used to indicate preferences (Boutilier

et al., 2004). Since CP-net represents a partial order

over outcome space, learning CP-nets can be seen as

a ranking learning of preferences from known pair-

wise comparisons (Liu et al., 2018). (Goldsmith et al.,

2008) investigated the computational complexity of

testing dominance and consistency in CP-nets, and

proved that complexity of testing dominance and or-

dering queries are in general NP-hard. CP-nets can

be cyclic or acyclic, but for the sake of intuition

and consistency, the CP-nets we describe default to

acyclic CP-nets. (Liu et al., 2018) learn structure of

CP-nets by calculating dependent degree among at-

tributes. However, most studies of structure learning

only focus on binary-valued CP-nets, which is limited

in the ﬁeld of automated negotiation.

(Dimopoulos et al., 2009) proposed an algorithm

that converts pairwise comparisons to binary-clauses

to learn structure of CP-nets. For employing it in

automated negotiation scenarios, we have extended

the algorithm by three aspects that will be described

in detail in Section 4. (Aydo

gan and Yolum, 2010)

ﬁrst apply CP-nets as preference representations to

utility-based automated negotiation, and extend the

algorithms in (Aydo

gan et al., 2015). However, this

is an estimate of the utility of preferences only if the

CP-nets is known, while our work focuses on learning

unknown CP-nets in automated negotiation scenarios.

3 PRELIMINARIES

In this section, we give a brief overview of the ba-

sic knowledge. We adopt a basic bilateral multi-

issue negotiation scenarios, which has been widely

used in the ﬁeld of negotiation. V = {X

,...,X

}

is the set of issues in negotiation domain. Each

issue X

is associated with a domain of values

DOM(X

) = {x

,...,x

}. The negotiation domain

Ω = DOM(X

) × · · · × DOM(X

) is the set of all pos-

sible negotiation outcomes o. o[X ] denotes the assign-

ment of issue X. The goal of negotiation is to reach an

agreement which is an acceptable outcome for all par-

ties. We denote the set of all assignments to X ⊆ V

by Asst(X ). For example, we set C = {C

}, then

Asst(C ) = Dom(C

) × Dom(C

). For the decision

maker, preference relationship follows a strict partial

order, which is indicated by the symbol ≺. If one

prefers o

to o

, then it can be denoted by o

≺ o

Next, we introduce the concepts of CP-nets and

preference graph (Boutilier et al., 2004).

Deﬁnition 1 (CP-nets). A CP-net is a directed acyclic

graph (DAG) model G, in which nodes represent is-

sues and edges represent the dependencies between

issues. If there is a directed edge from issue X

issue X

, then the preference of X

involves X

for the

user, which is denoted by Pare(X

) = {X

}. Each issue

∈ V holds a condition preference table CPT (X

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

384

Figure 1: A sample CP-net for travel domain with issues

location(L), season(S), duration(D).

which represents the preference ordering of assign-

ments of X for different assignments of Pare(X

) in the

G. If ∀X

∈ V , DOM(X

) is binary, it is called binary-

valued CP-net. If not, i.e., ∃X

∈ V , the amount of

possible assignments of DOM(X

) is more than 2, it is

called multi-valued CP-net.

The following is an example for a CP-net.

Example 1 (Travel Domain). Figure 1 illustrates a

CP-net that shows Justin’s preferences to travel with

three issues: Location, Season and Duration. In this

example, l

denotes Paris and l

denotes Hawaii; s

denotes Winter and s

denotes Summer; d

denotes

3days and d

denotes 7days. When Justin makes a

choice about the duration of the travel, the prefer-

ence for 3days and 7days is conditional. If Paris

and Winter are selected or Hawaii and Summer are

selected, he prefers 7days to 3days; If Paris and

Summer are selected or Hawaii and Winter are se-

lected, he prefers 3days; Note that, comparing the

preference of two outcomes, ancestral values domi-

nate over descendant values. In this example, no mat-

ter D takes d

or d

, all outcomes selecting l

and s

have priority over outcomes selecting l

and s

Deﬁnition 2 (Preference Graph.). Preference graph

is a DAG induced from the CP-net G. Nodes in pref-

erence graph stand for all outcomes in a negotiation

domain, in which the root node presents the worst out-

come for the user and the best outcome placed at the

leaf node. Each directed edge represents an improv-

ing ﬂip. By transitivity, if there exists a path in a pref-

erence graph from o

to o

, then o

and o

are com-

parable, and o

≺ o

, otherwise o

and o

are non-

comparable or called indifferent.

Figure 2 is a preference graph of the CP-net de-

scribed in Example 1. An edge from o

= l

to o

= l

in this preference graph denotes an

improving ﬂip on DOM(D), meaning that the user

prefers o

to o

[D] = d

and o

[D] = d

We will introduce the deﬁnition of preference

database, which will be used in our algorithms.

Figure 2: Preference graph induced from Figure 1.

Deﬁnition 3 (Preference Database). Given two out-

comes o and o

in a CP-net G, if o and o

are compa-

rable, they make up a comparable pairwise compari-

son stored in the preference database P . If o ≺ o

, it

denotes (o,o

), otherwise, it denotes (o

,o). When all

comparable pairwise comparisons derived from the

preference graph which is induced from given CP-

net are in the preference database, we call it stan-

dard preference database. When the set of compa-

rable pairwise comparisons derived from the CP-net

learned by given preference database, we call that

learned preference database.

In this section, we outlined the basics required for

this paper. In the next section, we will introduce the

module we propose and algorithms used in this paper.

4 USER MODELLING

4.1 Module for Preference Completion

Figure 3: The automated negotiation framework with mod-

ule for completion of user preference.

Due to the incomplete information, the agent

needs to estimate the user preference model before

conducting automated negotiation. We propose a

module to complete this task shown in Figure 3. Since

we assume that users preferences are represented by

CP-nets, the ﬁrst thing we address is structure learn-

ing of CP-nets. The structure of CP-net is learned

from a set of pairwise comparisons provided from the

user, and then the preference graph is induced from

Completion of User Preference based on CP-nets in Automated Negotiation

385

the learned structure. There may be some offers that

are not comparable based on the preference graph.

However, most negotiation strategies and opponent

modelings are based on quantitative preferences lead-

ing to a totally ordered set of outcomes. Therefore,

we use the appropriate heuristics method (Aydo

gan

et al., 2015) to transform qualitative preferences into

quantitative preferences.

4.2 Structure Learning of CP-nets

Algorithm 1: learn(Issue set V , preference database P ).

Output: a learned CP-net G with respect to P

1: G ⇐

0;R ⇐

0;X ⇐ V ; k ⇐ 0

2: Add all issues in V with empty CPT into G.

3: while k < |V | do

4: if k = 0 then

5: R ⇐ findRoots(P,X , G)

6: X ⇐ X \ R

7: else

8: added ⇐ extendNetwork(P ,X ,V , k,G)

9: X ⇐ X \ added

10: end if

11: if X =

0 then

12: return G

13: end if

14: end while

15: if X 6=

0 then

16: learningWithMaxSAT(P , X ,R ,G)

17: end if

18: return G

We present an algorithm to tackle the problem of

structure learning, which extends the algorithm pro-

posed by (Dimopoulos et al., 2009) to better accom-

modate automated negotiation scenarios. As shown in

Algorithm 1, main procedure learn() takes a prefer-

ence database P provided from user and the issue set

V as input, and outputs an acyclic CP-net that satis-

ﬁes the standard preference database as much as pos-

sible. At ﬁrst, the algorithm maintains an empty CP-

net G and a set X containing issues to be learned, k

denotes the number of provisional parents of issue X,

where the process loops until either k = |V | or the CP-

net G is constructed. Since the assignment of ances-

tor nodes (issues) impact the preferences of descen-

dant issues, accurate derivation of the root issues in

CP-nets is crucial. However, the original algorithm is

essentially an approximate learning algorithm, which

is not accurate enough. For the above reasons, ﬁrst

we extend the original algorithm as follows.

When k = 0, we call Algorithm 2 f indRoots() to

ﬁnd root issues in the CP-nets. Considering every X

in X , X will be a root issue if there exists an ordering

Algorithm 2: f indRoots(P ,X , G).

Output: issue set R

1: R ⇐

2: for X in X do

3: I ⇐ X \ X

4: if exist an ordering of values of X that satis-

ﬁes Comparisons = {P | o[I ] = o

[I ] } then

5: R .add(X)

6: createCPT (X,ordering)

7: end if

8: end for

9: return R

Algorithm 3: extendNetwork(P , X , V ,k,G).

Output: issue set added

1: added ⇐

2: for X in X do

3: U ⇐ provisionalParentSet(X,X ,G)

4: K ⇐ parentCombinations(U,k)

5: for K in K do

6: I ⇐ X \ (X ∪ K)

7: parentOrNot(K,X,I )

8: end for

9: if One of K ∈ K is the parent of X then

10: added.add(X)

11: end if

12: end for

13: return added

of values of X that satisﬁes comparisons set {P |

o[I ] = o

[I ]}, where I represents a subset of X except

X. That is, the preference ordering of X is not condi-

tioned by any assignments of the other issues. Finally

it creates the CPT (X) based on ordering. Once the

CPT (X) is created, X will be removed from the set

X .

When k > 0, we call extendNetwork() shown in

Algorithm 3, traversing X in the set X to extend

the G by completing CPT (X). During the travers-

ing, provisionalParentSet() returns a provisional par-

ent set of X, denoted by U, which guarantees that

the learned CP-net is acyclic. parentCombinations()

returns a set K of combinations of k elements se-

lected from U. During iterating through K in K ,

parentOrNot() decides whether K can be the par-

ent combination of X in G. parentOrNot() exam-

ines pairwise comparisons (k

) ∈ P , where

∈ Asst(K ), x

6= x

, x

∈ Asst(X), i

= i

∈ Asst(I), and chooses the suitable clauses in

: x

≺ x

and k

: x

≺ x

leading to no contradic-

tion among all clauses selected. Taking an example of

contradiction, a

: b

≺ b

, a

: b

≺ b

and a

: b

≺ b

have been selected, then the CPT (B) is induced as

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

386

: b

≺ b

. The above problem can be

converted into Boolean satisﬁability problem (SAT).

Since the number of clauses in the element of the set

are no more than 2, the SAT instance above is the 2-

SAT, which could be solved in polynomial time. In

this paper, we employ solvers (Morgado et al., 2014;

orensson and Een, 2005) for solving SAT. Each unit

can be separated into two parts to be encoded, one

is the assignment of K, and the other one is the re-

lationship between assignment of X . As an example,

: b

≺ b

can be encoded as α

, a

: b

≺ b

can be

encoded as ¬α

, and a

: b

≺ b

is encoded as β

. Fi-

nally, it solved the 2-SAT and writes into the CPT (X)

with the decoded results. We take an example for de-

scribing this process.

Example 2. Consider the issues A, B, C with values

}, {b

}, {c

} respectively. During

the invocation of parentOrNot({A},B, {C}) (deter-

mine whether {A} is the parent of B with the same

assignments of {C}), given pairwise comparisons are

as follow:

(1) a

≺ a

, (2) a

≺ a

(3) a

≺ a

, (4) a

≺ a

(5) a

≺ a

, (6) a

≺ a

Deduce these pairwise comparisons above:

(1) a

: b

≺ b

, (2) a

: b

≺ b

or a

: b

≺ b

(3) a

: b

≺ b

, (4) a

: b

≺ b

or a

: b

≺ b

(5) a

: b

≺ b

, (6) a

: b

≺ b

or a

: b

≺ b

We associate the elements of {A} with component of

Boolean variables as follows: the assignment a

⇒ α,

⇒ β. And the relationship b

≺ b

are associated

with subscript. Based on the above rules, the result-

ing SAT instance is (α

) ∧ (β

∨ α

) ∧ (α

) ∧ (¬β

∨

¬α

) ∧ (α

) ∧ (¬α

∨ ¬β

). And the solution of SAT

instance above are (α

,α

,¬β

). Consider-

ing ﬁrst three elements (α

,α

), they can be de-

coded as a

: b

≺ b

, a

: b

≺ b

and a

: b

≺

respectively, which can be deduced an ordering

: b

≺ b

and written into the CPT (B) with

: b

≺ b

. The remaining only have 2 clauses

: b

≺ b

, a

: b

≺ b

. According to transferability,

it could still deduce a

: b

≺ b

. Therefore, {A}

is the set of parent of B, and CPT (B) is created.

The second extension is described as follows:

Firstly, there may be such a situation that more than

one K satisﬁes being the parent of X , while only one

K can be parent of X , in principle. To cope with this

situation, we consider the count of clauses, K with

maximum count of clauses will be the parent of X.

Secondly, once the ordering is incomplete, it is neces-

sary to make a completion. Therefore, We use the

method BordaCount (Emerson, 2013) to determine

the incomplete position in the ordering.

Algorithm 4: learningWithMaxSAT(P ,X , R , G).

1: for X in X do

2: for R in R do

3: f it = Fitness(X,R)

4: end for

5: R

= argmax( f it)

6: R

is a parent of X, and create CPT (X)

7: end for

8: return

The following is the third extension of the original

algorithm. Back to the main procedure, if there are is-

sues remaining in the set X after completion of the

traversal on K, original algorithm will return False

to indicate failure of learning, which is not available

for automated negotiation scenarios. Therefore, we

calls learningWithMaxSAT () shown in Algorithm 4

to learning remaining issues. This function is sim-

ilar to the extendNetwork() shown in Algorithm 3.

For less complexity, the parents of remaining issues

X ∈ X is considered from R , and only one issue could

be the parent of X. The method that decides whether

R ∈ R can be the parent of X translates the prob-

lem into a SAT instance. But we only need to solve

for its maximum satisﬁable (Max-Sat) solution. We

choose the one with the maximum satisfaction rate

as the parent of X and create CPT (X ). When all

CPT (X), X ∈ V have been created, the CP-net G is

completed and main procedure learn() returns G.

4.3 Transformation of User Preferences

Given a CP-net, the ordering of the relationships

among the outcomes is a partial order sequence, so

there will be non-comparable pairwise comparisons

in most of the time. In order to better use various

strategies in automated negotiation scenarios, trans-

forming qualitative preferences into quantitative pref-

erences is useful that agent can get a total ordering

of outcomes and know all utility of outcomes in that

domain. The method Taxonomic Heuristic (TH) pro-

posed by (Aydo

gan et al., 2015) is used to handle this

problem. We brieﬂy summarized below. Considering

a preference graph induced from a given CP-net, the

root node keeps the worst outcome and the leaf node

keeps the best outcome for the user. That is, given

two outcomes, the dominance between them is deter-

mined by their depth (length of the longest path from

the root node to this node). The higher depth one is

assigned by higher utility.

U(o

) = Max(U(Parent(o

))) + ran (1)

According to Equation (1) , the outcome’s utility is

equals the maximum utility among its parents plus

Completion of User Preference based on CP-nets in Automated Negotiation

387

a random value ran ∈ (0, 1], which ensures its util-

ity is higher than its ancestors’ and maximize leaf

node’s teutility as well. Although the randomized

approach results in an unstable ordering among non-

comparable pairwise comparisons, it provides a ref-

erence to user for non-comparable pairwise compar-

isons, and comparable pairwise comparisons are not

affected. Hence, the overall impact is not signiﬁcant.

5 EXPERIMENTS

In order to demonstrate the effectiveness of our mod-

ule, the experiments were divided into two parts: one

is to evaluate the performance of structure learning

and the other is to demonstrate the feasibility of our

module in negotiation scenarios.

5.1 Performance of Structure Learning

To evaluate the performance of structure learning, we

consider experiments of learning CP-nets with 7 is-

sues. We consider 300 randomly generated CP-nets

with the number of edges from 1 to 10, where each as-

signment of edges randomly generates 30 CP-nets and

we ensure all CP-nets are acyclic and multi-valued.

To test learning performance with 20% of standard

database (including noise data), the metrics we se-

lected are the similarity of structure, error and accu-

racy of learning root issues. The formula of similarity

of structure is deﬁned as follows:

Similarity =

|V |

∑

n=1

sim(X

), (2)

where

sim(X

) =







score(X

) if X

is root issue,

/(e

+ r

)

|V |

otherwise,

(3)

score(X

) =







|V |

if X

is root issue,

0 otherwise.

(4)

In Equation (3), X

and X

denote an issue in learned

CP-net and original CP-net, respectively. r

denotes

the number of parent of X

learned accurately and e

denotes the number of parent of X

learned by error.

When Similarity = 1, it means the learned structure

is exactly the same as the given structure. The error

is the difference between learned preference database

and standard preference database. Equation (5) de-

scribes the formula for calculating error:

error =

num(incorrect pairwise comparisons)

num(standard preference database)

. (5)

Figure 4: This results of learning CP-nets in different edges.

num(incorrect pairwise comparisons) includes the

pairwise comparisons that are in standard prefer-

ence database but not in learned preference database

and are contrary to the facts by standard preference

database.

The experiment results of structure learning are

shown in Figure 4. The horizontal coordinate indi-

cates the edge number in a CP-net. Considering the

dominance of the CP-nets, the performance of learn-

ing the root issues accurately may be more important

than that of learning other issues in negotiation. The

blue line denotes the probability of accurately learn-

ing all root issues in the experiment. As we expected,

the performance of learning decreases with increasing

structural complexity. Results show that the structure

of the CP-net can be roughly learned with given data.

5.2 Application in Negotiation Scenario

To demonstrate the effectiveness of our framework,

we applied our module to automated negotiation sce-

narios and tested its performance. We randomly gen-

erated ﬁve domains with ﬁve issues for experiment.

The preference proﬁles are generated with CP-nets

model for two dummy users by given domains, but

the agents just know 20% of standard preference

database. Each domain is used for ten epochs of ne-

gotiation. For fairness, the agents will hold prefer-

ence proﬁle of counterpart to compete repeat, i.e., two

times of negotiation per epoch. We investigate three

test cases. In each case, two agents (A and B) with

the same bidding strategy compete with each other.

There are three subcases in each case. In the subcase

1, both agents use our module (denote as our.vs.our.).

In the subcase 2, agent A uses our module while agent

B does not. In the subcase 3, both two agents estimate

user model randomly. The classic time dependent tac-

tics proposed by (Faratin et al., 1998) are used for

each case. Its curve of utility thread and equation are

shown in Figure 5.

The utility threshold varies over time. When

β < 0, it adopts an aggressive static called Boulware;

When β = 0, the function curve is a straight line and

the static is called Linear; When β > 0, the agent

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

388

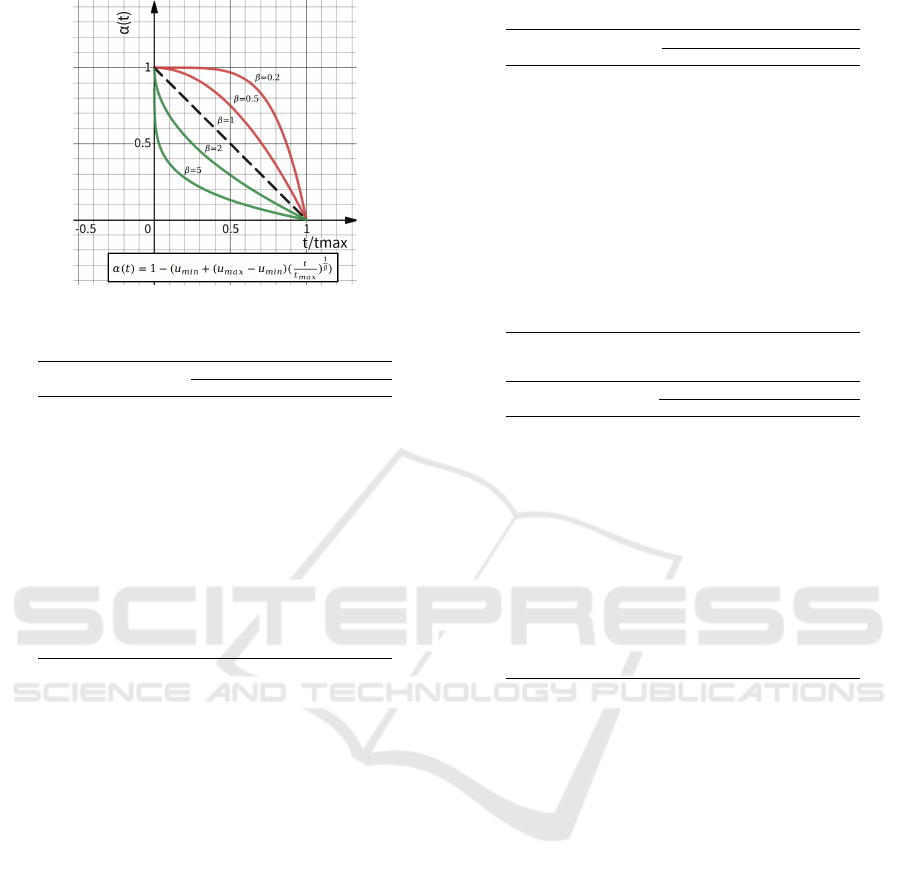
Figure 5: The curve of utility thread.

Table 1: The results of negotiation in the case Boulware.

Boulware

uti.A uti.B round soc.

Dom.1

our. vs. our. 0.46 0.48 451.20 0.94

our. vs. bas. 0.61 0.41 358.35 1.02

bas. vs. bas. 0.43 0.46 261.50 0.88

Dom.2

our. vs. our. 0.57 0.61 521.70 1.18

our. vs. bas. 0.82 0.64 395.40 1.45

bas. vs. bas. 0.50 0.56 342.90 1.05

Dom.3

our. vs. our. 0.62 0.61 509.90 1.23

our. vs. bas. 0.76 0.34 368.60 1.10

bas. vs. bas. 0.38 0.51 301.60 0.89

Dom.4

our. vs. our. 0.62 0.60 419.15 1.22

our. vs. bas. 0.78 0.33 396.35 1.11

bas. vs. bas. 0.51 0.42 272.00 0.93

Dom.5

our. vs. our. 0.68 0.66 276.35 1.35

our. vs. bas. 0.73 0.60 372.75 1.34

bas. vs. bas. 0.43 0.45 302.85 0.88

with this static called Conceder will make conces-

sions quickly. Each negotiation is limited to 1000

rounds, i.e., t

max

= 1000. The range of utility of

each outcome is normalized at [0,1], i.e., u

min

= 0

and u

max

= 1. The protocol used in this simulation

experiments is alternating-offers protocol. Both sides

take turns to alternate bids until time runs out or one

of agent offers to terminate the negotiation. If one of

agent offers to accept opponent’s offer, the agreement

is reached with the last bid offered.

The results of average utility, average round and

average social welfare with β = 0.5, β = 1 and β = 2

are shown in Table 1, Table 2 and Table 3, respec-

tively. It is intuitive that in any subcase, the use of

Conceder results in the minimum rounds per nego-

tiation. The results of subcase 2 in all cases show

that the average utility obtained by agent A is always

higher than that obtained by agent B, which veriﬁes

the effectiveness of our model for user modelling. By

comparing results in subcase 1 and subcase 3, average

social welfare obtained by agents in subcase 1 is more

than that in subcase 3. The negotiation in subcase 1

takes more time (average round) than that in subcase

3. Combining two analyses above, higher social wel-

Table 2: The results of negotiation in the case Conceder.

Conceder

uti.A uti.B round soc.

Dom.1

our. vs. our. 0.46 0.48 46.95 0.94

our. vs. bas. 0.57 0.38 39.25 0.94

bas. vs. bas. 0.42 0.44 9.85 0.86

Dom.2

our. vs. our. 0.58 0.63 73.70 1.21

our. vs. bas. 0.69 0.57 41.35 1.25

bas. vs. bas. 0.47 0.48 16.90 0.94

Dom.3

our. vs. our. 0.64 0.56 59.85 1.21

our. vs. bas. 0.75 0.31 26.95 1.06

bas. vs. bas. 0.46 0.40 9.50 0.85

Dom.4

our. vs. our. 0.61 0.61 30.35 1.21

our. vs. bas. 0.71 0.43 29.80 1.14

bas. vs. bas. 0.46 0.55 12.30 1.01

Dom.5

our. vs. our. 0.67 0.67 11.75 1.34

our. vs. bas. 0.70 0.59 33.25 1.28

bas. vs. bas. 0.47 0.48 12.05 0.95

Table 3: The results of negotiation in the case Linear.

Linear

uti.A uti.B round soc.

Dom.1

our. vs. our. 0.49 0.51 218.40 1.00

our. vs. bas. 0.58 0.42 369.45 1.00

bas. vs. bas. 0.44 0.49 76.10 0.93

Dom.2

our. vs. our. 0.64 0.64 266.95 1.28

our. vs. bas. 0.77 0.61 380.45 1.37

bas. vs. bas. 0.43 0.48 103.05 0.91

Dom.3

our. vs. our. 0.59 0.63 258.50 1.22

our. vs. bas. 0.73 0.35 404.95 1.08

bas. vs. bas. 0.43 0.42 73.05 0.85

Dom.4

our. vs. our. 0.58 0.62 168.00 1.20

our. vs. bas. 0.75 0.38 401.90 1.13

bas. vs. bas. 0.45 0.59 77.85 1.04

Dom.5

our. vs. our. 0.66 0.68 96.95 1.34

our. vs. bas. 0.72 0.62 360.00 1.34

bas. vs. bas. 0.45 0.49 102.35 0.95

fare was obtained despite the decline in utility thresh-

olds with the passage of time, which reﬂects that

agents with our model are willing to spend more time

on negotiation with opponent towards higher utility.

6 CONCLUSION

This paper studied how to complete user preference

with incomplete information in automated negotiation

scenarios where user preferences are represented by

CP-nets. Firstly, we extended the method of learn-

ing CP-nets (Dimopoulos et al., 2009) to reveal the

dependencies among issues, in which the extensions

including (1) special handling of the root issues to

learn more accurately; (2) optimising the choice of

provisional parents during learning structure; and (3)

avoiding failing to learn CP-nets. Secondly, we esti-

mate utility of offers by TH after completion of CP-

nets, making the preference representations of CP-

nets can be applied in automated negotiation. Finally,

we experimentally demonstrated the feasibility of our

module for completion of user preference in negoti-

ation. Much more could be done in the future. For

Completion of User Preference based on CP-nets in Automated Negotiation

389

example, due to the structures of CP-nets are inter-

pretative, users can easily express their attitude to-

wards the effect of preference completion, then how

to make agents interact with users efﬁciently to im-

prove the accuracy of completion of preference is one

of the most important problems should be address in

the future.

ACKNOWLEDGEMENTS

The works described in this paper are supported by

the National Natural Science Foundation of China un-

der Grant Nos. 62006085, 61772210 and U1911201;

Guangdong Province Universities Pearl River Scholar

Funded Scheme (2018); Project of Science and Tech-

nology in Guangzhou in China under Grant Nos.

202007040006 and 202102020948; Natural Science

Foundation of Guangdong Province in China under

Grant No. 2018A030310529; Project of Department

of Education of Guangdong Province in China under

Grant No. 2017KQNCX048.

REFERENCES

Amor, N. B., Dubois, D., Gouider, H., and Prade, H.

(2016). Graphical models for preference representa-

tion: An overview. In Scalable Uncertainty Manage-

ment, pages 96–111.

Aydo

gan, R., Baarslag, T., Hindriks, K. V., Jonker, C. M.,

and Yolum, P. (2015). Heuristics for using CP-nets

in utility-based negotiation without knowing utilities.

Knowledge and Information Systems, 45(2):357–388.

Aydo

gan, R. and Yolum, P. (2010). Effective negotiation

with partial preference information. In Proceedings

of the 9th International Conference on Autonomous

Agents and Multiagent Systems, pages 1605–1606.

Baarslag, T. (2016). Exploring the strategy space of negoti-

ating agents: A framework for bidding, learning and

accepting in automated negotiation. Springer.

Baarslag, T. and Gerding, E. H. (2015). Optimal incre-

mental preference elicitation during negotiation. In

Twenty-Fourth International Joint Conference on Ar-

tiﬁcial Intelligence, page 3–9.

Baarslag, T. and Kaisers, M. (2017). The value of infor-

mation in automated negotiation: A decision model

for eliciting user preferences. In Proceedings of the

16th Conference on Autonomous Agents and MultiA-

gent Systems, pages 391–400.

Boutilier, C., Brafman, R. I., Domshlak, C., Hoos, H. H.,

and Poole, D. (2004). CP-nets: A tool for representing

and reasoning with conditional ceteris paribus prefer-

ence statements. Journal of Artiﬁcial Intelligence Re-

search, 21:135–191.

Dimopoulos, Y., Michael, L., and Athienitou, F. (2009).

Ceteris paribus preference elicitation with predic-

tive guarantees. In Proceedings of the 21st Inter-

national Joint Conference on Artiﬁcial Intelligence,

pages 1890–1895.

Emerson, P. (2013). The original borda count and partial

voting. Social Choice and Welfare, 40(2):353–358.

Faratin, P., Sierra, C., and Jennings, N. R. (1998). Ne-

gotiation decision functions for autonomous agents.

Robotics and Autonomous Systems, 24(3-4):159–182.

Goldsmith, J., Lang, J., Truszczynski, M., and Wilson, N.

(2008). The computational complexity of dominance

and consistency in CP-nets. Journal of Artiﬁcial Intel-

ligence Research, 33:403–432.

Haddawy, P., Ha, V., Restiﬁcar, A., Geisler, B., and

Miyamoto, J. (2003). Preference elicitation via the-

ory reﬁnement. The Journal of Machine Learning Re-

search, 4:317–337.

Jennings, N. R., Faratin, P., Lomuscio, A. R., Parsons,

S., Wooldridge, M. J., and Sierra, C. (2001). Au-

tomated negotiation: Prospects, methods and chal-

lenges. Group Decision and Negotiation, 10(2):199–

215.

Kumar, S. and Mastorakis, N. E. (2009). A utility

based, multi-attribute negotiation approach for seman-

tic web services. WSEAS Transaction on Computers,

8(11):1733–1748.

Lafage, C. and Lang, J. (2000). Logical representation of

preferences for group decision making. In Proceed-

ings of the Seventh International Conference on Prin-

ciples of Knowledge Representation and Reasoning,

pages 457–468.

Liu, Z., Zhong, Z., Li, K., and Zhang, C. (2018). Struc-

ture learning of conditional preference networks based

on dependent degree of attributes from preference

database. IEEE Access, 6:27864–27872.

Morgado, A., Dodaro, C., and Marques-Silva, J. (2014).

Core-guided maxsat with soft cardinality constraints.

In International Conference on Principles and Prac-

tice of Constraint Programming, pages 564–573.

Springer.

Sanchez-Anguix, V., Tunalı, O., Aydo

gan, R., and Julian, V.

(2021). Can social agents efﬁciently perform in auto-

mated negotiation? Applied Sciences, 11(13):6022.

orensson, N. and Een, N. (2005). Minisat v1. 13-a

sat solver with conﬂict-clause minimization. SAT,

2005(53):1–2.

Towell, G. G. and Shavlik, J. W. (1994). Knowledge-based

artiﬁcial neural networks. Artiﬁcial intelligence, 70(1-

2):119–165.

Tsimpoukis, D., Baarslag, T., Kaisers, M., and Paterakis,

N. (2018). Automated negotiations under user prefer-

ence uncertainty: A linear programming approach. In

Agreement Technologies - 6th International Confer-

ence, AT 2018, Revised Selected Papers, pages 115–

129.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

390