Towards Model-driven Fuzziﬁcation of Adaptive Systems Speciﬁcation

Tomáš Bureš

, Petr Hn

etynka

, Martin Kruliš

and Jan Pacovský

Charles University, Faculty of Mathematics and Physics, Prague, Czech Republic

Keywords:

Adaptive Systems, Fuzziﬁcation, Machine Learning, Model-driven, Meta-models.

Abstract:

The position paper outlines a method transforming adaptation rules in a self-adaptive system to a machine

learning problem using neural networks. This makes it possible to endow a self-adaptive system with the

possibility to learn. At the same time, by controlling the degree to which this transformation is done, one can

scale the tradeoff between learning capacity and uncertainty in the self-adaptive system. The paper elaborates

this process as a model transformation pipeline. The pipeline starts with a model capturing the strict adaptation

rules. Then it is followed by multiple steps in which the strict rules are gradually fuzziﬁed by well-deﬁned

transformations. The last model transformation in the pipeline transforms the fuzziﬁed rules to a neural network

that can be trained using the traditional stochastic gradient descent method. We brieﬂy showcase this using two

examples from the area of collective adaptive systems.

1 INTRODUCTION

Nowadays, smart self-adaptive systems can be found

in almost all application domains — e.g., smart build-

ing management (smart heating, ventilation, physical

access control, etc.), smart cities (trafﬁc management),

emergency systems, smart agriculture, and production

management in Industry 4.0, to name just a few. In all

these systems, applications are composed of a rather

large number of components that cooperate on a com-

mon goal.

Cooperation among a group of components is typi-

cally speciﬁed via collaboration and adaptation rules.

These rules are domain- and application-speciﬁc and

are expressed as hard and soft constraints. Recent ap-

proaches to these systems started experimenting with

employing neural networks to better deal with situa-

tions that are not fully expected.

However, a discrete step from logical rules to neu-

ral networks typically means that one cannot easily

prescribe (at least some) behavior using rules, rather

everything has to be trained — this is because neural

networks work as a black-box.

Motivating this from the perspective of our re-

search, we have been quite successful in employing

the concept of autonomic component ensembles to de-

https://orcid.org/0000-0003-3622-9918

https://orcid.org/0000-0002-1008-6886

https://orcid.org/0000-0002-0985-8949

https://orcid.org/0000-0002-3895-7962

scribe group cooperation. An ensemble (Bures et al.,

2020) deﬁnes several conditions that are constraints

(temporal, spatial, and other) under which a group

(i.e., an instance of the ensemble) of components is

established. Evaluation of ensembles is continuous

and thus the groups of components are dynamic and

may overlap (a single component can be a member of

several ensemble instances at the same time). To ﬁnd

an assignment of components to ensemble instances, a

constraint solver is employed.

Over the years, we have beneﬁted from the con-

cept of ensembles in a number of projects from mul-

tiple different domains (IoT, smart farming, Industry

4.0). However, we have encountered two issues that

are pushing us to machine learning (using neural net-

works). First, we have to increasingly deal with uncer-

tainty in systems that the pre-deﬁned rules are not fully

ﬁt to handle. Second, for large systems with a high

number of components, the exponential complexity of

evaluating the rules using a constraint solver becomes

a problem (which is further aggravated by the need to

evaluate ensembles continuously at runtime).

Moving towards the neural network approach, we

reformulated the problem of ensemble evaluation from

a constrain solving one to classiﬁcation one and em-

ploy machine learning using neural networks. Our

initial experiments (Bureš et al., 2020) in this direction

are rather promising.

A big pitfall of this solution, when done trivially,

is that the abstractions used by the neural network

336

Bureš, T., Hn

etynka, P., Kruliš, M. and Pacovský, J.

Towards Model-driven Fuzziﬁcation of Adaptive Systems Speciﬁcation.

DOI: 10.5220/0010910800003119

In Proceedings of the 10th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2022), pages 336-343

ISBN: 978-989-758-550-0; ISSN: 2184-4348

are too different to the traditional logical rules. Many

practitioners thus typically opt to drop the natural un-

derstanding of the system (which is inherent when

using logical rules) and go for a black-box approach

represented by the neural network.

In our work, we advocate a compromise that brings

the better of both approaches: it preserves some level

of natural understanding of the system (which comes

from the logical rules) and it can learn to better deal

with not fully expected situations (which comes from

the neural network).

We outline this approach in this paper. The ap-

proach is model-based — it relies on a gradual transfor-

mation of models that capture the logical rules govern-

ing the operation of the system. Each step corresponds

to the fuzziﬁcation of the logical rules, gradually mov-

ing the logical rules towards a generic neural network

while keeping a clear relation to the original logical

rules.

The result of each of these model-transformation

steps yields a fully working system. Thus, the ap-

proach we present uses the model-transformation pro-

cess to create a family of systems, which all address

the same goal and only differ in the trade-off between

natural understandability and trainability.

The particular goal of this position paper is to pro-

pose (meta-)models that are used in the approach and

to design the overall approach as a model-driven trans-

formation pipeline.

To achieve the goal, the paper is structured as fol-

lows. Section 2 presents several motivation cases from

different domains. The (meta-)models and model-

driven pipeline are described in Section 3. In Section 4,

we discuss related work and Section 5 concludes the

paper.

2 ENSEMBLES AND

MOTIVATION CASES

As mentioned in the introduction, we are considering

self-adaptive systems that are speciﬁed via autonomic

component ensembles. Using this approach, entities

of a system are modeled as components, which are de-

ﬁned by their state (also called a knowledge). From the

point of interactions, a component is passive — i.e., it

does not actively communicate with other components.

The interaction is modeled via ensembles that deﬁne

conditions under which particular components are part

of the ensemble. A single component can be in mul-

tiple ensembles at the same time. The ensemble also

prescribes data interchange among components in the

ensemble and also prescribes group-wise tasks (e.g.,

coordinated movement). More details are provided

within the code examples in the rest of this section

where we discuss two motivation cases from two dif-

ferent domains. Both cases are taken from our recent

and ongoing projects with industrial partners.

2.1 Case #1 – Smart Farming

As the ﬁrst motivation case, we are using a simple but

real-life scenario from our ECSEL JU project AFar-

Cloud

, which focuses on smart farming. Figure 1

shows the example visualized in our simulator devel-

oped for demonstration of the project results.

Figure 1: Motivation case #1.

In the example, there are several ﬁelds with crop

(yellow ones in the ﬁgure) that needs protection from

ﬂocks of birds. To drive the birds out of these ﬁelds

(to areas that cannot be damaged by the birds — green

and brown ﬁelds on the ﬁgure), there is a set of drones.

They monitor the farm environment (temperature, hu-

midity, etc.) but also detect the ﬂocks. To effectively

drive the birds out, the drones need to cooperate (a

bigger ﬂock of birds requires more drones) and form

a temporary group. The battery of a drone has only a

limited capacity and thus the drones need to recharge

themselves (the chargers are depicted as rounded ar-

row blocks in the center). However, the charger can

accommodate only a limited number of drones at the

same time.

In the ensemble-based speciﬁcation, drones, charg-

ers, ﬁelds, and even ﬂocks are described as compo-

nents. The ﬂocks are beyond direct control, thus their

state is only observed and not affected by the ensem-

bles. For drone cooperation, there are several ensem-

bles deﬁned — e.g., one for creation of a drone forma-

tion for the ﬁeld protection, one for charging coordina-

tion, etc. A complete speciﬁcation of the example in

our DSL for ensembles can be found in (Bureš et al.,

2020).

https://www.ecsel.eu/projects/afarcloud

Towards Model-driven Fuzziﬁcation of Adaptive Systems Speciﬁcation

337

Listing 1 shows a high-level speciﬁcation of a con-

straint deﬁning a condition whether a particular drone

is low on battery and thus switches its operation task

(and can be subsequently selected by an ensemble re-

sponsible for the charger assignment).

1 rule GoToCharger(drone) {

2 condition {

3 drone.energy < ENERGY_TRESHOLD

4 }

5 action {

6 drone.task = GO_TO_CHARGER

7 }

8 }

Listing 1: Charging condition.

Similarly, there is a constraint when the drone is

close to a dangerous ﬂock and thus switches its op-

eration task to driving the ﬂock away — shown in

Listing 2. Here, the condition ﬁlters out nearby ﬂocks

(in terms of Euclidean distance as computed in a helper

predicate, which is also included) and then determines

whether at least one such ﬂock exists.

1 rule ScareFlock(drone) {

2 condition {

3 drone.knownFlocks.ﬁlter(ﬂock −>

4 distanceLessThan(drone.pos, ﬂock.pos, 10))

5 .size() > 0

6 }

7 action {

8 drone.task = SCARE_FLOCK

9 }

10 }

12 pred distanceLessThan(pos1, pos2, dist) {

13 sqrt((pos1.posX − pos2.posX) ^ 2 +

14 (pos1.posY − pos2.posY) ^ 2) < dist

15 }

Listing 2: Flock condition.

Finally, there is a constraint (Listing 3) selecting a

required number of active drones for given phase of

the day. It is based on an observation that the birds

are very active during the morning, somewhat active

during the afternoon, and sleeping during the night (but

at least a single drone is required always to monitor

environment at any given time). Here, the condition is

not speciﬁed as the rule is active always.

1 rule activeDrones() {

2 action {

3 activeDrones = switch (hour(NOW)) {

4 case 0..5: 1

5 case 5..11: 10

6 case 11..19: 5

7 case 19..24: 1

8 }

9 }

10 }

Listing 3: Active drones condition.

2.2 Case #2 – Access Control in

Industry 4.0

The second case is also a real-life scenario — this

time taken from our international project Trust 4.0.

The scenario primarily targets physical access con-

trol within a company. In the company, the workers

work on projects for different customers. Each of these

projects is assigned to a different group of workers (the

groups are disjoint). The reason for such an organi-

zation is protecting of customers intellectual property

and the workers from different teams cannot commu-

nicate and cannot even share the same room (with

exceptions of corridors, bathrooms, etc.). To ensure

these constraints, the workers are controlled in terms,

which rooms they should (or are allowed to) enter.

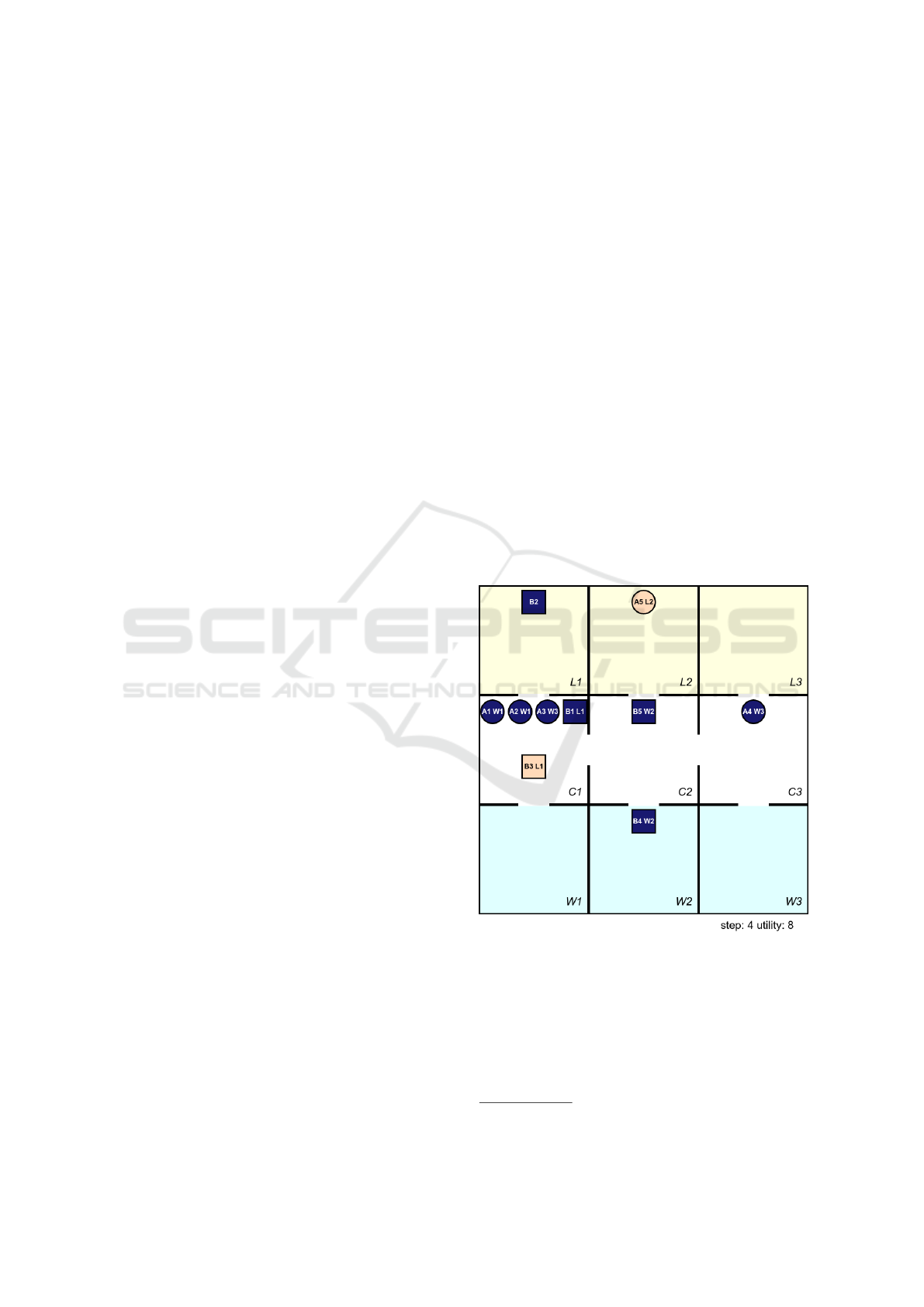
Figure 2: Motivation case #2.

Figure 2 shows a screenshot from our simulator of

the scenario (for a small number of rooms and work-

ers). In particular there are three working rooms (W1–

W3 at the bottom), three lunch rooms (L1–L3 at the

top), and three corridors in the middle. Circles and

squares represent workers — the shape distinguishes

afﬁnity of the worker to a particular team. Color of the

http://trust40.ipd.kit.edu/home/

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

338

shapes distinguishes mode of the worker (blue for the

working mode and orange for the want-to-eat mode).

Labels within the shape are IDs of the worker and

assigned room.

Since the capacity of the rooms is limited, the even

the workers from different teams need to share rooms.

In such case, the workers can share rooms if their

teams are declared as compatible. The compatibility

of teams is deﬁned explicitly via matrix — e.g., for

four teams (labeled A–D) the matrix can be visualized

as follows (check-mark represents team compatibility).

A predicate for identifying compatibility simply reads

the appropriate value in the matrix.

A B C D

A X X X

B X X X

C X X

D X X X X

Within the constraints of which workers are al-

lowed to meet and which are not, the system controls

the dynamic assignment of rooms such that the needs

of the workers (e.g., to work and to have lunch) are

satisﬁed.

3 MODEL-DRIVEN

FUZZIFICATION APPROACH

Although the speciﬁcation in the previous section

works well in fully anticipated situations, the fact that

it has no capacity to learn surfaces quickly when the

level of uncertainty increases.

In this section, we outline how to transform (re-

lying on the model transformation principles) a rule-

based system into a system that has capacity to learn

and that can eventually be implemented using a neural

network.

While we could replace the system with a generic

neural network (e.g., a multi-layer perceptron with sev-

eral hidden layers), we argue that this trivial solution

is too generic and any domain-speciﬁc knowledge en-

coded in the original rules would be lost. Instead, we

preserve the domain knowledge coming from the strict

adaptation rules and we transform them into “learnable

rules” that will be directly mappable to the correspond-

ing fragments of a neural network.

We perform this transformation in steps where the

result of each step is a working system with a certain

level of learning capacity. Each step fuzziﬁes the sys-

tem and increases its learning capacity (by replacing

some predicates with corresponding counterparts with

higher learning capacity).

The transformation can be shown on the condition

of the rule in Listing 1. Here, the less-than operator

and strict value are replaced with a “fuzzy” operator

isNotEnough

(Listing 4), which takes three parameters:

(1) a value to be tested, (2) minimal value, and (3) max-

imal value. After the transformation, the system has

the ability to learn this particular condition.

1 condition {

2 isNotEnough(drone.energy, min=0, max=100)

3 }

Listing 4: Charging condition fuzziﬁed.

The condition can be “fuzziﬁed” further (shown

in Listing 5) and replaced with a generic operator

hasRightValue1D

, which represents a general learn-

able interval. The

capacity

parameter expresses the

learning capacity, which determines the number of

neurons in the hidden layer in the underlying neural

network for training (the higher it is, the more complex

function it can learn).

1 condition {

2 hasRightValue1D(drone.energy,

3 min=0,

4 max=100,

5 capacity=20)

6 }

Listing 5: Charging condition fuzziﬁed — 2

level.

Similarly, the condition in Listing 2 can be up-

dated. Within the ﬁrst level of fuzziﬁcation via the

spatial operator

isCloseEnough

and within the sec-

ond level of fuzziﬁcation via the generic operator

hasRightValue2D

, which is shown in Listing 6. It is

the same operator as in the case of

hasRightValue1D

but this time for two-dimensional values (tuples).

1 condition {

2 drone.knownFlocks.ﬁlter(ﬂock −>

3 hasRigthValue2D[ﬂock.id](drone.pos,

min=(0,0), max=(100,100), capacity=20))

4 .size() > 0

5 }

Listing 6: Charging condition fuzziﬁed — 2

level.

For the drone selection based on time of the day

(Listing 3), the ﬁrst level of fuzziﬁcation is based on

the temporal operator

getValueBasedOnTime

, while

the second level is again via the

hasRightValue1D

op-

erator.

For fuzziﬁcation of the condition in the second

motivation case, the operator

isInRelation

with two

parameters is used in the ﬁrst level of fuzziﬁcation

while in the second level, there is the generic operator

hasRightCategories

. The operator takes a ﬁxed-size

vector of categorical values (in this particular case

Towards Model-driven Fuzziﬁcation of Adaptive Systems Speciﬁcation

339

Meta-model

of neural

networks

Meta-model

with fuzzy

condition

Meta-model

with strict

condition

transformation

Neural

networks

specification

transformation

n-th level

fuzzification

Specification

with strict

conditions

1st level

fuzzification

«instanceOf»

Figure 3: Transformation pipeline.

workers in a room) and it learns which combinations

of values correspond to the true output.

3.1 Model-driven Pipeline

As shown above, we propose a gradual transformation

of an adaptive system speciﬁcation with logical adap-

tation rules to a speciﬁcation with trainable rules. The

advantage of such an approach is that the speciﬁca-

tion of logical rules can be created by a domain expert,

which has no knowledge of the neural networks and the

construction of trainable rules, and these are generated

semi-automatically from the logical ones. The core of

the speciﬁcation (components and ensembles) remains

the same and only the conditions in the ensemble spec-

iﬁcations will be transformed. A modeling tool then

can easily assist developers during transformations,

i.e., it can navigate to conditions within the ensemble

deﬁnitions and propose a suitable transformation of

operators based on their operands and context.

Earlier in this section, we have showcased a two-

step transformation, but in general there can be any

number of them. The overall process is illustrated in

Figure 3.

To simplify the development of speciﬁcations and

allow for tool-support, we deﬁne the whole process

as a model-driven pipeline, where a developer starts

with a model and gradually executes transformations

on it to get a more detailed one that can be further

transformed to an executable speciﬁcation with neural

networks.

To support these transformations, we have created

a meta-model that is also shown in Figure 3 (the indi-

vidual speciﬁcations in the pipeline are models con-

forming to the meta-model). In detail, the meta-model

is described in the following section.

The exact transformation to the neural network (to-

gether with the meta-model of a neural network spec-

iﬁcation) is beyond the scope of this paper. Here we

elaborate the model-driven aspect of this approach. In

a nutshell, we transform each fuzzy condition to a frag-

ment of a neural network (e.g., the

hasRightValue1D

and

hasRightValue2D

get turned to an RBF neural net-

work layer

). The logical connections are then turned

to arithmetic operations over outputs of the network

corresponding to the operands.

3.2 Meta-model

We have created a single meta-model split into several

packages. Its overall structure is shown in Figure 4.

The core speciﬁcation concepts that are common to all

our models (i.e., deﬁnitions of components and ensem-

bles), are deﬁned in the

Components and Ensembles

package. Then, there are two additional packages that

merge with the core package. The ﬁrst of them deﬁnes

the operators for strict conditions while the second one

deﬁnes operators for fuzzy speciﬁcations.

Strict conditions

Fuzzy conditions

Component and Ensembles

«merge»

Figure 4: Meta-model structure.

Figure 5 shows an excerpt of the core

Components and Ensembles

package. Just to

brieﬂy overview it, there are Components and

Ensembles — both of them can have deﬁned

DataFields. Ensembles can be hierarchically nested

(the sub-ensembles association) and they have rules,

which based on Conditions, select the components to

be in the Ensemble. The Condition is composed of

condition expressions which are either a Predicate

or the Operator expression. The OperatorExpr class

is abstract and its concrete realizations are deﬁned

in particular packages based on the used level of the

speciﬁcation.

https://en.wikipedia.org/wiki/Radial_basis_function_

network

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

340

«MetaClass»

OperatorExpr

«MetaClass»

ConditionExpr

«MetaClass»

PredicateExpr

«MetaClass»

Condition

«MetaClass»

Rule

«MetaClass»

Ensemble

«MetaClass»

DataField

«MetaClass»

Component

expr

expression

selects

subensembles

Figure 5: Components and Ensembles package.

Figure 6 shows the main part of the

Strict conditions

packages. There are several

deﬁned operator expressions that extend the abstract

OperatorExpr class. The

ScalarThreshold

operator

declares, as its name suggests, a scalar comparison

with a given threshold. It has two arguments (omitted

in the ﬁgure to leave it concise) for a value and

threshold and then it has a ﬁeld for the kind of

comparison (less-than, greater-then, etc.). It is used

for modeling the condition from Listing 1. Similarly,

there is

EuclideanDistanceThreshold

that offers

a comparison of two-dimension values and it has

the same structure as the previous operator. It can

be used for the condition in Listing 2. Next, the

CategoricalSelection

is used for selecting a value

from several possibilities (categories) and it is used in

for modeling conditions in Listing 3 and compatibility

checking in the motivation case #2. Finally, there can

be deﬁned other operators (currently left as future

work).

Component and Ensembles

...other operators...

«MetaClass»

CategoricalSelection

«MetaClass»

EuclideanDistanceThreshold

+kind

«MetaClass»

ScalarThreshold

+kind

«MetaClass»

OperatorExpr

Figure 6: Strict conditions.

Finally, Figure 7 shows the main part of the

Fuzzy conditions

packages. As in the Strict pack-

age, there is a set of operator expressions extend-

ing the abstract OperatorExpr class. The operators

are those already introduced in the examples at the

beginning of this section. Additionally, there is

a direct relation with the strict operators. In par-

ticular, the

IsNotEnough

and

HasRightValue1d

are

fuzzy variants of the

ScalarThreshold

operator. Sim-

ilarly, the

IsCloseEnough

and

HasRightValue2d

cor-

respond to

EuclideanDistanceThreshold

and, ﬁnally,

the

IsInRelation

and

HasRightCategories

correspond

to the CategoricalSelection operator.

Component and Ensembles

«MetaClass»

IsInRelation

«MetaClass»

IsCloseEnough

«MetaClass»

IsNotEnough

...other operators...

«MetaClass»

HasRightCategories

«MetaClass»

HasRightValue2D

«MetaClass»

HasRightValue1D

«MetaClass»

OperatorExpr

Figure 7: Fuzzy conditions.

4 RELATED WORK

The main idea of our approach is to gradually trans-

form a system speciﬁcation with strict logical rules to

more fuzzy rules and ultimately towards a generic neu-

ral network and subsequent evaluation of a fuzzy logic

system. Thus, the related work areas are application of

neural network for representation of logical formulas

and applying them in adaptive systems. Also, as the

approach is based on models and transformation, the

related areas are usage of model-driven approaches in

adaptive systems.

The idea of using neural network for logic condi-

tions is not new and ﬁrst attempts can be found in (Li

et al., 2001), where a kind of calculus method to deter-

mine the truth-values of propositional logic formulas is

deﬁned. The recent approaches in this direction can be

found in (Shi et al., 2019; Riegel et al., 2020), where

more sophisticated neural networks are employed. We

in general take a similar approach, however we are

applying it in practice in the area of adaptive systems.

Most importantly, we shape it as a model transforma-

tion pipeline to integrate it better with MDD process.

As we move to the domain of adaptive systems,

there are also applications of neural networks and ma-

Towards Model-driven Fuzziﬁcation of Adaptive Systems Speciﬁcation

341

chine learning. A quite large area (but not directly

related) is anomaly detection in such systems (detect-

ing attacks, intrusions, etc.). An overview of such

techniques can be found in (Mohammadi Rouzbahani

et al., 2020).

There are also a number of closely related ap-

proaches that employ neural networks and machine

learning directly in the adaptation cycle. For example

in (Van Der Donckt et al., 2020), neural network-based

approach is applied during the analysis and planning

phase of the MAPE-K cycle to reduce adaptation space.

We propose to use neural networks in the same phases

but to fuzzify strict conditions and make them learn-

able. Similarly to the previous approach, neural net-

works are employed in (Gabor et al., 2020) as well to

reduce large adaptation space. Different application

of neural networks in adaptive systems can be found

in (Muccini and Vaidhyanathan, 2019), where they are

used to predict QoS parameters of a system and thus

allow for proactive adaptation.

A model-driven approaches to model and develop

adaptive systems can be found in several works, e.g.,

in (D’Angelo et al., 2018) and (Weyns and Iftikhar,

2019) but they do not employ any machine learning

methods. In the conclusion of the latter paper, the au-

thors plan to include them and in (Weyns et al., 2021),

the same authors propose inclusion of machine learn-

ing techniques to most of the phases of the adaptation

cycle (primarily to predict and optimize adaptation).

However, none of these inclusion follows the same or

similar approach as our one.

Conceptually similar approach is discussed

in (Ghahremani et al., 2018), where machine learning

techniques are utilized to train a model for rule-based

adaptation. Nevertheless, the authors use different

machine learning approaches than neural networks.

To sum up, there are numerous approaches com-

bining neural networks and adaptive systems, but none

of them uses the same direction as our one — that is

to view the integration of neural networks to adaptive

systems as a gradual model transformation process

which makes it possible to scale the learning capacity

of the system.

5 CONCLUSION

We have proposed an approach of gradual transforma-

tion of the traditional logical rule-based speciﬁcation

of adaptive systems into a speciﬁcation where the rules

are learnable and implemented as generic neural net-

works. As the paper is a position one, we are currently

working on an implementation of the approach. Partic-

ularly, we are focusing on two directions.

First, we are working on the complete speciﬁcation

of the meta-models and transformations. We plan to

employ a modeling tool (EMF

-based one), for which

we plan to create plugins assisting developers during

the transformations.

Second, we are working on the evaluation of the

approach. It means a deﬁnition of semantics of the

fuzzy operators — i.e., deﬁnition of a structure of

underlying neural networks and implementation of the

runtime environment for ensemble execution.

ACKNOWLEDGMENTS

This work has been partially supported by the Czech

Science Foundation project 20-24814J and also par-

tially supported by Charles University institutional

funding SVV 260451.

REFERENCES

Bureš, T., Gerostathopoulos, I., Hn

etynka, P., and Pacovský,

J. (2020). Forming Ensembles at Runtime: A Machine

Learning Approach. In Proceedings of ISOLA 2020,

Rhodes, Greece, volume 12477 of LNCS. Springer.

Bures, T., Gerostathopoulos, I., Hnetynka, P., Plasil, F., Krijt,

F., Vinarek, J., and Kofron, J. (2020). A language and

framework for dynamic component ensembles in smart

systems. International Journal on Software Tools for

Technology Transfer, 22(4):497–509.

D’Angelo, M., Napolitano, A., and Caporuscio, M. (2018).

CyPhEF: a model-driven engineering framework for

self-adaptive cyber-physical systems. In Companion

Proceedings of ICSE 2018, Gothenburg, Sweden, pages

101–104. ACM.

Gabor, T., Sedlmeier, A., Phan, T., Ritz, F., Kiermeier, M.,

Belzner, L., Kempter, B., Klein, C., Sauer, H., Schmid,

R., Wieghardt, J., Zeller, M., and Linnhoff-Popien, C.

(2020). The scenario coevolution paradigm: adaptive

quality assurance for adaptive systems. International

Journal on Software Tools for Technology Transfer,

22(4).

Ghahremani, S., Adriano, C. M., and Giese, H. (2018). Train-

ing Prediction Models for Rule-Based Self-Adaptive

Systems. In Proceedings of ICAC 2018, Trento, Italy.

Li, H., Qin, K., and Xu, Y. (2001). Dynamic neural net-

works for logic formula. In Proceedings of the 8th

international conference on information processing.

Mohammadi Rouzbahani, H., Karimipour, H., Rahimne-

jad, A., Dehghantanha, A., and Srivastava, G. (2020).

Anomaly Detection in Cyber-Physical Systems Using

Machine Learning. In Handbook of Big Data Privacy.

Muccini, H. and Vaidhyanathan, K. (2019). A Machine

Learning-Driven Approach for Proactive Decision

https://www.eclipse.org/modeling/emf/

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

342

Making in Adaptive Architectures. In Companion Pro-

ceedings of ICSA 2019, Hamburg, Germany.

Riegel, R., Gray, A., Luus, F., Khan, N., Makondo, N.,

Akhalwaya, I. Y., Qian, H., Fagin, R., Barahona,

F., Sharma, U., Ikbal, S., Karanam, H., Neelam, S.,

Likhyani, A., and Srivastava, S. (2020). Logical Neu-

ral Networks. arXiv:2006.13155 [cs].

Shi, S., Chen, H., Zhang, M., and Zhang, Y. (2019). Neural

Logic Networks. arXiv:1910.08629 [cs, stat].

Van Der Donckt, J., Weyns, D., Quin, F., Van Der Donckt,

J., and Michiels, S. (2020). Applying deep learning to

reduce large adaptation spaces of self-adaptive systems

with multiple types of goals. In Proceedings of SEAMS

2020, Seoul, Korea. ACM.

Weyns, D. and Iftikhar, M. U. (2019). ActivFORMS: A

Model-Based Approach to Engineer Self-Adaptive Sys-

tems. arXiv:1908.11179 [cs].

Weyns, D., Schmerl, B., Kishida, M., Leva, A., Litoiu, M.,

Ozay, N., Paterson, C., and Tei, K. (2021). Towards

Better Adaptive Systems by Combining MAPE, Con-

trol Theory, and Machine Learning. In Proceedings of

SEAMS 2021, Madrid, Spain, pages 217–223. IEEE.

Towards Model-driven Fuzziﬁcation of Adaptive Systems Speciﬁcation

343