Management of Groups of Passengers on Buses Considering the

Restrictions of COVID-19

Francesca Guerriero

, Martina Luzzi

and Giusy Macrina

Department of Mechanical, Energy and Management Engineering, University of Calabria, Italy

Keywords:

COVID-19, Social Distancing, Passenger Transportation, Group Seat Assignment Problem.

Abstract:

During the epidemiological emergency, the measures adopted by the governments to contain the spread of the

virus have caused heavy changes in the passenger transportation sector. In this work, we address the problem

of managing groups of passengers on buses considering COVID-19-related restrictions. We propose a linear

integer programming model to represent mathematically the bus group assignment problem, whose main aim

is to make the best seat-passenger assignment, in such a way that the social distancing constraints, imposed

for containing the spread of COVID-19, are satisﬁed. The developed formulation, accordingly to the current

Italian rules, considers not only the physical distancing among passengers, but also the possibility to allocate

household groups close to one another. The proposed model is tested empirically considering a real case

study of a bus company operating in Italy. The computational results reveal that our model could help the

transportation company to effectively manage the capacity, improve customer service, and maintain the social

distancing in order to prevent the risk of contagion, by maximizing the revenue.

1 INTRODUCTION

The ongoing global spread of COVID-19, started at

the beginning of 2020, dramatically affects global-

ized societies and economies. All the governments

prompted forceful measures for transmission contain-

ment, causing widespread social and economic dis-

ruptions. In this paper, we focus on the passengers

transportation service, more speciﬁcally on buses sec-

tor, considering the pandemic restrictions related to

the physical distancing. The report “Observatory on

mobility trends during the COVID-19 health emer-

gency”, drawn up by the Mission Technical Struc-

ture for the strategic direction, infrastructure devel-

opment and High Surveillance of the Italian Ministry

of Infrastructure and Transport (MIT), shows that, in

Italy, the journeys made through collective transporta-

tion services have undergone a more marked reduc-

tion compared to private/individual road transporta-

tion, reaching reductions even higher than 90% in

the period March-April 2020 compared to the pre-

COVID-19 period.

The second wave of spread of the virus and the

https://orcid.org/0000-0002-3887-1317

https://orcid.org/0000-0001-9193-4332

https://orcid.org/0000-0001-6762-3622

consequent restrictive mobility policies have pro-

duced less marked effects on collective transporta-

tion than those observed during the ﬁrst lockdown,

with maximum reductions of 60%. In particular,

high-speed rail journeys underwent a reduction of

up to almost 100% in the period March-April 2020.

This drastic peak was also recorded, in addition to

the restrictive measures adopted, in the face of a re-

duction in the offered services by more than 95%.

Movements on maritime services, instead, suffered a

slightly different reduction in passenger demand com-

pared to that observed for land services, with losses

that amounted to around 90-100% in the period April-

May 2020, and then began to grow, while still show-

ing a signiﬁcant reduction (about 20%) in passenger

demand in July 2020. Finally, travel on air services

has undergone a 99% reduction in both demand and

supply, which has started in March 2020 and reached

a minimum in the period April-May 2020, and then

slightly has begun to grow. On March 20, 2020, the

Italian shared regulatory protocol was adopted for the

containment of the spread of COVID-19 in the trans-

portation and logistics sector.

In the protocol, distance, protections and sanita-

tion become imperative indications for the safe use of

mobility services. The rules of distancing that regu-

late the “how to sit” on the various transportation vec-

Guerriero, F., Luzzi, M. and Macrina, G.

Management of Groups of Passengers on Buses Considering the Restrictions of COVID-19.

DOI: 10.5220/0010911300003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 67-76

ISBN: 978-989-758-548-7; ISSN: 2184-4372

tors are rigid, just because they could represent a vehi-

cle of contagion. Making collective passengers trans-

portation safe and acceptable is the main goal of all

the governments as well as of the transportation com-

panies. Proposing ﬂexible but effective solution for

managing the available seats on a vehicle, consider-

ing physical distancing, guaranteeing the safety of the

travellers and the containment of virus spread is cru-

cial. However, an inadequate allocation of passengers

may lead to an additional loss of revenues. Our main

goal is to propose an effective strategy that, on the one

hand, guarantees travellers safety, on the other one,

maximizes the revenues as much as possible. In par-

ticular, we propose a linear integer programming for-

mulation to represent the bus group assignment prob-

lem (BGAP, for short). The main aim is to manage the

bus capacity (i.e., available seats), by maximizing the

revenue and considering COVID-19 social distance

restrictions. The rest of the paper is structured as fol-

lows: Section 2 describes the state-of-art on passenger

transportation in the pandemic era and focuses on the

limitations and rules imposed in Italy on the collective

transportation. Section 3 presents a linear integer pro-

gramming formulation for the BGAP under COVID-

19 social distance in the case of bus passengers trans-

portation service. Computational experiments are dis-

cussed in Section 4, while Section 5 summarizes the

conclusions.

2 PASSENGER

TRANSPORTATION IN THE

PANDEMIC ERA

In this section, we ﬁrstly discuss brieﬂy about pas-

senger transportation, highlighting the importance of

this sector. Secondly, we focus on the impacts of

the Covid-19 pandemic on the collective passenger

transportation, by analyzing several scientiﬁc contri-

butions.

2.1 Passenger Transportation

Collective transportation provides everyone with per-

sonal mobility, giving each person the possibility to

perform his/her daily activities, such as accessing to

employment, schools, medical care, and community

resources, as well as his/her occasional ones, such

as reaching vacation spots. Collective transportation,

public or private, may include buses, trains, under-

ground rail systems, airplanes and also cars in the

context of sharing services (Ferrero et al., 2018).

Each type of transportation vector has its speciﬁc fea-

tures, for example, an airplane is faster than a bus,

however it is also more expensive. In general, among

the key factors that inﬂuence customers choice be-

tween alternative transportation modes, there are the

travel time, the cost and the convenience (Hancocka

et al., 2021). Another important aspect that inﬂu-

ences customers choice is the environmental sustain-

ability. Recent surveys, as the one carried by the

booking platform Omio (www.Omio.it), show that

potential customers prefer to select transportation so-

lutions, characterized by low emissions and small car-

bon footprint.

Collective mobility is central to the whole society,

hence, offering efﬁcient and effective services to cus-

tomers is a critical aspect for all companies operating

in this sector. To pursue this goal, it is important man-

aging the available and limited resources avoiding any

type of waste. Thus, ﬁnding methods that allow to op-

timize the capacity of the transportation vectors, try-

ing to maximize the revenue from the sold tickets, is a

very discussed topic. In fact, numerous authors have

already addressed it in the past, see, e.g., (Lin et al.,

2020; Wang et al., 2018; Ongprasert, 2006); however,

it still represents a challenge for researchers, scholars

and companies.

2.2 Consequences of the Pandemic on

Transportation

In the last two years, the pandemic has contributed

to increase the difﬁculties of managing capacity of

transportation vectors. The new regulations, imposed

to contain and stop the spread of infections on trans-

portation vectors, are conﬁgured as additional con-

straints that must be taken into account when manag-

ing the capacity. Indeed, the rules of social distancing

lead to a reduction of the bookable seats and, conse-

quently, to a lower possibility of obtaining revenues

deriving from the sales of tickets. Figure 1 shows the

conﬁguration that must be adopted by bus following

the social distancing rules. The capacity limitation

imposes that the seats adjacent to the one occupied

by a passenger are forbidden, and therefore cannot be

used to allocate other travelers.

For this reason, developing models that optimally

manage the allocation of passengers on transporta-

tion vectors, maximizing sales and consequently the

revenues, and respecting the distancing constraints is

a current challenge for both the scientiﬁc research

and the service providers operating in the passenger

transportation sector. Although the reference context

is new and constantly evolving, several authors have

already addressed this topic under different perspec-

tives and application ﬁelds. (Fischetti et al., 2021)

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

Figure 1: Layout and limitations of capacity on buses. The

green squares represent the bookable seats; while crossed

gray squares the forbidden seats, hence the not bookable

ones.

study the problem of locating facilities in a given

area, subject to social distancing constraints. The goal

is to maximize the area utilization, as well as min-

imize the overall virus spread among facilities, fol-

lowing the social distancing rules. They analyze the

similarities between this problem and that of locat-

ing wind turbines in an offshore area. In fact, sim-

ilarly to people who can infect each other, also tur-

bines located close to one another may to “infect”

each other by casting wind shadows (the so-called

“wake effect”), that cause production losses. The dis-

covery of this parallelism allows the authors to ap-

ply mathematical optimization algorithms originally

designed for wind farms, to produce optimized facil-

ity layouts, that minimize the overall risk of infec-

tion among customers. The results of the research

show that in the structure of the safest layouts, the

facilities are not equally distanced (as it is typically

believed), but a policy, that signiﬁcantly reduces the

overall risk of contagion, tends to concentrate the fa-

cilities on the border of the available area. (Barry

et al., 2021) consider a space allocation problem, that

incorporates social distancing constraints, while opti-

mising the number of available safe work-spaces, in

an on-site working scenario. The solution approach

is based on a bipartite graph of disconnected compo-

nents over a graph of constraints. The obtained results

are compared to a constrained random walk heuristic

and a linear programming approach. A few contri-

butions focused on the ﬁeld of collective passengers

transportation. (Salari R. et al., 2020) address the air-

plane passengers seat assignment problem, while en-

suring social distancing among passengers. The au-

thors propose a mixed integer integer programming

model to assign passengers to seats on an airplane,

such that two types of social distancing constraints

are satisﬁed. The ﬁrst type refers to passengers being

seated far enough away from each other. The metric

for this type of social distancing is how many passen-

gers are seated so close to each other as to increase the

risk of infection. The second one refers to the initial

model to determine seat assignments, that maximize

distance between seat assignments and the aisle. This

distance inﬂuences the health risk involved in pas-

sengers and crew members walking down the aisle.

Corresponding metrics for both passengers and crew

members health risks are included in the objective

function. The authors also provide an additional ver-

sion of the initial model, in order to determine the seat

assignments, that maximize the number of passengers

boarding an airplane while practicing social distanc-

ing among passengers. The study of (Gkiotsalitis and

De Weert, 2021) introduces a mixed-integer quadratic

program that sets the optimal frequencies of public

transportation lines and sub-lines, in order to conform

with the pandemic-imposed capacity restrictions. The

so called frequency setting model is tested on a net-

work containing high-demand bus lines and it demon-

strates that the revenue losses due to social distancing

can be reduced when implementing short-turning ser-

vice patterns. (Gongyu et al., 2021) redesign routes

and bus schedules for University of Michigan’s cam-

pus bus system, during the COVID-19 pandemic, with

the aim to balance individuals safety and operational

efﬁciency. In particular, they propose a hub-and-

spoke design and utilize real data of student activ-

ities to identify hub locations and bus stops to be

used in the new routes. (Moore et al., 2021) study

the seat assignments with physical distancing in pub-

lic transit considering a mixed-integer programming

model deﬁned to assign passengers to seats based on

the speciﬁc conﬁguration of the vehicle and desired

physical distancing requirement. They also develop a

Management of Groups of Passengers on Buses Considering the Restrictions of COVID-19

”household grouping heuristic” that allows household

members to seats near to each other without respect-

ing social distancing, and show that the proposed ap-

proach increases the capacity of the transit vehicles

(e.g., airplanes, school buses, and trains) without in-

creasing the risk of infection. The ongoing pandemic

of COVID-19 and the constant change of rules to ar-

rest the spread of the virus have been a high impact

on transportation sector. Providing ﬂexible models

to manage the capacity during these sudden events is

crucial for avoiding the service disruption. The ma-

jority of the reviewed works, focused on social dis-

tancing, hence on the reduction of the capacity of the

vehicles. However, only one work, i.e., (Moore et al.,

2021), considers the possibility to allocate household

groups on adjacent seats. In our work we focus on

this particular strategy, currently adopted in bus pas-

senger transportation. For this type of transport, in

fact, the current Italian rule establishes that the use of

adjacent seats is limited exclusively to cohabiting pas-

sengers in the same housing unit, as well as between

relatives and people who have stable interpersonal re-

lationships. It is clear that this possibility could lead

to a potential increase in the capacity of the vehicle

(i.e., number of allocable seats), and consequently an

increase in the number of sold tickets, hence to obtain

additional revenues. Our work present some similar-

ities with (Moore et al., 2021), in fact, they consider

the allocation of groups of people on a bus. How-

ever, the main difference is that (Moore et al., 2021)

consider a single-destination transportation service,

in our work, instead, we consider more lines and a

multi origin-destination scenario. In addition, (Moore

et al., 2021) propose a heuristic approach to allocate

the groups, while in our work we propose a mathe-

matical model to handle the problem.

3 A LINEAR PROGRAMMING

MODEL FOR GROUPS

ASSIGNMENT PROBLEM

UNDER COVID-19

RESTRICTIONS

We propose a mathematical model for managing dif-

ferent sized kin groups of passengers on the buses, re-

specting the social distancing limitations imposed by

the Italian government rule reported in the previous

section. The proposed model is an extension of the

BSAP (Bus Seat Assignment Problem) formulation

deﬁned by (Guerriero et al., 2020). As in (Guerriero

et al., 2020), we consider a passenger transportation

company that offers a transportation service from a

given set of origins to a given set of destinations. The

company sells a set of products to several groups of

customers on a given time horizon. Each product is

an origin-destination (OD) transportation service per-

formed by a bus. At each time of the planning hori-

zon, the company has to decide how to manage the

overall capacity in the most proﬁtable way.

Let E = {e

, . . . , e

} denote the set of n origins

and F = { f

, . . . , f

} the set of q destinations. A

generic product is denoted as the pair {(e, f ) : f >

e, e ∈ E, f ∈ F} and represents the OD transportation

service from the bus station e to the bus station f .

All the products are sorted in increasing order of the

origin bus station and stored in the set (EF), that is

(EF) = (e

, f

), . . . , (e

, f

), (e

, f

), . . . , (e

, f

). The

products offered by the company can be indexed as

p = (1, . . . , |(EF)|). We assume that the company per-

forms the transportation service using a set of buses,

each of them characterized by a given number of rows

i = 1, . . . m, each row is composed by a certain num-

ber of seats denoted by l. In addition, we also assume

that every bus has the same number of seats on each

row. The number of seats per each row multiplied by

the number of rows of the bus represents the seating

capacity of the bus. The buses have t lines, t = 1, . . . T

and C

is the capacity of line t that is the seating ca-

pacity of the bus, which runs on the line t. Each line t

consists of a given number of stops denoted as S

+ 1

including the starting and the terminal bus stations

and S

legs between each two bus stations. All the

products (i.e., OD transportation service) produced by

each line t, t = 1, . . . , T are stored in a sequence ac-

cording to the incremental order of f and e, that is

(EF)

= (1, 2)

, . . . , (1, S

+ 1)

, (2, 3), . . . , (S

, S

+ 1).

After numbering all the products in (EF)

from left to

right, we can get the product sequence indexed by the

serial number p

= (1, . . . , |(EF)

|). Let H

= h

, s =

1, . . . , S

, p

= 1 . . . , |(EF)

| denote a binary matrix,

each element being equal to 1 if product p

generated

by the line t uses leg s and zero otherwise. Each col-

umn of matrix H

contains all the information related

to the legs involved in the OD transportation services

provided by the line t. An example of matrix H

for a

line with S

= 5 stops and 10 products is reported in

Figure 2.

Product

Leg (1,2) (1,3) (1,4) (1,5) (2,3) (2,4) (2,5) (3,4) (3,5) (4,5)

(1, 2) 1 1 1 1 0 0 0 0 0 0

(2, 3) 0 1 1 1 1 1 1 0 0 0

(3, 4) 0 0 1 1 0 1 1 1 1 0

(4, 5) 0 0 0 1 0 0 1 0 1 1

Figure 2: Representation of of the matrix B, for a line with

5 stops and 10 products.

We assume that different lines can deliver the

same OD transportation service from e to f , that is

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

alternative products are available. Thus, in order to

handle this speciﬁc situation, a binary parameter γ

introduced to denote the relationship between product

p and line t. In particular, γ

= 1, if the transporta-

tion service p can be delivered by the line t, that is

(e, f ) ∈ (EF)

, and zero otherwise. Time is discrete,

and at each time period of the booking horizon, the

company has to decide on accepting/denying the re-

quest of a group of customers asking for a product p,

that is an OD transportation service. The capacity of

the system depends not only on the number of avail-

able seats for each row of a given line t = 1, . . . , T

but also by the size of the passenger group k with

k = 1, . . . , K, that is assigned to the considered row.

In fact, considering the restrictions in terms of social

distancing between people that are not kin, we can

allocate different types of groups on each row, with

various conﬁgurations. Let’s suppose that each row

of the bus contains 4 individual seats. In this case,

the possible assignment conﬁgurations for each row,

depending of the group size, are the following:

• a kin group of 4 people,

• a kin group of 3 people,

• 2 groups of 2 people,

• 2 groups of 1 person,

• 1 kin group of 2 people and 1 single passenger.

Figure 3 represents an example of a layout conﬁgu-

ration considering the limitation of capacity and the

allocation of the groups. To model all the possi-

ble conﬁgurations, we introduce the matrix B, whose

single element, denoted by b

i j

, represents the num-

ber of seats, including those required to ensure the

satisfaction of social distancing rule, used to allo-

cate on the row i of the line t a group of k people,

j = (k − 1)m + 1, . . . , km. A representation of the ma-

trix B, for the considered scenario, is given in Table 1,

in which the matrix B is built by considering 2 lines

t = 1, 2 and four group sizes k = 1, 2, 3, 4.

Table 1: Example of matrix B.

k=1 k=2 k=3 k=4

m m m m

2 0 0 ... 0 2 0 0 ... 0 4 0 0 ... 0 4 0 0 ... 0

t=1 0 2 0 ... 0 0 2 0 ... 0 0 4 0 ... 0 0 4 0 ... 0

0 0 2 ... 0 0 0 2 ... 0 0 0 4 ... 0 0 0 4 ... 0

m . . . .

. . . .

0 0 0 ... 2 0 0 0 ... 2 0 0 0 ... 4 0 0 0 ... 4

2 0 0 ... 0 2 0 0 ... 0 4 0 0 ... 0 4 0 0 ... 0

t=2 0 2 0 ... 0 0 2 0 ... 0 0 4 0 ... 0 0 4 0 ... 0

0 0 2 ... 0 0 0 2 ... 0 0 0 4 ... 0 0 0 4 ... 0

m . . . .

. . . .

0 0 0 ... 2 0 0 0 ... 2 0 0 0 ... 4 0 0 0 ... 4

The main goal is to maximize the total revenue

obtained from the accepted requests of a group of size

k for the product p on the booking horizon. Moreover,

Figure 3: Example of a bus layout conﬁguration consider-

ing the limitations of capacity and the allocation of kin’s

groups. The green squares represent the occupied seats;

while crossed gray squares the forbidden seats. In partic-

ular, from the top (ﬁrst line) to the bottom (octave line): a

group of one person, two groups of one person, a group of

four people, a group of three people, a group of one per-

son, a group of one person and a group of two people, two

groups of one person, two groups of two people.

it is assumed that booking requests made for groups

with k greater than one cannot be partially accepted.

A summary of the parameters and the variables of

the model is presented in what follows:

• R

the revenue associated to the product p for a

group of size k;

• d

the number of request for a product p made by

a group of size k;

• q the number of seats available on each row of the

buses;

• γ

, p = 1, . . . , |(EF)|, equal to 1 if the product p

can be delivered by using the line t and zero oth-

erwise;

• h

, s = 1, . . . , S

, p

= 1 . . . , |(EF)

| equal to 1 if

the leg s is used in the product p

and zero oth-

erwise. h

is an element of the matrix H intro-

duced above;

Management of Groups of Passengers on Buses Considering the Restrictions of COVID-19

• b

i j

represents the number of seats used to allocate,

on the row i of the line t, a group of k people,

j = (k − 1)m + 1, . . . , km. b

i j

is an element of the

matrix B introduced above;

• x

integer variables representing the number of

satisﬁed requests for the product p by the line t.

The BGAP under COVID-19 social distancing

rules is formulated as follows.

Max

|(EF)|

∑

p=1

∑

t∈T

∑

j=(k−1)m+1,...,k m

∑

k∈K

(1)

∑

t=1

∑

j=(k−1)m+1,...,k m

≤ d

p = 1, . . . , |(IJ)| , k = 1, ..., K (2)

|(EF)

∑

j=1,...,km

|(EF)|

∑

p=1

i j

≤ q t = 1, . . . , T, s = 1, . . . , S

(3)

i = 1, ..., m

≥ 0, integer p = 1, . . . , |(IJ)|, t = 1, . . . , T, j = 1, ..., km (4)

The objective function 1 represents the total rev-

enue obtainable. Equations 2 represent the demand

constraints and state that the demand for a product

p (transportation service) for a group of size k can

be satisﬁed with all the products generated by all

the lines t,t = 1, ..., T , that can deliver the consid-

ered transportation service. Equations 3 represent the

capacity constraints and they assure both the respect

of the social distance between different sized groups

and the right allocation of capacity on the rows of the

lines. Finally, constraints 4 deﬁne the variables do-

main.

Clearly, this model could be easily extended to any

type of transportation vector, by opportunely chang-

ing the capacity constraints considering the speciﬁc

features of the vector.

4 COMPUTATIONAL

EXPERIMENTS

In this section, we describe the computational results

collected to validate the proposed model. We used the

software AIMMS 4.75.3.6 and the commercial solver

Cplex 10.1, on an Intel Core i7-8565U CPU, 1.8 GHz,

8 GB of RAM.

The experimentation is divided into two main

parts: the ﬁrst one is aimed to assess the behaviour of

the proposed model in terms of solution quality; the

second one is devoted to investigate the performance

of the model in terms of scalability. The instances

used in the ﬁrst part of the computational study are

based on real data derived from www.simetbus.it: the

web site of a bus company operating in the south of

Italy, that is the Simet S.p.A.. Each instance is char-

acterized by a certain number of inter-regional lines,

with a capacity of 52 seats. In particular, the lay-

out of the bus operating a certain line is composed

of 13 rows, each of which is made by 4 seats. In addi-

tion, every line is composed of a given set of origin-

destination products. A different fare is associated to

each OD product for a group of size k. We consider

4 possible types of groups. In particular, a group can

be composed from a minimum of one person (a single

passenger) to a maximum of 4 people. In Table 2 we

reported the three lines considered for our tests, taken

from the Simet S.p.A. website.

Table 2: Characteristics of Instances: Lines and OD prod-

ucts.

Line1 Line2 Line3

origin destination origin destination origin destination

1 6 1 5 1 6

2 6 2 5 2 6

3 6 3 5 3 6

4 6 4 5 4 6

1 6 1 7

2 6 2 7

3 6 3 7

4 6 4 7

5 6 6 7

Looking at Table 2, the three lines and 7 cities

(origin or destination) numbered in ascending order

are reported on the columns. Each line is character-

ized by a set of OD products, depicted on each row of

each line. In particular, the Line1 has 4 OD products

with different origins but the same destination (i.e.,

6). Line 2 and Line 3 are composed of 9 OD prod-

ucts. In addition, we may notice that the lines have

in common some rides. For example, the product 1-6

is present in all the lines; hence, departing from the

origin 1, it is possible to reach the destination 6 by

using all the three lines. Regarding the legs, we may

say that the Line 1 has 4 legs, Line 2 is composed

of 5 legs, while Line 3 of 5 legs. The demand value

for each ride is randomly estimated. In the computa-

tional study we compare the results obtained by allo-

cating the customers using the proposed BGAP, with

two other seat allocation policies. In particular, in

the ﬁrst policy we consider a FIFO strategy in which

the demand of groups is allocated following the ar-

rival order, respecting social distance but without any

type of optimization. The second policy, named ”NO

GROUP”, consists in a strategy that does not consider

the possibility to allocate two or more relatives close

to one another. Table 3 summarizes the results. In

particular, the second, third and fourth columns report

the three strategies used to allocate passengers (i.e.,

solving the BGAP model, the FIFO strategy and the

NO GROUP strategy, respectively). On the rows, for

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

each strategy, we report the total revenues, expressed

in euro, the available seats, the occupied seats, the in-

terdicted seats (i.e., the number of seats that cannot be

occupied for maintaining the social distancing), and

the unoccupied seats (i.e., seats that remain empty be-

cause they can not satisfy the demand that arrives for

certain OD products).

Table 3: Computational results: BGAP vs FIFO vs NO

GROUP.

BGAP FIFO NO GROUP

Total Revenue 2.036,00 1.707,00 1.115,00

Available seats 156 156 156

Occupied seats 139 117 78

Interdicted seats 35 21 78

Unoccupied seats 0 18 0

The values, reported in Table 3, clearly show that

the highest value of revenue is obtained by applying

the BGAP model. Thus, the BGAP strategy is the

most effective compared with the FIFO and the NO

GROUP approaches. In particular, the BGAP model

leads to an increase in the revenue, over the other

two strategies, of about the 19.3% and 82.6%, respec-

tively. In addition, we can notice that BGAP ensures

the highest number of occupied seats and the lowest

number of interdicted seats compared with FIFO and

NO GROUP. Using the BGAP model to allocate the

passengers, the value of the occupied seats is 18.8%

and 78.2% higher than the FIFO and NO GROUP

approach, respectively. Thus the BGAP model al-

lows an effective management of the capacity. It it

worth noting that the sum of the values associated

with “Occupied seats”, “Interdicted seats” and “Un-

occupied seats” do not always correspond to the value

of “Available seats”.

This can be easily explained by taking into ac-

count that we have considered lines, characterized by

several stops, in correspondence of which passengers

can get on and off the vehicle. This means that some

seats could be interdicted and/or occupied more than

one time and, hence, counted more than once as occu-

pied or interdicted seats. To better clarify this issue,

let’s consider the stop 5 of the line 2 deﬁned in the

Table 2. At this stop all passengers whose destina-

tion is 5 get off, while those who must go from 5 to 6

get on. Consequently, the seats occupied by the pas-

sengers who get off at stop 5 become available and

thus they can be occupied again by passengers who

get on the bus at stop 5 to reach destination 6. Thus,

the same seat could be occupied by a passenger over

a leg and interdicted over another leg according to the

size of groups allocated on the row in which the seat

is located. In fact, as we can see in the second col-

umn of the Table 3, the sum of “Occupied seats” and

“Interdicted seats” is higher than the value associated

to the “Available seats”. Moreover, solving the model

does not require high computational time, about 0.02

second on average, hence it is also efﬁcient.

In the second part of the computational study,

aimed at evaluating the scalability of the proposed

model, we consider a set of randomly generated in-

stances of increasing size.

Table 4 provides, for each test problem, the number of

lines, the number of legs and the number of products.

For example, instance T 10 1 refers to a bus network

characterized by 10 lines, each line has 5 legs, and

5 available OD products. For each instance, demand

and revenue values are randomly generated in the in-

terval [0;10] and [5;300], respectively.

Table 5 summarizes the computational results ob-

tained by solving the BGAP model. In particular, for

each instance, it provides the objective function value

(column ”Revenue”) and the execution time (column

”Time”) in seconds.

Table 4: Test Problems.

Test Lines Legs Products

T 10 1 10 5 5

T 10 2 10 5 10

T 10 3 10 10 10

T 10 4 10 20 20

T 10 5 10 50 50

T 10 6 10 50 100

T 10 7 10 300 300

T 10 8 10 300 600

T 20 1 20 10 10

T 20 2 20 10 20

T 20 3 20 10 40

T 20 4 20 50 50

T 20 5 20 50 100

T 20 6 20 50 200

T 20 7 20 300 300

T 20 8 20 300 600

T 20 9 20 300 1200

T 50 1 50 50 50

T 50 2 50 50 100

T 50 3 50 300 300

T 50 4 50 300 600

T 50 5 50 500 500

T 50 6 50 500 1000

Looking at Table 5, it is easy to notice that the rev-

enues increase with the increasing of instances size.

This is an expected behaviour, since the higher the

demand and the capacity, the higher the revenue.

In order to analyze the dependency between the com-

putational overhead, required to solve the BGAP

model and the instances size, in Figures 4 – 8 we de-

pict the execution time as a function of instances char-

acteristics (i.e., number of lines, legs and products).

Management of Groups of Passengers on Buses Considering the Restrictions of COVID-19

Table 5: Computational Results on randomly generated in-

stances.

Test Revenue Time

T 10 1 13022 0.02

T 10 2 33433 0.02

T 10 3 31190 0.03

T 10 4 44375 0.03

T 10 5 57632 0.08

T 10 6 61593 0.33

T 10 7 63941 3.86

T 10 8 65324 8.91

T 20 1 33806 0.03

T 20 2 59243 0.08

T 20 3 93001 0.08

T 20 4 101655 0.42

T 20 5 111050 0.77

T 20 6 124264 0.77

T 20 7 126783 9.48

T 20 8 128991 18.2

T 20 9 130580 36.08

T 50 1 146102 0.44

T 50 2 236471 0.78

T 50 3 413181 25.45

T 50 4 664210 54.91

T 50 5 586031 96.19

T 50 6 965359 202.63

Figure 4: Execution time as a function of the number of

lines, with ﬁxed number of products and legs (50 legs, 50

products).

Focusing on the results depicted in Figures 4 - 7

we can notice that the higher the number of lines,

the higher the execution time. In particular, consid-

ering Figures 4 and 5, which refer to the results for

instances with 50 legs and 50 products, and 50 legs

and 100 products, respectively, it is evident that the

execution time sharply raises when the number of

lines increases from 10 to 20, then, after 20 lines, it

continues to slightly raise with respect to the number

of lines. Looking at Figures 6 and 7, which depict

the results obtained for instances with 300 legs and

300 products, and with 300 legs and 600 products,

respectively, it is easy to observe that the execution

time sharply increases with the increasing number of

Figure 5: Execution time as a function of the number of

lines, with ﬁxed number of products and legs (50 legs, 100

products).

Figure 6: Execution time as a function of the number of

lines, with ﬁxed number of products and legs (300 legs, 300

products).

Figure 7: Execution time as a function of the number of

lines, with ﬁxed number of products and legs (300 legs, 600

products).

lines. Thus, looking at Figure 8, which summarizes

the overall results obtained on all the classes of in-

stances, we can state that the feature, which inﬂuence

the most the computational overhead is the number of

legs, and consequently the number of products, while

the number of lines has not a relevant impact on the

execution time. The plots reported in the Figure 9,

which depict the execution time as a function of the

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

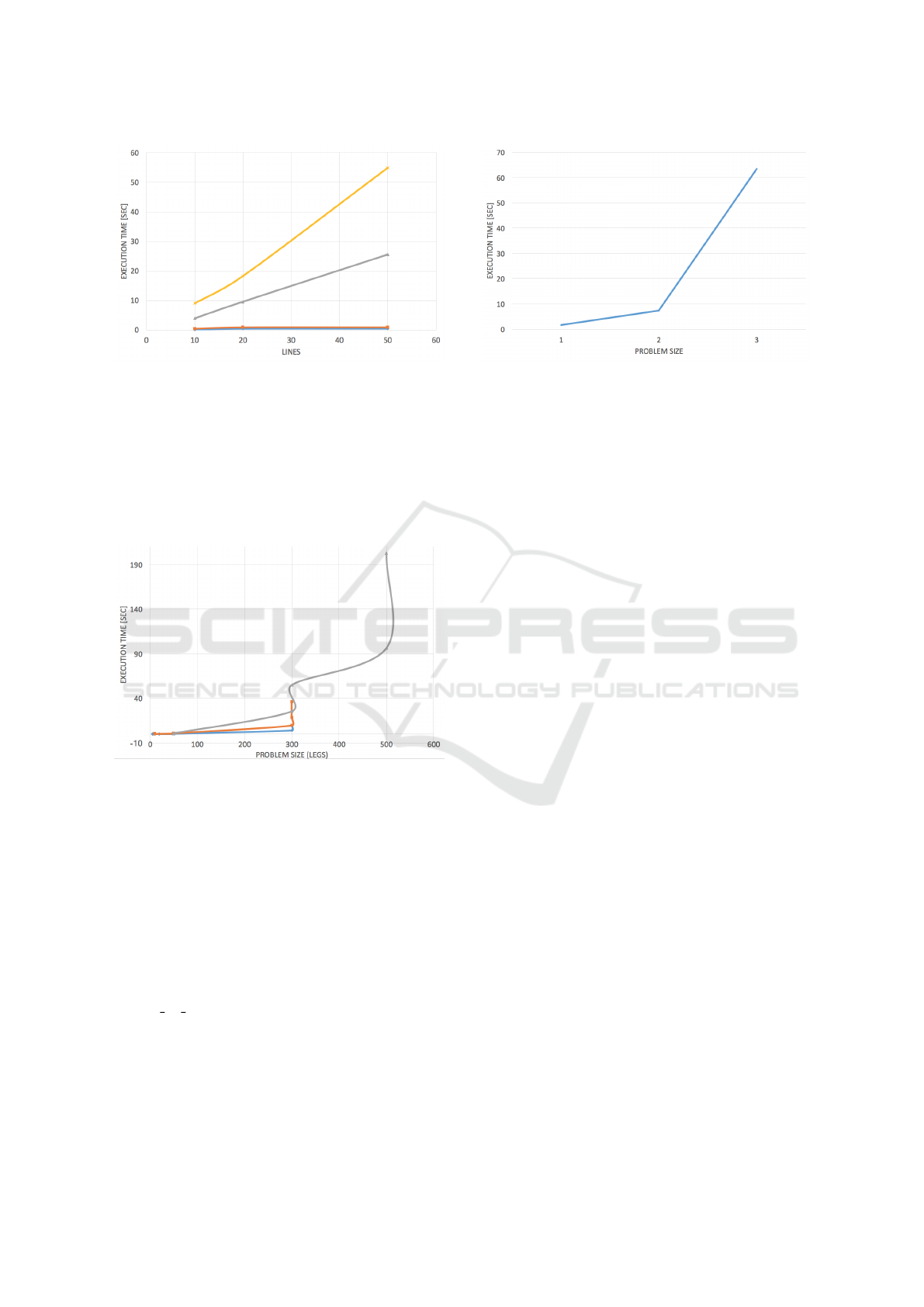
Figure 8: Execution time as a function of the number of

lines, with ﬁxed number of products and legs: Orange line:

instances with 50 legs, and 50 products; Blue line: instances

with 50 legs, and 100 products; Grey line: instances with

300 legs, and 300 products; Yellow line: instances with 300

legs, and 600 products.

number of legs, ﬁxing the number of lines, conﬁrm

the strictly dependence of the execution time on the

numbers of legs and products.

Figure 9: Execution time as a function of the number of

legs, with ﬁxed number of lines. Grey line: instances with

50 lines, Orange line: instances with 20 lines, Blue line:

instances with 50 lines.

Finally, looking at Figure 10 that represents the

trend of the average execution time with respect to

the increase of the problem size, we can notice that,

the computational time increases with the increasing

problem size, in terms of number of lines, number of

legs, and number of products considered, on average.

It is important to highlight that overall the reso-

lution of the BGAP model has short execution times,

i.e., in the order of minutes, even for large instances

(e.g., T 50 6). Thus, the BGAP model is efﬁcient for

ﬁnding optimal solutions also considering more real-

istic sized instances. We may conclude that the use of

the BGAP model allows to efﬁciently and effectively

manage the seats assignment and groups of passen-

gers, by optimizing the seats allocation, respecting the

rules of social distancing imposed to reduce the diffu-

Figure 10: Trend of the average execution time with respect

to the increasing problem size.

sion of the COVID-19 virus.

5 CONCLUSIONS

In this paper we have considered the problem of allo-

cating groups of passengers on the buses during the

pandemic time. The main goals are: creating safe

conﬁgurations by respecting social distancing, opti-

mally exploiting the capacity of vehicles and maxi-

mizing the revenue deriving by the sale of travel tick-

ets. In particular, we considered the possibility to al-

locate groups of relatives close to one other, follow-

ing the Italian rules currently adopted on the buses.

However, it is worth noting that this model could be

easily extended to any transportation vector type, by

modifying the capacity constraints, considering the

speciﬁc features of the transportation vector. In the

computational experiments, we made a comparison

between the results obtained with and without the ap-

plication of the proposed model. The results high-

lighted that our model provides more effective solu-

tions than the common FIFO or NO GROUP strate-

gies. In addition, we investigate the scalability of the

model, by considering a set of randomly generated in-

stances of increasing size. The results highlighted that

the computational times increase with the increasing

number of lines. However, solving the model requires

a reasonable amount of time. Thus, we may conclude

that our model could efﬁciently help the bus trans-

port company to optimize the managing of resource-

constrained buses and, at the same time, maximizing

the revenue, considering the rules of social distanc-

ing. Hence, our model represents a valid support tool

for managing the passengers seats allocation by min-

imizing the risk of contagion.

Management of Groups of Passengers on Buses Considering the Restrictions of COVID-19

REFERENCES

Barry, M., Gambella, C., Lorenzi, F., Sheehan, J., and

Ploennigs, J. (2021). Optimal seat allocation under

social distancing constraints. IBM Research Europe.

Ferrero, F., Perboli, G., Rosano, M., and Vesco, A. (2018).

Car-sharing services: An annotated review. In Sus-

tainable Cities and Society. Elsiever.

Fischetti, M., Fischetti, M., and Stoustrup, J. (2021). Safe

distancing in the time of covid-19. In European Jour-

nal of Operational Research. Elsevier.

Gkiotsalitis, K. and De Weert, Y. (2021). A covid-19 public

transport frequency setting model that includes short-

turning options. In Future Transportation 2021, 1,

3–20. https://doi.org/10.3390/ futuretransp1010002.

MDPI.

Gongyu, C., Xinyu, F., Huiwen, J., Xian, Y., and Siqian, S.

(2021). An optimization-and-simulation framework

for redesigning university campus bus system with so-

cial distancing. arXiv:2010.10630v3.

Guerriero, F., Luzzi, M., and Macrina, G. (2020). Revenue

management approach for passengertransport service:

an italian case study. In Optimization and Decision

Science 2020. Springer.

Hancocka, T. O., Hessa, S., Marley, A., and Choudhurya,

C. F. (2021). An accumulation of preference: Two al-

ternative dynamic models for understanding transport

choices. In Transportation Research Part B: Method-

ological Volume 149, Pages 250-282. Elsiever.

Lin, B., Xu, J., Chen, S., Feng, Y., and Li, Michael, Z.

(2020). A hybrid model for airline seat inventory con-

trol of the multi-leg problems. In Operations Research

Letters 48 291–296. Elsevier.

Moore, J. F., Carvalho, A., Davis, ABULHASSAN, Y., and

Megahed, F. M. (2021). Seat assignments with phys-

ical distancing in single-destination public transit set-

tings. In IEEE Access, vol. 9, pp. 42985-42993, 2021,

doi: 10.1109/ACCESS.2021.3065298. IEEE.

Ongprasert, S. (2006). Passenger behavior on revenue man-

agement systems of inter-city transportation. In Tech-

nical report, Graduate School of Engineering. Kochi

University of Technology, Japan.

Salari R., M., Milne, J., Delcea, C., Kattan, L., and Cotfas,

L.-A. (2020). Social distancing in airplane seat as-

signments. In Journal of Air Transport Management.

Elsevier.

Wang, W., Tang, O., and Huo, J. (2018). Dynamic capacity

allocation for airlines with multi-channel distribution.

In Journal of Air Transport Management 69 173–181.

Elsevier.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems