Molecular Fragments from Incomplete, Real-life NMR Data:

Framework for Spectra Analysis with Constraint Solvers

Haneen A. Alharbi

, Igor Barsukov

2 b

, Rudi Grosman

2 c

and Alexei Lisitsa

1 d

Department of Computer Science, University of Liverpool, Liverpool, U.K.

Institute of Systems, Molecular and Integrative Biology, University of Liverpool, Liverpool, U.K.

Keywords:

Constraint Satisfaction Problem, Constraint Programming, NMR Data Interpretation, Molecular Structure

Generation.

Abstract:

Nuclear Magnetic Resonance (NMR) spectroscopy is a powerful analytical tool that can be used in the eluci-

dation of chemical structures and is widely applied both in academia and industry. Despite using computer-

assisted structure elucidation systems, interpretation of NMR data is often laborious, requires high levels of

expertise and is not immune to ambiguities. In this multi-disciplinary study, we developed a design of a novel

system using a Constraint Satisfaction (CS) framework to utilise unannotated NMR spectra. Additionally,

our system allows the utilisation of complementary information obtained/known outside the scope of NMR.

Herein we describe a prototype implementation and its empirical evaluation on a set of amino acids, which are

a diverse class of important biological compounds. We further employ the CS approach to show the principle

limits (ambiguity) of the NMR method in molecular structure elucidation.

1 INTRODUCTION

Nuclear Magnetic Resonance (NMR) spectroscopy

is a cornerstone analytical method widely used both

in academia and industry. One of the main appli-

cations of this method is chemical structure eluci-

dation (Elyashberg and Williams, 2015). There are

different types of NMR techniques to collect par-

tial structural information on molecular structures of

substances under investigation. An example of the

type of structural information which can be obtained

from NMR spectra is that a molecule should con-

tain a Carbon (C) atom directly bonded to a Hydro-

gen (H) atom. Various other types of structural in-

formation are available from the spectra (Elyashberg

and Williams, 2015) which makes it possible to iden-

tify/elucidate the structure of the molecule, which

constitute the main goal of NMR analysis. The elu-

cidation process is complex, laborious and the re-

sults may be ambiguous, so the interpretationof NMR

spectra currently requires the involvement of human

experts. The research on the automation of the NMR

https://orcid.org/0000-0002-0281-8346

https://orcid.org/0000-0003-4406-9803

https://orcid.org/0000-0002-0233-7112

https://orcid.org/0000-0002-3820-643X

spectra interpretation and development of Computer-

Assisted Structure Elucidation (CASE) systems has

been conducted since the 1960s (Koichi et al., 2014)

and several such systems are available either as re-

search prototypes or commercial propositions (Burns

et al., 2019).

There are still many remaining challenges in

computer-assisted NMR analysis: full automation (or

greater degree of automation), managing the uncer-

tainty of spectra, handling the ambiguity of the anal-

ysis or dealing with the mixtures as opposed to pure

substances. The main task of NMR analysis lends it-

self very naturally to the CS area. Indeed, the par-

tial structural information obtained from NMR spec-

tra can be seen as a set of constraints, with an eluci-

dated molecular structure being a solution to this set

of constraints. This observation was a starting point

of our investigation and we found it quite surprising

that no attempts to apply generic CS techniques (as

opposed to specialised algorithms) to NMR analysis

have been made until very recently. In (Omrani and

Naanaa, 2016; Omrani and Naanaa, 2019) the authors

have demonstrated that the basic tasks of NMR analy-

sis can be solved by reformulation of the structural in-

formation obtained from NMR spectra as constraints

and the application of generic constraint solvers. The

open-source system (Omrani and Naanaa, 2019) al-

834

Alharbi, H., Barsukov, I., Grosman, R. and Lisitsa, A.

Molecular Fragments from Incomplete, Real-life NMR Data: Framework for Spectra Analysis with Constraint Solvers.

DOI: 10.5220/0010915800003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 834-841

ISBN: 978-989-758-547-0; ISSN: 2184-433X

lows applying basic types of NMR constraints as well

as user-speciﬁed allowed/forbidden molecular struc-

tures. While this work has demonstrated the viability

of the CS-based NMR analysis, important theoretical

and practical questions have been left open. First, the

power of the proposed method has been illustrated by

the case studies but was not systematically assessed.

Second, the NMR constraints were considered from

the idealised perspective, and no practical limitations

of the NMR method were taken into account. For

the latter, in the practice of NMR analysis, it is quite

common that some theoretically possible NMR con-

straints are not extractable from the spectra. Further-

more, the ambiguity of the NMR structure elucidation

was not addressed.

In this paper, we present the design of the system

for NMR interpretation/molecular structure elucida-

tion based on the CS. We take as a principle an inher-

ent incompleteness and uncertainty of NMR derivable

partial information about the molecular structures.

We consider several classes of constraints, including

chemical constraints, such as valency of atoms, NMR

constraints such as chemical bond connectivity and

other constraints coming either from other types of

analysis (e.g. mass spectrometry) or from the prac-

tical experience. We discuss the formulation of vari-

ous types of constraints and report on the experiments

with a prototype implementation on the classes of

amino acids. We also show that NMR analysis is in-

herently ambiguous, even when all theoretically pos-

sible NMR constraints are available, there are cases

when it is still impossible to uniquely identify the

molecular structure in question. Thus, we assess the

fundamental limitation of the NMR method itself.

2 PRELIMINARIES

We will represent the molecular structures as labelled

undirected multigraphs, which are formally deﬁned

as triples hV, e, li, where V is a set of vertices, e :

V × V → Z

≥

represents the multiplicity of edges be-

tween the vertices, and l : V → A labels the vertices

by the types of chemical elements. Here A is a set of

all chemical elements, including e.g.

for

hydrogen

for

carbon

, etc. We use multigraphs as opposed

to graphs to represent faithfully the cases of molec-

ular structures with multiple bonds between pairs of

atoms. A function v : A → Z

denotes the valency,

fundamental chemical characteristic of the atom types

that denotes the maximum capacity of making bonds.

For example v(H) = 1 and v(C) = 4.

We will deal in this paper with two main types of

2-D (two-dimensional) NMR spectra used in the elu-

cidation of molecular structures: Heteronuclear Sin-

gle Quantum Coherence (HSQC) and Heteronuclear

Multiple Bond Correlation (HMBC) experiments that

correlate signals of

C and

H atoms. Typically these

spectra are visualised as contour plots where the axes

coordinates are called chemical shifts with the units

of Hertz or the most commonly used normalised scale

parts per million (ppm) by convention.

A molecule’s structural information appears in the

spectra in the form of peaks shown as the small spots

at the intersection of the chemical shifts of the inter-

acting atoms (see Figure 1 (left) and (right) for peaks

in the HSQC and HMBC spectra, respectively). Each

peak in the HSQC spectrum corresponds to (or is gen-

erated by) a pair of

and

atoms with a direct bond

between them, meaning the graph-distance between

corresponding vertices in the representing multigraph

is 1. Similarly, the peaks in the HMBC spectrum iden-

tify the pairs of

and

atoms separated by two or

three bonds (i.e distance between corresponding ver-

tices in the multigraph is 2 or 3).

For both types of spectra, x-coordinate, and y-

coordinate of a peak represent chemical shifts of cor-

responding

and

atoms, respectively. The chemical

shifts of the atoms persist across different spectra and

different atoms may have the same (very close) chem-

ical shifts due to possible symmetries of the molecule.

Figure 1 illustrates these principles, where the molec-

ular structure in the middle produces HSQC (left) and

HMBC (right) spectra. The (in)equalities of chemi-

cal shifts are subject to possible measurement errors

and subtle differences in an experimental setup, and

they should be considered as approximate. We as-

sume here, as a starting point in constraints formu-

lation, that all necessary approximations/abstractions

have been done and it is ﬁrmly established which co-

ordinates (shifts) are equal and which are different.

This is sufﬁcient to formulate the basic NMR con-

straints (see Section 3.3). Furthermore, the informa-

tion about the shifts taking values in a speciﬁc range

is useful for NMR interpretation and to formulate fur-

ther NMR constraints (see Section 3.4).

The problem of NMR analysis/interpretation we

consider here can be reformulated as Given a set of

NMR-derivable constraints from HSQC and HMBC

spectra on the connections between atoms to gener-

ate all molecular multigraphs satisfying those con-

straints. Additional structural information derived

from other NMR experiments can be introduced by

extending the constraint set. The ultimate goal of

such an analysis is to identify the molecular structures

down to the least ambiguous set possible. In the next

section, we discuss the important aspects of constraint

formulation for this problem.

Molecular Fragments from Incomplete, Real-life NMR Data: Framework for Spectra Analysis with Constraint Solvers

835

Figure 1: The connectivity information from HSQC (left panel blue arrow) and HMBC (right panel red arrows) obtained for

alanine (middle panel). Additional NMR information such as chemical shifts can be added as optional constraints and are

planned to be implemented in the future. NMR Spectra are courtesy of James London.

3 CONSTRAINTS FOR NMR

ANALYSIS

In the constraint-based NMR analysis, several cat-

egories of constraints do naturally occur. Some of

them are absolute/rigid, in a sense, they have to be

present and satisﬁed in all reasonable scenarios of

analysis, while others are soft constraints that may

be present/absent and are not always required to be

satisﬁed. The latter categories reﬂect inherent incom-

pleteness, uncertainty and practical limitations of the

NMR method. Further to that, we consider two dif-

ferent settings for the analysis, in one we seek com-

plete solutions, meaning the full molecular structures,

in another, we seek incomplete molecular structures

or fragments. The incomplete setting is important, as

NMR-derivable information is often insufﬁcient to re-

cover the full molecular structure and other sources

of information are needed, but the recovered frag-

ments may be still useful for NMR spectra interpre-

tation. Yet another aspect of NMR interpretation is

whether an analysis of pure substances or mixtures is

required. All these variants of the problem affect the

ways some constraints are formulated. In this sec-

tion we discuss the constraints in an implementation-

independent form; the details of the implementation

of a prototype system can be found in Section 4.

3.1 Molecular Graph Representation

Constraints

The solutions of NMR CS are thought in terms of la-

belled undirected multigraphs, so the following rigid

constraints are necessary:

• e(x, y) ≥ 0 (M)ultigraph;

• e(x, y) = e(y, x) (U)ndirected;

• e(x, x) = 0 (N)o Loops;

Due to the additivity of NMR spectra when ap-

plied to mixtures as opposed to pure substances, NMR

derived constraints are related to all participating

molecules. In the case of the analysis of pure sub-

stances as opposed to the mixtures, the solutions need

to represent a single molecule, so the connectedness

constraint is required:

• the molecular multigraph is connected

(C)onnectedness

Notice that to consider the case of mixtures with

unknown numbers of components it is sufﬁcient just

to omit C constraint - the disconnected multigraphs

solutions will then include representations of the

molecular structures of the components. Due to the

complexity of the connectedness constraint, we pro-

pose to treat it at the post-processing stage, that is not

to include it as a constraint, generate all solutions and

then ﬁlter them on connectedness condition.

3.2 Basic Chemistry Constraints

All molecular structures are constrained by the va-

lency, the fundamental chemical property of the con-

stituting atoms. This imposes the following con-

straints depending on the settings:

• ∀x ∈ V d(x) = v(l(x)) (complete setting) (VC)

• ∀x ∈ V d(x) ≤ v(l(x)) (incomplete setting) (VI)

Here d(x) is a degree of a vertex x in a multigraph,

that is Σ

y∈V

e(x, y), v is a (predeﬁned) valency func-

tion, and l is a atom type labelling function.

3.3 NMR Constraints

It is signiﬁcant to express the HSQC and HMBC spec-

tra clearly in terms of constraints. The HSQC exper-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

836

iment identiﬁes a single bond between the pairs of

and

atoms and the HMBC spectroscopy detects cor-

related atoms separated by two or three bonds in the

multigraphs. Let the HSQC and HMBC spectra con-

tain the peaks p

i, j

with 1 ≤ i ≤ t

;1 ≤ j ≤ t

and q

k,m

with 1 ≤ k ≤ s

;1 ≤ m ≤ s

, respectively. Let the co-

ordinates (chemical shifts) of these peaks be (h

, c

)

and (h

, c

), respectively. We will use the following

useful abbreviations:

dist

(1)

(x, y) for e(x, y) > 0 (The HSQC peaks),

dist

(2)

(x, y) for ∃z (e(x,z) > 0 ∧ e(z, y) > 0),

and dist

(3)

(x, y) for ∃z, v (e(x, z) > 0 ∧ e(z, v) > 0 ∧

e(v, y) > 0) (The HMBC peaks).

Then basic NMR constraints are deﬁned as:

• ∃ ¯x∃ ¯y (HSQC( ¯x, ¯y) ∧ HMBC( ¯x, ¯y) ∧ ID( ¯x, ¯y))

(NMR)

where:

• ¯x = x

, . . . x

and ¯y = y

, . . . y

are sequences of

variables

• HSQC( ¯x, ¯y) is

i, j

(dist

(1)

, y

) ∧ l(x

) = H ∧

l(y

) = C)

• HMBC( ¯x, ¯y) is

k,m

((dist

(2)

, y

) ∨

dist

(3)

, y

)) ∧ l(x

) = H ∧ l(y

) = C)

• ID( ¯x, ¯y) is

6=c

6= x

) ∧

6=h

6= y

)

Thus, the basic NMR constraints assert the ex-

istence of pairs of

atoms satisfying necessary

distance conditions, imposed by HSQC and HMBC

spectra (HSQC( ¯x, ¯y), HMBC( ¯x, ¯y), respectively), as

well as by identity conditions (ID( ¯x, ¯y)). Notice that

in the case when some peak coordinates are equal

(within one spectrum or across both), e.g. c

= c

then

corresponding variables y

, y

are the same.

3.4 Further Constraints

3.4.1 Exact/Partial Formula Constraints

Due to the partiality of NMR-derived information,

any additional information can be very useful for

structure elucidation. Other forms of analysis, in-

cluding different variants of spectroscopy (e.g. Mass-

Spectroscopy (MS)), may provide partial or full in-

formation on a Molecular Formula (MF), that is the

count of different types of atoms involved in the

molecule. Thus, for any known count n of a type of

atom T involved in a molecule adds a formula con-

straint:

• |{x | l(x) = T}| = n (F)

Figure 2: The workﬂow of the system. Demonstrating how

the system works for different data inputs.

3.4.2 Optional Constraints

It is not uncommon to have prior information on ex-

pected or impossible fragments during structure elu-

cidation and use it as optional constraints. This infor-

mation can be derived either from the knowledge of

the work being done or from the NMR data itself. For

example, if the analysed mixture is obtained through

a chemical synthesis all the precursor materials used,

the by-products and the products are known. If no

cyclic structures (e.g phenyl rings) are present, this

information can be imposed as an optional constraint

to prohibit cyclic solutions. Similarly, any expected

fragments can also be forced to the solution space.

3.5 Post-processing

In the proposed design, we assume that some of the

constraints may be computationally expensive to deal

with by a generic constraint solving or depending on

the solver, may be infeasible to express in its input

language. In such cases, the constraints can be used

for ﬁltering the solutions at the post-processing stage.

In the implemented prototype we experimented with

the connectedness constraint being used for ﬁlter-

ing at the post-processing stage. Furthermore, post-

processing can be used to further reduce the number

of solutions by removing equivalent multigraphs. In

this vein, we experimented with partial/full isomor-

phism checks and ﬁltering of obtained multigraphs.

Molecular Fragments from Incomplete, Real-life NMR Data: Framework for Spectra Analysis with Constraint Solvers

837

4 PROPOSED FRAMEWORK

AND PROTOTYPE

IMPLEMENTATION

The proposed high-level design of the constraint-

based NMR interpretation system from the discussed

principles is presented in Figure 2. The system sup-

ports different sources of the input data - it may come

either as pre-processed experimental spectra (lists of

peaks/chemical shifts) or as ideal constraints gener-

ated from known molecular structures data (molecu-

lar ﬁles). The latter is used for the testing and the

investigation of inherent ambiguity related to the CS

approach for NMR data analysis. Once all constraints

are formulated, based on the input data, a generic

constraint solver is applied which results in the set

of all possible molecular structures (labelled multi-

graphs) satisfying the constraints. Post-processing

(e.g. connectedness, or isomorphism ﬁltering) is ap-

plied after that, and if the results remain ambigu-

ous/inconclusive, the set of constraints can be updated

and processing repeated.

The current prototype system is implemented in

Python and constraints programming platform Num-

berjack (Hebrard et al., 2010), and its constraint

solver Mistral (Hebrard, 2008) is used. The open-

source RDKit software (Landrum, 2016) is used

to handle the connection between atoms and draw

molecular structures. To identify isomorphic struc-

tures and to enumerate all nonisomorphic ones, we

used a standalone Nauty tool, which relies on canoni-

cal labelling algorithms (McKay and Piperno, 2014).

In this work we have used Nauty to check isomor-

phism of labelled graphs.

The performance of the system has been tested

by using known structures of chemical compounds.

Therefore, the NMR data for simple amino acids are

chosen from the Biological Magnetic Resonance Data

Bank (BMRB) website to be the data set for the sys-

tem (Ulrich et al., 2007).

5 EXPERIMENTS, RESULTS AND

EVALUATION

All the experiments were implemented on Intel Core

CPU’s with frequency 2.20 GHz running Ubuntu

18.04.5 and using 7 GB of RAM.

To test our approach we generated full sets of

HSQC and HMBC constraints for all 20 amino acids

from their chemical structures and calculated incom-

plete solutions and part of complete solutions (Ta-

ble 1 and 2, respectively). In each case, the solu-

tions were subsequently ﬁltered at the post-processing

stage to ﬁnd all connected and nonisomorphic multi-

graphs. In Table 1,

and

atoms were considered

in the incomplete setting experiment. For 18 out of

20 amino acids, we reported the number of all possi-

ble solutions with time in seconds and the number of

nonisomorphic structures with the time taken to ﬁl-

ter the solutions in seconds. For two amino acids, we

stated an ’out of memory’ case while running the sys-

tem. To tackle this case, we might need further op-

timisation for the current implementation, including

using different constraint solvers. Multiple solutions

were generated by the constraint solver for amino

acids, with the number of solutions increasing signif-

icantly with the increased complexity of the molec-

ular structure, represented by the number of atoms

in a Molecular Formula (MF). Much higher number

of solutions was generated when the MF was used as

additional source of constraints (complete solutions),

compared to the incomplete solution set. Isomorphic

ﬁltering only partially reduced the number of solu-

tions, demonstrating intrinsic ambiguity of the con-

straint sets.

Inspection of the partial solutions for alanine in

Figure 3 reveals several reasons for multiple solu-

tions. Most of the solutions are linear structures

where the

atom that does not have

atom attached

(no corresponding HSQC peak) is positioned either

at the end of the chain or between the two atoms

that have

atoms. This type of ambiguity is caused

by the intrinsic ambiguity of HMBC constraints that

correspond to either two or three-bond separation be-

tween the interacting atoms. This ambiguity can be

resolved by introducing additional NMR connectivity

constraints.

The second source of ambiguity is uncertainty in

the number of

atoms attached to each

. Since

has

Table 1: Incomplete solutions calculated for amino acids

using only NMR data as the input.

Amino acid MF Structures

# Sols Time (s) Nonisomorphic Time (s)

Alanine C

25 0.00 15 0.00

Arginine C

1952 0.32 716 0.00

Asparagine C

104 0.00 60 0.00

Aspartic acid C

104 0.00 60 0.00

Cysteine C

S 25 0.00 15 0.00

Glutamine C

456 0.04 172 0.00

Glutamic acid C

456 0.04 172 0.00

Glycine C

3 0.00 3 0.00

Histidine C

6204 0.81 2060 0.02

Isoleucine C

1977 0.33 427 0.01

Leucine C

2279 0.33 346 0.01

Lysine C

2555 0.42 676 0.01

Methionine C

S 910 0.11 163 0.00

Phenylalanine C

136221 35.85 30735 0.69

Proline C

603 0.12 85 0.00

Serine C

25 0.00 15 0.00

Threonine C

142 0.01 39 0.00

Tryptophan C

out of memory - - -

Tyrosine C

out of memory - - -

Valine C

603 0.14 85 0.00

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

838

a valency of four, a terminal

can have up to three

atoms attached, and

in the middle of the linear

chain can have maximum two

atoms. The num-

ber of

atoms can be determined in the multiplicity-

edited HSQC experiment. The number of possible

variants caused by these two ambiguities increase dra-

matically with the number of

atoms in the molecule,

as clearly seen from Table 1 and 2.

The third type of ambiguity is caused by the pos-

sibility to form cyclic compounds. Only single cycle

variant is possible with three

atoms, but in more

complex molecules the number of cycles can increase

signiﬁcantly. Small cycles of three and four atoms are

chemically unstable, which justiﬁes using additional

constraint that eliminate small cycles. Constraints on

the number of

atoms attached to

may automati-

cally eliminate cycles through the valencyconstraints.

Including the MF to generate complete solutions

increase the ambiguity for amino acids further (Table

2) because it introduced

and

atoms not detected

in the NMR experiments. As the result, only valency

constraints can be formulated for these atoms, allow-

ing them to take any position in the molecule. How-

ever, for molecules that only contain

and

atoms

the MF constraints maybe highly beneﬁcial because

they would eliminate structures with the incorrect to-

tal number of

atoms.

Our analysis highlights intrinsic ambiguity of

the NMR data and critical contributions from addi-

tional constraints for unambiguous determination of

the molecular structure. In the majority of CASE

systems, including the CS system of (Omrani and

Naanaa, 2016) the MF is required, and these con-

straints are rigidly embedded into the system; very

often the software would not run if these parameters

are not deﬁned. This limits the usability of the sys-

tems, as most of the time only partial information on

these parameters is available at best. It may also lead

to incomplete or incorrect results, as possible solu-

tion are not explored systematically. In contrast, our

system explicitly deﬁnes all constraints used in ﬁnd-

ing the solution and allows to explore the constraints

systematically. The system can be used with any set

of constraints, often incomplete, which allows its ap-

plication at all stages of the NMR analysis. The in-

spection of the results, as outlined above, can suggest

further experiments to eliminate ambiguities, until a

unique solution is found.

From a more theoretical perspective, we propose

to consider the obtained results in the complete set-

ting (including the formula) as evidence of the lim-

its of the NMR method itself. Indeed, in a consid-

ered variant of NMR analysis including HSQC and

HMBC spectra, even in the presence of all theoret-

Table 2: Complete solutions calculated for amino acids us-

ing NMR data and the MF as the inputs.

Amino acid MF Structures

# Sols Time (s) Nonisomorphic Time (s)

Alanine C

662 0.10 148 0.00

Cysteine C

S 8081 1.51 779 0.01

Glycine C

78 0.00 34 0.00

Leucine C

4091 2.41 136 0.00

Proline C

15066 3.69 764 0.03

Serine C

8081 1.51 783 0.01

Threonine C

24153 5.81 732 0.04

Valine C

2654 0.81 64 0.00

ically possible ideal NMR constraints (derived from

the known structure) the target structure can not be

identiﬁed uniquely. The numbers produced measure

an inherent ambiguity of the NMR method. We sus-

pect that it remains the case even in the presence of

further realistic constraints. The proposed CS-based

approach addresses such questions systematically and

this is a subject of our ongoing and future work.

6 RELATED WORK

The current study contributes to the existing knowl-

edge by addressing several structure elucidation prob-

lems. Unlike similar existing constrained structures

generating systems, the paper suggests an analytical

approach that considers being as realistic and practi-

cal as possible. As a result, the program generates

all possible structures based on real-world constraints,

considering the minimum available information.

There are a set of limitations that may affect the

molecular structure elucidation results. One poten-

tial drawback that might be encountered is the un-

certainty of NMR data, caused by the different envi-

ronments, especially during the acquisition of NMR

data, for solvent or temperature, which can create

signiﬁcant noise of the spectra data. Further im-

provements should be taken into account to tackle

these problems. In the literature, several approaches

have been proposed to develop CASE systems over

the past century. The Dendral project (Smith et al.,

1981), is a pioneer in structure elucidation systems

based on NMR spectra. The main aim of the Den-

dral group was to develop computer systems to assist

the chemists in identifying unknown chemical struc-

tures (Gray, 1988). The project’s main achievement

was to introduce the CASE systems’ idea to eluci-

date the chemical structure. There has been a sig-

niﬁcant increase in publications that document other

CASE systems’ approaches due to the development

of NMR techniques. The examples of these CASE

systems are SENECA platform-independent pack-

age (Steinbeck, 2001), MONOREG (Ferreira et al.,

Molecular Fragments from Incomplete, Real-life NMR Data: Framework for Spectra Analysis with Constraint Solvers

839

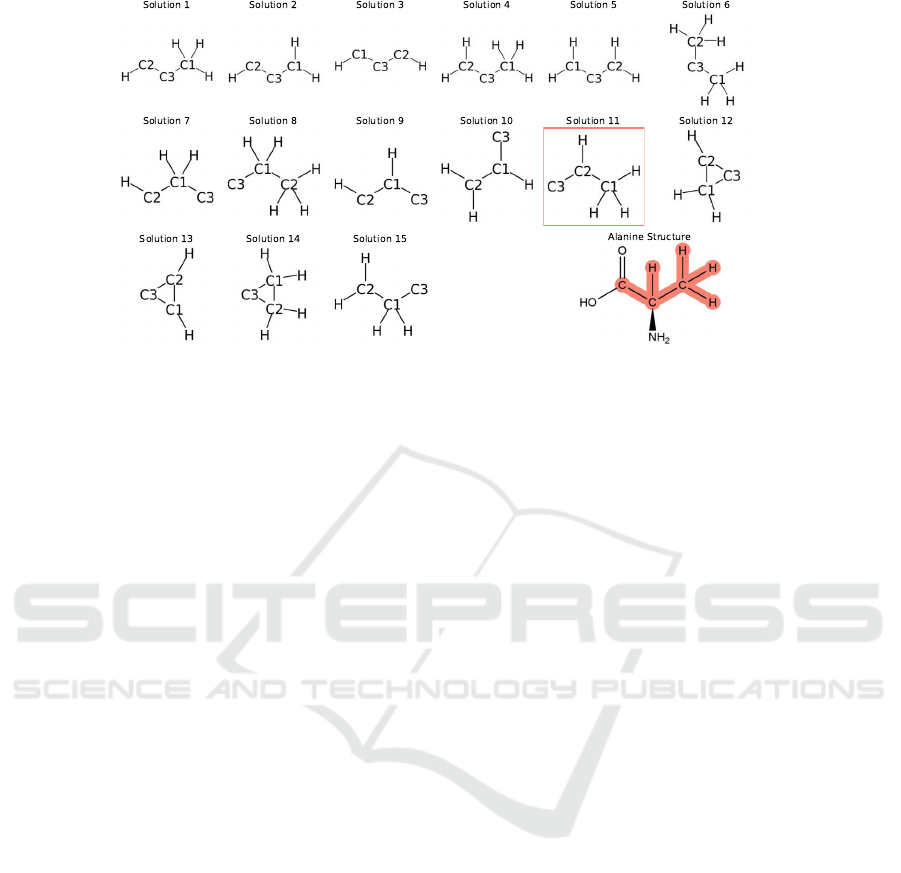
Figure 3: Solution multigraphs built from chemical and NMR constraints derived from alanine data. 15 multigraphs satisﬁed

the constraints and were connected and nonisomorphic. The box labelled (Solution 11) is the correct structure. The structure

at the bottom right is the complete structure of alanine and the highlighted parts in red corresponds to Solution 11.

2001), Bruker CMC-se program (Kessler and Gode-

johann, 2018), Logic for Structure Determination

(LSD) (Plainchont et al., 2013), Advanced Chem-

istry Development (ACD)/ Structure Elucidator Suite

(Elyashberg et al., 2002), Mestrelab MNova struc-

ture (Burns et al., 2019) and MOLGEN 5.0 (Gugisch

et al., 2015). The majority of these approaches rely

on complex sets of rules deﬁned by experts, and spe-

cialised algorithms, which limits their effectiveness

and adaptation for complex systems, such as molecu-

lar mixtures. The constraint-based systems, we argue

for in this paper, separate rules (constraints) formula-

tion and constraint solving, which make them much

more ﬂexible and adaptable. Such systems allow util-

ising the performance of generic constraint solvers.

According to (Omrani and Naanaa, 2016), the frame-

work of CS provides an effective solution to structure

elucidation problems. A program was developed to

generate molecular structures based on satisfying sev-

eral predeﬁned constraints. The ﬁrst constraint is the

MF. In addition, the number of bonds for each atom

and the type of bonds are given as inputs to their sys-

tem. The system can also impose substructures to ap-

pear in the results and forbid speciﬁc fragments to ex-

ist in the generated structures. The authors have pub-

lished a recent study describing a new open-source

system CP-MolGen (Omrani and Naanaa, 2019).

However, from a practical perspective, the amount

of minimum required information to use the frame-

work proposed by the authors is challenging to ob-

tain and even unfeasible in some cases. The MFs are

not always readily available. Determining the num-

ber of bonds may require extensive analytical data

from different instruments. A detailed map of spe-

ciﬁc distance between atoms is a complicated process

that usually is incomplete. For example, HMBC ex-

periments are used to map out the bond distances but

HMBC experiments cannot distinguish between two

or three bonds (Janovick et al., 2020). This infor-

mation needs to be inferred from other data available

similar to a CS approach. In practice, after obtaining

such detailed data elucidating the molecular structure

is a trivial process and using a constraint solver is gen-

erally not necessary.

Structure elucidation can be formulated as a more

generalised CS problem, and approximate solutions

can be proposed with a more realistic amount and

type of input information. All constraints can be for-

mulated exactly and explicitly, which allows avoiding

biased solutions. Such a CS approach to obtain a list

of approximations down to the least ambiguous set

would be more useful in practical applications. Such a

list of solutions can even indicate which experiments

to perform next to get a unique solution. In a typi-

cal NMR analysis, samples usually consist of chemi-

cal mixtures or contain contaminants that have signals

indistinguishable from the compounds of interest.

Thus, the amount of experimental NMR informa-

tion is very limited, which leads to incomplete con-

nectivity and a lack of separation of the observed sig-

nals into groups corresponding to different molecules.

Sometimes partial information on the MFs can be ob-

tained from the MS analysis, but cannot be related

to the NMR signals. These challenges are impossi-

ble to address with the reported CS implementation

of (Omrani and Naanaa, 2016). The CASE system

we have presented addresses this particular need and

allows obtaining a full list of possible chemical struc-

tures irrespective of the completeness of the NMR in-

formation. This creates a powerfulcomputational tool

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

840

for NMR data analysis and guidance for the selection

of additional experiments to establish an objectively

unique solution.

7 CONCLUSIONS

This paper presents a method of interpreting NMR

spectra data via the CS framework to generate molec-

ular multigraphs. Real-world chemical structures in-

stances demonstrate that obtaining constraints based

on NMR data is successfully predicts the correct

molecular multigraphs. While alternativeCS methods

exist, which can determine the correct structures for

the molecules based on several deﬁned constraints,

the interpretation of spectra data in our approach has

the advantage of generating the structures based on

the minimum available information as the case of the

real practical NMR instances. Although we solve

the structures predicting problems, we did not con-

sider more complex natural compounds. For instance,

chemical structures containing ring compounds and

the existence of symmetry for some atoms of the

structures. The main challenge would be that it can

not easily differentiate between the atoms as two or

more atoms will be had the same values of chemical

shifts. Further measures are suggested to improve the

performance and to predict robust and conﬁdent struc-

tures. The actions should deﬁne the most appropriate

methods to handle any uncertainty of NMR data as

this is more likely to be encountered in real instances

of spectra data.

REFERENCES

Burns, D. C., Mazzola, E. P., and Reynolds, W. F. (2019).

The role of computer-assisted structure elucidation

(case) programs in the structure elucidation of com-

plex natural products. Natural product reports,

36(6):919–933.

Elyashberg, M. and Williams, A. J. (2015). Computer-

based structure elucidation from spectral data.

Springer.

Elyashberg, M. E., Blinov, K. A., Williams, A. J., Mar-

tirosian, E. R., and Molodtsov, S. G. (2002). Appli-

cation of a new expert system for the structure eluci-

dation of natural products from their 1d and 2d NMR

data. Journal of natural products, 65(5):693–703.

Ferreira, M. J., Rodrigues, G. V., and Emerenciano, V. P.

(2001). Monoreg an expert system for structural elu-

cidation of monoterpenes. Canadian journal of chem-

istry, 79(12):1915–1925.

Gray, N. (1988). Dendral and meta-dendral—the myth and

the reality. Chemometrics and Intelligent Laboratory

Systems, 5(1):11–32.

Gugisch, R., Kerber, A., Kohnert, A., Laue, R., Meringer,

M., R¨ucker, C., and Wassermann, A. (2015). Molgen

5.0, a molecular structure generator. In Advances in

mathematical chemistry and applications, pages 113–

138. Elsevier.

Hebrard, E. (2008). Mistral, a constraint satisfaction li-

brary. Proceedings of the Third International CSP

Solver Competition, 3(3):31–39.

Hebrard, E., O’Mahony, E., and O’Sullivan, B. (2010).

Constraint programming and combinatorial optimisa-

tion in numberjack. In Lodi, A., Milano, M., and Toth,

P., editors, AI and OR Techniques in Optimization

Italy, June 14-18, 2010. Proceedings, volume 6140 of

Lecture Notes in Computer Science, pages 181–185.

Springer.

Janovick, J., Spyros, A., Dais, P., and Hatzakis, E. (2020).

4 - nuclear magnetic resonance. In Pico, Y., editor,

Chemical Analysis of Food (Second Edition), pages

135–175. Academic Press, second edition edition.

Kessler, P. and Godejohann, M. (2018). Identiﬁcation

of tentative marker in corvina and primitivo wines

with cmc-se. Magnetic Resonance in Chemistry,

56(6):480–492.

Koichi, S., Arisaka, M., Koshino, H., Aoki, A., Iwata, S.,

Uno, T., and Satoh, H. (2014). Chemical structure

elucidation from 13c NMR chemical shifts: Efﬁcient

data processing using bipartite matching and maximal

clique algorithms. Journal of chemical information

and modeling, 54(4):1027–1035.

Landrum, G. (2016). Rdkit: Open-source cheminformatics

software. GitHub and SourceForge, 10:3592822.

McKay, B. D. and Piperno, A. (2014). Practical graph

isomorphism, ii. Journal of symbolic computation,

60:94–112.

Omrani, M. A. and Naanaa, W. (2016). A constrained

molecular graph generation with imposed and forbid-

den fragments. In Proceedings of the 9th Hellenic

Conference on Artiﬁcial Intelligence, pages 1–5.

Omrani, M. A. and Naanaa, W. (2019). Constraints for gen-

erating graphs with imposed and forbidden patterns:

an application to molecular graphs. Constraints, pages

1–22.

Plainchont, B., de Paulo Emerenciano, V., and Nuzillard,

J.-M. (2013). Recent advances in the structure eluci-

dation of small organic molecules by the lsd software.

Magnetic Resonance in Chemistry, 51(8):447–453.

Smith, D. H., Gray, N. A., Nourse, J. G., and Crandell,

C. W. (1981). The dendral project: Recent advances

in computer-assisted structure elucidation. Analytica

Chimica Acta, 133(4):471–497.

Steinbeck, C. (2001). Seneca: A platform-independent,

distributed, and parallel system for computer-assisted

structure elucidation in organic chemistry. Jour-

nal of chemical information and computer sciences,

41(6):1500–1507.

Ulrich, E. L., Akutsu, H., Doreleijers, J. F., Harano, Y.,

Ioannidis, Y. E., Lin, J., Livny, M., Mading, S., Maz-

iuk, D., Miller, Z., et al. (2007). Biomagresbank. Nu-

cleic acids research, 36(suppl

1):D402–D408.

Molecular Fragments from Incomplete, Real-life NMR Data: Framework for Spectra Analysis with Constraint Solvers

841