Classiﬁcation Rules Explain Machine Learning

Matteo Cristani

1 a

, Francesco Olvieri

2 b

, Tewabe Chekole Workneh

1 c

, Luca Pasetto

1 d

and Claudio Tomazzoli

3 e

Department of Computer Science, University of Verona, Italy

School of Computer Science, Grifﬁth University, Brisbane, Australia

CITERA, University of Rome, Italy

Keywords:

Machine Learning, eXplainable AI, Approximation, Anytime Methods.

Abstract:

We introduce a general model for explainable Artiﬁcial Intelligence that identiﬁes an explanation of a Machine

Learning method by classiﬁcation rules. We deﬁne a notion of distance between two Machine Learning

methods, and provide a method that computes a set of classiﬁcation rules that, in turn, approximates another

black box method to a given extent. We further build upon this method an anytime algorithm that returns the

best approximation it can compute within a given interval of time. This anytime method returns the minimum

and maximum difference in terms of approximation provided by the algorithm and uses it to determine whether

the obtained approximation is acceptable. We then illustrate the results of a few experiments on three different

datasets that show certain properties of the approximations that should be considered while modelling such

systems. On top of this, we design a methodology for constructing approximations for ML, that we compare

to the no-methods approach typically used in current studies on the explainable artiﬁcial intelligence topic.

1 INTRODUCTION

The reproduction of results obtained by up-to-date

methods of Machine Learning (ML) and Deep Learn-

ing (DL) approaches, in a fashion that could be un-

derstood by humans is one of the emerging topics in

recent Artiﬁcial Intelligence studies. The overall idea

of explainable Artiﬁcial Intelligence lies on the possi-

bility of doing what is devised above.

If we look at the concepts underlying this very no-

tion, we observe a relevant distance between how a

ML, and in speciﬁc case, a DL system executes the

classiﬁcation and the natural way in which human be-

ings identify rules that execute similar analyses on the

same data. This discrepancy has been remarked in nu-

merous cases, and is one of the reasons why explain-

able artiﬁcial intelligence has emerged.

When looking at a set of data, we can regard them

as expression of implicit regularity, the discover of

https://orcid.org/0000-0001-5680-0080

https://orcid.org/0000-0003-0838-9850

https://orcid.org/0000-0001-5756-2651

https://orcid.org/0000-0003-1036-1718

https://orcid.org/0000-0003-2744-013X

which is indeed an intelligent process, and even a log-

ical base for an induction process to learn those regu-

larities. Given that we expect data to grow over time,

this process can be performed in two models:

• The data of a classiﬁcation system have at least a

partition of human - made labels. Therefore there

is the so called ground truth: a training set and

a test /validation set can be determined, while we

always have an execution dataset. After a train-

ing and validation phase over the training and test

sets, an algorithm can try and predict the values

against the execution dataset by looking at two or

more observation instants. This method is based

on the existence of a ground truth, so we name this

grounded model.

• The data of a classiﬁcation system do not have any

human - made labels. We need another classiﬁca-

tion algorithm (maybe a previously evaluated one)

so that a performance comparison can be made

over the execution dataset by looking at two or

more observation instants. This method does not

provide ground to the conclusions it takes, it only

validates a model against another one. Therefore

we name this model cross-validation model.

Cristani, M., Olvieri, F., Workneh, T., Pasetto, L. and Tomazzoli, C.

Classiﬁcation Rules Explain Machine Learning.

DOI: 10.5220/0010927300003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 897-904

ISBN: 978-989-758-547-0; ISSN: 2184-433X

897

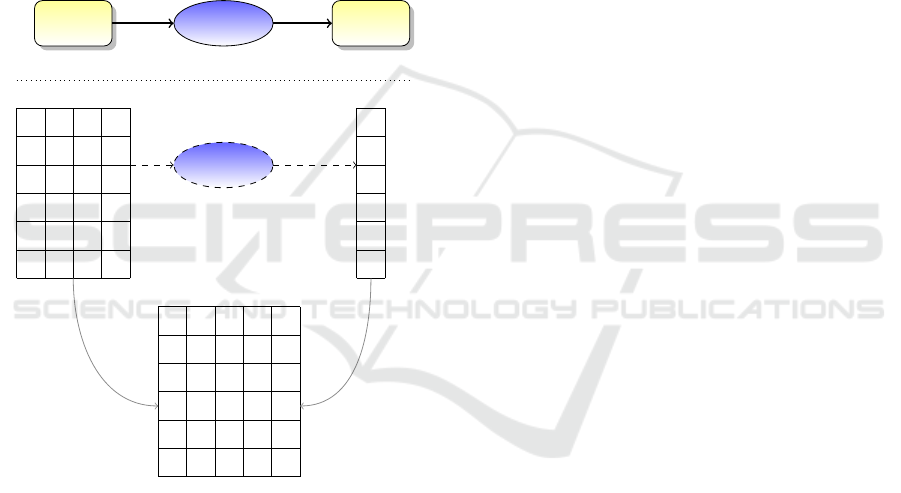
The basic idea of this paper is that a classiﬁca-

tion system C explains another classiﬁcation system

when two conditions hold:

• C is an approximation of C

, i.e., the way in which

C forecasts the results is close to the way in which

does so, and

• C is a readable rule-based systems. We will pro-

vide a non-formal deﬁnition of this concept of

readablility in the following paragraphs.

To better identify the underlying concept, we pro-

vide here a toy example about the basic notion of ex-

plainability.

Example 1. Consider a binary classiﬁcation system

that we can only observe as an input-output black box

technology, as illustrated in Figure 1. Assume that

Input Data

Classiﬁer

Output

Figure 1: A black box input-output data conﬁguration.

the rows in the table under analysis of the observed

classiﬁer respond to one association rule R1 and to an

association rule R2, each (for the sake of simplicity)

with a positive error of 3% and a negative error of 2%

The two rules establish

• R1 when the values in column F1 are greater than

a threshold value limit t

and the values in col-

umn F2 are less than a threshold value t

then

the classiﬁcation value on column C is true;

• R2 when the values in column F3 are greater than

a threshold value t

and the values in column F4

are less than a threshold value t

then the classi-

ﬁcation value on column C is true.

Now, the rule system {R1, R2} is an approxima-

tion of the black box that has a positive error of 3%

and a negative error of 2%.

Based on the idea illustrated above, we build a

model of explanation that can be summarised as fol-

lows: explaining means approximating with the con-

straint that an approximation is better when it is sim-

pler. Therefore, to devise a good technology for ex-

plaining a black-box system, we need to identify a

system that is readable and a hierarchy among read-

able systems that are as simpler and more accurate

(precise or recalling) as possible.

The rest of this paper is organised as follows. Sec-

tion 2 introduces some basic notions used in the rest

of the paper, and Section 3 discusses an algorithmic

approach based on the introduced notions. Section 5

reviews relevant literature, and Section 6 takes con-

clusions and sketches further work.

2 BASIC DEFINITIONS

We introduce, from scratch, some basic notions that

we are about to use in order to introduce a notion of

explainability that is to be formalised in the rest of

this paper. There is a large part of readers who might

consider this section very introductory. However, it

is important to get to the ground notions to highlight

how a notion of actual explainability should be intro-

duced.

Deﬁnition 1. Assume a collection of three datasets

hTrain, Test, Execi where: (i) the training set Train

and the test set Test are formed by the same n + 1

columns, and (ii) the execution set Exec is formed

by the ﬁrst n columns of training and test sets. We

name these n columns the classiﬁcation features and

the (n + 1) −th one the class.

The classiﬁcation problem consists in deﬁning a

method that learns the class classiﬁcation to the clas-

siﬁcation features from the training set, veriﬁes it on

the test set to provide its measures of accuracy, pre-

cision and recall and ﬁnally applies the classiﬁcation

to the execution test, where we expect the behaviour

of the classiﬁer will respect the measures taken on the

test set.

A system like the one just devised above is said

to be a classiﬁer. Every classiﬁer is intrinsically de-

scribed by its confusion matrix that is a k-entry ma-

trix establishing the relative account of elements (fre-

quency) in each class obtained for each value of the

classiﬁcation by the classiﬁer performed on the test

set. When the classiﬁer is binary (i.e., the classes

are only two), the matrix cells are named true pos-

itive (T P), false positive (FP), true negative (T N),

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

898

and false negative (FN), indicating the elements: (i)

correctly classiﬁed (true positive and true negative),

and (ii) incorrectly classiﬁed (false positive and false

negative). In general, when looking at the confu-

sion matrix we also use the acronyms P = T P + FN

for positive elements, N = T N + FP for negative ele-

ments, T = T P +FP for elements classiﬁed correctly,

F = FP + FN for elements classiﬁed incorrectly and

ﬁnally A = T P+FP+T N +FN for the size of test set

(namely all elements. We henceforth limit ourselves

in studying binary classiﬁers.

Accuracy is the frequency of a classiﬁer correct

answers. It is deﬁned as

a(C) =

T P + T N

= 1 −

Precision measures the probability of the classi-

ﬁer’s positive answers to be correct. In other terms,

the more a classiﬁer is precise, the fewer are the posi-

tive incorrect answers it gives. It is deﬁned by

p(C) =

T P

T P + FP

T P

Recall measures the probability of the classiﬁer’s

negative answers to be false. In other terms, the

higher is a classiﬁer’s recall, the more are the posi-

tive correct answers it gives. It is deﬁned by

r(C) =

T P

T P + FN

T P

Once we have trained a classiﬁer on the training

set, we can measure its behaviours in terms of quality

of the classiﬁcation on the test set.

We can now introduce a measure that has been

used in various applications of classiﬁcation rules,

and in general applies to rule-based systems includ-

ing decision trees. To do so, we start by formalising

the notion of classiﬁcation rules.

A simple value constraint may be either an equal-

ity constraint, where a feature is set to be valued

in a given way, an inequality constraint, that is the

opposite of the above, and a minority/majority con-

straint when it imposes the value of the feature to

span below/over a given value on the range of ad-

missible values for that feature. A minority/majority

constraint can be either weak (while including the ex-

treme value) or strong (while excluding the extreme

value). When the values of a feature are not or-

dered, then the equality/inequality constraints are the

only admissible ones. Boolean expressions on simple

value constraints are hence value constraints.

Deﬁnition 2. An classiﬁcation rule is a classiﬁer that

consists of a test of value constraints on the features

for a classiﬁcation problem that forecasts the class of

that problem.

It is not difﬁcult to show that every value con-

straint on an ordered domain can be represented by

a ﬁnite collection of intervals and semi-intervals,

along with a ﬁnite set of inequalities (Stergiou and

Koubarakis, 2000). Conversely, when a discrete un-

ordered and ﬁnite domain is involved, the largest

number of elements involved in a value constraint is

exactly the size of the domain minus 1. For instance,

if a ﬁnite domain is formed by three elements, then

admissible constraints are 7, corresponding to the re-

quest to range over a subset of the 3 elements.

R1 of Example 1 is a classiﬁcation rule. An classi-

ﬁcation rule system is a set of rules, that are to be ap-

plied disjunctively, and assumed to validate one single

class. The set {R1, R2} of Example 1 is a classiﬁca-

tion rule system. An element of the test or execution

set is classiﬁed by means of a rule system when it is

valued by at least one of the rule system in that class.

At a very simple level, we can introduce a notion

of complexity of a rule. A rule length is the sum of

intervals or the sum of disjoint values for unordered

and ﬁnite domains, for each feature.

Example 2. Consider a feature F1 ranging on natu-

ral numbers, and a feature F2 ranging on real num-

bers. A rule consists in the expression:

((1 ≤ F1 ≤ 12) ∨ (14 ≤ F1 ≤ 33))

∧ ((F2 6= 3.14) ∧ (F2 ≥ 2.72)) → True

The length of the above rule is 4, because the con-

straints appearing in it are formed in turn by two pairs

of constraints on two different features, both of length

two. Clearly, when a rule R has length l

and a rule

has length l

, then l

≤ l

is to be read R is shorter

than R

Two rules are in the containment order ⊆ (R1 ⊆

R2) iff when R2 is satisﬁed then R1 is satisﬁed. For

instance, consider a rule R

((1 ≤ F1 ≤ 12) ∨ (14 ≤ F1 ≤ 33)) → True

and a rule R

((1 ≤ F1 ≤ 12)) → True

and R

in the relation R

⊆ R

. In fact, when

is satisﬁed, R

is satisﬁed as well. A rule R is said

to be simpler than a rule R

when R is shorter than R

and R

⊆ R. Extensively, a rule set S

is simpler than

a rule set S

when each rule of S

is simpler than at

least one rule in S

We can provide an absolute measure of complex-

ity of a classiﬁcation rule system by computing its

volume a measure inspired by classic software met-

rics: the product of maximum length of a rule in the

system and number of rules. This notion of volumes

Classiﬁcation Rules Explain Machine Learning

899

presents two primary advantages that we need to con-

sider in this phase.

When two systems have the same volume they can

be rather different but may be reasonably similar in

terms of the effort we need to devise them. The com-

putation of rules is expensive both in terms of required

design effort, and in terms of the computational effort

to build the rules. Both effort of design and compu-

tational cost depend on the length of the rules and on

the number of rules. We could have considered length

of the rule system as the sum of lengths of the rules.

However, these would have made equivalent two sys-

tems in a way that is in fact independent of the number

of rules. This is actually different from what we ex-

pect to be a good explanation. In fact, an explanation

should be understandable, and therefore we expect it

to be made of simple rules and that these rules are

not too many. Obviously we should get a tradeoff,

for the ideal explanation would result, from the above

premises, the empty rule system. Therefore, volume

is a better measure of length, for it could accommo-

date, in the same volume, or roughly the same, a num-

ber of possible different explanations that are similar

in terms of design effort, and let us able to choose the

best ones, by considering the most accurate or precise

or recalling.

To summarise, the idea is that when two approx-

imations are comparable in terms of simplicity we

should choose the most accurate (precise, recalling),

and on the opposite, when two approximations are

comparable in terms of accuracy (respectively preci-

sion, recall) we should choose the simpler one.

We can shift our attention to the details of the ap-

proach, by devising a method to compute approxima-

tions for a black box classiﬁer. Consider a classiﬁer

C that we cannot look more in detail than by its be-

haviour, namely by looking at the results of the clas-

siﬁcation on an execution test, without knowing how

the results are obtained. The idea of the method is

to perform the classiﬁcation on a subset of the exe-

cution set, that we can control. On the input/output

behaviour of the classiﬁer we can build a training set,

that is used to extract a classiﬁcation rule set. We are

now able to build a confusion matrix and use it to de-

vise the correct understanding of the behaviour of the

classiﬁer.

Speciﬁcally, when such a method is computed, we

can state that a binary classiﬁer C has been approxi-

mated by a classiﬁcation rule system S with accuracy

α, precision π and recall ρ (by using the measures ob-

tained by the confusion matrix) with volume V . Ide-

ally, we should also derive the idea that a rule set

is a better approximation of a given classiﬁer when

it has the same accuracy (respectively precision, re-

call) but a smaller volume, or the same volume but a

better accuracy (respectively precision, recall). Obvi-

ously, the idea that accuracy, precision and recall re-

main the same (either alone or in triple) is unrealistic,

for these values are intrinsically unstable on classiﬁ-

cation rule setup. We can establish a range interval on

which accuracy, precision and recall are to be consid-

ered equivalent, that is the conﬁdence on that opera-

tion. The conﬁdence is thus a value χ such that when

accuracy (respectively, precision, recall) of a set S

is to be considered roughly the same of accuracy (re-

spectively, precision, recall) of a set S

is that because

|α(S

) − α(S

)|≤ χ (and correspondingly for π and

ρ).

Therefore, we can state that a rule set S

is a better

approximation of a rule set S

because S

has less vol-

ume than S

and they are ordered by better accuracy

(respectively, precision, recall) or at most roughly the

same.

3 ALGORITHMS FOR

EXPLAINING THE BLACK BOX

Given the analysis discussed above, we can devise a

method to compute optimal rule systems that approx-

imates a classiﬁer, or, on more practical design of the

method, a rule system that approximates a classiﬁer

with an acceptable accuracy (respectively precision,

recall). Consider an approximation S

. We can make

two kinds of operations. The former consists in look-

ing for admissible simpliﬁcations that preserve accu-

racy (respectively precision, recall) and reduce vol-

ume. The latter, on the opposite, looks for improve-

ment on the accuracy (respectively precision, recall)

but preserve volume.

At this point of this discussion, we need to specify

an important aspect of the concept of rule system we

have devised so far. The idea of disjunctive systems is

quite simple, and it is so for we can provide room for

constraints on the range by means of a method that

results polynomial on deterministic machines. The

majority of methods like Apriori as well as methods

for similar approaches to other rule system, as in, for

instance, decision trees, provide incremental compu-

tation of the rule system. Thus, a rule system is more

complex and potentially more accurate, precise and

recalling, then the rule system computed on the previ-

ous step by those methods. To obtain good explana-

tions we therefore should look at these methods with

a critical eye: the purpose of the computation is to

choose among the partial solutions obtained by these

methods that we consider good explanations, more

than good classiﬁers. In fact, we do not really have

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

900

a comparison with the ground truth, for the only ob-

ject we look at is a classiﬁer that acts in the realm

of the execution set. We should manage a choice of

the quality of the explanation by looking at the rel-

ative accuracy (respectively precision, recall) but we

cannot ensure that the approximation obtained only

introduces the errors we measure on the relative com-

parison, for new errors could have been introduced,

as well as errors made by the explained classiﬁer are

incorporated as well (and obviously we can also have

the opposite, inverted effect, where errors of the ex-

plained classiﬁer are corrected by the explanation).

The above reasoning can be described as the core

of the methodology we propose here. Let us sum-

marise the concept we are looking at:

1. We are given a black box classiﬁer C, for which

we aim at computing an acceptable explanation

2. We assume a partition of the domain classiﬁed by

C in two subsets Train and Test, where the classes

(positive and negative) are assigned;

3. We use the subset of the execution set Train to

devise a collection of rule classiﬁcation systems;

4. We choose among the systems computed in the

above Step 3 an explanation that has both a good

volume, and a good accuracy (respectively preci-

sion, recall).

Naturally, computing every possible system is un-

affordable, for even if the number might be ﬁnite, is

likely to be unacceptably large. A possible way to

overwhelm the mentioned drawback is to limit to a

method that works on incremental algorithm

At ﬁrst, as an initial perspective, we evaluate the

opportunity of applying the devised approach Con-

sider a feature F1 ranging over an inﬁnite range of

values. Given a set of records on which the train-

ing set sets the value of the row to true, we can col-

lect the values in total order by ordering algorithm in

O(n · log(n)). Once we have devised the correct or-

dering, the line of values can be marked by the class

elements true, and therefore partitioned into open in-

tervals.

For instance, assume that we have F1 valued

, a

, . . . , a

on n rows, and that a

and a

are val-

ued true, while a

is valued false, and a

and a

are both valued true. The interval partition is (F1 ≤

) ∨ (a

< F1 < a

) ∨ (F1 ≥ a

). Each single rule

generated in this way matches the training set with

no errors, but other disjunctive rules can be gener-

ated with errors as well. For instance, in particular

for discrete cases, we may have situations in which

a value is attributed to a feature and that feature has

some true and some false with that value. The major-

ity method chooses the most frequent among the two

cases, the unanimity method chooses true only when

all the cases unanimously give a true. Mix strategy

lies on the notion that instead of basic majority we

require qualiﬁed one to reinforce the method (that is

equivalent to mitigating the unanimity by requiring

a signiﬁcant percentage instead of 100%). Clearly,

generating rules on single feature does not improve

the results signiﬁcantly, for they could only be con-

sidered separately, and there is an extensive literature

on how to combine them that has shown to work only

in speciﬁc and limited conditions.

All the above notions are quite well-known from

Decision Tree approaches as well as association rules.

The novelty we introduce here is the idea that ap-

proximation is computed by using one of these ap-

proaches, and then evaluated by means of the notions

of relative accuracy (respectively precision, recall)

and total volume as a measure of the quality (sim-

plicity) of the approximation. If we thus consider an

approximation obtained by a rule set S we can state

that S is a good approximation when it is the simplest,

or when it has the best relative accuracy. Clearly the

two quantities are in tradeoff. It is very likely that the

simplest explanation would not result to be the most

relatively accurate, and the way around. If we start

with an Apriori method, we can simply generate the

ﬁt rules one at a time, and evaluate the resulting rule

set in terms of volume. Classic implementations of

Apriori allow us to do so, by invoking it on the ba-

sis of the step to be performed. Once we have in-

voked the algorithm, we can obtain the values of the

resulting approximation. During this process we can

keep information on the computed model by enumer-

ating the results along with the accuracy (respectively

precision, recall) and the volume. At the end of the

Apriori execution we can generate the partially or-

dered set of these approximations and choose the best

candidate, namely among the ones with optimal vol-

ume that with best accuracy (respectively precision,

recall). The volume and accuracy (respectively pre-

cision, recall) could be speciﬁed with a parameter of

rough equivalence, χ

, χ

(χ

, χ

) that is passed to the

algorithm itself.

4 EXPLANATION ALGORITHMS

The basic explanation method we introduce is exactly

the Apriori algorithm, that is trapped in each step of

the reﬁnement. Apriori algorithm. This is introduced

in Algorithm 1.

Classiﬁcation Rules Explain Machine Learning

901

Algorithm 1: Apriori algorithm.

1: L

← Frequent1 − itemset

2: k ← 2

3: while L

k−1

6= φ do

4: Temp ← candItemSet(L

k−1

)

5: C

← f reqO f ItemSet(Temp)

6: L

← compItemSetWithMinSup(C

, minsup)

7: k ← k + 1

8: end while

9: return L

With a little abuse of notation we assume here that

the algorithm we implement invokes Apriori until step

k, and left it suspensively waiting for another invoca-

tion (as in trap/interrupt parallelism methods). There-

fore we shall name this invocation by Apriori(k). Al-

gorithm 2 considers the measure λ, that could be ac-

curacy, precision or recall.

Substantially, Algorithm 1 is an anytime version

of the classic mining method for association rules.

We introduced this concept here, for three distinct rea-

sons.

• Firstly, we need a method that could be devised to

perform in practice. Every technique of associa-

tion rule generation is computationally expensive,

and since the computation of explanations is here

explorative, for we need to understand, at least

in principle, what explanation is the best, or, at

least, whether an explanation is acceptable, there

is a serious risk of not being able to conclude the

analysis within an even not particularly restrictive

practical time limit;

• Secondly, Apriori is a very basic approach, and

allow us to provide the second step of the investi-

gation, described in 6, where human in the loop

analysis is to be performed in order to validate

with a gold standard the introduced notion of vol-

ume;

• Thirdly, for we look at an explainability concept

that can be used even when we do not know what

features have been extracted (as in the deep learn-

ing approach) and aim at devising a very general

methodology for rule-based systems.

One main drawback of the above devised method

is the limited ability that it has to reﬁne the results.

In fact, by deﬁnition of the Apriori method, every

step increases the coverage given by the rules, and

on the same time it simpliﬁes the rules, by generat-

ing a classiﬁer that has a smaller or identical volume.

Therefore, the probability that the computed solution

is computed just at the end of the execution of the al-

gorithm is very high being the stability of the method

very unusual. The introduction of the χ values. The

Algorithm 2: Computing volume and accuracy algorithm.

1: Stack ←

2: k ← 1

3: while Apriori is not terminated, Increment k do

4: Invoke Apriori(k);

5: Compute Volume and λ of L

;

6: push Index of L

, volume, λ;

7: end while

8: return Stack optimal by (Volume, λ) extensively

considering the volume under the constraint of

range equivalence given by χ

and accuracy (re-

spectively precision, recall) under the appropriate

parameter χ

(with λ = α, π, ρ)

second, well known drawback, regards the types of

the data, that need to be discrete and ﬁnite. In fact,

with inﬁnite value ranges the predictive capability

of Apriori algorithm is very basic, while with Deci-

sion Trees we can have much better results, from this

viewpoint. However, while Apriori is deﬁnitely in-

terruptible, by means of the invocation parameter k,

as shown above, it does not make any sense to in-

terrupt a DT method, for the computation of the tree

could just be stopped over in the wrong deepening.

The only case in which this can be done is when the

method used to generate the tree starts from the root,

and goes, bread-width, downward. This is the case of

ID3. Again we could imagine to substitute the invo-

cation to Apriori(k) by the invocation to ID3(k) where

k denotes the level of the Decision Tree generated so

far, we obtain the very same method of Algorithm 2.

The usage of ID3 could, potentially, improve the

performances, while letting the underlying process

of explanation intact. In the future we shall explore

much more deeply methods that are based upon logic

programming, such as Inductive Logic Programming,

and Answer Set Programming.

To summarise the approach we consider two ex-

planations ordered when they are similar in terms of

volume and one is better than the other one in terms of

accuracy (respectively precision or recall), or on the

opposite, when they are similar in terms of accuracy

(respectively precision, recall) but one has a smaller

volume. Measuring volume is very easy for associ-

ation rules, and can be extended in a straightforward

way to decision trees. The very same notion cannot

be applied to black-box systems.

Let us consider a simple abstract example. As-

sume that we aim at approximating a black-box sys-

tem C. We can describe by hTrain, Test, Execi the

split of the input to C observed in a period of obser-

vation (data are randomly chosen to belong to Train

and Test). After this period, we can feed Algorithm

2 with Train set and compute alternative Apriori so-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

902

lutions to approximate the black-box. At top of the

stack at the end of the process we shall have an Apri-

ori set of rules that exhibit a good volume, in the sense

that this will be the best (minimum) volume obtained

by the anytime performance of the Apriori method.

While comparing two elements in the stack, we

may have either a better element that has less rules,

or a better element that has short maximum rule. On

the other side of the evaluation, when two Apriori so-

lutions are comparable in terms of volume, we may

choose the best one in terms of accuracy (precision,

recall). Notice that even a limited (within a given

threshold) loss in terms of accuracy (precision, recall)

or in terms of volume could be accepted as fruitful. In

fact, when the Apriori anytime method devised above

acts, we do not really know what is computed in terms

of rules, for we can drop rules based on the invoca-

tion by Algorithm 2. Essentially, as it is devised, the

method could use volume as an heuristic for a search

in the solution space in a potential implementation

based on efﬁcient search algorithms such as SMA

∗

Note that the interruptible method is based on the

very useful property of Apriori to discover rules in

order of length. Therefore, dropping a rule requires a

speciﬁc method. We have experimented two different

possible conditions:

• We may drop rules that have limited coverage.

This is a good idea in general, for they contribute

only a little to the usefulness of the approach.

However, typically, rule coverage decreases with

length, and therefore the dropping will not be par-

ticularly effective;

• We may drop rules based on their relationship

with shorter rules. For instance we do not need to

generate a rule that has a superset of antecedents

with respect to another rule already selected;

5 RELATED WORK

The long path that is bringing us from black box tech-

nologies, as for instance deep learning ones, to ex-

plainable solutions, has been only recently carried

out. Moreover, there is an open debate on the actual

features that we expect from an explainable system.

First of all, we have in mind two crucial points:

• Explainable systems should be readable by hu-

mans, but also should be usable in order to iden-

tify the meaning of the machine learning activity

that is performed;

• Explainability is both an issue of the design of a

system, and of the interpretation of them.

What are thus explainability it twofold: good ex-

planations for existing systems, and methodologies

to design new systems that behave in an explainable

way. On the way of this path we should consider the

explainability as a basic property. There has been a

recent focus on this very basic issue: how can we

measure explainability? Answers to this question are

central in the process of making our effort.

In a high level perspective, the study of Pedrycz et

al. (Pedrycz, 2021) has provided a speciﬁc viewpoint

on a variety of possible approaches to be employed

for explainability, while discussing, in particular, the

basic notion of explanation as a means to guarantee

coordination of different learning methods.

Very general viewpoint on explainability can be

found in the survey and also comparative study pro-

vided by Molnar et al. (Molnar et al., 2020) who re-

viewed critically the approaches developed so far on

the argument of approximation for explainability. On

research speciﬁc issues, we refer to the path of re-

search conducted by Mereani et al. since 2019’s pre-

liminary study (Mereani and Howe, 2019) and further

deepening (Mereani and Howe, 2021). For what con-

cerns deep learning explanations Soares et al. have

provided a comprehensive approach that could be

considered the counterpart of the neural network in-

vestigation of Mereani et al. (Soares et al., 2021).

Association rules have been speciﬁcally investi-

gated as means for explaining black boxes by Moradi

et al. (Moradi and Samwald, 2021).

6 CONCLUSIONS AND FURTHER

WORK

The promising results of this investigation are mainly

due to the intuition that a rule-based system can be

measured to perform better in terms of explainability

than a black-box one. In fact, deep learning methods

exhibit high accuracy, precision and recall for many

real-world cases in which perception is involved, but

when reasoning is involved than many aspects that

cannot be considered in deep learning take place.

First of all, as amplily argued in many studies con-

cerning hybrid reasoning (see, for instance, (Cristani

et al., 2018b; Cristani et al., 2018a)), the connection

between reasoning and decision making is strict, and

therefore data coming from observations, including

those related to perception are only a part of the deci-

sion process, for the knowledge we do have in front of

the perception inﬂuences our conclusions. Secondly,

practical usages of methods derived from Logic can

incorporate that knowledge in the decision process,

whilst perception-driven methods cannot.

Classiﬁcation Rules Explain Machine Learning

903

Further developments of this study will be fo-

cusing on three aspects: (1) the applicability of

logic programming methods, that some of the authors

have been dealing with before (Cristani et al., 2015;

Cristani et al., 2014; Olivieri et al., 2015; Cristani

et al., 2016b) when connected to machine learning

problems, (2) the usage of Inducive Logi Program-

ming appraoches as in (Lisi, 2008; Lisi, 2010; Lisi

and Straccia, 2013), and (3) the study of applications

in speciﬁc mining domains, including in particular

social network and the web, for process mining pur-

poses (Cristani et al., 2016a; Cristani et al., 2016c).

One important step that we shall carry out rather

immediately aims at deploying an experiment with

human subjects to validate the notion of volume as

a predictor, along with performance indices like ac-

curacy, precision and recall, of the judgment on ex-

plainations for a black-box system.

REFERENCES

Cristani, M., Domenichini, F., Olivieri, F., Tomazzoli, C.,

and Zorzi, M. (2018a). It could rain: Weather fore-

casting as a reasoning process. volume 126, pages

850–859.

Cristani, M., Fogoroasi, D., and Tomazzoli, C. (2016a).

Measuring homophily. volume 1748.

Cristani, M., Karaﬁli, E., and Tomazzoli, C. (2014). Energy

saving by ambient intelligence techniques. pages 157–

164.

Cristani, M., Karaﬁli, E., and Tomazzoli, C. (2015). Im-

proving energy saving techniques by ambient intel-

ligence scheduling. volume 2015-April, pages 324–

331.

Cristani, M., Olivieri, F., and Tomazzoli, C. (2016b). Auto-

matic synthesis of best practices for energy consump-

tions. pages 154–161.

Cristani, M., Olivieri, F., Tomazzoli, C., and Zorzi, M.

(2018b). Towards a logical framework for diagnostic

reasoning. Smart Innovation, Systems and Technolo-

gies, 96:144–155.

Cristani, M., Tomazzoli, C., and Olivieri, F. (2016c).

Semantic social network analysis foresees message

ﬂows. volume 1, pages 296–303.

Lisi, F. (2008). Building rules on top of ontologies for the

semantic web with inductive logic programming. The-

ory and Practice of Logic Programming, 8(3):271–

300.

Lisi, F. (2010). Inductive logic programming in databases:

From datalog to DL+log. Theory and Practice of

Logic Programming, 10(3):331–359.

Lisi, F. and Straccia, U. (2013). Dealing with incomplete-

ness and vagueness in inductive logic programming.

volume 1068, pages 179–193.

Mereani, F. and Howe, J. (2019). Exact and approximate

rule extraction from neural networks with boolean fea-

tures. pages 424–433.

Mereani, F. and Howe, J. (2021). Rule extraction from neu-

ral networks and other classiﬁers applied to xss detec-

tion. Studies in Computational Intelligence, 922:359–

386.

Molnar, C., Casalicchio, G., and Bischl, B. (2020). Inter-

pretable machine learning – a brief history, state-of-

the-art and challenges. Communications in Computer

and Information Science, 1323:417–431.

Moradi, M. and Samwald, M. (2021). Post-hoc explana-

tion of black-box classiﬁers using conﬁdent itemsets.

Expert Systems with Applications, 165.

Olivieri, F., Cristani, M., and Governatori, G. (2015). Com-

pliant business processes with exclusive choices from

agent speciﬁcation. Lecture Notes in Computer Sci-

ence (including subseries Lecture Notes in Artiﬁcial

Intelligence and Lecture Notes in Bioinformatics),

9387:603–612.

Pedrycz, W. (2021). Design, interpretability, and explain-

ability of models in the framework of granular com-

puting and federated learning.

Soares, E., Angelov, P., Costa, B., Castro, M., Nageshrao,

S., and Filev, D. (2021). Explaining deep learn-

ing models through rule-based approximation and vi-

sualization. IEEE Transactions on Fuzzy Systems,

29(8):2399–2407.

Stergiou, K. and Koubarakis, M. (2000). Backtracking al-

gorithms for disjunctions of temporal constraints. Ar-

tiﬁcial Intelligence, 120(1):81–117.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

904