An Atypical Metaheuristic Approach to Recognize an Optimal

Architecture of a Neural Network

Abishai Ebenezer M. and Arti Arya

PES University, Bangalore, India

Keywords:

Artiﬁcial Neural Networks (ANNs), Structural Design, Water Cycle Algorithm (WCA), Water Wave Opti-

mization (WWO), Metaheuristic Algorithm.

Abstract:

The structural design of an Artiﬁcial Neural Network (ANN) greatly determines its classiﬁcation and regres-

sion capabilities. Structural design involves both the count of hidden layers and the count of neurons required

in each of these hidden layers. Although various optimization algorithms have proven to be good at ﬁnding

the best topology for a given number of hidden layers for an ANN, there has been little work done in ﬁnding

both the optimal count of hidden layers and the ideal count of neurons needed in each layer. The novelty

of the proposed approach is that a bio-inspired metaheuristic namely, the Water Cycle Algorithm (WCA) is

used to effectively search space of local spaces, by using the backpropagation algorithm as the underlying

algorithm for parameter optimization, in order to ﬁnd the optimal architecture of an ANN for a given dataset.

Computational experiments have shown that such an implementation not only provides an optimized topology

but also shows great accuracy as compared to other advanced algorithms used for the same purpose.

1 INTRODUCTION

As humans, it is quite natural to be inspired by nature

and carry that inspiration , irrespective of the domain,

into building our own designs and structures. Re-

searchers in computer science, and speciﬁcally, deep

learning, have been inspired by nature as well and

have long been trying to build models that exhibit or

replicate what the human brain can accomplish. Our

brain contains millions of neurons, and what is more

interesting is that these neurons are assembled per-

fectly in order for us to make both simple and com-

plex decisions. Deep learning practitioners are often

confronted with the dilemma of having to manually

design a structure while building an ANN. With the

advent of various kinds of bio inspired algorithms,

it is now possible to draw inspiration from nature

while building an ANN wherein the main goal is to

ﬁnd the global optimum. This could also be applied

to the problem of structural optimization where the

search space consists of all the possible ANN struc-

tures. On earth, water is known to ﬂow downwards

in its liquid form due to gravity. Therefore, streams

ﬂow into rivers while rivers ﬂow into the sea. The

sea is synonymous to global minimum/optimum. Wa-

https://orcid.org/0000-0002-4470-0311

ter from the sea then evaporates forming clouds fol-

lowed by the raining process which leads to formation

of streams and the cycle goes on. For minimization

problems, the water cycle provides a natural analogy.

And just as all streams and rivers ﬂow into the sea,

agents employed in ﬁnding a global minimum in the

search space could be made to follow a similar move-

ment.

The human brain has approximately 86 billion

neurons (Azevedo et al., 2009) assembled perfectly

to perform complex computations and make fast de-

cisions, demonstrating that the structure of an ANN

goes a long way in determining its accuracy and efﬁ-

ciency. Those who build and create ANNs are often at

a loss to know what the structure of their ANN must

be. After numerous trial and error manual iterations,

the ﬁnal structure that they adopt would most prob-

ably, not be the most optimal architecture. If more

hidden layers or more neurons are used than needed,

it would lead to excessive training time and faulty re-

sults due to overﬁtting, especially when the training

data set is large. When the number of neurons and

hidden layers used is lesser than required, it would

lead to underﬁtting and the features present in the data

would not be learnt by the ANN. An optimal structure

means efﬁcient use of compute resources and precise

learning of features present in the data for ANNs.

Ebenezer M., A. and Arya, A.

An Atypical Metaheuristic Approach to Recognize an Optimal Architecture of a Neural Network.

DOI: 10.5220/0010951600003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 917-925

ISBN: 978-989-758-547-0; ISSN: 2184-433X

917

This paper proposes a novel approach to cope

with the variable dimensions of the structure opti-

mization using a combination of the Water Cycle Al-

gorithm (WCA) for structure optimization and back-

propagation for parameter training (Eskandar et al.,

2012). The WCA has been applied to two levels of

search spaces - the global search space and the lo-

cal search space of each particle in the global popula-

tion, in order to return the most optimal structure for

an ANN given a particular dataset. The primary goal

of this proposed methodology is to do better and im-

prove upon the existing approaches, while also prov-

ing the fact that bio-inspired metaheuristics can ef-

fectively be used in the ﬁeld of Neural Architecture

Search.

2 LITERATURE REVIEW

Methods used for Neural Architecture Search could

broadly be classed into two - traditional methods and

non-traditional methods. Traditional optimization

methods have predominantly been calculus based.

Guliyev et al.(Guliyev and Ismailov, 2018b) proved

that a neural network having two neurons in one hid-

den layer, and all weights having a ﬁxed value equal

to 1, could accurately approximate any continuous

univariate function. The disadvantage of the pro-

posed methodology is that it could not approximate

all continuous multivariate functions. The same au-

thors then overcame this drawback by proving that,

by considering the Euclidean Space to consist of d di-

mensions and by using a neural network having two

hidden layers, wherein the count of hidden neurons

it contains is 3d+2, any continuous d-variable func-

tion could be correctly approximated(Guliyev and Is-

mailov, 2018a).

Ludwig(Molino et al., 2019) is an AutoML model

created by Uber Research, used for deep learning

model training by passing their data through an API.

Ludwig uses an encoder-combiner-decoder model

and acts like a black-box which abstracts the process

of model training. Although Ludwig achieves great

results, researchers still look for solutions to ﬁnd the

optimal structure of a deep feed-forward neural net-

work which would enhance our understanding and

perception of the underlying working of deep feed-

forward neural networks.

Cai et al. suggested a technique to ascertain the

ideal count of neurons required in a neural network

having just one hidden layer, by using data normal-

ization and singular value decomposition(Cai et al.,

2019). The count of hidden neurons would then be

determined by the main eigen values. Pablo et al.

suggested a non-iterative method for ﬁnding the opti-

mal count of neurons in a singly hidden layered neu-

ral network while pruning the hidden neurons with

respect to harmonic mean(Henr

ıquez and Ruz, 2018).

Hence, it is observed that although traditional meth-

ods have been able to achieve an acceptable level of

performance for ﬁnding the optimal count of neurons

in shallow neural networks, it still fails to resolve the

issue of ascertaining both the ideal/near optimal count

of hidden layers as well as the ideal count of hidden

neurons for a deep neural network.

Neural Architecture Search has been an evolving

ﬁeld of research, especially in the recent past. A sur-

vey on various approaches to this problem was done

by a team of researchers from IBM Research and is

presented in (Wistuba et al., 2019). This survey pre-

sented a comprehensive study of the different kinds

of search spaces that have been adopted and many

traditional and non-traditional approaches have been

explored. The survey also presented the various cate-

gories of optimization methods that have been used to

traverse and explore the search space. Although the

survey does not touch upon the use of bio-inspired al-

gorithms, the authors have elaborately speciﬁed con-

tributions belonging to the class of evolutionary algo-

rithms in the ﬁeld of Neural Architecture Search.

Bio-inspired algorithms simulate biological evo-

lution in nature and have proven to show remark-

able results for solving complex optimization tasks.

Kennedy and Eberhart created the ﬁrst ever bio-

inspired algorithm - Particle Swarm Optimization

(PSO)(Kennedy and Eberhart, 1995). PSO takes

inspiration from the way a ﬂock of birds search

for food. PSO has been a popular choice for

bio-inspired algorithms, especially due to its easy-

to-understand methodology and simple implemen-

tation. Similarly, researchers have developed bio-

inspired algorithms that simulate the collaborative

characteristics of schools of ﬁsh(Zhang et al., 2014),

ant colonies(Dorigo and Di Caro, 1999) and even

bats(Gandomi et al., 2013). These algorithms con-

sider properties speciﬁc to the biological species and

translates them into equations. These new equa-

tions then give rise to a bio-inspired algorithm which

can then be used in various engineering optimization

tasks. PSO has also been used for both parameter op-

timization(Qolomany et al., 2017) and structure opti-

mization(Chhachhiya et al., 2017). Due to its highly

simplistic nature, PSO falls short in terms of the ﬁnal

results obtained.

The Water Wave Optimization (WWO) is a rela-

tively recent bio-inspired optimization algorithm, de-

veloped in 2015(Zheng, 2015). This algorithm takes

inspiration from shallow water wave models, wherein

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

918

the solution is represented by a wave. It involves

the use of three different operators - namely prop-

agation, refraction, and breaking. Zhou et al. pro-

posed a methodology to use the WWO algorithm for

simultaneously solving both parameter optimization

and structure optimization(Zhou et al., 2018). Al-

though the algorithm did achieve competitive perfor-

mance, it did have a few drawbacks. For parameter

optimization, the WWO algorithm was much slower

compared to the back propagation algorithm. One of

the main disadvantages in the application of WWO to

the problem of structure optimization is that the count

of hidden layers has to be preset by the user before

the start of computation. The problem of structure

optimization, where the optimal count of hidden lay-

ers and the optimal count of neurons required in each

of the hidden layers, still remains to be solved in a

manner wherein the user themselves does not have to

specify the exact count of hidden layers.

The WCA, developed in 2012, inspired by the wa-

ter cycle on earth(Eskandar et al., 2012), presents it-

self as a natural choice for an optimization algorithm

that can be used in multidimensional space. Water at

higher level ﬂows to a lower level, under the inﬂuence

of gravity and this analogy is especially suited for

the minimization paradigm for the speciﬁc engineer-

ing problems. The combination of WCA, backprop-

agation and the use of both global and local search

spaces, has proven to show competitive results in var-

ious constrained engineering optimization problems

and upon being used in the proposed approach in this

paper, shows great promise in solving the structure

optimization problem for deep neural networks.

Poongodi et al. (Poongodi et al., 2021) presented

a trained XGBoost model that was able to predict the

taxi trip durations having an RMSE value of 0.39,

and concluded that XGBoost performed better than

a Multi-layer Perceptron (MLP) model. Although the

exact MLP structure that they have used is not ex-

actly known, the structure evidently was not an opti-

mal structure, as shown in section 5.

3 THE WATER CYCLE

ALGORITHM

As suggested by its name, the process of water cy-

cle is the main motivation behind the WCA(Eskandar

et al., 2012). This algorithm captures the ﬂow of

rivers and streams downstream into the sea. The

sea represents the global minimum. This is because

streams ﬂow into rivers, which then ﬂow into the sea

which is the universal lowest region. To begin with,

the raining process occurs, which leads to the forma-

tion of streams. The raining process creates the ini-

tial population of streams in a random manner. The

best stream of the initial population is selected as the

sea. In case of a minimization problem like the prob-

lem of structure optimization for ANNs, this means to

search for the stream with the highest ﬁtness value i.e.

the stream with the least value of cost function (mean

squared error).

Subsequently, a number of good streams (other

than the sea) are chosen as rivers. This number is one

of the parameters given by the user, and its value can

be decided on the basis of the extent of exploration

required. The other streams ﬂow towards the rivers or

the sea.

The term particle in context of neural architecture,

refers to an individual object that collaborates with

other similar objects to achieve a common objective.

In the case of the WCA, particle and stream are equiv-

alent and may be used interchangeably.

The initial step of creating the population of

streams i.e. the raining process, involves creating

an array of randomly generated integers in a given

range. These integers represent the particle’s location

deﬁned in the search space. The range of the ran-

domly generated integers by the algorithm is another

parameter required from the user. Let’s assume the

population size is N

pop

. Hence, an array with N

pop

el-

ements would be created, each specifying a randomly

generated integer in the given range representing po-

sition of the stream/particle in the search space. The

ﬁtness value of each stream can be found using a ﬁt-

ness function F. Considering a speciﬁc element i.e. an

integer representing a particular stream to be X, F(X)

would then return the ﬁtness value of the particular

stream X , where n simply signiﬁes that X is the nth

stream in the population.

The sea represents the best stream i.e. the best po-

sition reached so far in the search space. Therefore,

the sea is selected as the best individual i.e. the sea is

the element which has the least value of cost function

in the array, which means that at all times, the ele-

ment having the highest ﬁtness value would be cho-

sen as the sea. Consider a variable N

, which is the

count of rivers (as provided by the user) in addition to

the single sea. Also, N

streams

is deﬁned as the size of

the remaining population i.e. the streams that are not

rivers or the sea.

The quantity of water that ﬂows into a particular

river or sea varies for each river and the sea. The ﬂow

of water into each river or the sea is deﬁned by a vari-

able NS

and can be calculated using the below equa-

tions as described in (Eskandar et al., 2012):

streams

= N

pop

− N

(1)

An Atypical Metaheuristic Approach to Recognize an Optimal Architecture of a Neural Network

919

= round(



F(X)

∑

i=1

F(X)



× N

streams

) (2)

n = 1,2,....,N

i+1

Str

= p

Str

+ rand ∗ C ∗ (p

− p

Str

) (3)

i+1

Str

= p

Str

+ rand ∗ C ∗ (p

Sea

− p

Str

) (4)

As mentioned in (Sadollah et al., 2016), Equation

(3) represents streams that would ﬂow into the corre-

sponding rivers and Equation (4) represents streams

that would ﬂow into the corresponding sea.

i+1

= p

+ rand ∗ C ∗ (p

Sea

− p

) (5)

Str

represents the position of the particular

stream at the ith timestep. Str signiﬁes a particular

’Stream’ and R signiﬁes a particular ’River’. NS

the count of streams that would ﬂow into that particu-

lar river or sea.

In order to avoid premature convergence i.e. to

avoid getting stuck in a local minimum, an evapora-

tion operation is deﬁned which involves the evapora-

tion of sea water. The evaporation process is enabled

when the river and the sea are separated by a very

small distance d i.e. when the below criteria is satis-

ﬁed.



Sea

− p



< d (6)

i = 1,2,3,...,N

- 1

d is a near zero number, and d is an important fac-

tor in the exploration phase of the WCA. If the evap-

oration operation as in Equation (6), is satisﬁed, the

raining process is then performed, which thus gives

rise to new streams in the population, which are ini-

tialised randomly. The value of d is determined at

every time step using the following equation -

t+1

= d

−

(7)

t = 1,2,3,...,m. m is the maximum count of iterations.

A higher value of d signiﬁes lower search intensity

while a lower value of d encourages the intensity of

exploration closer to the sea.

This entire water cycle procedure is then repeated

for as many iterations as required in order to identify

the most optimal region/point in the search space.

The motivation towards adopting the WCA for

ﬁnding the optimal architecture of an ANN is its sim-

plicity and ease of implementation. It was proposed

as a general solution for constrained optimization and

engineering design problems. Its functioning, which

is easily understandable as it is derived from the water

cycle, is highly relatable to ﬁnd the global minimum

in multidimensional space. The novelty of the pro-

posed methodology elevates the level of performance,

as shown in the subsequent sections, thus stressing

more on the proposed approach.

4 PROPOSED APPROACH TO

ARCHITECTURAL

OPTIMIZATION FOR ANNs

The approach suggested in this paper involving the

use of global and local search spaces, the WCA algo-

rithm, as well as the back-propagation algorithm is a

signiﬁcant upgrade compared to approaches taken in

the past. Not only does the unconventional approach

proposed in this paper solve the problem of optimiz-

ing the count of neurons in each of the n hidden layers

but also uses the WCA algorithm to ﬁnd out the ideal

value of n itself.

The global search space represents the error as a

function of the count of hidden layers. The ﬁtness

of each stream in the main space is determined by

the least value of cost function(error) that can be ob-

tained by using that particular number of hidden lay-

ers. Each particle contains the information as to the

least possible error and the corresponding conﬁgura-

tion i.e. the count of hidden layers and the count of

neurons required in each of the hidden layers. The

central focus in this section is the approach that or-

chestrates the movement of these particles in both

the global search space as well as every local search

space.

The WCA is applied at the global and local levels

for the structure optimization problem (as shown in

Figure 1). As mentioned earlier, two types of spaces

would be considered to cope with variable dimension

problem. The global search space represents the count

of hidden layers. The population of streams/particles

would then search this space to determine what would

be the best number of hidden layers. Considering that

the initial population of streams would be used to as-

certain the ideal count of hidden layers required, each

stream in itself represents a search space (local) which

contains all the possible conﬁgurations for that par-

ticular count of hidden layers as represented by the

stream. WCA is again applied in this local search

space of each stream to ﬁnd out the best conﬁgura-

tion i.e. the optimal count of neurons in each of the

hidden layers for the speciﬁc number of hidden layers

(this number is the parent stream in the global space).

Having explained why the WCA has been cho-

sen as a part of this study, the reason why back-

propagation seems a more suitable choice in the lo-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

920

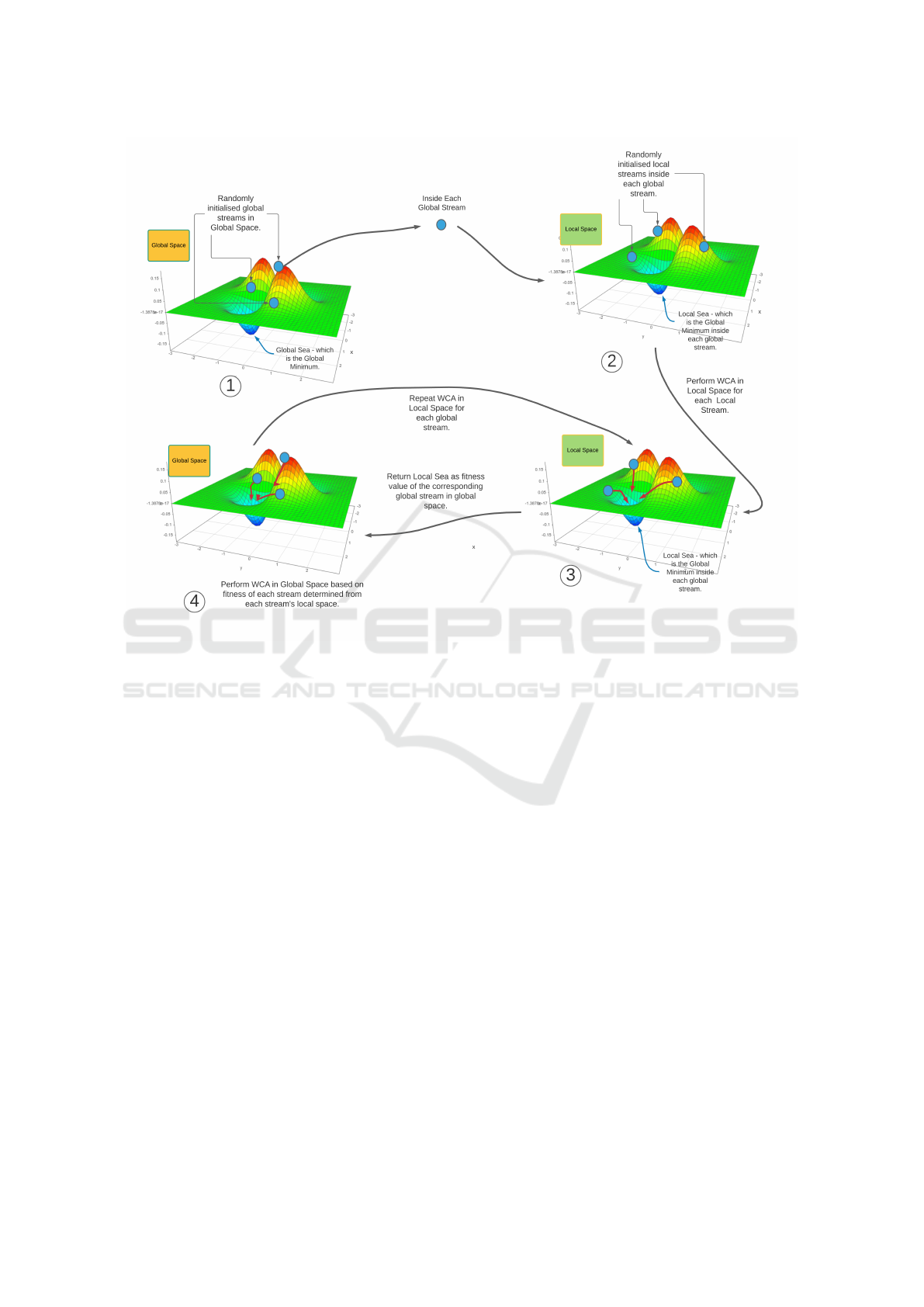
Figure 1: The proposed approach using WCA for optimal architecture search.

cal search space to train an ANN for parameter opti-

mization must be mentioned. The entire search space,

which includes the global search space and all the

local search spaces put together, is very large, and

hence, the optimization algorithm used must be able

to explore the local search spaces in a swift manner.

Although the WCA is sufﬁciently efﬁcient, it isn’t the

fastest optimization algorithm. Therefore, to enhance

the performance of the system, backpropagation has

been used for parameter optimization. Backpropaga-

tion is one of the most preferred algorithms for pa-

rameter optimization due to its easy implementation

and comparatively lesser run-times.

The proposed novel approach involves applying

the WCA algorithm at two levels (as shown in Figure

2) - the global search space and local search spaces,

while using back-propagation to train the ANN i.e.

for parameter optimization. A population of streams

is created randomly, wherein each stream contains

a randomly generated integer value (within a range

speciﬁed by the user) which represent the count of

hidden layers. The goal now is to assign a ﬁtness

value to each stream. The ﬁtness value of each stream

would represent how close or far the particular stream

is from its ﬁnal goal. The ﬁtness value of each stream

in the global search space is determined by the value

of the cost function of the best conﬁguration for that

particular number of hidden layers, as represented by

the stream in the global search space. For example, if

a stream S contains the integer X, the ﬁtness value

assigned to this stream would be the value of cost

function of the best conﬁguration containing the op-

timal count of neurons in each of the X hidden lay-

ers. Therefore, for a stream to be considered a ’good’

stream (like a river or the sea), then it must have a

higher ﬁtness value i.e. a lower value of cost function.

The sea would have the highest ﬁtness value followed

by the rivers and so on.

The goal now is to ﬁnd the ’best conﬁguration’

for X hidden layers. The local search space of each

stream can be intuitively visualized as a search space

within the stream in the global search space i.e. a

search space within a search space. The local search

space represents the entire set of possible conﬁgura-

tions for X layers. WCA is applied in this local search

space as well. An initial population of streams is cre-

ated, wherein the streams represent an array of inte-

gers. The ith element in the array represents the count

of neurons in the ith hidden layer. For example, con-

sider an array A = ( A

, A

,...,A

), where A

is the

number of neurons in the ith hidden layer. Unlike the

global search space which initially seemed only to be

An Atypical Metaheuristic Approach to Recognize an Optimal Architecture of a Neural Network

921

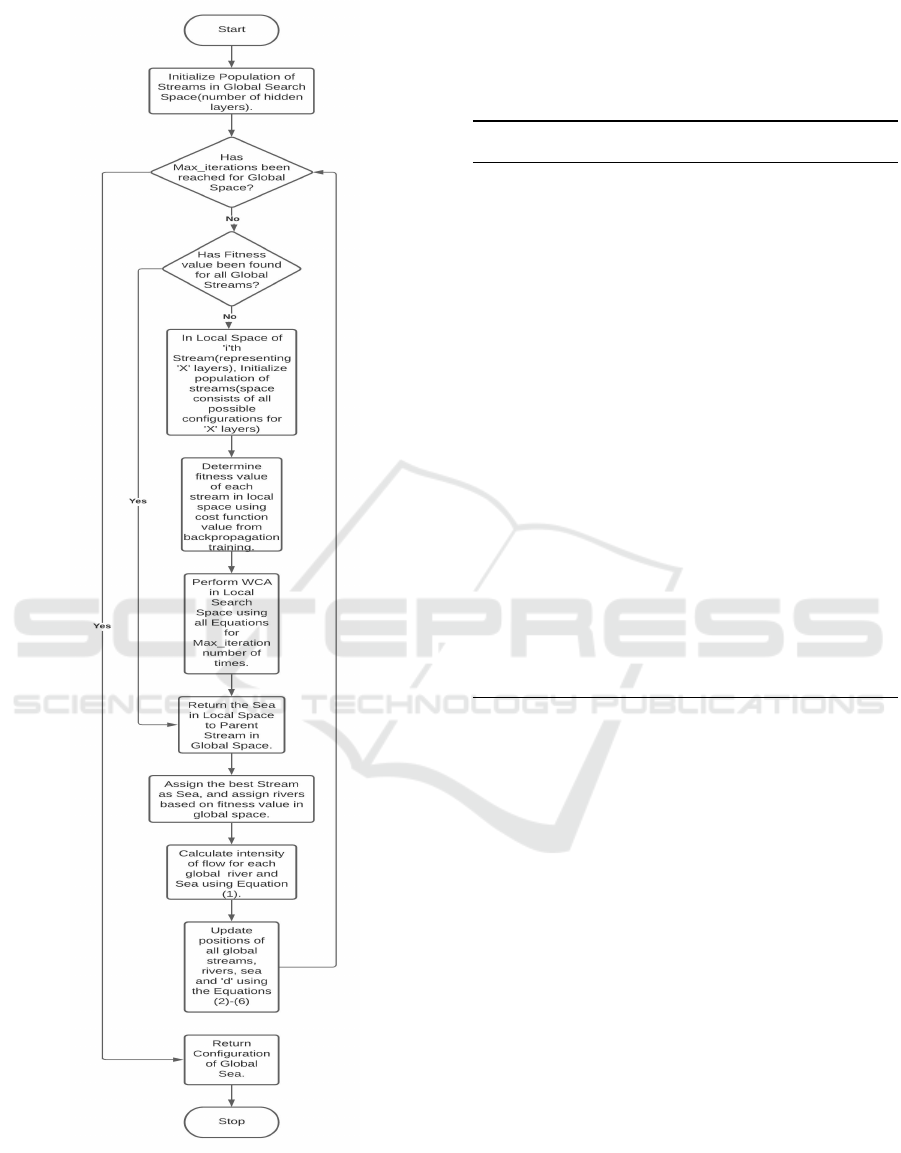
Figure 2: Flowchart of Proposed Approach.

a single dimension problem, the local search space is

an X dimensional problem (X is used here in the same

sense as mentioned previously), where X is an integer

in the range speciﬁed initially by the user.

Algorithm 1: Applying WCA for Architecural Optimiza-

tion.

Initialize a population of streams Global

Streams

ran-

domly;

while Max.Iterations for Global Space has not

been reached do

for all SεGlobal

Streams

Initialize a population of streams Local

Streams

randomly;

while Max. Iterations for Local Space has not

been reached do

Determine ﬁtness of each stream in

Local

Streams

;

Update the position of each stream using

Equations (1)-(6);

Update position of Local Sea of S;

end while

return Stream with maximum ﬁtness in

Local

Streams

as ﬁtness of S;

end for

Update position of all streams in Global

Streams

using the equations;

Update position of Global Sea;

end while

return Global Sea and its Local sea

During the step of calculating the new values of

position of both streams and rivers using Equations

(1) to (6), the stream is considered to be an X di-

mensional particle. The cost function i.e. the ﬁtness

value of all streams would be determined by the cost

function of an optimally trained ANN (using back-

propagation with a necessary and sufﬁcient amount of

training epochs) with hidden layers as speciﬁed by the

array contained in the particular stream. The WCA

process is then repeated for a particular number of it-

erations, as speciﬁed by the user. The stream with

the highest ﬁtness value i.e. the sea present in the

global search space is returned. Therefore, the stream

in the global search space contains 3 different values

- the number of hidden layers, an integer array of size

X (obtained from local search space) and the ﬁtness

value which is the cost function of the ANN sufﬁ-

ciently trained using back-propagation (obtained from

the local search space). In the global space, only the

count of hidden layers is used to update the positions

of the rivers and streams. This process is repeated un-

til the desired accuracy is achieved. Upon conclusion

of the ﬁnal iteration in the global space, the stream

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

922

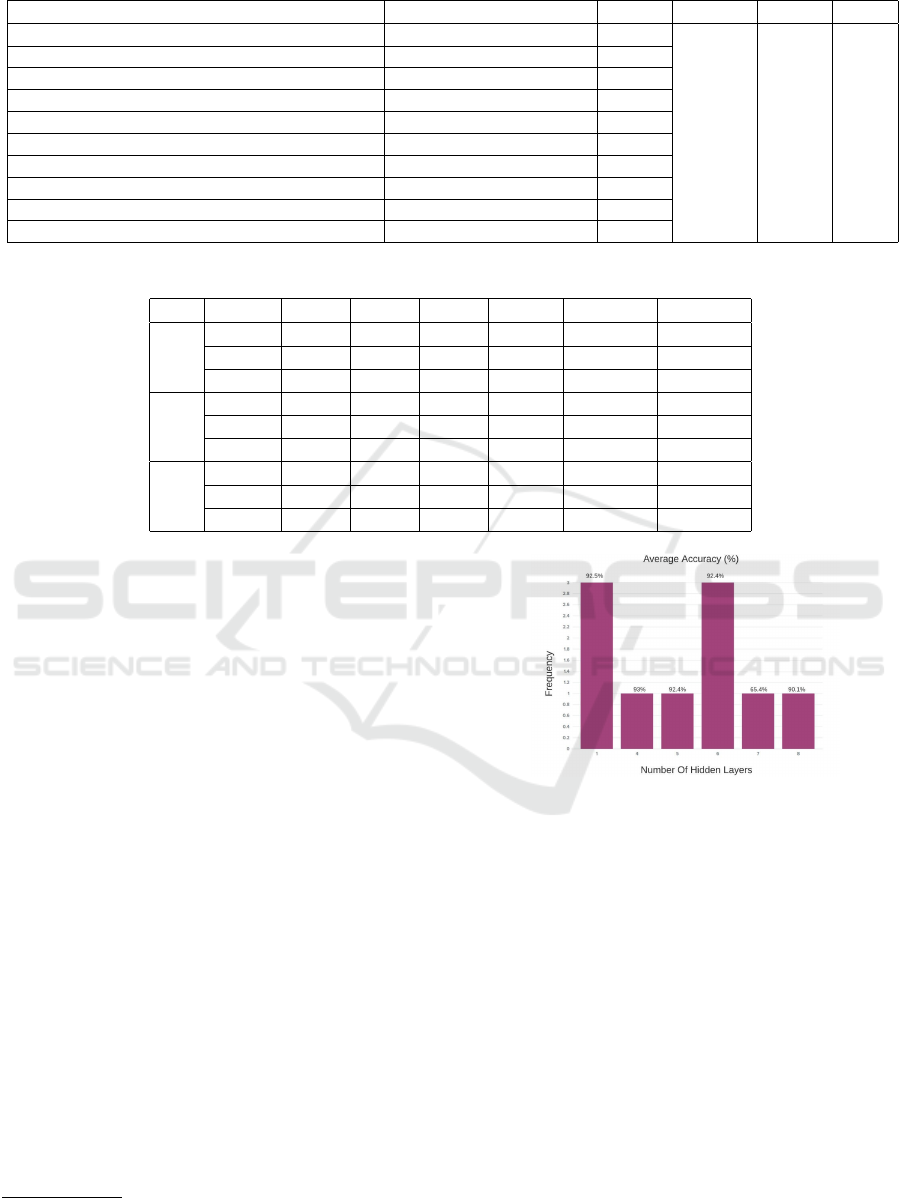
Table 1: Results on New York Taxi Trip Duration Dataset.

Neurons in each hidden layer Number of hidden layers RMSE Average Min Max

[300, 113, 1, 88, 101] 5 0.3751

[139, 223, 42] 3 0.3848

[218, 126, 157, 75] 4 0.3799

[255, 157, 173] 3 0.3786

[183, 61, 99, 265, 218, 296, 139, 265, 286, 51] 10 0.3911

[224, 94, 128, 272, 47, 177, 137, 1] 8 0.387

[218, 242, 81, 131, 155, 242, 82, 275] 8 0.3793

[57, 84, 42, 142, 195, 50, 124, 140, 191] 9 0.396

[245, 300, 230, 108, 110, 138, 1, 37, 24, 276] 10 0.3764

[106, 270, 87] 3 0.3845

0.3833 0.3751 0.396

Table 2: Results on the WINE Dataset for WCA as compared to WWO.

T:V Metric GA PSO BBO WWO WCA(1) WCA(2)

2:3

Max 84.11 94.39 86.92 98.13 95.28 98.11

Min 79.44 93.46 83.18 96.26 94.34 90.57

Mean 81.7 93.69 84.89 96.65 94.528 94.85

3:2

Max 84.87 94.12 88.24 97.48 98.59 98.59

Min 82.35 90.76 85.71 97.48 92.96 92.96

Mean 83.6 92.23 86.86 97.48 95.212 96.16

4:1

Max 80.56 97.22 88.89 100 100 100

Min 77.78 97.22 77.78 100 94.28 94.29

Mean 79.32 97.22 81.38 100 98.284 98.44

with the highest ﬁtness value i.e. the sea, which con-

tains the optimal count of hidden layers, ideal count of

neurons required in each hidden layer and its ﬁtness

value is returned to the user. Algorithm 1 describes

the application of WCA for architectural optimization

for ANNs.

5 RESULTS AND DISCUSSION

The WCA is a simple yet intuitive optimization meta-

heuristic algorithm(Eskandar et al., 2012). Other

bio-inspired algorithms have also been developed,

amongst which the WWO algorithm has been able to

achieve state-of-the-art results(Zhou et al., 2018).

The proposed model was executed on the New

York Trip Duration dataset

10 times, and the results

obtained have been shown in Table 1. The conﬁgura-

tion of the proposed model was the same as that used

for the previous experiments. The New York Trip Du-

ration dataset consists of taxi trips data such as pickup

time and date, drop off time and date, geo-coordinates

of pickup and drop off, number of passengers and sev-

eral other variables, wherein the duration of each taxi

trip is to be predicted. A sample of one million rows

were taken out of the the 1458644 rows available in

the training dataset. The range of number of hidden

https://www.kaggle.com/c/nyc-taxi-trip-duration/data

Figure 3: Frequency and Average Accuracies on all the

suggested count of hidden layers for the Phishing Websites

Dataset(Vrban

c, 2020).

layers (input parameter) was conﬁgured to be between

1 and 10 and the count of neurons in each layer ranges

between 1 and 300. Also, d, mentioned in Equation

(6), is set to 0.01 for all the performed experiments,

as suggested in (Sadollah et al., 2016). Table 1 shows

that the proposed methodology is able to ﬁnd various

optimal architectures for this dataset. 8 out of the 10

proposed structures have an RMSE value below 0.39,

which is slightly better than the XGBoost model pre-

sented in (Poongodi et al., 2021) - previously consid-

ered to work better than an MLP model. This shows

that the proposed approach is able to ﬁnd optimal ar-

chitectures for neural networks whose performance

can match and even better those of other supervised

machine learning algorithms, even when other ma-

An Atypical Metaheuristic Approach to Recognize an Optimal Architecture of a Neural Network

923

Table 3: Results on Phishing Websites Dataset for 1 and 6 Hidden Layers.

Neurons in Each Hidden Layer Number Of Hidden Layers Accuracy (%) Average Max

[87,48,55,59,67,100] 6 93.12

92.43 93.12[30,28,52,98,49,65] 6 92.03

[100,78,74,40,20,57] 6 92.14

[78] 1 94.03

92.50 94.03[76] 1 91.82

[100] 1 91.66

chine learning learning algorithms were previously

perceived to perform better than an MLP model, as

is the case here.

The WINE Dataset (Dua and Graff, 2017) is a

popular dataset based on classiﬁcation output. The

main task here is to correctly classify the category of

wine based on parameters such as color, acidity etc.

The proposed algorithmic approach was executed 30

times (30 was decided randomly, for the main purpose

of presenting how well the proposed method performs

over multiple executions), while the range of number

of hidden layers (input parameter) was between 1 to

10 and the count of neurons in each layer ranges be-

tween 1 and 100 for the remaining performed exper-

iments. Conﬁgurations having 2 hidden layers was

suggested 11 out of the 30 times it was executed,

proving that the proposed approach works well for

such benchmark datasets.

The proposed approach performs at par with the

WWO algorithm, and has performed better than algo-

rithms like Particle Swarm Optimization (PSO), Ge-

netic Algorithms (GA) and Biogeography-based opti-

mization (BBO) and ﬁnds the optimal count of hidden

layers as well as optimal count of neurons in each hid-

den layer, and hence, specifying the number of hidden

layers beforehand is not a requirement. In Table 2, the

ﬁrst column T:V represents the ratio of size of training

dataset to validation dataset. The results shown have

been obtained using the WINE dataset. As stated in

(Zhou et al., 2018), the time taken by backpropagation

for parameter optimization in the local search space

is least, and hence serves as the motivation for using

backpropagation in the proposed approach. WCA(1)

and WCA(2) represent two different conﬁgurations.

WCA(1) was conﬁgured with 6 streams in the global

space and 4 streams in each local space. WCA(2) was

conﬁgured with 5 streams in the global space and 5

streams in each local space. Both were conﬁgured to

suggest the number of hidden layers within the range

of 1 to 10 and the count of neurons in each layer be-

tween 1 and 100.

As seen from Table 2, the proposed approach

using WCA falls slightly short as compared to the

WWO. This is not to be mistaken that the pro-

posed approach is in any way inferior to the WWO.

The main shortcoming of the approach that uses the

WWO, is that the number of hidden layers has to be

speciﬁed by the user beforehand, whereas this is al-

ready taken care of in the proposed approach using

WCA. The fact that the proposed approach suggests

both the count of hidden layers as well as the count

of neurons in each hidden layer, while maintaining

an accuracy that is almost at par with a state-of-the-

art bio-inspired approach like WWO and achieving

an accuracy better than older approaches such as GA,

PSO and BBO shows the superiority of the proposed

methodology.

It was also tested on the the Phishing Websites

Dataset(Vrban

c, 2020)

. Generally, while creating

an ANN for a dataset having thousands of rows and

a large number of features to be learnt, ANN cre-

ators naturally use a large count of layers and neu-

rons. Such an extensive architecture may not always

be necessary, as proved by the following experiment.

The Phishing Websites Dataset contains 88647 rows

and 112 columns. As depicted in Figure 3, the pro-

posed approach was executed 10 times for this dataset

and both one hidden layer and six hidden layers were

suggested 3 times each, whereas the remaining num-

ber of hidden layers were suggested only once. Al-

though the number of features to be learnt are high,

on executing the approach proposed in this paper, it

was found that one hidden layer, containing 78 neu-

rons was able to achieve an accuracy of just over

94%, using 3000 training epochs and at a learning

rate of 0.001. Table 3 shows the results obtained

for one and 6 hidden layers with the mentioned num-

ber of neurons in each hidden layer. This goes on to

show that this proposed approach not only works well

with small datasets, but can easily be scaled to large

real world datasets as well, which is easily achievable

given the power and capabilities of modern day com-

puting hardware.

6 CONCLUSION

The novel approach proposed in this paper shows its

capability in coping with the variable dimension prob-

lem of architecture optimization by achieving state-

https://data.mendeley.com/datasets/72ptz43s9v/1

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

924

of-the-art results. This goes on to prove not only that

metaheuristic algorithms are capable of being used ef-

fectively and accurately in multidimensional space,

but also the use of global and local search spaces in

ﬁnding the ideal/near optimal count of hidden lay-

ers (global) as well as the ideal/near optimal count of

neurons in each hidden layer (local). Computation-

ally performed tests conﬁrm this by showing that the

approach proposed in this paper achieves competitive

results to other algorithms that have been developed

lately, like the WWO algorithm, while also going one

step further by ﬁnding the optimal count of hidden

layers without the need of user intervention. As a

part of extending the scope of this approach, progress

is being made on adapting this methodology to more

state-of-the-art algorithms and evaluating their perfor-

mance. Also, efforts are being made to minimize the

expanse of the overall search space.

REFERENCES

Azevedo, F. A., Carvalho, L. R., Grinberg, L. T., Farfel,

J. M., Ferretti, R. E., Leite, R. E., Filho, W. J., Lent,

R., and Herculano-Houzel, S. (2009). Equal numbers

of neuronal and nonneuronal cells make the human

brain an isometrically scaled-up primate brain. Jour-

nal of Comparative Neurology, 513(5):532–541.

Cai, G.-W., Fang, Z., and Chen, Y.-F. (2019). Estimating

the number of hidden nodes of the single-hidden-layer

feedforward neural networks. In 2019 15th Interna-

tional Conference on Computational Intelligence and

Security (CIS), pages 172–176.

Chhachhiya, D., Sharma, A., and Gupta, M. (2017). De-

signing optimal architecture of neural network with

particle swarm optimization techniques speciﬁcally

for educational dataset. In 2017 7th International

Conference on Cloud Computing, Data Science En-

gineering - Conﬂuence, pages 52–57.

Dorigo, M. and Di Caro, G. (1999). Ant colony optimiza-

tion: a new meta-heuristic. In Proceedings of the 1999

Congress on Evolutionary Computation-CEC99 (Cat.

No. 99TH8406), volume 2, pages 1470–1477 Vol. 2.

Dua, D. and Graff, C. (2017). UCI machine learning repos-

itory.

Eskandar, H., Sadollah, A., Bahreininejad, A., and Hamdi,

M. (2012). Water cycle algorithm – a novel meta-

heuristic optimization method for solving constrained

engineering optimization problems. Computers &

Structures, 110-111:151–166.

Gandomi, A. H., Yang, X.-S., Alavi, A. H., and Talata-

hari, S. (2013). Bat algorithm for constrained opti-

mization tasks. Neural Computing and Applications,

22(6):1239–1255.

Guliyev, N. J. and Ismailov, V. E. (2018a). Approximation

capability of two hidden layer feedforward neural net-

works with ﬁxed weights. Neurocomputing, 316:262–

269.

Guliyev, N. J. and Ismailov, V. E. (2018b). On the approxi-

mation by single hidden layer feedforward neural net-

works with ﬁxed weights. Neural Networks, 98:296–

304.

Henr

ıquez, P. A. and Ruz, G. A. (2018). A non-iterative

method for pruning hidden neurons in neural net-

works with random weights. Applied Soft Computing,

70:1109–1121.

Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-

mization. In Proceedings of ICNN’95 - International

Conference on Neural Networks, volume 4, pages

1942–1948 vol.4.

Molino, P., Dudin, Y., and Miryala, S. S. (2019). Ludwig: a

type-based declarative deep learning toolbox.

Poongodi, M., Malviya, M., Kumar, C., et al. (2021). New

York City taxi trip duration prediction using MLP and

XGBoost. Int J Syst Assur Eng Manag.

Qolomany, B., Maabreh, M., Al-Fuqaha, A., Gupta, A., and

Benhaddou, D. (2017). Parameters optimization of

deep learning models using particle swarm optimiza-

tion. In 2017 13th International Wireless Communi-

cations and Mobile Computing Conference (IWCMC),

pages 1285–1290.

Sadollah, A., Eskandar, H., Lee, H. M., Yoo, D. G., and

Kim, J. H. (2016). Water cycle algorithm: A detailed

standard code. SoftwareX, 5:37–43.

Vrban

c, G. (2020). Phishing websites dataset.

Wistuba, M., Rawat, A., and Pedapati, T. (2019). A survey

on neural architecture search.

Zhang, C., Zhang, F.-m., Li, F., and Wu, H.-s. (2014). Im-

proved artiﬁcial ﬁsh swarm algorithm. In 2014 9th

IEEE Conference on Industrial Electronics and Ap-

plications, pages 748–753.

Zheng, Y.-J. (2015). Water wave optimization: A new

nature-inspired metaheuristic. Computers & Opera-

tions Research, 55:1–11.

Zhou, X.-H., Xu, Z.-G., Zhang, M.-X., and Zheng, Y.-J.

(2018). Water wave optimization for artiﬁcial neu-

ral network parameter and structure optimization. In

Qiao, J., Zhao, X., Pan, L., Zuo, X., Zhang, X., Zhang,

Q., and Huang, S., editors, Bio-inspired Computing:

Theories and Applications, pages 343–354, Singa-

pore. Springer Singapore.

An Atypical Metaheuristic Approach to Recognize an Optimal Architecture of a Neural Network

925