The Problem with ‘Dimensionless Quantities’

B. D. Hall

Measurement Standards Laboratory of New Zealand, New Zealand

Keywords:

SI, Quantities, Units, Dimensions.

Abstract:

Many diﬀerent quantities can be described as ‘dimensionless’ and have the same SI unit “one”, so their diﬀerent

natures cannot be determined from the unit name alone. In scientiﬁc unit systems like the SI, a set of base

quantities and associated units can lead to such many-to-one relationships between quantities, dimensions,

and units. So, it is necessary to understand how the mechanism of dimensions in unit systems works before

trying to design more general formats for the expression of quantities. In the familiar expression of physical

quantities, like mass, energy, etc, dimensions play a role when converting between unit systems or changing

unit preﬁxes. So, it is often assumed that the notion of dimension is general. However, this paper explains that

is not so: dimensions do not apply to all expressions of quantities. By recognising that there diﬀerent types

of measurement scale, the role played by dimensions in systems like the SI can be seen as secondary to the

importance to the kind of quantity being expressed. There is a need to provide a unique way of identifying

each kind of quantity: dimensions and unit names are not able to fulﬁl this requirement.

1 INTRODUCTION

Digital support for physical quantities and units is

an elusive goal. In spite of eﬀorts from as early as

the 1970s (Cleaveland, 1975; Gehani, 1977), noth-

ing seems to have found acceptance yet in quite the

same way as, say, numerical formats for representing

real numbers (e.g., the IEEE 754 Standard for Float-

ing Point Arithmetic). Perhaps one reason for slow

progress is that there is a wide variety of ways that

measurements can be expressed, reﬂecting the diver-

sity of measurement methods. There do not appear to

be clear guidelines on how to cater for diﬀerent types

of measurement. The international metrology and sci-

entiﬁc communities have embraced the International

System of Units (SI) (BIPM, 2019), however, the SI

notation has, for pragmatic reasons, some shortcom-

ings (Foster, 2009; Mills, 2009).

The International Committee for Weights and

Measures (CIPM) has recognised the need to coor-

dinate digitalisation of the international measurement

system and established a Task Group on the Digital

SI (CIPM, 2019), supported by a team of experts. In

early 2021, this team made a public request for use-

cases to identify situations where digitalisation of ex-

isting metrological infrastructure might improve out-

comes or address diﬃculties. This paper presents a

https://orcid.org/0000-0002-4249-6863

preliminary analysis of one of those use-cases, which

identiﬁed redundant or ambiguous unit deﬁnitions as

a problem for interoperability.

For instance, if the

context in which units appear does not identify the

intended quantity, there are quite a few SI units that

are potentially ambiguous: heat capacity and entropy

(kg ⋅ m

⋅ s

−2

⋅ K

−1

), electric current and magnetomo-

tive force (A), torque and energy (kg ⋅ m

⋅ s

−2

), quan-

tities expressed in terms of inverse time (s

−1

), and

the gray and sievert (m

⋅ s

−2

) (BIPM, 2019, §2.3.4).

More generally, there is a large number of so-called

dimensionless quantities that all have the SI unit one.

The intent of this paper is to shed some light on the

internal mechanisms of unit systems like the SI. The

ambiguity attributed to some unit names arises from a

policy to compose the names for derived units from

the dimensional expression for the quantity and the

names of base units. The names produced this way are

helpful mnemonic devices when evaluating unit con-

version factors, however, unique names for each quan-

tity cannot be guaranteed. This is particularly obvious

in the case of dimensionless quantities.

By clarifying relationships between quantities, di-

mensions, and units, we show that support for a wider

range of expressions for measured quantities could be

The opinions expressed in this paper are those of the

author and are not necessarily shared by other members of

the CIPM Expert Group.

116

Hall, B.

The Problem with ‘Dimensionless Quantities’.

DOI: 10.5220/0010960300003119

In Proceedings of the 10th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2022), pages 116-125

ISBN: 978-989-758-550-0; ISSN: 2184-4348

developed. Dimensions and units play a role when

converting between diﬀerent unit systems, but only

when quantities are expressed on a particular type

of measurement scale. The more general problem

of converting expressions between diﬀerent types of

scale should be recognised. This leads us to suggest a

diﬀerent way of organising support for quantities and

units.

2 QUANTITIES, DIMENSIONS,

UNITS, AND SCALES

In the 9

edition of the SI Brochure, we read that

(BIPM, 2019, §2.1)

The value of a quantity is generally expressed

as the product of a number and a unit. The unit

is simply a particular example of the quantity

concerned which is used as a reference, and

the number is the ratio of the value of the quan-

tity to the unit.

This is presumably an interpretation of the ﬁrst para-

graph of the Preliminary chapter on measurement of

quantities in the Treatise on Electricity and Magnetism

(Maxwell, 1873)

Every expression of a Quantity consists of two

factors or components. One of these is the

name of a certain known quantity of the same

kind as the quantity to be expressed, which is

taken as a standard of reference. The other

component is the number of times the stan-

dard is taken in order to make up the required

quantity. The standard is technically called

the Unit, and the number is called the Numer-

ical Value of the quantity.

Maxwell’s description of units is an early instance of

metadata: a unit name (or symbol) is associated with

a value to allow the expression of a quantity to be in-

terpreted correctly in the context of diﬀerent systems

of units. To see this, it is helpful to think in terms

of a producer and a consumer of data. A producer

expresses a quantity (a numerical value with a unit)

in such a way that consumers may interpret it cor-

rectly. Consumers ultimately need a numerical value

for computation. So, the producer’s expression of a

quantity, with a unit name, has to be reconciled with

the consumer’s measurement system. Maxwell de-

scribes this (Maxwell, 1873),

. .. a person of any nation, by substituting

for the diﬀerent [unit] symbols the numerical

value of the quantities as measured by his own

national units, would arrive at a true result.

So, the unit name is a place-holder for the appropriate

numeric conversion factor (a numeric variable). This

factor is not known to the producer, because it depends

on the consumer context. Interoperability is enabled

by assigning the appropriate conversion factor in dif-

ferent measurement systems.

For instance, a minimum height requirement for

Police recruits may be expressed in imperial units as,

say, 5 f t 8 in. If this requirement is needed in a con-

text that uses SI units, appropriate values for unit sym-

bols are substituted: ft = 0.3048 and in = 0.0254 (the

values of one foot and one inch when measured in

metres). So, the minimum height in an SI context is

5 × 0.3048 + 8 × 0.0254 = 1.727.

It is perhaps important to emphasize that our con-

cern here is to communicate information about mea-

sured quantities. Maxwell was, of course, interested in

providing a concise mathematical formulation of the

physics of electromagnetism. By introducing the idea

of a unit system, he was able to describe relations be-

tween quantities without concern for units. This ab-

straction of quantities is now very familiar. For ex-

ample, a relation like Newton’s second law, 𝒇 = 𝒎𝒂,

is understood to be unit-independent; that is, the law

holds in any coherent unit system (the law is consid-

ered to hold even if system is not coherent, but one ad-

ditional numerical factor may be required). The terms

𝒇 , 𝒎, and 𝒂, in such equations are not simple numeric

variables; they are usually called quantities (bold italic

terms are used here for quantities).

Now, the relationship between an abstract unit-

independent quantity and a producer expression for

that quantity is of interest. Consider speed, which may

be deﬁned without reference to units as 𝒗 = 𝒍∕𝒕, where

𝒕 is the time taken to cover a distance 𝒍. To express a

particular speed, a producer will assign a number to

{𝑣} and the name of the unit, or its symbol, to 𝑉 (e.g.,

mile-per-hour, knot, etc.). So, 𝒗 = {𝑣}𝑉 expresses a

speed in a general sense and 1.5 m ⋅ s

−1

is a particular

speed. The term 𝑉 is a place-holder for the unit name;

it is called the dimension of the quantity (Barenblatt,

1987). Valid substitutions for 𝑉 are names, or sym-

bols, for units for speed.

The general quantity expression for speed can be

related to expressions for length and time by substitut-

ing for each term in the deﬁning equation,

𝒗 =

𝒍

𝒕

= {𝑣}𝑉

{𝑙}𝐿

{𝑡}𝑇

= {𝑙∕𝑡}𝐿𝑇

−1

Here terms in braces are values and dimensions are in

upper-case letters. The sense in which 𝐿 can be di-

vided by 𝑇 is that numbers (conversion factors) are

ultimately assigned to the unit names substituted for

The Problem with ‘Dimensionless Quantities’

117

these dimensions. When the expression of a quantity

is reduced to a number in a particular unit system, the

unit terms act as conversion factors. This is quite im-

portant: when units for length and time change, an ex-

pression like 𝐿𝑇

−1

describes the scaling required for

a speed (the factor for speed is equal to the conversion

factor for the unit of length divided by the conversion

factor for the unit of time).

Starting with a small independent basis set of

quantities (mass, length, and time), and using (unit-

independent) equations of physics, Maxwell deﬁned

other quantities of interest. This simultaneously es-

tablished relationships between the units chosen to ex-

press those quantities. The resulting structure is useful

when converting between unit systems, because con-

version factors can be derived from the base units. To

this end, derived unit names often encode a quantity’s

dependence on base quantities. For example, the name

of the SI unit for acceleration is “metre-per-second-

per-second” (m ⋅ s

−2

), which is obtained by substitut-

ing ‘metre’ and ‘second’ into the dimensional expres-

sion 𝐿𝑇

−2

Because unit names are derived from dimensional

expressions, they encode the scaling relationships but

the nature of the derived quantity is not necessarily

captured. The SI Brochure concedes that . .. several

diﬀerent quantities may share the same SI unit (BIPM,

2019, §2.3.4). The most obvious examples are the

many diﬀerent kinds of dimensionless quantities that

all have the SI unit one. This unit indicates that no

scaling is needed when base units change (e.g., an as-

pect ratio does not depend on units of length), but the

unit name gives no hint as to the nature of the quan-

tity itself. There are also dimensioned quantities in the

SI that are indistinguishable, such as torque and work

which have the dimension 𝑀 𝐿

𝑇

−2

. The SI includes

some special unit names to try to mitigate this prob-

lem. For instance, plane angle may be expressed in

rad or in m ⋅ m

−1

, activity in Bq or in s

−1

, etc. Nev-

ertheless, the composed names for these units are also

considered valid.

The construction of a system of quantities must

assume that the multiplication and division of terms

in deﬁning equations is meaningful (like 𝒗 = 𝒍∕𝒕 and

𝒇 = 𝒎𝒂). However, that places limits on the type of

measurement scale that can be used to express terms:

only ratio scales (Stevens, 1946), which are charac-

terised by a scale-independent zero, are acceptable

(e.g., the foot, inch, furlong and metre are all ratio

scales for length; on each, zero corresponds to the

same length).

However, there are other types of scale in use,

which should be considered. Stevens identiﬁed four

categories of scale and Chrisman added several more

levels (Chrisman, 1995; Chrisman, 1998). The scales

identiﬁed by Stevens can be classiﬁed by the mathe-

matical transformations that leave a scale’s form in-

variant; the four scales are called: nominal, ordinal,

interval and ratio.

For instance, if 𝑥 and 𝑥

′

are values for the same

quantity expressed on diﬀerent ratio scales, there will

be some conversion factor 𝐾 such that 𝑥

′

= 𝐾 𝑥, which

preserves the form of the scale. For interval scales,

an aﬃne transformation of the form 𝑥

′

= 𝐾 𝑥 + 𝑂 is

needed (c.f., conversion between Fahrenheit and Cel-

sius); for ordinal scales, a monotonic increasing func-

tion 𝑥

′

= 𝑓 (𝑥) is required. We may think of these

diﬀerent forms of transformation as generalisations of

the simple conversion factors that convert between ra-

tio scales for things like mass and length.

If diﬀerent types of scale are an important classi-

ﬁer, the term ‘quantity’ must be given some consid-

eration. In the most general sense, a quantity may

be thought of as an attribute of some phenomenon,

body or substance, that can be distinguished quali-

tatively and determined quantitatively (BIPM et al.,

1984, §1.01). Such a quantity might be expressed on

any of Stevens’s scales (e.g., a body can be determined

to have a temperature, that temperature can be mea-

sured on an ordinal scale by a thermochromic device,

or on an interval scale by a domestic thermometer, or

on a ratio scale by a radiation thermometer). How-

ever, this interpretation of the term quantity may be

too broad for our purposes and could lead to confu-

sion. As already noted, the terms in unit-independent

equations—which are often referred to as quantities—

are not quantities in this general sense.

To a physicist or applied mathematician, it is al-

most universally assumed, although rarely acknowl-

edged, that ‘quantity’ is used in the restricted sense

that applies to unit-independent expressions. The

terms appearing in equations such as Newton’s law

stand for a quantity that can be expressed on a ratio

scale. A great deal of published material on quanti-

ties, units, and dimensions is written from this point

of view. Because of this, we believe that ‘quantity’

must be used in this restricted sense, and be quali-

ﬁed appropriately when a diﬀerent notion is intended

(such as, ‘ordinal quantity’ or ‘interval quantity’; to

indicate the more general sense ‘general quantity’ or

‘kind of quantity’ may be used ). This means that all

quantities have an associated dimension, and perhaps

a dimensional expression related to the quantity def-

inition. Conversely, the notion of dimension is only

meaningful for quantities in the stricter sense; it does

not apply to any other types of measurement scale, be-

cause simple scaling does not leave those scales in-

variant. This limitation of dimensions is often misun-

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

118

derstood.

Indeed there appears to be little awareness about

the diﬀerent types of measurement scale. A recent re-

view, by Grozier, found that the distinction between

unit dependence and independence is often unclear.

He observed “. . . unit-invariance does not appear to

have yet entered the scientiﬁc mainstream; instead,

formulae which are unit-invariant are often not recog-

nised as such, and formulae that are unit-dependent

are often wrongly taken to be of universal application”

(Grozier, 2020). This observation is somewhat alarm-

ing and suggests that, in striving for more autonomous

digital systems, we must apply stricter discipline when

describing physical data and metadata.

2.1 Quantity and Scales

The qualiﬁed terms ‘nominal quantity’, ‘ordinal quan-

tity’, or ‘interval quantity’ may be used to refer to

quantities expressed on corresponding types of scale.

The arithmetic, ordering and equivalence operations

that apply to data expressed on the diﬀerent scales can

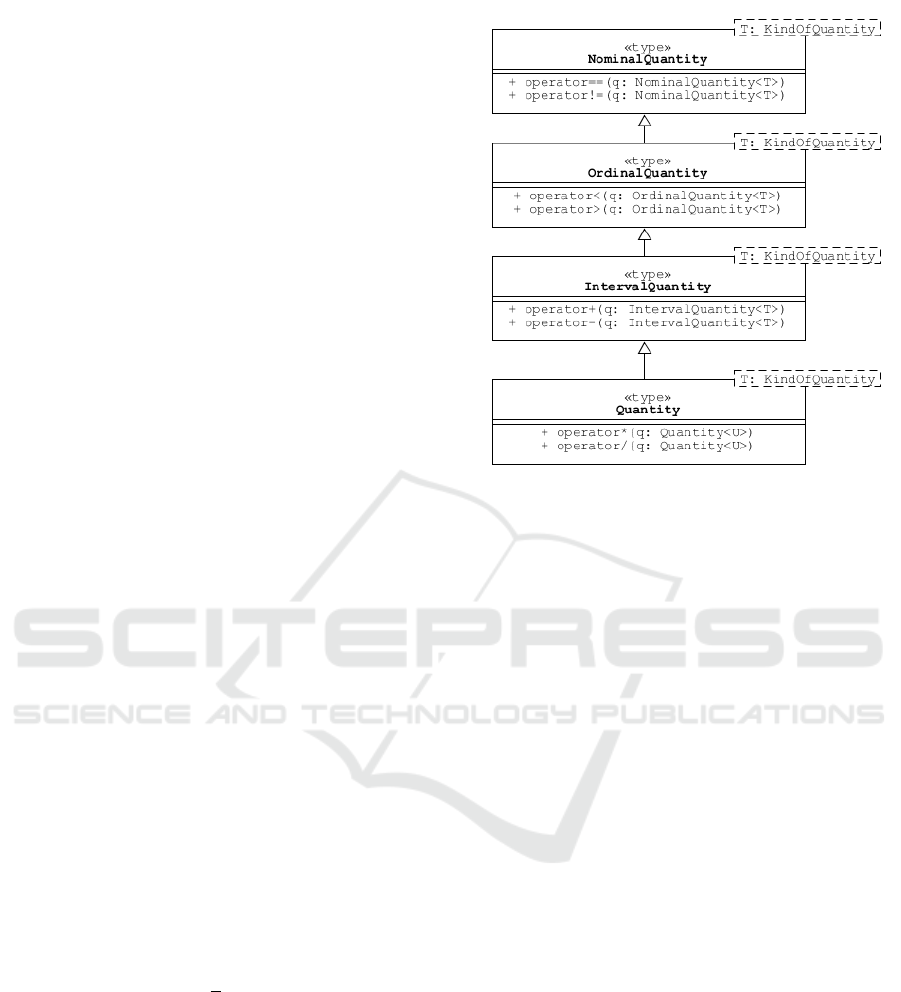
be organised as shown in the class diagram in Fig-

ure 1. The base class corresponds to a nominal quan-

tity; one can only determine whether an object pos-

sesses a particular nominal quantity or not. However,

an ordinal quantity has a magnitude that can be mean-

ingfully compared; although, it is not meaningful to

compare the diﬀerences between pairs of magnitudes.

For an interval quantity, the diﬀerence between mag-

nitudes is meaningful but not ratios of the magnitudes

(e.g., if the air temperature yesterday was 15 °C and

today it is 20 °C, it makes sense to say that it is 5 °C

warmer today, but not that it is 33 % warmer). Finally,

because ratio scales have a natural zero (e.g., zero feet

is the same as zero metres, etc), ratios of magnitudes

are meaningful.

In terms of software, distinguishing between the

diﬀerent levels of expression could exert tighter con-

trol over declarations and assignments to variables.

For instance, the physics equation

𝑬 =

𝒌

𝑻 (1)

is unit-independent; 𝑬, 𝒌

and 𝑻 represent quantities:

𝑬 is the average translational kinetic energy of atoms

in an ideal gas, 𝒌

is a proportionality constant be-

tween energy and temperature, called the Boltzmann

constant, and 𝑻 is thermodynamic temperature. Now,

the relationship between quantities on either side of

this equation is constrained and so the types chosen to

represent terms can be validated. If the result of the

expression is declared an energy, and a term associ-

ated with 𝑻 is declared a temperature, then the term

representing the Boltzmann constant must be declared

Figure 1: This UML class diagram shows a simple inher-

itance relationship between four diﬀerent levels of expres-

sion for a general quantity. Stevens identiﬁed nominal, or-

dinal, interval and ratio scales as diﬀerent levels of expres-

sion (Stevens, 1946). It is useful to formalise these levels

(and perhaps others (Chrisman, 1995; Chrisman, 1998)), in

terms of the operations that are meaningful for data. Use

of the term ‘quantity’ here, for ratio scales, corresponds to

common usage in physical science; the more general sense

of quantity is represented by the template parameter for a

particular kind of quantity. Note the product and quotient

operations deﬁned for a Quantity<T> may take a diﬀer-

ent quantity kind argument Quantity<U>. These operations

generally return a diﬀerent quantity kind too (not shown).

a quantity that relates temperature to energy. This con-

sistency check could be regarded as application of the

principle of dimensional homogeneity, which requires

that the dimensions of each term in a unit-independent

equation be the same. However, ambiguity between

quantities can still arise if the homogeneity principle

is applied using a ﬁxed set of base dimensions, such

as in the SI. To avoid this, some form of unambiguous

representation of the quantities themselves is required

and, if quantity expressions are to be checked, some

way of representing relationships among quantities is

also needed. How to provide this information is an

open question, which will be discussed further below.

Let us suppose that appropriate quantity-speciﬁc

terms have been declared to represent equation (1).

The computation itself can only be carried out when

quantities are expressed on appropriate an appropriate

choice of ratio scales (for instance, in SI units). How-

ever, if the data assigned to terms are not immediately

in the correct form, a digital system could apply cer-

tain pre- or post-processing steps automatically. For

The Problem with ‘Dimensionless Quantities’

119

instance:

1. Appropriate conversion factors could be applied,

if the assigned data were expressed as a quan-

tity, but not in the units required. For example,

there is an Imperial scale for absolute tempera-

ture called Rankine (symbol

◦

R). If a value for

𝑻 were expressed in

◦

R, the conversion factor

273.15∕491.67 = 0.555 56 K∕

◦

R could be applied

to obtain an expression in kelvin.

2. Conversion of interval-quantity data to a suitable

quantity scale could be carried out. For exam-

ple, an absolute temperature expressed in degrees

Fahrenheit could be converted to kelvin by an

aﬃne transform. This would also coerce the data

type from IntervalQuantity<Temperature> to

Quantity<Temperature>, but the legitimacy of

this operation could be determined by the system,

because the kind of quantity—temperature—is the

same.

3. The format for reporting results could be adapted

to user requirements. For example, quantities that

are subject to formal regulations generally require

metrological traceability to SI units. Nevertheless,

reporting in customary units may be desirable re-

quiring conversion of results to a diﬀerent form.

Such conversion might also involve type-coercion

to interval or ordinal quantities.

4. If a particular assignment cannot be made le-

gitimately, an exception could be raised to pro-

vide an opportunity for further ad hoc pro-

cessing. For example, if temperature data

were expressed as an ordinal quantity (i.e.,

as an OrdinalQuantity<Temperature>), auto-

matic conversion to a quantity is illegal. Neverthe-

less, information about the quantity could perhaps

be handled by an exception. For instance, an upper

or lower bound on temperature might be known,

so a range of corresponding results could be eval-

uated.

3 THE PROBLEM WITH

‘DIMENSIONLESS

QUANTITIES’

The title of this paper is intended to draw attention

to the predominance of base dimensions as a proxy

for quantities in our thinking and, indeed, to how mis-

leading that is. Introducing the notion of scales (lev-

els of measurement) has shown that the notion of a

dimension applies only to quantities expressed on a

ratio scale. There are more general aspects that must

be captured. Indeed, were it not for the overwhelm-

ing use of ‘quantity’ in scientiﬁc literature, we would

have suggested that ‘dimension’ could be adopted as

a name for the (ratio) quantity type. Unfortunately,

‘quantity’ and ‘dimension’ have become hopelessly

entangled (Emerson, 2005).

So, if there is a problem with dimensionless quan-

tities, it appears to be a semantic one. A physicist

would consider quantities, such as the gain of an am-

pliﬁer, a refractive index, or an emissivity, to tran-

scend measurement; a property would be assumed to

exist independently of any consideration about how

to measure it. Yet, a physicist would also take for

granted that mathematical models—unit-independent

equations—could incorporate terms for quantities like

ampliﬁer gain, refractive index, etc, which are dimen-

sionless. This restricts the expression of those terms

to ratio scales (there could be no such thing as a ‘di-

mensionless interval quantity’, for example).

The fact that a particular unit can be used to ex-

press several diﬀerent quantities is not a problem. The

unit one is appropriate for all dimensionless quantities,

because it indicates to the consumer that the value in

the producer expression does not require conversion.

Nonetheless, the expression of a dimensionless quan-

tity is not a pure number: it is merely insensitive to

changes in the units of the measurement system. The

unit one arises from arithmetic cancellation of dimen-

sion variables (factors, or equivalently unit names).

For example, an aspect ratio is the ratio of two lengths

𝒂 =

𝒍

Using the full expression of quantities

{𝑎}𝐴 =

{𝑙

}𝐿

{𝑙

}𝐿

{𝑙

}

{𝑙

}

because the factor 𝐿∕𝐿 reduces to unity for any choice

of unit and so 𝐴 = 1.

Dimensionless quantities arise when there is com-

plete cancellation of dimension variables or unit

names, however partial cancellation can occur as well.

Perhaps the best-known example is that of work and

torque (both having the derived SI unit kg ⋅ m

⋅ s

−2

These quantities would have diﬀerent dimensions, and

therefore diﬀerent names, if angle were included as a

base quantity in the system (Brownstein, 1997). How-

ever, angle is deﬁned as a ratio of lengths in the SI and

so its role in the deﬁnition of torque escapes from the

dimensional representation. Other examples of ambi-

guity were given in the Introduction. Again, this is

not the symptom of a problem: there should not be

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

120

an expectation that a unit name will uniquely iden-

tify a quantity. Dimensional expressions will always

correctly represent the conversion factors needed to

change units, but that is all.

4 ORGANISING INFORMATION

The more general notion of quantity is a common

thread among the diﬀerent forms of expression for

quantities. For example, temperature may be ex-

pressed in kelvin, in degrees Celsius, in degrees

Fahrenheit, or in comparison to some particular ref-

erence temperature, and we may legitimately convert

between diﬀerent forms of expression as long as the

kind of quantity—temperature—remains common to

each. So, to represent quantities and units of measure-

ment in digital systems, the kind of quantity should be

given prominence. Furthermore, to enable interoper-

ability among systems, identiﬁers for diﬀerent kinds

of quantity, as well as units of measurement, should

be standardised.

The task of developing detailed digital registers

containing information about the huge number of

common units and even greater number of quantity

kinds is daunting. Nevertheless, a number of ini-

tiatives do provide references for units of measure.

These projects have established substantial user com-

munities and are well maintained. All, however, have

adopted internal structures based on the Maxwellian

model for unit systems. We brieﬂy present three of

these projects.

UCUM: The Uniﬁed Code for Units of Measure

(UCUM) in clinical information systems claims to

provide a complete and unambiguous coding sys-

tem for units.

"The Uniﬁed Code for Units of Measure is a code

system intended to include all units of measures

being contemporarily used in international sci-

ence, engineering, and business. The purpose is to

facilitate unambiguous electronic communication

of quantities together with their units (Schadow

et al., 1999)."

UCUM is designed around the mathematical prop-

erties of a ﬁxed basis of units. Unit are deﬁned by a

numeric factor and a sequence of base-unit expo-

nents. Units for interval quantities are treated as

exceptions (“special units”) and there is also the

notion of “arbitrary unit”, which bears no relation

to any other unit. A unit may also be adorned with

a textual “annotation”, although this does not con-

tribute to the unit semantics.

OM: The Ontology of units of Measure (OM) pro-

vides a conceptual framework for units of mea-

surement (Rijgersberg et al., 2013). It implements

classes, instances, and properties intended to be

used to represent measurement concepts and in-

cludes various systems of units.

The notion of quantity corresponds to the narrow

sense of the term. However, OM distinguishes be-

tween a ‘measure’ and a ‘scale’, the former cor-

responding to the expression of a quantity and

the latter to the expression of an interval quan-

tity. This allows OM to use the degree Celsius and

the degree Fahrenheit in two quite diﬀerent ways

(given in the OM documentation as an example).

Temperature can be expressed on an ‘scale’, which

allows an oﬀset origin, so 0 °C ≠ 0 °F ≠ 0 K, or, as

a ‘measure’, it is admissible to write 0 °C = 0 °F =

0K, where the expressions represent quantities (in

this case, temperature diﬀerences).

QUDT: The Quantity Units Dimensions and Types

(QUDT) ontology is intended to model quantities,

units, numerical values, and data types to store and

manipulate these objects (QUDT, 2021).

QUDT’s semantics are constructed on a basis set

of quantities and units and it claims to establish a

relationship between units and quantity kinds by

the internal representation of dimensions. This

claim will be limited, because a dimensional rep-

resentation cannot uniquely identify quantities.

However, to overcome some of the problems asso-

ciated with dimensionless quantities, QUDT uses

a numerator and denominator of dimensional ex-

ponents in the internal representation.

The interest in ontologies is intended to capture con-

ceptual information (knowledge) to associate with em-

pirical data stored in digital records. If this is done

consistently on a large scale it may enable applica-

tions of artiﬁcial intelligence (AI) and machine learn-

ing (ML) on large heterogeneous collections of phys-

ical data.

The fact that ontologies have so far focused on the

narrow meaning of quantity may not be an immediate

problem, if applications of AI and ML use scientiﬁc

data. However, poor representation of metrological

concepts in knowledge discovery tools is ultimately of

concern. Vast quantities of physical data will be gen-

erated by digital sensor networks and much of this data

will not be expressible as quantities. How is this data

to be represented in a way that autonomous machines

could make use of it?

We must recognise that the general notion of quan-

tity is fundamental and distinct from units and also

that units may be used to express more than just

simple ratio quantities. It is necessary to uniquely

identify kinds of quantity independently of units.

The Problem with ‘Dimensionless Quantities’

121

The full expression of a quantity has to include: a

value, a unit and a quantity kind, as indicated by the

QuantityExpression class shown in Figure 2.

Figure 2: The digital expression of a quantity will be com-

posed of: a value, a unit, and a quantity kind. This would

be applicable to all of the types shown in Figure 1 (a ‘mixin’

class). The properties of diﬀerent kinds of quantity would be

handled by applications, so only a unique identiﬁer is shown.

An elegant feature of Maxwellian unit systems is

that a producer of data need not anticipate consumers’

requirements: consumers are responsible for conver-

sions from the producer’s unit. So, a digital unit must

also carry enough information to allow conversion. A

simple schema for digital units is shown in Figure 3. A

unit must uniquely identify the combination of: a unit

name, a unit system and a type of scale. For example,

degrees Celsius in the SI system would have two dig-

ital units: one for temperature expressed as an inter-

val quantity, the other for temperature as a ratio quan-

tity. These units would avoid an existing source of

ambiguity, where a consumer does not know whether

a temperature expressed in degrees Celsius is oﬀset.

A temperature diﬀerence expressed in degrees Cel-

sius would use the digital unit for a quantity, whereas,

an absolute temperature expressed in degrees Celsius

would use the unit for an interval quantity.

Figure 3: A digital unit carries information about the context

of an expressed quantity to allow conversion to an equivalent

form in a diﬀerent context. The identiﬁer must be unique to

the combination of the name, the unit system (e.g., SI, CGS,

etc), and the type of scale (ratio, interval, etc).

To convert between diﬀerent expressions of a

quantity may involve more than just a multiplicative

factor. Conversion functions depend on the types of

scale involved and hence on the producer (source) and

consumer (destination) units, as indicated in Figure 4.

Figure 4: Unit conversion will apply an operation to the nu-

meric value of an expressed quantity. The appropriate con-

version function depends on both the source (producer) and

destination (consumer) units (src_unit and dst_unit).

An authoritative register of quantities and ex-

tended unit representations would be convenient to

support the expression of quantities and units. En-

during unique identiﬁers are needed for both quantity

kinds and units, and a central reference of unit con-

version operations is also desirable. Figure 5 shows

the idea. Of course, such a repository would be likely

to curate more extensive information about the quan-

tities, units and unit systems, as is the case for UCUM,

OM, and CUDT.

5 DIMENSIONLESS QUANTITY

CALCULUS

Inferring the type of quantity that results from an ar-

bitrary computation has often been a motivation for

looking at digital representations for quantities and

units (e.g., (Kennedy, 2010)). However, that is a dif-

ferent problem to developing suitable formats for the

full expression of quantities.

The notion of quantity used in calculations is lim-

ited to expressions on ratio scales and only fairly ba-

sic operations are permissible (essentially just arith-

metic). Type-inference for such calculations must ex-

ploit a notion of quantity that is independent of base

units and dimensions. The idea of using the base di-

mensions of a unit system to generate an abstract lat-

tice of distinct quantities fails to distinguish between

all possibilities (De Boer, 1995). However, by sep-

arating unit representations from quantities, progress

can be made. Recent work has shown that many dif-

ﬁcult cases can be handled by declaring quantities of

importance in context (Hall, 2020).

Dimensionless quantities are considered a special

case in computations. They are often regarded as pure

numbers. However, this point of view should not be

adopted for digitalisation of quantity calculus. Di-

mensionless quantities are indeed diﬀerent from di-

mensioned quantities, but only by virtue of their dif-

ferent scaling behaviour when units change.

To see this more clearly, consider a length 𝒍. The

dimension of 𝒍 is 𝐿 and the dimension of 𝒍

is 𝐿

So, the sum 𝒍 +𝒍

cannot be expressed as a quantity in

the form 𝒒 = {𝑞}𝑄; that is why this operation is not

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

122

Figure 5: An authoritative register of information would be needed to support interoperability of digital representations for

quantities and units. Enduring and unique identiﬁers are needed for both quantity kinds and (digital) units, and a central

reference for operations to convert between diﬀerent units is also desirable.

permitted. On the other hand, for a dimensionless as-

pect ratio 𝒂, we may indeed express the sum of powers

𝒂 + 𝒂

+ ⋯ as a quantity (each term is dimensionless).

For this reason it is meaningful, and therefore permis-

sible, to apply more general mathematical functions

to the value of a dimensionless quantity. A diﬀerent

quantity will generally result, but both will be dimen-

sionless. For example, the trigonometric sine function

transforms an angle (angle is a dimensionless SI quan-

tity and the sine function can be expressed as Taylor

series) into a quantity that may be interpreted as the

ratio of perpendicular sides in a right triangle.

6 DISCUSSION

The SI provides a framework for eﬀective communi-

cation of information about physical quantities, but the

fundamental assumption, that . . . a quantity is gener-

ally expressed as the produce of a number and a unit

is too limited. A third aspect is needed: the quantity

must be identiﬁed. It is the absence of this additional

information that makes dimensionless quantities hard

to handle.

If we accept that each kind of quantity must be

identiﬁed independently of the unit in which it is ex-

pressed, then the stage is set for much informative

quantity expressions. The diﬀerent levels of measure-

ment (scales) that are used in society can be handled

directly, not as exceptions, and the semantics associ-

ated with expressed values can be properly captured.

One of the arguments for adopting SI units over

conventional units is that conversion between units

would not be needed if everyone used the SI. How-

ever, conventional units have proved very resistant to

change and the ubiquity of digital systems now greatly

facilitates conversions. Moreover, SI units do not ap-

ply to most non-ratio scale expressions.

An important class of such measurements are com-

monly reported in SI units although they cannot be

expressed on ratio scales. Many measurements of ma-

terial properties fall into this category (Kirkham and

White, 2018). Such measurements may follow a stan-

dardised procedure that renders values for a particular

purpose. However, when measured by diﬀerent proce-

dures, the same nominal property may give quite dif-

ferent results. The characterisation of viscosity is one

example where there are literally dozens of methods

(for details, see (Kirkham and White, 2018)). In such

cases, expressed quantities could be better handled by

identifying the method used with the quantity kind.

This would prevent misinterpretation.

In 2019, the SI underwent a very signiﬁcant

change when exact values for seven ‘deﬁning con-

stants’ were adopted as a way of constructing the sys-

tem (BIPM, 2019). This ﬁnally retired ‘base units’, al-

though they have been retained to support legacy ver-

sions of the SI and the SI notation. Emphasis is now

placed on the equations of physics that establish re-

lationships among quantities. So, although the unit

of speed remains the ‘metre-per-second’, we might

equally think of it as ‘SI-speed’; there would be no

harm in doing so. The change to the SI adds weight to

our suggestion that each digital unit deserves an indi-

vidual unique identiﬁer. There is no hierarchy among

units to be captured in the representation.

It is not possible to attribute a cost due to in-

correct interpretations of physical data. A few well-

known stories, like the NASA Mars Climate Ob-

server (Oberg, 1999), or the Gimli Glider incident

(Wikipedia, 2021a), are often cited to motivate the

need for better handling of units. The huge disruption

caused by the practice of storing a year as two dec-

imal digits (the Year 2000 problem) has been better

documented (Wikipedia, 2021b). Another, less well-

known, story involves the construction of a bridge

over the Rhine river, where there was confusion about

height expressed on interval scales (BBC, 2014). The

so-called ‘height above sea level’ is an interval scale

for length, because the origin—sea level—is arbitrar-

The Problem with ‘Dimensionless Quantities’

123

ily deﬁned. In Germany, sea level is taken with re-

spect to the North Sea, whereas Switzerland refers to

the Mediterranean Sea. These heights are not equiv-

alent, there is a nominal diﬀerence of 27 cm between

them. So, when a bridge was built between Germany

and Switzerland, at Laufenburg, the diﬀerence be-

tween expressions of height needed to be accounted

for, but was mishandled, resulting in a 54 cm height

diﬀerence between the Swiss and German sides. Ev-

eryone would agree, it seems, that more reliable ways

of communicating information about physical quanti-

ties are needed, as well as a greater awareness of the

metrological concepts involved.

7 CONCLUSIONS

In summary, the problem with dimensionless quanti-

ties, and more generally with dimensions themselves,

is that often it is incorrectly assumed that a dimension

or a unit can identify a corresponding quantity. We

have explained how the manipulation of conventional

units, as explained by Maxwell, can lead to such am-

biguity. This is not a problem with the units, rather

it is a misinterpretation of their role. Several obser-

vations can be made: dimensional expressions, and

compound unit names based on such expressions, can-

not reliably identify quantities; however, dimensional

expressions can always be relied upon to obtain con-

version factors when units change.

The mathematical modelling of a system of quan-

tities, like the SI, assumes that quantities are expressed

on ratio scales. However, other types of scale are

important too. To accommodate a wider range of

measurements, quantity expressions should be gener-

alised. The various levels of measurement proposed

by Stevens and Chrisman oﬀer a useful classiﬁcation

of scales and can be used to implement wider sup-

port for physical data. The diﬀerent levels can be rep-

resented by simple hierarchical inheritance structures

(like Figure 1).

The term ‘quantity’ must be handled carefully.

The common use of quantity by physical scientists

should be adopted for expressions on ratio scales

and the more general notion of quantity—as a prop-

erty that exists without consideration for a particular

form of expression—should be suitably qualiﬁed. The

terms ‘nominal quantity’, ‘ordinal quantity’, and ‘in-

terval quantity’ could be adopted to refer to expres-

sions on nominal, ordinal, or intervals scales and other

terms may be introduced if the levels proposed by

Chrisman are adopted.

The more general notion of quantity is fundamen-

tally important. Conversion between diﬀerent expres-

sions of the same quantity may be possible, up or

down a hierarchy of scales (e.g., a body might be

deemed to have a temperature (nominal), that temper-

ature could be ranked against other temperatures (or-

dinal), or given a value in degrees Celsius (interval),

or kelvin (ratio)). For this reason, Figure 1 used the

parameter T to represent the kind of quantity. A digi-

tal system should adopt suitable unique identiﬁers for

each general quantity. Having these identiﬁers avail-

able would immediately resolve the diﬃculties that

prompted the preparation of this report.

ACKNOWLEDGEMENTS

The author is grateful to Vladimir Bubanja and Joe

Borbely for careful review of this manuscript. This

work was funded by the New Zealand government.

REFERENCES

Barenblatt, G. I. (1987). Dimensional analysis. Gordon and

Breech.

BBC (2014). The Laufenburg bridge. https://www.bbc.

co.uk/news/magazine-27509559 (accessed 28 Dec.

2021).

BIPM (2019). The International System of Units. BIPM,

Sèvres, France, 9

edition.

BIPM, ISO, IEC, and OIML (1984). Vocabulary of metrol-

ogy, Part 1, basic and general terms (international).

International Organisation for Standardization.

Brownstein, K. (1997). Angles—let’s treat them squarely.

American Journal of Physics, 65(7):605–614.

Chrisman, N. R. (1995). Beyond stevens: A revised ap-

proach to measurement for geographic information. In

AUTOCARTO-CONFERENCE, pages 271–280.

Chrisman, N. R. (1998). Rethinking levels of measurement

for cartography. Cartography and Geographic Infor-

mation Systems, 25(4):231–242.

CIPM (2019). CIPM Task Group on the Digital SI. (ac-

cessed 29 August 2021). https://www.bipm.org/en/

committees/ci/cipm/wg/cipm-tg-dsi.

Cleaveland, J. C. (1975). Pouches, a programming language

construct encouraging redundancy. Msc, University of

California, Los Angeles–Computer Science.

De Boer, J. (1995). On the history of quantity calculus and

the international system. Metrologia, 31(6):405.

Emerson, W. H. (2005). On the concept of dimension.

Metrologia, 42(4):L21–L22.

Foster, M. P. (2009). Disambiguating the SI notation would

guarantee its correct parsing. Proceedings of the Royal

Society A: Mathematical, Physical and Engineering

Sciences, 465(2108):1227–1229.

Gehani, N. (1977). Units of measure as a data attribute.

Computer Languages, 2(3):93–111.

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

124

Grozier, J. (2020). Should physical laws be unit-invariant?

Studies in History and Philosophy of Science Part A,

80:9–18.

Hall, B. D. (2020). Software for calculation with physi-

cal quantities. In 2020 IEEE International Workshop

on Metrology for Industry 4.0 & IoT, pages 458–463.

IEEE.

Kennedy, A. (2010). Types for Units-of-Measure: Theory

and Practice. In Horváth, Z., Plasmeijer, R., and Zsók,

V., editors, Central European Functional Program-

ming School, volume 6299, pages 268–305. Springer

Berlin Heidelberg, Berlin, Heidelberg. Series Title:

Lecture Notes in Computer Science.

Kirkham, H. and White, R. (2018). Pure and applied mea-

surement: The need for expanded education. IEEE

Instrumentation & Measurement Magazine, 21(6):52–

59.

Maxwell, J. C. (1873). A Treatise on Electricity and Mag-

netism. Clarendon Press, Oxford.

Mills, I. (2009). Conventions for writing the values of

quantities in the SI. Proceedings of the Royal Society

A: Mathematical, Physical and Engineering Sciences,

465(2108):2313–2316.

Oberg, J. (1999). Why the Mars probe went oﬀ course. IEEE

Spectrum, December:34–39.

QUDT (2021). Quantity, Unit, Dimension and Type. (ac-

cessed 26 March 2021). DOI: 10.25504/FAIRshar-

ing.d3pqw7.

Rijgersberg, H., van Assem, M., and Top, J. (2013). Ontol-

ogy of units of measure and related concepts. Semantic

Web, 4(1):3–13. https://github.com/HajoRijgersberg/

OM.

Schadow, G., McDonald, C. J., Suico, J. G., Föhring, U.,

and Tolxdorﬀ, T. (1999). Units of measure in clinical

information systems. Journal of the American Medical

Informatics Association, 6(2):151–162. https://ucum.

nlm.nih.gov/.

Stevens, S. S. (1946). On the theory of scales. Science,

103(2684):677 – 680.

Wikipedia (2021a). Gimli Glider. https://en.wikipedia.org/

wiki/Gimli_Glider (accessed 28 Dec. 2021).

Wikipedia (2021b). Year 2000 problem. https://en.

wikipedia.org/wiki/Year_2000_problem (accessed 28

Dec. 2021).

The Problem with ‘Dimensionless Quantities’

125