Acousto-optic k-space Filtering of Optical Beams

Konstantin B. Yushkov

National University of Science and Technology “MISIS”, 4 Leninsky Prospekt, Moscow 119049, Russia

Keywords:

Acousto-optics, Tunable Filter, Spatial Filter, Phase Imaging, Optical Trapping.

Abstract:

Acousto-optic tunable ﬁlters (AOTFs) can be used for spatial ﬁltering of optical beams. A noncollinear AOTF

has a tunable ring-shaped transfer function determined by geometry of the refractive index surface in a uniaxial

crystal. Different axially symmetric transfer functions can be synthesized using multi-frequency ultrasonic

signals. In the report, theory of AOTF-based spatial ﬁltering of optical beams is summarized. Speciﬁc transfer

function of the AOTF — bandpass spatial frequency ﬁlter — enables hyperspectal phase imaging in dark-ﬁeld

mode using incoherent illumination. Operation of a dynamic ring-shaped optical trap based on the noncollinear

AOTF is demonstrated.

1 INTRODUCTION

Acousto-optic tunable ﬁlters (AOTF) ﬁnd broad ap-

plications as hyperspectral imaging devices (wide-

aperture monochromators and programmable multi-

window ﬁlters) in the ﬁelds of biophotonics, remote

sensing, and space research (Lu and Fei, 2014; Ko-

rablev et al., 2018; Genchi et al., 2021). Besides that,

AOTFs are also capable of tunable spatial ﬁltering of

optical beams. This feature has been known since

1980-ies (Balakshy, 1984), but only a few of its appli-

cations in Optics, Photonics, and Laser Physics have

been reported until recently (Balakshy and Voloshi-

nov, 2005; Balakshy and Kostyuk, 2009). In this re-

port, fundamentals and novel applications of AOTF-

based optical beam shaping are observed.

Anisotropic acousto-optic diffraction in Bragg

regime is used in AOTFs. It is a tree-wave mixing

linear optical interaction, which is governed by the

phase matching condition. Ultrasonic wave produces

periodic modulation of refractive index in an interac-

tion medium — a volume phase grating to which a

reciprocal grating vector can be assigned. Efﬁcient in-

teraction is only possible if momentum of interacting

waves is conserved. Thus, Bragg phase matching de-

termines wavelength and angular selectivity that en-

ables design of tunable optical ﬁlters. Interaction of

ﬁnite-size optical beams is analyzed using plane wave

decomposition. As the result, the acousto-optic ﬁl-

ter can operate as a tunable k-space ﬁlter of optical

beams.

https://orcid.org/0000-0001-9015-799X

Figure 1: Noncollinear paratellurite AOTF: (a) real-size

photograph; (b) acoustic ﬁeld visualization: left — 0

or-

der; right — 1

order; white rectangle — optical aperture;

yellow rectangle — piezotransducer (PT).

A paratellurite (TeO

) single crystal AOTF de-

signed and fabricated in-house (NUST “MISIS”) is

shown in Fig. 1 (a). There are two beams at the AOTF

output: the 0

and the 1

diffraction orders, Fig. 1 (b).

The AOTF demonstrates diffraction efﬁciency over

98% in the optical aperture area (5 × 5 mm

) and ho-

mogeneity of the diffracted ﬁeld intensity within 15%

r.m.s.

Yushkov, K.

Acousto-optic k-space Filtering of Optical Beams.

DOI: 10.5220/0010972700003121

In Proceedings of the 10th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2022), pages 69-75

ISBN: 978-989-758-554-8; ISSN: 2184-4364

2 FUNDAMENTALS

2.1 AOTF Transfer Function

The transfer function of a linear space-invariant op-

tical system is deﬁned as a transmission coefﬁcient

of the angular spectrum (Goodman, 2005). The

ﬁrst-order transmission coefﬁcient of a Bragg grating

is derived from plane-wave coupling-of-modes the-

ory (Yariv and Yeh, 1984):

;F) =

+ R

;F)

sin

+ R

;F), (1)

where Q is the coupling coefﬁcient and R(k

;F)

is the phase mismatch depending transverse compo-

nents of the wave vector k

and k

and ultrasound fre-

quency F provided optical frequency λ is given.

The mismatch R(k

;F) is calculated from a 3D

wave vector diagram, see Fig. 2. AOTFs are designed

in uniaxial crystals using their birefringence. To ob-

tain wide acceptance angle, which is necessary for

image processing, noncritical phase matching (NPM)

geometry is chosen. Angular bandwidth of NPM is

directly related to curvature of the optical wave nor-

mal surface in the crystal (Yushkov, 2021; Yushkov

and Naumenko, 2021). It follows from differential ge-

ometry of wave normal surfaces that two fundamental

topologies of phase matching in the neighborhood of

NPM points are elliptical and hyperbolic. The NPM

frequency F

npm

is a local minimum of F(k

) for the

elliptical topology and the saddle point for the hyper-

bolic one. Topological transition between these ge-

ometries takes place only at certain direction of ultra-

sound, which are determined only by principal values

of dielectric permittivity tensor (Yushkov and Nau-

menko, 2021). The vector diagram in Fig. 2 illustrates

conical phase matching in a positive uniaxial crystal.

Explicit expression for R(k

;F) in a non-

collinear acousto-optic diffraction geometry in uniax-

ial crystals can be found elsewhere (Yushkov et al.,

2020a; Yushkov et al., 2020b). Figure 3 shows a

typical phase matching surface in k-space (k

∝ δθ

Intensity transfer function

) = |H

(2)

can be readily visualized in experiment. The setup for

transfer function visualization is schematically shown

in Fig. 4 (a). A collimated laser beam is focused onto

an AOTF. An output polarizer is used to select one

of the diffraction orders. The output beam is cap-

tured from a screen with a CCD. Experiment in Figs 4

Figure 2: 3D wave vector diagram of anisotropic Bragg

diffraction: (a) deﬁnition of angular coordinates for off-

axial diffraction in a uniaxial crystal; (b) conical phase

matching in the neighborhood of the noncritical phase

matching geometry. Reproduced under Open Access Li-

cence from (Yushkov et al., 2020a),

2020 OSA.

Figure 3: Zero phase mismatch surface: the case of non-

collinear AOTF. Reproduced under Open Access Licence

from (Gorevoy et al., 2021),

2021 OSA.

(b)-(d) shows the transfer function T

measured ex-

perimentally. Paratellurite AOTF with acoustic beam

orientation α = 9.06

◦

and λ = 532 nm laser were

used, the transfer functions were measured at RF sig-

nal frequencies of 132.4, 133.0, and 133.6 MHz. The

ﬁrst result is a low-pass angular frequency ﬁlter with

maximum transmission at k

= k

= 0 at F ≈ F

npm

132.4 MHz. The other results demonstrate a tunable

bandpass ﬁlter with almost circular phase matching

locus k

+ k

= ρ

(F) with ρ

∝ (F − F

npm

). Simula-

tions show that at low paratellurite crystal cut angles

(α . 12

◦

) the transfer function asymmetry manifests

itself mainly as the shift of the transfer function cen-

ter (Yushkov et al., 2020b).

2.2 Optical System Layouts

Two common optical schemes for AOTF-based opti-

cal beam shaping systems are shown in 5: the confo-

cal one and the Fourier-transform one. For simplicity,

both optical schemes in Fig. 5 are shown with unity

scaling factors and equal focal lengths f of front-end

and back-end optics. A general case of arbitrary focal

lengths can be analyzed in the same way. Beam stops

PHOTOPTICS 2022 - 10th International Conference on Photonics, Optics and Laser Technology

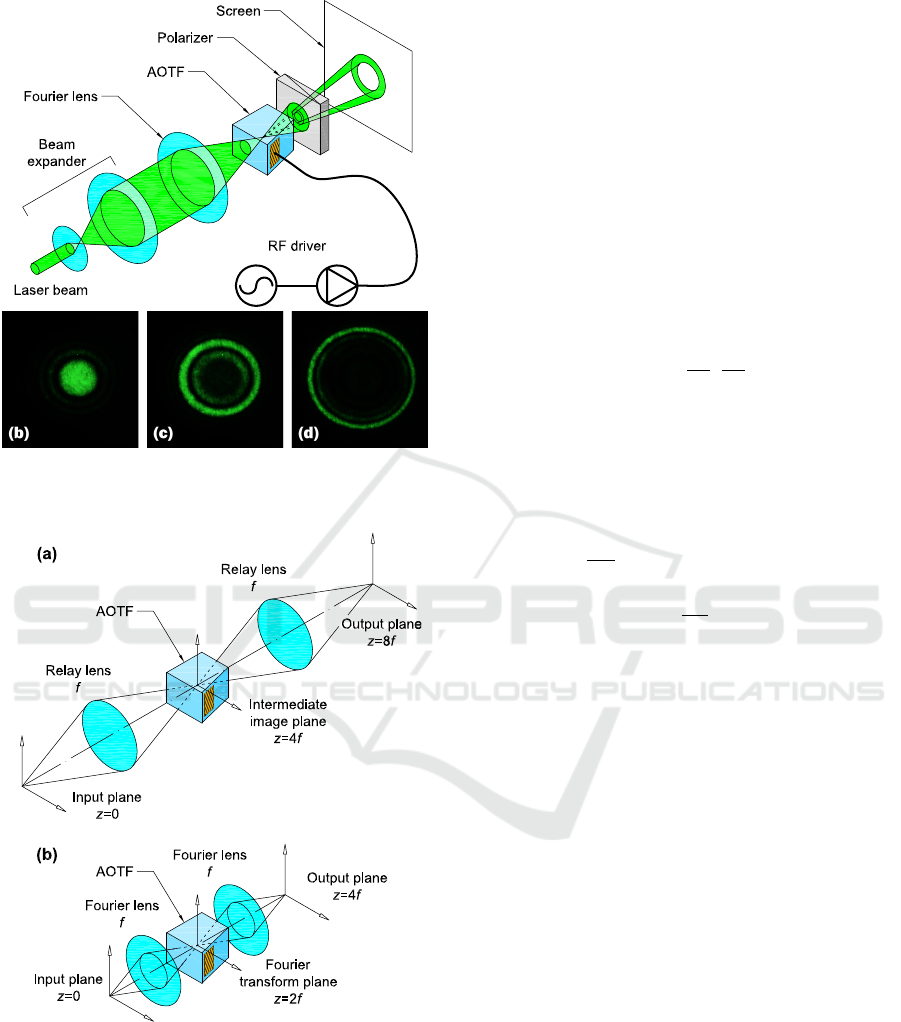
Figure 4: Visualization of AOTF transfer function: (a) ex-

periment scheme; (b)-(d) ﬁrst-order AOTF transfer func-

tions measured at different signal frequencies.

Figure 5: Two principal layouts of AOTF-based spatial ﬁl-

tering schemes: (a) confocal scheme; (b) Fourier-transform

scheme.

to separate the diffraction orders are assumed but not

plotted.

The confocal system shown in Fig. 5 (a) performs

direct k-space ﬁltering of the optical beam:

out

) = H

). (3)

In this scheme, the input ﬁeld U

(x,y) is relayed to

the AO interaction plane and its angular spectrum is

unaltered. The diffracted ﬁeld has the angular spec-

trum modiﬁed according to Eq. (3).

The confocal optical scheme is typical for low-

aberration hyperspectral imaging systems (Suhre

et al., 2004). Annular transfer function of the AOTF

enables application of this scheme for hyperspectral

imaging in dark ﬁeld mode. Application of this new

imaging modality for phase imaging is discussed in

Sec. 3.1.

The Fourier-transform optical scheme shown in

Fig. 5 (b). In this scheme, the AOTF transfer func-

tion is a complex-valued multiplier in the output ﬁeld

distribution:

out

(x,y) = H



λ f



(x,y) (4)

where the scaling factor between k-space and coor-

dinate space (x,y) is λ f : x/(λ f ) = k

and y/(λ f ) =

. Derivation of Eq. (4) simply follows from prop-

erties of optical Fourier transform performed by a

lens (Goodman, 2005):

(x,y) =

iλ f

+∞

−∞

)×

exp



−

2πi

λ f

(xx

+ yy

)



(5)

is the optical ﬁeld at the Fourier plane z = 2 f (i.e., at

the AOTF input), and

) = −iλ fU

(−λ f k

,−λ f k

) (6)

is its plane wave spectrum. Equation (4) explicitly

follows from applying the optical Fourier transform

twice.

Fourier-transform scheme is an effective solution

for laser beam shaping. Dynamic annular optical trap

based on this principle is described in Sec. 3.2.

2.3 Laser Beam Shaping

Laser beam shaping is a new branch in acousto-optic

instrumentation, which broadens the range of applied

problems in science and engineering solved with the

usage of the effect of light diffraction by ultrasound

(Yushkov et al., 2018). In can extend operation rates

of current beam shaping methods (Dickey, 2014) up

to 100 kHz owing to fast response of AOTFs and other

acousto-optic devices.

Transfer function analysis in Sec. 2.1 was made

under assumption of single-frequency RF signals re-

sulting in a periodic phase grating with unique grat-

ing vector k

. A straightforward way to synthesize

transfer functions with variable transmission width is

Acousto-optic k-space Filtering of Optical Beams

to apply multifrequency RF signals. Each monochro-

matic component of ultrasound will provide phase

matching at its own locus of spatial frequencies re-

sulting in broadening of the transfer function or gen-

eration of multiple independent rings. Acoustic time

aperture of the AOTF, τ

, is the minimum time re-

quired to change transfer function. The time aperture

is reciprocal to RF phase matching bandwidth δF.

In order to provide controllable phase relations be-

tween components of the RF signal, one can use dis-

persive waveform synthesis (Yushkov et al., 2019b).

The ultrasonic signal S(t) is calculated as the Fresnel

transform (i.e., Fourier transform with quadratic spec-

tral phase factor) of the transmission window function

W (F

S(t) =

∑

k=1

W (F

)exp



πiF

∆F



exp(−2πiF

t), (7)

where ∆F is the effective FWHM signal bandwidth;

the number of sampling points is determined from the

Nyqist criterion, K = 2∆Fτ

; and the frequency grid

centered at the frequency F

= ∆F

2k − K − 1

K − 1

+ F

. (8)

Equation (7) was derived to comply with the period-

icity property of discrete Fourier transform. The cen-

tral frequency F

can be chosen arbitrarily that allows

continuous tuning of the transmitted interval of spatial

frequencies.

The signal S(t) is sampled and synthesized using

an RF arbitrary waveform generator (AWG). In eq. (7)

it was assumed that two conditions are met to provide

stationary AOTF transmission with minimized distor-

tions:

1. RF signal period equals the AOTF time aperture

;

2. the transmission window satisﬁes the uncer-

tainty relation for chirped pulses (Yushkov et al.,

2021b).

The dispersive waveform synthesis method enables

such output modes as ﬂat-top laser beam shaping and

generation of bottle laser beams with variable diam-

eter and wall thickness (Yushkov et al., 2021a). The

examples of Gaussian laser beam shaping are shown

in Fig. 6. Panels (a) and (c) were obtained with single-

frequency RF signals corresponding to Fig. 4; panels

(b) and (d) were obtained with multi-frequency RF

signals synthesized according to (7).

Figure 6: Laser beam shaping with a noncollinear AOTF:

(a) low-pass spatial ﬁltering; (b) ﬂat-top beam shaping; (c)

band-pass spatial ﬁltering; (d) bottle beam shaping. Repro-

duced from (Yushkov et al., 2021a),

2021 SPIE–OSA.

Figure 7: Experimental setup for hyperspectral phase imag-

ing based on AOTF operation in dark-ﬁeld mode: red ar-

rows — optical path. Reproduced under Open Access Li-

cence from (Yushkov et al., 2020a),

2020 OSA.

3 APPLICATIONS OVERVIEW

3.1 Phase Imaging

Angular selectivity of acousto-optic Bragg diffraction

can be used for physical-level phase imaging. For ex-

ample, it has been previously shown that differential

phase imaging can be obtained with gradient transfer

functions of an AOTF (Balakshy and Kostyuk, 2009;

Balakshy, 2018).

The confocal AOTF scheme, Fig. 5, can process

optical images in dark ﬁeld mode that enables phase

imaging. Coherent phase imaging system is a bright-

ﬁeld light microscope with narrowband object illumi-

nation and a confocal hyperspectral imaging system

placed at the microscope output optical port (Yushkov

et al., 2016). Changing the frequency of ultrasound,

one can select the spatial frequency transmitted by

the AOTF and therefore to change object visualiza-

tion mode.

Phase imaging with broadband incoherent illumi-

nation requires a system modiﬁcation since differ-

ent wavelength of the input light will be efﬁciently

diffracted at different spatial frequencies. When a

plane wave passes through a phase object its an-

gular spectrum is broadened because of scattering.

Lower spatial frequencies of the optical beam are

blocked by a spatial light modulator (SLM) placed

PHOTOPTICS 2022 - 10th International Conference on Photonics, Optics and Laser Technology

Figure 8: Demonstration of acousto-optic phase imaging:

(a) reference image captured with an RGB camera; (b)

bright-ﬁeld spectral image; (c) dark-ﬁeld phase image; (d)

false-color fusion of amplitude-and-phase modulation. Re-

produced under Open Access Licence from (Yushkov et al.,

2020a),

2020 OSA.

in a Fourier-conjugated plane of the system (Yushkov

et al., 2019a; Yushkov et al., 2020a). Higher spatial

frequencies that contain only the scattered light are

transmitted to satisfy dark ﬁeld phase imaging prin-

ciple. Then the conical beam is spectrally ﬁltered by

the AOTF. According to the phase matching surface

symmetry, all components of the conical beam are

diffracted by the AOTF within the same wavelength

window. Matched spectral and spatial ﬁltering results

in high resolution wide-ﬁeld phase imaging.

When the spatial light modulator is switched off,

the AOTF operates in a regular bright-ﬁeld spectral

imaging mode. That allows correct calibration of

phase imaging and false-color fusion of phase-and-

amplitude modulation. An example of phase imaging

is shown in Fig. 8.

3.2 Optical Trapping

The phenomenon of optical trapping has been known

for four decades (Ashkin, 1992). The range of appli-

cation of optical traps and tweezers covers many dis-

ciplines ranging from microbiology to manipulation

of cold atoms. The technology of optical traps is con-

stantly being improved, and recently a need has arisen

for dynamical generation of various geometrical con-

ﬁgurations of optical traps, which requires advanced

methods of laser beam shaping. One of such meth-

ods is a noncollinear AOTF based laser beam shap-

ing. The use of several frequencies to feed the AOTF

makes it possible to synthesize various radial ﬁeld dis-

tributions and to tune them with sub-10-µs response

time.

Experimental setup of a ring-shaped optical trap

is shown in Fig. 9 (Obydennov et al., 2021a; Oby-

dennov et al., 2021b). The optical scheme is a modi-

ﬁed Fourier-transform scheme, Fig. 5 (b), with an ad-

ditional relay lens group between the AOTF and the

second Fourier lens. The relay optics performs laser

beam magniﬁcation and transport from the AOTF to

the back focal plane of a microscope objective, which

is the second Fourier lens. Thus, the angular aper-

ture of the AOTF was matched with the aperture of

Figure 9: Optical trapping setup based on a noncollinear

AOTF: CCD — imaging camera; DM — long-pass dichroic

mirror; L1, L2, L3 — lenses; LED — light emitting diode

for illumination; MO — microscope objective; P — thin-

ﬁlm polarizer; green arrows — laser beam path at 532 nm;

cyan arrows — illumination path at 460 nm.

the objective. Laser radiation with the wavelength of

532 nm was used. Passing through the expander, the

laser beam was focused by means of a Fourier lens

into the volume of a noncollinear paratellurite AOTF

specially optimized and fabricated for this work. The

operating frequency of the ﬁlter in the wide-aperture

diffraction geometry is 132.35 MHz, the bandwidth

is 0.24 MHz. The 0

diffraction order at the AOTF

output was blocked by a thin-ﬁlm polarizer. The ob-

jective converted the ring-shaped angular spectrum of

the beam into spatial intensity distribution, which ex-

poses the sample.

The sample was a suspension of polystyrene mi-

crospheres with an average diameter of 10 µm. The

liquid phase of the suspension was deionized water

with the addition of a liquid antiseptic and a surfactant

to prevent adhesion. The suspension was placed in a

special reaction cell made of cover glass. To visualize

the sample, we used a transmission K

ohler illumina-

tion system with a blue diode light source. Passing

through the sample, the radiation was collected by an

objective and imaged onto on the CCD matrix through

a dichroic mirror and a tube lens.

Demonstration of the annular trap operation is

shown in Fig. 10. The radius of the trapping ring was

controlled by changing the RF signal frequency in the

range from 132.4 to 134.0 MHz. A programmable

AWG was used for this purpose. Panel (a) shows

opration of the trap in a static mode, the radius of the

ring being ﬁxed. In this particular example, the mi-

crospheres are arranged in a circle with the radius of

80 µm at F = 134.0 MHz. A dynamic trap is shown

in panels (b) and (c): the RF signal had sawtooth fre-

quency sweep resulting in generation of a series of

convergent or divergent trapping rings. As the result,

the microspheres were either aggregated in the center

of the trap or repulsed from the center.

Acousto-optic k-space Filtering of Optical Beams

Figure 10: Optical trapping demonstration: (a) static single-ring trap; (b) aggregation of particles by dynamic converging-ring

trap; (c) disaggregation of particles by dynamic diverging-ring trap.

4 DISCUSSION

Diffraction efﬁciency of an AOTF is one of the key

performance parameters in applications. According

to Eq. 1, for a plane wave component without mis-

match max H

= 1 when Q = 1 and R(k

;F) = 0.

In practice, the efﬁciency can be rather close to 1.

Visualization of the 0

diffraction order in Fig. 1

demonstrates overall efﬁciency above 98% within the

whole active aperture of the AOTF. Thus, overall op-

tical losses in the AOTF including Fresnel reﬂections

can be well below 5% for linearly polarized light.

In optical beam shaping applications described in

Sec. 3 the beams are spatially ﬁltered by the AOTF,

thereby the overall throughput is an integral of the op-

tical beam angular spectrum multiplied by the trans-

fer function H

. In the case of phase imaging, the

optical beam is pre-ﬁltered by the dark-ﬁeld Fourier-

plane ﬁlter implemented on the SLM. Therefore an-

gular spectrum of the beam is already matched with

the annular AOTF transfer function and the polariza-

tion at the SLM output is linear as required for the

AOTF. In the case of annular optical trap, a Gaussian

input beam was used at the AOTF input. For this rea-

son, lower spatial frequencies of the beam were not

used and the diffracted beam intensity was few per-

cent of the input beam even though the diffraction efﬁ-

ciency for phase-matched components of the angular

spectrum was above 95%. Optimization of the sys-

tem throughput by means of refractive ﬂat-top beam

shaping (Laskin et al., 2011; Dickey, 2014) before the

AOTF will be a plot for future work.

Another potential advancement in AOTF-based

laser beam shaping is related to using biaxial crys-

tals. The topology of the transfer function depends

on local curvature of the optical wave normal surface

in the phase matching region of the k-space (Yushkov

and Naumenko, 2021). In a uniaxial crystal, there are

only three types on the NPM transfer function, one

of them being the annular transfer function discussed

in this work. In biaxial crystals, the geometry of the

wave normal surface is more complicated, and other

topologies of the transfer function may exist enabling

asymmetrical transfer functions, one dimensional tun-

able k-space ﬁltering, and high-order NPM geome-

tries.

ACKNOWLEDGEMENTS

The author thanks contributions to this work from the

Acousto-Optical Research Center team.

The research was supported by the Russian Sci-

ence Foundation (RSF) under project 21-12-00247.

REFERENCES

Ashkin, A. (1992). Forces of a single-beam gradient laser

trap on a dielectric sphere in the ray optics regime.

Biophys. J., 61(2):569–582.

Balakshy, V. (1984). Acoustooptical cell as the space fre-

quency ﬁlter. Sov. J. Commun. Technol. Electron.,

29(8):1610–1616.

Balakshy, V. (2018). Acousto-optic visualization of optical

wavefronts. Appl. Opt., 57(10):C56.

Balakshy, V. and Kostyuk, D. (2009). Acousto-optic image

processing. Appl. Opt., 48(7):C24.

Balakshy, V. and Voloshinov, V. (2005). Acousto-optic im-

age processing in coherent light. Quantum Electron.,

35(1):85–90.

Dickey, F., editor (2014). Laser Beam Shaping: Theory and

Techniques. CRC Press, Boca Raton, FL, 2nd edition.

Genchi, L., Bucci, A., Laptenok, S., Giammona, A., and

Liberale, C. (2021). Hadamard-transform spectral

acquisition with an acousto-optic tunable ﬁlter in a

broadband stimulated raman scattering microscope.

Opt. Express, 29(2):2378–2386.

Goodman, J. (2005). Introduction to Fourier Optics.

Roberts, New York, 3rd edition.

Gorevoy, A., Machikhin, A., Martynov, G., and Pozhar,

V. (2021). Spatiospectral transformation of noncol-

PHOTOPTICS 2022 - 10th International Conference on Photonics, Optics and Laser Technology

limated light beams diffracted by ultrasound in bire-

fringent crystals. Photonics Res., 9(5):687.

Korablev, O., Belyaev, D., Dobrolenskiy, Y., Trokhi-

movskiy, A., and Kalinnikov, Y. (2018). Acousto-

optic tunable ﬁlter spectrometers in space missions.

Appl. Opt., 57(10):C103–C119.

Laskin, A., Shcherbakov, A., Molchanov, V., Laskin, V.,

and Makarov, O. (2011). Developing the refractive

light beam shapers as lossless apodization systems

suppressing the side-lobes in Fourier transform opti-

cal systems. Proc. SPIE, 8011:80110L.

Lu, G. and Fei, B. (2014). Medical hyperspectral imaging:

a review. J. Biomed. Opt., 19(1):010901.

Obydennov, D., Yushkov, K., and Molchanov, V. (2021a).

Acousto-optic annular beam shaping for optical traps

and lattices. Proc. SPIE, 11926:1192610.

Obydennov, D., Yushkov, K., and Molchanov, V. (2021b).

Ring-shaped optical trap based on acousto-optic tun-

able spatial ﬁlter. Opt. Lett., 46(18):4494.

Suhre, D., Denes, L., and Gupta, N. (2004). Telecentric

confocal optics for aberration correction of acousto-

optic tunable ﬁlters. Appl. Opt., 43(6):1255–1260.

Yariv, A. and Yeh, P. (1984). Optical Waves in Crystals.

Wiley, New York.

Yushkov, K. (2021). Noncritical acousto-optic Bragg phase

matching: Analysis of orthorhombic and monoclinic

crystal systems. Appl. Opt., 60(24):7113.

Yushkov, K., Champagne, J., Kastelik, J.-C., Makarov, O.,

and Molchanov, V. (2020a). AOTF-based hyperspec-

tral imaging phase microscopy. Biomed. Opt. Express,

11(12):7053.

Yushkov, K., Champagne, J., Kastelik, J.-C., and

Molchanov, V. (2019a). Hyperspectral phase imaging

with a spatially matched acousto-optical tunable ﬁlter.

Proc. SPIE, 10890:108900V.

Yushkov, K., Chizhikov, A., Makarov, O., and Molchanov,

V. (2020b). Optimization of noncollinear AOTF de-

sign for laser beam shaping. Appl. Opt., 59(27):8575.

Yushkov, K., Gurov, V., and Molchanov, V. (2021a). En-

gineering of aotf transfer function for phase imaging

microscopy and optical trapping. In European Confer-

ences on Biomedical Optics 2021 (ECBO), OSA Tech-

nical Digest, page ETu3B.5, Munchen, Germany. Op-

tical Society of America.

Yushkov, K., Makarov, O., and Molchanov, V. (2019b).

Novel protocol of hyperspectral data acquisition by

means of an acousto-optical tunable ﬁlter with synthe-

sized transmission function. Opt. Lett., 44(6):1500.

Yushkov, K., Molchanov, V., Balakshy, V., and Mant-

sevich, S. (2018). Acousto-optical transfer func-

tions as applied to laser beam shaping. Proc. SPIE,

10744:107440Q.

Yushkov, K., Molchanov, V., Belousov, P., and Abrosi-

mov, A. (2016). Contrast enhancement in microscopy

of human thyroid tumors by means of acousto-

optic adaptive spatial ﬁltering. J. Biomed. Opt.,

21(1):016003.

Yushkov, K., Molchanov, V., and Khazanov, E. (2021b).

Uncertainty relation in broadband laser pulse shaping.

Phys. Uspekhi, 64(8):828.

Yushkov, K. and Naumenko, N. (2021). Optical beam

diffraction tensor in birefringent crystals. J. Opt.,

60(9):095602.

Acousto-optic k-space Filtering of Optical Beams