Predicting the Intended Action using Internal Simulation of Perception

Zahra Gharaee

Computer Vision Laboratory (CVL), Department of Electrical Engineering,

University of Link

oping, 581 83 Link

oping, Sweden

Keywords:

Intention Prediction, Internal Simulation, Self-organizing Neural Networks, Action Recognition, Cognitive

Architecture.

Abstract:

This article proposes an architecture, which allows the prediction of intention by internally simulating per-

ceptual states represented by action pattern vectors. To this end, associative self-organising neural networks

(A-SOM) is utilised to build a hierarchical cognitive archi- tecture for recognition and simulation of the skele-

ton based human actions. The abilities of the proposed architecture in recognising and predicting actions is

evaluated in experiments using three different datasets of 3D actions. Based on the experiments of this article,

apply- ing internally simulated perceptual states represented by action pattern vectors improves the perfor-

mance of the recognition task in all experiments. Furthermore, internal simulation of perception addresses

the problem of having limited access to the sensory input, and also the future prediction of the consecutive

perceptual sequences. The performance of the system is compared and discussed with similar architecture

using self-organizing neural networks (SOM).

1 INTRODUCTION

For efﬁcient Human-Robot-Interaction, it is important

that the robot can predict the behaviour of the human,

at least for the nearest future. In Human-Human in-

teraction we do this by reading the intentions of oth-

ers. This is done using our capacity for mind reading,

intention recognition is one of the core processes of

mind reading (Bonchek-Dokow and Kaminka, 2014),

where we simulate the thoughts of others. We can

predict about behavior and mental states of another

person based on our own behavior and mental states

if we were in his/her situation. This occurs by simu-

lating another person’s actions and the stimuli he/she

is experiencing using our own behavioral and stim-

ulus processing mechanisms (Breazeal et al., 2005;

Bonchek-Dokow and Kaminka, 2014). The overar-

ching question of this article is to develop a compu-

tational model of an artiﬁcial agent for intention pre-

diction, the ability to extend an incomplete sequence

of actions to its most likely intended goal.

1.1 Theoretical Background

The perceptual processes normally elicited by some

ancillary input can be mimicked by the brain (Hess-

https://orcid.org/0000-0003-0140-0025

low, 2002). This relates to an idea that higher organ-

isms are capable of simulating perception, which is

supported by a large number of evidences. As shown

by several neuroimaging experiments, the activity in

visual cortex when a subject imagines a visual stimu-

lus resembles the activity elicited by a corresponding

ancillary stimulus (Kosslyn et al., 2001; Bartolomeo,

2002).

The idea of perceptual simulation can help in at

least two major applications in a perceptual system.

First is the internal simulation when there is a lim-

ited access to the sensory input, and second is the

future prediction of the consecutive perceptual se-

quences. According to (Johnsson et al., 2009), the

subsystems of different sensory modalities of a multi-

modal perceptual system are associated with one an-

other. Therefore, suitable activity in some modalities

that receive input can elicit activity in other sensory

modalities as well. The ability of internal simula-

tion can facilitate the activation in the subsystems of a

modality even when there is no or limited sensory in-

put but instead there is activity in subsystems of other

modalities.

Moreover, in different perceptual subsystems

there is a capacity to elicit continued activity even in

the absence of sensory input. In other words, the per-

ceptual process does not stop when the sensory input

is blocked but rather continues by internally simulate

626

Gharaee, Z.

Predicting the Intended Action using Internal Simulation of Perception.

DOI: 10.5220/0010977600003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 626-635

ISBN: 978-989-758-547-0; ISSN: 2184-433X

 2022 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

the sequences of perceptions as proposed in the neu-

roscientiﬁc simulation hypothesis (Hesslow, 2002).

This continuity is an important feature of a perceptual

system especially for the circumstances in which the

connection to the sensory input is somehow reduced.

Empirical studies of rodents’ memory have also

shown that the hippocampus stores and reactivates

episodic memories ofﬂine (Stoianov et al., 2020).

Based on these ﬁndings, the rodent hippocampus in-

ternally simulates neural activations (so called re-

plays) in phases of wakeful rest during spatial navi-

gation, as well as during subsequent sleep, which re-

semble sequences observed during animal’s real ex-

periences (Buzs

aki, 2015).

Since, these internally simulated hippocampal se-

quences during sleeping or wakeful resting depict

paths to future goals rather than only past trajecto-

ries, it is hard to believe that the hippocampus does

only “replay” past experiences of a memory buffer.

Therefore, it can somehow be considered in the role of

planning and imagination (Pfeiffer and Foster, 2013);

trajectories that have never been directly explored but

yet reﬂect prior spatial knowledge (Liu et al., 2018;

Dragoi and Tonegawa, 2013) or for future event loca-

tions (

Olafsd

ottir et al., 2015).

To demonstrate this feature of hippocampus, a hi-

erarchical generative model of hippocampal forma-

tion is proposed in (Stoianov et al., 2020), which or-

ganizes sequential experiences to a set of coherent

but mutually exclusive spatio-temporal contexts (e.g.,

spatial maps). They have also proposed that the in-

ternally generated hippocampal sequences stem from

generative replay, or the ofﬂine re-sampling of ﬁctive

experiences from the generative model.

More importantly, the continuous perceptual sim-

ulation mechanism can facilitate the anticipation of

future sequences of perceptions, the prediction, that

normally follows a certain perception within a modal-

ity, and also over different modalities. This occurs

only if the modalities are associated in an appropri-

ate manner. For example, a thunder light seen, would

yield an anticipation of hearing a sound to be followed

soon.

However, prediction of future sequences of per-

ception is extremely important in different aspects of

life such as rational decision making or social inter-

action. Recent developments in the conceptualization

of the brain processing have shown the predictive na-

ture of the brain, the predictive coding or predictive

processing views ((Clark, 2013; Friston, 2010)).

In fact, many perceptual phenomena can only be

understood by assuming that meaningful perception

is not just a matter of processing incoming informa-

tion, but it is largely reliant on prior information since

the brain often unconsciously and compellingly as-

sumes (or infers) non-given information to construct

a meaningful percept (Pezzulo et al., 2019). From a

neuroscience perspective also, the theory of ”predic-

tive coding” ((Friston, 2005)) describes how sensory

(e.g., visual) hierarchies in the brain may combine

prior knowledge and sensory evidence, by continu-

ously exchanging top-down (predictions) and bottom-

up (prediction error) signals.

An important application of predictive processing

lies in the recognition of others’ distal intentions. This

plays a substantial role in recognizing actions per-

formed by others in advance to be prepared for plan-

ning to make an appropriate reaction for example in

the case of social interactions.

A computationally-guided explanation of distal

intention recognition derived from theories of compu-

tational motor control is proposed by (Donnarumma

et al., 2017). Based on the control theory (Pezzulo

and Cisek, 2016), proximal actions have to simultane-

ously fulﬁll the concurrent demands of ﬁrst-order as

well as higher-order planning. As an example, in per-

forming action ’grasping an object’, ﬁrst-order plan-

ning determines object handling grasp trajectory ac-

cording to immediate task demands (e.g., tuning to

the orientation or the grip size for an object to be

grasped) while the higher-order planning alters one’s

object manipulation behavior not only on the basis of

immediate task demands but also on the basis of the

next tasks to be performed. Based on this view, it is

necessary to simultaneously optimize proximal com-

ponents of an action like reaching and grasping a bot-

tle as well as distal components (intentions) of an ac-

tion sequence such as pouring water or rather moving

the bottle.

On the other hand, based on the affordance com-

petition hypothesis (Cisek, 2007), the processes of ac-

tion selection (what to do?) and speciﬁcation (how

to do it?) occur simultaneously and continue even

during overt performance of movements. Accord-

ing to this hypothesis, complete action plans are not

prepared for all possible actions at a given moment.

There are only actions speciﬁed, which are currently

available ﬁrst and next many possible actions are

eliminated from processing through selective atten-

tion mechanisms. Attention processing limits the sen-

sory information that is transformed into representa-

tions of action.

Therefore, according to affordance competition

hypothesis (Cisek, 2007), complete action planning is

not proposed even for the ﬁnal selected action. Even

in cases of highly practiced behaviours, no complete

pre-planned motor program or the entire desired tra-

jectory appears to be prepared. This hypothesis em-

Predicting the Intended Action using Internal Simulation of Perception

627

phasises on a continuous simultaneously processing

of action selection and speciﬁcation until the ﬁnal

goal is achieved.

According to (Vinanzi et al., 2019) there is a pre-

liminary distinction between goal and intention. The

goal represents a ﬁnal desired state while the intention

incorporates both a goal and an action plan to achieve

it. Knowing this distinction, in both approaches pre-

sented above (Donnarumma et al., 2017; Cisek, 2007)

human is involved in an ongoing process of simulta-

neous planning for selecting and performing the ac-

tions required to address an intention or to achieve a

particular goal.

Prediction of future sequences of state and the in-

ternal simulation of the self-or the other’s perception

(reading the other’s intention) facilitates this ongoing

process by providing a priori-knowledge about the fu-

ture. One way to model the internal simulation of per-

ception is to apply Associative Self-Organizing Map

(A-SOM) neural networks (Johnsson et al., 2009).

This model is developed and utilized in a number of

applications such as action simulation and discrimi-

nation (Buonamente et al., 2015; Buonamente et al.,

2013), letters prediction in text (Gil et al., 2015) and

music simulation (Buonamente et al., 2018).

1.2 Applications of Reading Intention

There are a number of approaches performing some

practical applications to somehow address the prob-

lem of robots reading intentions. Among them there

is the Hierarchical Attentive Multiple Models for Ex-

ecution and Recognition (HAMMER) architecture as

a representative example of the generative embodied

simulationist approach to understanding intentions

(Demiris, 2007). HAMMER uses an inverse–forward

model coupling in a dual role: either for executing an

action, or for perceiving the same action when per-

formed by a demonstrator, the imitator processes the

actions by analogy with the self—“what would I do if

I were in the demonstrator’s shoes?”.

Another approach proposed by (Dominey and

Warneken, 2011) is built to test the cooperation, a

robotic system for cooperative interaction with hu-

mans in a number of experiments designed to play

game in collaboration. A probabilistic hierarchical

architecture of joint action is presented in (Dindo

and Chella, 2013), which models the casual relations

between observables (movements) and their hidden

causes (goals, intentions and beliefs) in two levels: at

the lowest level the same circuitry used to execute the

self-actions is re-enacted in simulation to infer and

predict actions performed by the partner, while the

highest level encodes more abstract representations,

which govern each agent’s observable behavior.

The study presented in (Sciutti et al., 2015) pro-

poses taking into consideration the human (and robot)

motion features, which allow for intention reading

during social interactive tasks. In (Vinanzi et al.,

2019) a cognitive model is developed to perform in-

tention reading on a humanoid partner for collabo-

rative behavior towards the achievement of a shared

goal by applying the experience.

Using intention inference to predict actions per-

formed by others is proposed in a Computational

Cognitive Model (CCM) inspired by the biological

mirror neurons (Ang et al., 2012), which applies sim-

ulation theory concept of perspective changing and

how one’s decision making mechanism can be in-

ﬂuenced by mirroring other’s intentions and actions.

The method presented in (Karasev et al., 2016) also

predicts long-term pedestrian motions by using the

discrete-space models applied to a problem in con-

tinuous space.

Recognizing plans together with the actions per-

formed, by developing a hybrid model is proposed in

(Granada et al., 2017), which combines a deep learn-

ing architecture to analyze raw video data to identify

individual actions and process them later by a goal

recognition algorithm using a plan library to describe

possible overarching activities. Inferring and predic-

tion of intentions for communicative purposes is done

in other approaches like; the prediction of intentions

in gaze-based interactions (Bednarik et al., 2012),

inferring communicative intention from images (Joo

et al., 2014) and predicting human intentions and tra-

jectories in video streams (Xie et al., 2017).

2 PROPOSED ARCHITECTURE

Action recognition architecture, ﬁgure(1), is consists

of ﬁve layers: preprocessing layer, A-SOM layer, or-

dered vector representation layer, SOM layer and the

output layer. Shown by ﬁgure(1), native input is com-

posed of consecutive 3D posture frames and external

input is the activity map of A-SOM layer. It is pos-

sible to use different types of input data as the exter-

nal input. For example, the main modality of a sys-

tem like vision can produce the native input and other

modalities like auditory or olfactory can be used to

generate external inputs. Learning of A-SOM layer is

done using native and external inputs.

Training A-SOM layer, original pattern vectors of

action sequences are created using total activity of

the network. An original pattern vector is created by

connecting consecutive activation of neural map when

consecutive posture frames are received as the native

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

628

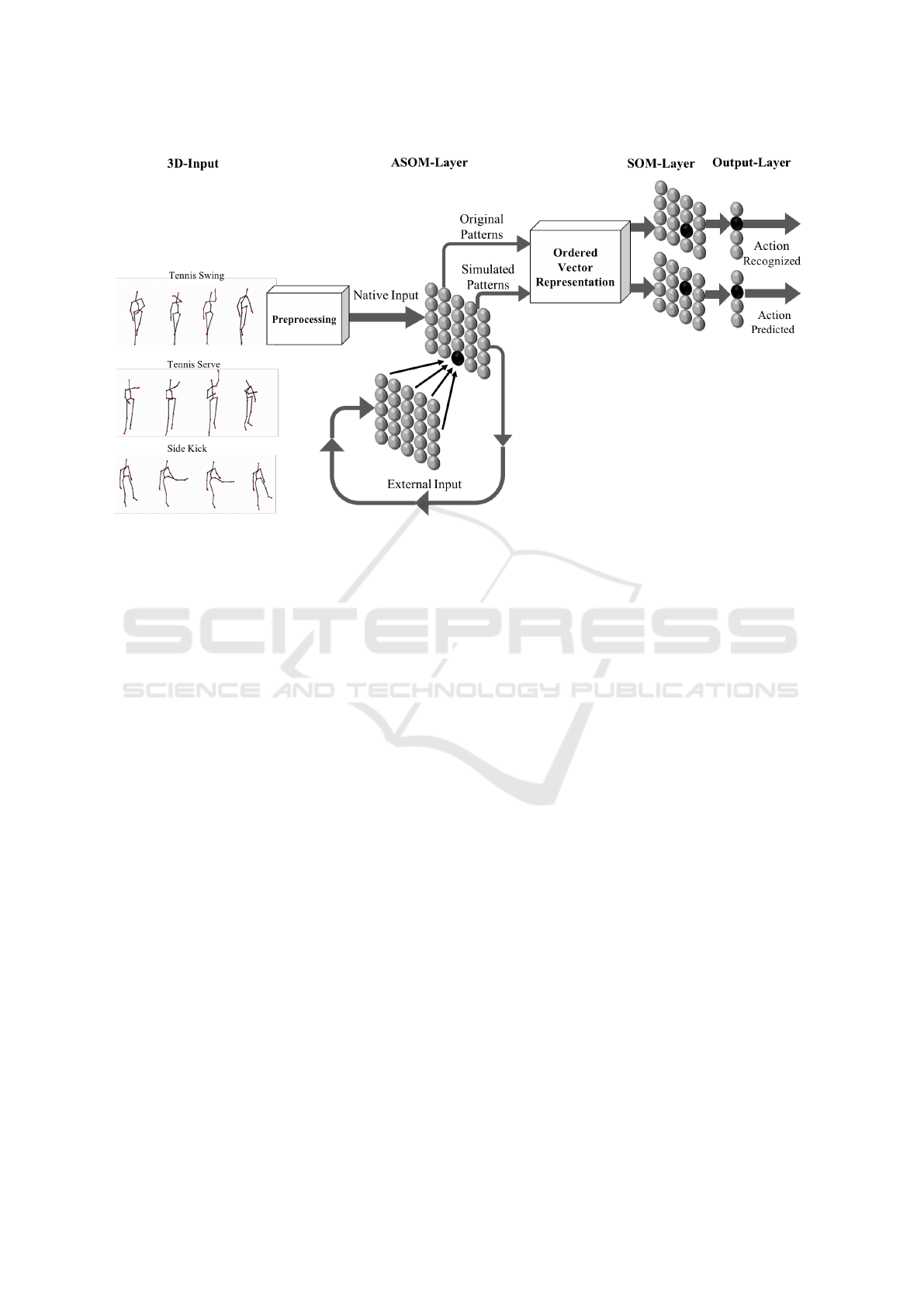
Figure 1: The architecture proposed using ASOM neural networks.

input by the network. Simulated pattern vectors are

generated using external inputs only. To this end, par-

tial native input is received by trained A-SOM.

The original as well as simulated patterns are next

received by ordered vector representation layer to pro-

duce time invariant action pattern vectors as, which is

given to SOM- and output layers. Finally, action pre-

dicted from original patterns is compared with the one

predicted from simulated patterns.

2.1 Input Data and Preprocessing

The input space is composed of 3D skeleton-based

human actions sequences captured by Kinect sensor.

Each dataset contains a number of action sequences

while each sequence is composed of consecutive pos-

ture frames. Every posture frame contains 3D infor-

mation of skeleton joints, shown in ﬁgure(1).

Preprocessing layer uses three main functions to

process input data: ego-centered coordinate trans-

formation, scaling and attention mechanism. Ego-

centered coordinate system is to make a human pos-

ture invariant of having different orientations towards

the camera while acting. Scaling function used to

similarly scale all posture frames to be invariant of

having different distances to the camera. Attention

mechanism selects skeleton joints based on their ve-

locity, the joints moving the most play the main role

in acting. A thorough description about the design

and implementation of the preprocessing functions is

presented in (Gharaee, 2020a). The presentation of

this layer is not among the main scopes of this article.

2.2 A-SOM Layer

A-SOM neural network of this paper is a self-

organizing map (SOM), which learns to associate its

native activity from the native input with a number of

external activities from a number of external inputs.

The input to the system at each time step t is:

X(t) =

{

(t),x

(t),..., x

(t)

}

, (1)

where x

(t) ∈ R

is the native input received by

the main SOM and x

(t) ∈ R

and 1 < i < r are the

r external inputs received by the r number of external

SOMs.

The network consists of an I × J grid of neurons

with a ﬁxed number of neurons and a ﬁxed topol-

ogy. Each neuron n

i j

is associated with r + 1 weight

vectors, among them one weight vector, w

i j

∈ R

, is

used to parametrize native input and the remaining r

weight vectors, w

i j

∈ R

i j

∈ R

,..., w

i j

∈ R

are used to parametrize external inputs. Weight vec-

tors are initialized by real numbers randomly selected

from a uniform distribution between 0 and 1.

At each time step, the network receives input

shown by (1) and the native input of each neuron rep-

resenting the distance to the input vector is calculated

based on the Euclidean metric as:

i j

(t) = ||x

(t) − w

i j

(t)||

, (2)

where ||.|| shows l

norm. The native activity is

calculated by applying an exponential function to the

Predicting the Intended Action using Internal Simulation of Perception

629

native input and passing it over a soft-max function

computed as:

i j

(t) =

exp

i je

max

k∈I×J

exp

i je

, (3)

where z

i je

= exp(

−z

i j

(t)

) and σ is the exponential

factor to normalize and increase the contrast between

highly activated and less activated areas, k ranges

over the neurons of the network grid and s

exp

shows

the soft-max exponent. The external activities cor-

responding to the external inputs are also calculated

based on the Euclidean metric:

i j

(t) = e

−||x

(t)−w

i j

, (4)

where p ranges over the external inputs 1 < p < r

and σ is the exponential factor to normalize and in-

crease the contrast between highly activated and less

activated areas. Having the native activity shown by

(3) and external activities shown by (4), the total ac-

tivity of the network is calculated as:

i j

(t) =

r + 1

i j

(t) +

p=r

∑

p=1

i j

(t)

. (5)

Next is to ﬁnd the winning neuron n

based of the

network total activity Y

i j

as:

= argmax

i j

(t), (6)

where i and j ranges over the rows and columns of

the network grid. By calculating the winner the native

weights are tuned by:

i j

(t + 1) = w

i j

(t) + α(t)G

i jw

(t)



(t) − w

i j

(t)



(7)

The term 0 ≤ α(t) ≤ 1 shows the learning adap-

tation strength, which starts with a value close to 1

and decays by time as α(t) → α

min

when t → ∞. The

neighborhood function G

i jw

(t) = e

−

||d

−d

i j

2ρ

(t)

(t) is a

Gaussian function decreasing with time, and d

∈ R

and d

i j

∈ R

are location vectors of winner n

and

neuron n

i j

respectively. The term ρ(t) also shows

adaptation over the neighborhood radius, which starts

with full length of the grid and decays by time as

ρ(t) → ρ

min

when t → ∞. Thus the winner neuron

receives the strongest adaptation and the adaptation

strength decreases by increasing distance from the

winner. As a result the further the neurons are from

the winner, more weakly their weights are updated.

The weights of the external inputs on the other hand

are updated as the following:

i j

(t + 1) = w

i j

(t)+ β(t)x

(t)

i j

(t) − y

i j

(t)

, (8)

where β(t) is a constant adaptation strength and p

ranges over the external inputs 1 < p < r.

2.3 Ordered Vector Representation

Layer

This layer is designed to create input data to SOM-

layer (Gharaee, 2020a) by extracting unique activa-

tion patterns of A-SOM-layer and segmenting them

into the vectors having equal number of activity seg-

ments. Therefore, it conducts two operations, ﬁrst the

subsequent repitition of similar activations is mapped

into a unique activation and then, all action pattern

vectors are ordered to represent vectors of equal ac-

tivity segments.

To this end, pattern vector with the maximum

number of activations is extracted and the number

of its activations is calculated by K

max

= max

∈V

where v

shows one activity pattern vector, V shows

the set of all activity pattern vectors and k

represents

the number of activations of v

The goal is to increase the number of activations

for all activity pattern vectors to K

max

by inserting

new activations while preserving spatial geometry of

the original pattern vectors trained by A-SOM layer.

Therefore, for each activity pattern vector, the approx-

imately optimal distance d

between two consecutive

activations is calculated as:

max

N−1

∑

n=1

n+1

− a

, (9)

where a

= [x

] is an activation in the 2D map

and N shows the total number of activations for the

corresponding activity pattern vector.

To ﬁnd the location of a new insertion, the dis-

tance between a consecutive pair of activations is cal-

culated using `

norm as d

n+1

− a

and if

> d

, new activation a

is inserted on the line

connecting a

to a

n+1

with a distance of d

from a

through solving system equation of:

sys =

(

(1) :

−y

n+1

−y

−x

n+1

−x

(2) :

− a

= d

(10)

where a

= [x

] and a

n+1

= [x

n+1

] and

= [x

If d

< d

, new activation a

is inserted on the

line connecting a

n+1

to a

n+2

with a distance of d

− d

from a

n+1

solving system equations of:

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

630

sys =

(

(3) :

−y

n+1

n+2

−y

n+1

−x

n+1

n+2

−x

n+1

(4) :

− a

n+1

= d

(11)

and, a

n+1

is removed from the corresponding pat-

tern vector.

Insertion of new activations continues until the to-

tal number of activity segments of the corresponding

pattern vector becomes equal to K

max

2.4 SOM Layer

The SOM-layer used in this article designed with a

grid of I ×J neurons with a ﬁxed number of neurons

and a ﬁxed topology. Each neuron n

i j

is associated

with a weight vector w

i j

∈ R

having the same dimen-

sion K as the input vector x(t). For a squared SOM

the total number of neurons is the number of rows

multiply by the number of columns. All elements of

the weight vectors are initialized by real numbers ran-

domly selected from a uniform distribution between 0

and 1.

At time t, each neuron n

i j

receives the input vec-

tor x(t) ∈ R

. The net input z

i j

(t) = ||x(t) − w

i j

(t)||

at time t is calculated based on the Euclidean met-

ric. Activation of each neuron is calculated using (3)

while y

i j

(t) = y

i j

(t). Applying activity matrix Y

i j

(t),

winning neuron having the strongest activation value

is received using (6) and, therefore, weight vectors of

all neurons w

i j

are adapted using (7).

2.5 Output Layer

The output layer is designed as one-layer supervised

neural network, which receives as its input the activ-

ity traces of the SOM-layer. The output-layer consists

of a number of neurons N and a ﬁxed topology. The

number N is determined by the number of classes rep-

resenting actions names. Each neuron n

is associated

with a weight vector w

∈ R

. All the elements of

the weight vector are initialized by real numbers ran-

domly selected from a uniform distribution between

0 and 1, after which the weight vector is normalized,

i.e. turned into unit vectors.

At time t each neuron n

receives an input vector

x(t) ∈ R

. The activity y

of the neuron n

is calculated

using the standard cosine metric:

x(t) · w

(t)

||x(t)||.||w

. (12)

During the learning phase the weights w

are

adapted as:

(t + 1) = w

(t) + γx(t) [y

− d

], (13)

Table 1: Table shows settings of the parameters of the ar-

chitecture. α, β and ρ are initialized according to the initial

values α

, β

and ρ

and updated by decay values α

, β

and

using (14), until they approach a ﬁnal value, α

, β

and

Hyper-Parameter-Settings

Parameters A-SOM SOM

Neurons 900 1600

σ 10

exp

10 10

, α

0.1, 0.99, 0.01 0.1, 0.99, 0.01

, ρ

30, 0.999, 1 30, 0.999, 1

, β

0.35, 1.0, 0.01 -

Metric Euclidean Euclidean

Epoch 300 1500

where γ is a constant adaptation strength and is set

to 0.35. The term y

is the predicted activation by the

network and d

is the desired activation of neuron n

3 EXPERIMENTS

In this section the experiments showing the accuracy

of the architecture are presented. To this end, three

skeleton based action datasets are used to run the ex-

periments. All settings of the system hyperparameters

are shown in Table (1). According to Table (1), α, β

and ρ are calculated at each time step using:

X(t) ← X

− X(t)) + X (t), (14)

where X(t) shows the values of the changing parame-

ters, α, β and ρ, at current time step t, X

shows ﬁnal

values of the parametrs and X

is a decaying rate.

Input. Input data is composed of consecutive pos-

ture frames of skeleton represented by 3D joint posi-

tions captured by a Kinect sensor shown in ﬁgure(1).

Three datasets of actions are presented in the follow-

ing. For all experiments, 10-fold cross validation ap-

proach is used to split a dataset into training, vali-

dation and test sets. To this end, a test set contain-

ing 25% of action sequences is randomly selected for

each dataset. The remaining 75% of action sequences

are randomly splitted into 10 folds through which one

is used for validation and the remaining are used for

training the system. The best performing model on

the validation set in terms of recognition accuracy is

ﬁnally selected and tested on the test set.

MSRAction3D 1 dataset by (Wan, 2015) contains

287 action sequences of 10 different actions per-

formed by 10 different subjects in 2 to 3 different

events. The actions are performed using whole body

of the performer, arms as well as legs. Each posture

Predicting the Intended Action using Internal Simulation of Perception

631

frame contains 20 joint positions represented by 3D

Cartesian coordinates. The actions are: 1.Hand Clap,

2.Two Hands Wave, 3.Side Boxing, 4.Forward Bend,

5.Forward Kick, 6.Side Kick, 7.Still Jogging, 8.Ten-

nis Serve, 9.Golf Swing, 10.Pick up and Throw.

MSRAction3D 2 dataset (Wan, 2015) contains

563 action sequences achieved of 20 different ac-

tions performed by 10 different subjects in 2 to 3 dif-

ferent events. The actions are: 1.High Arm wave,

2.Horizontal Arm Wave, 3.Using Hammer, 4.Hand

Catch, 5.Forward Punch, 6.High Throw, 7.Draw X-

Sign, 8. Draw Tick, 9. Draw Circle, 10.Tennis Swing,

11.Hand Clap, 12.Two Hands Wave, 13.Side Boxing,

14.Forward Bend, 15.Forward Kick, 16.Side Kick,

17.Still Jogging, 18.Tennis Serve, 19.Golf Swing,

20.Pick up and Throw.

Florence3DActions dataset by (Seidenari et al.,

2013) contains 215 action sequences of 9 different

actions performed by 10 different subjects in 2 to 3

different events. This dataset consist of 3D Carte-

sian coordinates of 15 skeleton joints. The actions

are: 1.Wave, 2.Drink from a Bottle, 3.Answer Phone,

4.Clap Hands, 5.Tight Lace, 6.Sit down, 7.Stand up,

8.Read Watch, 9.Bow. The actions are

Experiments are designed and implemented to

present the ability to recognize human actions and

to compare it with SOM architecture proposed in

(Gharaee et al., 2017a). Next, there are illustrations

showing the internally simulated action patterns com-

pared with the original ones. Finally, the accuracy of

the architecture in predicting intended actions using

simulated perception is presented and compared with

the results when using the original perception.

Action Recognition. To evaluate the ability of the

system in action recognition tasks, experiments are

designed using three different datasets of actions and

the results are presented in Table(2). Based on the

results, the system recognizes actions with about the

same accuracy as SOM-architecture (Gharaee, 2018;

Gharaee et al., 2017a; Gharaee et al., 2017b; Gharaee

et al., 2017c). However there is a slight drop in accu-

racy using MSRAction3D 1 and Florence3DActions

datasets. One explanation for this reduction is when

receiving external inputs together with native inputs,

dimension of input data increases and, therefore, there

is more complexity in learning input space.

Perception Simulation Action patterns vectors are

created by training A-SOM layer. Using one di-

mension of external input together with action inputs

makes the system capable of accomplishing the inter-

nal simulation task. To evaluate this capacity, A-SOM

layer was fully trained using all input resources: na-

Table 2: Performance in action recognition using three dif-

ferent datasets of human 3D actions. The results of test

experiments are presented when SOM and A-SOM neural

network are applied. SOM results shows the accuracy of the

framework proposed by (Gharaee et al., 2017a). MSR(1,2)

are MSRAction3D dataset by (Wan, 2015) and Florence is

the Florence3DAction dataset by (Seidenari et al., 2013).

Datasets

Networks MSR(1) MSR(2) Florence

SOM 86.00% 59.61% 72.22%

A-SOM 86.50% 72.22% 74.10%

tive and external inputs. Original patterns were cre-

ated and the system received partial native input in

several experiments to generate simulated patterns.

Figure(2) presents simulated and original patterns

together. In each row, it shows when certain percent-

age of native input is deducted and replaced by zero

padding, the system has to internally simulate patterns

using external input only. As plots show, the system

can successfully simulate action patterns similar to

the original ones.

Recognition using Simulated Perception. To eval-

uate the ability of the system in predicting intended

actions, simulated patterns were given to SOM- and

output layer in different experiments. The accuracy

of predicting actions using simulated patterns is pre-

sented in Table(3).

Shown by Table(3), accuracy drops almost around

5% up until simulating 35% of action patterns. Above

35% of simulation, performance reduction is much

more signiﬁcant. Prediction errors in recognizing ac-

tions when using simulation is shown in ﬁgure(3).

4 DISCUSSION

The architecture proposed in this article is capable of

simulating perception and applying it in predicting the

intended action. This occurs by using associative self-

organizing neural networks (A-SOM). Using A-SOM

layer with association (external inputs) force the sys-

tem to simulate the perception in the absence of na-

tive input. Three different action 3D datasets are used

in various experiments to evaluate the system perfor-

mance.

Among related approaches using A-SOM neural

network are those proposed by (Buonamente et al.,

2013; Buonamente et al., 2015; Buonamente et al.,

2018; Gil et al., 2015). However, in (Buonamente

et al., 2018), the authors used A-SOM in simulat-

ing musics and in (Gil et al., 2015), they focused

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

632

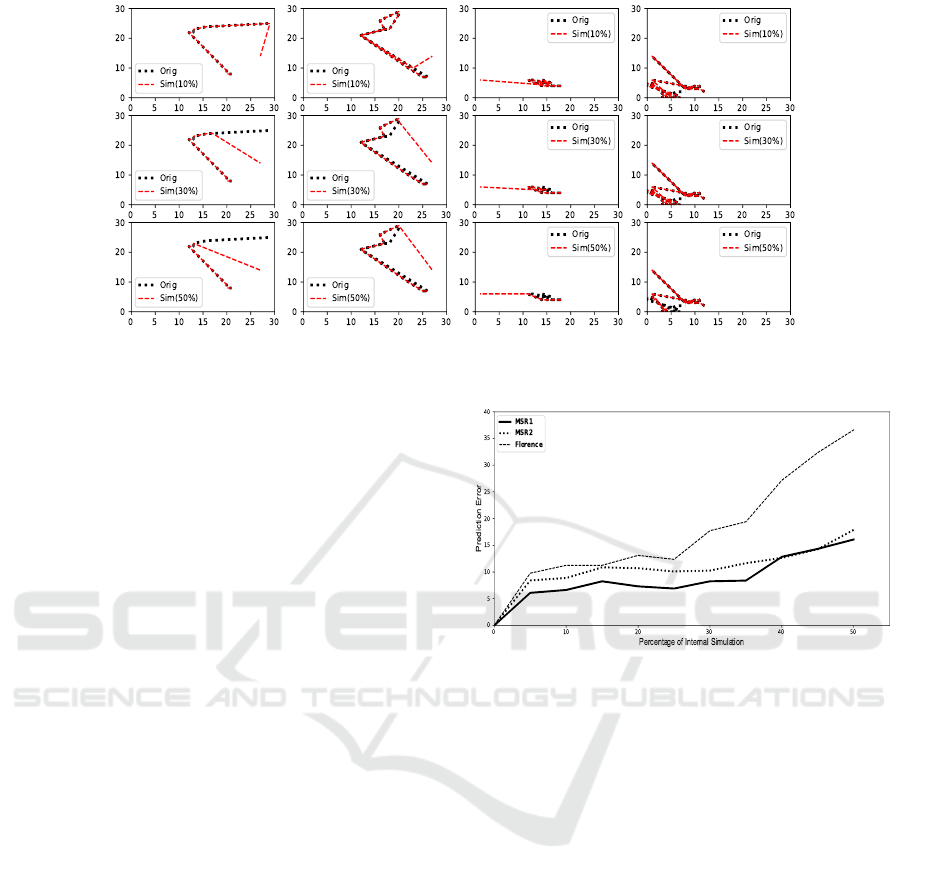
Figure 2: Internal Simulation of action patterns for three different action sequences. Each row shows the comparison of

internally simulated patterns of a certain percentage of data input with the original ones.

on predicting sequences of letters using a supervised

architecture based on the recurrent associative SOM

(SARASOM).

Using the system presented in (Buonamente et al.,

2013; Buonamente et al., 2015), the authors have

shown the A-SOM abilities in discriminating and sim-

ulating actions. The dataset used in these studies is

composed of black and white contours recorded with

only two human performers (Andreas and Hedlena)

who perform a set of 13 different actions, one per-

forms actions for the training set and the other for the

test set.

The method proposed by (Buonamente et al.,

2015) uses A-SOM to discriminate actions by de-

tecting the center of activities, however no result

is reported and the authors mentioned their goal as

presenting investigations of self-organising princi-

ples leading to the emergence of sophisticated social

abilities like action and intention recognition. Fur-

thermore, the approaches proposed by (Buonamente

et al., 2013; Buonamente et al., 2015), have not shown

when and how simulated information can be used.

In this article, the experiments are designed us-

ing three different datasets of actions (Wan, 2015;

Seidenari et al., 2013) having a larger number of se-

quences in comparison to (Buonamente et al., 2013;

Buonamente et al., 2015) and the experiments are de-

signed to show the abilities of A-SOM neural net-

works in simulating perception and applying it to ac-

complish a higher level task, which is predicting the

intended actions.

Other related approaches address the problem

of robots reading intentions by designing experi-

ments based on a collaborative task (Dominey and

Warneken, 2011; Vinanzi et al., 2019; Demiris, 2007),

such as playing game between a human and a robotic

arm (Dominey and Warneken, 2011), or a humanoid

Figure 3: Prediction errors using simulated information

with three different datasets to show how much internal sim-

ulation decreases the accuracy by modifying the percentage

of simulating perception.

(Vinanzi et al., 2019). In these studies reading the

intentions occurs through continuous collaboration,

like by asking questions. While in the experiments of

this study the system applies its learned knowledge to

make simulations and uses the simulated information

for the prediction.

In other approaches using images or video streams

to predict human intentions and trajectories in video

streams (Xie et al., 2017) and to recognize activities

and plans (Granada et al., 2017), the focus is to read

intentions in activities rather than actions, while the

approach proposed in this article concentrates on pre-

dicting the intended actions to be performed using

only the motion trajectories. Moreover, the study pre-

sented in this article does not make use of other enti-

ties or objects to recognize or predict the intention.

Predicting the Intended Action using Internal Simulation of Perception

633

Table 3: Overall test results of predicting the intended action applying varying percentages of the internally simulated action

patterns using three different datasets of human 3D actions. Prediction results are presented in percentage. MSR(1,2) is

MSRAction3D dataset by (Wan, 2015) and Florence is the Florence3DAction dataset by (Seidenari et al., 2013)

Internal simulation (%)

Datasets 0 5 10 15 20 25 30 35 40 45 50

MSR(1) 86.50 80.41 79.87 78.24 79.19 79.60 78.24 78.11 73.65 72.16 70.41

MSR(2) 72.22 63.81 63.35 61.34 61.50 62.11 61.96 60.57 59.57 57.95 54.32

Florence 74.10 72.22 70.74 70.74 68.89 69.63 64.26 62.59 54.81 49.63 45.37

5 CONCLUSION

In conclusion, associative self-organizing maps are

employed in a cognitive architecture to predict the in-

tended action using internal simulation of perception

in the absence of native input. Running several exper-

iments using three different datasets of actions show

the accuracy of the proposed framework in recogniz-

ing and predicting the intended actions. In future,

developing the architecture applying information of

prediction and objects involved in action to improve

segmention of a sequence recognized online (Gharaee

et al., 2016; Gharaee, 2020b) is crucial.

ACKNOWLEDGEMENTS

This work was partially supported by the Wallen-

berg AI, Autonomous Systems and Software Program

(WASP) funded by the Knut and Alice Wallenberg

Foundation.

REFERENCES

Ang, J. H. B., Teow, L. N., and Ng, G. W. (2012). Intent

inference and action prediction using a computational

cognitive model. In 2012 15th International Confer-

ence on Information Fusion, pages 1338–1344. IEEE.

Bartolomeo, P. (2002). The relationship between visual per-

ception and visual mental imagery: a reappraisal of

the neuropsychological evidence. Cortex, 38(3):357–

378.

Bednarik, R., Vrzakova, H., and Hradis, M. (2012). What

do you want to do next: a novel approach for intent

prediction in gaze-based interaction. In Proceedings

of the symposium on eye tracking research and appli-

cations, pages 83–90.

Bonchek-Dokow, E. and Kaminka, G. A. (2014). To-

wards computational models of intention detection

and intention prediction. Cognitive Systems Research,

28:44–79.

Breazeal, C., Buchsbaum, D., Gray, J., Gatenby, D., and

Blumberg, B. (2005). Learning from and about oth-

ers: Towards using imitation to bootstrap the social

understanding of others by robots. Artiﬁcial life, 11(1-

2):31–62.

Buonamente, M., Dindo, H., Chella, A., and Johns-

son, M. (2018). Simulating music with as-

sociative self-organizing maps. Biologically

Inspired Cognitive Architectures, 25:135–140.

DOI:https://doi.org/10.1016/j.bica.2018.07.006.

Buonamente, M., Dindo, H., and Johnsson, M. (2013). Sim-

ulating actions with the associative self-organizing

map. In In International Workshop on Artiﬁcial In-

telligence and Cognition (AIC), volume 1100, pages

13–24.

Buonamente, M., Dindo, H., and Johnsson, M. (2015).

Discriminating and simulating actions with the as-

sociative self-organising map. Connection Science,

27(2):118–136.

Buzs

aki, G. (2015). Hippocampal sharp wave-ripple: A

cognitive biomarker for episodic memory and plan-

ning. Hippocampus, 25(10):1073–1188.

Cisek, P. (2007). Cortical mechanisms of action selection:

the affordance competition hypothesis. Philosophical

Transactions of the Royal Society B: Biological Sci-

ences, 362(1485):1585–1599.

Clark, A. (2013). Whatever next? predictive brains, situated

agents, and the future of cognitive science. Behavioral

and brain sciences, 36(3):181–204.

Demiris, Y. (2007). Prediction of intent in robotics and

multi-agent systems. Cognitive processing, 8(3):151–

158.

Dindo, H. and Chella, A. (2013). What will you do next?

a cognitive model for understanding others’ inten-

tions based on shared representations. In International

Conference on Virtual, Augmented and Mixed Reality,

pages 253–266. Springer.

Dominey, P. F. and Warneken, F. (2011). The basis of shared

intentions in human and robot cognition. New Ideas

in Psychology, 29(3):260–274.

Donnarumma, F., Dindo, H., and Pezzulo, G. (2017). Sen-

sorimotor coarticulation in the execution and recogni-

tion of intentional actions. Frontiers in Psychology,

8:237.

Dragoi, G. and Tonegawa, S. (2013). Distinct pre-

play of multiple novel spatial experiences in the rat.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

634

Proceedings of the National Academy of Sciences,

110(22):9100–9105.

Friston, K. (2005). A theory of cortical responses. Philo-

sophical transactions of the Royal Society B: Biologi-

cal sciences, 360(1456):815–836.

Friston, K. (2010). The free-energy principle: a uni-

ﬁed brain theory? Nature reviews neuroscience,

11(2):127–138.

Gharaee, Z. (2018). Action in Mind: A Neural Net-

work Approach to Action Recognition and Seg-

mentation. Lund University: Cognitive Science.

DOI:https://arxiv.org/abs/2104.14870.

Gharaee, Z. (2020a). Hierarchical growing grid

networks for skeleton based action recogni-

tion. Cognitive Systems Research, 63:11–29.

DOI:https://doi.org/10.1016/j.cogsys.2020.05.002.

Gharaee, Z. (2020b). Online recognition of un-

segmented actions with hierarchical som architec-

ture. Cognitive Processing, 22:77–91. DOI:

https://doi.org/10.1007/s10339-020-00986-4.

Gharaee, Z., G

ardenfors, P., and Johnsson, M. (2016).

Action recognition online with hierarchical self-

organizing maps. In Proceedings of Interna-

tional Conference on Signal Image Technology

and Internet Based Systems(SITIS), pages 538–544.

DOI:10.1109/SITIS.2016.91.

Gharaee, Z., G

ardenfors, P., and Johnsson, M. (2017a).

First and second order dynamics in a hier-

archical som system for action recognition.

Applied Soft Computing, 59:574–585. DOI:

https://doi.org/10.1016/j.asoc.2017.06.007.

Gharaee, Z., G

ardenfors, P., and Johnsson, M. (2017b).

Hierarchical self-organizing maps system for ac-

tion classiﬁcation. In Proceedings of the In-

ternational Conference on Agents and Artiﬁcial

Intelligence (ICAART), pages 583–590. DOI:

10.5220/0006199305830590.

Gharaee, Z., G

ardenfors, P., and Johnsson, M. (2017c). On-

line recognition of actions involving objects. Bio-

logically Inspired Cognitive Architectures, 22:10–19.

DOI:10.1016/j.bica.2017.09.007.

Gil, D., Garcia-Rodriguez, J., Cazorla, M., and Johnsson,

M. (2015). Sarasom: a supervised architecture based

on the recurrent associative som. Neural Computing

and Applications, 26(5):1103–1115.

Granada, R. L., Pereira, R. F., Monteiro, J., Ruiz, D. D. A.,

Barros, R. C., and Meneguzzi, F. R. (2017). Hybrid

activity and plan recognition for video streams. In

Proceedings of the 31st. AAAI Conference: Plan, Ac-

tivity and Intent Recognition Workshop, 2017, Estados

Unidos.

Hesslow, G. (2002). Conscious thought as simulation of be-

haviour and perception. Trends in cognitive sciences,

6(6):242–247.

Johnsson, M., Balkenius, C., and Hesslow, G. (2009). Asso-

ciative self-organizing map. In In the proceedings of

the International Joint Conference on Computational

Intelligence (IJCCI).

Joo, J., Li, W., Steen, F. F., and Zhu, S.-C. (2014). Vi-

sual persuasion: Inferring communicative intents of

images. In Proceedings of the IEEE conference on

computer vision and pattern recognition, pages 216–

223.

Karasev, V., Ayvaci, A., Heisele, B., and Soatto, S. (2016).

Intent-aware long-term prediction of pedestrian mo-

tion. In 2016 IEEE International Conference on

Robotics and Automation (ICRA), pages 2543–2549.

IEEE.

Kosslyn, S. M., Ganis, G., and Thompson, W. L. (2001).

Neural foundations of imagery. Nature reviews neuro-

science, 2(9):635–642.

Liu, K., Sibille, J., and Dragoi, G. (2018). Generative pre-

dictive codes by multiplexed hippocampal neuronal

tuplets. Neuron, 99(6):1329–1341.

Olafsd

ottir, H. F., Barry, C., Saleem, A. B., Hassabis, D.,

and Spiers, H. J. (2015). Hippocampal place cells con-

struct reward related sequences through unexplored

space. Elife, 4:e06063.

Pezzulo, G. and Cisek, P. (2016). Navigating the affordance

landscape: feedback control as a process model of be-

havior and cognition. Trends in cognitive sciences,

20(6):414–424.

Pezzulo, G., Maisto, D., Barca, L., and Van den Bergh, O.

(2019). Symptom perception from a predictive pro-

cessing perspective. Clinical Psychology in Europe,

1(4):1–14.

Pfeiffer, B. E. and Foster, D. J. (2013). Hippocampal

place-cell sequences depict future paths to remem-

bered goals. Nature, 497(7447):74–79.

Sciutti, A., Ansuini, C., Becchio, C., and Sandini, G.

(2015). Investigating the ability to read others’ inten-

tions using humanoid robots. Frontiers in psychology,

6:1362.

Seidenari, L., Varano, V., Berretti, S., Del Bimbo, A., and

Pala, P. (2013). Recognizing actions from depth cam-

eras as weakly aligned multi-part bag-of-poses. In

Proceedings of the IEEE Conference on Computer Vi-

sion and Pattern Recognition Workshops (CVPRW),

pages 479–485. DOI: 10.1109/CVPRW.2013.77.

Stoianov, I., Maisto, D., and Pezzulo, G. (2020). The

hippocampal formation as a hierarchical generative

model supporting generative replay and continual

learning. bioRxiv. DOI:10.1101/2020.01.16.908889.

Vinanzi, S., Goerick, C., and Cangelosi, A. (2019). Min-

dreading for robots: Predicting intentions via dynam-

ical clustering of human postures. In 2019 Joint IEEE

9th International Conference on Development and

Learning and Epigenetic Robotics (ICDL-EpiRob),

pages 272–277. IEEE.

Wan, Y. W. (accessed 2015). Msr action recognition

datasets and codes.

Xie, D., Shu, T., Todorovic, S., and Zhu, S.-C. (2017).

Learning and inferring “dark matter” and predicting

human intents and trajectories in videos. IEEE trans-

actions on pattern analysis and machine intelligence,

40(7):1639–1652.

Predicting the Intended Action using Internal Simulation of Perception

635