Development of a New Fundamental Period Formula for Steel
Structures Considering the Soil-structure Interaction with the Use of
Machine Learning Algorithms
Ashley Megan van der Westhuizen
1
, George Markou
1
and Nikolaos Bakas
2
1
Department of Civil Engineering, University of Pretoria, South Africa
2
Department of RnD, RDC Informatics, Athens, Greece
Keywords: Seismic Design, Fundamental Period, Steel Structures, Nonlinear Regression, Soil-structure Interaction,
Machine-Learning Algorithms.
Abstract: The fundamental period of buildings is an important parameter when designing seismic resistant structures.
The current formulae proposed in design codes for determining the fundamental period of steel structures
cannot accurately predict the fundamental period of real structures. In addition, most of the current formulae
only consider the height of the structure in their formulation, while soil structure interaction (SSI) and the
orientation of the I-columns that influence the fundamental period are usually neglected. This research focuses
on the use of machine learning algorithms to obtain a new formula that accounts for different geometrical
features of the superstructure, where the SSI effect is also considered. After training and testing a 40-feature
formula, an additional 138 out-of-sample numerical results were used to further test the accuracy of the
proposed formula’s prediction abilities. The validation resulted in a correlation of 99.71%, which suggests
that the proposed formula exhibits high predictive features for the steel structures considered in this study.
1 INTRODUCTION
An important structural feature related to the dynamic
response of a structure is the fundamental period
(Young, 2011). Current building codes use empirical
equations to predict the fundamental period of
structures (Jiang et al., 2020, Taljaard et al., 2021 and
Gravett et al., 2021). For determining the
fundamental period of buildings, current international
codes have oversimplified formulae as they require
only the height of the structure and do not account for
the actual 3D geometry of the building nor account
for the interaction between the superstructure and
substructure.
The following design formulae are currently used
in the estimation of the fundamental period of steel
structures:
EC8:
𝑇

=𝐶


𝐻
)
.
Where:
𝐶

= 0.085 for momen
t
resistant space steel frames
𝐶

= 0.075 for eccentrically
b
raced steel frames
(1)
ASCE 7-05:
𝑇

= 0.0724

𝐻
)
.
for steel
moment-resisting frames
𝑇

= 0.0731

𝐻
)
.
for
eccentrically braced steel
frames
(2)
(3)
Another formula proposed by Cinitha (2012) also
takes into account the plan area of the building

𝐿×𝐵
)
and can be seen below:
𝑇

=𝐶


𝐿∙𝐵
)
.∙
(4)
With
𝐶

= 0.0247𝑒
.∙
(5)
𝛼 = 0.4473𝑒
.∙
(6)
Another work was also presented by Nassani,
2014, where a simple model for calculating the
fundamental period of vibration in steel structures
was presented. The proposed formulae in the
aforementioned research works do not consider the
SSI effect, therefore, the development of a formula
that will be able to account this important feature is
required. The phenomenon of SSI involves a
multidisciplinary field of structural mechanics, soil
mechanics and structural dynamics (Jayalekshmi and
Chinmayi, 2013 and Gravett et al., 2021). It has been
952
van der Westhuizen, A., Markou, G. and Bakas, N.
Development of a New Fundamental Period Formula for Steel Structures Considering the Soil-structure Interaction with the Use of Machine Learning Algorithms.
DOI: 10.5220/0010978400003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 3, pages 952-957
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

found that the SSI can increase the fundamental
period, thus is an important consideration when
determining the fundamental period of a structure
(Khalil et al., 2007 and Mourlas et al., 2020).
According to the research gap discussed in this
section, the objective of this research work is to
develop a new formula for predicting the fundamental
period of steel structures that considers the SSI effect.
Additionally, the proposed formula considers other
parameters such as the base conditions and
orientation of the I-columns. A total of 576 numerical
models using Reconan FEA (2020) were created to
obtain a dataset containing 1,152 numerical results.
The dataset is used to train a machine learning
algorithm to formulate a 40-feature formula, using a
higher order NLR model, which was then validated
through the use of out-of-sample data. It is important
to note here that the ability of Reconan FEA to predict
the fundamental period of structures was validated
through the use of experimental data found in the
international literature (Mourlas et al., 2019 and
Mourlas et al., 2021).
2 MACHINE LEARNING
There are 18 independent variables used in this
research work to train the machine learning
algorithm. These include the initial parameters such
as soil depth, Young’s Modulus of soil, height, length
and width of the superstructure, and the orientation of
the I-columns. The modified parameters added during
the training procedure to improve the predictability of
the developed closed form solution included
ln

𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 + 1
)
and


.
Algorithm 1: Higher Order Regression.
Input: XX (matrix of Independent Variables), YY (Vector of
Dependent Variable),
nlf (number of nonlinear features to be kept in the model)
Output: Prediction Formulae
1. Create all nonlinear features
*
(anlf)
2. For i from 1 to nlf do
3. For j from 1 to anlf do
4. Add j
th
feature to the model
5. Calculate Prediction Error, MAPE
j
**
6. End
7. Keep in the model the j
th
feature which yields the
minimum prediction error
5. End
Return: Prediction Formula
*with all inter-items combinations up to the 3
rd
degree,
**Mean Absolute Percentage Error (MAPE).
The features were created to contain a
combination of the parameters up to the third degree
(Dimopoulos and Bakas, 2019). The algorithm was
set to use 85% of the data to train the algorithm and
15% of the data to test the proposed fundamental
period formula. The algorithm shown below
represents the applied procedure for developing the
proposed formula (Gravett et al., 2021).
3 DEVELOPMENT OF
NUMERICAL MODELS AND
DATASET
The main challenge for proposing a new design
formula is in the development of a sufficient number
of models that have varying soil depths, number of
stories, plan area and orientation of I-columns. In
addition to the test dataset, a validation dataset is
developed that contains the numerically obtained
fundamental period results of models that foresee out-
of-sample parameters as discussed below.
The finite element software Femap is used to
graphically create the models and Reconan FEA
(2020) is used to analyse and obtain the fundamental
periods numerically. The models were created using
a varying number of stories, bays and base conditions.
The development of the models started with an initial
model, which is a single storey, single bay structure
with a height of 3.5 m and a raft foundation assuming
a fixed base (see Figure 1). The geometry of the single
bay has a length of 5 m (in the x-direction) and a
width of 3 m (in the y-direction). The initial model
was used to develop additional building geometries
by altering the number of stories, number of spans,
depth of soil and orientation of I-columns.
Figure 1: Initial model.
Development of a New Fundamental Period Formula for Steel Structures Considering the Soil-structure Interaction with the Use of Machine
Learning Algorithms
953

The initial model was modified to develop new
models that foresaw 2, 4, 6, 8 and 10 stories, each
with a 3.5 m height. Each of these models were then
modified to contain single, double, and triple spans
along the x-axis and, single and double spans along
the y-axis. The largest total plan area used to develop
the dataset foresaw a 15x6 m plan view, where the
smallest was 5x3 m.
The models were further modified to include the
SSI effect as seen in Figure 2. The discretization of
the soil domain foresaw depths of 1, 5, 12.5, 22.5 and
37.5 m. It is important to note that the superstructure
was discretized through the use of Natural Beam-
Column Flexibility-Based (NBCFB) finite elements,
where the raft slab and the soil domain were
discretized through 8-noded isoparametric
hexahedral elements. Three soil types were
considered in this research investigation, namely: soft
soil with a Young’s modulus of 65 MPa, soft to
medium soil with a Young’s modulus of 350 MPa and
medium soil with a Young’s modulus of 700 MPa.
(
a
)
(
b
)
Figure 2: 2-storey steel building. Triple span in long
direction, double span in short direction (a) fixed base wit
h
raft foundation (b) flexible base with soil hexahedral mesh.
Table 1 contains the minimum and maximum
values that each parameter had according to the
design of the geometrical features of the buildings
and the soil domains.
Table 1: Minimum and maximum parameter values for
model development.
Parameter Minimum Maximum
Soil Depth [m] 1 37.5
Soil E [kPa] 65 000 700 000
Height [m] 3.5 35
Length (along x-axis) [m] 5 15
Width (along y-axis) [m] 3 6
After the construction of the initial numerical
models that foresaw the use of the positioning of the
steel IPE columns’ section along a specific direction,
the number of models was increased by changing the
orientation of the columns’ section by 90
o
. The
columns’ strong axis orientation was modified from
being parallel to the global x-axis to being parallel to
the global y-axis direction of the structure, thus
allowing the investigation of this feature on the
fundamental period. It is important to note here that
the IPE200 section was used for all beams and the
IPE300 for constructing all columns.
Additionally, the slabs of the buildings were
assumed to be reinforced concrete (RC) slabs and
were modeled as diaphragms with a mass equal to the
mass of a 150 mm thick slab that foresees a live load
of 2 kN/m
2
.
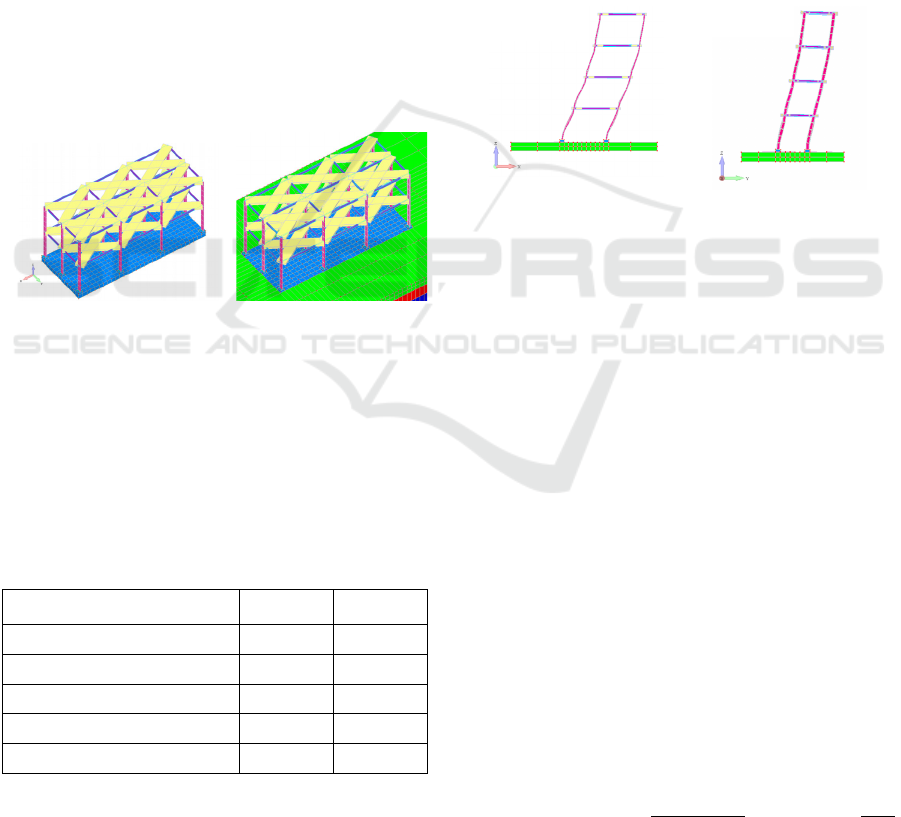
Figure 3 shows the first two modal shapes of a 4-
storey, 1-bay steel building with 1 m soft soil.
(
a
)
(
b
)
Figure 3: Modal shape (a) 1 and (b) 2 of a 4-storey, 1-
b
a
y
steel buildin
g
founded on 1 m dee
p
soft soil.
4 PROPOSED FUNDAMENTAL
PERIOD FORMULA
The proposed formula for determining the
fundamental period of steel structures was
determined from the numerical results of 1,152 data
points. The formula contains 40-features, which are a
combination of the following parameters:
𝑇 is the fundamental period (s)
𝐷

is the depth of soil (m)
𝐸 is the soils Young’s Modulus (kPa)
𝐻 is the building height (m)
𝐿 is the length of the building parallel to the
oscillating direction (m)
𝐵 is the width of the building perpendicular to
the oscillating direction (m)
𝐶𝑂 is the orientation of the columns (either a 1
or 2)
𝑙𝑃𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 is ln

𝑃𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 + 1
)
i.e., 𝑙𝐷

=
ln

𝐷

+1
)
𝐼𝑛𝑣𝑃𝑎𝑟𝑎𝑚𝑒𝑡𝑒r is


i.e., 𝐼𝑛𝑣𝐷

=




The developed formula is given in Equation 7. It
must be noted here that numerous formulae have been
T
1
=1.524 s T
2
=0.518
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
954

investigated that foresaw 5, 10 and 20 features, where
it was found that the 40-feature formula was able to
provide with the highest accuracy in terms of fitting
into the training and test data, but most importantly in
terms of predicting accurately the out-of-sample data
compared to other machine learning generated
formulae.
Figure 4: Relationship between numerically predicted and
formula predicted fundamental periods on test and train
dataset.
𝑇 =0.194630 ∙𝑙𝐻

+0.0580556 ∙ 𝐶𝑂

∙𝐵
−9.39027 ∙𝐼𝑛𝑣𝐶𝑂∙𝐼𝑛𝑣𝐵∙𝑙𝐵
−8.49213 ∙𝐼𝑛𝑣𝐿∙𝐶𝑂∙𝐻
−41.8498 ∙𝐼𝑛𝑣𝐶𝑂∙𝑙𝐿∙𝐻
−8.14564 ∙𝐼𝑛𝑣𝐸∙𝐸∙𝐻−0.800465 ∙𝐶𝑂∙𝐵∙𝐻
+114.808 ∙𝐼𝑛𝑣𝐶𝑂∙𝐼𝑛𝑣𝐵∙𝐻
+46.6778 ∙𝐼𝑛𝑣𝐶𝑂∙𝐼𝑛𝑣𝐵

+0.0631499 ∙ 𝐵

∙𝐻
+4.20803 ∙𝑙𝐵∙𝐶𝑂∙𝐻−0.144945 ∙𝑙𝐿∙𝐻∙𝐿
+0.847694 ∙𝐵∙𝐻∙𝐼𝑛𝑣𝐿+9.37930 ∙𝐼𝑛𝑣𝐿

∙𝐻
−1.08930 ∙𝐼𝑛𝑣𝐶𝑂

∙𝐿+4.04342 ∙𝐼𝑛𝑣𝐿
−0.251627 ∙𝐼𝑛𝑣𝐿∙𝐶𝑂∙𝐵
−0.00783561 ∙𝐼𝑛𝑣𝐵∙𝑙𝐶𝑂∙𝑙𝐸
+0.523388 ∙𝑙𝐿

∙𝐼𝑛𝑣𝐶𝑂
+0.0947335 ∙𝐼𝑛𝑣𝐻∙𝑙𝐻∙𝐿
+46.8309 ∙𝐼𝑛𝑣𝐸∙𝐻∙𝑙𝐷𝑠+0.00764850 ∙𝑙𝐻∗𝐵
+0.000161108 ∙𝑙𝐿∙𝐿∙𝑙𝐸
−20.5554 ∙𝐼𝑛𝑣𝐸∙𝐶𝑂∙𝐷𝑠
−0.00474725 ∙𝐼𝑛𝑣𝐿

∙𝐼𝑛𝑣𝐷𝑠
+2.73101 ∙𝐼𝑛𝑣𝐿∙𝐼𝑛𝑣𝐻∙𝐶𝑂
+0.403996 ∙𝐼𝑛𝑣𝐶𝑂∙𝑙𝐵∙𝐿
−0.0105914 ∙𝑙𝐿∙𝐿∙𝐵
−0.228100 ∙𝑙𝐵

∙𝐶𝑂
+0.00265642 ∙𝐼𝑛𝑣𝐿∙ 𝐻

−2.58386 ∙𝐼𝑛𝑣𝐵∙𝐼𝑛𝑣𝐻∙𝐶𝑂
+5.84142 ∙𝐼𝑛𝑣𝐶𝑂∙𝐻∙𝐿
+29.5168 ∙𝐼𝑛𝑣𝐶𝑂∙𝐻
+0.849560 ∙𝐼𝑛𝑣𝐿∙𝑙𝐻∙𝐶𝑂
−2.14776 ∙𝐼𝑛𝑣𝐵∙𝑙𝐻∗𝑙𝐶𝑂
+1.34222 ∙𝑙𝐵∙𝑙𝐻∙𝐼𝑛𝑣𝐻
−0.00333495 ∙𝑙𝐸∙𝐿∙𝐼𝑛𝑣𝐻
−2.64111 ∙𝐼𝑛𝑣𝐵

∙𝐼𝑛𝑣𝐻
+71.1358 ∙𝐼𝑛𝑣𝐻∙𝐷𝑠∙𝐼𝑛𝑣𝐸
−17.9194 ∙𝐼𝑛𝑣𝐸∙𝑙𝐸∙𝑙𝐿−1.16636
(7)
Figure 4 shows the similarity ratio of the proposed
formula compared to the numerically predicted data
used to train and test the developed relationship. The
correlation ratio was found to be 99.95% as it derives
from the training and testing procedure.
5 FURTHER VALIDATION OF
THE PROPOSED FORMULA
A set of 138 fundamental periods were generated
through the use of additional models that were not
used during the training and testing procedure so as
to investigate the performance of the proposed 40-
feature formula when out-of-sample data are used.
The validation dataset was created using random
parameter values not included in the train and test
datasets. 3, 5, 7 and 9-storey models and models with
Young’s modulus of 10 MPa and 100 MPa were used.
Figure 5 shows two of these models that were
developed for the validation stage that foresaw 5 and
9 storeys. The out-of-sample parameters were
assumed to validate whether the new proposed
formula would be able to accurately predict the
fundamental period of steel structures that had
parameter values that differ from those that were used
to train and test the predictive model.
(
a
)
(
b
)
Figure 5: (a) 5-storey, 1-bay, (b) 9-storey, 3-bay 5m soil
models developed for validation stage.
The numerically predicted periods were plotted
against those obtained using the proposed formula as
seen in Figure 6. By evaluating the correlation
between the numerically predicted periods and those
obtained using the proposed formula, it is observed
that a high correlation (𝑅

= 99.71%) was achieved.
This shows that the formula yields a high accuracy
prediction and can be used to predict the fundamental
period of framed steel structures that have
geometrical features within the limits presented in
Table 1.
y = 0,9994x + 0,0008
R² = 0,9995
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
0 0,5 1 1,5 2 2,5 3 3,5 4 4,5
Formula Predicted Period [s]
Numerically Predicted Period [s]
Development of a New Fundamental Period Formula for Steel Structures Considering the Soil-structure Interaction with the Use of Machine
Learning Algorithms
955

Figure 6: Relationship between numerically predicted and
formula predicted fundamental periods on the out-of-
sample validation dataset.
Table 2: Comparison of fundamental period error
predictions on the validation dataset.
Description Formula Mean absolute error
40-feature formula Equation 7 2.8%
EC8 Equation 1 76%
ASCE Equation 2 76%
Cinitha (2012) Equation 4 92%
Table 2 shows the comparison between the
numerically obtained fundamental periods and those
obtained using the proposed formula as well as the
formulae currently found in design codes and the
international literature. It is evident that the current
design codes estimate the fundamental period with a
high mean absolute error as compared to the new
proposed formula.
6 CONCLUSIONS AND
RECOMMENDATIONS
A newly proposed formula for predicting the
fundamental period of steel structures with the use of
machine-learning algorithms was presented. The
proposed formula considers the depth of soil,
Young’s modulus of soil, height and plan area of the
structure, as well as the orientation of the I-columns.
The 40-feature formula proposed was developed
using an algorithm combining the parameters using a
higher order NLR.
The proposed fundamental period formula was
tested on out-of-sample steel structures, where a
correlation of 99.71% was achieved. This shows that
the proposed formula produces accurate results and
can be further used to predict the fundamental period
of out-of-sample results. Design code formulae for
the calculation of the fundamental period of steel
structures were compared to the proposed formula,
where it was found that the proposed predictive
model derived a 27 times smaller mean absolute error.
In addition to that, the proposed fundamental period
formula was found to be superior to other existing
proposed equations found in the international
literature when used on the under-study datasets.
The study focuses on steel structures with regular
plans. To expand the dataset and further investigate
the dynamic response of steel framed structures,
irregular in plan buildings will be investigated, where
braced and infill frames will be modeled in future
research work. Finally, for each type of steel framing
system, larger models will be created to develop
formulae that will be applicable to a broader spectrum
of frame geometries.
REFERENCES
Cinitha, A 2012. A rational approach for fundamental
period of low and medium rise steel building frames.
International Journal of Modern Engineering Research,
2(5):3340-3346.
Dimopoulos, T and Bakas, N 2019. Sensitivity analysis of
machine learning models for the mass appraisal of real
estate. Case study of residential units in Nicosia,
Cyprus. Remote sensing, 11(24):3047
Gravett, Z D, Mourlas, C, Taljaard V L, Bakas, P N,
Markou, G and Papadrakakis, M 2021. New
Fundamental Period Formulae for Soil-Reinforced
Concrete Structures Interaction Using Machine
Learning Algorithms and ANNs. Soil Dynamics and
Earthquake Engineering, 144: 106656
Jayalekshmi, B and Chinmayi, H 2013. Effect of soil
flexibility on lateral natural period in RC framed
buildings with shear wall. International Journal of
Innovative Research in Science, Engineering and
Technology, 2(6):2067-2076.
Jiang, R, Jiang, L, Hu, Y, Jiang, L and Ye, J 2020. A
simplified method for fundamental period prediction of
steel frames with steel plate shear walls. The structural
design of tall and special buildings, 29(7):1-15.
Khalil, L, Sadek, M and Shahrour, I 2007. Influence of the
soil–structure interaction on the fundamental period of
buildings. Earthquake engineering & structural
dynamics, 36(15):2445-2453.
Mourlas, C, Markou, G and Papadrakakis, M 2019.
Accurate and Computationally Efficient Nonlinear
Static and Dynamic Analysis of Reinforced Concrete
Structures Considering Damage Factors. Engineering
Structures, 178:258–285.
Mourlas, C, Khabele, N, Bark, H A, Karamitros, D, Taddei,
F, Markou, G and Papadrakakis, M 2020. The Effect of
Soil-Structure Interaction on the Nonlinear Dynamic
Response of Reinforced Concrete Structures.
y = 1,0171x - 0,0442
R² = 0,9971
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
00,511,522,533,544,5
Formula Predicted Period [s]
Numerically Predicted Period [s]
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
956

International Journal of Structural Stability and
Dynamics, 20(13): 2041013 doi:10.1142/S02194554
20410138
Mourlas, C. and Markou, G. 2020. ReConAn v2.00 Finite
Element Analysis Software User's Manual.
Nassani, D E 2014. A simple model for calculating the
fundamental period of vibration in steel structures.
APCBEE procedia, 9:339-346.
Reconan FEA v2.00, User’s Manual. 2020.
https://www.researchgate.net/publication/342361609_ReC
onAn_v200_Finite_Element_Analysis_Software_User
's_Manual
Spijkerman, Z, Bakas, N, Markou, G and Papadrakakis, M
2021. Predicting the Shear Capacity of Reinforced
Concrete Slender Beams Without Stirrups by Applying
Artificial Intelligence Algorithms. COMPDYN 2021,
27-30 June 2021, Streamed from Athens, Greece.
Taljaard, V L, Gravett, D Z, Mourlas, C, Bakas, N, Markou,
G and Papadrakakis, M 2021. Development of a New
Fundamental Period Formula by Considering Soil-
Structure Interaction with the Use of Machine Learning
Algorithms, COMPDYN 2021, 27-30 June 2021,
Streamed from Athens, Greece.
Young, K C 2011. An Investigation of the Fundamental
Period of Vibration of Irregular Steel Structures. The
Ohio State University.
Development of a New Fundamental Period Formula for Steel Structures Considering the Soil-structure Interaction with the Use of Machine
Learning Algorithms
957