A Data-Driven Methodology for Pre-Flight Trajectory Prediction

Gaetano Zazzaro

, Francesco Martone, Gianpaolo Romano, Antonio Vitale

and

Edoardo Filippone

CIRA (Italian Aerospace Research Centre), Via Maiorise snc, Capua (CE), Italy

Keywords: Data Driven, Data Mining, Machine Learning, Trajectory Prediction, Uncertainties.

Abstract: This paper presents a data-driven methodology, named P4T, for the trajectory prediction from long to short

term before scheduled time of flight, developed within the framework of the PIU4TP project. The

methodology is aimed to support the Network Manager in the air traffic flow and capacity management,

allowing the optimization of flight distribution among sectors and flight routes, the anticipation of air traffic

flow requests and the identification in advance of potential conflicts. The proposed approach applies machine

learning and data mining techniques to perform data analysis and to correctly identify, from historical data,

the aircraft expected behaviour, in terms of flight path selection. The main peculiarity of this approach is the

exploitation of the uncertainties on current forecasts of some relevant mission and aircraft parameters to

compute trajectory prediction outcomes enriched with associated probabilistic information. The preliminary

validation of the methodology using simulated data highlighted very promising results.

1 INTRODUCTION

Trajectory Prediction (TP) is one of the most relevant

capability and need of the current and, above all, the

future management of air traffic, in its expected

implementation of the Trajectory Based Operations

paradigm. Indeed, it supports the activities

concerning demand-capacity balance, identification

of hotspots and preventive mitigation of potential

conflicts. Therefore, the TP process is used by several

actors involved in the traffic planning and

management, starting even long time before the

actual flight execution. A lot of efforts have been

done to develop TP algorithms that can meet the

stringent safety requirements typical of the aviation

sector. The traditional approach uses a model-based

deterministic forecast of the trajectories without any

quantification of the uncertainty affecting the

prediction (Engage, 2019). However, the TP process

is uncertain by its nature, indeed it predicts actual

trajectories by using models, which are

approximation of the reality affected by a given

accuracy, and uncertain input data, such as weather

forecast, Air Traffic Control (ATC) practices, and

aircraft actual performance.

https://orcid.org/0000-0001-6042-6650

https://orcid.org/0000-0001-9675-5245

This paper presents the TP approach developed in

the PIU4TP project (Zazzaro et al., 2020), financed

by SESAR within the Engage KTN framework, and

applicable to the strategic and pre-tactical phases of

the Air Traffic Management (ATM). It is a data-

driven methodology that builds the predictive model

of flight trajectories by using Data Mining (DM) and

Machine Learning (ML) techniques. The innovation

of the approach consists in the computation of 4-

dimensional (4D) TP enriched with its relevant

probabilistic information, which is obtained by

exploiting the uncertainty inherently connected to the

data used as inputs by the TP process. The prediction

of the 3D spatial trajectory consists, for the scope of

this work, in the identification of the most suitable

flight plan among several possible, whereas the

prediction of the fourth dimension of the flight plan,

that is the computation of the time of arrival in each

waypoint (WP), is performed by solving a regression

problem. Actually, there is a large number of

parameters that can affect the optimal flight plan

selection. Few, among the most relevant ones, have

been considered in the development of the proposed

methodology. In fact, the aim is to demonstrate a

proof of concept and to investigate how the

188

Zazzaro, G., Martone, F., Romano, G., Vitale, A. and Filippone, E.

A Data-Driven Methodology for Pre-Flight Trajectory Prediction.

DOI: 10.5220/0010985300003191

In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2022), pages 188-197

ISBN: 978-989-758-573-9; ISSN: 2184-495X

information about significant parameters can be

exploited in an integrated manner to perform in

advance a reliable prediction of the flown trajectory.

Although the method was designed in this simplified

scenario, all the steps that define the proposed

approach can be applied to any set of uncertain inputs.

Indeed, the methodology takes the form of a lifecycle

model for the analysis and modelling of flight paths

in the context of TP and allows to add new input

variables and external parameters by iterating through

the phases of the lifecycle. The defined methodology

was preliminarily validated using simulated data and

the obtained results seem very promising. The use of

simulated data is due to the lack of comprehensive

open access datasets of real aircraft trajectories and

information concerning the parameters that influence

these trajectories. Moreover, the simulated data allow

to test the methodology in a controlled environment,

that is, the value of the parameters of interest and the

rules and the assumptions that lead to perform the

flight along a specific flight plan are perfectly known;

thus, the capabilities and limitations of the proposed

approach can be fully assessed.

This paper is structured as follows: Section 2

summarizes previous works on the TP topic. Section

3 and Section 4 present the operational scenario

defined for the methodology design and validation

and the developed methodology, respectively.

Section 5 discusses the preliminary methodology

evaluation results. Conclusions are in Section 6.

2 RELATED WORK

The evolution towards trajectory-based ATM has led

in recent years to a great deal of interest in the

development of methodologies for predicting aircraft

trajectories. The position of an aircraft in its trajectory

can be estimated using physical models of the

dynamics of the aircraft subject to the different forces

acting on it (gravity, drag, etc.). These model-based

methods require the solution of differential equations

with the precise estimation of a number of parameters

characterizing the response of the aircraft. Aircraft

databases provide theoretical model specifications

and related specific datasets to simulate the behaviour

of any aircraft and is often used for aircraft TP (Nuic

et al., 2010). Point mass models are widely used to

simulate aircraft motion (Schuster, 2015), (Fukuda et

al., 2010). By combining the calculation model, intent

of the aircraft and environmental conditions the

accuracy of the predicted trajectory can be improved

(Alligier et al., 2013), (Zhang et al., 2018). Most of

the relevant parameters in model-based TP methods

are difficult to measure with a satisfying level of

accuracy, in particular the weather data and the

aircraft mass change during flight. Instability in the

predicted position of the aircraft may arise, limiting

the applicability of these techniques to short-term or

to portions of the overall flight.

ML methods are gaining more and more attention

given the resurgence of interest in the field of AI with

the successful application of neural nets in the field of

computer vision, natural language processing,

automatic translation and others. As an alternative to

model-based solutions a data-driven approach

represents a viable solution to the problem of TP

(Wang et al., 2017), (Fernandez et al., 2017). It uses

a collection of past flown trajectories to statistically

predict the behaviour of future flights by exploiting

all the information implicitly included in the

historical data. A stepwise regression method may be

used in TP integrating meteorological data to predict

the arrival time (de Leege et al., 2013). A direct linear

regression model using a dataset of radar trajectories

for short to mid-term aircraft TP has been developed

and tested on a large database of flights over Europe

(Tastambekov et al., 2014). Deep Neural Nets also

have been exploited to address the problem of TP.

Casting this problem as a flight sequence estimation,

a recurrent Neural Net can be trained to predict

aircraft position in discrete time steps (Wu et al.,

2017), (Park et al., 2018). A comparative study

showed that deep learning algorithms have

impressive performance when compared with other

traditional approach (Guan et al., 2016). With the

improving quality and growing volume of the data

collected in ATC systems, data-driven methods have

become mainstream in current aircraft TP research

and may allow overcoming the limitations of model-

based approach. The problem of TP when

uncertainties in the input variables are considered has

emerged in the recent years, and research activities

are on-going on the topic. It is one of the main

objectives of this paper. In previous work this

problem has been faced by using model-based

approach, coupled with probabilistic or uncertainty

propagation methodologies (Rodriguez-Sanz et al.,

2019), (Rivas et al., 2017), and data-driven approach

(Ma and Tian, 2020), (Zeh et al., 2020), (Zhang et al.,

2020).

3 OPERATIONAL SCENARIO

The design and validation of the TP methodology

require the definition of an operational scenario and

the collection of all the relevant data (historical data,

A Data-Driven Methodology for Pre-Flight Trajectory Prediction

189

in terms of flown trajectories and related forecasts).

The scenario definition includes the selection of the

considered airspace, routes and aircraft, the

identification of the parameters that affect the flight

plan, and the definition of the time frame in which the

TP shall be carried out. All the data that characterize

the scenario are generated in simulation, providing a

wide and complete database. The simulated data are

computed using some assumptions that however do

not affect the generality of the developed

methodology. The following subsections detail both

the considered scenario and the process for simulated

data generation.

3.1 Scenario Definition

Two routes within the European airspace were

selected: London Heathrow Airport (ICAO code:

EGLL) to Athens Eleftherios Venizelos Airport

(ICAO code: LGAV) and London Gatwick Airport

(ICAO code: EGKK) to Malta International Airport

(ICAO code: LMML). Both routes are executed by

several airliners, fly through different national

airspaces and go across different airspace sectors. It

is assumed that each route can be performed using

one out of twelve possible flight plans (three different

lateral flight plans which can be performed at four

different cruise flight levels), defined by departure

and destination airports and a list of waypoints (WPs).

A generic short/medium range aircraft has been

chosen to perform the flights, with take-off weight

varying in the range 50-80 tons. Actually, there is a

large number and types of parameters that can affect

flight plan selection and request for a flight plan

change both during pre-flight planning and flight

execution. The defined scenario considers two of

these parameters, that are relevant in the strategic and

pre-tactical phases, namely actual aircraft take-off

weight (TOW) and weather conditions. In fact, the

actual TOW affects the climbing performance of the

aircraft (Zeh et all., 2020), (Uzun and Koyuncu,

2017), and the selection of the optimal flight level, as

described in (AIRBUS, 1998). The effects of weather

conditions on the performed flight plan are widely

known and reported in several works in the literature

(Rivas, Franco and Valenzuela, 2017), (de Leege, van

Paassen and Mulder, 2013), (Sankararaman and

Daigle, 2017). For the sake of simplification, other

effects such as the pilot intent, FMS performance,

ATC tactical intervention, are not considered in the

generation of simulated data.

The methodology shall be applicable in strategic

and pre-tactical phases, therefore a time window of

15 days before the scheduled date of flight (denoted

as Tf) is considered. In details, TP is performed at

three relevant dates: 15 days, 5 days and 1 day before

Tf, denoted with Tf-15, Tf-5 and Tf-1, respectively.

Simulated data concerning meteorological conditions

and estimated TOW, including related uncertainties,

are computed in these dates and in the day of flight.

3.2 Simulated Data Generation

The information about a huge number of flights shall

be available to design and validate a data-driven TP

methodology. For each flight the following data are

required:

 the set of possible flight plans that can be flown

along the selected route;

 the weather forecasts (and their probabilistic

characterization) along the flight route, in each

date of the TP computation and the actual

weather conditions on the day of the flight;

 the TOW estimations (and their probabilistic

characterization) in each date of the TP

computation and the actual TOW during the

flight;

 the actual flown trajectory the day of flight.

The set of possible flight plans for each route was

selected through the analysis of the data available on

the website https://www.flightradar24.com and

defined by a list of WPs downloaded from the website

www.flightplandatabase.com.

The ERA5 database of the European Centre of

Medium-range Weather Forecast-ECMWF (ERA5,

2021) was used to get 3D (longitude, latitude,

pressure altitude) weather data. Several datasets,

including wind intensity and direction and

atmospheric temperature, were used; they refer to all

the days of October and November from 1979 to 2013

at 2pm. Weather data are evaluated in each WP of all

the possible flight plans for the selected route,

through an interpolation of the grid provided by

ERA5. The ERA5 also provides the uncertainties for

the weather forecasts (Haiden et al., 2019) that apply

back till to 15 days before the date, and this is also a

leading reason for selecting 15 days as the time range

of our scenario. In the defined scenario, along with

the forecast at Tf-15, Tf-5 and Tf-1 dates, an

uncertainty is associated to each variable that

characterize the weather conditions, as provided in

(Haiden et al., 2019). It is assumed that the forecast

of the atmospheric parameters are stochastic variables

with a Uniform distribution. Once the atmospheric

parameters are available, the No-Fly Zones can be

computed as the airspace region where wind intensity

exceeds a pre-defined threshold.

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

190

The TOW forecast and actual values vary among

two precise limits, the Operating Empty Weight

(OEW) and the Maximum Take-Off Weight

(MTOW). These values for most of the aircraft are

available in the literature (AIRBUS, 1998). The TOW

forecast at each prediction date is obtained through a

random draw, assuming a Uniform stochastic

distribution within the allowable range. The

uncertainty on the estimated value depends on how

much in advance with respect to the scheduled flight

date the estimation is computed (it decreases while

approaching the flight date) and it is defined as a

percentage of the whole range of variation.

Computed weather conditions and take-off

weight on the day of flight are inputs for the selection

of the flown flight plan among the possible options.

Specifically, as detailed before, the presence of the

No-Fly Zones is determined by the weather, whereas

the TOW defines, for a given aircraft and cost index

selected by the operator, the climbing performance,

the optimal cruise altitude and the optimal Mach

number, denoted as ECON Mach (AIRBUS, 1998). It

is worthy to remark that the weather conditions could

also contribute to determine the optimal flight level,

because the relation between TOW and optimal cruise

altitude (flight level), for a fixed cost index, varies

with the atmospheric temperature. Based on these

considerations, the following rules apply to select the

most suitable flight plan (among the available ones

for the considered route):

 the selected lateral flight plan shall avoid the

NFZs;

 the selected flight level shall be the optimal one

with respect to the take-off weight.

The definition of the 4D flight plan requires the

computation of the time of arrival in each WP. It is

performed through kinematic equations, assuming

that the flight is executed flying at ECON Mach. In

computing the time to reach the WPs in the first legs

of a flight plan, the climb performance of the aircraft

is also considered by adding to the estimated time an

additional delay. This climb performance is available

in the open literature for some aircraft models

(AIRBUS, 1998).

Using the data generation process above

described, 2052 simulated flights were computed for

the route from London to Athens, and 2023 simulated

flights for the route from London to Malta. Globally,

there are 20 variables comprised in the simulated data

related to aircraft state, weather condition, take-off

weight and the relative uncertainties. For each

simulated flight these variables are provided at each

prediction date (predicted values of the variables and

related uncertainties) and at the date of flight (actual

flown values of the variables). Table I shows the list

of the variables.

Table 1: List of simulated variables.

Variable Descri

tion Units

WP_ID Way

oint (WP) Identifie

Lon WP longitude deg

Lat WP latitude de

T Temperature

VnW

North component of wind

eed on WP

m/s

VeW

East component of wind

eed on WP

m/s

VdW

East component of wind

eed on WP

m/s

W Take-off weight kg

FL Flight level 100s ft

PrFL

Probability associated to the

flight level

M Mach numbe

PrM

Probability associated to the

Mach numbe

Speed with respect to the

groun

m/s

ETime

Time needed to cover the

distance between two

consecutive WPs

(

ETA

)

4 METHODOLOGY

DEVELOPMENT

The development of the methodology, named P4T,

was carried out in three phases: domain and data

understanding, data preparation, and training of the

models.

4.1 Domain and Data Understanding

The domain understanding included the fixing of the

objectives of the data analysis goals and the

assessment of the situation. In particular, it concerned

the mapping from domain issues to data analysis

problems. As a result, the domain objective in the P4T

methodology, consisting in the prediction of the flight

path, has been translated into a data analysis

objective, which consists of a multiclass classification

with respect to the flight plan prediction (both lateral

and vertical), and of a regression, regarding the

estimation of the time of arrival on the WPs of the

flight plan.

For the lateral and vertical flight plan, the problem

to address can be stated as: predict which flight plan,

among N possible ones, will be selected for the

A Data-Driven Methodology for Pre-Flight Trajectory Prediction

191

execution of the flight. The input variables considered

are: forecast and related uncertainties of weather

conditions (temperature and wind speed components)

at each WP of the flight plan and of take-off weight.

The prediction of the time of arrival on the WPs

(ETA) is a classical regression problem having as

input variables the sequence of the WPs, the forecast

of temperature and horizontal wind direction (east

and north components) at each WP, and of take-off

weight. The examination of the simulated data has

showed that there is a one-to-one correspondence

between the flight level and the optimal cruising

Mach number of the aircraft, so that, once established

the value of the flight level, the Mach is uniquely

defined. This is perfectly reasonable in a first

approximation, taking apart the possible variation due

to the necessity to compensate for the effects of the

wind speed along the route. So, temperature and take-

off weight contain all the information to predict the

cruising airspeed. For this reason, in the regression

model for the estimation of ETA, these variables are

considered as input to the model and not the estimated

cruising speed or flight level.

4.2 Data Preparation

Different strategies were used to construct the

datasets needed in the modelling phase for lateral

flight plan and flight level classifications and for the

estimation of the time of arrival.

Regarding the prediction of the lateral flight plan,

separate datasets were built for each of the selected

route and for each time frame before the estimated off

block time (EOBT). Since it is assumed that the

definition of the lateral flight plan and the choice of

the cruise flight level may be taken as independent,

different datasets for the prediction of these two target

variables were built. Once fixed the route and the time

frame, the simulated dataset provides for each flight,

the alternative flight plans along with the related

forecasted weather conditions, as well as the

estimated take-off weight. The datasets for the

prediction of the lateral flight plan contain vectors

with the following structure:

𝑇

()

,𝑉



()

,𝑉



()

,𝑉



()

,…,𝑇

()

,𝑉



()

,𝑉



()

,𝑉



()



(1)

where 𝐿 is the number of WPs in the flight plan. The

components of these vectors are only the weather

variables, i.e. the temperature 𝑇 and the three

components of the wind speed along the three

directions north 𝑉



, east 𝑉



, and down 𝑉



In order to consider the uncertainties, the value of

the weather variables used to construct the input

vectors for modelling is drawn from a gaussian

distribution centred on the simulated value and with

standard deviation σ=∆/3, where ∆ is the associated

uncertainty. The choice of σ is made to have a

gaussian ample enough to take all the interval of

uncertainty of the weather variable, i.e. 6 σ=2 ∆. This

sampling is repeated for a fixed number of times.

Then, for the components of the vector (1), we have:

𝑇

(



)

𝒩

(𝑇



(



)

,∆𝑇

(



)

/3)

(2)

𝑉



()

𝒩

(𝑉



(



)

,∆𝑉



(



)

/3)

(3)

where 𝑖=1,…,𝐿, 𝑗=𝑁,𝐸,𝐷, and 𝑇



()

and 𝑉



()

are

the values of T and V

at WP i-th as provided by the

available input data. The target variable for the training

of the models is the label corresponding to the lateral

flight plan used for the execution of the flight.

The procedure used to construct the dataset for the

prediction of the flight level is similar. The flight

level is a characteristic of the flight, not of the single

flight plan, and it is assumed that the choice of the

flight level depends mainly on the take-off weight and

on the mean temperature in the zone of flight.

The dataset for the training of the models for the

prediction of the flight level is made up of vectors

with the following simple structure:

(

𝑇



,𝑊

)

(4)

where 𝑇



is calculated by taking all the WPs of all the

possible lateral flight plans, and 𝑊 is a value

repeatedly drawn from a gaussian distribution centred

on the value of the take-off weight, denoted as 𝑊



, as

provided by the input data and having 1/3 of the

uncertainty ∆𝑊 as standard deviation. Then, for the

target variable, to each possible flight level is given

as label an integer from 1 to the number of possible

flight levels. The target variable for the training of the

model is the label corresponding to the flight level

used for the execution of the flight.

The dataset for the regression problem of

estimating the time of arrival on the WPs of the lateral

flight plan was built starting from the data of the

simulated flights, i.e. those referring to the day of

flight (see Table 1). These variables refer to the flight

plan used during the execution of the flight and carry

no uncertainties. Therefore, a data-driven model of

the aircraft dynamics was built by exploiting one

dataset for each of the two routes considered. Each

dataset contains rows with the following structure:

(

𝑑,𝑏,𝑇,𝑉



,𝑉



,𝑊

)

(5)

where 𝑑 is the distance between two consecutive

WPs of the same flight calculated along a loxodrome,

b is the track angle between the two WPs, 𝑇, 𝑉



and

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

192

𝑉



are evaluated at the starting WP. The dependency

on other estimated parameters, such as the flight level

or the Mach number, is not introduced into the

regression model since the temperature and the take-

off weight should contain enough information to let

the model gain a knowledge about the cruise speed of

the aircraft. The analysis focused on the cruising

phase of the flight, leaving out the climbing from the

departure airport to the cruising flight level and the

descending phase to the arrival airport.

The modelling datasets obtained with these

procedures are split into training and test sets. The

training sets are used for the construction and

optimization of the predictive models, while the test

sets are kept apart for the final evaluation of the

performance of the models.

4.3 Modeling

In order to select the best model for the problem at

hand, part of the available training dataset is used as

a validation dataset useful for tuning the model’s

hyperparameters.

In the development of the methodology both

holdout and a k-fold cross-validation (with k=10)

have been used, obtaining very similar results, so in

the following only the results for the cross validation

are reported, separately for the prediction of the flight

plan and the prediction of the ETAs.

The three timeframes in which TP is carried out

have been dealt with the same procedure and there

were not special difficulties and limitations

encountered during the training of the models.

An information-gain based filter has been used to

reduce the number of input variables to the most

significant ones. Several different models were tested

in the development of the methodology varying their

specific hyperparameters: inductive decision trees

with variable depth, random forests with variable

number of decision trees, Bayesian Networks with

different number of parent nodes and Neural

Networks with variable number of units in the hidden

layer. We found that the models showing the best

performance in classification were inductive decision

trees and random forests (Tan et al., 2019). Decision

trees were used for both the route and for almost all

the timeframes for the prediction of both the

horizontal flight plan and the flight level with three

exceptions, all regarding the prediction of the lateral

flight plan: a random forest with 20 decision trees was

used for the London-Malta route at Tf-5 and two

random forests with 250 decision trees were used for

both the routes one day before EOBT. In Table 2 and

3 are reported the results obtained for the accuracy in

the prediction of the lateral flight plan. The training

datasets are substantially balanced, especially the one

for the London-Malta route, while the one for the

London-Athens route presents a slight imbalance in

favour of the first lateral flight plan, as highlighted in

Table 4. As can be seen from the tables, the ability of

the models to make correct predictions for the long

term, 15 days before take-off, is better than that of a

classifier that assigns labels randomly. In this time

frame, for the London-Athens route, the model tends

to prefer the first plane of lateral flight, this could be

a further sign of imbalance in the dataset. The results

improve, however, rapidly as the temporal distance

from EOBT decreases, a sign that the models have

been able to effectively learn the information useful

for the classification.

Table 2: Results for horizontal flight plan prediction.

Route

Accuracy

Tf-15 Tf-5 Tf-1

London

–

Athens 38.5% 53.4% 99.9%

London

–

Malta 35.8% 81.2% 99.9%

Table 3: Results for flight level prediction.

Route

Accuracy

Tf-15 Tf-5 Tf-1

London

–

Athens 46.7% 69.9% 88.7%

London

–

Malta 44.2% 72.3% 90.3%

Table 4: Composition of the training dataset for horizontal

flight plan prediction.

Flight plan London – Athens London – Malta

1 36.6% 32.2%

2 30.1% 33.0%

3 33.3% 34.8%

Table 5: Composition of the training dataset for flight level

prediction.

Flight level London – Athens London – Malta

330 23.5% 25.0%

350 31.7% 29.6%

370 27.1% 27.7%

390 17.7% 17.7%

For the flight level, the training datasets show a

more marked imbalance (see Table 5), once again

lower in the case of the London-Malta route. The

models perform better than the random classifier

starting from 15 days before EOBT and the rate of

correct classification increases steadily approaching

the day of the flight.

Using one-hot encoding the components of the

output vectors are all positive numbers that sum to 1

and thus may be interpreted as a probability

A Data-Driven Methodology for Pre-Flight Trajectory Prediction

193

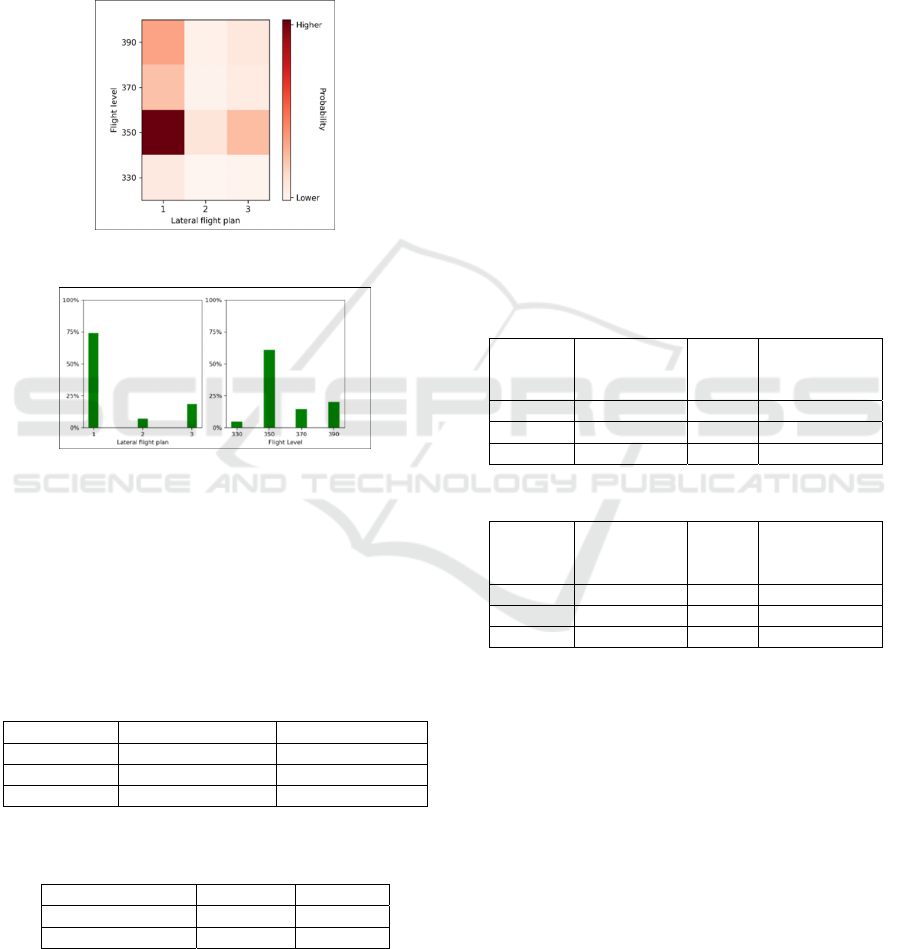
distribution over the possible lateral flight plans (flight

levels) given the vector of inputs. The output of the

model is the lateral flight plan or flight level to which

corresponds the highest probability. Since the choice

of the lateral flight plans and of the flight level are

considered as independent, the product of these proba-

bilities gives the overall probability for the selection of

a flight plan (lateral + vertical), that can be represented

as a heat-map (Figure 1) or a bar plot graph (Figure 2).

Figure 1: Heat-map representation of the joint probability.

Figure 2: Bar plot representation of the joint probability.

As said above, the dataset used for the prediction

of the time of arrival was built starting from the data

relative to the executed flight and carry no

uncertainties. The datasets were almost balanced in

terms of the flight plan used for the flights, for both

the two selected routes (Table 6).

Table 6: Composition of the training dataset for prediction

of the time of arrival.

Fli

lan London – Athens London – Malta

1 36.2% 32.0%

2 30.1% 33.0%

3 33.7% 35.0%

Table 7: Training results for prediction of the time of

arrival.

Route MSE (s

) MAE (s)

London

–

Athens 10.5 1.8

London

–

Malta 4.8 1.4

Also, four different regression algorithms were

tested, optimizing their respective hyperparameters

against a validation dataset: decision trees with

variable depths, random forests with different number

of decision trees, AdaBoost regressors based on

decision trees by varying the depth of the trees and

the number of estimators, artificial Neural Networks

with variable number of hidden layer units. The

models giving the best performance for both the

London-Athens route and the London-Malta route

were two random forest regressor models with 150

estimators, the MSE (Mean Squared Error) and MAE

(Mean Absolute Error) are reported in Table 7.

5 METHODOLOGY

EVALUATION

The evaluation of the performance of a model is of

paramount importance to assess the real capability of

the model to be used in a production environment. To

this end part of the available data is to be kept apart

in a test dataset not used in any step of the

training/validation process.

Table 8: Test results for the route London-Athens.

Time

before

EOBT

Horizontal

flight plan

Flight

level

Flight plan

(horizontal +

vertical)

Tf-15 31% 48% 12%

Tf-5 63% 67% 42%

Tf-1 78% 88% 68%

Table 9: Test results for the route London-Malta.

Time

before

EOBT

Horizontal

flight plan

Flight

level

Flight plan

(horizontal +

vertical)

Tf-15 34% 48% 13%

Tf-5 76% 66% 50%

Tf-1 83% 89% 74%

The test dataset for the evaluation of the models

trained in the P4T methodology comprise 100

randomly chosen flights for each of the selected

routes, with data referring to 15 days, 5 days and 1

day before the EOBT and to the day of execution of

the flight. It is worth pointing out a major difference

between the training/validation dataset and the test

dataset. As described in the previous paragraph, the

training dataset is built by sampling the input

variables from certain distributions defined by their

respective uncertainty, so from each simulated flight

in the training set we get M different records

corresponding to the same target flight plan. The

dataset obtained by this procedure is then split

randomly into a training and a validation dataset,

these two sets are disjoint but it may be possible that

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

194

records referring to the same flight may be present in

both sets. The test dataset, instead, is made up by all

the records of all the flights taken apart for the

evaluation of the models. Since the choice of the

lateral flight plan and of the flight level are considered

as independent, the prediction of the flight plan is a

two steps process that can be performed in parallel.

The M vectors obtained through the sampling

procedure are used as input to the model for the

prediction of the lateral flight plan to obtain M

different predictions, the final output of the model is

the one recurring most often (majority voting). For

the prediction of the flight level there is a unique

vector as input to the model and the output is the most

probable flight level (one-hot encoding).

The performance of the predictive models on the

test dataset are presented in Table 8 for the route from

London to Athens and in Table 9 for the route from

London to Malta. It is worthy to note that a classifier

that chooses the lateral flight plan and the flight level

completely randomly should have an accuracy of

about 8.33%, so even in the long-term case Tf-15 the

accuracy in predicting the flight plan (horizontal and

vertical) is still significantly better than a random

classifier. These results confirm the overall good

performance of the models, in particular the accuracy

of the prediction increases remarkably as the time of

the departure closes in and the forecast values of the

input variables get closer to the values experienced

during the execution of the flight and the

corresponding uncertainties get smaller.

A sequence of WPs is needed as input to test the

performance of the regression model for estimating the

arrival times. These WPs are provided by the model for

the lateral flight plan prediction. The same flights used

to test the models for the prediction of the flight plans

were considered. To assess the performance of the

regression model, the predicted and actual flight times

were compared. But, since the predicted flight plan

may differ from the actual flight plan, instead of

comparing the arrival times on the individual WPs, the

overall duration of the cruise phase was compared.

In Figure 3 there are the histograms of the

absolute values of the difference between the actual

and the predicted duration of the cruise flight for the

route from London to Malta for all the considered

time frames before the EOBT. For this route, the

cruise flight extends for 21 WPs with a duration that

ranges from about 1.5 to about 2.5 hours. It is evident

that the performance of the model gets better

approaching the day of the flight. A similar pattern is

obtained for the route London-Athens: approaching

the EOBT the number of flights with a prediction

error in the range 0-5 minutes increases steadily, with

a corresponding reduction in the number of flights

with high prediction errors. It is expected that the

error in time prediction is related to the error in the

prediction of the horizontal flight plan. In fact, to give

an idea of the improving performance of the

regression model when the horizontal flight plan is

correctly predicted, Figure 4 shows the absolute value

of the error limited only to the flights with a correct

prediction of the lateral flight plan for the route

London-Malta; similar results were obtained for the

other route. For both the routes, the error doesn’t

exceed 360 seconds (6 minutes), and the number of

flights with a value of the error below 120 s increases

remarkably approaching the day of the flight.

Another view of the results is presented in Figure

5, which includes three scatter plots for the London-

Malta route, one for each considered time frame,

going from left to right, Tf-15, Tf-5 and Tf-1. The

plots report the actual duration of the cruise phase of

the flight on the x-axis and the predicted duration on

the y-axis. Each point represents a flight with a color

that depends on the correctness of the prediction of

the 3D flight plan: violet both horizontal and vertical

flight plan are correctly predicted, blue only the

vertical flight plan prediction is correct, light blue

only the horizontal flight plan prediction is correct,

yellow both are incorrectly predicted. The nearer the

point to the bisector, line in red, the lesser is the error

in the prediction of the duration of the cruise flight.

The figure confirms that if both lateral flight plan and

flight level or if only lateral flight plan are correctly

predicted then the error on the predicted duration is

very low. Very similar results were obtained for the

route from London to Athens.

6 CONCLUSIONS AND FUTURE

WORKS

This paper presented a data driven methodology for

trajectory prediction on long, medium and short

terms, developed within the framework of the

PIU4TP project. Its main peculiarity is the capability

to manage the uncertainties that by nature affect the

input data to the trajectory prediction process.

The proposed approach was developed and tested

using a simplified use case, based on simulated data.

Specifically, only two factors that influence the

selection of the optimal flight plan were considered,

that is, weather conditions and take-off weight. Indeed,

the objective is to demonstrate a proof of concept and

to provide evidences of the proposed methodology

applicability and potential benefits arising from its use.

A Data-Driven Methodology for Pre-Flight Trajectory Prediction

195

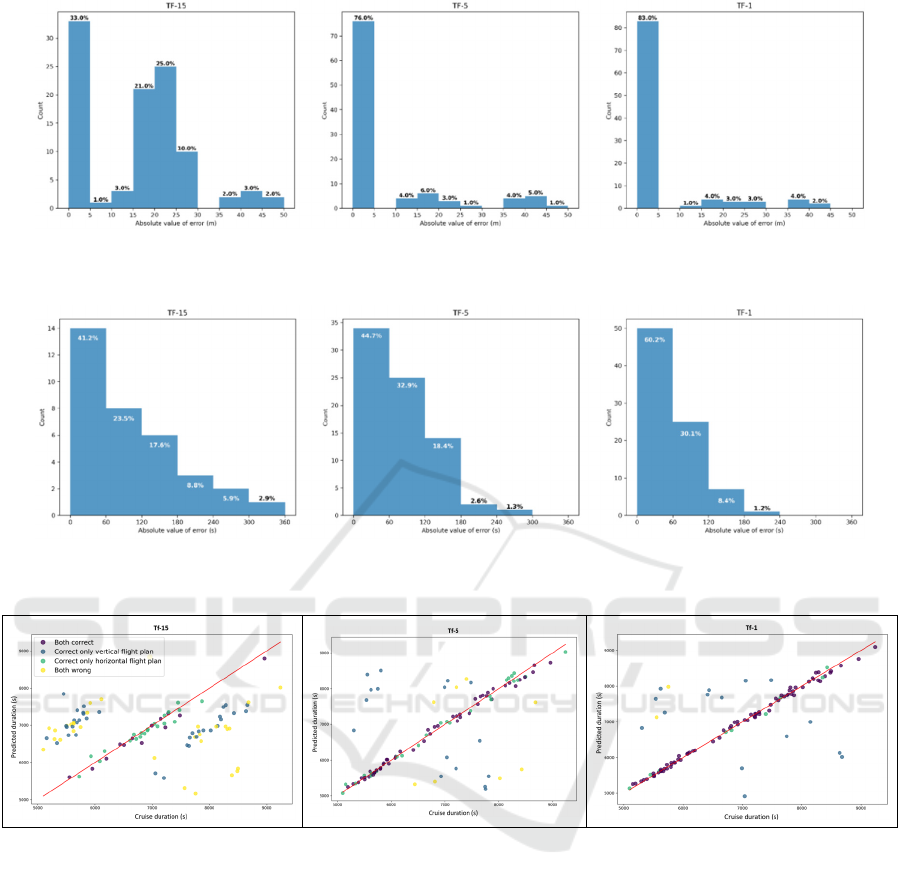
Figure 3: London-Malta route, histograms of the absolute difference between actual and predicted duration, in minutes (m),

of the cruise flight.

Figure 4: London-Malta route, histograms of the absolute difference between actual and predicted duration, in seconds (s), of

the cruise flight limited only to the flights with a correct prediction of the flight plan.

Figure 5: London-Malta scatter-plots of the actual vs. the predicted duration of the cruise flight.

The simulated data were produced within the

framework of the PIU4TP project by defining suitable

simulation models and exploiting the data found in

the open access databases. Preliminary assessment of

the methodology highlighted that it is able to catch

the information that are available in the input data,

including the related uncertainties, and to exploit

them to reliably predict in advance the flown

trajectory. The methodology’s output includes a

complete spatial prediction of the flight plan

(horizontal and vertical) enriched with an estimation

of the time of flight (limited to the cruise phase of the

flight). The probability of the prediction is provided,

too. The accuracy of the prediction depends on the

time in advance with which it is computed and

increases sharply as the time approaches the day of

the flight, reaching values around 70% one day before

the EOBT. This behaviour is due to the weather

forecasts improve and the uncertainties on the input

data reduce as the EOBT approaches. When the three-

dimensional spatial flight plan is correctly predicted,

the estimation of the duration of the cruise phase of

the flight is very accurate, too, with a worst-case error

less than 6 minutes also on long term prediction.

Finally, the achieved percentage of correct

predictions for the horizontal flight plan at Tf-1 (from

78% to 83%) is in line with the ones presented in

(Cordero et al., 2018), where the success rate of the

predictions performed 8 hours before EOBT varies

between 82% and 90%. It shall be considered that in

the two works the predictions are performed at

different time frames (24 hours versus 8 hours before

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

196

flight schedule) and that different scenarios are

considered.

In order to further mature the concept, future

research shall focus on more complex use cases,

which consider a wider set of input parameters, and

analyze actual flight data.

ACKNOWLEDGEMENTS

The PIU4TP project has received funding from the

SESAR Joint Undertaking under the European

Union’s Horizon 2020 research and innovation

programme under grant agreement No 783287.

REFERENCES

AIRBUS (1998). Getting to grips with the cost index. In

Flight Operations Support & Line Assistance, Issue II.

Alligier, R., Gianazza, D., and Durand, N. (2013). Learning

the aircraft mass and thrust to improve the ground-

based trajectory prediction of climbing flights. In

Transportation Research Part C: Emerging

Technologies, Vol. 36, pp. 45-60.

Cordero, J. M., et al. (2018). Traffic Characterization for a

Dynamic and Adaptive Trajectory Prediction Data-

Driven Approach. In 10

SESAR Innovation Days.

de Leege, A., van Paassen, M., Mulder, M. (2013). A

machine learning approach to trajectory prediction. In

AIAA Guidance, Navigation, and Control (GNC)

Conference. AIAA.

Engage Thematic challenge 2 (2019). Data-driven

trajectory prediction. Engage KTN, Edition 3.0.

ERA5 (2021). Reanalysis dataset. At

https://www.ecmwf.int/en/forecasts/datasets/reanalysis

-datasets/era5. ECMWF.

Fernández, E. C., et al. (2017). DART: A Machine-

Learning Approach to Trajectory Prediction and

Demand-Capacity Balancing. In Seventh SESAR

Innovation Days. SESAR.

Fukuda, Y., Shirakawa, M., Senoguchi, A. (2010).

Development and evaluation of trajectory prediction

model. In Proceedings of 27th International Congress

of the Aeronautical Sciences (ICAS).

Guan, X., Lv, R., Sun, L., Liu, Y. (2016). A study of 4D

trajectory prediction based on machine deep learning.

In Proceedings of the 2016 12thWorld Congress on

Intelligent Control and Automation (WCICA).

Haiden, T., et al. (2019). Evaluation of ECMWF forecasts,

including the 2019 upgrade. In ECMWF Technical

Memoranda. ECMWF

Ma, L., Tian, S. (2020). A hybrid CNN-LSTM model for

aircraft 4D trajectory prediction. In IEEE Access, vol.

8, pp. 134668-134680. IEEE.

Nuic, A., Poles, D., Mouillet, V. (2010). BADA: An

advanced aircraft performance model for present and

future ATM systems. In International Journal of

Adaptive Control & Signal Processing, Vol. 24, pp.

850- 866.

Park, S.H.; Kim, B.; Kang, C.M.; Chung, C.C.; Choi, J.W.

(2018). Sequence-to-sequence prediction of vehicle

trajectory via LSTM encoder-decoder architecture. In

Proceedings of the 2018 IEEE Intelligent Vehicles

Symposium (IV).

Rivas, D. Franco, A., Valenzuela, A. (2017). Analysis of

aircraft trajectory uncertainty using Ensemble Weather

Forecasts. In Proceedings of 7

European Conference

for Aeronautics and Space Sciences (EUCASS).

Rodríguez-Sanz, A., et al. (2019). 4D-trajectory time

windows: definition and uncertainty management. In

Aircraft Engineering and Aerospace Tech., Vol. 91 No.

5, pp. 761-782.

Sankararaman, S., Daigle, M. (2017). Uncertainty

quantification in trajectory prediction for aircraft

operations. In AIAA Guidance, Navigation, and Control

(GNC) Conference. AIAA.

Schuster, W. (2015). Trajectory prediction for future air

traffic management–complex manoeuvres and taxiing.

In Aeronaut. J., Vol. 119 No. 1212, pp. 121–143.

Tan, P. N., Steinbach, M., Karpatne, A., Kumar, V. (2019).

Introduction to Data Mining. Pearson. 2

edition.

Tastambekov, K., Puechmorel, S., Delahaye, D., Rabut, C

(2014). Aircraft trajectory forecasting using local

functional regression in Sobolev space. In Transp. Res.

Part C Emerg. Technol., Vol. 39, pp. 1–22.

Uzun, M., Koyuncu, E. (2017). Data-driven trajectory

uncertainty quantification for climbing aircraft to

improve ground-based trajectory prediction. In

ANADOLU Univ. J. Sci. Technol. - Appl. Sci. Eng., pp.

323–345.

Wang, Z., Liang, M., Delahaye, D. (2017). Short-term 4D

Trajectory Prediction Using Machine Learning

Methods. In Seventh SESAR Innovation Days. SESAR.

Wu, H.; Chen, Z.; Sun, W.; Zheng, B.; Wang, W. (2017).

Modeling Trajectories with Recurrent Neural

Networks. In Proceedings of the Twenty-Sixth

International Joint Conference on Artificial

Intelligence (IJCAI).

Zazzaro, G., et al. (2020). P4T: A Methodology to Support

the Flight Trajectory Prediction. In Tenth SESAR

Innovation Days. SESAR.

Zeh, T., Rosenow, J., Alligier, R., Fricke, H. (2020).

Prediction of the propagation of trajectory uncertainty

for climbing aircraft. In Proceedings of AIAA/IEEE

39th Digital Avionics Systems Conference (DASC).

Zhang, J., Liu, J., Hu, R., Zhu, H. (2018). Online four-

dimensional trajectory prediction method based on

aircraft intent updating. In Aerosp. Sci. Technol., Vol.

77, pp. 774–787.

Zhang, X., Mahadevan, S. (2020). Bayesian neural

networks for flight trajectory prediction and safety

assessment. In Decision Support Systems, Vol. 131.

A Data-Driven Methodology for Pre-Flight Trajectory Prediction

197