
Nonlinear Complementarity Problems for n-Player Strategic
Chance-constrained Games
Shangyuan Zhang
1,2 a
, Makhlouf Hadji
1 b
, Abdel Lisser
2 c
and Yacine Mezali
1 d
1
Institut de Recherche Technologique SystemX, 8 Avenue de la Vauve, 91120 Palaiseau, France
2
CentraleSupelec, L2S, Université Paris Saclay, 3 Rue Curie Joliot, 91190, Gif-sur-Yvette, France
Keywords:
Chance-constrained Optimization, Game Theory, Nonlinear Complementarity Problem, Normal/Cauchy
Distribution.
Abstract:
In this paper, we focus on n-player strategic chance-constrained games where the payoff of each player fol-
lows either Cauchy or normal distribution. We transform the Nash equilibrium problem into its equivalent
nonlinear complementarity problem (NCP) through the Karush-Kuhn-Tucker (KKT) conditions. Then, we
prove the existence of the Nash equilibrium by the mean of Brouwer’s fixed-point theorem. In order to show
the efficiency of our approach, we perform numerical experiments on a set of randomly generated instances.
1 INTRODUCTION
Nash equilibrium is a crucial concept widely studied
in game theory literature. John Von Neumann proved
the existence of mixed strategy saddle point equilib-
rium for two-player finite zero-sum games (Neumann,
1928). John Nash extended this result to finite games
with n players and deterministic payoffs (Nash et al.,
1950).
In real-life problems, games input data might be
affected by different uncertainty sources leading to
numerous studies on games under uncertainty, namely
stochastic games. The oligopoly market is a typical
example where the payoff of each player is a random
variable. Generally, the players in an oligopoly mar-
ket are risk neutral. Therefore, they consider the ex-
pectation of random payoffs and constraints (De Wolf
and Smeers, 1997; DeMiguel and Xu, 2009; Jadamba
and Raciti, 2015; Ravat and Shanbhag, 2011; Valen-
zuela and Mazumdar, 2007; Xu and Zhang, 2013).
When the players are risk averse, chance-
constrained games can be used efficiently (Charnes
and Cooper, 1963; Cheng and Lisser, 2012; Prékopa,
2013). In (Singh et al., 2016a), the authors prove the
existence of Nash equilibrium for an n-player finite
strategic chance-constrained game under elliptical
a
https://orcid.org/0000-0003-0230-8618
b
https://orcid.org/0000-0003-1048-753X
c
https://orcid.org/0000-0003-1318-6679
d
https://orcid.org/0000-0003-1912-9093
distributions. Furthermore, (Singh et al., 2016b) show
that a Nash equilibrium problem for a two-player ran-
dom bi-matrix game is equivalent to a linear com-
plementarity problem (LCP, for short) when each
player’s payoff follows independent Cauchy distribu-
tions. When the player’s payoffs are normally dis-
tributed, Nash equilibrium is equivalent to a nonlinear
complementarity problem (NCP, for short). In (Singh
and Lisser, 2018), the authors characterized the set
of Nash equilibria of a chance-constrained game us-
ing the solution set of a variational inequality prob-
lem. In the case where the probability distributions
are not known in advance, (Singh et al., 2017) stud-
ied distributionally robust chance-constrained games.
Various approaches were considered in the literature
for chance-constrained two-player stochastic zero-
sum games (Blau, 1974; Cassidy et al., 1972; Charnes
et al., 1968; Cheng et al., 2016; Song, 1992).
In addition, stochastic games with deterministic
payoffs and chance-constrained strategies were also
studied in the literature. For the case of two-player
zero sum games, (Singh and Lisser, 2019) show that
the saddle point is equivalent to a primal-dual pair of
second order cone programs. As for the n-player gen-
eral sum games with joint chance constraints, (Peng
et al., 2018) show the existence of Nash equilibrium
when the random linear constraints are independently
normally distributed.
In this paper, we extend the two-player results in
(Singh et al., 2016b) to the case of n-player stochastic
games. We show that the Nash equilibrium problem
94
Zhang, S., Hadji, M., Lisser, A. and Mezali, Y.
Nonlinear Complementarity Problems for n-Player Strategic Chance-constrained Games.
DOI: 10.5220/0011005600003117
In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 94-104
ISBN: 978-989-758-548-7; ISSN: 2184-4372
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

can be reformulated as an NCP when the player’s pay-
off follows either Logistic or Normal distributions.
We also prove the existence of Nash equilibrium un-
der different conditions using Brouwer’s fixed-point
theorem. As for the numerical experiments, we solve
several randomly generated game instances to show
the performance of our approaches. Unlike (Singh
et al., 2016b), we solve instances where the size
ranges from (2 × 2) to (6 × 6 × 6 × 6 × 6 × 6).
The chance-constrained game model can be ap-
plied to solve real-life problems, e.g., competition
in electricity markets (Lee and Baldick, 2003) and
decision-making for autonomous vehicles (Black-
more et al., 2006). When it comes to the electric-
ity market, companies seek to maximize their profits
by controlling prices or production quantities. As the
reward function is random, we can model this situ-
ation by our chance-constrained game model to de-
termine each company’s Nash equilibrium strategy.
In the decision-making process, autonomous vehi-
cles seek to avoid potential collisions with obstacles
while taking into account perceptional errors and en-
vironmental disturbances (Blackmore et al., 2006). In
the case of multiple vehicles, the chance-constrained
game theoretical framework can be used to model the
vehicles decisions under uncertainty.
The remainder of this paper is organized as fol-
lows: Section 2 introduces our chance-constrained
modelling framework. In Section 3, we prove the
existence of Nash equilibrium by Brouwer’s fixed-
point theorem, and reformulate our stochastic chance-
constrained games as an NCP. Section 4 is dedicated
to numerical simulations. Finally, Section 5 con-
cludes the paper.
2 CHANCE-CONSTRAINED
GAMES
We consider an n-player chance-constrained finite
strategic game with random payoffs. Let I =
{1, 2, 3, . . . n} be the set of players. A
i
, i ∈ I is the ac-
tion set of player i with components a
i
. The set of
mixed strategies of player i includes all probability
distributions over its action set, defined by the follow-
ing k-simplex:
X
i
= {τ
i
∈ R
k+1
|
k+1
∑
j=1
τ
i j
= 1, τ
i j
≥ 0}, (1)
where τ
i j
is the jth component of vector τ
i
, k = |A
i
|−
1 with |A
i
| the cardinality of the set A
i
. Specifically,
τ
i j
is the probability for the player i to choose the jth
action in A
i
. Let X =
∏
n
i=1
X
i
be the set of strategy
profiles for all players with components τ ∈ X. The
pure strategy set of player i is defined by
Y
i
= {y
i
∈ X
i
| ∃ j ∈ {1, 2, ..|A
i
|}, s.t. y
i j
= 1}, (2)
which is a subset of X
i
. The set of pure strategy pro-
files for all players is defined by Y =
∏
n
i=1
Y
i
, with
y ∈ Y its element. In order to describe the strategy of
one specific player in response to other players, we
denote X
−i
=
∏
n
j=1, j6=i
X
j
the strategy set of all play-
ers except player i, with components τ
−i
∈ X
−i
. Sim-
ilarly, we denote Y
−i
=
∏
n
j=1, j6=i
Y
j
where y
−i
∈ Y
−i
is
the related generic element.
We assume that the pure strategy y based payoff
of player i denoted by r
ω
i
(y) is a random variable.
Given the payoff corresponding to each pure strat-
egy, the payoff of player i for a mixed strategy τ ∈ X
is a linear combination of pure-strategy payoffs, i.e.,
r
ω
i
(τ) =
∑
y∈Y
n
∏
k=1
τ
k j
y
k
r
ω
i
(y), (3)
where j
y
k
is the index of y
i
’s component.
In a chance-constrained game, the objective of
each player is to maximize the expected payoff under
a given level of confidence, i.e.,
u
α
i
i
(τ) = sup{u|P(r
w
i
(τ) ≥ u) ≥ α
i
}. (4)
In the next section, we show the existence of Nash
equilibrium for the chance-constrained games, and
derive the NCP reformulations.
3 NCP FOR n-PLAYER
CHANCE-CONSTRAINED
GAME
In this section, we assume that the random pay-
offs of each player follow two probability distribu-
tions, namely Cauchy and Normal distributions. For
each distribution, we derive a deterministic equivalent
NCP.
3.1 Independent Cauchy Distributed
Payoffs
We assume that the pure strategy payoffs for
all players follow independent Cauchy distribu-
tion, i.e. r
ω
i
(y) ∼ C(µ
i
(y), σ
i
(y)) for all y ∈ Y .
Then, for a mixed strategy τ ∈ X, the payoff
r
ω
i
(τ) =
∑
y∈Y
∏
n
k=1
τ
k j
y
k
r
ω
i
(y) of player i is Cauchy
distributed with µ
i
(τ) =
∑
y∈Y
∏
n
k=1
τ
k j
y
k
µ
i
(y) and
σ
i
(τ) =
∑
y∈Y
∏
n
k=1
τ
k j
y
k
σ
i
(y). Therefore, Z
C
i
=
Nonlinear Complementarity Problems for n-Player Strategic Chance-constrained Games
95

r
ω
i
−µ
i
(τ)
σ
i
(τ)
follows a standard Cauchy distribution
C(0, 1). Let F
−1
Z
C
i
be the quantile function of the stan-
dard Cauchy distribution.
For each player i, the chance-constrained payoff
with confidence level α
i
is:
u
α
i
i
(τ) = sup{u|P(r
w
i
(τ) ≥ u) ≥ α
i
}
= sup{u|P(
r
w
i
(τ) − µ
i
(τ)
σ
i
(τ)
≥
u −
∑
y∈Y
∏
n
k=1
τ
k j
y
k
µ
i
(y)
∑
y∈Y
∏
n
k=1
τ
k j
y
k
σ
i
(y)
) ≥ α
i
}
= sup{u|F
Z
C
i
(
u −
∑
y∈Y
∏
n
k=1
τ
k j
y
k
µ
i
(y)
∑
y∈Y
∏
n
k=1
τ
k j
y
k
σ
i
(y)
)
≤ 1 − α
i
}
=
∑
y∈Y
n
∏
k=1
τ
k j
y
k
µ
i
(y)
+ F
−1
Z
C
i
(1 − α
i
)
∑
y∈Y
n
∏
k=1
τ
k j
y
k
σ
i
(y)
=
∑
y∈Y
n
∏
k=1
τ
k j
y
k
(µ
i
(y) + F
−1
Z
C
i
(1 − α
i
)σ
i
(y))
=
∑
y∈Y
n
∏
k=1
τ
k j
y
k
A
i
(y)
= V
T
i
(τ
−i
)τ
i
,
(5)
where V
i
(τ
−i
) ∈ R
|A
i
|
.
V
i
(τ
−i
) =
∑
y
−i
∈Y
−i
A
i
(y
1
i
, y
−i
)
∏
n
k=1, k6=i
τ
k j
y
k
)
.
.
.
∑
y
−i
∈Y
−i
A
i
(y
m
i
, y
−i
)
∏
n
k=1, k6=i
τ
k j
y
k
)
.
.
.
∑
y
−i
∈Y
−i
A
i
(y
|A
i
|
i
, y
−i
)
∏
n
k=1, k6=i
τ
k j
y
k
)
,
(6)
where y
j
i
∈ R
|A
i
|
is a unit vector with jth element
equal to 1.
3.1.1 Existence of Nash Equilibrium
In the following, we prove the existence of Nash equi-
librium for stochastic games with Cauchy distribu-
tion.
Theorem 1. There always exists a Nash equilib-
rium for every n-player strategic chance-constrained
game, where the payoff of each player is indepen-
dently Cauchy distributed.
The proof of this theorem is similar to the proof
given in (Nash, 1951).
3.1.2 NCP Formulation
Given a strategy profile τ of all players, the chance-
constrained payoff of player i is u
α
i
i
(τ) = V
T
i
(τ
−i
)τ
i
.
The best response of player i, given the strategy pro-
file τ
−i
for all other players, can be obtained by solv-
ing the following optimization problem:
max
τ
i
V
T
i
(τ
−i
)τ
i
s.t.
|A
i
|
∑
j=1
τ
i j
= 1,
τ
i j
≥ 0, ∀ j ∈ {1, 2, ..., |A
i
|}.
(7)
The objective function in (7) is concave subject to
linear constraints. Hence, Slater’s condition is satis-
fied and the KKT conditions are necessary and suffi-
cient for optimality.
By KKT conditions, the best response of player i
can be reformulated as follows:
0 ≤ τ
i
⊥ −V
i
− λ
i
1
1
|e
i
|
+ λ
i
2
1
|e
i
|
≥ 0,
0 ≤ λ
i
1
⊥
|A
i
|
∑
j=1
τ
i j
− 1 ≥ 0,
0 ≤ λ
i
2
⊥ 1 −
|A
i
|
∑
j=1
τ
i j
≥ 0,
(8)
where 1
n
denotes all-ones vector with size n.
Putting together the KKT conditions for all play-
ers, we obtain the Nash equilibrium of the chance-
constrained game by solving the following NCP:
0 ≤ ζ ⊥ G(ζ) ≥ 0, (9)
where
ζ = (τ
1
, τ
2
, ..., τ
n
, λ
1
1
, λ
1
2
, ..., λ
n
1
, λ
n
2
) ∈ R
∑
i=1
n|A
i
|+2n
,
(10)
and
G(ζ) =
−V
1
− λ
1
1
1
|A
1
|
+ λ
1
2
1
|A
1
|
−V
2
− λ
2
1
1
|A
2
|
+ λ
2
2
1
|A
2
|
.
.
.
−V
n
− λ
n
1
1
|A
n
|
+ λ
n
2
1
|A
n
|
∑
|A
1
|
j=1
τ
1 j
− 1
1 −
∑
|A
1
|
j=1
τ
1 j
∑
|A
2
|
j=1
τ
2 j
− 1
1 −
∑
|A
2
|
j=1
τ
2 j
.
.
.
∑
|A
n
|
j=1
τ
n j
− 1
1 −
∑
|A
n
|
j=1
τ
n j
. (11)
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
96

3.2 Independent Normally Distributed
Payoffs
In the following, we consider normally dis-
tributed pure strategy payoffs for all the play-
ers. Thus, for a mixed strategy τ ∈ X , the
payoff r
ω
i
(τ) =
∑
y∈Y
∏
n
k=1
τ
k j
y
k
r
ω
i
(y) of player
i follows a normal distribution N(µ
i
(τ), σ
2
i
(τ))
with µ
i
(τ) =
∑
y∈Y
∏
n
k=1
τ
k j
y
k
µ
i
(y) and σ
2
i
(τ) =
∑
y∈Y
∏
n
k=1
τ
2
k j
y
k
σ
2
i
(y).
Therefore, Z
N
i
=
r
ω
i
−µ
i
(τ)
σ
i
(τ)
follows a standard nor-
mal distribution N(0, 1). Let F
−1
Z
N
i
be the quantile
function of the standard normal distribution.
For each player i, the chance-constrained payoff
with confidence level α
i
is:
u
α
i
i
(τ) = sup{u|P(r
w
i
(τ) ≥ u) ≥ α
i
}
= sup{u|P(
r
w
i
(τ) − µ
i
(τ)
σ
i
(τ)
≥
u −
∑
y∈Y
∏
n
k=1
τ
k j
y
k
µ
i
(y)
q
∑
y∈Y
∏
n
k=1
τ
2
k j
y
k
σ
2
i
(y)
) ≥ α
i
}
= sup{u|F
Z
N
i
(
u −
∑
y∈Y
∏
n
k=1
τ
k j
y
k
µ
i
(y)
q
∑
y∈Y
∏
n
k=1
τ
2
k j
y
k
σ
2
i
(y)
)
≤ 1 − α
i
}
=
∑
y∈Y
n
∏
k=1
τ
k j
y
k
µ
i
(y)+
F
−1
Z
C
i
(1 − α
i
)
s
∑
y∈Y
n
∏
k=1
τ
2
k j
y
k
σ
2
i
(y)
= P
T
i
(τ
−i
)τ
i
+C
i
kQ
1
2
i
(τ
−i
)τ
i
k,
(12)
where C
i
= F
−1
Z
C
i
(1 − α
i
) and P
i
(τ
−i
) ∈ R
|A
i
|
,
P
i
(τ
−i
) =
∑
y
−i
∈Y
−i
(µ
i
(y
1
i
, y
−i
)
∏
n
k=1, k6=i
τ
k j
y
k
)
.
.
.
∑
y
−i
∈Y
−i
(µ
i
(y
m
i
, y
−i
)
∏
n
k=1, k6=i
τ
k j
y
k
)
.
.
.
∑
y
−i
∈Y
−i
(µ
i
(y
|A
i
|
i
, y
−i
)
∏
n
k=1, k6=i
τ
k j
y
k
)
,
(13)
and Q
1
2
i
(τ
−i
) ∈ M
|A
i
| ×|A
i
|
is a diagonal matrix
Q
1
2
i
(τ
−i
) =
q
1
2
1
(τ
−i
) . . . 0
.
.
.
.
.
.
.
.
.
0 . . . q
1
2
|A
i
|
(τ
−i
)
, (14)
where q
1
2
m
(τ
−i
) =
q
∑
y
−i
∈Y
−i
(σ
2
i
(y
m
i
, y
−i
)
∏
n
k=1, k6=i
τ
2
k j
y
i
).
3.2.1 Existence of Nash Equilibrium
Lemma 1. If a function f (x) is strictly concave
and continuous on a compact convex set, then
argmax
x
f (x) is a single-valued correspondence.
Proof. A continuous function can always reach its
maximum on a compact set. A strictly concave func-
tion on a convex set has no more than one maximum.
Thus, the function f has one maximum, which im-
plies that argmax
x
f (x) is a single-valued correspon-
dence.
Theorem 2. Consider an n-player chance-
constrained strategic game. If the pure strategy
payoff of each player follows an independent normal
distribution, then the Nash equilibrium exists for
confidence level α ∈ [0.5, 1).
Proof. Firstly we construct a function
br
i
(τ) = argmax
τ
∗
i
(u
i
(τ
∗
i
, τ
−i
) − ||τ
∗
i
− τ
i
||). (15)
For α ∈ [0.5, 1), br
i
is well-defined since f
i
(τ
−i
) =
u
i
(τ
∗
i
, τ
−i
) − ||τ
∗
i
− τ
i
|| is a strictly concave function.
Therefore argmax
τ
−i
f
i
(τ
−i
) is a singleton by lemma
1. As f
i
(τ
−i
) is continuous, we can prove that br
i
(τ)
is a continuous function by the Maximum theorem.
By concatenating br
i
, we have
br(τ) =
n
∏
i=1
br
i
(τ
−i
). (16)
Since br is a continuous function from a con-
vex compact subset to itself, according to Brouwer’s
fixed-point theorem, there exists a point τ
∗
where τ
∗
=
br(τ
∗
). Based on the definition of br, we can conclude
that τ
∗
is a Nash equilibrium for this game.
3.2.2 NCP Formulation
For a given strategy profile τ
−i
for all other players
and α ∈ [0.5, 1), a best response strategy of player i
can be obtained by solving the following optimization
problem:
max
τ
i
P
T
i
(τ
−i
)τ
i
+C
i
kQ
1
2
i
(τ
−i
)τ
i
k
s.t.
|A
i
|
∑
j=1
τ
i j
= 1,
τ
i j
≥ 0, ∀ j ∈ {1, 2, ..., |A
i
|}.
(17)
Nonlinear Complementarity Problems for n-Player Strategic Chance-constrained Games
97

Here the objective function is concave and the
constraints are linear, thus Slater’s condition holds
and the KKT conditions are both necessary and suffi-
cient for optimality.
By KKT conditions, the best response of player i
can be reformulated as follows
0 ≤ τ
i
⊥ − P
i
(τ
−i
) −C
i
Q
i
(τ
−i
)τ
i
kQ
1
2
i
(τ
−i
)τ
i
k
− λ
i
1
1
|e
i
|
+ λ
i
2
1
|e
i
|
≥ 0,
0 ≤ λ
i
1
⊥
|A
i
|
∑
j=1
τ
i j
− 1 ≥ 0,
0 ≤ λ
i
2
⊥ 1 −
|A
i
|
∑
j=1
τ
i j
≥ 0.
(18)
Putting together the KKT conditions for all play-
ers, we can obtain the Nash equilibrium of the
stochastic game by solving the following NCP:
0 ≤ ζ ⊥ G(ζ) ≥ 0, (19)
where
ζ = (τ
1
, τ
2
, ..., τ
n
, λ
1
1
, λ
1
2
, ..., λ
n
1
, λ
n
2
) ∈ R
∑
i=1
n|A
i
|+2n
,
(20)
and
G(ζ) =
−P
1
(τ
−1
) −C
1
Q
1
(τ
−1
)τ
1
kQ
1
2
1
(τ
−1
)τ
1
k
− λ
1
1
1
|e
1
|
+ λ
1
2
1
|e
1
|
−P
2
(τ
−2
) −C
2
Q
2
(τ
−2
)τ
2
kQ
1
2
2
(τ
−2
)τ
2
k
− λ
2
1
1
|e
2
|
+ λ
2
2
1
|e
2
|
.
.
.
−P
n
(τ
−n
) −C
n
Q
n
(τ
−n
)τ
n
kQ
1
2
n
(τ
−n
)τ
n
k
− λ
n
1
1
|e
n
|
+ λ
n
2
1
|e
n
|
∑
|A
1
|
j=1
τ
1 j
− 1
1 −
∑
|A
1
|
j=1
τ
1 j
∑
|A
2
|
j=1
τ
2 j
− 1
1 −
∑
|A
2
|
j=1
τ
2 j
.
.
.
∑
|A
n
|
j=1
τ
n j
− 1
1 −
∑
|A
n
|
j=1
τ
n j
.
(21)
4 NUMERICAL EXPERIMENTS
In this section, we generate random instances in Mat-
lab and we use PATH Solver to come up with Nash
equilibrium.
PATH Solver is an implementation of a stabi-
lized Newton method for the solution of the Mixed
Complementarity Problem (MCP) (Dirkse and Ferris,
1995). For our concern, once the analytic form of
G(x) and its Jacobian is known and coded, we can
directly use PATH to solve our NCP.
As a matter of illustration, we give two examples
of (3 × 3 × 3) random games with different distribu-
tions and then analyze the corresponding results.
4.1 (3 × 3 × 3) Random Games with
Cauchy Distribution
Three examples of randomly generated (3 × 3 × 3)
games, following independent Cauchy distribution
C
i
(a) ∼ (µ(a), σ(a)), are given below. The mean µ
and deviation σ are uniformly generated between 1
and 3 as follows:
1.
µ
1
(:, :, 1) =
1 1 2
2 3 1
1 3 1
, µ
1
(:, :, 2) =
2 1 3
3 1 2
1 2 2
,
µ
1
(:, :, 3) =
2 1 2
1 3 2
3 1 3
σ
1
(:, :, 1) =
1 2 1
3 2 2
3 2 2
, σ
1
(:, :, 2) =
3 2 2
3 3 3
2 2 3
,
σ
1
(:, :, 3) =
2 1 1
2 1 3
2 2 1
µ
2
(:, :, 1) =
1 2 2
1 1 1
1 3 3
, µ
2
(:, :, 2) =
3 1 1
2 2 2
1 2 3
,
µ
2
(:, :, 3) =
1 1 1
1 2 1
1 2 3
σ
2
(:, :, 1) =
1 2 2
3 2 3
3 1 2
, σ
2
(:, :, 2) =
2 2 2
1 3 3
2 2 1
,
σ
2
(:, :, 3) =
3 1 3
3 1 1
3 2 3
µ
3
(:, :, 1) =
1 3 3
2 3 2
2 3 3
, µ
3
(:, :, 2) =
1 2 2
1 2 2
3 3 3
,
µ
3
(:, :, 3) =
3 1 2
2 3 1
1 1 3
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
98

σ
3
(:, :, 1) =
3 1 1
2 3 2
2 1 1
, σ
3
(:, :, 2) =
3 1 3
3 2 2
3 2 3
,
σ
3
(:, :, 3) =
2 1 2
2 1 3
3 1 3
2.
µ
1
(:, :, 1) =
1 1 1
1 1 2
1 2 3
, µ
1
(:, :, 2) =
2 1 3
2 2 1
2 3 1
,
µ
1
(:, :, 3) =
2 1 1
2 3 1
2 1 1
σ
1
(:, :, 1) =
2 3 1
2 3 3
1 3 3
, σ
1
(:, :, 2) =
3 2 1
3 1 1
3 2 3
,
σ
1
(:, :, 3) =
1 2 3
1 2 2
1 1 3
µ
2
(:, :, 1) =
2 1 3
2 2 1
1 1 3
, µ
2
(:, :, 2) =
2 1 3
3 2 3
3 2 1
,
µ
2
(:, :, 3) =
1 2 1
2 2 3
1 1 3
σ
2
(:, :, 1) =
2 3 1
3 3 2
1 2 1
, σ
2
(:, :, 2) =
1 1 2
1 1 1
3 1 3
,
σ
2
(:, :, 3) =
1 2 1
1 1 1
1 3 1
µ
3
(:, :, 1) =
1 3 1
1 2 3
2 1 3
, µ
3
(:, :, 2) =
2 2 1
1 1 1
3 3 3
,
µ
3
(:, :, 3) =
2 3 3
2 3 2
3 1 2
σ
3
(:, :, 1) =
1 2 1
3 3 2
2 1 2
, σ
3
(:, :, 2) =
3 1 3
3 1 3
3 1 3
,
σ
3
(:, :, 3) =
1 1 2
3 2 3
1 1 2
3.
µ
1
(:, :, 1) =
1 2 3
1 2 2
2 2 2
, µ
1
(:, :, 2) =
2 1 2
3 2 3
3 2 1
,
µ
1
(:, :, 3) =
1 2 2
1 2 2
3 2 2
σ
1
(:, :, 1) =
3 1 1
2 1 2
3 1 2
, σ
1
(:, :, 2) =
2 3 1
3 3 1
2 3 3
,
σ
1
(:, :, 3) =
1 3 3
2 2 3
2 2 2
µ
2
(:, :, 1) =
2 1 1
1 1 2
2 3 3
, µ
2
(:, :, 2) =
2 3 1
3 3 1
2 2 2
,
µ
2
(:, :, 3) =
1 2 3
1 3 2
3 2 3
σ
2
(:, :, 1) =
3 3 3
2 3 2
1 1 3
, σ
2
(:, :, 2) =
3 3 2
1 2 1
3 3 1
,
σ
2
(:, :, 3) =
2 3 1
3 1 1
3 2 1
µ
3
(:, :, 1) =
3 2 3
2 1 2
1 1 3
, µ
3
(:, :, 2) =
3 3 3
2 3 2
3 1 3
,
µ
3
(:, :, 3) =
2 1 2
2 2 3
3 3 3
σ
3
(:, :, 1) =
2 1 3
1 2 3
2 2 3
, σ
3
(:, :, 2) =
3 2 3
2 1 2
3 1 3
,
σ
3
(:, :, 3) =
1 1 1
2 2 2
2 2 1
For the above randomly generated examples, the
mean and the deviation of each player’s payoff use
(3 × 3 × 3) tensors since there are 3 players in the
Nonlinear Complementarity Problems for n-Player Strategic Chance-constrained Games
99

game and each player has 3 actions to choose. For in-
stance, if each player chooses the first action as their
strategy, then the payoff for player 1 follows a Cauchy
distribution with mean parameter µ = 1 and scale pa-
rameter σ = 1. Table 1 summarizes the Nash equi-
librium of the three examples for different confidence
levels α. Column 1 presents the index of examples.
Columns 2-4 contain the different confidence levels α
for the chance-constrained game. The Nash equilib-
rium of the game is given in Columns 5-7.
4.2 (3 × 3 × 3) Random Games with
Normal Distribution
Similarly, three instances of randomly generated (3 ×
3 × 3) games, following independent normal distribu-
tion N
i
(a) ∼ (µ(a), σ
2
(a)), are given below. The mean
µ and deviation σ are uniformly generated between 1
and 3 as follows:
1.
µ
1
(:, :, 1) =
3 1 2
1 1 2
3 2 3
, µ
1
(:, :, 2) =
1 3 1
3 2 2
3 2 3
,
µ
1
(:, :, 3) =
1 3 2
1 3 3
1 3 3
σ
2
1
(:, :, 1) =
9 1 1
4 9 1
4 1 4
, σ
2
1
(:, :, 2) =
4 1 1
9 9 1
9 1 1
,
σ
2
1
(:, :, 3) =
4 4 4
4 4 4
1 9 1
µ
2
(:, :, 1) =
2 1 3
2 1 2
1 1 3
, µ
2
(:, :, 2) =
2 2 3
2 3 1
1 2 2
,
µ
2
(:, :, 3) =
2 3 1
3 1 1
3 2 2
σ
2
2
(:, :, 1) =
4 4 1
1 9 4
1 4 9
, σ
2
2
(:, :, 2) =
9 4 4
1 4 9
4 1 1
,
σ
2
2
(:, :, 3) =
4 4 4
4 4 1
9 1 9
µ
3
(:, :, 1) =
3 3 2
1 1 1
3 3 2
, µ
3
(:, :, 2) =
3 3 2
1 3 2
2 2 3
,
µ
3
(:, :, 3) =
3 3 2
2 3 1
2 3 1
σ
2
3
(:, :, 1) =
1 9 9
9 9 1
9 4 1
, σ
2
3
(:, :, 2) =
4 9 1
1 4 1
1 9 9
,
σ
2
3
(:, :, 3) =
9 1 9
1 4 9
4 4 9
2.
µ
1
(:, :, 1) =
1 2 3
1 3 3
3 2 3
, µ
1
(:, :, 2) =
3 3 1
1 3 2
1 1 3
,
µ
1
(:, :, 3) =
2 2 2
1 2 1
3 2 1
σ
2
1
(:, :, 1) =
4 9 4
1 1 4
9 9 9
, σ
2
1
(:, :, 2) =
9 1 9
4 9 9
1 9 9
,
σ
2
1
(:, :, 3) =
4 4 9
4 1 4
1 4 4
µ
2
(:, :, 1) =
2 1 2
3 3 1
1 3 1
, µ
2
(:, :, 2) =
1 1 1
2 2 3
3 1 1
,
µ
2
(:, :, 3) =
1 2 1
2 1 2
1 3 1
σ
2
2
(:, :, 1) =
4 9 4
9 4 4
4 4 9
, σ
2
2
(:, :, 2) =
4 4 9
1 4 9
9 9 1
,
σ
2
2
(:, :, 3) =
4 9 4
4 1 1
9 9 4
µ
3
(:, :, 1) =
1 2 1
3 3 1
3 3 2
, µ
3
(:, :, 2) =
3 3 3
3 3 1
1 1 2
,
µ
3
(:, :, 3) =
2 1 3
2 1 3
1 2 1
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
100

Table 1: Nash equilibrium for various values of α for Cauchy distribution.
No.
α Nash Equilibrium
α
1
α
2
α
3
x
∗
y
∗
z
∗
1
0.4 0.4 0.4 (0, 1, 0) (1, 0, 0) (0.667, 0, 0.333)
0.5 0.5 0.5 (0, 1, 0) (0, 1, 0) (1, 0, 0)
0.7 0.7 0.7 (0, 1, 0) (0, 1, 0) (0, 0, 1)
2
0.4 0.4 0.4 (0.442, 0, 0.558) (0, 0, 1) (0, 0, 1)
0.5 0.5 0.5 (0, 0, 1) (1, 0, 0) (0, 1, 0)
0.7 0.7 0.7 (0, 0, 1) (0, 0, 1) (1, 0, 0)
3
0.4 0.4 0.4 (0, 0.775, 0.225) (0, 1, 0) (0, 1, 0)
0.5 0.5 0.5 (0, 0, 1) (0, 0, 1) (0, 0, 1)
0.7 0.7 0.7 (0, 0, 1) (0, 0, 1) (0, 0, 1)
σ
2
3
(:, :, 1) =
1 9 4
4 1 1
1 1 1
, σ
2
3
(:, :, 2) =
9 9 9
9 4 9
9 1 4
,
σ
2
3
(:, :, 3) =
1 4 1
1 9 9
9 4 1
3.
µ
1
(:, :, 1) =
2 3 1
2 3 3
2 1 2
, µ
1
(:, :, 2) =
2 2 2
2 3 1
2 2 2
,
µ
1
(:, :, 3) =
2 1 1
1 1 2
3 3 1
σ
2
1
(:, :, 1) =
1 4 1
9 1 1
1 1 4
, σ
2
1
(:, :, 2) =
4 9 4
4 4 1
9 4 4
,
σ
2
1
(:, :, 3) =
9 9 9
9 1 4
1 1 1
µ
2
(:, :, 1) =
3 2 2
3 3 1
3 1 2
, µ
2
(:, :, 2) =
1 1 1
3 1 1
1 1 1
,
µ
2
(:, :, 3) =
1 2 1
1 1 3
1 2 1
σ
2
1
(:, :, 1) =
1 4 1
9 1 1
1 1 4
, σ
2
1
(:, :, 2) =
4 9 4
4 4 1
9 4 4
,
σ
2
1
(:, :, 3) =
9 9 9
9 1 4
1 1 1
µ
3
(:, :, 1) =
3 3 2
1 3 3
1 1 2
, µ
3
(:, :, 2) =
2 3 3
3 3 1
2 1 3
,
µ
3
(:, :, 3) =
2 3 3
2 2 3
3 3 2
σ
2
3
(:, :, 1) =
1 1 9
4 4 9
9 1 1
, σ
2
3
(:, :, 2) =
9 9 1
1 4 1
1 9 1
,
σ
2
3
(:, :, 3) =
4 4 9
9 4 4
4 1 1
For the above randomly generated examples, the
mean and the deviation of each player’s payoff use
(3 × 3 × 3) tensors. Considering the first example, if
each player chooses the first action as their strategy,
the payoff for player 1 follows a normal distribution
with mean parameter µ = 3 and variance parameter
σ
2
= 9. Table 2 summarizes the Nash equilibrium
in the same way as Table 1. Column 1 presents the
index of examples. Columns 2-4 show the different
confidence levels α for the chance-constrained
game. The Nash equilibrium of the game is given in
Columns 5-7.
Nonlinear Complementarity Problems for n-Player Strategic Chance-constrained Games
101
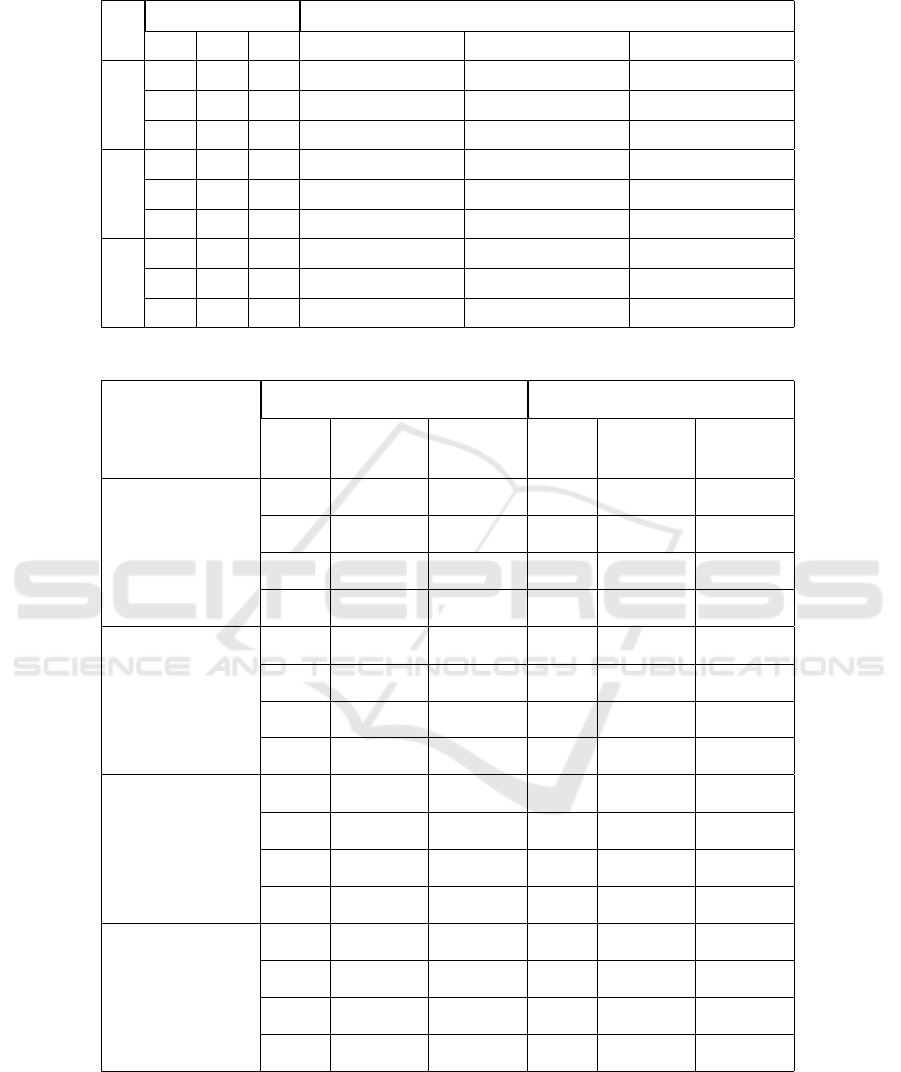
Table 2: Nash equilibrium for various values of α for normal distribution.
No.
α Nash Equilibrium
α
1
α
2
α
3
x
∗
y
∗
z
∗
1
0.6 0.6 0.6 (0, 0, 1) (0, 0.187, 0.813) (0.092, 0.909, 0)
0.7 0.7 0.7 (0, 0, 1) (0, 0, 1) (0.673, 0.327, 0)
0.8 0.8 0.8 (0, 0, 1) (0.194, 0.229, 0.577) (0.764, 0.236, 0)
2
0.6 0.6 0.6 (0.623, 0, 0.377) (1, 0, 0) (0.424, 0.576, 0)
0.7 0.7 0.7 (0.851, 0.149, 0) (0.395, 0.386, 0.219) (0, 1, 0)
0.8 0.8 0.8 (0.067, 0.861, 0.069) (0.322, 0.678, 0) (0.771, 0.229, 0)
3
0.6 0.6 0.6 (0, 0.457, 0.543) (0, 0.291, 0.71) (0.058, 0 , 0.942)
0.7 0.7 0.7 (0, 0.626, 0.374) (0.072, 0.206, 0.722) (0.264, 0 , 0.736)
0.8 0.8 0.8 (0, 0, 1) (0, 1, 0) (0, 0, 1)
Table 3: Comparison of success rate and running time.
Game type
Cauchy distribution Normal distribution
α success
rate
average
time(s)
α success
rate
average
time(s)
2 × 2
0.2 100% 0.0128 0.6 99% 0.0389
0.4 100% 0.0122 0.7 95% 0.0449
0.6 100% 0.0107 0.8 90% 0.0487
0.8 100% 0.0098 0.9 86% 0.0509
3 × 3 × 3
0.2 100% 0.0463 0.6 98% 0.2198
0.4 100% 0.0378 0.7 92% 0.2419
0.6 100% 0.0420 0.8 86% 0.3398
0.8 100% 0.0337 0.9 83% 0.3264
4 × 4 × 4 × 4
0.2 100% 1.1165 0.6 96% 4.5894
0.4 100% 1.0237 0.7 90% 5.4259
0.6 100% 0.8908 0.8 87% 7.4005
0.8 100% 0.7670 0.9 86% 6.5441
5 × 5 × 5 × 5 × 5
0.2 81% 39.8803 0.6 64% 144.8211
0.4 80% 48.8849 0.7 52% 196.6912
0.6 89% 44.9324 0.8 67% 201.4756
0.8 94% 36.1606 0.9 86% 126.2685
4.3 Numerical Results for Large Size
Game Instances
Here we solve large size instances with up to (5 × 5 ×
5 × 5 × 5) games.
The NCPs are implemented in Matlab and solved
by PATH on Intel Core i72,6 GHz with 32GB RAM.
We randomly generated 100 tests of several groups
of different game sizes and confidence levels for
both distributions, then we computed the average
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
102

running time and the success rate in relation of
solved instances by PATH solver. Table 3 summa-
rizes the numerical results for different sizes of the
chance-constrained games. Column 1 presents the
size of the game instances. Columns 2-4 show the
confidence level α, success rate and average CPU
time for problems under Cauchy distribution, respec-
tively. Columns 5-7 provide the same information as
Columns 2-4 for problems under normal distribution.
As shown in Table 3, the average CPU time for
the instances up to (4 × 4 × 4 × 4) is within 1 sec-
ond, whilst (5 ×5 ×5 ×5) instances are solved within
49 seconds. Games with Cauchy distributions have
100% success rates for all the instances except (5 ×
5 × 5 × 5) instances where the success rates range
from 81% up to 94%. As for normal distribution
games, the success rate ranges from 52% for the large
instance to 99% for the smallest instances. In addi-
tion, we also solve game instances with size (6 × 6 ×
6×6 ×6 ×6) within 30 minutes. PATH failed to solve
game instances with more than (6 ×6 ×6 ×6× 6 ×6).
5 CONCLUSION
In this paper, we solved the Nash equilibrium prob-
lem with n-player chance-constrained games. We
proved the existence of Nash Equilibrium for stochas-
tic games with Cauchy and normal distributions.
We derive a deterministic equivalent NCP for these
games.
In order to show the performances of our ap-
proaches, we generated random instances and used
the PATH solver to solve the related NCPs.
For future work, we will consider different dis-
tributions for the addressed stochastic games and ap-
ply our approach to real-life applications, e.g., au-
tonomous vehicles.
REFERENCES
Blackmore, L., Li, H., and Williams, B. (2006). A proba-
bilistic approach to optimal robust path planning with
obstacles. In 2006 American Control Conference,
pages 7–14. IEEE.
Blau, R. A. (1974). Random-payoff two-person zero-sum
games. Operations Research, 22(6):1243–1251.
Cassidy, R., Field, C., and Kirby, M. (1972). Solution of a
satisficing model for random payoff games. Manage-
ment Science, 19(3):266–271.
Charnes, A. and Cooper, W. W. (1963). Determinis-
tic equivalents for optimizing and satisficing under
chance constraints. Operations research, 11(1):18–
39.
Charnes, A., Kirby, M. J., and Raike, W. M. (1968). Zero-
zero chance-constrained games. Theory of Probability
& Its Applications, 13(4):628–646.
Cheng, J., Leung, J., and Lisser, A. (2016). Random-
payoff two-person zero-sum game with joint chance
constraints. European Journal of Operational Re-
search, 252(1):213–219.
Cheng, J. and Lisser, A. (2012). A second-order cone
programming approach for linear programs with joint
probabilistic constraints. Operations Research Let-
ters, 40(5):325–328.
De Wolf, D. and Smeers, Y. (1997). A stochastic version of
a stackelberg-nash-cournot equilibrium model. Man-
agement Science, 43(2):190–197.
DeMiguel, V. and Xu, H. (2009). A stochastic multiple-
leader stackelberg model: analysis, computation, and
application. Operations Research, 57(5):1220–1235.
Dirkse, S. P. and Ferris, M. C. (1995). The path solver:
a nommonotone stabilization scheme for mixed com-
plementarity problems. Optimization methods and
software, 5(2):123–156.
Jadamba, B. and Raciti, F. (2015). Variational inequal-
ity approach to stochastic nash equilibrium problems
with an application to cournot oligopoly. Journal of
Optimization Theory and Applications, 165(3):1050–
1070.
Lee, K.-H. and Baldick, R. (2003). Solving three-player
games by the matrix approach with application to an
electric power market. IEEE Transactions on Power
Systems, 18(4):1573–1580.
Nash, J. (1951). Non-cooperative games. Annals of mathe-
matics, pages 286–295.
Nash, J. F. et al. (1950). Equilibrium points in n-person
games. Proceedings of the national academy of sci-
ences, 36(1):48–49.
Neumann, J. v. (1928). Zur theorie der gesellschaftsspiele.
Mathematische annalen, 100(1):295–320.
Peng, S., Singh, V. V., and Lisser, A. (2018). General sum
games with joint chance constraints. Operations Re-
search Letters, 46(5):482–486.
Prékopa, A. (2013). Stochastic programming, volume 324.
Springer Science & Business Media.
Ravat, U. and Shanbhag, U. V. (2011). On the characteriza-
tion of solution sets of smooth and nonsmooth convex
stochastic nash games. SIAM Journal on Optimiza-
tion, 21(3):1168–1199.
Singh, V. V., Jouini, O., and Lisser, A. (2016a). Existence of
nash equilibrium for chance-constrained games. Op-
erations Research Letters, 44(5):640–644.
Singh, V. V., Jouini, O., and Lisser, A. (2016b). Solv-
ing chance-constrained games using complementar-
ity problems. In International Conference on Opera-
tions Research and Enterprise Systems, pages 52–67.
Springer.
Singh, V. V., Jouini, O., and Lisser, A. (2017). Distribu-
tionally robust chance-constrained games: existence
and characterization of nash equilibrium. Optimiza-
tion Letters, 11(7):1385–1405.
Nonlinear Complementarity Problems for n-Player Strategic Chance-constrained Games
103

Singh, V. V. and Lisser, A. (2018). Variational inequality
formulation for the games with random payoffs. Jour-
nal of Global Optimization, 72(4):743–760.
Singh, V. V. and Lisser, A. (2019). A second-order cone
programming formulation for two player zero-sum
games with chance constraints. European Journal of
Operational Research, 275(3):839–845.
Song, T. (1992). On random payoff matrix games. In Sys-
tems and Management Science by Extremal Methods,
pages 291–308. Springer.
Valenzuela, J. and Mazumdar, M. (2007). Cournot prices
considering generator availability and demand un-
certainty. IEEE Transactions on power systems,
22(1):116–125.
Xu, H. and Zhang, D. (2013). Stochastic nash equilibrium
problems: sample average approximation and applica-
tions. Computational Optimization and Applications,
55(3):597–645.
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
104
