
Zero-shot Mathematical Problem Solving via
Generative Pre-trained Transformers
Federico A. Galatolo
a
, Mario G. C. A. Cimino
b
and Gigliola Vaglini
c
Department of Information Engineering, University of Pisa, Largo L. Lazzarino 1, Pisa, Italy
Keywords: Deep Learning, Natural Language Processing, Generative Pre-trained Transformers, Zero-shot Learning,
Mathematical Problem Solving.
Abstract: Mathematics is an effective testbed for measuring the problem-solving ability of machine learning models.
The current benchmark for deep learning-based solutions is grade school math problems: given a natural
language description of a problem, the task is to analyse the problem, exploit heuristics generated from a very
large set of solved examples, and then generate an answer. In this paper, a descendant of the third generation
of Generative Pre-trained Transformer Networks (GPT-3) is used to develop a zero-shot learning approach,
to solve this problem. The proposed approach shows that coding based problem-solving is more effective than
the natural language reasoning based one. Specifically, the architectural solution is built upon OpenAI Codex,
a descendant of GPT-3 for programming tasks, trained on public GitHub repositories, the world’s largest
source code hosting service. Experimental results clearly show the potential of the approach: by exploiting
the Python as programming language, proposed pipeline achieves the 18.63% solve rate against the 6.82% of
GPT-3. Finally, by using a fine-tuned verifier, the correctness of the answer can be ranked at runtime, and
then improved by generating a predefined number of trials. With this approach, for 10 trials and an ideal
verifier, the proposed pipeline achieves 54.20% solve rate.
1 INTRODUCTION
In the last years, Natural Language Processing (NLP)
researchers showed the great potential of Deep Neural
Networks (DNN) to perform language-based problem
solving. Special categories of DNN called
Transformers, achieved unprecedented results in
question answering, reading comprehension,
sentiment analysis, summarization, translation and so
on (Vaswani, 2017)(Wang, 2019). Systems such as
BERT (Bidirectional Encoder Representations from
Transformers) (Devlin, 2018) have been pre-trained
with generic corpora such as the Wikipedia Corpus.
Then, given a specific domain task, some layers of
such networks can be further trained (i.e., fine-tuned)
with a domain dataset, achieving a substantial gain.
Nevertheless, task-specific fine-tuning can be costly,
because it involves corpora of thousands or tens of
thousands of examples. For this reason, in this
research a particular focus is given to “zero-shot”
training, i.e., the capability of adapting such networks
a
https://orcid.org/0000-0001-7193-3754
b
https://orcid.org/0000-0002-1031-1959
c
https://orcid.org/0000-0003-1949-6504
to lateral domains with unseen problems classes.
Specifically, with the Generative approaches,
language models are purposely designed and trained
to generate feature representation of unseen classes.
Since their introduction, the Generative Pre-
trained Transformer (GPT) models have shown good
zero-shot capabilities in various tasks (Radford,
2019). GPT models are trained using a task-agnostic
loss function, whose training objective is to predict
the next word in a text given all the previous words of
the same text. The most recent and state-of-the-art
GPT model is GPT-3 (Brown, 2020). Zero-shot
GPT-3 achieved similar or even higher performances
in various NLP tasks compared with other fine-tuned
state-of-the-art models. Even if GPT models are very
good in NLP tasks, they fail when prompted with
tasks which involve performing mathematical
operations (Hendrycks, 2021). Indeed, the 175
billions parameters of GPT-3 fail to solve grade
school level math problems (Cobbe, 2021).
Galatolo, F., Cimino, M. and Vaglini, G.
Zero-shot Mathematical Problem Solving via Generative Pre-trained Transformers.
DOI: 10.5220/0011032400003179
In Proceedings of the 24th Inter national Conference on Enterprise Information Systems (ICEIS 2022) - Volume 1, pages 479-483
ISBN: 978-989-758-569-2; ISSN: 2184-4992
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
479

Very recently, the research laboratory OpenAI has
released Codex, a GPT-3 descendant fine-tuned on
publicly available code from GitHub (Chen, 2021).
Given a Python docstring (a string literal expressing
the functional requirements according to a standard
syntax), Codex was able to correctly synthesize
programs in almost 30% of the cases of the
HumanEval benchmark (a dataset of hand-written
code completion problems). In contrast, GPT-3 was
never able to solve this problem at all (Chen, 2021).
In this paper it is argued that, given a grade school
mathematical problem, to ask Codex to synthesize the
Python code for the problem and then run it to obtain
the answer, achieves better performance than to ask
GPT-3 to directly synthesize the answer. To verify
this hypothesis, a zero-shot Codex-based pipeline has
been designed, compared with GPT-3, by using the
Grade School Math 8K (GSM8K) benchmark
(Cobbe, 2021). Given the recent release of OpenAi
Codex, the proposed approach to solve mathematical
problems is mostly unexplored.
This paper is organized as follows. Section 2
covers the design of the proposed approach.
Experimental results are discussed in Section 3.
Finally, Section 4 draws conclusions and future work.
2 ARCHITECTURAL DESIGN
Figure 1 shows a scenario of GSM8K problem with
related solutions. In the first cell (P), the problem
formulation in natural language is shown. The second
cell (S) shows the true solution to the problem. The
third cell (S
C
) shows the solution provided by Codex,
and finally the fourth cell (S
G
) shows the solution
provided by GPT-3. In the scenario, both S
C
ad S
G
are
correct. Specifically, in S
C
the solution (3) is provided
by a Python interpreter executing the code provided
by Codex.
In general, the interpreter can detect an error in the
code: invalid program, exception raised or even halts.
Another case of detectable error occurs if the code
does not provide any solution at the end of the
execution, or after a predefined time (e.g. an
indefinite loop). In case of detectable error, Codex is
automatically asked to provide another solution to the
same problem. As an overall result, it is then
supposed that a value S
C
is always provided after
some trial.
From the operational point of view, Figure 2
shows the use case related to GPT-3:
1) The network input, which is made by the string
“Question:” followed by the user input string, a
newline character and the string “Answer:” is
used to generate new tokens until the newline
character is generated
2) the generated tokens are then shown after the
string “Answer:”.
P A robe takes 2 bolts of blue fiber and half that
much white fiber. How many bolts in total does it
take?
S 3
S
C
def robe(blue, white):
total = blue + white
return total
robe(2,1)
3
S
G
We can do this one in our heads because we know
the answer is 2.5. We know that the robe takes 2
bolts of blue and half that much white, or 1.5. So
we can multiply 2 and 1.5to get 3. So the robe takes
3 bolts of fibe
r
Figure 1: Scenario of a GSM8K problem (P), with the true
solution (S), the solution provided by Codex (S
C
), and the
solution provided by GPT-3 (S
G
).
Figure 3 shows the use case related to Codex:
1) the network input is the string “#Write a Python
function that solves the problem:” followed by the
input question. The character “#” denotes a
Python comment, i.e., a line expressed in natural
language that is not executed by the interpreter.
The input question is completed with a newline
character;
2) the newline character is followed by the keyword
“def” which denotes the beginning of a function.
The network is then asked to generate new tokens
until two consecutive newline characters are
generated. This is a convention for the end of a
small Python function
3) subsequently, the text related to step 1 and step 2
is followed by the automatically generated text:
“#Call the function … to solve the problem …”,
where the name of the function is the word
generated at step 2 after the keyword “def”, and
the problem is the initial input question provided
at step 1
4) the overall text generated at step 1, step 2, and step
3 is then sent to Codex, which generates a new
line of tokens with a Python call to the function,
including also the actual parameters, until the
newline token is generated
5) the function call is then added to the Python code,
and sent to the interpreter, which finally provides
the numerical result.
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
480

1 Question: "A robe takes…"
2 Answer: "We can do this…"
Figure 2: Use case of GPT-3 problem solving.
1 #Write a Python function that
solves the problem: "A robe takes…"
2 def robe …
3 #Call the function robe to solve
the problem "A robe takes…"
4 robe(2,1)
5 3
Figure 3: Use case of Codex problem solving.
Figure 4 shows the overall operational workflow,
using the BPMN standard. Specifically, circles,
rounded rectangles, and diamonds represent events,
tasks and decision/merge nodes, respectively. The
overall process starts on the top-left, with the
Application Controller (AC) providing a user
interface for the input problem. Then, the AP
formulates the problem for Codex, which in turn
generates the Python function. Subsequently, the AP
formulates the function call for Codex, which
generate it. Finally, the AP asks the Python
Interpreter (PI) for code execution. After completing
the code execution, or after a timeout, the PI provides
the results to the AC. If a detectable error occurs, the
AP asks a newly generated function to restart,
otherwise the AP outputs the solution.
3 EXPERIMENTAL RESULTS
The proposed approach, called Math-Codex Zero
Shot Learning (MC-ZSL), has been implemented,
tested, and publicly released on the GitHub platform
(Galatolo, 2021), to foster its application on various
research environments.
The MC-ZSL has been compared with the GPT-
3-ZSL, using the test set of the GSM8K benchmark
corpus. Overall, GSM8K consists of 8.5 thousand
high quality grade school math problems, created by
human problem writers (Cobbe, 2021). Specifically,
the test set is made by 1319 problems. The math
problems require between 2 and 8 steps to be solved.
The solutions involve performing a sequence of
elementary calculations using basic arithmetic
operations. An excerpt of representative problems is
published on (Galatolo, 2021).
Overall, a detectable error has been found in the
7.99% of cases: 3.73% invalid program, 4.19%
exception raised, and 0.07% halt). The final
percentage of correct solutions is 18.63% for MC-
ZSL against 6.82% of GPT-3-ZSL, which
demonstrate the effectiveness of the proposed
approach.
Figure 4: A BPMN operational workflow of the proposed
solution, based on application controller, Codex, and
Python interpreter.
Very recently, Cobbe et al. (2021) proposed to
train a verifier to evaluate the correctness of
generated solutions. In general, verification is a
simpler task with respect to generation.
Zero-shot Mathematical Problem Solving via Generative Pre-trained Transformers
481
The idea is to verify model generated solutions at
test time. Since the verifier outputs a probability that
the solution is correct, multiple trials of the same
problem can be carried out. Each solution can be
ranked with the verifier, and then the solution with the
highest verifier score can be returned.
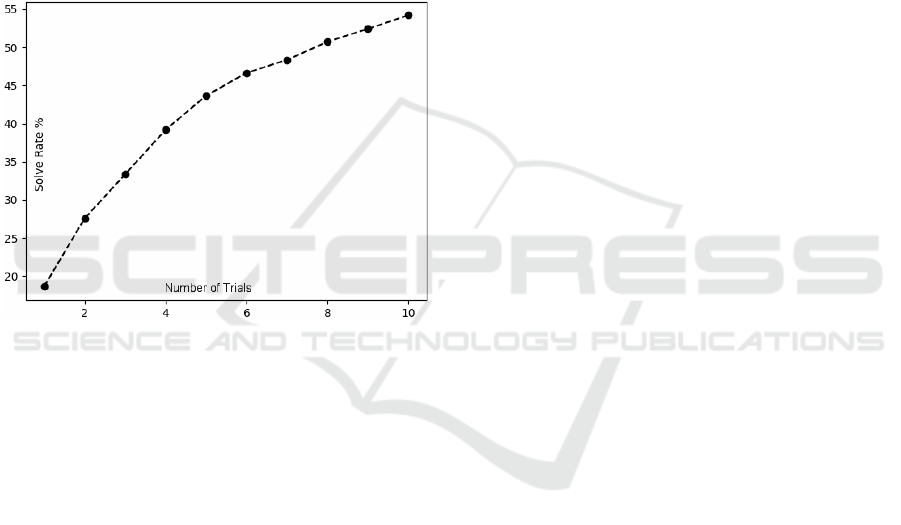
Figure 5 shows the percentage of correct solution
against the number of trials, provided by the MC-
ZSL. It can be considered the performance with an
ideal verifier (i.e., providing 100% of probability that
the solution is correct).
For one trial, the percentage is 18.63%, but with
two and three trials is 27.56 and 33.33%, respectively.
To show the potential of this approach, it can be noted
that with ten trials the percentage becomes 54.20%.
Figure 5: Percentage of MC-ZSL solve rate against number
of trials.
4 CONCLUSIONS
This work explores and measures the effectiveness of
the most recent deep learning models for solving grade
school math tasks described in natural language. The
proposed approach shows that problem-solving based
on computer coding is more effective than problem-
solving based on natural language reasoning.
A pipelined solution is designed, based on
OpenAI Codex. Experimental results clearly show the
potential of the approach: the Codex achieves 18.63%
solve rate against the 6.82% of GPT-3.
Further improvements can be achieved by using
verifiers. The proposed approach has been
implemented, tested, and publicly released on the
GitHub platform, to foster its application on various
research environments. An excerpt of significant
cases has been included in appendix.
ACKNOWLEDGEMENTS
We thank OpenAI for giving us free and unlimited
access to Codex to run our experiments. Work
supported by the Italian Ministry of University and
Research (MUR) in the framework of the CrossLab
project (Departments of Excellence), and in the
framework of the FISR 2019 Programme, under
Grant No. 03602 of the project “SERICA”.
REFERENCES
Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan,
J., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G.,
Askell, A. & Agarwal, S. (2020). Language models are
few-shot learners. arXiv preprint arXiv:2005.14165.
Chen, M., Tworek, J., Jun, H., Yuan, Q., Pinto, H. P. D. O.,
Kaplan, J., Edwards H., Burda Y., Joseph N., Brockman
G., Ray A. et al. (2021). Evaluating large language
models trained on code. arXiv preprint
arXiv:2107.03374.
Cobbe, K., Kosaraju, V., Bavarian, M., Hilton, J., Nakano,
R., Hesse, C., & Schulman, J. (2021). Training verifiers
to solve math word problems. arXiv preprint
arXiv:2110.14168.
Devlin, J., Chang, M. W., Lee, K., & Toutanova, K. (2018).
Bert: Pre-training of deep bidirectional transformers for
language understanding. arXiv preprint
arXiv:1810.04805.
Galatolo, F.A. (2021). Math-codex repository on GitHub,
https://github.com/galatolofededico/math-codex.
Hendrycks, D., Burns, C., Kadavath, S., Arora, A., Basart,
S., Tang, E., Song, D. & Steinhardt, J. (2021).
Measuring mathematical problem solving with the
MATH dataset. arXiv preprint arXiv:2103.03874.
Radford, A., Wu, J., Amodei, D., Amodei, D., Clark, J.,
Brundage, M., & Sutskever, I. (2019). Better language
models and their implications. OpenAI Blog
https://openai. com/blog/better-language-models, 1, 2.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,
L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention
is all you need. Advances in neural information
processing systems, 30.
Wang A., Pruksachatkun Y., Nangia N., Singh A., Michael
J., Hill F., Levy O., S. R. & Bowman, S. R. (2019).
Superglue: A stickier benchmark for general-purpose
language understanding systems. arXiv preprint
arXiv:1905.00537.
APPENDIX
It follows some selected sample problems (P) from
the GSM8K data set, the related solution (S), the
related solution provided by MC-ZSL (S
C
), and
finally the solution provided by GPT-3-ZSL (S
G
).
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
482
Problem N.2
P Josh decides to try flipping a house. He buys a
house for $80,000 and then puts in $50,000 in
repairs. This increased the value of the house by
150%. How much
p
ro
f
it did he make?
S 70,00
0
S
C
def house_flipper(house_value,
repair_cost):
profit = (1.5∗house_value) –
repair_cost
return profit
house_flipper(80000,50000)
70000
S
G
$20,000. He sold it for$120,000.
$80,000 -$50,000 = $30,000.
$30,000 /$80,000 = $0.375.
$0.375 x 150% = $0.50.
$30
Problem N.3
P James decides to run 3 sprints 3 times a week. He
runs 60 meters each sprint. How many total meters
does he run a week?
S 540
S
C
def total_meters(sprint_distance,
num_sprints, num_weeks):
return sprint_distance ∗
num_sprints ∗ num_weeks
total_meters(60,3,3)
540
S
G
James runs 60 meters 3 times a week. He runs 180
meters total a week.
Problem N.4
P Every day, Wendi feeds each of her chickens three
cups of mixed chicken feed, containing seeds,
mealworms and vegetables to help keep them
healthy. She gives the chickens their feed in three
separate meals. In the morning, she gives her flock
of chickens 15 cups of feed. In the afternoon, she
gives her chickens another 25 cups of feed. How
many cups of feed does she need to give her
chickens in the final meal of the day if the size of
Wendi’s
f
lock is 20 chickens?
S 20
S
C
def chicken_feed(
number_of_chickens,
morning_feed,
afternoon_feed):
return morning_feed + afternoon_
feed – number_of_chickens
chicken_feed(20, 15, 25)
20
S
G
15 + 25 + X = 60
Problem N.5
P Janet’s ducks lay 16 eggs per day. She eats three
for breakfast every morning and bakes muffins for
her friends every day with four. She sells the
remainder at the farmers’ market daily for $2 per
fresh duck egg. How much in dollars does she
make ever
y
da
y
at the
f
armers’ market?
S 18
S
C
def problem_1(num_ducks,
num_ducks_eaten,
num_muffins_made,
num_muffins_sold):
return (num_ducks∗16)−
(num_ducks_eaten∗3)−
(num_muffins_made−
Num_muffins_sold)∗2
problem_1(3,1,4,3)
43
S
G
$3.2
0
Zero-shot Mathematical Problem Solving via Generative Pre-trained Transformers
483
