Expressing Adaptations to Take into Account in Generator-based
Exercisers: An Exploratory Study about Multiplication Facts
Pierre Laforcade
1 a
, Emeric Mottier
1
, S
´
ebastien Jolivet
2,3 b
and B
´
er
´
enice Lemoine
1
1
LIUM Computer Science Laboratory, Le Mans University, Laval, France
2
IUFE, University of Geneva, Switzerland
3
LDAR, University of Paris, France
Keywords:
Adaptation, Generation, Modeling, Didactic, Metamodeling.
Abstract:
This paper intends to explore how the generation logic and the elements involved are expressed from the
teachers’ viewpoint, in the context of learning games. We present an interview-based exploratory study:
preparation, realization, analysis, and findings. From the results we also propose a dedicated metamodel to
capture these expressed elements and logic. We evaluate this metamodel by developing a high-level generator
component about the practice of times tables.
1 INTRODUCTION
Serious games can be wearing for the users when ac-
tivities are repetitive or redundant, or when the games
present an imbalance of challenge relative to the skill
level of the players (Streicher and Smeddinck, 2016).
This is especially true when considering declarative
knowledge (explicit knowledge of facts) that requires
repetition for encouraging their memorization, gen-
eralizations, and retention (Kim et al., 2013). Seri-
ous games targeting such knowledge should then pro-
pose or generate a wide variety of adapted learning
game activities. Designing a generator in charge of
this need is a complex task involving different actors’
viewpoints and different dimensions about the adapta-
tion to take into account (didactic, pedagogical, gam-
ing, motivational, . . . ) (Laforcade, 2020).
This paper is about the design of generators of
learning activities in the context of serious games ded-
icated to declarative knowledge. Our interest is about
the complex adaptations that cannot be easily taken
into account by the learning game at run-time, like
the objective to consider or the specification of the
game or learning components involved into the activ-
ity to propose. As a first step we intend to explore
how the generation logic and the elements involved in
the runtime generations are expressed from the teach-
ers’ viewpoint. Because we put aside the gaming
a
https://orcid.org/0000-0001-8498-2731
b
https://orcid.org/0000-0003-3915-8465
dimension, one can consider the generated activities
to study as adapted exercises for training declarative
facts. This paper relates then the preparation, real-
ization, analysis, and findings of an interview-based
exploratory study we conducted, focusing on the mul-
tiplication tables as a case study. We also propose a
first attempt to formalize the expressed elements and
logic for an high-level generation.
This article is structured as follows: in Section II
we briefly present some research works dealing with
the design of generators for adaptation purposes. In
Section III and IV, we present our exploratory study
and analysis of the results, respectively. In Section
V we propose a metamodeling approach to capture
invariants and variants expressed by teachers. Finally,
Section VI is about the application and evaluation of
our proposed metamodel.
2 RELATED WORKS
As stated by (Streicher and Smeddinck, 2016), ”de-
spite remarkable progress in AI in recent years,
adding adaptivity or personalization features to seri-
ous games in a fully automated manner [..] is not
yet easily feasible”. Past and current research works
dealing with adaptivity focus on different purposes
(recommandation, personalization, etc.), targets (con-
tent, learning objects, scenarios, etc.), and methods /
techniques (Vandewaetere et al., 2011) (Streicher and
242
Laforcade, P., Mottier, E., Jolivet, S. and Lemoine, B.
Expressing Adaptations to Take into Account in Generator-based Exercisers: An Exploratory Study about Multiplication Facts.
DOI: 10.5220/0011033100003182
In Proceedings of the 14th International Conference on Computer Supported Education (CSEDU 2022) - Volume 1, pages 242-249
ISBN: 978-989-758-562-3; ISSN: 2184-5026
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Smeddinck, 2016). They also differ in focusing more
on the learning dimension (Wilson and Scott, 2017)
or the gamification dimension (B
¨
ockle et al., 2017).
Research has already tackled the need for analysis
frameworks helping identify and specify various in-
volved models: learner models, domain models, game
models, etc. Also, various approaches and techniques
have been proposed to implement various adaptive
systems. Nevertheless, the design of generators is
barely considered (specify all involved models as well
as the generation logic using them). Such formal-
ized models (machine-readable models) can be used
to drive the development of the generator component
but can also be useful to evaluate, and validate the
generation behavior as well as the involved elements
before the development phase: changes at this step
will be less expensive than changes occurring during
the re-engineering of the overall serious game.
(Sehaba and Hussaan, 2013) proposed a generic
architecture for personalizing a serious game scenario
according to learners’ competencies and interaction
traces. The architecture is organized in three layers:
domain concepts, pedagogical resources and game re-
sources . Their proposal allows the generation of three
successive scenarios (conceptual, pedagogical and se-
rious game) according to the three presented layers.
In past research works, from the Escape It! (Lafor-
cade and Laghouaouta, 2019), we tackled the issue of
generating adapted learning game scenarios. We pro-
posed a specific modeling approach. It is based on
a metamodel specifying at first the domain elements
according to both a 3-incremental-perspective on the
resulting scenario, and a 3-dimensions specification
of domain elements. The approach proposes to model
the game description and the learner’s profile as input
models for the generator that will produce the adapted
scenario as an output model. Nevertheless, the gener-
ation rules and the mapping rules between the diffi-
culty levels and the game objects involved within a
scene resolution, are not explicit: they are hard-coded
in the generator. These domain rules cannot be easily
adjusted. Some studies have to be conducted to ex-
plore how making the generation logic more explicit
and changeable.
3 EXPLORATORY STUDY
3.1 Overview
The objective is to collect and analyze information
about how the generation of adapted exercises should
be addressed according to the viewpoint of people in-
terested in using such learning games with students:
i.e. mainly teachers. We on purpose decided to re-
strict the adaptation to the learning dimension, i.e.
putting aside for now the game dimension (indeed,
teachers cannot be considered as game experts).
The analysis of the collected data will help us in
identifying and characterizing how participants ex-
press the adaptations to take into account for the gen-
eration of adapted exercises. We are also interested in
understanding how they proceed, what elements and
rules they identify and how they express them.
The didactic context for this experiment is about
the multiplication tables training. The fictive learn-
ing game to design aims at providing learners with
adapted training sessions. The participants are peo-
ple who could be involved in the design of this fic-
tive TEL-system in order to represent the didactic and
pedagogical viewpoints. Because of the exploratory
context, we decided to conduct these first experiments
with a single participant at a time (among the 11 par-
ticipants), according to the following protocol.
3.2 Protocol
The protocol is illustrated in Figure 1. Because of the
lockdown context occurring during this experiment
(from May to June 2021) these steps have been de-
signed for distant interviews.
Figure 1: The different steps of the protocol with informa-
tion about the average time and the use of documents.
Pre Interview. This first step is a semi-structured in-
terview based on a list of subjects to question the
participant. First questions are about the partic-
ipants’ identity, current or past teaching activi-
ties. Secondly, we guide them to present their own
experiences about adaptation within their daily
teaching activities.
Introduction. We introduce to them the didactic
context about the training of multiplication tables.
We present a fictive serious game based wherein
the training occurs during multiple sessions, each
one proposing students with an individualized ses-
sion generated by the system to match their needs
and preferences. The current focus on the ’learn-
Expressing Adaptations to Take into Account in Generator-based Exercisers: An Exploratory Study about Multiplication Facts
243

ing’ dimension is presented, explaining we put
aside for now the ’gaming’ dimension. This in-
troduction step is supported by a slide-based doc-
ument they can see during the presentation. This
allows us to show examples of maths questions
and answer modalities (Figure 2), defining what a
question and an exercise are. Our objective is to
give them a shared starting point about the genera-
tion target but no information about the sources to
consider and how the generation should proceed.
Figure 2: Information showed to participants during the in-
troduction step (assembly of translated parts from the orig-
inal slide-based document).
Production. We ask participants to think about the
adaptations to consider, the target elements (no
restriction to the ones we show them) and source
elements to consider (the instruction is given on
the last slide of the previous step). We encourage
them not to restrict their imagination to techni-
cal considerations or about how could be collected
some learners’ information. We also ask them to
put down in writing or figures a maximum of their
thoughts (no constrained formalism) using simple
paper-based notes. We let them make this pro-
duction by themselves but allow them to ask any
questions wherever they need. They can use all
the time they need up to 30 minutes maximum.
Collect. In this short step, participants take some
photos of their paper notes and send them to us
by email.
Discussion. Within this step, participants present
their ideas. The objective is twofold: being able to
interpret and understand their notes, and making
them detail their findings. This step is much more
a discussion than a presentation but our questions
are only intending to ask them details, not struc-
turing or guiding the discussion.
Post Interview. This last step is another semi-
structured interview based on predetermined
questions. Some of these questions are about
summarizing the identified adaptations, others are
about the production step itself: how they pro-
ceed to identify them, how they consider their
production, if some guidance were missing, etc.
We then finally discuss the specification and us-
ages of adaptation/generation elements and rules
by teachers.
In order to find some participants, we contacted
at first official french organisms related to the edu-
cational field for elementary and middle schools (tar-
geted audience for the training of multiplication ta-
bles). Based on the limited positive answers, we used
the snowball sampling technique by asking first par-
ticipants to give us some contacts about other poten-
tial interested participants.
3.3 Collected Data
We realized 11 interviews remotely using a video-
conferencing system. 9 participants accepted to be
recorded (video and sound). The participants’ profiles
are outlined in Table 1.
The interviews last between 1 and 2 hours, 1.5
hours on average. The shorter step was the produc-
tion one. For 4 participants on 11, the production has
required interactions and exchanges, mixing up the
production and discussion steps. We tried not to influ-
ence and simply guide them to detail their thoughts.
All participants put down their production on paper
that we collected.
Table 1: Participants’ main working activity.
ID Main information
#1 6
th
grade retired teacher
#2 Middle maths teacher
#3 Maths division pedagogical advisor
#4 2
nd
Grade teacher in a priority education zone
#5 Recently graduated of a primary school
teaching Master diploma
#6 2
nd
Grade teacher
#7 5
th
Grade teacher
#8 5
th
Grade teacher in a priority education zone
#9 Instructor about teaching adaptations for
children with Autism Syndrom Disorder
#10 2
nd
Grade teacher
#11 Maths assistant professor in College
4 ANALYSIS AND MAIN
FINDINGS
The pre- and post-interviews and productions answers
were analyzed based on the participants’ notes, the
CSEDU 2022 - 14th International Conference on Computer Supported Education
244

recorded interviews (including production step) and
our own. We highlight the main findings.
Former or current teachers have different experi-
ences about adaptation in classrooms. It goes from
simple additional guidance of students with difficul-
ties, to content and exercises dedicated to specific stu-
dents or groups. Most of the time, content and exer-
cises are the same for all students, with some optional
additional resources delivered to the fastest students.
Participants’ productions are mainly driven by
their own experience about teaching and adaptation
on their daily teaching routine. Most of them started
by identifying learner-independent information about
how to practice the training of multiplication tables:
order for the tables, difficulty levels based on chang-
ing the answer modalities, ordering or not the mul-
tiplication facts, varying the information to find (the
product at first, one of the operands in a second time),
etc. Some participants consider that mixing up dif-
ferent tables is possible when these tables have been
at first achieved independently. Other times, partici-
pants consider the explicit combinations of different
tables or specific number facts. They also consider
the training objectives and activities according to the
learner’s grade from 2nd to 6th.
Participants take into account the learner when
considering that each generated exercise has to cope
with the current learner’s progress within his learn-
ing path. Some objectives are prerequisites for oth-
ers whereas various objectives can be performed in-
dependently. Based on their experience using existent
maths serious games, two participants proposed to as-
sociate different learning paths to groups of student,
according to their level. Finally, only the participant
#9 (no teaching expertise) expressed learner-centered
needs for adapted and progressive difficulty inside
and outside the generated exercises, but without being
able to express how to put into practice this difficulty
in regard to this mathematical context. Only a few
of the participants proposed to use learners’ previous
incorrect answers to drive the difficulty level of the
generated questions or for proposing tricky choices.
It is worth notice that no participant expressed
generation rules or adaptation rules in general. They
mainly focused on the elements to consider, not on
how they will be used to really generate exercises
adapted to learners. In relation to the post-interview
answers, we observe that the participants were gener-
ally satisfied of their production, and had not felt the
need for more guidance (except the ones who required
our intervention). They do not use any particular for-
malism, their notes are mainly hand-written sentences
without any schema or graphic representation, except
the use of arrows to link ideas.
5 CAPTURING THE DIDACTIC
FACET FOR GENERATING
ADAPTED EXERCISES
The main finding of these interviews is that most of
the participants dealt with the generation of adapted
exercises on a very didactic viewpoint. They fol-
lowed a top-down approach, thinking about, at first,
on learning paths of objectives and activities that can
be relevant for most learners. They could identify
groups of learners requiring dedicated paths but rarely
focused on a single learner. Their approach were
more about personalizing general-purpose activities
than taking into account every individual’s needs as
a starting point. Participants were naturally thinking
about the didactic facet but failed to explicit specific
adaptation or generation rules. However, an implicit
and shared generation logic can be identified.
Because the didactic facet of generating adapted
exercises is fundamental and must be tackled as a very
first step, we decided to focus on it.
5.1 Objectives and Method
In order to capture the didactic facet we propose a
metamodel specifying most of the information ex-
pressed by the participants. Because of the inherent
subjectivity of metamodels it is worth noting that it
can still be debatable or not convenient to cover in-
formation and needs of other teachers. However, our
proposition relies on a generic structure that can be
convenient for other didactic contexts.
Also, our objectives are to i/ verify the metamodel
expressiveness to model the complete perspective of
some participants’ viewpoint, and ii/ prove that such
models can drive the partial generation of adapted ex-
ercises (machine-readable with no ambiguity).
5.2 In-depth Interviews
We decided to propose another interview to two par-
ticipants in order to deepen and develop their ideas
about what to consider and how to use it to gener-
ate adapted training exercises about the multiplication
facts. These two participants were #3 and #8.
Each interview took approximately one hour and
a half. They both occurred at distance using a video-
conferencing system. They were free to start from
scratch or from their previous notes. We guide them
to express their ideas on the following subjects, ex-
tracted from all the previous interviews: What are the
objectives? Are these objectives composed of sub-
objectives or different difficulty levels? How all these
Expressing Adaptations to Take into Account in Generator-based Exercisers: An Exploratory Study about Multiplication Facts
245

elements are related to the didactic field of the multi-
plication tables? How these elements are sequenced?
Are there some prerequisites or dependencies? How
these elements are associated to learners? What de-
fines a generated activity? How these activities are
related to the objectives or other elements? How the
generator component should decide which objective
to deal with? How to choose the activity to generate
if several are related to the elected objective?
They were free to express any idea. We do not
impose them to deal with these subjects in this order.
5.3 The Metamodel
All elements from the two in-depth interviews, added
to those always collected, led us to specify the meta-
model illustrated in Figure 3. It captures invariants
and variants into concepts, properties and relations.
We used the Ecore format (Steinberg et al., 2009) to
build the metamodel.
5.3.1 Overview
The metamodel is composed of 3 inter-related parts
(different colors in Figure 3), each one having its own
root element. This 3 parts composition is related to
the 3 perspectives from (Laforcade and Laghouaouta,
2019). The top and main part concerns the specifica-
tion of the teachers’ viewpoint (Domain root). Mod-
els in conformance to this part can be considered as
the domain models required by the generation pro-
cess. For now, these domain models only deal with
the didactic and pedagogical facets. Other dimen-
sions, like the game-based motivational dimension,
will be considered and specified in this part.
The second part is the one starting with the Con-
text element: it models the learner models, i.e., the in-
formation about one learner that will be used to drive
the generation of an adapted exercise. This part of the
metamodel has some relations to the first domain part.
Finally, the third and last perspective specifies the
elements to generate. This part also refers to the do-
main part.
5.3.2 Generic Elements
Although this metamodel is related to the training
context of multiplication tables, some information are
generic enough to be relevant for other didactic con-
texts about declarative knowledge.
The Domain root element is composed of three
container elements: Scenarios, Declarative Knowl-
edge, and Activities. Scenarios gathers all different
learning scenarios that a teacher can declare. A Sce-
nario is a set of Objective. It corresponds to the di-
dactic concept of learning trajectory (Diwan et al.,
2019)(Mendes et al., 2021). Each Objective has a
list of Level that will support the learning progress
or difficulty for a same objective. An Objective can
have some prerequisites, each Prerequisite referenc-
ing a Level, from another objective, that should be
achieved. When the referenced level is the last one
of an objective it means that the overall objective has
to be achieved. The different learning activities are
declared as ActivityType. They define various param-
eters about the activity to generate. A Level references
one of these activity types.
Every Learner is associated to a Scenario. Enroll-
ments could have been made by the intermediary of
groups or the entire class but, according to the gener-
ation viewpoint, the generator only requires the infor-
mation of the learning path for the considered learner.
A Learner is then associated to a set of CurrentObjec-
tiveLevel. They relate to a Level, and can also relate to
one Level among the ones associated to that objective,
in order to specify if this objective/level are achieved
or still in progress.
Unlike our previous works (Laforcade and
Laghouaouta, 2019), the generation does not have the
same three iterative and incremental steps. In our con-
text, we first have to select only one objective to con-
sider. We then select the only one activity type defined
for the selected objective. We consider these two
steps as the high-level exercise. Finally, the next step
will consist in generating an ordered list of questions,
sometimes including several answer options (the low-
level exercise). The HighLevelExercise is then the
only element to generate considering our decision to
restrict this study to the two first generation steps.
It is worth noting that the metamodel do not tackle
the rules about how levels or objectives are achieved,
or how the learner information are tracked and iden-
tified: it only considers what has to be provided for
being used by the generation logic.
5.3.3 Context-related Information
The metamodel also captures (see Figure 3) some in-
formation related to the training of times tables.
From the domain part, these information are about
the knowledge to train and the activity types that char-
acterize different training configurations. In the con-
text of multiplication tables, this knowledge is about
the tables, composed of multiplication facts (multi-
plicand and multiplier), to consider. It is possible to
declare particular set of multiplication facts (for ex-
ample all facts equals to 12: ’3 × 4’, ’4 × 3’, ’6 × 2’,
’2 × 6’, ’1 × 12’, ’12 × 1’). Teachers can then asso-
ciate an objective to one or several set of multipli-
cation facts. Sometimes, teachers also need to de-
CSEDU 2022 - 14th International Conference on Computer Supported Education
246

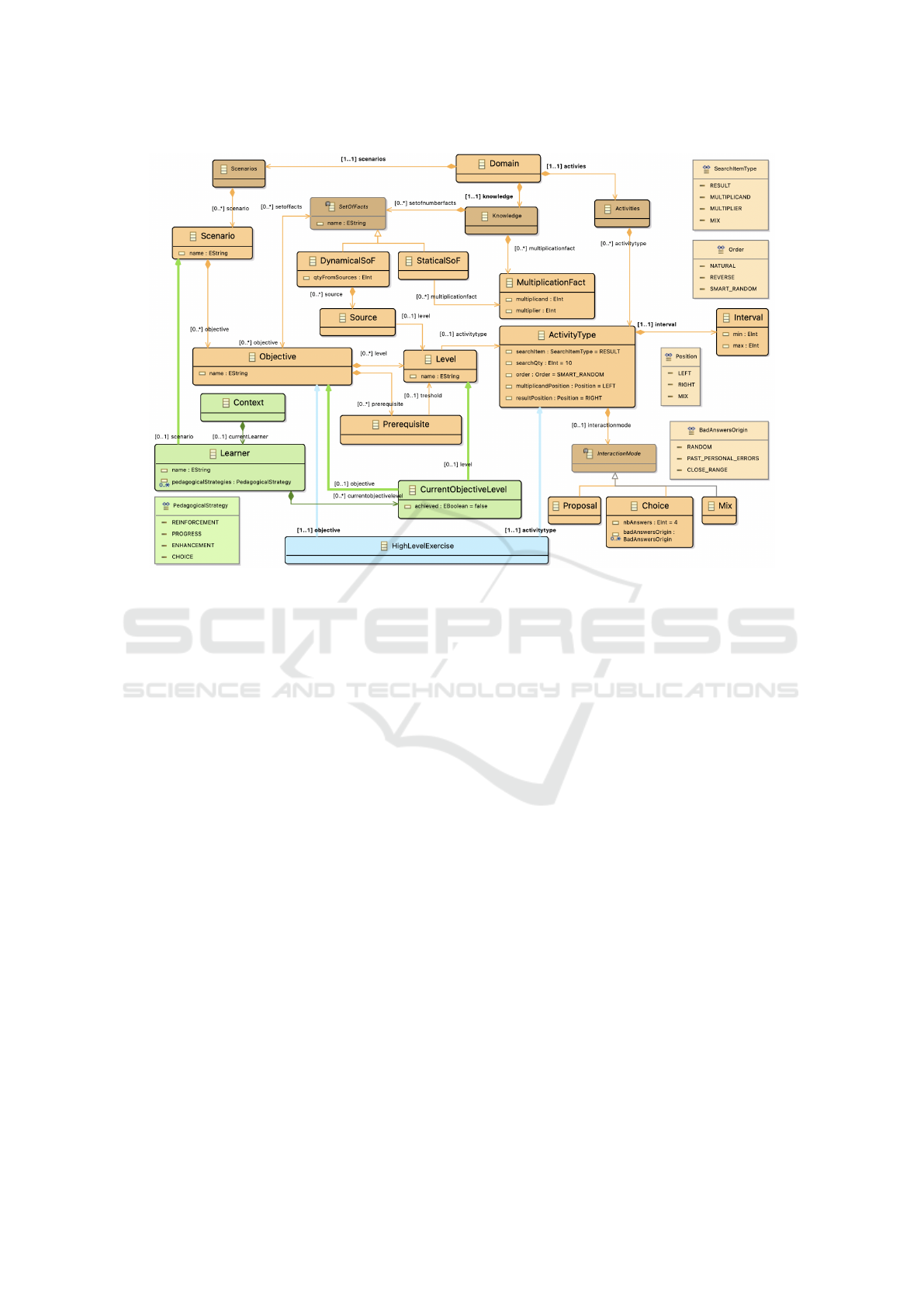
Figure 3: Metamodel capturing information required to realize a generation of adapted exercises from a teacher viewpoint.
fine dynamical set of facts. For example, the objec-
tive mastering the mix of 2 simple tables can be set
to concern 2 tables from a specified range (for exam-
ple tables 2, 3 and 5) in accordance to the first two
ones available from each learner’s progress. To this
end, the associated knowledge will be a Dynamical-
SoF with a qtyFromSources attribute set to 2, and hav-
ing 3 Source referencing, for example, the fourth level
(on 5) of 3 objectives concerning the tables 2, 3 and
5. The two first achieved objectives/levels referenced
by these 3 sources will provide their own SetOfFacts.
The characteristics of the activity types are also
context-sensitive. Teachers express these parameters:
the search item to identify (multiplicand, multiplier,
product or a mix). The quantity of facts to consider
(picked up from the pool of facts associated to the
objective that is refilled with the same sources when
empty). The questions order: original pool order, re-
verse, or ”smart” random (i.e. a fact cannot be chosen
randomly twice while the pool is not empty). The dis-
play of the products on the left or right of the equals
sign (e.g., ’3×? = 15’ or ’15 = 3×?”) ; the mix value
means that ’left’ or ’right’ is chosen for each ques-
tion. The multiplier interval as min and max values
(for examples ”1-10”, ”2-9”, ”1-5”, ”6-12”, etc.). The
position of the multiplicand: for example, if we con-
sider multiplicand 2 times multiplier 5, we can pro-
pose ”2×5” or ”5×2” ; this can be useful to represent
tables according to the teacher’s viewpoint or to gen-
eralize the understanding of the multiplication tables
by provide learners with some randomized position
for each question (mix value). Lastly, the answering
mode among ’proposal’ (learners have to submit an
answer), ’choices’ (learners choose between different
proposals), or a ’mix’ of both (randomized mode at
runtime for every question). Note that the ’choices’
mode can also set the number of proposals and how
they are proposed (random values, values close to the
good answer, previous false answers of the learner).
A combination of values allow teachers to specify
the kind of activity they want for a tuple <objective,
level>. It is very useful to propose a progressive chal-
lenge for the different levels of an objective. It also
allows to take into account the various learners’ au-
dience and current understanding of these multiplica-
tion facts and other underlying multiplication-related
knowledge like commutativity, division, etc.
Teachers also express several pedagogical strate-
gies to decide which objective choose among the eli-
gible ones. An eligible objective is an objective with-
out prerequisite or one with achieved prerequisites.
Sometimes, teachers prefer encouraging the master-
ing of an objective (enhancement strategy), i.e. pro-
gressing into the levels, before dealing with other ob-
jectives. The progress strategy encourages newly eli-
gible objectives or the tuples <objective, level> that
are prerequisites to other objectives. Other strategies
can focus on reinforcement former achieved objec-
Expressing Adaptations to Take into Account in Generator-based Exercisers: An Exploratory Study about Multiplication Facts
247

tives based on multiplication facts that have been met
and answered incorrectly in other in-progress objec-
tives, or simply to let the choice of the objectives to
the learner. Teachers can define a list of strategies
for every learner (individually or as a group). Either
way, at the generation time, the context model pre-
cises the strategies for the learner concerned. Strate-
gies are then sequentially applied until an eligible ob-
jective can be selected.
6 APPLICATIONS
6.1 Evaluating the Expressiveness
The metamodel has been been build upon informa-
tion from in-depth interviews with teachers. It could
then be considered straightforward to verify that its
expressiveness allows the modeling of these teachers’
viewpoint. Nevertheless, metamodeling is also a sub-
jective and tooled activity which can lead to some dif-
ferences between the resulting metamodel and the in-
tentions to model. We then specified the two partici-
pants’ viewpoints as domain model conformed to our
metamodel proposition, from the Domain root.
It is also important to verify that the expressed do-
main models can also be handled appropriately in or-
der to participate in the generation of HighlevelExer-
cise models, by using some context models.
6.2 Simulating a High-level Generation
We aim at generating, for now, high-level models in
accordance with the context and domain models given
as inputs. A low-level generation will then focus on
generating an exercise with questions and/or choices
according to the selected activity type and multiplica-
tion facts. One can notice that this second generation
will used the previous high-level models as inputs as
well as other required information from the context
(e.g. the learner’s previous incorrect answers for the
considered facts) or from the domain.
The generation to simulate concerns the high-level
part. We already modeled two domain models accord-
ing to the viewpoint of the two teachers. In order to
simulate the generation, we need a dedicated tooling
framework, test-cases using specific context models,
and some generic generation rules.
6.2.1 Verification Process and Tooling
Framework
The verification process we followed consist of these
steps: 1/ Use of the EMF framework to generate Java
code allowing to load, save and handle models con-
formed to the metamodel; 2/ Specification of a do-
main model for the two in-depth teachers’ viewpoints;
3/ Development of a generic code (only based on the
structure and generic semantics of the metamodel)
able to generate high-level exercises (using the code
from step 1); 4/ Identification and modeling of limit
value tests, for each domain model, as context mod-
els; 5/ Testing and comparisons with expected results.
6.2.2 Generation Rules
We highlight in Algorithm 1 the main steps of the gen-
eration rules as a generic algorithm that is convenient
for different didactic contexts.
Algorithm 1: Generic high-level generation algorithm.
1: collect all available objectives for the learner refer-
enced in the context model;
2: filter the eligible objectives (no prerequisites or
achieved prerequisites);
3: apply the strategies associated to the considered
learner, according to their definition order, until
one strategy implies the qualification of an objec-
tive;
4: select the appropriate level for this objective (last
unachieved level, otherwise the first level);
5: select the related activity type for this tuple <ob-
jective, level>;
6: create an output model conformed to our meta-
model and built from the HighLevelExercise root.
6.2.3 Context Models, Predictions and Results
As preconditions, we states that there is always at
least one available objective and one eligible objec-
tive. Indeed, the contrary will mean that the domain
model is not correctly defined. We consider for now
that it will be the responsibility of future ”authoring
tool” to ensure these preconditions.
For both specified domain models, we identified
an average of 20 limit value tests in order to ver-
ify specific situations (for examples, a very first gen-
eration wherein the learner has no CurrentObjec-
tiveLevel, objectives with zero, one or all prerequi-
sites that are achieved, behavior of the different strate-
gies application, etc.
To this end, we modeled as much fictive context
models as test cases. We manually identified the set
of possible predictions, i.e. tuples of objectives/levels.
We compared these predictions with the results ob-
tained from our high-level generator component using
one context model and one domain model at a same
time. The objective was twofold: help us developing
the generator code, and verify its final behavior.
CSEDU 2022 - 14th International Conference on Computer Supported Education
248

7 ONGOING WORKS
We planned to continue this exploratory study and
(meta-)modeling approach by the following perspec-
tives: i/ considering the low level generation into
the three inter-related parts of the metamodel (do-
main/context/exercise); ii/ taking into account ad-
ditional pedagogical information like feedbacks to
give and post-actions to realize after correct or in-
correct answers; Indeed, gamified learning experi-
ences should have early, frequent, meaningful and
rapid feedback (Faiella and Ricciardi, 2015); iii/ ex-
perimenting the specification of domain models (pro-
cess and tooling) directly by teachers thanks to user-
friendly authoring-tools; iv/ exploring the gaming
facet to generate not only learning exercises but also
gaming activities. Indeed, tailoring gamification is a
current trend in the educational context (Klock et al.,
2020)(Rodrigues et al., 2020).
This last perspective is very important. It will
tackle the need for some new adaptations to learn-
ers’ gaming preferences, based on different gameplay,
game mechanisms, and aesthetics, to identify and de-
sign correctly, in order to better engage and motivate
learners to practice the multiplication exercises.
8 CONCLUSIONS
This article intended to explore how the genera-
tion logic and the underlying elements involved are
expressed from the teachers’ viewpoint in learning
games. First, we conducted an interview-based ex-
ploratory study about the training of times tables. We
related its preparation and analysis. This work led us
to collect many information about a didactic-centered
viewpoint of adaptations to take into account although
no explicit generation rules has been identified. Nev-
ertheless, these information can be used to capture the
didactic facet of the generation.
We then proposed, as a second contribution, a
metamodel specifying all these information. The
metamodel has generic concepts, properties and rela-
tions that can be relevant for other didactic contexts
about declarative knowledge centered. The meta-
model also embeds context-related information about
the times table context. This metamodeling approach
allows to capture invariant informations as well as
generation variants whose semantics can be taken into
account in the generic generation logic by considering
the input models given to the generator.
REFERENCES
B
¨
ockle, M., Novak, J., and Bick, M. (2017). Towards
adaptive gamification: A synthesis of current devel-
opments.
Diwan, C., Srinivasa, S., and Ram, P. (2019). Automatic
Generation of Coherent Learning Pathways for Open
Educational Resources. In Transforming Learning
with Meaningful Technologies, volume 11722, pages
321–334. Springer International Publishing.
Faiella, F. and Ricciardi, M. (2015). Gamification and learn-
ing: a review of issues and research. 11(3):10.
Kim, J. W., Ritter, F. E., and Koubek, R. J. (2013). An in-
tegrated theory for improved skill acquisition and re-
tention in the three stages of learning. 14(1):22–37.
Klock, A. C. T., Gasparini, I., Pimenta, M. S., and Hamari,
J. (2020). Tailored gamification: A review of litera-
ture. 144:102495.
Laforcade, P. (2020). Generation of adapted learning sce-
narios in a serious game: Lessons learnt. In Games
and Learning Alliance, volume 12517, pages 13–23.
Springer International Publishing. Series Title: Lec-
ture Notes in Computer Science.
Laforcade, P. and Laghouaouta, Y. (2019). Generation of
adapted learning game scenarios: A model-driven en-
gineering approach. In Computer Supported Educa-
tion, volume 1022, pages 95–116. Springer Interna-
tional Publishing. Series Title: Communications in
Computer and Information Science.
Mendes, F., Brocardo, J., and Oliveira, H. (2021). Build-
ing Opportunities for Learning Multiplication, pages
241–264. Springer International Publishing.
Rodrigues, L., Toda, A. M., Palomino, P. T., Oliveira, W.,
and Isotani, S. (2020). Personalized gamification:
A literature review of outcomes, experiments, and
approaches. In Eighth International Conference on
Technological Ecosystems for Enhancing Multicultur-
ality, pages 699–706. ACM.
Sehaba, K. and Hussaan, A. M. (2013). GOALS: generator
of adaptive learning scenarios. 8(3):224.
Steinberg, D., Budinsky, F., Paternostro, M., and Merks,
E. (2009). EMF: Eclipse Modeling Framework 2.0.
Addison-Wesley Professional, 2nd edition.
Streicher, A. and Smeddinck, J. D. (2016). Personalized and
Adaptive Serious Games. In D
¨
orner, R., G
¨
obel, S.,
Kickmeier-Rust, M., Masuch, M., and Zweig, K., ed-
itors, Entertainment Computing and Serious Games,
volume 9970. Springer International Publishing. Se-
ries Title: Lecture Notes in Computer Science.
Vandewaetere, M., Desmet, P., and Clarebout, G. (2011).
The contribution of learner characteristics in the de-
velopment of computer-based adaptive learning envi-
ronments. Computers in Human Behavior, 27(1):118–
130.
Wilson, C. and Scott, B. (2017). Adaptive systems in educa-
tion: a review and conceptual unification. The Inter-
national Journal of Information and Learning Tech-
nology, 34(1):2–19.
Expressing Adaptations to Take into Account in Generator-based Exercisers: An Exploratory Study about Multiplication Facts
249