Testing an Eco-Cooperative Adaptive Cruise Control System in a

Large-scale Metropolitan Network

Hao Chen

and Hesham A. Rakha

Charles E. Via, Jr. Department of Civil and Environmental Engineering, Virginia Tech Transportation Institute, Virginia

Polytechnic Institute and State University, 3500 Transportation Research Plaza, Blacksburg, VA 24061, U.S.A.

Keywords: Eco-driving, Large-scale Traffic Network, Vehicle Engine Type, Signalized Intersections, Energy Optimized

Solution, Connected and Automated Vehicles.

Abstract: This study implements and tests an Eco-Cooperative Adaptive Cruise Control at Intersections (Eco-CACC-I)

system in a large-scale metropolitan network to quantify the system-level performance considering different

vehicle powertrains, connected automated vehicle (CAV) market penetration rates, and congestion levels.

Specifically, three vehicle powertrains are considered in this study, including internal combustion engine

vehicles (ICEVs), battery electric vehicles (BEVs) and hybrid electric vehicles (HEVs). This study integrates

the Eco-CACC-I controller with different fuel/energy consumption models, so that the controller can compute

energy-optimized solutions to assist ICEVs, BEVs and HEVs traverse signalized intersections. A simulated

traffic network in the Greater Los Angeles Area including the downtown LA and the immediate vicinity is

used to implement and test the Eco-CACC-I controller. The test results demonstrate that the controller

produces positive impacts on saving fuel/energy consumption, reducing travel time and delays on urban

networks for different combinations of CAV market penetration and congestion levels.

1 INTRODUCTION

Studies have showed that vehicle acceleration,

deceleration maneuvers and idling events near

signalized intersections increase vehicle energy

consumption and emission levels on arterial road,

since vehicle are forced to stop ahead of traffic signals

when encountering red indications, producing shock

waves within the traffic stream (Barth &

Boriboonsomsin, 2008). The communications

between vehicles (V2V) and between vehicles and

infrastructure (V2I) provide additional data for

researchers to develop control strategies such as eco-

driving systems to optimize vehicle trajectories in the

vicinity of signalized intersections to enhance

mobility and reduce vehicle fuel consumption and

emissions (Saboohi & Farzaneh, 2008).

Most of the studies in this area have focused on

developing eco-driving strategies for ICEVs, since

the current car market is dominated by fuel-powered

vehicles. For example, a cooperative adaptive cruise

control system using SPaT information was proposed

https://orcid.org/0000-0001-8272-734X

https://orcid.org/ 0000-0002-5845-2929

to minimize the absolute acceleration levels of

vehicles and reduce vehicle fuel consumption levels

(Malakorn & Park, 2010). A dynamic programming-

based fuel-optimization strategy was developed using

recursive path-finding principles, and evaluated the

developed strategy using an agent-based modeling

approach (Kamalanathsharma & Rakha, 2014).

Moreover, an eco-driving system entitled Eco-CACC

for fuel-powered vehicles was developed, and field

tests were conducted to demonstrate that the

developed system can efficiently reduce stop-and-go

traffic and produce significant fuel and delay savings

of 31% and 9%, respectively (Almannaa, Chen,

Rakha, Loulizi, & El-Shawarby, 2019).

With the rapid growth of electric vehicles in the

past decade, recently some researchers have started to

develop speed control strategies for electric vehicles,

including BEVs and HEVs. For instance, an eco-

driving technique for BEVs was developed in

(Miyatake, Kuriyama, & Takeda, 2011), and the

vehicle trajectory control problem was formulated as

an optimization problem to minimize the summation

Chen, H. and Rakha, H.

Testing an Eco-Cooperative Adaptive Cruise Control System in a Large-scale Metropolitan Network.

DOI: 10.5220/0011039200003191

In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2022), pages 265-272

ISBN: 978-989-758-573-9; ISSN: 2184-495X

265

of vehicle power. However, a simple energy model

was used by assuming that the recharge efficiency is

a constant value. Another BEV eco-driving algorithm

was proposed in (Zhang & Yao, 2015), in which an

energy consumption model based on the VT-Micro

model was developed for different operation modes

of BEVs, then an eco-driving model for a single

signalized intersection was proposed using the

developed energy model. However, the proposed

energy consumption model was a statistical model

based on limited collected data, thus the accuracy

may not be good enough for the purpose of

developing an optimal control strategy for dynamic

vehicle maneuvers. The same energy consumption

model was used in (Qi, Barth, Wu, Boriboonsomsin,

& Wang, 2018) to develop a connected eco-driving

system for BEVs. However, the case study used a

2012 Ford Escape with a hybrid engine to represent

the performance of an actual BEV. A more robust

algorithm which uses a realistic energy consumption

model for BEV was developed in (Chen & Rakha,

2020) and the simulated test results demonstrated the

benefits of the developed controller to save energy

consumption and delays. An extension work further

expanded the controller to HEVs, and the test results

from an arterial corridor with three signalized

intersections demonstrated that the proposed system

can effectively reduce stop-and-go traffic in the

vicinity of signalized intersections (Chen & Rakha,

2021).

Most of existing studies investigated the eco-

driving strategies for a single vehicle engine type.

Moreover, the developed algorithms were generally

tested using simplified or small traffic networks, and

none of these studies investigated the performance on

large-scale traffic networks calibrated to real traffic

conditions. Considering the abovementioned

problems, this study implements and tests an Eco-

CACC-I system using a large-scale metropolitan

network to investigate the system-level performances

for different vehicle powertrains (ICEV, BEV and

HEV), CAV market penetration rates and congestion

levels. Based on the previous work, the optimal speed

profiles for different vehicle powertrains are

generally very different under certain conditions,

such as different speed limits and roadway grades.

This study integrates the Eco-CACC-I controller with

different fuel/energy consumption models, so that the

controller can compute energy-optimized solutions to

assist ICEVs, BEVs and HEVs traverse signalized

intersections. A simulated traffic network in the

Greater Los Angeles Area including the downtown

LA and the immediate vicinity is used to implement

and test the Eco-CACC-I controller. The test results

demonstrate the controller can effectively reduce

stopped delay and energy consumption for ICEV,

BEV and HEV in the LA network.

2 Eco-CACC-I CONTROLLER

In this study, the Eco-CACC-I controller uses eco-

driving strategy to compute real-time fuel/energy-

optimized speed profile for assist vehicles pass

signalized intersections. Our previous work

developed various Eco-CACC-I systems for vehicles

with different engine types, including ICEV, BEV

and HEV. In this study, we use the same Eco-CACC-

I framework we developed in previous work, and

incorporate the energy models of ICEV, BEV and

HEV so that the controller can work with different

vehicle types in large-scale traffic network.

2.1 Eco-CACC-I Algorithm

The control region is defined as vehicles follow the

recommended speed by Eco-CACC-I from a distance

upstream of the signalized intersection (defined as

) to a distance downstream of the intersection

(defined as d

down

), as the Eco-CACC-I algorithm

optimizes speed profile for vehicle approaching and

leaving signalized intersections. Upon approaching a

signalized intersection, the vehicle may accelerate,

decelerate, or cruise (maintain a constant speed)

based on a number of factors, such as vehicle speed,

signal timing and phase, distance to the intersection,

road grade, headway distance, etc. Considering that

the vehicle may or may not need to decelerate when

approaching the traffic signal, two cases are

considered to develop the Eco-CACC-I strategies.

Case 1 doesn’t require the vehicle to decelerate to

pass the signalized intersection. In this case, the

cruise speed for the vehicle to approach the

intersection during the red indication can be

calculated by Equation (1) to maximize the average

vehicle speed during the control region.

𝑢



𝑚𝑖𝑛

𝑑



𝑡



,𝑢





)

In case 2, the vehicle’s energy-optimized speed

profile is illustrated in Figure 1. After entering the

control region, the vehicle with the initial speed of

u(t

) needs to brake at deceleration level denoted by

a, then cruise at a constant speed of u

to approach the

signalized intersection. After passing the stop bar, the

vehicle should increase speed to u

per the vehicle

dynamics model, and then cruise at u

until the vehicle

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

266

leaves the control region. In this case, The following

optimization problem is formulated to compute the

optimum vehicle speed profile, and the only unknown

variables are the upstream deceleration rate a and the

downstream throttle f

Figure 1: Vehicle optimum speed profile.

Assuming a vehicle enters the Eco-CACC-I

control region at time t

and leaves the control region

at time t

+T, the objective function entails

minimizing the total energy consumption as

𝑚𝑖𝑛 𝐸𝐶𝑢



𝑡















𝑑𝑡

(2)

where EC denotes the energy consumption at instant

t. The energy models for ICEVs, BEVs and HEVs are

presented in Equations (5) ~ (10). The constraints to

solve the optimization problem can be built according

to the relationships between vehicle speed, location,

acceleration/deceleration as presented below:

𝑢



𝑡



⎩

⎪

⎨

⎪

⎧

𝑢



𝑡



𝑢



𝑡





𝑎𝑡

𝑢



𝑡



𝑢



𝑡



𝑡𝑡



𝑡



𝑡𝑡



𝑢



𝑡∆𝑡



𝑢



𝑡































∆𝑡

𝑢



𝑡



𝑢



𝑡



𝑡𝑡



𝑡



𝑡𝑡



𝑇

(3)

𝑢



𝑡





𝑡

𝑎𝑡



𝑢





𝑡



𝑡





𝑑



𝑢



𝑢



𝑡





𝑎



𝑡



𝑡





𝑢



𝑡











𝑑𝑡  𝑢





𝑡



𝑇𝑡





𝑑



𝑢



𝑡





𝑢



𝑎



𝑎𝑎



𝑓





𝑓





𝑓



𝑢



0

(4)

In Equation (3), u(t) is the velocity at instant t; m is

the vehicle mass; 𝑎



𝑡



𝑑𝑣𝑡𝑑𝑡

⁄

is the

acceleration of the vehicle in [m/s

] ( 𝑎



𝑡



takes

negative values when the vehicle decelerates);

function F denotes vehicle tractive force and function

R represents all the resistance forces (aerodynamic,

rolling, and grade resistance forces). Note that the

maximum deceleration is limited by the comfortable

threshold felt by average drivers. The throttle value f

ranges between f

min

and f

max

. Dynamic programming

(DP) is used to solve the problem by constructing a

graph of the solution space by discretizing the

combinations of deceleration and throttle values and

calculating the corresponding energy consumption

levels; the minimum path through the graph computes

the energy-efficient trajectory and optimum

parameters (Guan & Frey, 2013).

2.2 Energy Consumption Models

The energy consumption models for ICEVs, BEVs

and HEVs are the key inputs to the abovementioned

objective function to solve the optimization problem.

In this study, the fuel/energy consumption models for

various vehicle powertrains are selected by

considering: (1) speed and grade data are the only

required input for the energy models, and vehicle

engine data are not required so that the optimization

problem can be easily solved; (2) the energy models

have been validated and demonstrated to produce

good accuracy compared to empirical data; (3)

models can be easily calibrated to a specific vehicle

type using public data and/or the EPA combined fuel

economy data. By considering those factors, the

following fuel/energy models for ICEV, BEV and

HEV are selected in this study.

The Virginia Tech Comprehensive Power-based

Fuel Consumption Model (VT-CPFM) type 1 is

selected to estimate the instantaneous fuel

consumption rate for ICEV (Park, Rakha, Ahn, &

Moran, 2013). The VT-CPFM utilizes instantaneous

power as an input variable and can be easily

calibrated using publicly available fuel economy data

(e.g., Environmental Protection Agency [EPA]-

published city and highway gas mileage). The VT-

CPFM is formulated as below.

𝐹𝐶



𝑡



𝑎



𝑎



𝑃



𝑡



𝑎



𝑃𝑡



∀ 𝑃𝑡0

𝑎



∀ 𝑃



𝑡



0

(5)

𝑃



𝑡



𝑚𝑎



𝑡



𝑚𝑔∙

𝐶



1000



𝑐



𝑢



𝑡



𝑐







𝜌



𝐴



𝐶



𝑢





𝑡



𝑚𝑔 𝜃𝑢𝑡

(6)

Where FC

ICEV

(t) is the fuel consumption rate for

ICEV; α



, α



and α



are the model parameters that

can be calibrated for a particular vehicle using public

available vehicle specification information from

manufacturer; P(t) is the instantaneous total power

(kW); 𝑔 [m/s

] is the gravitational acceleration; 𝜃 is

the road grade; 𝐶



,𝑐



and 𝑐



are the rolling resistance

parameters that vary as a function of the road surface

type, road condition, and vehicle tire type; 𝜌



[kg/m

] is the air mass density; 𝐴



] is the frontal

Testing an Eco-Cooperative Adaptive Cruise Control System in a Large-scale Metropolitan Network

267

area of the vehicle, and 𝐶



is the aerodynamic drag

coefficient of the vehicle.

This study uses the Virginia Tech Comprehensive

Power-based EV Energy consumption Model (VT-

CPEM) compute instantaneous energy consumption

levels for BEV (Fiori, Ahn, & Rakha, 2016). The VT-

CPEM only requires the instantaneous speed and the

EV characteristics as input to compute the

instantaneous power consumed. One of the major

advantages of VT-CPEM is that it captures

instantaneous braking energy regeneration, which is

not available in most BEV energy models. The VT-

CPEM model is summarized as below.

𝐸𝐶





𝑡







𝑃





𝑡



∙𝑑𝑡

(7)

𝑃



𝑡

⎩

⎨

⎧

𝑃





𝑡



𝜂



∙𝜂

∙

𝜂



 𝑃



∀ 𝑃



𝑡0

𝑃





𝑡



∙𝜂



∙𝜂



∙𝜂



∙𝜂



∀ 𝑃



𝑡0

 𝑃



(8)

𝜂



𝑡𝑒



.









(9)

where EC

BEV

represents the energy consumption for

BEV; P

is the power consumed by (regenerated to)

the electric motor; Pw denotes the power at the

wheels computed in Equation (6); P

Aux

is the power

consumed by the auxiliary systems; η

and η

are the

driveline efficiency and the efficiency of the electric

motor, respectively; η

denotes the efficiency from

battery to electric motor; η

represents the

regenerative braking energy efficiency, which can be

computed using Equation (9).

An HEV energy consumption model developed in

(Ahn & Rakha, 2019) is selected to compute

instantaneous energy consumption levels for HEVs.

The model was developed after analyzing field data

and HEV energy consumption behaviors. First, the

amount of fuel consumed is proportionally related to

both the vehicle power and speed; second, the HEV

operates in EV mode when the power is less than 0;

third, the HEV utilizes only an electric mode when

the speed is lower than an EV mode speed (u

) and

the required power is lower than a specific power

). This model only requires instantaneous speed as

input and can be easily calibrated with high accuracy

to match field data. The HEV energy consumption

model is formulated as below.

𝐹𝐶





𝑡





⎩

⎪

⎨

⎪

⎧

𝐹𝐶





for 

𝑃0

𝑢𝑢



and 𝑃𝑃



𝑎𝑏∗𝑢



𝑡





𝑐∗𝑃



𝑡



𝑑∗𝑃



𝑡





for

𝑃0 and 𝑢𝑢



𝑢𝑢



and 𝑃𝑃



(10)

where FC

HEV

(t) is the fuel consumption rate for HEV,

and FC

EV_mode

is the fuel consumption rate in EV

mode and estimated as average fuel consumption in

EV mode; P(t) is the instantaneous total power and

can be computed using Equation (6); and u is the

instantaneous vehicle speed. Statistical analysis of the

empirical data found that the optimum values for v

and P

are 32 km/h, and 10 kW, respectively (Ahn &

Rakha, 2019).

3 CASE STUDY

3.1 The Simulated Traffic Network

In this study, INTEGRATION was used as the

simulation tool to simulate the traffic network in the

Greater Los Angeles Area including the downtown

LA and the immediate vicinity. INTEGRATION is an

integrated simulation and traffic assignment model

that creates individual vehicle trip departures based

on an aggregated time-varying O-D matrix. In

consideration of traffic control devices and gap

acceptance, INTEGRATION moves vehicles along the

network in accordance with embedded preset traffic

assignment models and the Rakha-Pasumarthy-

Adjerid (RPA) car-following model. A more-detailed

description of INTEGRATION is provided in the

literature (Aerde & Rakha, 2007a, 2007b).

Different data sources are used to build the

microscopic network, including NavTeq for

generating nodes and links, OpenStreetMap for

creating intersection traffic control information, and

Google Maps for validating road attributes – the

number of lanes, one-way streets, speed limits, bus

lane locations, etc. The simulated traffic network in

LA includes 1625 nodes, 3561 links and 457 signals.

A static O-D demand file was generated using

QueensOD (Rakha & Lucic, 2002), a software

application developed by VTTI researchers.

QueensOD estimates the most-likely time-dependent

static O-D using observed link traffic flows, observed

link turning movement counts, link travel times, and

a seed matrix. QueensOD iteratively minimizes the

error between the observed link volumes and

estimated link flow to generate a most-likely O-D

matrix that is as close as possible to the seed matrix.

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

268

In this study, the median of the traffic count data for

ten randomly selected Tuesdays and Wednesdays in

2014, which were provided by the Caltrans

Performance Measurement System (PEMS), were

used as the input observed link flow data for

QueensOD.

The simulation results were compared against the

traffic count data from PEMS and the corresponding

R values were computed. The statistical analysis

demonstrated that the simulated network is highly

accurate by comparing to the field data collected in

LA. More detailed information of the simulated LA

traffic network can be found in (Du, Rakha, Elbery,

& Klenk, 2018; Elbery, Devorak, Du, Rakha, &

Klenk, 2019).

3.2 Test the Eco-CACC-I Controller

The Eco-CACC-I controller was implemented into

the simulated LA network using the INTEGRATION

software. The Eco-CACC-I controller was enabled on

all the 457 signalized intersections in the LA network.

In particular, 1,606 arterial links (including both

upstream and downstream links) that are controlled

by traffic signals for vehicle entering or existing are

selected to implement the Eco-CACC-I controller. An

experiment design was conducted to test the

performances of the LA network in two scenarios

(base case, Eco-CACC-I), under the combinations of

vehicle type (ICEV, BEV and HEV), traffic demand

(no congestion - 25% demand, mild congestion - 50%

demand and heavy congestion - 100% demand), and

level of market penetration (LMP) rate of the

controlled vehicles (1%, 2%, 5%, 10%, 20%, 25%,

50%, 75% and 100%). It should be noted that 100%

demand was calibrated by one-hour real traffic data

under weekday morning peak traffic conditions,

which represents heavy traffic congestion. Note that

the Eco-CACC-I controllers are disabled in the base

case, and the controllers are enabled on the selected

1,606 arterial links in the Eco-CACC-I case. Each

scenario was simulated using 10 different random

number seeds to address the stochastic characteristics

of real-world traffic conditions, we should point out

that all results reported below are averages across the

10 runs. The comparisons of the test results in two

scenarios are presented as below.

Figure 2: The savings of Eco-CACC-I vs. base for BEV under different CAV market penetration and congestion levels.

Testing an Eco-Cooperative Adaptive Cruise Control System in a Large-scale Metropolitan Network

269

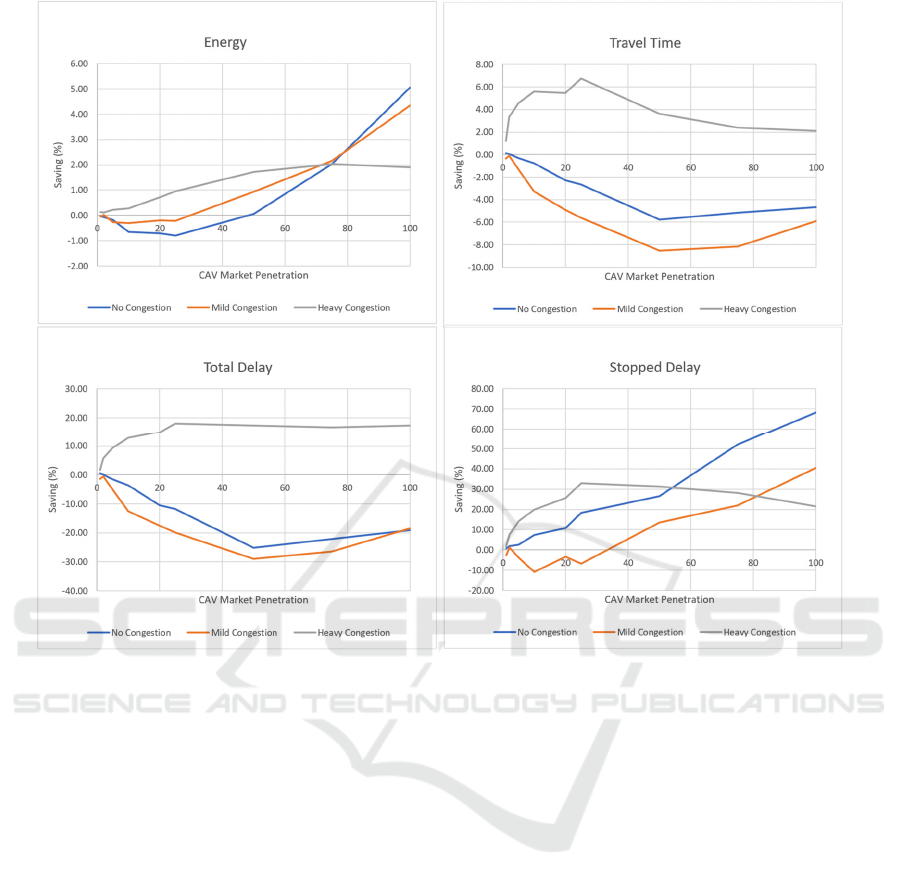
Figure 3: The savings of Eco-CACC-I vs. base for BEV under different CAV market penetration and congestion levels.

Figure 2 illustrates the savings in fuel, travel time,

total delay and stopped delay associated with the

application of the Eco-CACC-I controller for ICEV.

The test results indicate that the Eco-CACC-I

controller reduced the fuel consumption of ICEVs by

up to 6.4%, travel time by up to 8.7%, total delay by

up to 21.5%, stopped delay by up to 68.5%. We

performed t-tests and found the results to be

statistically significant. Figure 2 also demonstrates

that the Eco-CACC-I controller effectively improves

the fuel efficiency of ICEVs in heavily congested

conditions, but the controller increases fuel

consumption by up to 4% when the congestion levels

are low. This is due to the fact that the entire network

uses dynamic vehicle routing and an adaptive traffic

signal controller that continuously changes the traffic

signal timings, which makes the control of the vehicle

very challenging given the continuous stochastic

changes in the system. In addition, the study found

that the Eco-CACC-I controller is most effective for

ICEVs on fuel consumption, travel time, and total

delay when the CAV MPR is 25% and the roads are

heavily congested. The results also indicate that the

Eco-CACC-I controller can effectively reduce ICEV

stopped delay in various congestion levels. The

savings of stopped delay are generally increased with

higher MPRs when the congestion levels are low. The

maximal savings of stopped delay are 68% and 41%

for no congestion and mild congestion levels for a

100% MPR.

Figure 3 illustrates the savings in energy, travel

time, total delay and stopped delay associated with

using the Eco-CACC-I controller for BEV. The

simulation results demonstrate that the Eco-CACC-I

controller produces energy savings of BEVs up to

5.05% (p-value < 0.01) on the LA network. The

energy consumption savings increase as the CAV

MPR increases for all congestion levels. The study

found that the BEV energy savings for no congestion

and mild congestion cases are greater than those of

heavy congestion cases when the CAV MPR is 100%.

Figure 3 also demonstrates that the Eco-CACC-I

controller reduces BEV travel times and the total

delays in the heavily congested cases. In particular,

the controller produces savings in travel time by up to

6.8% (p-value < 0.01) and total delay by up to 17.9%

(p-value < 0.01) at a 25% CAV MPR in heavily

congested

conditions. However, Figure 3 also

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

270

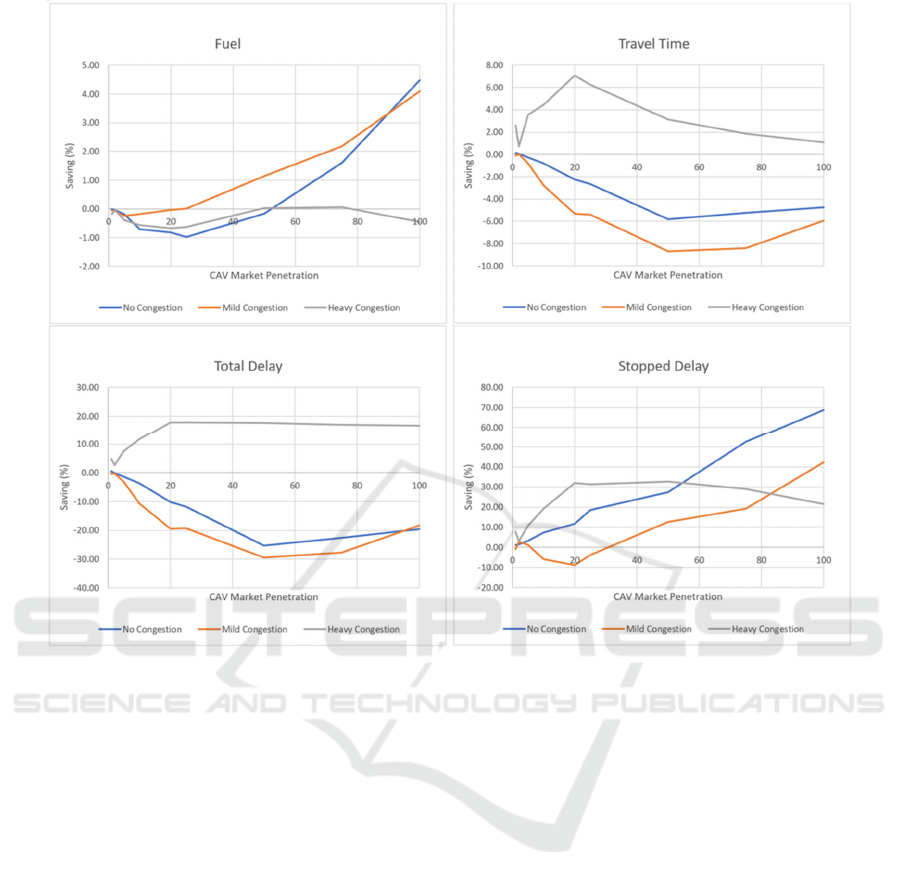
Figure 4: The savings of Eco-CACC-I vs. base for HEV under different CAV market penetration and congestion levels.

demonstrates that the Eco-CACC-I increases both

travel time and total delay in the no congestion and

mild congestion cases when BEV powertrains are

considered. The simulation results indicate that the

BEV Eco-CACC-I controller can effectively reduce

stopped delay under various congestion levels. The

savings in stopped delay generally increase with

higher CAV MPRs for no and mild congestion

conditions. The study found that the Eco-CACC-I

produced savings in BEV stopped delay by up to

68.2% (p-value < 0.01) with a 100% CAV MPR and

no congested conditions.

Figure 4 illustrates the savings in fuel, travel time,

total delay and stopped delay by using the Eco-

CACC-I controller for HEV. The simulation study

found that the Eco-CACC-I controller reduced the

fuel consumption of HEVs by up to 4.5% (p-value <

0.01) when the CAV MPR is 100% with no

congestion in the LA network. The study found that

Eco-CACC-I increased the fuel consumption of

HEVs for most cases. However, Eco-CACC-I

reduced the fuel consumption of HEVs for high CAV

MPR cases (75% and 100%) in no congestion and

mild congestion cases. Figure 4 also demonstrates

that the Eco-CACC-I reduces the travel time by up to

7.1% (p-value < 0.01) and total delay by up to 17.8%

(p-value < 0.01), and stopped delay by up to 32.8%

(p-value < 0.01). The study found that Eco-CACC-I

is most effective on travel time, total delay, and

stopped delay for HEVs when CAV MPRs are

between 20% and 50% and when roadways are

heavily congested. However, Eco-CACC-I is not

effective when the roads are not congested or are

mildly congested. The results also indicate that the

Eco-CACC-I controller can effectively reduce

stopped delay under various congestion levels. The

savings in stopped delay generally increase with

higher CAV MPRs in low to mild traffic congestion.

4 CONCLUSIONS

This study implements and tests an Eco-CACC-I

system on a large-scale metropolitan network to

quantify the system-level impact considering

different vehicle powertrains, CAV market

penetration rates and congestion levels. Specifically,

Testing an Eco-Cooperative Adaptive Cruise Control System in a Large-scale Metropolitan Network

271

three powertrains are considered in this study,

including ICEVs, BEVs and HEVs. This study

integrates the Eco-CACC-I controller with different

fuel/energy consumption models, so that the

controller can compute energy-optimized solutions to

assist ICEVs, BEVs and HEVs traverse signalized

intersections. A simulated traffic network in the

Greater Los Angeles Area including the downtown

LA and the immediate vicinity is used to implement

and test the Eco-CACC-I controller. The test results

demonstrate that the controller has positive impacts

on reducing fuel/energy consumption, travel time,

total and stopped delay, for ICEVs, BEVs and HEVs

for different combinations of CAV market

penetration and congestion levels. More data analysis

on links with or without Eco-CACC-I controllers, and

the further tests to combine Eco-CACC-I with other

controllers (such as freeway speed harmonization,

platooning, eco-routing, etc.) will be considered in

the future work.

ACKNOWLEDGEMENTS

This work was funded by the Department of Energy

through the Office of Energy Efficiency and

Renewable Energy (EERE), Vehicle Technologies

Office, Energy Efficient Mobility Systems Program

under award number DE-EE0008209.

REFERENCES

Release 2.30 for Windows: User's Guide – Volume I:

Fundamental Model Features. M. Van Aerde & Assoc.,

Ltd., Blacksburg.

Release 2.30 for Windows: User's Guide – Volume II:

Advanced Model Features. M. Van Aerde & Assoc.,

Ltd., Blacksburg.

Ahn, K., & Rakha, H. A. (2019). A Simple Hybrid Electric

Vehicle Fuel Consumption Model for Transportation

Applications Electric and Hybrid Vehicles.

Almannaa, M. H., Chen, H., Rakha, H. A., Loulizi, A., &

El-Shawarby, I. (2019). Field implementation and

testing of an automated eco-cooperative adaptive cruise

control system in the vicinity of signalized

intersections. Transportation Research Part D:

Transport and Environment, 67, 244-262.

Barth, M., & Boriboonsomsin, K. (2008). Real-world

carbon dioxide impacts of traffic congestion.

Transportation Research Record: Journal of the

Transportation Research Board(2058), 163-171.

Chen, H., & Rakha, H. A. (2020). Battery Electric Vehicle

Eco-Cooperative Adaptive Cruise Control in the

Vicinity of Signalized Intersections. Energies, 13(10),

2433.

Chen, H., & Rakha, H. A. (2021). Developing a Hybrid

Electric Vehicle Eco-Cooperative Adaptive Cruise

Control System at Signalized Intersections. Retrieved

from

Du, J., Rakha, H. A., Elbery, A., & Klenk, M. (2018).

Microscopic simulation and calibration of a large-scale

metropolitan network: Issues and proposed solutions.

Retrieved from

Elbery, A., Devorak, F., Du, J., Rakha, H. A., & Klenk, M.

(2019). Large-scale Agent-based Multi-modal

Modeling of Transportation Networks.

Fiori, C., Ahn, K., & Rakha, H. A. (2016). Power-based

electric vehicle energy consumption model: Model

development and validation. Applied Energy, 168, 257-

268.

Guan, T., & Frey, C. W. (2013). Predictive fuel efficiency

optimization using traffic light timings and fuel

consumption model. Paper presented at the Intelligent

Transportation Systems-(ITSC), 2013 16th

International IEEE Conference on.

Kamalanathsharma, R., & Rakha, H. (2014). Agent-Based

Simulation of Ecospeed-Controlled Vehicles at

Signalized Intersections. Transportation Research

Record: Journal of the Transportation Research

Board(2427), 1-12.

Malakorn, K. J., & Park, B. (2010). Assessment of mobility,

energy, and environment impacts of IntelliDrive-based

Cooperative Adaptive Cruise Control and Intelligent

Traffic Signal control. Paper presented at the

Sustainable Systems and Technology (ISSST), 2010

IEEE International Symposium on.

Miyatake, M., Kuriyama, M., & Takeda, Y. (2011).

Theoretical study on eco-driving technique for an

electric vehicle considering traffic signals. Paper

presented at the Power Electronics and Drive Systems

(PEDS), 2011 IEEE Ninth International Conference on.

Park, S., Rakha, H., Ahn, K., & Moran, K. (2013). Virginia

tech comprehensive power-based fuel consumption

model (VT-CPFM): model validation and calibration

considerations. International Journal of Transportation

Science and Technology, 2(4), 317-336.

Qi, X., Barth, M. J., Wu, G., Boriboonsomsin, K., & Wang,

P. (2018). Energy Impact of Connected Eco-driving on

Electric Vehicles Road Vehicle Automation 4 (pp. 97-

111): Springer.

Rakha, H., & Lucic, I. (2002). Variable power vehicle

dynamics model for estimating truck accelerations.

Journal of transportation engineering, 128(5), 412-419.

Saboohi, Y., & Farzaneh, H. (2008). Model for optimizing

energy efficiency through controlling speed and gear

ratio. Energy Efficiency, 1(1), 65-76.

Zhang, R., & Yao, E. (2015). Eco-driving at signalised

intersections for electric vehicles. IET Intelligent

Transport Systems, 9(5), 488-497.

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

272