
Towards a Performance Model for Byzantine Fault Tolerant Services
Thomas Loruenser
a
, Benjamin Rainer and Florian Wohner
1 b
AIT Austrian Institute of Technology GmbH, Giefinggasse 4, Vienna, Austria
Keywords:
Fault Tolerance, Performance Modelling, Performance Evaluation.
Abstract:
Byzantine fault-tolerant systems have been researched for more than four decades, and although shown possi-
ble early, the solutions were impractical for a long time. With PBFT the first practical solution was proposed
in 1999 and spawned new research which culminated in novel applications using it today. Although the safety
and liveness properties of PBFT-type protocols have been rigorously analyzed, when it comes to practical
performance only empirical results —often in artificial settings— are known and imperfections on the com-
munication channels are not specifically considered. In this work we present the first performance model for
PBFT that specifically considers the impact of unreliable channels and the use of different transport protocols
over them. We also performed extensive simulations to verify the model and to gain more insight into the
impact of deployment parameters on the overall transaction time. We show that the usage of UDP can lead to
significant speedups for PBFT protocols compared to TCP when tuned accordingly, even over lossy channels.
1 INTRODUCTION
Cloud services have become pervasive in our daily
life for both the private and business sector. Nowa-
days many companies rely on cloud services because
they provide a reasonable and convenient alternative
to in-house solutions. Although the availability and
durability of individual offerings can be quite good,
combining them into virtual multi-cloud applications
can be very challenging, especially if the connectivity
is not ideal and high robustness is needed. Typically,
protocols that tolerate Byzantine faults are needed in
this setting, but implementing well-performing solu-
tions has proven challenging. The most promising ap-
proaches are based on Practical Byzantine Fault Tol-
erance (PBFT), originally introduced by Castro and
Liskov (2002). PBFT is a 3-phase protocol that re-
lies only on a weak synchrony assumption to guar-
antee safety and liveness even over unreliable chan-
nels. It is known to perform well in local LAN set-
tings with high-bandwidth connectivity and low la-
tency, but we found the performance achieved in typ-
ical multi-cloud settings disappointing.
In this work we take a deep dive into the net-
work layer and protocols for PBFT implementations
for lossy and medium to high latency channels. To
the best of our knowledge, we present the first ap-
a
https://orcid.org/0000-0002-1829-4882
b
https://orcid.org/0000-0002-8641-7522
proach for a performance model of PBFT. We an-
alyze the core 3-phase view-consensus protocol in
PBFT without additional features like leader change
and checkpointing and develop an analytical perfor-
mance model for success probability and latency of
transactions. Then we present simulation results and
analyze systems performance using TCP and UDP as
transport protocols. We further explore the param-
eters available for tuning such systems and evaluate
the model with extensive simulations and provide cri-
teria for system design and a hybrid transport mode
that is able to increase performance by making use of
both TCP and UDP. The results are then compared to
a real implementation in a comparable environment.
The remainder of the paper is organized as fol-
lows. In the rest of this section we briefly discuss our
motivation and relevant related work. In Section 2 we
present the analytical model and Section 3 provides
a performance evaluation of our service in different
configurations. Section 4 summarizes the paper and
provides an outlook on future work.
1.1 Motivation
Our analysis was motivated by the performance prob-
lems encountered in the deployment and operation
of robust and secure multi-cloud storage solutions
(Loruenser et al., 2015; Happe et al., 2017), which
suffer from worse connectivity compared to LAN or
178
Loruenser, T., Rainer, B. and Wohner, F.
Towards a Performance Model for Byzantine Fault Tolerant Services.
DOI: 10.5220/0011041600003200
In Proceedings of the 12th International Conference on Cloud Computing and Services Science (CLOSER 2022), pages 178-189
ISBN: 978-989-758-570-8; ISSN: 2184-5042
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

single-cloud settings. However, the problem applies
to all types of robust multi-cloud services. In general,
a multi-cloud deployment over different administra-
tive domains (clouds) has the advantage over single-
cloud deployments that there is no need to fully rely
on a single provider and even better security and avail-
ability can be achieved (Sell et al., 2018).
Our scenario deals with networks that are less re-
liable than pure LAN implementations, but still have
reasonable connectivity, especially in the optimistic
case without node failures. PBFT is designed for this
type of channel with weak synchrony, where mes-
sages are eventually delivered after a certain time
bound ∆t, which is in principle unknown to the pro-
tocol designer. Generally, it provides safety as long
as less than one third of the nodes are malicious and
it can also cope with unreliable channels. The safety
properties of PBFT holds even when the delay is vi-
olated, and only its liveness guarantees depend on
the weak synchrony assumptions. In essence, PBFT
is a leader based consensus protocol with a 3-phase
epoch (or view) consensus for safety in asynchronous
networks and a weak leader election mechanism to
achieve progress, i.e., it is a good compromise for our
use case. However, even when the weak synchrony
assumptions hold, weakly synchronous protocols de-
grade significantly in throughput when the underly-
ing network is unpredictable or unreliable. Ideally,
we would like a protocol whose throughput closely
tracks the network’s performance especially for the
optimal case of no faults, but under the assumption of
unreliable transport.
1.2 Related Work
When designing reliable services, two classes of fail-
ures are prominent: Byzantine and crash faults. The
latter describe systems that either work correctly or
do not respond at all after an (initial) failure. In con-
trast, Byzantine faults allow for arbitrary failures and
thus do not limit an attacker’s capabilities regarding
corrupted nodes. However, a malicious attacker is not
able to break cryptography or read internal state of
honest nodes.
A commonly used protocol in the Byzantine set-
ting is Practical BFT (PBFT) (Castro and Liskov,
2002) and its variants Zyzzyva (Kotla et al., 2007) and
Aardvark (Clement et al., 2009). It is leader based and
utilizes majority voting between all involved servers
and strong cryptography to provide message ordering
and strong consistency in the face of Byzantine faults.
To allow for majority voting, active servers with com-
munication channels between them are mandatory.
Two types of deployments for BFT based consen-
sus mechanisms can typically be distinguished, LAN
and blockchain. If deployed in a closed network
within a single administrative domain, e.g. as a LAN
based distributed lock manager like the ”5 Chubby
nodes within Google” environment, best performance
is achieved with the usage of UDP for message trans-
mission. However, as the experiments of (Chondros
et al., 2012) showed, due to congestion, packet loss
can occur even in the ideal LAN setting, and the trig-
gered view-changes severely degrade performance.
If PBFT based consensus is used in (permis-
sioned) blockchain protocols, different assumptions
and requirements hold (Kwon, 2014; Yin et al., 2018;
Miller et al., 2016), and results cannot easily be ported
from one world to the other. Many transactions
are typically batched, and consensus is organized in
epochs comprising all currently pending transactions.
Moreover, transaction times are typically amortized
values, which makes sense in the blockchain setting
with a continuous incoming stream of transactions
and enough buffered transactions in each epoch. The
models also assume that a reliable channel can al-
ways be established with little overhead over unreli-
able channels and that the network buffers at nodes
are infinite. In practice, they typically apply TCP or
its secure variant TLS if authenticity is required.
When it comes to performance analysis of BFT
protocols, benchmarking is typically used to compare
and estimate the performance of protocols (Gupta
et al., 2016). The only known more systematic ap-
proach was presented in (Sukhwani et al., 2017),
which use Stochastic Reward Nets (SRN) to model
“mean time to complete consensus”. However, they
model the network as a reliable channel where the rate
of message transmission between all pairs of peers is
the same and fit individual distributions from mea-
surements.
In summary, a large body of research exists in
BFT and many protocols have been proposed and
benchmarked, but only little is known when it comes
to performance modeling of such protocols.
2 MODELING PACKET LOSS
In this section we briefly review the PBFT protocol
and develop a performance model that specifically
considers unreliable communication channels, which
is always the case in real systems. Due to space con-
straints we will focus on modeling transaction success
and leave the model of transaction latency for the ex-
tended version. We therefore compare the usage of
the UDP and TCP transport protocols, and their im-
pact on the performance of basic PBFT transactions.
Towards a Performance Model for Byzantine Fault Tolerant Services
179
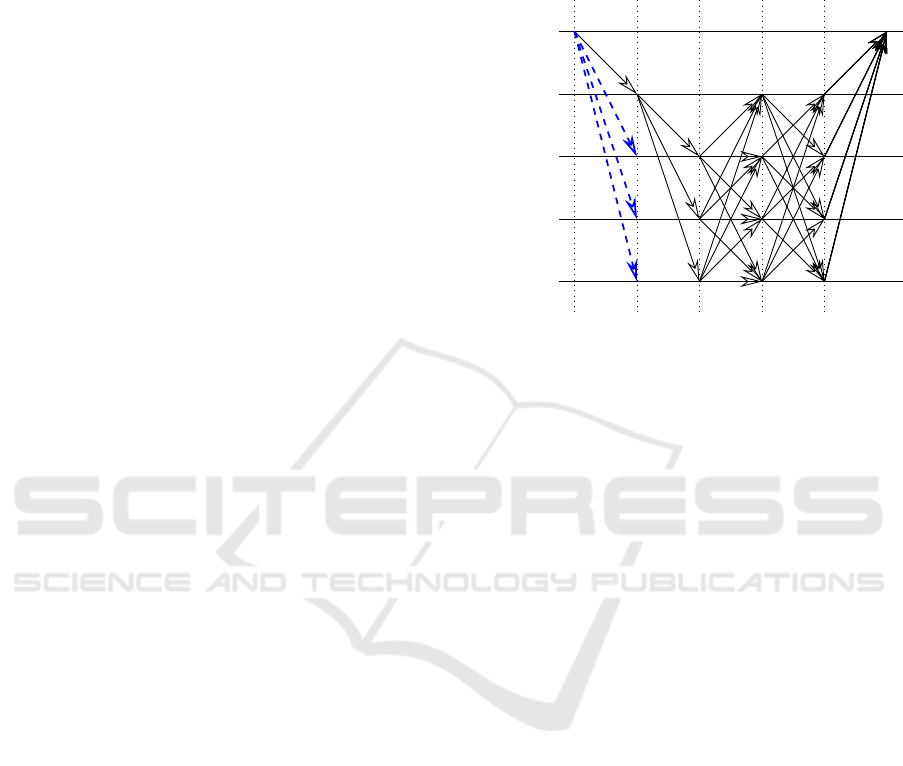
For our analysis we look at the optimistic case with
no malicious behavior during the phases, which was
most suitable for our use case. However, the model
itself is generic and can easily be adapted to various
scenarios by changing parameters accordingly.
2.1 PBFT Protocol
PBFT basically resembles a state replication mecha-
nism that can work over unreliable channels and guar-
antee safety and liveness even in asynchronous envi-
ronments such as the Internet. For this, it needs at
minimum 3 f +1 nodes, tolerating up to f of them be-
ing arbitrarily faulty in the Byzantine model. The full
protocol is leader-based as shown in Figure 1, and the
core view-consensus protocol comprises three phases
which on a high level work as follows. Being leader-
based, one node takes over leadership in linearizing
transactions for a given period of time, the so-called
view, which can also be changed if enough nodes are
not satisfied with the current leader (view-change).
During a view, the leader is getting transaction re-
quests from clients and orders them by assigning a
transaction identifier. However, because the client
does not know the current leader, it sends the request
to all nodes. For our analysis, which is only looking
at the performance of the leader consensus, this part
shown in blue can be omitted. Having received the
request, the leader broadcasts a PRE-PREPARE mes-
sage. If nodes receive a PRE-PREPARE they check
transaction data and send a PREPARE message to all
other nodes if it is consistent with their state. If nodes
receive enough PREPARE messages from other nodes
they enter the prepared state and send a COMMIT
message to all other nodes. A node transitions into
the committed state if it has received at least 2 f + 1
(also including its own) COMMIT messages, and fi-
nally send a REPLY message to the client. The client
considers the transaction to be committed when it has
received f +1 identical REPLY messages. In fact, if f
malicious node are still present in the committed state
a total of 2 f +1 REPLY messages can be required for
the majority voting at the client.
The protocol provides safety by only progressing
if an honest majority is assured (at least 2 f + 1 nodes
are in the same state). Furthermore, the commit phase
is used to guarantee this property within views and
the commit phase is needed to assure it over view
changes. Finally, liveness is guaranteed if the net-
work satisfies weak synchrony conditions, which is
often a reasonable assumption but could lead to large
timeouts in software implementations and bad perfor-
mance when the right timeout has to be found. Weak
synchrony means that eventually after a bounded time
Client
Primary
Replica
Replica
Replica
REQUEST
PRE-PREP
PREPARE
COMMIT
RESULT
Figure 1: Message flow diagram of PBFT with the extended
first phase. Altered phases and communications are high-
lighted by red.
∆t the network becomes synchronous.
The PBFT protocol also applies cryptography to
implement authentic channels and transaction certifi-
cates. As an adversary cannot break cryptography
this reduces its capacity on the channel to delaying
and deleting messages, i.e., he cannot introduce new
messages from nodes he is not controlling. From a
practical perspective, however, an attacker will not al-
ways have control over all communication channels
between all nodes and this model seems unnecessarily
restrictive when it comes to performance evaluation.
For real-world applications, especially in the multi-
cloud setting, it is therefore reasonable to assume that
if an attacker compromises one node, it has full con-
trol over it and can control all incoming and outgo-
ing messages of that node, but it is not able to con-
trol the channels between honest nodes. This is the
underlying idea of our approach, in fact, the generic
model building even starts from a non-compromised
state, but with realistic channels. If the adversary can
arbitrarily delay all messages, performance modeling
would not be possible.
We model and analyze the optimistic case with no
malicious nodes present but possibly adverse and un-
reliable network conditions. The goal of this first ap-
proach is to fully leverage the redundancy inherent
in PBFT to achieve short transaction times in opti-
mal cases. Note that in the case of errors we can al-
ways fall back to a standard implementation for non-
optimistic case with known performance degradation.
CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science
180

2.2 Modeling Transaction Success
As mentioned before, if requests time-out a view
change is triggered. These view changes inflict high
resource costs (especially on the network level); in
addition new requests can only be executed after the
view change has been completed. Thus, it would be
beneficial to know (or at least estimate) the probabil-
ity that the system is able to successfully process a
request a priori. This knowledge could significantly
improve the overall system performance because if
an unreliable transport mechanism, i.e., UDP, is used
the system may switch over to reliable network com-
munication, i.e., TCP, if the chance of a view change
increases.
The employed PBFT protocol heavily relies on
network communication between the replicas. Thus,
delay and packet loss can have a tremendous impact
on the overall system performance. There are basi-
cally two transport protocols: UDP (connectionless)
and TCP (connection oriented). Both protocols are
suited for our system (both provide disadvantages and
advantages), however, UDP employs the least over-
head and delay while TCP requires maintaining a con-
nection and provides a reliable transport service. In
order to minimize communication overhead and de-
lay, UDP is favored. However, with increasing packet
loss, we may run into the problem that nodes do not
receive at least 2 f + 1 messages from other nodes in
a phase (cf. Figure 1). If this applies to more than
2 f + 1 nodes, phases cannot be accepted anymore be-
cause of missing (distinct) messages and, therefore,
requests will time-out. This leads to re-requesting
timed-out requests and finally ends in even more re-
quests timing-out. Thus, if the packet loss increases,
TCP intuitively becomes superior to UDP, while trad-
ing performance for reliability. Thus, the question
“when should TCP be used instead of UDP?” arises.
For the following considerations f ∈ [0,b
n−1
3
c], in or-
der to have more than f correct working replicas we
need n − 2 f > f ⇒ n > 3 f replicas, thus the smallest
number of needed replicas is 3 f +1 assuming f faulty
ones. In the following we will provide a criterion
which answers the aforementioned question based on
probability theory.
Intuition tells us, that we would switch over to
TCP if the expected number of nodes that receives
more than 2 f + 1 message is less than 2 f + 1 in order
to have enough replicas transitioning between the de-
clared PBFT phases. Our goal is it to investigate how
errors in the actual transmission between the BFT
protocol phases propagate and how these errors influ-
ence the successful completion of a given transaction
under the assumption of f faulty nodes. Without loss
of generality, we assume that multicast is not in place
and, therefore, nodes have to rely on unicasts. If mes-
sages are attacked by man-in-the-middle attacks and
are altered (thus altering the recalculated digest) we
assume that the message is lost.
Taking a look at Figure 1 and having in mind that
messages may get lost we have the following phases
if a request is received by the primary:
(i) PRE-PREPARE: The primary sends a PRE-
PREPARE message to all nodes (including itself).
Nodes can only successfully commit a transac-
tion if they successfully accept all phases, this
also includes the reception of a PRE-PREPARE
message which actually fires off the consensus
protocol. Assuming that there is packet loss, m
out of n − 1 (m,n ∈ N,m ≤ n) nodes may re-
ceive a PRE-PREPARE message. The primary it-
self sends n −1 PRE-PREPARE messages to only
n − 1 nodes.
(ii) PREPARE: m + 1 (accounting for the primary)
nodes broadcast a PREPARE message to all n
nodes. Each node has to receive at least 2 f + 1
PREPARE messages to successfully accept the
PREPARE phase and in order to transition into the
next phase. We start with m + 1 nodes and may
end up with only k out of m + 1 nodes (k, m,n ∈
N,k ≤ m ≤ n) receiving at least 2 f +1 PREPARE
messages. A node in this phase will only need to
receive 2 f distinct PREPARE messages from m
nodes because one message is sent to itself.
(iii) COMMIT: k nodes transition into this phase and
broadcast a COMMIT message to all n nodes.
Since only k nodes successfully accepted the pre-
vious phase we again have at most k nodes which
can successfully accept the last phase. Thus, we
have j out of k nodes ( j, k, m,n ∈ N, j ≤ k ≤
m ≤ n) which again need 2 f messages from k − 1
nodes.
(iv) REPLY: j nodes arrive in this phase and will send
a REPLY to the client. The client sees its request
as fulfilled if it receives f + 1 identical REPLY
messages, i.e., f + 1 REPLY messages in total
(best case), or 2 f +1 messages if malicious nodes
are also considered (worst case), out of j possible
ones.
We denote the random variables for the phases as fol-
lows: M (PRE-PREPARE), K (PREPARE), J (COM-
MIT), and S (REPLY). We do not take into account
the reception of a request. If a request is not received,
no transaction will be triggered. The final number
of nodes, thus, relies on the number of nodes that
are able to successfully accept each phase. We as-
sume that the probability of successfully transmitting
Towards a Performance Model for Byzantine Fault Tolerant Services
181

P(S = s,J = j,K = k,M = m) =
j
s
p
s
l
(1 − p
l
)
j−s
k
j
P
T
(X ≥ 2 f |k − 1)
j
(1 − P
T
(X ≥ 2 f |k − 1))
k− j
m + 1
k
P
T
(X ≥ 2 f |m)
k
(1 − P
T
(X ≥ 2 f |m))
m+1−k
n − 1
m
p
m
l
(1 − p
l
)
n−1−m
(1)
a packet is independent and identically distributed.
The expected value E[S,J ≥ 2 f + 1,K ≥ 2 f + 1, M ≥
2 f + 1] as a function of successful transmitting a mes-
sage/packet, should suffice the following properties:
(i) Let f ∈ [0,b
n−1
3
c], ∀p
l,i
, p
l, j
∈ ]0,1[, p
l,i
≤ p
l, j
:
E[S,J ≥ 2 f + 1,K ≥ 2 f + 1,M ≥ 2 f + 1](p
l,i
) ≤
E[S,J ≥ 2 f + 1,K ≥ 2 f + 1,M ≥ 2 f + 1](p
l, j
).
(ii) Let p
l
∈ ]0,1[: E[S, J ≥ 2 f
i
+1, K ≥ 2 f
i
+1, M ≥
2 f
i
+1] ≥ E[S,J ≥ 2 f
j
+1, K ≥ 2 f
j
+1, M ≥ 2 f
j
+
1], ∀ f
i
, f
j
∈ [0, b
n−1
3
c], f
i
≤ f
j
.
The probability that a client receives s replies from
j nodes, where l out of k nodes accepted the COM-
MIT phase, k out of m nodes accepted the PRE-
PARE phase, and m out of n nodes successfully re-
ceived a PRE-PREPARE message is given by Equa-
tion 1. We define p
l
as the probability for success-
fully transmitting a packet with length l (we will
later derive this probability or provide means to mea-
sure it). The actual probability p
l
does depend on
the underlying transport protocol T . Furthermore,
P
T
(X = k|n, p
l
) denotes the probability that k out of n
packets/messages are successfully transmitted given
p
l
using transport protocol T . The following result
provides an estimate of the expect value which can be
evaluated fast.
Proposition 2.1. Let 1 ≤ f ≤ b
n−1
3
c, then we have
the following inequality for E[S,J ≥ 2 f +1,K ≥ 2 f +
1,M ≥ 2 f + 1]:
E[S,J ≥ 2 f + 1,K ≥ 2 f + 1,M ≥ 2 f + 1] ≥ p
2
l
n
·
n−2
∑
m=0
n − 2
m
p
m
l
(1 − p
l
)
n−2−m
P
T
(X ≥ 2 f |m + 1)
2n+2
(2)
The estimate for the expected value provides a fast
computation of the expected value without the need
of computing many binomial-coefficients which is in
general slow if n gets big.
2.3 TCP vs. UDP
In the following we derive the probability P
T
for UDP.
Assume that the probability p(l) of encountering a
packet loss when a message (with length l) is trans-
mitted using UDP is given. Then p
l,U DP
:= p(l) be-
cause UDP does not bother whether a message has
been successfully sent. The probability of receiving j
out of n messages using UDP reads as
P
UDP
(X = j|n) =
n
j
p(l)
j
(1 − p(l))
n− j
. (3)
For UDP we use P
UDP
as an instantiation of P
T
in
Equation 1. The service provider may use the ex-
pected value E[S,J ≥ 2 f + 1,K ≥ 2 f + 1,M ≥ 2 f +
1] to decide whether it should switch from a UDP
based transmission to TCP. A criteria for switching
the transport protocol could be E[S, J ≥ 2 f + 1,K ≥
2 f + 1, M ≥ 2 f + 1] < 2 f + 1 or Equation 2 because
at least f + 1 (in the best case) or 2 f + 1 (in the
worst case) replies are needed by the client accepting
the transaction. With TCP we gain reliable connec-
tions at the expense of (even more) delay (and time
until a phase completes). Thus, we want to mini-
mize the impact of re-transmissions. Therefore, we
would like to know how many re-transmissions of
a single message do we need on average such that
E[S,J ≥ 2 f + 1,K ≥ 2 f + 1,M ≥ 2 f + 1] ≥ 2 f + 1.
Using TCP we assume a constant transaction success
probability of one, assuming an infinite number of re-
transmissions, but employing higher latency because
of the acknowledgment mechanism and potential re-
transmissions.
In order to shed some light on the probability
and expected value of TCP re-transmissions, we as-
sume that TCP connections are already set up and
we only account for the transmission of data seg-
ments/messages. Again, we assume that the proba-
bility of successfully transmitting a packet of length
l over the wire/channel is given by p(l). However, a
segment is only successfully transmitted using TCP
if we receive an acknowledgment (ACK) otherwise
a time-out will trigger, and a re-transmission of the
segment will be initiated. Therefore, both (segment
+ ACK) have to be transmitted successfully. We do
not consider any extensions of TCP. A message may
be divided into several segments which all have to be
successfully transmitted. The probability of success-
fully transmitting a segment reads as
P(¬M|p) = p(l)(1 − p(ACK)) + (1 − p(l))
P(M|p) = p(l)p(ACK).
If p(l) ≈ p(ACK) then we have P(M|p) = p(l)
2
,
in general we have p(l) ≤ p(ACK) and we obtain
CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science
182

P(M|p) ≥ p(l)
2
. We derive the probability of suc-
cessfully transmitting a segment with a certain num-
ber of allowed re-transmissions m ∈ N
0
by Equa-
tion 4. In order to derive the probability of success-
ful transmitting a TCP segment, we model this pro-
cess (X
n
)
n∈N
by a Markov chain with the state space
Ω = {1, 2} with the following transition matrix
P =
1 0
P(M|p) 1 − P(M|p)
.
According to the Kolmogorov – Chapman equation
we obtain for P
RETCP
(M|m, p)
P(X
m
= 1|X
0
= 2) = P
m
2,1
= P(M|p)
m
∑
k=0
(1−P(M|p))
k
.
(4)
Equation 4 can be easily verified by applying induc-
tion.
Proposition 2.2. Let (Ω,A ,P
RETCP
) be a probabil-
ity space, where Ω = {M,¬M}, with the states ac-
counting for a successful and not successful transmis-
sion of a TCP segment. Where, (P
RETCP
) is condi-
tional probability measure given a certain number of
re-transmissions m ∈ N
0
. Then the following holds
lim
m→∞
P
RETCP
(M|m, p) = 1.
Corollary 2.1. Equation 4 can also be written as
P
RETCP
(M|m) = 1 − (1 −P(M|p))
m+1
.
A message sent by our BFT solution may be
split up into several TCP segments. Assuming an
i.i.d. packet loss, the success probability of a mes-
sage which is divided into u different segments finally
reads as
p
l,TCP
:= P
u
\
j=1
M
j
|m, p
!
=
u
∏
j=1
P
RETCP
(M
j
|m, p) =
(1 − (1 − P(M
1
|p))
m+1
)
u−1
(1 − (1 − P(M
k
|p))
m+1
),
(5)
there are k segments where k − 1 are of the same size
and the k-th segment may have a smaller length than
its predecessors. Then the probability that a replica
receives k messages using TCP reads as
P
TCP
(X = k|n, p
l
) =
n
k
p
k
l,TCP
(1 − p
l,TCP
)
n−k
.
The probability that i replicas receive at least 2 f mes-
sages (excluding the self-message) reads as
P(Y = i, X ≥ 2 f ) =
n
i
P
TCP
(X ≥ 2 f |n − 1)
i
(1 − P
TCP
(X ≥ 2 f |n − 1))
n−i
.
Proposition 2.3. Let 1 ≤ f ≤ b
n−1
3
c, then we ob-
tain the following inequality and lower bound on the
needed re-transmissions:
E
TCP
[S,J ≥ 2 f + 1,K ≥ 2 f + 1,M ≥ 2 f + 1] ≥
n(1 − (1 − p(l)
2
)
r+1
)
u·n+(2n−2)·(n−1)
(6)
In order to have at least 2 f + 1 replicas that success-
fully reply to the client we need at most
r =
&
log
1−p(l)
2
1 −
2 f + 1
n
(u·n+(2n−2)·(n−1))
−1
!
− 1
'
(7)
re-transmissions using TCP.
Proposition 2.3 provides a rule of thumb for the
number of needed re-transmissions for each TCP
transmission such that in the end the client receives
enough replies. We may also use the insights gained
by Equation 7 for UDP. If we set P(M|p) = p(l) we
have the case of UDP. In this case we have an esti-
mate on how often each BFT node hast to duplicate
(incl. sending) a message. Thus, before switching to
TCP, the BFT system may try to send each message r
times.
2.4 Exploring the Design Space
In the following we discuss the most important pa-
rameters and improvements to tune system deploy-
ment to optimize the performance.
Forward Error Correction (Repetition Code). To
improve the probability for a packet being transmit-
ted successfully without the introduction of hand-
shake protocols like TCP we could apply forward
error correction (FEC) mechanisms. The simplest
way would be to apply repetition codes, which send
the data multiple times. In case of immediate re-
transmission with UDP a new p
l
2
and p
l
3
for having
an additional re-transmission or two additional im-
mediate re-transmissions respectively would decrease
the packet loss substantially for our channel model
with i.i.d. loss (p
l
2
= 1 − (1 − p
l
)
2
= 2p
l
− p
2
l
and
p
l
3
= 1 − (1 − p
l
)
3
)
Additional Redundancy in Nodes. An alternative
solution would be the use of additional nodes beyond
the optimal 3 f +1 robustness bound. For the standard
case with reliable channels it does not make sense to
go beyond the optimal number of nodes, because no
robustness is gained. However, from a performance
perspective, increasing the amount of nodes 3 f +1+x
leads to higher success probabilities in the UDP case
and could improve system performance if switching
to TCP could be pushed to higher error rates or even
avoided for the expected communication channels.
Towards a Performance Model for Byzantine Fault Tolerant Services
183

Nevertheless, increasing the number of nodes also re-
quires an increase in the quorum size for the protocol
to d
n+ f +1
2
e, which is not considered in the formulas
above but will be used in the simulations.
3 PERFORMANCE EVALUATION
In order to investigate the performance of the pro-
posed approach and to validate the theoretical results
we simulated the BFT protocol as described in Sec-
tion 2. We selected OMNet++ 5.6
1
as the underly-
ing simulation environment and use INET 3
2
as the
network simulator on top of which we implemented
the altered PBFT protocol using TCP and/or UDP as
transport protocol for exchanging messages on the ap-
plication layer. We use a simplified topology where n
replicas are connected through a router. Additionally,
we benchmarked a real PBFT implementation devel-
oped in a project for multi-cloud storage to verify the
results from the event simulation and test improve-
ments. For our evaluations we set the requirement of
f + 1 REPLY messages needed to succeed, which also
assumes honest behavior in the last phase. This was
done to see, what performance can be achieved with
different communication protocols for the fully opti-
mistic case, where the first f + 1 REPLY messages
are sufficient for immediate encoding. Furthermore,
in our simulation we did not consider the computation
times of nodes. Especially the overhead of the crypto-
graphic mechanisms also needed in a full implemen-
tation are assumed to be negligible for this analysis.
3.1 Model Validation
For the first experiment we set the bandwidth of each
link (between node and router) to 100 Mbps, and the
delay is truncated normal distributed (always ≥ 0)
with mean 20ms and a variance of 5ms. We varied the
bit error rate of the channel from 0 to 13·10
−5
in 10
−5
steps and measured the actual packet loss seen at the
transport layer. We used 20 replicas, a message size
of 128 bytes, and we assumed the maximum num-
ber of faulty nodes (6 in the case of 20 nodes). For
each simulation run we did 100 requests and for each
simulation parameter configuration we did 20 repeti-
tions. Figure 2 depicts the probability using the model
provided in Equation 1 (P
succ
:= P(S ≥ 2 f + 1,J ≥
2 f + 1,K ≥ 2 f + 1, M ≥ 2 f + 1)) and the data ob-
tained by the experiment. It is evident that the theo-
retical model fits the observed experimental data.
1
https://github.com/inet-framework/inet/issues/75
2
https://inet.omnetpp.org/
0.00 0.05 0.10 0.15 0.20 0.25 0.30
Packet loss
0.00
0.25
0.50
0.75
1.00
Success probability
Theory
Measured with errorbar
Figure 2: Transaction success probability as a function of
packet loss obtained by experiments vs. Equation 1 using
UDP.
Even if the theoretical model fits the experimen-
tal data it is not feasible to work with the exact for-
mula for larger deployments, especially if we want to
know how many nodes are at least expected to reply
to the client. Figure 3 provides a graphical compari-
son between the exact result and the estimate given in
Equation 2.1 and shows a good fit between model and
simulation.
0.00 0.05 0.10 0.15 0.20 0.25 0.30
Packet loss
0
5
10
15
20
E[X]
Exact
Estimate
Figure 3: Comparison between the exact expected value
(solid blue line) of replicas replying to the client being ver-
ified by experiments and the estimate given in Equation 2.1
(dashed red line) for the case of UDP transmission. The
parameters in order to obtain these expected values are the
same as for the experiment.
The relation is mainly governed by the length of
the packets transmitted. The length of the packets are
rather short, however, to cope for possible different
packet lengths we use the packet error rate for com-
parison which makes the results independent of vari-
ations in packet length.
3.2 Simulation Results
To better understand and improve the UDP behavior
we explore the design space available to improve suc-
cess rates and analyze their impact on the latency.
Two immediate and easy to realize options exist for
the improvement of the success probability of indi-
vidual transactions P
succ
. One is to increase the re-
CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science
184
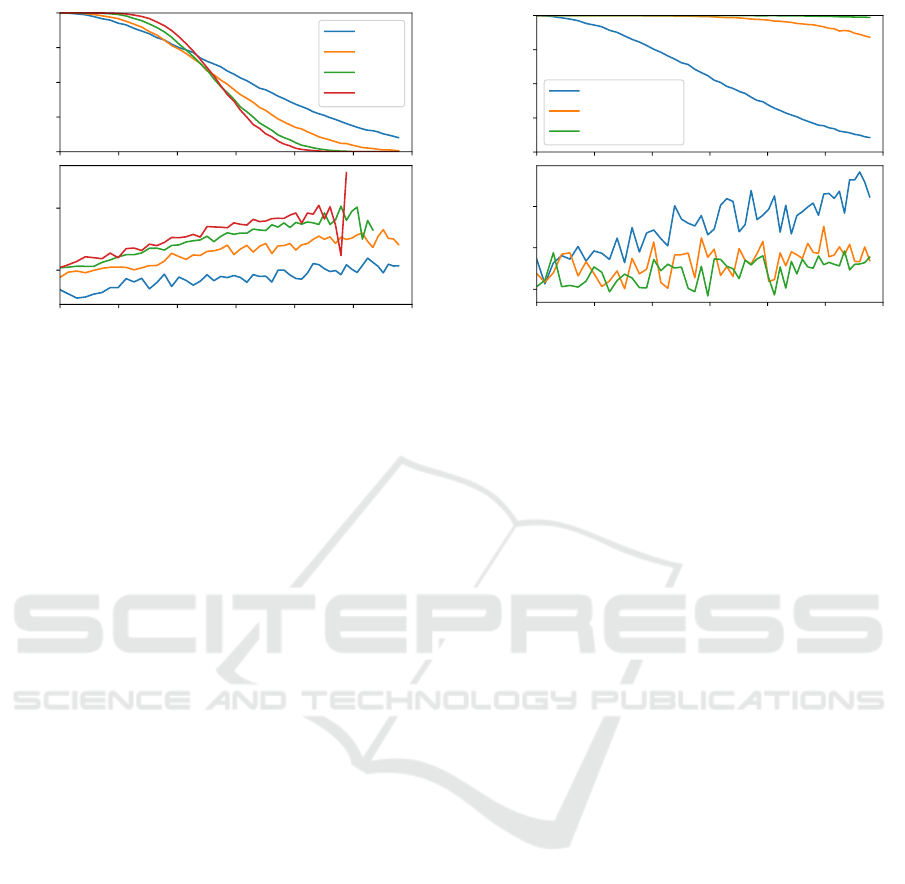
0
25
50
75
100
Success probability
n=4
n=7
n=13
n=19
0.00 0.05 0.10 0.15 0.20 0.25 0.30
Packet Loss
0.16
0.18
Transaction time in s
Figure 4: Success probability over increasing packet loss
for UDP with different f and minimum node configuration
n = 3 f + 1.
dundancy of nodes and the other to better cope for
channel losses by means of forward error correction
(FEC).
To prevent transactions from failing by losing syn-
chronization at certain nodes, increasing the number
of nodes seems a good way to increase resilience.
However, the main configuration parameters of a BFT
system (n, f ) cannot be freely chosen and have to ful-
fill certain requirements. In general, a setting with
n = 3 f + 1 is believed to be optimal and typically
used, as the quorum size is also minimal with 2 f + 1.
We therefore compared settings with different robust-
ness f from a performance point of view and for the
suitability of UDP. The results are shown in Figure 4,
and it can be seen that with increasing number of
nodes n, the success probability P
succ
also increases.
For settings with an intermediate number of nodes
(e.g. n >= 19) we see high transaction success even
for substantial packet loss, which indicates that appli-
cation of UDP is practical. Furthermore, as expected
the transaction times are much better with UDP com-
pared to protocols using acknowledgements and only
slightly increases with higher packet loss and number
of nodes.
If FEC is used, repetition codes are the most ef-
ficient solution in our case, as the amount of pack-
ets should be kept low and only short messages are
exchanged in multiple rounds. The effect of repeti-
tion codes is shown in Figure 5. As expected it raises
P
succ
substantially by reducing the effective packet
loss on the channels through proactive retransmission
of packages. This comes at the cost of an (unneces-
sary) increase of messages transmitted. Interestingly,
the overall transaction time is not affected if enough
bandwidth is available and the good timing behavior
0
25
50
75
100
Success probability
f=1, n=4, r=0
f=1, n=4, r=1
f=1, n=4, r=2
0.00 0.05 0.10 0.15 0.20 0.25 0.30
Packet Loss
0.150
0.155
0.160
ransaction time in s
Figure 5: Success probability over increasing packet loss
for UDP with f = 1 and increasing repetitions r.
is maintained in all situations.
Given an accurate channel model and some band-
width left on the network, this method turned out to be
the most effective. However, if the channel changes
behavior or is not known at all, this approach could
lead to completely different results, e.g., for burst fail-
ures this FEC strategy would fail. Additionally, over-
head on the network is produced and it should only
be used if enough bandwidth is available and no addi-
tional congestion is induced.
Finally, besides the evident options presented
above, it is natural to ask if going beyond optimal con-
figurations of n = 3 f +1 could make sense from a per-
formance point of view, although not necessary from
a robustness perspective. We suspected that adding
additional nodes could help to improve UDP usage
even with certain packet loss, but is was not clear how
it would impact the overall latency and how big the
improvement in success probability would be. In Fig-
ure 6 we show the results of this analysis. With addi-
tional nodes the success probability with lossy links
can be increased and at the same time we get even
shorter transaction times. The effect is best seen for
small configurations which can benefit from this idea.
Nevertheless, because PBFT is a quorum based pro-
tocol, nodes have to be added pairwise. Adding a sin-
gle node to an optimal configuration degrades perfor-
mance, because the required quorum also increases,
i.e., if more than (n + f )/2 servers have to be in the
same phase, the servers have to wait for more PRE-
PARE and COMMIT messages.
Finally, in our simulations we also verified that
TCP behaves worse for increasing packet loss as is
shown in Figure 7. Even for no losses the transaction
time was already almost twice as high as with UDP.
This can be easily explained by the basic nature of
Towards a Performance Model for Byzantine Fault Tolerant Services
185

0
25
50
75
100
Success probability
n=4
n=6
n=8
0.00 0.05 0.10 0.15 0.20 0.25 0.30
Packet Loss
0.150
0.155
0.160
0.165
Transaction time in s
Figure 6: Success probability over increasing packet loss
for UDP with f = 1 and increasing node redundancy.
Figure 7: Success probability over increasing packet loss
for TCP with f = 1 and increasing node redundancy.
TCP using acknowledgements. Even worse, with in-
creasing packet loss the transaction time started to rise
to unexpectedly high values in the seconds range and
due to timeout behavior we even saw some transac-
tions not finishing. This result confirmed our findings
from the first experiments mentioned in Section 1.1.
Although TCP is an extremely versatile and at-
tractive protocol for many situations to build reli-
able channels over unreliable ones, for the BFT type
of interactive protocols with many short messages
sent among nodes it turned out to be not a good
fit. This is also aligned with our intuition of TCP
being throughput optimized for channels with high
bandwidth-delay product. Nevertheless, in situations
with a lot of uncertainty about the channel and high
losses it can be a valuable tool to increase the trans-
action rate in such rough conditions. Surprisingly we
also found that the success probability was not 1 in
all situations, and even with long timeouts some of the
transactions did not complete in scenarios with higher
packet loss. This is because of the limit of 12 retrans-
missions in the TCP implementation of INET.
Finally, we also tried to compare different TCP
types to show their behavior, but we could find no
significant differences between the algorithms imple-
mented in INET (Tahoe, Reno, New Reno). This may
be due to a known problem of this framework (Varga,
2015).
3.3 System Measurements
In addition to the simulation, we also performed
measurements on a real implementation done in
Python (Loruenser et al., 2015). To establish sim-
ilar conditions for our comparison we opted for an
emulated network on a single Linux PC deployment
where each node was run as a separate instance and
the local network stack was used for communication.
To evaluate different networking conditions the Linux
netem kernel module (Hemminger, 2005) was used to
provoke packet delay and network loss. This setup
provided the stable and controllable environment we
needed to verify the results of the simulation and the
analytical model. For the measurements the same
channel settings were used as in the simulation, i.e.
normally distributed network latency with 40ms mean
and 10ms variance (equals 20ms mean and 5ms vari-
ance in the star topology used in the simulation) with
an additional packet loss varying from 0 to 30%.
0
25
50
75
100
Success probability
n=4 (meas)
n=4 (sim)
n=6 (meas)
n=6 (sim)
n=8 (meas)
n=8 (sim)
0.00 0.05 0.10 0.15 0.20 0.25 0.30
Packet Loss
0.15
0.16
0.17
0.18
Transaction time in s
Figure 8: Comparison of measured value from implementa-
tion to simulated vales for UDP. Measured values are drawn
with continuous lines and simulated values dashed.
The comparison of the measurements and the sim-
ulation is shown in Figure 8. Overall, the measure-
CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science
186

ments taken from the PBFT implementation show a
very good match to the simulated results and show
that model and simulation are correct and can be used
to estimate performance. The success probability in
particular resembles the simulated values well. The
measured latency shows a smoother behavior over in-
creasing packet loss corresponding to smaller vari-
ances in the measurements which can be attributed to
buffering effects in the software and OS stack used.
We also found a slightly higher transaction time in the
real implementation for increased packet loss, how-
ever, even for very high packet loss it was within 10%
margins.
Additionally, in our protocol analysis we found
that especially the PRE-PREPARE phase is suscepti-
ble to packet loss and could greatly impact the overall
performance in terms of successful transaction termi-
nation. This is due to the leader-based structure of the
core view-consensus protocol in PBFT. In such a pro-
tocol one node initializes the transactions by distribut-
ing relevant data to all other nodes, the backups. In
this phase the protocol has less redundancy compared
to later phases. Interestingly, adding redundancy by
message repetition only in this phase gives a high in-
crease in success probability with relatively low addi-
tional communication cost. With one re-transmission
in the PRE-PREPARE phase only n − 1 packets are
added, compared to n
2
packets per retransmission in
the other phases, but the success probability can be
substantially increased. To verify this behavior we
measured the increase in success probability for one
and two retransmissions in the PRE-PREPARE phase.
0.00 0.05 0.10 0.15 0.20 0.25 0.30
0
20
40
60
80
100
Success probability
n=4 (r
pp
= 0)
n=4 (r
pp
= 1)
n=4 (r
pp
= 2)
n=6 (r
pp
= 0)
n=6 (r
pp
= 1)
n=6 (r
pp
= 2)
n=8 (r
pp
= 0)
n=8 (r
pp
= 1)
n=8 (r
pp
= 2)
Figure 9: Measured success probability with retransmission
only in the pre-prepare phase. Lines without retransmission
are depicted as continuous lines and results with 1 (2) re-
transmission of pre-prepare messages are drawn with dash-
dot (dashed) style.
The results are presented in Figure 9, and the
data show that adding one retransmission in the PRE-
PREPARE phase leads to the same or even higher
P
success
as adding a full additional node for redun-
dancy, but saves a lot of communication overhead.
Given a total of (r
pp
+1)n+2n
2
+ f +1 messages sent
in the view-consensus protocol with its three phases,
with r
pp
being the number of retransmission in the
pre-prepare phase, the overhead introduced with one
additional retransmission is low. For systems which
tolerate one faulty node out of 4 nodes we get about
11% of message overhead, with 5 nodes we see 9%
overhead and about 7.7% overhead are required for 6
nodes. This leads to a significant improvement com-
pared to the communication overhead introduced by
adding an additional node without retransmission to
increase P
succ
, i.e., a total of 53% more messages must
be sent if n is increased from 4 to 5. Nevertheless,
both measures can be combined to get UDP perfor-
mance up to 5% packet loss and more if two addi-
tional nodes are combined with retransmission in the
pre-prepare phase as an example.
3.4 Interpretation
From this result, we see that careful design on the
network layer is essential for PBFT and protocols
with similar communication patterns to achieve best
performance in challenging network settings. Espe-
cially multi-cloud configurations fall in this category,
but single cloud deployments with a certain level of
geo-separation could also introduce substantial laten-
cies. As can be seen from the measurements taken at
CloudPing (Matt, 2020), latencies between continents
are crucial, for example between Europe and North
America, where they range from 100 − 150ms (50th
percentile). Even within a single continent they are
the dominating factor for BFT performance, e.g., they
go up to 40ms (50th percentile) for servers within Eu-
rope. Thus even intra-region BFT will face substan-
tial latencies and has to rely on UDP for performance
reasons. However, if UDP is used, its performance
should not degrade if higher packet loss is encoun-
tered and switching to TCP should be avoided if high
transaction rates are required.
In general, it is desirable to use UDP and to avoid
TCP wherever possible, because it leads to unaccept-
able performance degradation for higher error rates
on the transmission channel. Although from a ro-
bustness point of view there is no reason to use more
than 3 f + 1 nodes to run a PBFT system, when it
comes to unreliable communication it turns out that
adding nodes is a means to improve the redundancy
on the network layer. Additionally, the use of repe-
tition codes can also lead to significant performance
improvements as UDP can be used over TCP even
Towards a Performance Model for Byzantine Fault Tolerant Services
187

in situations with increased packet loss. If the chan-
nel behavior is known in advance we recommend to
configure the deployment adequately to stay in the
UDP regime. In the end, for our type of applica-
tion a dedicated network protocol would be desirable
which adaptively optimizes retransmissions and other
parameters without increasing latency.
Adaptive and Hybrid Network Layer. From the
structure of the communication pattern it turned out
that unreliable channels have different impact in
different phases. A node missing a single PRE-
PREPARE message could already be out of sync for
the current transaction, contrary if f PREPARE mes-
sages do not arrive, it will still have enough infor-
mation to proceed. This shows that especially the
first broadcast from the primary is relatively more im-
portant than the rest of the messages and measures
taken to increase its probability of success will have a
disproportionate impact on the success of the whole
transaction. It could therefore make sense to use
TCP only for this phase, or, as we have done, to pro-
actively repeat this message once or twice.
Byzantine Case. If f nodes really behave fully mali-
cious, their messages are ignored by the honest nodes
if they do not follow the protocol. Therefore, the best
they can do to slow down transactions—and therefore
slow down service time—is to delay their transmis-
sions or remain silent. For the network layer this
would mean that no redundancy is left to cope with
packet loss as all 2 f + 1 honest nodes have to reach
the final state for the transaction to complete and in
this case packet loss would be fatal. However, by
increasing the redundancy beyond 3 f + 1 nodes we
reach the same regimes as presented above. In fact
if 5 f + 1 nodes are used we reach in the worst case
similar success probabilities, because such a system
would require a 3 f + 1 quorum and leave 2 f over-
all redundancy in the system, i.e. f Byzantine nodes
and f honest nodes whose message do not need to
arrive. However, this is only true if the adversary
does not have access to the channels between honest
nodes, which was the assumption we started from. Al-
ternatively, the implementation can always fall back
to TCP and therefore emulate reliable channels over
unreliable ones, if the packet loss or the number of
node failures is too big for UDP usage. In essence,
the safety property of the system is never compro-
mised, only performance is improved in rather opti-
mistic scenarios.
4 CONCLUSIONS AND FUTURE
WORK
In this work we present the impact of packet loss and
latency as well as transport protocols on the perfor-
mance of BFT systems. We provide an analytical
framework and validate three obtained analytical for-
mulas by simulations. We further explored the design
space available for PBFT deployments to optimize
performance and the results have also been compared
to a real implementation. However, we did not yet
complete our discussion where we would like to pose
questions on the transaction time if we employ reli-
able and/or unreliable network communication. We
also considered only basic transactions and did not in-
corporate view-change protocols and garbage collec-
tion mechanisms. For a complete picture of the over-
all performance these steps should be also analyzed
and optimized. Thus, we have to leave this investi-
gation to future work. Additionally, it is worth study-
ing variants of PBFT, and related distributed protocols
in general, that use slightly modified communication
patterns but could benefit from our treatment.
ACKNOWLEDGEMENTS
This work has received funding from the European
Union’s Horizon 2020 research and innovation pro-
gramme under grant agreement No 890456 (SlotMa-
chine) and the Austrian Research Promotion Agency
under the Production of the Future project FlexProd
(871395).
REFERENCES
Castro, M. and Liskov, B. (2002). Practical Byzantine Fault
Tolerance and Proactive Recovery. ACM Trans. Com-
put. Syst., 20(4):398–461.
Chondros, N. et al. (2012). On the Practicality of Practi-
cal Byzantine Fault Tolerance. volume LNCS-7662
of Middleware 2012, pages 436–455, Montreal, QC,
Canada. Springer.
Clement, A. et al. (2009). Aardvark: Making Byzan-
tine Fault Tolerant Systems Tolerate Byzantine Faults.
Symposium A Quarterly Journal In Modern Foreign
Literatures, pages 153–168.
Gupta, D., Perronne, L., and Bouchenak, S. (2016). BFT-
Bench: Towards a practical evaluation of robustness
and effectiveness of BFT protocols. In Lecture Notes
in Computer Science, volume 9687, pages 115–128.
Springer Verlag.
Happe, A., Wohner, F., and Lor
¨
unser, T. (2017). The
Archistar Secret-Sharing Backup Proxy. In Proceed-
CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science
188

ings of the 12th International Conference on Avail-
ability, Reliability and Security, ARES ’17, pages
88:1—-88:8, New York, NY, USA. ACM.
Hemminger, S. (2005). Network Emulation with NetEm,
https://wiki.linuxfoundation.org/networking/netem.
Kotla, R. et al. (2007). Zyzzyva: Speculative Byzantine
Fault Tolerance. In SOSP ’07, pages 45–58. ACM.
Kwon, J. (2014). TenderMint : Consensus without Mining.
https://tendermint.com/.
Loruenser, T., Happe, A., and Slamanig, D. (2015). Archis-
tar: Towards secure and robust cloud based data shar-
ing. In 2015 IEEE 7th International Conference on
Cloud Computing Technology and Science (Cloud-
Com), pages 371–378.
Matt, A. (2020). AWS Latency Monitoring,
https://www.cloudping.co/grid. Accessed 2020-
12-10.
Miller, A. et al. (2016). The Honey Badger of BFT proto-
cols. In Proceedings of the ACM Conference on Com-
puter and Communications Security, volume 24-28-
Octo, pages 31–42. Association for Computing Ma-
chinery.
Sell, L., Pohls, H. C., and Lorunser, T. (2018). C3S: Cryp-
tographically combine cloud storage for cost-efficient
availability and confidentiality. In Proceedings of the
International Conference on Cloud Computing Tech-
nology and Science, CloudCom, volume 2018-Decem,
pages 230–238.
Sukhwani, H. et al. (2017). Performance Modeling of PBFT
Consensus Process for Permissioned Blockchain Net-
work. In SRDS, volume 2017-Septe, pages 253–255.
IEEE.
Varga, A. (2015). TCP Tahoe/Reno/NewReno strange
behaviors. Online: https://github.com/inet-
framework/inet/issues/75.
Yin, M. et al. (2018). HotStuff: BFT Consensus in the Lens
of Blockchain. http://arxiv.org/abs/1803.05069.
Towards a Performance Model for Byzantine Fault Tolerant Services
189
