Decentralized Platoon Management and Cooperative Cruise Control

of Autonomous Cars with Manoeuvre Coordination Message

Reza Dariani

, Giovanni Lucente and Julian Schindler

Institute of Transportation Systems, German Aerospace Center, Lilienthalplatz 7, Braunschweig, Germany

Keywords: Cooperative Trajectory Planning, Platooning, Cacc, Vehicle Automation, Manoeuvre Coordination Message.

Abstract: Recent development of Vehicle-to-Vehicle (V2V) technologies enables the vehicles to communicate with

each other and coordinate their manoeuvres. With such technologies an Advanced Driving Assistance System

(ADAS) such as Adaptive Cruise Control (ACC) can be pushed to another level in conditional and highly

automated vehicles, i.e. a network of cooperative connected vehicles in the form of Cooperative ACC (CACC)

or even a platoon. In this paper, based on V2V communication between automated vehicles by using

Manoeuvre Coordination Message (MCM), a decentralized platoon management is designed and

implemented to manage the platooning state of each vehicle and when the vehicles are in a platoon or joining

one, a cruise controller is designed and implemented to guarantee the desired headway to a preceding vehicle.

1 INTRODUCTION

An average driver has a very slow reaction time,

around 2.3 seconds (McGehee, Mazzae, & Baldwin,

July 2000). Driver errors play the most important

role, with 94%, in a crash of light vehicles, based on

the research done at National Motor Vehicle Crash

Causation Survey (NMVCCS) (Transportation,

March 2018). That is why the modern vehicles are

equipped with a high number of sensors and

Advanced Driver Assistance Systems (ADAS) to

inform, warn and even intervene in critical driving

situations. As further development of such systems,

the partially-automated and automated driving

functions aim to take the driver partially or

completely out of the driving process.

It is not far from imagination to think that in near

future the traffic network will be a mixture of cars

with different levels of automation. The conditional

and highly automated vehicles (SAE3 & 4 level)

(SAE International, 2021) will soon be on the road.

These cars not only can monitor and sense the

environment and plan and drive a trajectory, they can

also cooperate with each other as well as with C-ITS

infrastructure. This cooperation enabled by

communication technologies, can be used to

https://orcid.org/0000-0002-1091-8793

https://orcid.org/0000-0001-5398-8217

coordinate the manoeuvre between automated

vehicles. This coordination may be in the form of

connected cruise control or a platoon. Vehicle

platooning in general is a method, in which a string of

vehicles drives together while keeping certain inter-

vehicular distances (or time-headways) by using

various types of sensors and ways of communication,

see Figure 1, which results in a more optimal use of

the traffic network.

This paper describes the aspects of vehicle

automation and focuses particularly on a proposed

trajectory planning module and decision-making

module, see Figure 2. The decision-making module

deals mostly with cooperation aspects of vehicle

automation and it also analyses the road geometry,

other road users and information received via

communication and defines a strategy for the

trajectory planning module. A platoon management

module in the form of state machines has been

designed as part of the decision-making module

which deals with platooning vehicle states. How one

car can form a platoon with another car and under

which conditions that is possible; are the questions

that can be answered through platoon management or

platoon logic concepts. Based on the defined strategy

from the decision-making module, the trajectory

planner plans an optimal trajectory and delivers the

Dariani, R., Lucente, G. and Schindler, J.

Decentralized Platoon Management and Cooperative Cruise Control of Autonomous Cars with Manoeuvre Coordination Message.

DOI: 10.5220/0011043400003191

In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2022), pages 281-289

ISBN: 978-989-758-573-9; ISSN: 2184-495X

281

vehicle actuators input to the vehicle controller. The

vehicle controller itself consists of several feedback

and feedforward controllers to guarantee that the

vehicle follows the planned trajectory. Another

important part of the decision-making module, is the

cooperative cruise controller which calculates a

velocity for the vehicle based on the information

received about the preceding vehicle via V2V

communication. Driving with that velocity results in

driving with shorter headway to the preceding vehicle.

The majority of the research on the idea of

platooning has been conducted in a highway-based

situation. However, recently the research work has

turned towards platooning in urban areas, where

platooning is mostly linked to efficient intersection

passing rather than reducing air drag. Although

requiring a high amount of flexibility, the idea of

urban platooning has already been tested in public

traffic (Schindler, et al., 2020) (Dariani & Schindler,

2019). However, it is still far from being normalized

or standardized. The communication network needed

for cooperation in this paper is only based on the

preceding vehicle and no other information such as

leader information is required. That makes the

cooperation very dynamic especially in urban areas in

which the string of the vehicles mostly does not have

a common destination and the vehicles drive together

only for few intersections. In this case forming and

resolving a platoon is very dynamic and adaptive to

urban area scenarios.

Figure 1: String of vehicles driving with CACC.

The main focus on this paper is on the trajectory

planner and the decision making. Although the

decision-making modules focuses on many aspects

such as behaviour and intention prediction of other

participants as well as analysing road geometry

(Dariani & Schindler, 2019), in this paper only

platooning related functionalities of the decision-

making module are discussed.

The outline of the paper is as follows, chapter 2

describes the vehicle automation and briefly explains

the trajectory planner and decision-making module.

In Chapter 3 the trajectory planner is explained.

Chapter 4 is about the decision-making module with

the focus on the platoon management module and the

cruise controller. In Chapter 5 the functionality of the

designed algorithms has been proven in simulations

and tests in public traffic in a complex urban area, and

finally Chapter 6 is conclusion.

2 VEHICLE AUTOMATION

The Automated Driving Open Research (ADORe)

developed by the Institute of Transportation Systems

of the German Aerospace Center (DLR), also

available open source (Hess, et al., 2017), is a

modular software library and toolkit for decision

making, planning, control and simulation of

automated vehicles has been used for this work, see

Figure 2. As the same software is used in simulation

and in research vehicles, the simulation experiments

are very close to reality. Although many modules

remain unchanged in this work such as Navigation,

Controller, Data Model, etc., several modules have

been completely changed or modified explicitly for

this research work, such as Decision-Making,

especially the platoon management module,

Trajectory Planning and cruise controller.

Figure 2: ADORe modular architecture.

For Trajectory planning an optimal control

approach is used which makes the planned trajectory

the solution of a nonlinear optimization problem. One

powerful method to solve a sequence of nonlinear

Optimal Control Problems (OCP) is Sequential

Quadratic Programming (SQP). The Newton method

or quasi-Newton method finds a point where the

gradient of the objective function of the OCP

vanishes. The Newton or quasi-Newton method

requires a starting point or an initial solution and the

quality of the initial solution has high impact on the

convergence rate of the optimization problem and

consequently on the calculation time. Therefore, an

initial solution is calculated based on the shortest path

connecting current vehicle position to destination,

which is already available via “Navigation” module.

A “Decision-Making” module is designed on top of

the trajectory planner to define the strategical and

tactical tasks for the planner, i.e. the long- and short-

term tasks. Mainly due to the complexity of the non-

linear optimization problem, the planning horizon, ,

has its real-time limitation and cannot merge to

infinite. But the decision-making horizon can be

extended to the vehicle perception sensors vision

range or even to the communication range, which

permits the trajectory planner to take required actions

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

282

for events out of the trajectory planner horizon and

also, any possible cooperation between the vehicles,

such as platooning, is decided by this module. Figure

3 illustrates the planning horizon, green area, versus

the decision-making horizon, red area.

Another important part of the decision-making

module is the cruise controller. Although it is called a

controller, it does not have any direct interaction with

vehicle actuators. Instead, while forming or driving in

a platoon, based on the states of the preceding vehicle

i.e. position and velocity, received via V2V, it

calculates a velocity which results in a desired

headway with preceding vehicle. This velocity is

passed to the trajectory planner as a driving task, and

the trajectory planner plans a trajectory based on the

suggested velocity.

The next chapter describes the concept and

functionality of the trajectory planner.

Figure 3: Trajectory planning horizon (green) vs. decision

making horizon (red).

3 TRAJECTORY PLANNER

The trajectory planner consists of different

components in which a non-linear optimal control

problem is the core component. And as already

mentioned an initial solution as optimization starting

point is needed. Some of the main parts of the

trajectory optimization are explained here.

• Optimal Control Problem OCP:

The nonlinear optimization problem is defined as

min(

,)

(1)

with differential equation modelling the vehicles

dynamics and nonlinear constraints

 =



(,)

(2)





(,)



(3)

as well as states and inputs boundaries









(4)









(5)

The optimal control problem non-linearity and

also high length of the planning course make the

optimal control problem numerically difficult to solve

and also it requires high computational time. A

possibility to deal with this problem is using Moving-

Horizon approach (MHA) (Gerdts, 2003). In this

approach, the global optimization problem covering

the complete driving task is portioned into several

local optimal sub-problems of second, or planning

horizon, which are comparatively easier to solve. The

local optimal control problem structure is similar to

the global problem just that not the whole driving

course is considered.

Figure 4: The Moving-Horizon approach.

That is very similar to how the human driver drives,

i.e., in real driving scenario, the driver has limited

information about the road and knows only about the

area ahead. The moving-horizon approach also

updates the optimal control problem by saving the

solution for a part of the problem, , named increment

as a portion of horizon , and used it as the starting

point for the next optimal sub-problem, see Figure 4.

• Vehicle Model:

To describe vehicle dynamics the single-track

model also known as bicycle model is used. The

vehicle is regarded as a rigid body moving in the -

plane and combines both wheels per axle into one. In

the vehicle model roll and pitch angles are neglected

and the tire dynamics are approximated by linear tire

characteristic with saturation. The vehicle model (1)

has the following state vector  (6) and control vector

 (7).



=[,,,,,,,



]

(6)

=[



,



] (7)

Decentralized Platoon Management and Cooperative Cruise Control of Autonomous Cars with Manoeuvre Coordination Message

283

The states variables are vehicle position in global

coordinates [,], vehicle yaw angle  and yaw rate

̇, vehicle velocity , vehicle chassis sideslip angle ,

steering angle  and steering rate 



. The control

variables are steering angle acceleration 



guarantee that the vehicle applied steering angle  is

smooth (two times continuous differentiable) and

longitudinal force 



.The systems of differential

equations is discretized by applying Runge-Kutta

integration of fourth order as numerical integrator,

with step size of Δ and planning horizon of , see

Figure 4.

• Objective Function:

The desired driving behaviour is the result of an

objective function definition of the optimal control

problem. Therefore, the objective function must

result in a collision free and comfortable trajectory.

The objective function can be written as (8)



(,)=



ℒ

(,)

(8)

Index ℒstands for Lagrange term, equation (9) which

is an additional state inside the Ordinary Differential

Equation (ODE) of the vehicle model (2). Steering

rate 



and steering acceleration 



are inside the

objective function to make the steering behaviour

smooth and avoid uncomfortable steering wheel

impulse. Δis the difference between desired speed

and vehicle current speed. The desired speed in non-

cooperative model is calculated based on the

Intelligent Driver Model integrated in the decision-

making module, and in the cooperative mode, i.e.

platooning, it is calculated by the platoon controller.

Δ is the lateral vehicle distance to the center line. 



and 



are acceleration and jerk in the transverse and

longitudinal direction as comfort parameter. The last

two terms will not prevent rapid change of direction

therefore is introduced to attenuate high yaw rates.

And  is a diagonally matrix containing weighting

coefficients of each component.



ℒ

(

,

)

= ℒ(



,



,∆,∆,









,)











(9)

4 DECISION MAKING

In order to take a decision for autonomous vehicles

such as current driving speed, keeping the lane or

changing the lane and etc. the dynamic of the traffic

participants must be considered and based on that

their trajectory and intention must be precited.

While normal driving, the Intelligent Driver

Model (IDM) is used in Decision Making module to

calculate the velocity. IDM is a time-continuous car-

following model with the following ordinary

differential equations











=



(10)











=1−













−



∗

(





,Δ



)













(11)

where,



∗

(





,Δ



)

=



+



−





Δ

√



(12)

These are the velocity and acceleration equations for

any vehicle . 



is the net distance to the preceding

vehicle, 



is the position of the vehicle . Δ



is the

velocity difference, 



is the desired velocity, which

is the velocity at which the ego vehicle would drive

on any empty road, 



is the minimum desired net

distance between ego vehicle and preceding vehicle,

 is the desired time headway,  is the maximum

possible acceleration and  is the comfortable

braking deceleration. And finally, exponent  is

usually set to 4.

In this paper the main focus is on the cooperation,

especially from platooning point of view, which is the

platoon management and the cruise controller

module, more information about other parts of

Decision-Making module can be found in (Dariani &

Schindler, 2019).

4.1 Platoon Management

The platoon management module is a sub-module of

the decision making. The main task of the platoon

management is to determine if the platooning with the

preceding vehicle is possible or not. In that event, this

module based on the information received from

preceding vehicle via V2V communication, predict

its intention and based on that the platooning state is

defined. The platoon management module is state

machine based and can be used in the CACC mode as

well as Platoon mode. In the previous work done in

the European Horizon 2020 project MAVEN, an

extended CAM message was used for platooning

information (Schindler, Dariani, Rondinone, &

Walter, Dynamic and flexible platooning in urban

areas, March 2018) (Schindler, Dariani, Rondinone,

& Walter, Implementation and testing of dynamic and

flexible platoons in urban areas, 2019). The problem

with that approach was that the extended message

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

284

was not a standard message and only the vehicles

inside the context of the project could understand and

interpret the message. In this work we have used the

Manoeuvre Coordination Message (MCM), which is

a prominent candidate for becoming a standard

message used to coordinate manoeuvres between

automated vehicles (Lehmann & Wolf, 2018).

Although this message is not designed for platooning,

it is more capable for such an approach than standard

CAM messages, as it contains also the planned

trajectory of an automated vehicle. Here, the sketched

draft of the MCM used in H2020 TransAID is used

without modifications (Schindler, 2019). In this

chapter the platoon management state machines are

explained.

The platoon management consists of two state

machines, Platooning state machine and Distance

state machine. As illustrated in Figure 5, each vehicle

that can form a platoon has an implemented set of two

separate state machines that cover the multiple

potential states for platooning. The primary platoon

state machine, which displays the vehicle’s current

platooning status, serves as the foundation for all

operations. There’s also the distance state machine,

which is in charge of keeping track of the distance to

the preceding car or opening up a space, mostly to

react to a merge of other cars into the current ego lane.

Both state machines are explained briefly in the next

subsections, respectively.

The platoon state machine depicts the vehicle’s

overall condition. It specifies whether the

autonomous vehicle is now capable of driving in a

platoon or not. If the vehicle is unable to create or join

a platoon, e.g. due to a failure in the communication

module, or when the platooning mode has been

disabled by the driver, the platooning state machine

activates a transition to the state “Not able”. As a

result, while in this mode, the vehicle must maintain

a normal distance from other vehicles, therefore the

distance state machine has the state “Normal

Distance”. The state "able" is a composite state. This

is the state machine’s default initial state. It is divided

into four sub-states. “Want to form”, “Joining a

platoon”, “in a platoon” and “Leaving a platoon”.

The state "want to form" is a sub-state of the

composite state "able". This is the “able”

composite state’s initial state. The vehicle is

attempting to form a platoon in this state. It is

unrelated to any circumstance. It primarily acts as a

state indicating that the vehicle is interested in

platooning and that the system can presently form a

platoon.

Figure 5: Platoon management state machines.

The state "joining" is a sub-state of the composite

state "able". The vehicle is joining a platoon in this

state. To look at it another way, the vehicle is in this

state to achieve the desired time headway to the

preceding vehicle. In this state, the distance state

machine has a transition to “close distance” state. In

the state "in a platoon" the vehicle is acting as a full

platoon member. Besides, the vehicle is still

interested in forming a platoon if it is the last or the

first vehicle of the platoon. The distance state

machine remains in “close distance” state.

The state "leaving" indicates that the vehicle is

currently leaving the platoon. The vehicle is not

interested in forming or joining another platoon as

long as it is in this state. When a single vehicle leaves

the platoon, the condition "leaving" is reached. The

distance state machine has a transition from “close

distance” to “normal distance”.

As already mentioned, in this work no platooning

specific message is used, therefore the platooning

state of the other road user is unknown and it must be

predicted. It is though enough to know if the

preceding vehicle is “able” or “not able” to do

platooning or if it has “Want to form” or “leaving”

state. And these states can be implicitly extracted

from the MCM message.

MCM has several containers and data frames, see

(Schindler, 2019), but important for platooning use

cases are the following:

Decentralized Platoon Management and Cooperative Cruise Control of Autonomous Cars with Manoeuvre Coordination Message

285

Tolerated Distance Ahead: it is the distance to the

trajectory points that other vehicles have to respect

when they want to accept a desired trajectory of

someone else.

Tolerated Distance Behind: it is the distance to

the trajectory points that the other vehicles have to

respect when they want to accept a desired trajectory

of someone else.

Planned Trajectory: it is the future trajectory of

the vehicle.

Target Automation Level: it is the SAE level of

the automation.

Hence in the context of platooning, if a vehicle

has an automation level greater or equal to 3 and

broadcasts its current trajectory, then it has the “able”

state, otherwise it is “not able”. Though the level of

automation and current trajectory information are not

enough, they must be combined with the tolerated

distance ahead and behind to implicitly predict if the

vehicle is in the state “want to form” or “leaving”. A

vehicle which has the desire to form or join a platoon

has a relatively short tolerated distance ahead and

behind compare to the “leaving” vehicle. The exact

distance threshold can be calculated based on the

platooning desired time headway and velocity.

Although the current platoon management is

simpler compared to the MAVEN project (Schindler,

Dariani, Rondinone, & Walter, Dynamic and flexible

platooning in urban areas, March 2018) (Schindler,

Dariani, Rondinone, & Walter, Implementation and

testing of dynamic and flexible platoons in urban

areas, 2019), many transitions remain unchanged or

very similar.

Cooperative Cruise Controller

As explained, the cooperative cruise controller is a

part of the decision-making process which runs in

parallel to the trajectory planner and based on the

latest information received via V2V communication

calculates a desired velocity which must be followed

in order to maintain the desired headway with

preceding vehicle.

In this paper we present two different approaches

for the controller. The first one is a simple PD

controller (13) and the second approach is an optimal

control approach.



(



)

=





(



)

+



()



(13)

The designed PD controller is based on the gap

regulation controller for a cooperative ACC system of

Milanes et. al. (Milanes, et al., 2014). In our

approach, unlike (Milanes, et al., 2014) no leader

information is needed. Design a controller which uses

not only preceding vehicle information, but also a

leader results in string stability when the vehicles

drive with extreme short distance. Anyhow that is not

the main focus of this paper. On the other hand, in a

string of several vehicles the V2V information must

be analysed and be sorted to find out which

information belongs to the preceding and which

information belongs to the leader. And based on that

information a mapping on a HD map must be done to

calculate the net distance between ego and preceding

vehicle, as well as between ego and leader vehicle.

We believe for urban cooperation, considering the

urban environment dynamic, an extreme short

headway is not necessary, neither safe, therefore

preceding vehicle information might be enough to

design a cooperative cruise controller, but it does not

guarantee the string stability.

In Figure 6, () denotes the vehicle model; the

car-following policy with respect to the preceding

vehicle can be represented with terms 



(); 



() is

the controllers that control the time-gap error with

respect to the preceding vehicle; () represents the

time delay in wireless communication; 



and 



are the control actions for the ego and the preceding

vehicle, respectively.

One of them is in charge of maintaining

the present speed, but instead of using the ego

vehicle’s or preceding vehicle’s speed as a feed-

forward term, the preceding vehicle’s target speed is

used. This allows for faster vehicle reaction to speed

changes and shorter transition times between throttle

and brake actuations. The other term aims to keep the

errors in the preceding 



() vehicle as little as

possible.





(



)

=



+



(14)

The car-following policy can be defined as





(



)

=ℎ



(



)

(15)

where ℎ



is the time-gap target value to the preceding

vehicle. The wireless communication system was

expected to have no delay for the controller design,

i.e., 

(



)

=1.

Figure 6: PD platoon controller.

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

286

Despite the fact that the PD controllers are easy to

implement and they are effective, they do not use the

full potential of the MCM which is the use of the

current trajectory of the preceding vehicle. The PD

controller requires only the next velocity and position

of the vehicle. That is why with PD controller the

transition from “normal distance” to “close distance”

is not always smooth and comfortable, but once that

the desired headway is reached, the PD controller

functions properly. The above-mentioned problem is

due the fact that in order to reach the desired time

headway when the current time headway is bigger

than the desired, an acceleration is calculated also

when the preceding vehicle has a lower velocity or

even stand-still. To overcome this problem, a second

controller is designed for this work which uses the

complete trajectory of the preceding vehicle, included

in MCM, and calculates a velocity for the future time

horizon. The predictive nature of this controller will

avoid the above-mentioned problem.

A simple vehicle longitudinal dynamics model is

used for the optimal control with the following states;

longitudinal acceleration, longitudinal velocity,

progress which is the longitudinal position of the

vehicle and an extra state for the Lagrange term of the

objective function. The input, to be found by the

optimizer, is the desired acceleration. 



represents

the engine dynamics.

 =

−





 =

(16)

=

As mentioned, the objective function has only

Lagrange part (17), as an extra state inside ODE of

the vehicle longitudinal dynamics model.



ℒ

,= ℒ

(

,,Δ

)











(17)

The preliminary objective is to keep the desired time

headway . At low velocities the time headway will

not guarantee a safe behaviour, that is why distance 

between ego and the preceding vehicle is calculated

and the objective is to not pass the defined minimum

distance. Δ is the difference of the velocity between

the preceding vehicle and ego vehicle. This term

makes the transition from “Normal distance” to

“close distance” smooth and comfortable, especially

while joining a low speed or standing still preceding

vehicle. Boundaries can be applied to the states and

input such as defining the maximum and minimum

velocity, and acceleration. The boundaries and engine

dynamics (16) make the optimization result feasible

and customized for the vehicle dynamics.

5 TESTS AND VALIDATION

As previously mentioned, the simulation has been

done in ADORe which contains all of the necessary

data and components to create simulation scenarios

with a large number of vehicles that can interact with

one another and act like actual automobiles in diverse

urban roads. The implementation in ADORe is very

similar to the real-world implementation. All the

simulation cars are equipped with MCM senders and

receivers. Each car has also virtual sensors which are

used to create an environment model. Figure 7

illustrates the simulation environment of ADORe

(Hess, et al., 2017).

Although many scenarios can be tested in

simulation, our focus is on the functionality of the

predictive controller while joining a low speed

preceding. In urban scenario, forming or joining at

intersection is common, especially when

infrastructure plays a role in traffic coordination.

Joining a low speed or stand still vehicle is probable,

but as mentioned, the PD cruise controller does not

behave smooth in this case. That is why Figure 8

illustrates the ego vehicle velocity, calculated with

predictive controller, while joining and forming a

platoon with a preceding vehicle with velocity zero

which is 100 meters ahead. The ego vehicle can have

a maximum velocity of 13.6 [/] but the vehicle

does not exceed 9[/], as the velocity is calculated

for a horizon of time and it is foreseen that a

deceleration is required. That is why the ego vehicle

decelerates smoothly till stand still.

Figure 7: An example of ADORe simulation environment.

Decentralized Platoon Management and Cooperative Cruise Control of Autonomous Cars with Manoeuvre Coordination Message

287

Figure 8: Velocity of the go while joining a stand still

preceding.

After several promising simulated runs the

developed prototype has been tested under real

conditions using DLR’s test vehicles on a public

urban road. In this paper the main focus is on the

urban driving scenario which was done on a street in

Braunschweig-Germany by two highly automated

vehicles of the German Aerospace Center’s Insitute

of Transportation Systems (DLR), namely FASCarE

and ViewCar 2, See Figure 9. Both cars have a similar

sensor setup. In addition, both cars are equipped with

V2X communication modules. Figure 10 illustrates

the part of the road that has been used for the real

urban scenario. As illustrated, the testing road has an

intersection and traffic light phase is communicated

via I2V communication to the vehicles. For the urban

scenario the PD controller has been used

Figure 11 illustrates the velocities of the

preceding vehicle and ego in urban environment.

Both vehicles had a safety driver on-board and at a

given moment the automation has been activated and

the data was recorded. After activation, both vehicles

are in fully autonomous mode. Some important

moments are numbered in figure 11. At “1”, the

platoon management module of the ego vehicle, the

follower, has been switched to “forming” and “close

distance”, which resulted in acceleration of the

following vehicle and closing the gap between two

vehicles. At “2” the both vehicles are “in platoon”.

While remaining in platoon, at “3” both vehicles

approaching the intersection that has a red traffic

light. Keeping the platoon stable while reducing

speed till stand still is the main reason of choosing

this road for validation. Both vehicles wait till green

traffic light and after that they accelerate and remain

in platoon till end of the track.

6 CONCLUSIONS

In this paper a decentralized approach for platoon

management and control has been presented. The

platoon management deals with platooning state of

each vehicle, and the cooperative cruise controller

calculates a velocity which must be followed in order

to be in a stable platoon. Both of these modules are a

part of decision-making module. Trajectory planner

receives the tasks from decision-making module and

plan a trajectory. The trajectory planner and decision-

making module functionalities have been approved in

simulation, using ADORe and with real urban

scenario test with two autonomous cars of German

Aerospace Center.

As next step, the predictive controller can be

tested in urban scenario and also in simulation with a

string of several vehicles.

Figure 9: DLR’s test vehicles.

Figure 10: Urban road used for validation. Braunschweig-

Germany.

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

288

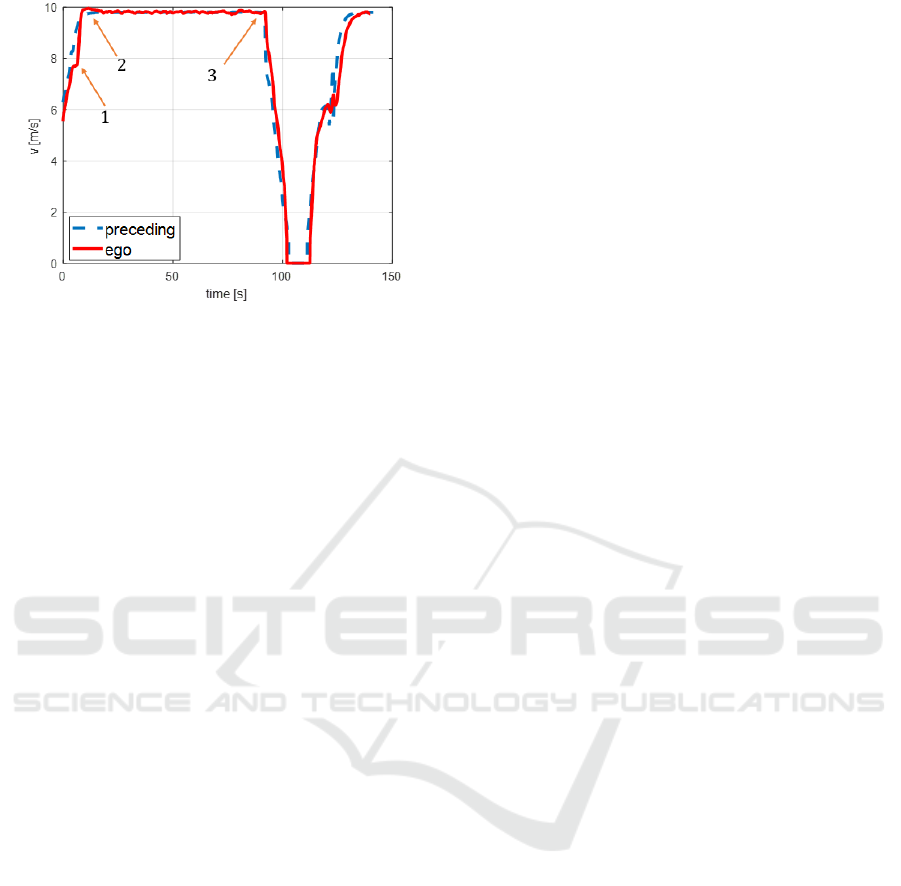
Figure 11: Velocity of the preceding and ego vehicle.

REFERENCES

Dariani, R., & Schindler, J. (2019). Cooperative Strategical

Decision and Trajectory Planning for Automated

Vehicle in Urban Areas. IEEE International

Conference on Vehicular Electronics and Safety

(ICVES).

Gerdts, M. (2003). A moving horizon technique for the

simulation of automoile test drives. Journal of applied

mathematics and mechanics.

Hess, D., Lapoehn, S., Nichting, M., Lobig, T., Behrisch,

M., Dariani, R., Schindler, J. (2017). ADORe. Von

ADORe: https://projects.eclipse.org/proposals/eclipse-

automated-driving-open-research-adore abgerufen

Lehmann, B. G., & Wolf, L. (2018). A Generic Approach

towards Maneuver Coordination for Automated

Vehicles. 21st International Conference on Intelligent

Transportation Systems (ITSC). Maui, Hawaii, USA.

McGehee, D., Mazzae, E., & Baldwin, G. (July 2000).

Driver Reaction Time in Crash Avoidance Research:

Validation of A Driving Simulation Study On A Test

Track. Proceedings of the Human Factors and

Ergonomics Society Annual Meeting.

Milanes, V., Shladover, S., Spring, J., Nowakowski, C.,

Kawayoe, H., & Nakamura, M. (2014). Cooperative

Adaptive Cruise Control in Real Traffic Situations.

IEEE Transactions On Intelligent Transportation

Systems, Vol. 15, NO. 1.

SAE International. (3. May 2021). Von

https://www.sae.org/blog/sae-j3016-update abgerufen

Schindler, J. (2019). TransAid Deliverable 7.2: System

prototype demonstration.

Schindler, J., Dariani, R., Rondinone, M., & Walter, T.

(2018). Dynamic and flexible platooning in urban areas.

AAET Braunschweig-Germany.

Schindler, J., Dariani, R., Rondinone, M., & Walter, T.

(2019). Implementation and testing of dynamic and

flexible platoons in urban areas. AAET. Braunschweig-

Germany.

Schindler, R., Blokpoe, R., Rondinone, R., Walter, T.,

Pirbyl, O., Hagen, S., Dariani, R. (2020). MAVEN

Deliverable 6.4: Integration Final Report.

Transportation, U. D. (March 2018). Critical reasons for

crashes investigated in the national motor vehicle crash

causation survey. NHTSA's National Center for

Statistics and Analysis.

Decentralized Platoon Management and Cooperative Cruise Control of Autonomous Cars with Manoeuvre Coordination Message

289