Optimal Placement of Micro-services Chains in a Fog Infrastructure

Claudia Canali

, Giuseppe Di Modica

, Riccardo Lancellotti

and Domenico Scotece

Department of Engineering ”Enzo Ferrari”, University of Modena and Reggio Emilia, Modena, Italy

Department of Engineering and Computer Science, University of Bologna, Bologna, Italy

Keywords:

Micro-services Placement, Fog Computing, Genetic Algorithms, Performance Evaluation.

Abstract:

Fog computing emerged as a novel approach to deliver micro-services that support innovative applications.

This paradigm is consistent with the modern approach to application development, that leverages the compo-

sition of small micro-services that can be combined to create value-added applications. These applications

typically require the access from distributed data sources, such as sensors located in multiple geographic lo-

cations or mobile users. In such scenarios, the traditional cloud approach is not suitable because latency

constraints may not be compatible with having time-critical computations occurring on a far away data-center;

furthermore, the amount of data to exchange may cause high costs imposed by the cloud pricing model. A

layer of fog nodes close to application consumers can host pre-processing and data aggregation tasks that can

reduce the response time of latency-sensitive elaboration as well as the trafﬁc to the cloud data-centers. How-

ever, the problem of smartly placing micro-services over fog nodes that can fulﬁll Service Level Agreements

is far more complex than in the more controlled scenario of cloud computing, due to the heterogeneity of

fog infrastructures in terms of performance of both the computing nodes and inter-node connectivity. In this

paper, we tackle such problem proposing a mathematical model for the performance of complex applications

deployed on a fog infrastructure. We adapt the proposed model to be used in a genetic algorithm to achieve

optimized deployment decisions about the placement of micro-services chains. Our experiments prove the

viability of our proposal with respect to meeting the SLA requirements in a wide set of operating conditions.

1 INTRODUCTION

According to the OpenFog Consortium Byers and

Swanson (2017), ”... fog computing is a horizontal

system-level architecture that distributes computing,

storage, control, and networking functions closer to

users along a cloud-to-things continuum”. The fog

paradigm grounds on the idea that by putting comput-

ing resources closer to both mobile users and sensors,

a better guarantee of service quality can be ensured

in all demanding scenarios that cloud computing has

proven unﬁt to serve.

If on the one hand the fog has shown the poten-

tial to provide such a guarantee, on the other one a

typical fog data center is not even comparable to a

cloud one in terms of both offered computing capac-

ity and homogeneity of owned resources. Unlike the

cloud, the fog fails to provision ﬂexibility and large

availability of resources to requesting users. A fog-

based computing environment typically requires that

accurate schemes of resource management and ser-

vice allocation are put into force in order to sustain the

promised service quality. Furthermore, a fog infras-

tructure is a geographically distributed system, mean-

ing that network-related delay in fog-to-fog commu-

nications are typically not negligible, thus placing ad-

ditional concerns for the deployment of complex ap-

plications.

In the depicted computing context, we deal with

the service placement problem, i.e., the problem of

how to best place services on the limited resources of-

fered by the fog in a way that meets the performance

expectation of service consumers. In particular, we

consider the common case of applications composed

of multiple and interconnected micro-services, which

in turn can be deployed independently of each other in

any of the available fog resources. The employment

of small software computing units rather than mono-

lithic applications makes the service placement prob-

lem even harder, as the number of potential micro-

service/resource mappings may grow very high.

In this paper, we tackle the deﬁnition of an analyti-

cal model to represent the placement of micro-service

based software applications on the computing nodes

Canali, C., Di Modica, G., Lancellotti, R. and Scotece, D.

Optimal Placement of Micro-services Chains in a Fog Infrastructure.

DOI: 10.5220/0011049500003200

In Proceedings of the 12th International Conference on Cloud Computing and Services Science (CLOSER 2022), pages 199-206

ISBN: 978-989-758-570-8; ISSN: 2184-5042

199

of a fog data center. We leverage the potential of ge-

netic algorithms to propose a strategy that explores

the space of service-resource mappings to discover

the conﬁguration that best matches the end users ex-

pectation in terms of service response time. Finally,

we discuss the results of tests run to assess the vi-

ability of the proposed strategy on several boundary

conditions.

In summary, the paper proposes the following in-

novative contributions:

• an analytical framework to model the placement

of micro-service chains in a fog environment;

• an optimal placement strategy leveraging a ge-

netic algorithm approach;

• a sensitivity analysis aimed to assess the ability of

the devised strategy to ﬁnd suitable solutions.

The rest of the paper is structured in the following

way. In Section 2, we report a survey of the state of art

addressing the placement of services in fog infrastruc-

tures. In Section 3, we introduce the motivation of the

paper along with a basic use case scenario. We dis-

cuss a theoretical model to represent the performance

of services deployed in a fog infrastructure in Section

4. In Section 5, we present the results of experiments

aimed at evaluating the proposed approach. Finally, in

Section 6 we conclude the paper and anticipate some

future directions of the work.

2 LITERATURE REVIEW

While service placement in terms of Virtual Machine

allocation in cloud datacenters has been extensively

studied Mann (2015); Canali and Lancellotti (2017),

the placement of micro-services over the nodes of a

fog computing infrastructure has received far less at-

tention.

Several studies propose mechanisms for service

placement over the geographically distributed nodes

of a fog infrastructure starting by the simplifying as-

sumption that an IoT application only consist of one

independent micro-service. Among them, the solu-

tion proposed in Yu et al. (2018) is based on an opti-

mization model to jointly study application placement

and data routing. The authors in Skarlat et al. (2017)

proposes a solution for the placement of IoT services

on fog resources, taking into account their QoS re-

quirements. They rely on the concept of fog colonies

and model the fog service placement problem as an

Integer Linear Programming problem. The study pre-

sented in Canali and Lancellotti (2019) proposes for

the ﬁrst time a service placement for fog comput-

ing systems based on genetic algorithms, demonstrat-

ing the efﬁcacy of this kind of solution in a fog en-

vironment. However, in the reality complex appli-

cations usually are made up of multiple dependent

micro-services, while all the cited studies did not con-

sider the existence of a chain of multiple dependent

services and the consequent constraints, that signiﬁ-

cantly increase the complexity of the solution.

Other studies focus on service placement in com-

bined fog-to-cloud architectures Souza et al. (2018);

Gupta et al. (2017); Yousefpour et al. (2017). The

study in Souza et al. (2018) proposes novel strate-

gies to ofﬂoad services execution within the whole set

of cloud and fog resources, according to the speciﬁc

services needs and resources characteristics. The so-

lutions proposed in Gupta et al. (2017); Yousefpour

et al. (2017) place services with low latency require-

ments on the fog nodes, not powerful enough to host

all services. In our solution, we focus on placing

the micro-services only on the nodes of the fog layer

in order to maximize the user satisfaction, assuming

that, for the considered service chains, fog nodes are

able to process every request.

Only a minor number of studies have consid-

ered the problem of modeling the service chains and

their placement over the fog nodes. Among them,

some solutions are based on completely distributed

approaches Kayal and Liebeherr (2019); Xiao and

Krunz (2017). In Kayal and Liebeherr (2019) authors

seek to optimize energy consumption and communi-

cation costs based on a game-theoretic approximation

method. In Xiao and Krunz (2017), fog nodes cooper-

atively determine the optimal amount of workload to

be forwarded and processed by each other to improve

the users’ quality of experience. On the other hand,

in Santos et al. (2020) a centralized service chain con-

troller optimizes the placement of service chains in

fog environments.Our solution relies on Genetic Al-

gorithms to cope with the non linear nature of the

optimization problem used to minimize the response

time of the service chains, and proposed a wide sen-

sitivity analysis to consider the impact of varying ser-

vice chain length, load level and number of fog nodes.

3 MOTIVATING SCENARIO

The fog computing paradigm aims at compensating

the inability of cloud computing to guarantee low

latency requirements typically required by applica-

tions in IoT contexts. This is typically achieved by

deploying services close to the source of data they

need to process and/or users they need to serve. Un-

fortunately, the processing and storage power of fog

nodes is limited compared with that offered by the

CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science

200

Microservice-node mapping Request load

Inter-node virtual network link

Figure 1.

cloud. Furthermore fog resources are typically het-

erogeneous, i.e., computing nodes provided in the fog

may exhibit non-uniform capacity. In such an envi-

ronment it is paramount to devise smart resource allo-

cation mechanisms that optimise resource occupancy

and grant service level agreements at the same time.

The problem is further exacerbated by the fact that

an application is often composed of multiple, smaller

micro-services that, in their turn, can be deployed in

any of the available fog nodes independently of each

other.

In this paper, we tackle a typical problem of ser-

vice placement in a fog environment. Input to the

problem are: i) a set of applications subject to SLAs;

ii) a list of fog nodes with known capacity features;

iii) a demand for applications whose expected load in

the short-to-mid term is known a priori. We aim to

ﬁnd an optimal application deployment scheme that

meet customers’ SLAs. Also, assuming that all appli-

cations are natively decomposed into smaller micro-

services, when seeking for optimal micro-service to

node placement, we will also monitor metrics such as

the average number of nodes spanned by applications,

the network delay the deployment incurs into and the

load balance.

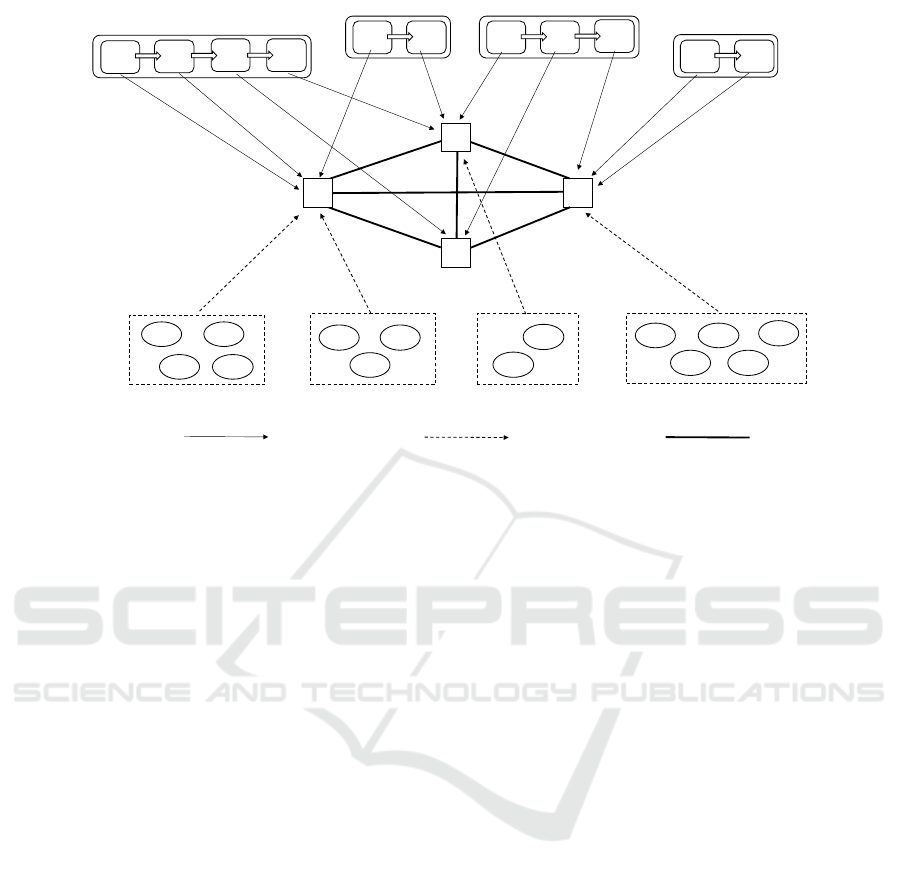
In Figure 1, we depict a sample service deploy-

ment scenario where four distinct applications are

placed on four fog nodes. The applications will serve

requests originated by four groups of end users. Each

group of users targets just one application. The way

user requests are conveyed to the targeted application

running in the fog layer is not relevant for the purpose

of this work. In the ﬁgure, each application is mod-

eled by means of a service chain composed of at least

two micro-services. Without loss of generality, we as-

sume that a service chain c

is actually implemented

by pipelining an ordered sequence of micro-services

i j

, j ∈ 1,2,...n. For j > 1, m

i j

takes input from

i( j−1)

and, for j < n sends its output to m

i( j+1)

. The

micro-service occupying the ﬁrst position in the chain

) will take c

input while m

ends the processing

either sending the results to a cloud-based storage or

by sending the ﬁnal result back trough the chain to re-

questing users. By length of a service chain we will

refer to the number of micro-services composing the

chain. Micro-services composing a service chain may

be placed into one or multiple fog nodes. Obviously,

the number of fog nodes hosting a service chain may

not exceed the service chain length. In its turn, a fog

node may host micro-services belonging to different

service chains. In the ﬁgure, service chain c

’s three

micro-services are hosted by three distinct fog nodes,

while the entire service chain c

is placed in one fog

node. A fog node f

is the recipient of all user re-

quests addressed to the service chain(s) having their

ﬁrst micro-service hosted by f

. By way of exam-

ple, fog node f

will receive all requests addressed

to service chain c

and c

, as f

is hosting m

and

which are the ﬁrst micro-service in the service

chains c

and c

, respectively. Fog nodes show differ-

ent computing capacity and are interconnected with

each other via homogeneous high-speed network.

In this paper, we focus on the performance rep-

resented by the time taken by the application to re-

ply to an end user’s request (i.e., the service response

time). Such an index is affected by some factors,

Optimal Placement of Micro-services Chains in a Fog Infrastructure

201

among which the most impacting ones are i) the ap-

plication’s request load, ii) the average service time of

all micro-services composing the service chain, and

iii) the computing capacity of fog nodes hosting the

micro-services. We aim to deﬁne a service placement

strategy that, taking in consideration the mentioned

boundary conditions, strives to minimize the applica-

tions response time.

4 PERFORMANCE MODEL

We now discuss the theoretical model used to de-

scribe the service placement problem as well as the

heuristic approach adopted to solve the problem. We

consider a framework such as the one described in

Section 3, with service chains composed of multiple

micro-services that needs to be deployed on a set of

fog nodes. Each chain receives data or activation re-

quests that can be either generated by devices or by

mobile users. We call these sources of events simply

sensors.

4.1 Performance Metric

In our formulation, the main performance metric is

the application response time, that is the time incur-

ring between the moment a sensor sends some data

and the time the service chain has processed the re-

quest. Indeed, optimizing this metric brings beneﬁts

with respect to several other more specialized perfor-

mance indicators. For example, signiﬁcantly unbal-

anced load may cause overload on part of the fog in-

frastructure, with a resulting penalty on the response

time; in a similar way, a placement that distributes the

micro-services of a service chain on many fog nodes

incur in a higher network-related delay compared to a

solution that tries to place micro-services on the same

or on nearby nodes. In our model we explicitly intro-

duce a maximum acceptable response time for each

service chain, that is the considered SLA.

In the following model, we refer to notation pre-

sented in Table 1, that can be used as a summary. For

the sake of brevity, we identify a micro-service sim-

ply as m, without explicitly showing the double index

of service chain and progressive position within the

chain as in Sec. 3.

The ﬁst critical element of our model is the per-

formance of a single micro-service. Service time of a

generic micro-service m is modeled with a Gaussian

distribution with average S

and standard deviation

. The service time corresponds to the time mea-

sured at server side to process a request when the ser-

vice is located on a fog node in an idle status. Service

Table 1: Notation and parameters for the proposed model.

Model parameters

M Set of micro-services

F Set of fog nodes

C Set of service chains

Incoming req. rate to micro-service m

Incoming req. rate to fog node f

Incoming req. rate to service chain c

Λ Incoming global request rate

Avg. service time for micro-service m

Standard deviation of S

Computational power of fog node f

Avg. response time for services on node f

Avg. response time for service chain c

R Global avg. response time

SLA

SLA of service chain c

Services order of execution in a chain

, f

network delay between nodes f

and f

Model indices

f A fog node

c A service chain

m A micro-service

Decision variables

m, f

Allocation of micro-service m to fog f

time contains no network delay nor waiting time due

to other services being processed.

For the purpose of model description, we make

the assumption that the system is in a steady state

condition, i.e., fog nodes are not overloaded. As

such, we can assume that, in every micro-service of

a service chain, the incoming load equals the out-

going load, i.e., for a generic service chain c ∈ C ,

= λ

∀m

∈ c. Furthermore, we anticipate

that the decisions on the placement of services will

be represented by a matrix of Boolean variables X =

m, f

,m ∈ M , f ∈ F } being x

m, f

= 1 ⇐⇒ service m

is assigned to fog node f .

A micro-service must be assigned to exactly one

fog node. However, multiple micro-services may co-

exist on a fog node, and the incoming requests may

be interleaved and enqueued. To model the perfor-

mance of a fog node we recur to a queuing theory

model for a multi-class application. We assume each

fog node f to be target of this multi-class workload.

Each class is one of the micro-services allocated on

the fog node f . As the service time of each micro-

service is a Gaussian distribution, the resulting multi-

class system will present a service time described as

a mixture of Gaussian distributions. Furthermore, we

consider that each node is characterized by a compu-

tational power P

that represents a speedup factor for

the service time. The resulting composite service time

can thus be described with an average value S

and a

CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science

202

standard deviation σ

as follows:

∑

m∈M

m, f

(1)



∑

m∈M

m, f

+ σ

)



− S

(2)

where λ

∑

m∈M

m, f

is the total incoming load

on node f . From this deﬁnition, we can derive the

expected response time R

for node f from the Pol-

laczek Khinchin formula:

= S

+ σ

1 − λ

(3)

For a generic service chain c, the response time R

is the sum of the response times of the nodes where

the micro-services belonging to that chain have been

deployed, plus the network delay associated with

the data transfer between each couple of subsequent

micro-services in the chain.

∑

m∈c

m, f

· R

∑

, f

∈F

∑

∈c

· x

, f

· x

, f

· δ

, f

(4)

where o

represents the order of execution of

micro-services in service chain c. Speciﬁcally

= 1 ⇐⇒ m

≺ m

, meaning that service m

is ahead of m

in the service chain.

4.2 Optimization Problem

We now present the optimization problem that de-

scribes the allocation of micro-services on the fog

nodes. We rely on the notation in Table 1 and exploit

the performance metrics introduced in Section 4.1.

minob j(X) =

∑

c∈C

(5)

subject to:

∑

f ∈F

m, f

= 1 ∀m ∈ M , (6)

∀ f ∈ F , (7)

< T

SLA

∀c ∈ C , (8)

m, f

= {0, 1}, ∀m ∈ M , f ∈ F , (9)

The objective function (5) is the weighted sum of

the response time of each service chain, that is calcu-

lated using Eq. (4). The weights w

are chosen in a

way that

∑

c∈C

= 1. In the basic deﬁnition of the

problem we can simply assume that w

= λ

/Λ, that

is, weights are proportional to the incoming trafﬁc in

each service chain (Λ is the sum of all λ

,s ∈ S ).

The optimization problem is characterized by

three constraints. The constraint expressed in Eq. (6)

imposes that each micro-service need to be allocated

on one and only one fog node. The constraint ex-

pressed in Eq. (7) imposes that fog nodes need not to

be in an overload condition (if the average processing

rate is 1/S

, this is the maximum allowed incoming

trafﬁc). The next constraint, in Eq. (8) ensures the

respect of the SLA for each service chain. Finally,

Eq. (9) describes the Boolean nature of the decision

variable.

4.3 Genetic Algorithm

The considered problem has a nonlinear nature (due

to its objective function) that makes it difﬁcult to ﬁnd

a solution. To tackle it, we adopted a heuristic ap-

proach inspired to evolutionary algorithms. Evolu-

tionary algorithms have been largely used in litera-

ture Binitha et al. (2012); Yusoh and Tang (2010) to

cope with cloud and fog infrastructure management

problems. In this paper, we leverage a heuristic ap-

proach based on Genetic Algorithms (GAs).

We brieﬂy recall the main elements of a genetic

algorithm. The solution is encoded in a chromosome

composed by genes that represent the single parame-

ters characterizing a solution of the problem. In the

solution we consider a population of individuals, be-

ing each individual a potential solution of the problem

described by the individual chromosome. The initial

population is randomly generated.

In our problem, we map the optimization model

described in Section 4.2 by deﬁning a chromosome

as a set of M = |M | genes, with M being the num-

ber of micro-services. Each gene is an integer num-

ber between 1 and F = |F |, that is the number of fog

nodes. The generic m

gene in a chromosome g

can be deﬁned as: g

= { f : x

m, f

= 1}. By virtue of

constraint (6), only one fog node will host the micro-

service m, so the encoding of the chromosome will

automatically produce solutions that satisfy Eqs. (6)

and (9).

To each individual we assign a value of the ﬁt-

ness score, that is based on the objective function

of the optimization problem deﬁned in Eq. (5). To

take full advantage of the genetic algorithm poten-

tial, we should allow the genetic pool to roam free

over the possible conﬁgurations. This approach con-

ﬂicts with constraints (7) and (8) concerning the fog

node overload and SLA satisfaction. Instead of em-

bedding the notion of unacceptable solution in the

Optimal Placement of Micro-services Chains in a Fog Infrastructure

203

problem encoding, we prefer to cope with this fea-

ture of the problem using the ﬁtness function. Specif-

ically, individuals providing a solution featuring one

or more overloaded fog nodes are characterized by a

poor ﬁtness score (we consider in Eq. (3) that λ

0.999; furthermore we multiply the response time by

1 + λ

− 1/S

to make the penalty proportional to the

overload level). In a similar way we introduce a sig-

niﬁcant penalty when one or more chains don’t meet

their SLA. As a consequence, such individuals are

likely to be pruned from the genetic pool.

In the genetic algorithm, the population evolves

through a set of generations aiming to reach higher

ﬁtness scores through a set of operators. Speciﬁcally,

in our experiments we consider a random mutation

operator to explore new areas of the solution space;

a uniform crossover to merge individuals; and a tour-

nament selection to select the ﬁttest individuals for

the next generation. The genetic algorithm has been

implemented using the DEAP

library. Preliminary

tests were carried out to tune the main algorithm pa-

rameters. Speciﬁcally, in our analysis we consider a

mutation and crossover probability (that is the prob-

ability of an individual to be chosen for mutation

and crossover, respectively) such that: P

mut

= 0.8%,

= 0.8%. From the same preliminary tuning we set

the initial population to 600 individuals and the gen-

erations to 600.

5 EXPERIMENTAL RESULTS

5.1 Experimental Setup

In this section, we discuss a set of experiments we

ran to assess the ability of the proposed GA-based ap-

proach to ﬁnd suitable solution to the service place-

ment problem in a fog infrastructure.

In our analysis, we generate several random prob-

lems with pre-deﬁned characteristics and evaluate the

quality of the solution found by our heuristic.

Each problem is deﬁned in terms of:

• Service chain length L

, that is the number of

micro-services composing a chain;

• Service time of a service chain S

;

• Average network delay δ between two fog nodes;

• Problem size, that is the number of fog nodes and

of service chains considered.

In our analysis we consider chains of equal length,

that is L

= |{m ∈ c}| is constant ∀c ∈ C . The impact

DEAP: Distributed Evolutionary Algorithms in Python

- https://deap.readthedocs.io/en/master/

of this parameter is evaluated in Section 5.2, while in

the other analyses we consider chains composed of 5

micro-services.

Throughout our experiments, the incoming load is

set in such a way that the average utilization of fog

nodes is in the order of 60%.

Concerning the problem size, the number of nodes

can be identiﬁed as |F |, while the number of chains

is |C |. As default values, used everywhere except for

the scalability evaluation of Section 5.3, we consider

a set of 10 fog nodes supporting 4 service chains.

For this analysis we assume that the SLA is set to

10× the service time of the chain, that is a common

value used in cloud applications. In our experiments,

this SLA is automatically satisﬁed as long as no over-

load occurs, motivating our choice of not performing

a speciﬁc analysis with respect to this parameter.

We consider the the response time of the service

chains and the average number of hops in the chain

deployments, normalized against the chain length

(ranging in [0, 1]) as signiﬁcant performance mea-

sure in our analyses. Another critical performance

metric of interest is the Jain index: fairness measure

that quantiﬁes the ability of the genetic algorithm to

achieve load balancing over the fog infrastructure.

The Jain index is deﬁned as J = 1/(1 +

CoV(ρ

)

), where ρ

is the utilization of each node

f ∈ F and CoV(·) is the coefﬁcient of variation (i.e.,

the ratio between standard deviation and mean) com-

puted over all fog nodes. An index of 1 means perfect

balancing, while a lower value means that the load is

unevenly distributed among the fog nodes.

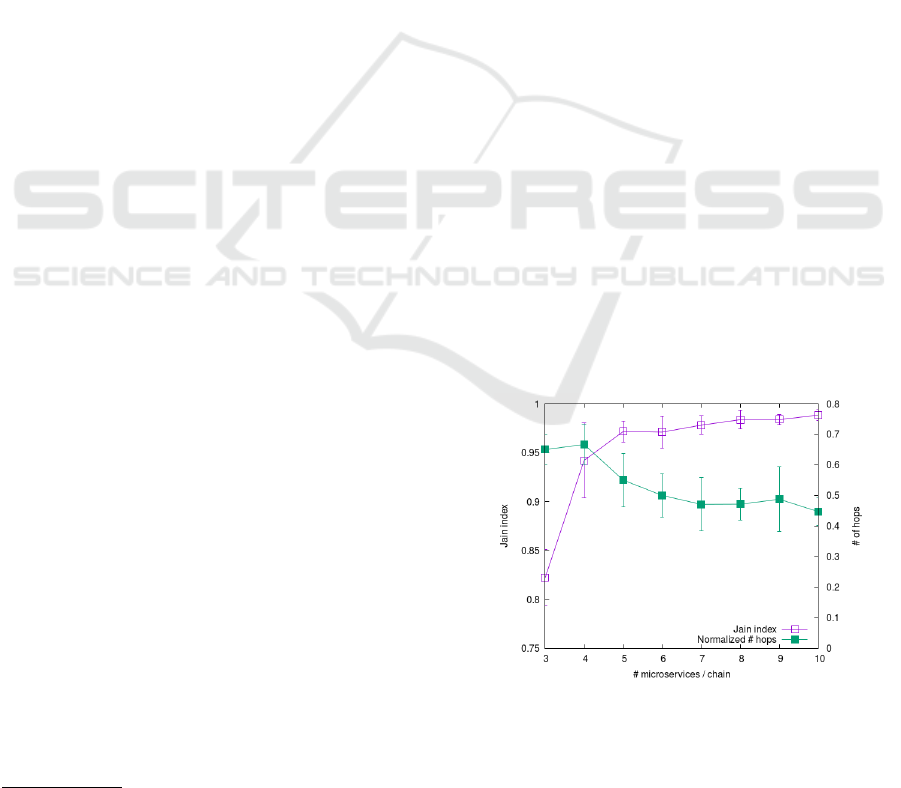
5.2 Sensitivity to Service Chain Length

Figure 2: Load balancing and hops vs. chain length L

Fig. 2 shows the Jain index (purple line with empty

squares) and the average number of hops of each

chain (green line with ﬁlled squares) as a function of

the service chain length L

. We observe that, when

CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science

204

the number of micro-services in a chain is low, the

load balancing is difﬁcult as there are long services

that, alone, can exhaust the processing power of a

fog node. On the other hand, as we have multiple,

smaller service (that is, when L

is higher), the ability

of the genetic algorithm to ﬁnd a good load balanc-

ing is proved by the Jain index value being close to

1. At the same time, due to the ﬁner-grain placement

options, also the average number of hops for each ser-

vice is reduced by roughly 35%, conﬁrming the abil-

ity of the proposed algorithm to reduce the impact of

network delays, being the normalized number of hops

close to 0.5, meaning that, on average, every two ser-

vices in a chain, there is one hop.

Figure 3: Response times vs. chain length L

Fig. 3 shows the average response time for dif-

ferent service chains length. The poor load balanc-

ing for low values of L

causes an increase of the

average response time as local near-overload condi-

tion may arise on some fog nodes. The purple aura

provides a measure of the variance of response times

within each problem (dark purple) and between differ-

ent problems (light purple). Due to the coarse-grained

placement when L

< 5 we observe both a response

time higher by up to 30% compared to longer service

chains and an increase of the variance of the samples

by a factor of 4.

5.3 Scalability Analysis

Finally, in Fig. 4 we report the study on the algorithm

scalability as the number of fog nodes |F | grows by

5× from 5 to 25 nodes. The number of service chains

|C | is increased proportionally from 2 to 10, with each

chain hosting 5 services. We observe that, as the con-

ﬁguration space to explore increases, the genetic algo-

rithm presents a steady growth in the execution time

(green line with ﬁlled squares). This result can be ex-

plained by considering that the chromosome length

corresponds to the number of micro-services to place.

Figure 4: Response and execution time vs. |F |.

As the chromosome grows, the cost of most genetic

operators (from the computation of the objective func-

tion to mutation and crossover) increases, thus caus-

ing the growth in the execution time that is nearly

doubled as the problem size increases by 5×. Also,

as the search space for the solutions grows, the ge-

netic algorithm is less effective in identifying the best

solutions. This explains the growth of the response

time (54%) as well as its standard deviation (more

than 4×), suggesting that for extremely large prob-

lems the algorithm may provide lower quality solu-

tions.

6 CONCLUSIONS AND FUTURE

WORK

Starting from applications designed as chains of

micro-services, we propose a model to optimize the

placement of these services over the nodes of the fog

infrastructure. Our model considers both the network

delay effect and the impact of computational load

over the achieved performance, taking into account

the inherent heterogeneity in the service time of the

various micro-services and in the computation power

of each fog node. In our paper we propose the perfor-

mance model, its application to an optimization prob-

lem for the deployment of fog applications and a ge-

netic algorithm heuristic for the problem solution. A

thorough experimental evaluation demonstrates that

our approach can provide adequate deployment solu-

tions, respecting SLA requirements, for a wide range

of service chain characteristics, load conditions and

problem sizes. This paper is just a ﬁrst step in a new

research line. Our future research directions spans

both the modeling, with more complex problems and

SLA formulations, and the evaluation, to test our ap-

proach with realistic fog applications through small-

scale prototypes and large-scale simulations.

Optimal Placement of Micro-services Chains in a Fog Infrastructure

205

REFERENCES

Binitha, S., Sathya, S. S., et al. (2012). A survey of bio in-

spired optimization algorithms. International Journal

of Soft Computing and Engineering, 2(2):137–151.

Byers, C. and Swanson, R. (2017). Openfog consor-

tium openfog reference architecture for fog comput-

ing. OpenFog Consortium Archit. Working Group,

Fremont, CA, USA, Tech. Rep. OPFRA001, 20817.

Canali, C. and Lancellotti, R. (2017). Scalable and auto-

matic virtual machines placement based on behavioral

similarities. Computing, 99(6):575–595.

Canali, C. and Lancellotti, R. (2019). A Fog Computing

Service Placement for Smart Cities based on Genetic

Algorithms. In Proc. of International Conference

on Cloud Computing and Services Science (CLOSER

2019), Heraklion, Greece.

Gupta, H., Vahid Dastjerdi, A., Ghosh, S. K., and Buyya,

R. (2017). ifogsim: A toolkit for modeling and

simulation of resource management techniques in

the internet of things, edge and fog computing en-

vironments. Software: Practice and Experience,

47(9):1275–1296.

Kayal, P. and Liebeherr, J. (2019). Distributed service

placement in fog computing: An iterative combina-

torial auction approach. In 2019 IEEE 39th Interna-

tional Conference on Distributed Computing Systems

(ICDCS), pages 2145–2156.

Mann, Z. A. (2015). Allocation of virtual machines in cloud

data centers—a survey of problem models and opti-

mization algorithms. ACM Computing Surveys, 48(1).

Santos, J., Wauters, T., Volckaert, B., and De Turck, F.

(2020). Towards delay-aware container-based service

function chaining in fog computing. In NOMS 2020

- 2020 IEEE/IFIP Network Operations and Manage-

ment Symposium, pages 1–9.

Skarlat, O., Nardelli, M., Schulte, S., and Dustdar, S.

(2017). Towards qos-aware fog service placement. In

2017 IEEE 1st International Conference on Fog and

Edge Computing (ICFEC), pages 89–96.

Souza, V., Masip-Bruin, X., Mar

ın-Tordera, E., S

anchez-

opez, S., Garcia, J., Ren, G., Jukan, A., and Juan

Ferrer, A. (2018). Towards a proper service place-

ment in combined Fog-to-Cloud (F2C) architectures.

Future Generation Computer Systems, 87:1–15.

Xiao, Y. and Krunz, M. (2017). Qoe and power efﬁciency

tradeoff for fog computing networks with fog node co-

operation. In IEEE INFOCOM 2017 - IEEE Confer-

ence on Computer Communications, pages 1–9.

Yousefpour, A., Ishigaki, G., and Jue, J. P. (2017). Fog

computing: Towards minimizing delay in the internet

of things. In 2017 IEEE International Conference on

Edge Computing (EDGE), pages 17–24.

Yu, R., Xue, G., and Zhang, X. (2018). Application provi-

sioning in fog computing-enabled internet-of-things:

A network perspective. In IEEE INFOCOM 2018

- IEEE Conference on Computer Communications,

pages 783–791.

Yusoh, Z. I. M. and Tang, M. (2010). A penalty-based

genetic algorithm for the composite saas placement

problem in the cloud. In IEEE Congress on Evolu-

tionary Computation, pages 1–8.

CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science

206