
Predicting Multiple Traffic Features using a Spatio-Temporal Neural
Network Architecture
Bogdan Ichim
1,2
and Florin Iordache
1
1
Faculty of Mathematics and Computer Science, University of Bucharest, Str. Academiei 14, Bucharest, Romania
2
Simion Stoilow Institute of Mathematics of the Romanian Academy, Str. Calea Grivitei 21, Bucharest, Romania
Keywords: Long Short-Term Memory Network (LSTM), Graph Convolutional Network (GCN), Neural Networks,
Traffic Models, Time-Series.
Abstract: In this paper we present several experiments done with a complex spatio-temporal neural network
architecture, for three distinct traffic features and over four time horizons. The architecture was proposed in
(Zhao et al., 2020), in which predictions for a single traffic feature (i.e. speed) were investigated. An
implementation of the architecture is available as open source in the StellarGraph library (CSIRO's Data61,
2018). We find that its predictive power is superior to the one of a simpler temporal model, however it
depends on the particular feature predicted. All experiments were performed with a new dataset, which was
prepared by the authors.
1 INTRODUCTION
Traffic forecasting is the process of studying traffic
features (including standard data like flow, speed
and occupancy) and predicting their trends over a
short or long interval of time. It plays an important
role inside a modern traffic management system, but
also provides information in advance for traffic
participants, allowing them to choose time optimal
travel routes. Overall, it is a key element for
improvements of the travel efficiency.
However, performing traffic forecasting is a
quite challenging undertaking. There exist complex
spatio-temporal interdependencies that affect its
performance.
In this paper we present experiments done with a
complex spatio-temporal neural network architecture
which was very recently proposed in (Zhao et al.,
2020), its implementation called GCN-LSTM being
made available as open source in the StellarGraph
library (CSIRO's Data61, 2018).
In (Zhao et al., 2020) the authors made
predictions only for speed data, this being the only
temporal traffic feature available in the two datasets
used by the authors. We wanted to see if this
architecture delivers also superior performance for
forecasting other temporal traffic features. Therefore
we have prepared a new dataset using data
publically available from the Caltrans Performance
Measurement System (PeMS, 2019). This new
dataset includes three time-series of traffic features:
flow, speed and occupancy. Then we have compared
the predictions made by the more complex GCN-
LSTM model with the predictions made with a
simpler LSTM model for all three temporal traffic
features and for various time horizons. We have
found that, in almost all experiments (with just one
exception), the GCN-LSTM model provides better
predictions.
Therefore, the contributions in this paper are the
following:
We have prepared a new dataset. It will be
useful also for other experiments. This new
dataset contains real time-series for three
different traffic features;
We have studied the effect on predictions of
various hyperparameters settings for the more
complex GCN-LSTM model. For finding the
best values, we have made experiments with
several different parameters settings for the
amount of hidden units on both the GCN and
the LSTM layers and we automatically select
the best of them for making predictions.
We have investigated the suitability of the
GCN-LSTM model for making predictions on
various new time-series of traffic features,
Ichim, B. and Iordache, F.
Predicting Multiple Traffic Features using a Spatio-Temporal Neural Network Architecture.
DOI: 10.5220/0011062900003191
In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2022), pages 331-337
ISBN: 978-989-758-573-9; ISSN: 2184-495X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
331

different from the (only) speed time-series
which were studied in (Zhao et al., 2020).
The prepared dataset, together with the
implementation used for experiments, is available on
demand from the authors.
2 RELATED WORK
Forecasting traffic features in order to build
intelligent traffic management systems is a major
research topic nowadays. There are many traffic
forecasting approaches which were investigated by
various authors. Nowadays, following the rapid
development in the field of deep learning (Silver et
al., 2016), (Silver et al., 2017), (Moravčík et al.,
2016), new neural networks architectures have
received particular attention. When benchmarked
versus other models, they are capable of achieving
the top results.
Many of the old approaches are forecasting just
one temporal feature. Others ignore completely the
spatial features, behaving like the traffic information
is not at all constrained by the traffic infrastructure.
However, it is quite clear that fully using both the
spatial and all available temporal information is the
answer for performant traffic forecasting.
The traffic information is inherently related to
graph like domains, due to the inherent topology of
the roads networks. In the recent years a new
architecture of neural networks, called Graph
Convolutional Network (GCN), was developed in
order to deal with this kind of information. It is a
generalization of the standard Convolutional Neural
Networks (CNN) architecture in the case of data
available on graph domains. For more about GCN
we point the reader to (Bruna et al., 2014), (Henaff
et al., 2015), (Atwood and Towsley, 2016), (Niepert
et al., 2016), (Kipf and Welling, 2017) and
(Hechtlinger et al., 2017). Remark that, since its
introduction, the GCN architecture has proven
superior performance for many applications.
The ability of GCN to handle information on
graph domains has motivated several authors to
develop various GCN architectures for forecasting
traffic features. One of the first attempts in this
direction was made by (Li et al., 2018), the authors
proposing a model that can make use of the spatial
features by computing random walks on graphs.
This was quickly followed by several papers, like for
example (Yu et al., 2018), (Zhao et al., 2020) and
(Zhang et al., 2020), in which various authors
propose different spatio-temporal neural network
architectures for traffic forecasting. In general, in
these papers only one particular temporal feature
(i.e. speed) was used for training and predicting.
Following this line of research, in this paper we
investigate if one particular spatio-temporal neural
network architecture may be used for forecasting
other temporal traffic features and if it provides
similar performance.
3 METHODOLOGY
3.1 Problem Statement
The scope of this paper is to simultaneously predict
multiple traffic features over a certain time horizon
using both the historical traffic data collected by
sensors and the spatial information about the
location of the sensors on the roads. More precisely,
we are interested in predicting the following traffic
features: flow, speed and occupancy. These features
are simultaneously collected in the data available
from the Caltrans Performance Measurement System
(PeMS, 2019).
Let 𝑆 be the number of sensors in the data. We
use a matrix 𝐴∈ℝ
for representing the spatial
information about the sensors. The matrix 𝐴 contains
weights 𝑎
∈
0,1
and it is called the adjacency
matrix. The weight 𝑎
is set to be 0 if there is a
significant distance or there is no road connection
between the two sensors 𝑖 and 𝑗. It is set to be close
to 1 if there exist a road connection between the two
sensors 𝑖 and 𝑗 and also the distance between them is
rather small.
Let 𝑁 be the number of samples. For each
feature 𝑓 the 𝑆 time-series collected by the sensors
are contained in a feature matrix 𝐵
∈ℝ
. Then,
at a certain time 𝑡, the vector 𝐵
,
∈ℝ
contains the
values collected by all sensors for the feature 𝑓.
Let 𝑇 be a time horizon. Assuming that an
adjacency matrix 𝐴 and a feature matrix 𝐵
are
given, then the problem of spatio-temporal
forecasting of the traffic feature 𝑓 for the time
horizon 𝑇 is the problem of learning a mapping
function 𝑚 (i.e. a model) such that
𝐵
,
𝑚
𝐴;𝐵
,
,…,𝐵
,
,𝐵
,
.
VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems
332
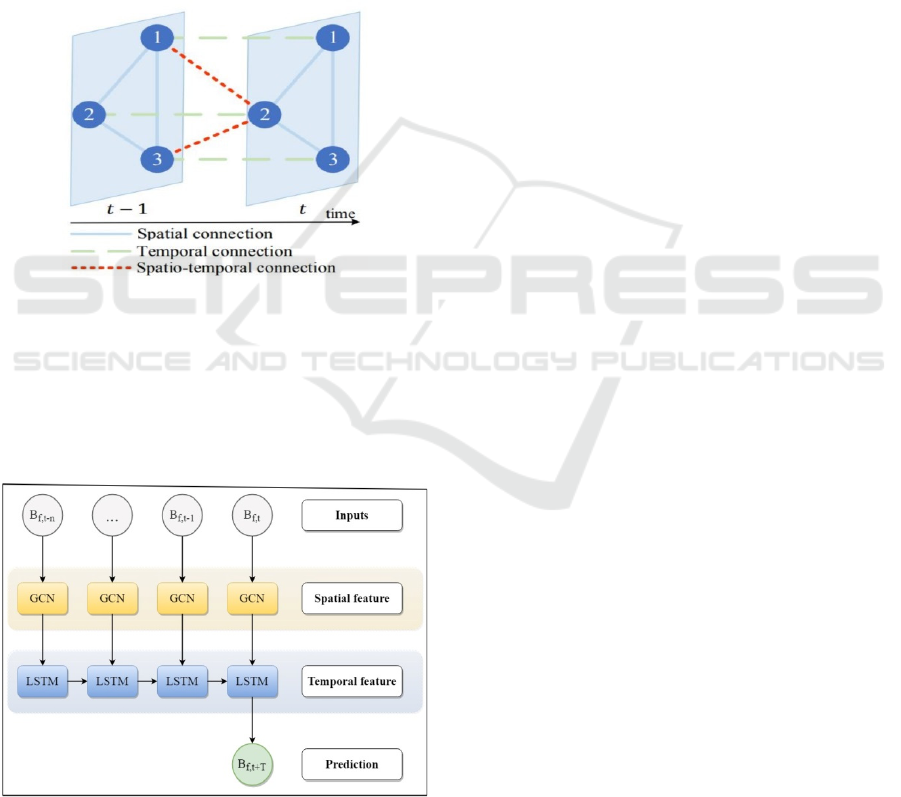
3.2 The Architecture of GCN-LSTM
Model
The key idea behind the construction of a spatio-
temporal neural network is illustrated in Figure 1.
Assume that the nodes 1,2,3 in the graph pictured
below represent three traffic sensors. A certain
traffic feature read by sensor 2 at timestamp 𝑡 may
explicitly be related (by spatial connections) to the
data read by sensors 1 and 3 at timestamp 𝑡, and to
the data read by sensor 2 at timestamp 𝑡1 (by the
temporal connection). Moreover, there exist implicit
spatio-temporal connections with the data read by
sensors 1 and 3 at timestamp 𝑡 1.
Figure 1: The spatial and temporal connections among
sensors arranged in a graph.
The architecture of the GCN-LSTM model
which is available as open source in the StellarGraph
library (CSIRO's Data61, 2018) was inspired by the
ideas proposed in (Zhao et al., 2020) and it is
illustrated in Figure 2.
Figure 2: The architecture of the GCN-LSTM model. For
each feature 𝑓 the 𝑆 time-series are used as input and the
final prediction is obtained by passing them through the
GCN and the LSTM layers.
According to (Zhao et al., 2020) and (CSIRO's
Data61, 2018) the GCN-LSTM model consists of
two distinct parts: the GCN layers and the LSTM
layers. The number and the size of GCN layers and
the LSTM layers, as well as the number of LSTM
cells are user defined. Remark that Gated Recurrent
Units (GRU) are used in (Zhao et al., 2020) instead
of LSTM, however in practice there are not any
significant differences between them and are equally
effective for various tasks. The basic operating
principles of both the GRU and LSTM are
approximately the same, according to (Chung et al.,
2020).
As can be seen in Figure 2, the GCN layers are
used first in order to capture the spatial relationships
between sensors. The information is added to the
(temporal) information contained by the inputted
time series. Remark that this part of the model can
be adapted for predicting the value of a certain
traffic feature on a future timestamp based only on
its current values across the sensors graph (at single
timestamp). However, the temporal information is
also very important for predictions, so for obtaining
the best results a subset of the time-series of values
of the traffic feature (as measured at several
previous timestamps across the sensors) should be
used in order to predict its value at a future
timestamp. For achieving this, in a second step the
time-series (now augmented with spatial features)
are inputted into the LSTM layers. (The number of
LSTM cells is given by the length of the subset of
the time-series used for training.) The final results
are obtained by passing through a dropout and a
dense layer. According to experimental results
(CSIRO's Data61, 2018), their usage leads to
improvement in performance and prevents over-
fitting.
In summary, the GCN-LSTM model may be
used for capturing both the spatial and the temporal
dynamics.
3.3 Dataset
For our experiments we have prepared a new dataset
using traffic data collected from various roads in the
State of California. The data is aggregated from
sensors positioned on the freeways of the state and it
is stored and publically available in the Caltrans
Performance Measurement System (PeMS, 2019), a
web platform where users can analyse and export
traffic information. The data was automatically
collected from the website using a Python script.
Since the PeMS data contains many sensors for
which the values of the corresponding features are
Predicting Multiple Traffic Features using a Spatio-Temporal Neural Network Architecture
333

not measured, but instead are imputed by the system
or simply not available, one important step in
preparing the dataset was to choose several sensors
for which as many as possible real observed values
are available and which are also relatively close
together. Using the plot on a map of the sensors and
their associated percentage of real observed values,
40 sensors found in all directions of a 4-way
interchange have been manually selected. They are
represented in Figure 1.
Figure 3: Map of the manually selected sensors. The
colours represent the corresponding traffic direction.
For the selected sensors, our dataset contains
time-series for all the traffic features studied in this
paper, i.e. flow, speed and occupancy. The time
period included in the dataset is from the 1
st
of April
to the 30
th
of April 2019. For each sensor
measurements are done every 5 minutes, so that a
full day of measurements contains 288 observations.
The system also offers a metadata file which
contains structured descriptions of each individual
sensor. From the data provided for each sensor the
following features are useful for computing spatial
information: freeway number, direction, latitude and
longitude.
3.4 Technical Implementation
For the implementation of the machine learning
models the Python libraries Tensorflow, Keras and
StellarGraph were used. Tensorflow (Google Brain,
2016) is a library developed by Google for
implementing machine learning applications. On top
of Tensorflow, another package has been built,
named Keras (Chollet, 2015). It contains
implementations of machine learning algorithms that
are very popular and may be used to define and train
models that combine them, as layers. StellarGraph
(CSIRO's Data61, 2018) is another library based on
TensorFlow that aims to help implementing graph
convolutional neural network architectures. The
open source implementation in StellarGraph of the
architecture proposed in (Zhao et al., 2020) was used
for the experiments presented in this paper.
4 EXPERIMENTS
4.1 Performance Metrics
For the purpose of measuring the performance of the
tested models, we have used in our experiments
three standard performance metrics that evaluate the
distance between the ground truth (i.e. the real, as
measured in traffic feature y
i
) and the computed
model prediction for the same feature. Assume that
the testing dataset contains 𝑁 samples (epochs) of
the form
𝑥
,𝑦
and 𝑚 is the model under
consideration. Denote by 𝑦
the mean of 𝑦
.Then
the prediction of the model for 𝑦
is 𝑚
𝑥
and we
have:
Root Mean Squared Error (RMSE):
𝑅𝑀𝑆𝐸
𝑚
𝑦
𝑚𝑥
;
Mean Absolute Error (MAE):
𝑀𝐴𝐸
𝑚
|
𝑦
𝑚𝑥
|
;
The Coefficient of Determination (R
2
):
𝑅
𝑚
1
𝑦
𝑚𝑥
∑
𝑦
𝑦
.
More precisely, the first two metrics are
measuring the model prediction error. They should
be interpreted as follows: the smaller is the number
computed, the better is the model. The capability of
the model to make good predictions is measured by
the coefficient of determination. Its interpretation is:
the closer to 1 is the number computed (by definition
it is always smaller than 1), the better is the model.
4.2 Tuning Model Parameters
For hyperparameters tuning a grid search is done in
order to find the best amount of hidden units on both
VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems
334

the GCN and the LSTM layers. The best settings are
automatically selected for making predictions.
Table 1: Measuring the GCN-LSTM performance for
predicting flow with variable amount of hidden units and
under different time horizons.
Time GCN
LSTM
64 128 256
15 min
16 25.55 21.69 22.88
32 23.97 23.38 21.18
64 24.45 22.57 21.51
30 min
16 28.29 26.80 27.22
32 31.55 27.85 26.24
64 26.66 25.74 24.86
45 min
16 30.99 27.56 28.49
32 29.41 28.50 28.27
64 29.39 30.06 29.02
60 min
16 33.55 34.70 32.50
32 32.78 33.71 30.36
64 33.36 29.87 30.33
Table 2: Measuring the GCN-LSTM performance for
predicting speed with variable amount of hidden units and
under different time horizons.
Time GCN
LSTM
64 128 256
15 min
16 51.90 51.77 48.74
32 50.00 49.10 46.48
64 48.95 49.76 43.60
30 min
16 80.46 74.87 77.11
32 82.95 78.08 72.43
64 79.29 77.48 75.94
45 min
16 95.26 94.33 97.12
32 95.75 93.23 93.94
64 96.05 94.80 90.07
60 min
16 111.20 106.79 123.63
32 110.45 107.35 111.23
64 117.64 106.60 114.93
Table 3: Measuring the GCN-LSTM performance for
predicting occupancy with variable amount of hidden units
and under different time horizons.
Time GCN
LSTM
64 128 256
15 min
16 27.91 24.51 25.28
32 27.37 24.46 24.58
64 26.53 24.86 22.64
30 min
16 31.42 30.81 30.26
32 31.80 30.04 30.37
64 31.70 30.75 30.45
45 min
16 34.97 34.08 34.10
32 34.23 34.65 34.46
64 34.66 33.50 35.28
60 min
16 38.43 37.98 38.95
32 37.35 37.43 37.34
64 38.25 36.74 36.07
The optimal number of hidden units found for
each feature and under each time horizon is marked
by bold numbers in the Tables 1, 2 and 3. Note that
the MSE numbers in these tables are scaled; smaller
numbers indicate better performance of the model.
4.3 Experimental Results
The performance of the GCN-LSTM model is
compared with the performance of a LSTM model
(Hochreiter et al., 1997), which is used as a baseline.
This allows us to see the combined spatio-temporal
prediction capability of the model.
The final results of our experiments are
contained in Table 4. We have compared the
predictions made by the two models for 4 times
horizons (15 min., 30 min., 45 min. and 60 min) and
for 3 different traffic features (flow, speed and
occupancy). From the total of 12 experiments made,
the GCN-LSTM model has provided better results
Table 4: Experimental Results.
Time Metric
LSTM GCN_LSTM
flow spee
d
occupanc
y
flow spee
d
occupanc
y
15 min
RMSE 48.7111 6.4772 0.0492 42.5435 7.117
6
0.0433
MAE 34.3575 3.5623 0.0273 30.5658 4.3369 0.0217
R
2
0.9396 0.8142 0.6452 0.9471 0.775
7
0.7253
30 min
RMSE 56.0602 9.5153 0.0549 46.9174 8.8095 0.0485
MAE 40.6417 5.4586 0.0329 34.1318 5.2449 0.0257
R
2
0.9077 0,5993 0.5568 0.9354 0.6566 0.6543
45 min
RMSE 62.9085 10.4843 0.0581 48.1666 8.9197 0.0499
MAE 47.1767 6.3406 0.0364 35.2929 5.5909 0.0278
R
2
0.8833 0.5139 0.5061 0.9319 0.6482 0.6342
60 min
RMSE 71.9628 11.5291 0.0609 51.2077 9.8415 0.0501
MAE 54.5468 7.6336 0.0394 37.9371 6.0044 0.0277
R
2
0.8466 0.4126 0.4548 0.9223 0.5720 0.6321
Predicting Multiple Traffic Features using a Spatio-Temporal Neural Network Architecture
335
than the LSTM model in 11 experiments. There
exists 1 experiment (marked with italics in Table 4)
in which the results obtained with the LSTM model
were superior.
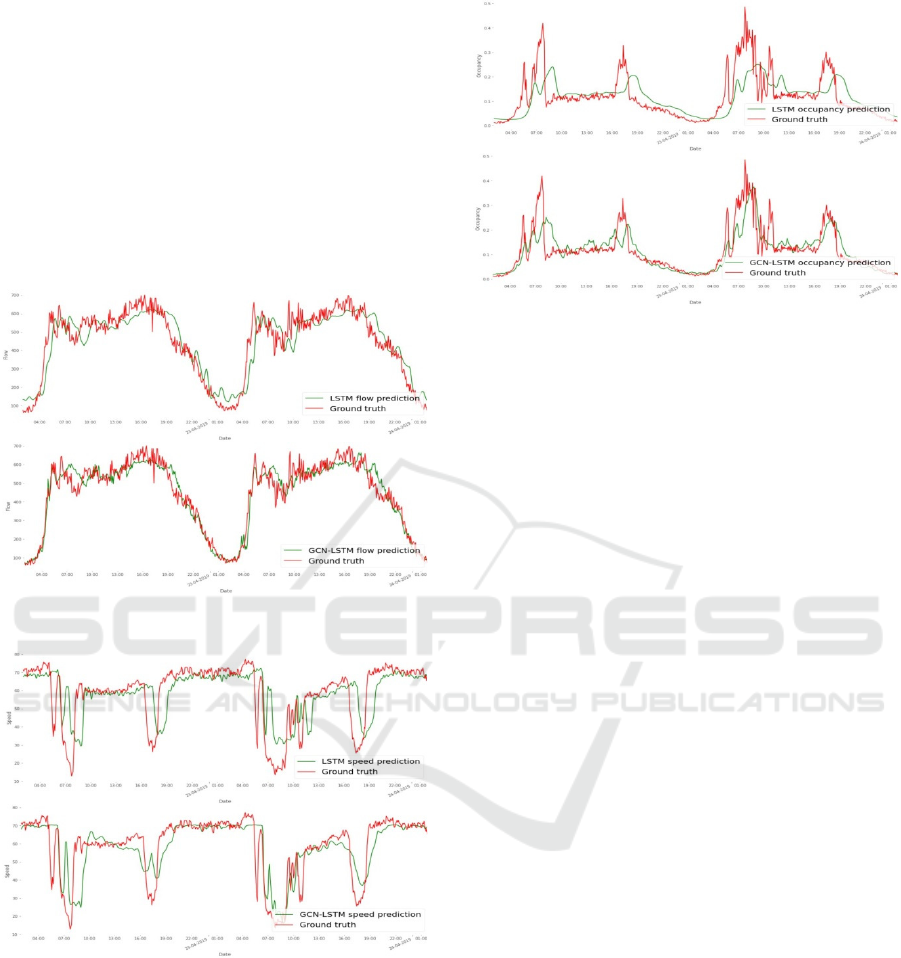
4.4 Visual Interpretation of the Results
For providing a better understanding of the results,
we have selected one particular sensor and the
predictions made by the two models for the 60
minutes time horizon on a 2-days subset of test set
are visualized in the Figures 2, 3 and 4.
Figure 4: LSTM and GCN-LSTM flow predictions.
Figure 5: LSTM and GCN-LSTM speed predictions.
Together with the numerical data for
performance in Table 4, these figures show:
Especially over longer time horizons the more
complex spatio-temporal neural network
architecture has better prediction capability
than the simpler temporal neural network
architecture. In other words, adding the spatial
information to the model leads to a significant
improvement of its predictive power;
Figure 6: LSTM and GCN-LSTM occupancy predictions.
The prediction performance depends on the
predicted traffic feature. As one can clearly
see by comparing Figures 2 and 3, as well as
from Table 4, there exist a difference in the
performance of both models for predicting
flow and speed. The flow predictions of both
models are significantly better than those for
speed.
5 CONCLUSIONS AND FUTURE
WORK
In this paper we present several experiments done
with a complex spatio-temporal neural network
architecture, which was initially proposed in (Zhao
et al., 2020), for 3 distinct traffic features and over 4
time horizons. First, we have found that, in almost
all cases, the predictive power of this new
architecture is superior to the one of a simpler
temporal model. We conclude that there exists
strong evidence that adding the spatial information is
very important. Second, unlike in the setup
considered in (Zhao et al., 2020) and also in other
related papers (where only one traffic feature is
investigated), we were interested to study the
performance of the architecture for various traffic
features, all of them being important for example
when building a modern traffic management system.
We have found that the architecture does not deliver
uniform performance across all traffic features, its
performance seem to depend heavily on the
particular feature used.
Our future work plan is to conduct more
experiments with several architectures proposed
very recently by various authors, as for example in
(Li et al., 2018), (Yu et al., 2018) and (Zhang et al.,
2020). We hope to find an architecture that does
VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems
336

deliver uniform performance, independent on the
particular feature predicted. Since we have seen that
using spatial information in almost all studied cases
improves the overall performance of the model, we
also intend to experiment with new, better ways of
processing it.
ACKNOWLEDGEMENTS
This work was partially supported by a grant of the
Romanian Ministry of Education and Research,
CCCDI - UEFISCDI, project number PN-III-P2-2.1-
PTE-2019-0817, within PNCDI III.
REFERENCES
Atwood, J., Towsley, D. (2016). Diffusion-convolutional
neural networks. In NIPS'16, Proceedings of the 30th
International Conference on Neural Information
Processing Systems, 2001 – 2009.
Bruna, J., Zaremba, W., Szlam, A., LeCun, Y. (2014).
Spectral Networks and Locally Connected Networks
on Graphs. In ICLR 2014, Proceedings of the 2th
International Conference on Learning
Representations, pages 1 – 14.
Chollet, F., & others (2015). Keras. Available online at:
https://github.com/fchollet/keras.
Chung, J., Gulcehre, C., Cho, K., Bengio, Y. (2014).
Empirical Evaluation of Gated Recurrent Neural
Networks on Sequence Modeling. Presented in NIPS
2014, Deep Learning and Representation Learning
Workshop. Preprint arXiv: 1412.3555.
CSIRO's Data61 (2018). StellarGraph Machine Learning
Library. Online at https://stellargraph.readthedocs.io/.
Google Brain (2016). TensorFlow: A system for large-
scale machine learning. In OSDI'16, Proceedings of
the 12th USENIX conference on Operating Systems
Design and Implementation, pages 265 – 283.
Hechtlinger, Y., Chakravarti, P., Qin, J. (2017). A
generalization of convolutional neural networks to
graph-structured data. Preprint arXiv: 1704.08165.
Henaff, M., Bruna, J., LeCun, Y. (2015). Deep
convolutional networks on graph-structured data.
Preprint arXiv:1506.05163.
Hochreiter, S., Schmidhuber, J. (1997). Long short-term
memory. Neural Computation 9, pages 1735 – 1780.
Kipf, T., Welling, M. (2017). Semi-Supervised
Classification with Graph Convolutional Networks. In
ICLR 2017, Proceedings of the 6th International
Conference on Learning Representations, pages 1 –
14.
Li, Y., Yu, R., Shahabi, C., Liu, Y. (2018). Diffusion
Convolutional Recurrent Neural Network: Data-
Driven Traffic Forecasting. In ICLR 2018,
Proceedings of the 6th International Conference on
Learning Representations, pages 1 – 16.
Moravčík, M., Schmid, M., Burch, N., Lisý, V., Morrill,
D., Bard, N., Davis, T., Waugh, K., Johanson, M.,
Bowling, M. (2017). Deepstack: Expert-level artificial
intelligence in heads-up no-limit poker. Science 356,
pages 508 – 513.
Niepert, M., Ahmed, M., Kutzkov, K. (2016). Learning
convolutional neural networks for graphs. In ICML
2016, Proceedings of the 33rd International
Conference on Machine Learning, pages 2014 – 2023.
PeMS, Caltrans Performance Measurement System
(2019). Data avaible at https://pems.dot.ca.gov/.
Silver, D. et al. (2016). Mastering the game of go with
deep neural networks and tree search. Nature 529,
pages 484 – 489.
Silver, D. et al. (2017). Mastering the game of go without
human knowledge. Nature 550, pages 354 – 359.
Yu, B., Yin, H., Zhu, Z. (2018). Spatio-Temporal Graph
Convolutional Networks: A Deep Learning
Framework for Traffic Forecasting. In Proceedings of
the Twenty-Seventh International Joint Conference on
Artificial Intelligence, IJCAI-ECAI-2018, pages 3634
– 3640.
Zhang, Q., Chang, J., Meng, G., Xiang, S., Pan, C. (2020).
Spatio-Temporal Graph Structure Learning for Traffic
Forecasting. In Proceedings of the Thirty-Fourth AAAI
Conference on Artificial Intelligence, 1177 – 1185.
Zhao, L., Song, Y., Zhang, C., Liu, Y., Wang, P., Lin, T.,
Deng, M., Li H. (2020). T-GCN: A Temporal Graph
Convolutional Network for Traffic Prediction. IEEE
Transactions on Intelligent Transportation Systems
21, pages 3848 – 3858.
Predicting Multiple Traffic Features using a Spatio-Temporal Neural Network Architecture
337
