Transfer Learning Gaussian Anomaly Detection by Fine-tuning

Representations

Oliver Rippel

1 a

, Arnav Chavan

, Chucai Lei

and Dorit Merhof

1 b

Institute of Imaging & Computer Vision, RWTH Aachen University, Aachen, Germany

Indian Institute of Technology, ISM Dhanbad, India

Keywords:

Anomaly Detection, Anomaly Segmentation, Transfer Learning, PDF Estimation, Visual Inspection.

Abstract:

Current state-of-the-art anomaly detection (AD) methods exploit the powerful representations yielded by

large-scale ImageNet training. However, catastrophic forgetting prevents the successful ﬁne-tuning of pre-

trained representations on new datasets in the semi-supervised setting, and representations are therefore com-

monly ﬁxed. In our work, we propose a new method to overcome catastrophic forgetting and thus successfully

ﬁne-tune pre-trained representations for AD in the transfer learning setting. Speciﬁcally, we induce a multi-

variate Gaussian distribution for the normal class based on the linkage between generative and discriminative

modeling, and use the Mahalanobis distance of normal images to the estimated distribution as training ob-

jective. We additionally propose to use augmentations commonly employed for vicinal risk minimization in

a validation scheme to detect onset of catastrophic forgetting. Extensive evaluations on the public MVTec

dataset reveal that a new state of the art is achieved by our method in the AD task while simultaneously

achieving anomaly segmentation performance comparable to prior state of the art. Further, ablation studies

demonstrate the importance of the induced Gaussian distribution as well as the robustness of the proposed

ﬁne-tuning scheme with respect to the choice of augmentations.

1 INTRODUCTION

Anomaly detection (AD) in images is concerned with

ﬁnding images that deviate from a prior-deﬁned con-

cept of normality, and poses a fundamental com-

puter vision problem with application domains rang-

ing from industrial quality control (Bergmann et al.,

2021) to medical image analysis (Schlegl et al., 2019).

Extending AD, anomaly segmentation (AS) tries to

identify the visual patterns inside anomalous images

that constitute the anomaly. In general, AD/AS tasks

are deﬁned by the following two characteristics

1. Anomalies are rare events, i.e. their prevalence in

the application domain is low.

2. There exists limited knowledge about the anomaly

distribution, i.e. it is ill-deﬁned.

Together, these characteristics result in AD/AS

datasets that are heavily imbalanced, often containing

only few anomalies for model veriﬁcation and testing.

https://orcid.org/0000-0002-4556-5094

https://orcid.org/0000-0002-1672-2185

For a general, exhaustive overview of AD we refer the

reader to (Ruff et al., 2021).

As a consequence, AD/AS algorithms focus on

the semi-supervised setting, where exclusively nor-

mal data is used to establish a model of normal-

ity (Bergmann et al., 2021; Schlegl et al., 2019;

Ruff et al., 2018). Since learning discriminative rep-

resentations from scratch is difﬁcult (Rippel et al.,

2021c), state-of-the-art methods leverage representa-

tion gained by training on ImageNet (Deng et al.,

2009) as the basis for AD/AS (Rippel et al., 2021b;

Defard et al., 2020; Andrews et al., 2016; Bergmann

et al., 2020; Cohen and Hoshen, 2020; Christiansen

et al., 2016; Perera and Patel, 2019; Li et al., 2021).

Fine-tuning these representations on the dataset

at hand now offers the potential of additional perfor-

mance improvements. However, ﬁne-tuning is hin-

dered by catastrophic forgetting, which is deﬁned as

the loss of discriminative features initially present in

the model in context of AD (Deecke et al., 2021).

In fact, ﬁne-tuning is so difﬁcult that it is simply

foregone in the majority of AD/AS approaches (re-

fer also Section 2.1). While methods have been pro-

posed to tackle catastrophic forgetting (Reiss et al.,

2021; Deecke et al., 2020; Perera and Patel, 2019;

Liznerski et al., 2021; Ruff et al., 2020; Deecke

Rippel, O., Chavan, A., Lei, C. and Merhof, D.

Transfer Learning Gaussian Anomaly Detection by Fine-tuning Representations.

DOI: 10.5220/0011063900003209

In Proceedings of the 2nd International Conference on Image Processing and Vision Engineering (IMPROVE 2022), pages 45-56

ISBN: 978-989-758-563-0; ISSN: 2795-4943

et al., 2021), they currently ignore the feature correla-

tions inherent to the pre-trained networks (refer Fig-

ure 1, (Rodr

ıguez et al., 2017; Ayinde et al., 2019)).

Moreover, many of the aforementioned methods em-

ploy synthetic anomalies as surrogates for the true

anomaly distribution to generate a supervised loss, a

concept called outlier exposure (OE) (refer Figure 1)

(Hendrycks et al., 2019). While performance gains

have been reported here, a signiﬁcant dataset bias is

also induced by OE (Ye et al., 2021).

Our contributions are as follows:

• Based on ﬁndings from (Lee et al., 2018) and

(Rippel et al., 2021c), we induce a multivariate

Gaussian for the normal data distribution in the

transfer learning setting, incorporating the fea-

ture correlations inherent to the pre-trained net-

work. We thus propose to ﬁne-tune the pre-trained

model by minimizing the Mahalanobis distance

(Mahalanobis, 1936) to the estimated Gaussian

distribution using normal data only, and forego

OE to avoid incorporating an additional dataset

bias. We furthermore show how the proposed ob-

jective relates to and extends the prior-used opti-

mization functions.

• We propose an early stopping criterion based

on data augmentations commonly used in semi-

supervised learning for vicinal risk minimization

(VRM) (Chapelle et al., 2001; Hendrycks et al.,

2020) to detect onset of catastrophic forgetting.

• We demonstrate the effectiveness of both propos-

als using the public MVTec dataset (Bergmann

et al., 2021), and perform extensive ablation stud-

ies to investigate the sensitivity of our approach

with respect to the chosen augmentation schemes.

2 RELATED WORK

Features generated by large-scale dataset training

(e.g. ImageNet) are commonly employed in literature

to achieve AD/AS on new tasks in a transfer learning

setting.

2.1 Fixed Representations

The representations of the pre-trained network are

commonly ﬁxed to prevent catastrophic forgetting. To

nevertheless improve AD/AS performance even with

ﬁxed representations, Bergmann et al. (Bergmann

et al., 2020) employ a two-stage knowledge distil-

lation framework to achieve AD and AS in a trans-

fer learning setting. Here, they directly regress

the intermediate representations of a ResNet18 (He

Train Val Test

OE + spherical cluster

Proposed method

Figure 1: Comparison of the proposed method and related

ﬁne-tuning approaches. Anomalies (shown in red) are often

subtle, and state-of-the-art methods use either them or syn-

thetic anomalies (shown in yellow) for OE. However, do-

ing so introduces a signiﬁcant bias (Ye et al., 2021). More-

over, state-of-the-art ﬁne-tuning methods ignore the feature

correlations inherent to the pre-trained network (Rodr

ıguez

et al., 2017; Ayinde et al., 2019). In the proposed method,

these correlations are taken into account by means of the

Gaussian assumption. Furthermore, we argue that augmen-

tations used for VRM (shown in green) are well-suited for

detecting the onset of catastrophic forgetting, and can thus

be used to validate semi-supervised training that uses nor-

mal data only (shown in blue). Thereby, the bias induced

by OE is reduced/circumvented. A dot in the scatter plot

corresponds to a complete image.

et al., 2016) pre-trained on ImageNet. Furthermore,

Rudolph et al. (Rudolph et al., 2021) ﬁt an uncon-

strained probability distribution by means of Normal-

izing Flows (Rezende and Mohamed, 2015) to the

nominal class.

Moreover, features from pre-trained networks are

also used as the basis for classical AD methods.

For example, Andrews et al. (Andrews et al., 2016)

ﬁt a discriminative one-class support vector machine

(SVM) (Sch

olkopf et al., 2001) to features extracted

from intermediate layers of a VGG (Simonyan and

Zisserman, 2015) network. Furthermore, k-NN has

also been used to realize AD/AS on pre-trained fea-

tures (Cohen and Hoshen, 2020). Last, generative al-

IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering

gorithms such as Gaussian AD (Christiansen et al.,

2016; Sabokrou et al., 2018; Defard et al., 2020; Rip-

pel et al., 2021c) are also commonly employed.

2.2 Fine-tuning Representations

Even though it offers potential beneﬁts, ﬁne-tuning

approaches are limited by onset of catastrophic for-

getting. In contrast to the typical continual learning

scheme, catastrophic forgetting in AD/AS is incurred

by the unavailability of anomalous data. As a conse-

quence, discriminative feature combinations initially

present in the pre-trained network are lost during ﬁne-

tuning, since they are most likely absent/missing in

the normal data (Tax and M

uller, 2003; Rippel et al.,

2021c). Ultimately this leads to a reduced AD/AS

performance.

Due to the absence of anomalies, ﬁne-tuning ap-

proaches base their learning objective on the con-

centration assumption instead, i.e. they try to ﬁnd

a compact description of the normal class in high-

dimensional representations. The most commonly

used optimization formulation for this is the Deep

support vector data description (SVDD) objective

(Ruff et al., 2018), deﬁned as

min

∑

i=1

∥Φ(x

;W ) − c∥

∑

l=1

∥W

∥

. (1)

Here, Φ : R

C×H×W

→ R

is a neural network

parametrized by its weights W = {W

, ..., W

}, and

a hypersphere is minimized around the cluster center

c subject to L

weight regularization, with ∥·∥

de-

noting the Frobenius norm.

To now overcome catastrophic forgetting, three

main procedures have been proposed in literature: (I)

Perera & Patel (Perera and Patel, 2019) jointly opti-

mize Equation 1 together with the original task to en-

sure that the original feature discriminativeness does

not deteriorate. Speciﬁcally, they use the arithmetic

mean as c and L

norm over the L

norm in Equa-

tion 1, and perform joint optimization with ImageNet-

1k training. Joint optimization, however, requires ac-

cess to the original dataset, which may not always

be feasible. (II) Reiss et al. (Reiss et al., 2021)

propose to make use of elastic weight consolidation

(EWC)(Kirkpatrick et al., 2017), a technique pro-

posed in continual learning, to overcome catastrophic

forgetting. This method, however, also requires ac-

cess to the original dataset, which may again not al-

ways be feasible. (III) Deecke et al. (Deecke et al.,

2021) propose to make use of L

regularization with

respect to the initial, pre-trained weights, arguing that

only subtle feature adaptations should be necessary

when ﬁne-tuning. Alternatively, they also propose to

learn only a modulation of frozen features by means

of newly introduced, residual adaptation layers, in-

stead of tuning them directly.

All the aforementioned techniques can be applied

in combination with OE (Hendrycks et al., 2019).

Here, either synthetic anomalies or datasets disjoint to

the target domain are used as surrogate anomalies to

facilitate training of supervised, discriminative mod-

els. Ruff et al. (Ruff et al., 2020) formulate a hyper-

sphere classiﬁer (HSC) to incorporate OE to the Deep

SVDD objective. Speciﬁcally, they optimize

min

∑

i=1

∥Φ(x

;W )∥

− (1 − y

)log



1 − exp(−∥Φ(x

;W )∥



(2)

where y

denotes whether a sample is either normal

= 1) or anomalous (y

= 0). While generalization

to anomalies unseen during training has been demon-

strated for OE (Hendrycks et al., 2019), a bias is un-

doubtedly introduced by this method. Speciﬁcally, Ye

et al. (Ye et al., 2021) show that labeled anomalies dif-

fering subtly from the normal class have a large im-

pact in OE, possibly degrading performance on un-

seen anomaly types that are also similar to the normal

class. They further show that empirical gains can only

be guaranteed when anomalies are used for OE that

differ strongly from the normal class instead.

Nevertheless, gains have been reported by ap-

proaches that incorporate OE, such as CutPaste (Li

et al., 2021) or fully convolutional data descriptor

(FCDD) (Liznerski et al., 2021). Here, CutPaste fol-

lows a two-stage procedure, i.e. ﬁne-tuning a super-

vised classiﬁer by means of OE with carefully crafted,

synthetic anomalies followed by Gaussian AD as pro-

posed in (Rippel et al., 2021c). FCDD applies the

HSC objective to spatial feature maps, i.e. intermedi-

ate representations of a pre-trained network that still

possess spatial dimensions, to ﬁne-tune the network

directly. Similar to CutPaste, they also use carefully

crafted, synthetic anomalies for OE.

Out of all related works, only FCDD and CutPaste

evaluate performance on a dataset where normal and

anomalous classes differ subtly, namely the MVTec

dataset (Bergmann et al., 2021).

3 TRANSFER LEARNING

GAUSSIAN ANOMALY

DETECTION

In our work, we propose to ﬁne-tune the represen-

tations of pre-trained networks based on the Gaus-

sian assumption. A motivation behind the seemingly

Transfer Learning Gaussian Anomaly Detection by Fine-tuning Representations

overly simplistic Gaussian assumption can be inferred

from Lee et al. (Lee et al., 2018). Here, authors have

induced a Gaussian discriminant analysis (GDA) for

out-of-distribution (OOD) detection. Investigations

into the unreasonable effectiveness of the Gaussian

assumption by Kamoi and Kobayashi (Kamoi and

Kobayashi, 2020) have revealed that feature combina-

tions containing low variance for the normal/nominal

class are ultimately those discriminative to the OOD

data. Independent investigations into the same phe-

nomenon for AD by Rippel et al. (Rippel et al., 2021c)

have revealed the same ﬁnding for the transfer learn-

ing setting. However, despite its elegant simplicity

and outstanding performance, the Gaussian assump-

tion has not yet been used to ﬁne-tune pre-trained fea-

tures for AD.

The Gaussian distribution is given by

µ,Σ

(x) :=

(2π)

|detΣ|

−

(x−µ)

⊤

−1

(x−µ)

, (3)

with D being the number of dimensions, µ ∈ R

being

the mean vector and Σ ∈ R

D×D

being the symmetric

covariance matrix of the distribution, which must be

positive deﬁnite.

Under a Gaussian distribution, a distance measure

between a particular point x ∈ R

and the distribu-

tion is called the Mahalanobis distance (Mahalanobis,

1936), given as

M(x) =

(x − µ)

⊤

−1

(x − µ). (4)

Let us compare the Mahalanobis distance (Equa-

tion 4) to the Deep SVDD objective (Equation 1).

When imposing a univariate Gaussian with zero mean

and unit-variance per feature, the Mahalanobis dis-

tance reduces to the L

distance to the mean, reca-

pitulating the original Deep SVDD objective with L

norm instead of L

norm. In other words, minimiz-

ing the Deep SVDD objective in conjunction with L

norm implicitly assumes that features follow indepen-

dent, univariate Gaussians with zero-mean and unit-

variance. This assumption, however, is in disagree-

ment with ﬁndings in literature, where strong corre-

lations have been observed across deep features ex-

tracted from convolutional neural networks (CNNs)

(Rodr

ıguez et al., 2017; Ayinde et al., 2019). Our in-

duced multivariate Gaussian prior thus actually im-

poses a lesser inductive bias than the Deep SVDD

objective, and allows for more ﬂexible distributions.

Internal experiments furthermore showed that iden-

tical performance could be achieved when decorre-

lating the pre-trained features by means of Cholesky

decomposition prior to training them with the Deep

SVDD objective.

Since others (Cohen and Hoshen, 2020; Defard

et al., 2020; Liznerski et al., 2021) have demonstrated

that good AS performance can be achieved by uti-

lizing intermediate feature representations that main-

tain spatial dimensions, we propose to apply the Ma-

halanobis distance to Gaussians ﬁtted to intermedi-

ate feature representations as well. Speciﬁcally, let

Φ : R

C×H×W

→ R

be a CNN with its intermedi-

ate mappings denoted as Φ

: R

m−1

×H

m−1

×W

m−1

→

×H

×W

. Then, the Mahalanobis distance of Φ

is a given by applying Equation 4 to each spatial el-

ement independently, yielding a matrix A

of size

× W

. Note that we account for small local

changes in image composition by modeling µ inde-

pendently per location & tie Σ across locations. This

has shown superior performance for ﬁxed features al-

ready in (Rippel et al., 2021a), and we furthermore

assess its effectiveness in Section 4.2.1. Furthermore,

we use max(A) to give an anomaly score per level

m of Φ, which is also used for optimization. Using

max(A) over mean(A) is motivated by (Defard et al.,

2020), which have shown that strong AD results can

be achieved by aggregating in such a manner for ﬁxed

representations. We argue that, when ﬁne-tuning AD,

one wants to modify exactly those feature combina-

tions that are currently most perceived to be anoma-

lous for normal images, in order to ensure that the true

data distribution ﬁts the estimated Gaussian distribu-

tion better, and assess its effects in Section 4.2.1.

Our overall minimization objective is thus

min

n · m

∑

i=1

∑

max(A

(Φ(x

;W ))). (5)

Note that the parameters µ

and Σ

of the Gaussians

are not learned. Instead, we use the empirical mean

and estimate Σ

using shrinkage as proposed by

Ledoit et al. (Ledoit et al., 2004), and leave them ﬁxed

afterwards. Doing so yields a stronger bias and has

shown to prevent catastrophic forgetting in prior ex-

periments.

For AS, we propose to upsample A

using bi-

linear interpolation similarly to (Cohen and Hoshen,

2020; Defard et al., 2020) over Gaussian interpola-

tion. Bilinear interpolation is free of hyperparame-

ters and thus more robust while simultaneously offer-

ing competitive results (selection of the Gaussian in-

terpolation kernel was shown to have a strong effect

on AS performance in (Liznerski et al., 2021)). Af-

ter their respective upsampling, pixel-wise averaging

across all heatmaps yields the overall anomaly score

map.

Note that while OE could be easily integrated into

our proposed approach by maximizing Equation 5 for

synthetic anomalies, we forego it to avoid the induc-

IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering

tion of an additional bias incurred by providing surro-

gates for the anomaly distribution (Ye et al., 2021).

3.1 Early Stopping via VRM

While we forego OE, we still need to detect onset of

catastrophic forgetting. To this end, we propose to ap-

proximate the compactness/discriminativeness of the

learned distribution. Speciﬁcally, we argue that a

good model should be able to distinguish between

subtle variations of the normal data and the normal

data itself as a surrogate for AD performance. We

therefore sample the vicinity of the normal data dis-

tribution by employing augmentations used for VRM

in semi-supervised learning schemes (refer Figure 1).

Afterwards, we measure the capability of a tuned net-

work Φ to distinguish between subtle vicinal varia-

tions and normal data by means of area under the

receiver operating characteristic (ROC) curve (AU-

ROC) as surrogate of the model’s discriminativeness.

We select both best model state based on this crite-

rion and perform early stopping should AUROC no

longer improve. As multiple augmentation schemes

have been proposed for VRM in literature, we com-

pare AugMix (Hendrycks et al., 2020) with CutOut

(DeVries and Taylor, 2017) to investigate the depen-

dence of early stopping on augmentation types. Ad-

ditionally, we compare with Confetti noise, but note

that this has been introduced as a surrogate for the

anomaly distribution originally in (Liznerski et al.,

2021).

We furthermore note that validating the model by

assessing its capability to distinguishing between sub-

tle variations and normal data could introduce an ad-

ditional bias. We argue however, that this bias should

be less strong than when using these subtle variations

for OE directly, and show this to be the case in Sec-

tion 4.2.

4 EXPERIMENTS

First, we brieﬂy introduce the dataset used for evalu-

ating our approach as well as the employed metrics.

4.1 Dataset and Evaluation Metrics

We use the public MVTec dataset (Bergmann et al.,

2021) to test and compare our approach with litera-

ture. The reasons for this are two-fold: First, MVTec

consists of subtle anomalies in high-resolution im-

ages as opposed to the AD tasks commonly con-

structed from classiﬁcation datasets (e.g. one-versus-

rest based on CIFAR-10 (Liznerski et al., 2021)).

Therefore, MVTec is more challenging and indicative

of real-world AD/AS performance. Second, MVTec

provides binary segmentation masks that can be used

to evaluate AS performance, which is infeasible for

classiﬁcation datasets. MVTec itself consists of 15

industrial product categories in total (10 object and 5

texture classes), and contains 5354 images overall.

To evaluate AD performance, we report the AU-

ROC, a metric commonly used to evaluate binary

classiﬁers (Ferri et al., 2011). For AS, we report the

pixel-wise AUROC as well as the per-region-overlap

(PRO) curve until 30% false positive rate (FPR) as

proposed in (Bergmann et al., 2020). While pixel-

wise AUROC represents an algorithm’s capability of

identifying anomalous pixels, PRO focuses more on

an algorithm’s performance at detecting small, locally

constrained anomalies.

4.2 Anomaly Detection

We ﬁrst assess whether our proposed ﬁne-tuning ap-

proach improves AD performance.

Training & Evaluation Details. We perform a 5-

fold evaluation over the training set of each MVTec

category, training an EfﬁcientNet-B4 (Tan and Le,

2019) to minimize the objective given by Equation 5,

and split the training dataset into 80% used for train-

ing and 20% used for validation. We choose Efﬁ-

cientNet based on its strong ImageNet performance

(Tan and Le, 2019), as architectures with stronger Im-

ageNet performance have been shown to yield bet-

ter features for transfer learning in (Kornblith et al.,

2019), which has been further conﬁrmed for trans-

fer learning in AD (Rippel et al., 2021c). Moreover,

EfﬁcientNet-B4s have been shown to offer a good

trade-off between model complexity and AD perfor-

mance (Rippel et al., 2021c). To demonstrate the gen-

eral applicability of our approach, we omit the selec-

tion of best-performing feature levels, simply extract-

ing the features from every “level” of the Efﬁcient-

Net as denoted in (Tan and Le, 2019). We also train

models to minimize the Deep SVDD (Equation 1) and

FCDD objectives. Here, we apply our early stopping

criterion to both objectives, and simultaneously use

the synthetic anomalies for OE in the FCDD objec-

tive. This is done to factor out differences in model

performance yielded by changing the underlying fea-

ture extractor (to the best of our knowledge, Deep

SVDD and FCDD objectives have not yet been ap-

plied to EfﬁcientNets for transfer learning AD in the

ﬁne-tuning setting). All models are trained using a

batch size of 8, Adam optimizer (Kingma and Ba,

2015) and a learning rate of 1.0 × 10

−6

. The small

Transfer Learning Gaussian Anomaly Detection by Fine-tuning Representations

learning rate is motivated by the fact that the feature

representations are already discriminative as is (refer

e.g. to the ﬁxed baseline in Table 1), and only need to

be tuned slightly. Furthermore, BatchNormalization

(Ioffe and Szegedy, 2015) statistics were kept frozen,

as dataset sizes are too small to re-estimate them re-

liably. Training was stopped when validation AU-

ROC performance did not improve for 20 epochs, and

70% of validation data was augmented and marked

as anomalous. We randomly sample 10 times the

length of our validation dataset for validation to better

approximate overall population characteristics, and

sample augmentations from all VRM-schemes with

equal probability (refer also Section 4.2.1). In all ex-

periments, we report µ± standard error of the mean

(SEM) aggregated over the 15 MVTec categories.

Results. Analyzing results (Table 1), it can be seen

that our proposed transfer learning scheme improves

over the baseline (frozen features), increasing AD

performance from 96.3 ± 1.1 to 97.1 ± 0.8 AUROC

and setting a new state-of-the-art in AD on the public

MVTec dataset. Furthermore, it can be seen that the

Gaussian assumption is important, since SVDD and

FCDD objectives are already outperformed by our

baseline where no ﬁne-tuning of feature representa-

tions occurs (90.5±2.7 and 87.0±3.6 vs. 96.3 ±1.1).

Still, it should be noted that ﬁne-tuning using our pro-

posed early stopping criterion improves results also

here (86.7 ± 3.5 to 90.5 ± 2.7 and 87.0 ± 3.6). Com-

paring Deep SVDD and FCDD performances, it can

be seen that worse AD performance is achieved when

using the subtle variations for OE rather than just us-

ing them for model validation.

4.2.1 Ablation Studies

Next, we perform ablation studies to quantify

the effects of proposed early stopping procedure,

parametrization of the Gaussian distribution + aggre-

gation of spatial anomaly scores on AD performance.

Proposed Early Stopping Procedure. We perform

two different experiments to assess effects of the pro-

posed early stopping procedure.

First, we investigate effects of early stopping it-

self, comparing the proposed approach to both (I) the

training for a ﬁxed number of epochs (250 speciﬁ-

cally) and (II) the early stopping without sampling the

vicinity of the normal data distribution. Here, we use

the minimum loss of Equation 5 over the validation

set as an early stopping criterion and omit sampling

the vicinity, focussing only on how well the normal

data ﬁts the distribution.

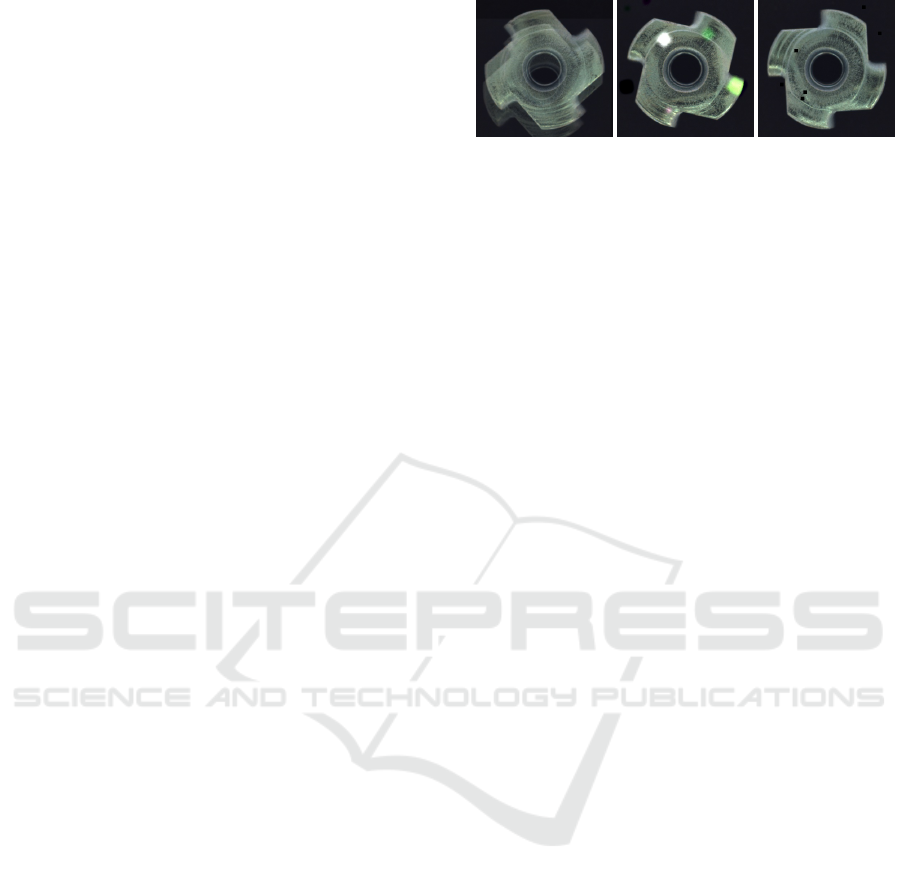
(a) (b) (c)

Figure 2: Reference synthesis results generated by (a) Aug-

Mix, (b) Confetti and (c) CutOut for the metal nut class.

Assessing results (Table 2), it can be seen that our

proposed early stopping criterion is the only method

that improves results. Furthermore, early stopping

based on validation loss alone leads to worse results

than training for a ﬁxed number of epochs. Thus, val-

idation loss alone is unable to detect onset of catas-

trophic forgetting. It should also be noted that man-

ually tuning the number of ﬁxed epochs for training

could have eventually led to improved results. Such

a tuning, however, would need to be performed in a

dataset speciﬁc manner and is not needed by our pro-

posed early stopping criterion.

Second, we assess the method’s sensitivity with

respect to the chosen VRM-type. To this end, we per-

form an additional ablation study, varying the sever-

ity of AugMix (Hendrycks et al., 2020) and investi-

gate the suitability of CutOut (DeVries and Taylor,

2017) and Confetti noise (Liznerski et al., 2021). We

sample the depth of AugMix uniformly from [1, 3],

as further increasing the depth produced too strong

variations in image appearance. We also investigate

beneﬁts yielded by combining different augmenta-

tion schemes, where the augmentation of a sample

is drawn randomly from {AugMix, CutOut, Confetti}

with equal probability. A reference image for each

synthesis procedure is shown in Figure 2.

Assessing results (Table 3), it can be seen that

all augmentation schemes improve results over the

baseline, where feature adaptation is omitted (Ta-

ble 1). Furthermore, AugMix outperforms the other

two methods slightly, and the performance is invariant

to the severity of applied augmentations. Last, when

jointly applying all augmentations, the same perfor-

mance is reached as when applying only the best aug-

mentation. This indicates that augmentation schemes

do not affect each other negatively, and reduces the

complexity of the approach: One can simply pool

multiple augmentation strategies and still achieve the

overall best performance.

Gaussian Types & Aggregation. We also investi-

gate the effects of both different distribution types ﬁt

to the normal class and spatial aggregation of anomaly

scores on AD performance. Speciﬁcally, we compare

IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering

Table 1: Comparison to the state of the art for AD. We report µ ± SEM AUROC scores in percent aggregated over all MVTec

categories. Note that values reported for GeoTrans and GANomaly were taken from (Fei et al., 2020), and values reported for

US from (Zavrtanik et al., 2020). Abbreviations: SEM = standard error of the mean.

Approach Feature type Mean ↑ SEM ↓

GeoTrans (Golan and El-Yaniv, 2018) Scratch 67.2 4.7

GANomaly (Akc¸ay et al., 2018) Scratch 76.1 1.6

ARNet (Fei et al., 2020) Scratch 83.9 2.8

RIAD (Zavrtanik et al., 2020) Scratch 91.7 1.8

US (Bergmann et al., 2020) Scratch 87.7 2.8

SPADE (Cohen and Hoshen, 2020) Frozen 85.5 —

Differnet (Rudolph et al., 2021) Frozen 94.7 1.3

PaDiM (Defard et al., 2020) Frozen 95.3 —

Patch SVDD (Yi and Yoon, 2020) Scratch 92.1 1.7

Triplet Networks (Tayeh et al., 2020) Scratch 94.9 1.2

CutPaste (Li et al., 2021) Tuned 96.6 1.1

Gaussian AD (Rippel et al., 2021c) Frozen 95.8 1.2

Gaussian ﬁne-tune (ours) Tuned 97.1 0.8

Frozen 96.3 1.1

Deep SVDD Tuned 90.5 2.7

Frozen 86.7 3.5

FCDD Tuned 87.0 3.6

Table 2: Effects of early stopping criterion on ﬁne-tuning

AD performance.

Method Mean ↑ SEM ↓

Vicinity sampling via VRM 97.1 0.9

Fixed epochs 96.3 1.2

Validation loss 95.4 1.2

No Training 96.3 1.1

Table 3: Effect of VRM-type on AD performance.

Method Mean ↑ SEM ↓

AugMix

sev = 3 97.1 0.8

sev = 4 97.0 0.9

sev = 5 97.0 0.8

sev = 6 97.0 0.8

sev = 7 97.1 0.8

Confetti noise 96.7 1.0

CutOut 96.6 1.0

All 97.1 0.8

a global Gaussian distribution (shared µ and Σ across

all spatial locations of a “level”), a tied Gaussian dis-

tribution (individual µ and tied Σ) as well as local

Gaussian distributions (individual µ and Σ per loca-

tion). Except for the parametrization of the Gaussian,

training details are identical as before. For the ag-

gregation methods, we compare mean and maximum

aggregation for generation of image-level AD scores.

Table 4: Effect of different types of distribution/aggregation

methods on AD performance.

Method Mean ↑ SEM ↓

Global Gaussian

aggregation = mean 93.7 2.3

aggregation = max 96.9 0.9

One Gaussian per location

aggregation = mean 97.3 0.8

aggregation = max 97.3 0.8

Tied Gaussian

aggregation = mean 93.0 2.3

aggregation = max 97.1 0.8

When assessing results (Table 4), it can be seen

that maximum aggregation performs best across all

methods. Furthermore, effects of max aggregation

are stronger for the global as well as the tied Gaus-

sian distribution than the local Gaussian ﬁt per loca-

tion. Overall, AD performance of the local Gaussian

model is best. However, it also has the highest mem-

ory requirement, increasing the overall memory foot-

print of the method by a factor of 10. Notably, it also

has the highest base AD performance and only negli-

gible gains are achieved by ﬁne-tuning. It is therefore

infeasible in practice, and not regarded further.

4.2.2 Anomaly Segmentation

Since our approach maintains spatial resolution of

anomaly scores, AS can also be achieved similarly to

Transfer Learning Gaussian Anomaly Detection by Fine-tuning Representations

(Liznerski et al., 2021; Defard et al., 2020).

Training & Evaluation Details. To factor out ef-

fects of pre-trained model selection on AS perfor-

mance and give a fair comparison to competing ﬁne-

tuning methods, we also report AS performance of

EfﬁcientNet-B4s ﬁne-tuned with either FCDD + OE

or Deep SVDD. All other hyperparameters are same

as in Section 4.2.

Results. Assessing results, it can be seen that our

proposed ﬁne-tuning scheme improves both AUROC

(Table 5) and PRO (Table 6) scores. This is in con-

trast to Deep SVDD, where both AUROC and PRO

decrease upon ﬁne-tuning. Conversely, the FCDD

objective also improves AS performance, and we

achieve higher AUROC values for FCDD than re-

ported in (Liznerski et al., 2021). Furthermore, dif-

ferences across the ﬁne-tuning objectives are much

lower for AS than for AD. Compared to state-of-the-

art AS methods, our method achieves similar AUROC

scores, and slightly lower PRO scores.

In addition to quantitative evaluations, we also

assess segmentation results qualitatively, showcasing

representative results in Figure 3. Here, it can be seen

that our approach performs well on low-level, textu-

ral anomalies (e.g. the “print” on the hazelnut as well

as the “glue” on the leather). However, it fails to

segment/capture high-level, semantic anomalies such

as the “cable swap” or “scratches” (“scratches” may

be similar in appearance to the background texture in

context of the class wood).

5 DISCUSSION

In our work, we have proposed to ﬁne-tune pre-

trained feature representations for AD using Gaussian

distributions, and motivated this by the linkage be-

tween generative and discriminative modeling shown

in (Lee et al., 2018; Kamoi and Kobayashi, 2020;

Rippel et al., 2021c). We have also proposed to use

augmentations commonly employed for VRM to de-

tect onset of catastrophic forgetting, avoiding the bias

likely induced by sampling the anomaly distribution

for OE (Ye et al., 2021).

Evaluations on the public MVTec dataset have

revealed that the proposed ﬁne-tuning based on the

Gaussian assumption achieves a new state-of-the-art

in AD and improves AS performance (Table 1, Ta-

ble 5 and Table 6). Ablation studies demonstrated

that onset of catastrophic forgetting can be reliably

detected using our proposed early stopping criterion

(Table 2). We have furthermore shown that the choice

(a)

(b)

Figure 3: Representative successful segmentations as well

as failure cases of our approach. We show representative

successful segmentations as well as failures for three cate-

gories (a) as well as three texture (b) classes of the MVTec

dataset. Left shows the input image, the middle the ground-

truth segmentation mask, and the right the heatmap gener-

ated by our approach. Heatmaps are scaled such that the

value range across all test images is mapped to the interval

[0, 255].

of augmentation scheme only has a limited inﬂuence

on the detection of catastrophic forgetting. Moreover,

ensembling multiple augmentation schemes yields re-

sults equal to that of the best scheme applied individ-

ually (Table 3). Our proposed early stopping regime

should thus be transferable also to other ﬁne-tuning

approaches and can easily integrate additional aug-

mentation schemes such as the one proposed in (Li

et al., 2021).

IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering

Table 5: AUROC scores in percent for pixel-wise segmentation. We report µ±SEM across MVTec categories. Values reported

for US were sourced from (Zavrtanik et al., 2020).

Approach Feature type Mean ↑ SEM ↓

CAVGA-R

(Venkataramanan et al., 2020) Scratch 89.0 —

RIAD (Zavrtanik et al., 2020) Scratch 94.2 1.3

VAE-Attention (Liu et al., 2020) Scratch 86.1 2.3

US (Bergmann et al., 2020) Scratch 93.9 1.6

SPADE (Cohen and Hoshen, 2020) Frozen 96.0 0.9

PaDiM (Defard et al., 2020) Frozen 97.5 0.4

Patch SVDD (Yi and Yoon, 2020) Scratch 95.7 0.6

FCDD (Liznerski et al., 2021) Tuned 92.0 —

CutPaste (Li et al., 2021) Tuned 96.0 0.8

Gaussian ﬁne-tune (ours) Tuned 96.5 0.8

Frozen 96.4 0.7

Deep SVDD Tuned 95.1 0.9

Frozen 95.2 0.9

FCDD Tuned 96.2 0.6

Table 6: Area under the PRO curve as deﬁned by (Bergmann et al., 2021; Bergmann et al., 2020) up to a false positive rate of

30%. Values for state-of-the-art methods are directly taken from the corresponding sources. We report µ±SEM values.

Approach Feature type Mean ↑ SEM ↓

SPADE (Cohen and Hoshen, 2020) Frozen 91.7 1.4

PaDiM (Defard et al., 2020) Frozen 92.1 1.1

US (Bergmann et al., 2020) Frozen 91.4 2.0

Gaussian ﬁne-tune (ours) Tuned 88.7 1.7

Frozen 88.5 1.6

Deep SVDD Tuned 88.7 1.9

Frozen 88.9 2.0

FCDD Tuned 89.7 1.6

We furthermore remarked in Section 3.1 that a

bias may still be introduced even when using subtle

augmentations for model validation rather than OE,

but argued that this bias would most likely be lower.

Results showed that Deep SVDD outperforms FCDD

with respect to AD (Table 1), supporting this claim.

While FCDD did outperform Deep SVDD with re-

spect to AS, this can be attributed by the segmen-

tation mask generated for the synthetic Confetti and

CutOut augmentations, which provide additional in-

formation about anomaly localization leveraged by

FCDD. Therefore, one should train FCDD without

exploiting the synthetic segmentation masks in future

work to fully validate our claim.

During our evaluations, we moreover found that

FCDD achieves better AS than reported in (Lizner-

ski et al., 2021). This can be in part attributed to

the fact that we apply FCDD to multiple levels of

the pre-trained CNN. Furthermore, we use features

of an EfﬁcientNet-B4 compared to the VGG16 used

in (Liznerski et al., 2021), and network architectures

with better ImageNet performance have been shown

to be more suited for transfer learning in (Kornblith

et al., 2019).

5.1 Limitations

While both AD and AS could be improved by ﬁne-

tuning, our approach failed to segment high-level,

semantic anomalies (cf. Figure 3). High-level, se-

mantic anomalies are undoubtedly more difﬁcult to

detect than low-level anomalies, as they require a

model of normality that is deﬁned on an abstract un-

derstanding of the underlying image domain (Ahmed

and Courville, 2020; Deecke et al., 2021). Acquir-

ing such abstract understanding has proven difﬁcult

for CNNs, as evidenced by their texture-bias (Geirhos

et al., 2019; Hermann et al., 2020). Potentially, learn-

ing these concepts could be achieved by employing

the self-attention mechanism (Vaswani et al., 2017),

and a lesser texture bias was observed for vision trans-

formers (ViTs) (Dosovitskiy et al., 2021) recently

Transfer Learning Gaussian Anomaly Detection by Fine-tuning Representations

(Naseer et al., 2021). Thus, one should try to apply

features of ImageNet pre-trained ViTs to the AS task

in future work. As an alternative, one could also try

to leverage features yielded by either object detection

or segmentation networks, which have been shown to

generate features that maintain stronger spatial acuity

(Li et al., 2019). They have furthermore been shown

to improve AS performance when used as the basis

for transfer learning AS (Rippel and Merhof, 2021).

Moreover, we limited our evaluations to the public

MVTec dataset. In future work, we will therefore

revalidate our approach on additional datasets used in

literature, such as CIFAR-10 (Ahmed and Courville,

2020). Last, anomalies may also occur for multi-

modal normal data distributions (Rippel et al., 2021d;

Deecke et al., 2021), and our current ﬁne-tuning pro-

cedure can not be applied here. Here, less constrained

priors such as Gaussian mixture models or normaliz-

ing ﬂows (Rezende and Mohamed, 2015) may be used

instead.

6 CONCLUSION

In our work, we have demonstrated that ﬁne-tuning of

pre-trained feature representations for transfer learn-

ing AD is possible using a strong Gaussian prior,

achieving a new state-of-the-art in AD on the public

MVTec dataset. We have further shown that augmen-

tations commonly employed for VRM can be used

to detect onset of catastrophic forgetting, which typ-

ically hinders transfer learning in AD. Here, ablation

studies revealed that our method is robust with re-

spect to the chosen synthesis scheme, and that com-

bining multiple schemes is also feasible. Together,

this demonstrated the general applicability of our ap-

proach.

REFERENCES

Ahmed, F. and Courville, A. (2020). Detecting semantic

anomalies. Proceedings of the AAAI Conference on

Artiﬁcial Intelligence, 34(04):3154–3162.

Akc¸ay, S., Atapour-Abarghouei, A., and Breckon, T. P.

(2018). GANomaly: Semi-supervised anomaly detec-

tion via adversarial training. In Asian Conference on

Computer Vision, pages 622–637. Springer.

Andrews, J., Tanay, T., Morton, E. J., and Grifﬁn, L. D.

(2016). Transfer representation-learning for anomaly

detection. JMLR, Multidisciplinary Digital Publish-

ing Institute.

Ayinde, B. O., Inanc, T., and Zurada, J. M. (2019). Regu-

larizing deep neural networks by enhancing diversity

in feature extraction. IEEE Transactions on Neural

Networks and Learning Systems, 30(9):2650–2661.

Bergmann, P., Batzner, K., Fauser, M., Sattlegger, D., and

Steger, C. (2021). The mvtec anomaly detection

dataset: A comprehensive real-world dataset for un-

supervised anomaly detection. International Journal

of Computer Vision.

Bergmann, P., Fauser, M., Sattlegger, D., and Steger,

C. (2020). Uninformed students: Student-teacher

anomaly detection with discriminative latent embed-

dings. In Proceedings of the IEEE/CVF Conference

on Computer Vision and Pattern Recognition, pages

4183–4192.

Chapelle, O., Weston, J., Bottou, L., and Vapnik, V. (2001).

Vicinal risk minimization. In Leen, T., Dietterich, T.,

and Tresp, V., editors, Advances in Neural Informa-

tion Processing Systems, volume 13. MIT Press.

Christiansen, P., Nielsen, L. N., Steen, K. A., Jørgensen,

R. N., and Karstoft, H. (2016). Deepanomaly: Com-

bining background subtraction and deep learning for

detecting obstacles and anomalies in an agricultural

ﬁeld. Sensors, 16(11):1904.

Cohen, N. and Hoshen, Y. (2020). Sub-image anomaly

detection with deep pyramid correspondences. arXiv

preprint arXiv:2005.02357.

Deecke, L., Ruff, L., Vandermeulen, R. A., and Bilen, H.

(2020). Deep anomaly detection by residual adapta-

tion. arXiv preprint arXiv:2010.02310.

Deecke, L., Ruff, L., Vandermeulen, R. A., and Bilen, H.

(2021). Transfer-based semantic anomaly detection.

In Meila, M. and Zhang, T., editors, Proceedings of

the 38th International Conference on Machine Learn-

ing, volume 139 of Proceedings of Machine Learning

Research, pages 2546–2558. PMLR.

Defard, T., Setkov, A., Loesch, A., and Audigier, R. (2020).

Padim: a patch distribution modeling framework for

anomaly detection and localization. arXiv preprint

arXiv:2011.08785.

Deng, J., Dong, W., Socher, R., Li, L., Li, K., and Fei-Fei,

L. (2009). ImageNet: A large-scale hierarchical im-

age database. In 2009 IEEE Conference on Computer

Vision and Pattern Recognition, pages 248–255.

DeVries, T. and Taylor, G. W. (2017). Improved regular-

ization of convolutional neural networks with cutout.

arXiv preprint arXiv:1708.04552.

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn,

D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer,

M., Heigold, G., Gelly, S., Uszkoreit, J., and Houlsby,

N. (2021). An image is worth 16x16 words: Trans-

formers for image recognition at scale. In Interna-

tional Conference on Learning Representations.

Fei, Y., Huang, C., Jinkun, C., Li, M., Zhang, Y., and Lu, C.

(2020). Attribute restoration framework for anomaly

detection. IEEE Transactions on Multimedia.

Ferri, C., Hern

andez-Orallo, J., and Flach, P. A. (2011). A

coherent interpretation of AUC as a measure of aggre-

gated classiﬁcation performance. In Proceedings of

the 28th International Conference on Machine Learn-

ing (ICML-11), pages 657–664.

IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering

Geirhos, R., Rubisch, P., Michaelis, C., Bethge, M., Wich-

mann, F. A., and Brendel, W. (2019). Imagenet-

trained CNNs are biased towards texture; increasing

shape bias improves accuracy and robustness. In In-

ternational Conference on Learning Representations.

Golan, I. and El-Yaniv, R. (2018). Deep anomaly detec-

tion using geometric transformations. In Advances in

Neural Information Processing Systems, pages 9758–

9769.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 770–778.

Hendrycks, D., Mazeika, M., and Dietterich, T. (2019).

Deep anomaly detection with outlier exposure. In In-

ternational Conference on Learning Representations.

Hendrycks, D., Mu, N., Cubuk, E. D., Zoph, B., Gilmer, J.,

and Lakshminarayanan, B. (2020). AugMix: A sim-

ple data processing method to improve robustness and

uncertainty. Proceedings of the International Confer-

ence on Learning Representations (ICLR).

Hermann, K. L., Chen, T., and Kornblith, S. (2020). The

origins and prevalence of texture bias in convolutional

neural networks. In Larochelle, H., Ranzato, M., Had-

sell, R., Balcan, M., and Lin, H., editors, Advances

in Neural Information Processing Systems 33: An-

nual Conference on Neural Information Processing

Systems 2020, NeurIPS 2020, December 6-12, 2020,

virtual.

Ioffe, S. and Szegedy, C. (2015). Batch normalization: Ac-

celerating deep network training by reducing inter-

nal covariate shift. In Proceedings of the 32nd In-

ternational Conference on International Conference

on Machine Learning - Volume 37, ICML’15, page

448–456, Lille, France. JMLR.org.

Kamoi, R. and Kobayashi, K. (2020). Why is the ma-

halanobis distance effective for anomaly detection?

arXiv preprint arXiv:2003.00402.

Kingma, D. P. and Ba, J. (2015). Adam: A method for

stochastic optimization. In Bengio, Y. and LeCun,

Y., editors, 3rd International Conference on Learn-

ing Representations, ICLR 2015, San Diego, CA, USA,

May 7-9, 2015, Conference Track Proceedings.

Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J.,

Desjardins, G., Rusu, A. A., Milan, K., Quan, J.,

Ramalho, T., Grabska-Barwinska, A., et al. (2017).

Overcoming catastrophic forgetting in neural net-

works. Proceedings of the national academy of sci-

ences, 114(13):3521–3526.

Kornblith, S., Shlens, J., and Le, Q. V. (2019). Do better

imagenet models transfer better? In Proceedings of

the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 2661–2671.

Ledoit, O., Wolf, M., et al. (2004). A well-conditioned

estimator for large-dimensional covariance matrices.

Journal of Multivariate Analysis, 88(2):365–411.

Lee, K., Lee, K., Lee, H., and Shin, J. (2018). A simple uni-

ﬁed framework for detecting out-of-distribution sam-

ples and adversarial attacks. In Advances in Neural

Information Processing Systems, pages 7167–7177.

Li, C.-L., Sohn, K., Yoon, J., and Pﬁster, T. (2021). Cut-

paste: Self-supervised learning for anomaly detection

and localization. In 2021 IEEE/CVF Conference on

Computer Vision and Pattern Recognition (CVPR),

pages 9659–9669.

Li, H., Singh, B., Najibi, M., Wu, Z., and Davis, L. S.

(2019). An analysis of pre-training on object detec-

tion. arXiv preprint arXiv:1904.05871.

Liu, W., Li, R., Zheng, M., Karanam, S., Wu, Z., Bhanu, B.,

Radke, R. J., and Camps, O. (2020). Towards visually

explaining variational autoencoders. In Proceedings

of the IEEE/CVF Conference on Computer Vision and

Pattern Recognition (CVPR).

Liznerski, P., Ruff, L., Vandermeulen, R. A., Franks, B. J.,

Kloft, M., and M

uller, K. R. (2021). Explainable deep

one-class classiﬁcation. In International Conference

on Learning Representations.

Mahalanobis, P. C. (1936). On the generalized distance in

statistics. National Institute of Science of India.

Naseer, M. M., Ranasinghe, K., Khan, S. H., Hayat, M.,

Shahbaz Khan, F., and Yang, M.-H. (2021). Intriguing

properties of vision transformers. Advances in Neural

Information Processing Systems, 34.

Perera, P. and Patel, V. M. (2019). Learning deep features

for one-class classiﬁcation. IEEE Transactions on Im-

age Processing, 28(11):5450–5463.

Reiss, T., Cohen, N., Bergman, L., and Hoshen, Y. (2021).

Panda: Adapting pretrained features for anomaly de-

tection and segmentation. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition (CVPR), pages 2806–2814.

Rezende, D. and Mohamed, S. (2015). Variational infer-

ence with normalizing ﬂows. In Bach, F. and Blei,

D., editors, Proceedings of the 32nd International

Conference on Machine Learning, volume 37 of Pro-

ceedings of Machine Learning Research, pages 1530–

1538, Lille, France. PMLR.

Rippel, O., Haumering, P., Brauers, J., and Merhof, D.

(2021a). Anomaly detection for the automated visual

inspection of pet preform closures. In 2021 26th IEEE

International Conference on Emerging Technologies

and Factory Automation (ETFA), volume 1.

Rippel, O. and Merhof, D. (2021). Leveraging pre-trained

segmentation networks for anomaly segmentation. In

2021 26th IEEE International Conference on Emerg-

ing Technologies and Factory Automation (ETFA),

pages 01–04.

Rippel, O., Mertens, P., K

onig, E., and Merhof, D. (2021b).

Gaussian anomaly detection by modeling the distribu-

tion of normal data in pretrained deep features. IEEE

Transactions on Instrumentation and Measurement,

70:1–13.

Rippel, O., Mertens, P., and Merhof, D. (2021c). Model-

ing the distribution of normal data in pre-trained deep

features for anomaly detection. In 2020 25th Inter-

national Conference on Pattern Recognition (ICPR),

pages 6726–6733.

Rippel, O., M

uller, M., M

unkel, A., Gries, T., and Merhof,

D. (2021d). Estimating the probability density func-

tion of new fabrics for fabric anomaly detection. In

Transfer Learning Gaussian Anomaly Detection by Fine-tuning Representations

10th International Conference on Pattern Recognition

Applications and Methods (ICPRAM).

Rodr

ıguez, P., Gonz

alez, J., Cucurull, G., Gonfaus, J. M.,

and Roca, F. X. (2017). Regularizing cnns with lo-

cally constrained decorrelations. In 5th International

Conference on Learning Representations, ICLR 2017,

Toulon, France, April 24-26, 2017, Conference Track

Proceedings. OpenReview.net.

Rudolph, M., Wandt, B., and Rosenhahn, B. (2021). Same

same but differnet: Semi-supervised defect detection

with normalizing ﬂows. In Winter Conference on Ap-

plications of Computer Vision (WACV).

Ruff, L., Kauffmann, J. R., Vandermeulen, R. A., Mon-

tavon, G., Samek, W., Kloft, M., Dietterich, T. G., and

uller, K. R. (2021). A unifying review of deep and

shallow anomaly detection. Proceedings of the IEEE,

pages 1–40.

Ruff, L., Vandermeulen, R., Goernitz, N., Deecke, L., Sid-

diqui, S. A., Binder, A., M

uller, E., and Kloft, M.

(2018). Deep one-class classiﬁcation. In Dy, J. and

Krause, A., editors, Proceedings of the 35th Interna-

tional Conference on Machine Learning, volume 80

of Proceedings of Machine Learning Research, pages

4393–4402, Stockholmsm

assan, Stockholm Sweden.

PMLR.

Ruff, L., Vandermeulen, R. A., Franks, B. J., M

uller, K.-R.,

and Kloft, M. (2020). Rethinking assumptions in deep

anomaly detection. arXiv preprint arXiv:2006.00339.

Sabokrou, M., Fayyaz, M., Fathy, M., Moayed, Z., and

Klette, R. (2018). Deep-anomaly: Fully convolutional

neural network for fast anomaly detection in crowded

scenes. Computer Vision and Image Understanding,

172:88–97.

Schlegl, T., Seeb

ock, P., Waldstein, S. M., Langs, G., and

Schmidt-Erfurth, U. (2019). f-AnoGAN: Fast unsu-

pervised anomaly detection with generative adversar-

ial networks. Medical image analysis, 54:30–44.

Sch

olkopf, B., Platt, J. C., Shawe-Taylor, J., Smola, A. J.,

and Williamson, R. C. (2001). Estimating the support

of a high-dimensional distribution. Neural computa-

tion, 13(7):1443–1471.

Simonyan, K. and Zisserman, A. (2015). Very deep con-

volutional networks for large-scale image recognition.

In Bengio, Y. and LeCun, Y., editors, 3rd Interna-

tional Conference on Learning Representations, ICLR

2015, San Diego, CA, USA, May 7-9, 2015, Confer-

ence Track Proceedings.

Tan, M. and Le, Q. V. (2019). EfﬁcientNet: Rethinking

model scaling for convolutional neural networks. In

Chaudhuri, K. and Salakhutdinov, R., editors, Pro-

ceedings of the 36th International Conference on Ma-

chine Learning, ICML 2019, 9-15 June 2019, Long

Beach, California, USA, volume 97 of Proceedings

of Machine Learning Research, pages 6105–6114.

PMLR.

Tax, D. M. and M

uller, K.-R. (2003). Feature extraction for

one-class classiﬁcation. In Artiﬁcial Neural Networks

and Neural Information Processing—ICANN/ICONIP

2003, pages 342–349. Springer.

Tayeh, T., Aburakhia, S., Myers, R., and Shami, A. (2020).

Distance-based anomaly detection for industrial sur-

faces using triplet networks. In 2020 11th IEEE An-

nual Information Technology, Electronics and Mobile

Communication Conference (IEMCON), pages 0372–

0377.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, L. u., and Polosukhin,

I. (2017). Attention is all you need. In Guyon,

I., Luxburg, U. V., Bengio, S., Wallach, H., Fer-

gus, R., Vishwanathan, S., and Garnett, R., editors,

Advances in Neural Information Processing Systems,

volume 30. Curran Associates, Inc.

Venkataramanan, S., Peng, K.-C., Singh, R. V., and Ma-

halanobis, A. (2020). Attention guided anomaly lo-

calization in images. In Vedaldi, A., Bischof, H.,

Brox, T., and Frahm, J.-M., editors, Computer Vision

– ECCV 2020, pages 485–503, Cham. Springer Inter-

national Publishing.

Ye, Z., Chen, Y., and Zheng, H. (2021). Understanding the

effect of bias in deep anomaly detection. In Zhou,

Z.-H., editor, Proceedings of the Thirtieth Interna-

tional Joint Conference on Artiﬁcial Intelligence, IJ-

CAI 2021, Virtual Event / Montreal, Canada, 19-27

August 2021, pages 3314–3320. ijcai.org.

Yi, J. and Yoon, S. (2020). Patch svdd: Patch-level svdd for

anomaly detection and segmentation. In Proceedings

of the Asian Conference on Computer Vision (ACCV).

Zavrtanik, V., Kristan, M., and Sk

caj, D. (2020). Recon-

struction by inpainting for visual anomaly detection.

Pattern Recognition, page 107706.

IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering