A Symbolic Time Constraint Propagation Mechanism Proposal for
Workflow Nets
Lorena Rodrigues Bruno and St
´
ephane Julia
Federal University of Uberl
ˆ
andia, Uberl
ˆ
andia-MG, Brazil
Keywords:
Time Petri Net, Symbolic Expression, Workflow Net, Linear Logic, Forward Propagation, Backward
Propagation.
Abstract:
The model of a Workflow Management System should describe the time constraints of resources over the
activities of the corresponding business process. In general, typical temporal phenomena include activity
execution delays, limits to the occurrence of valid intervals over the activities, limits to valid intervals over
resources (limit to resources life cycle), limits to duration of process execution, time distance between two
activities, etc. In this study, a Workflow net model incremented with time intervals to describe the duration
of activities and waiting times is presented. To define the execution of activities minimum and maximum
intervals, a time constraint propagation mechanism based on the sequent calculus of Linear Logic and on
symbolic dates is proposed.
1 INTRODUCTION
Workflow Management Systems are systems that
manage the execution of Workflow processes (Mu-
rata, 1989). A Workflow process represents the se-
quence of activities that have to be executed by mem-
bers of the same working group, while respecting
some conditions that determine their order of execu-
tion, in order to treat specific cases and to reach a
well-defined goal.
Petri nets (Murata, 1989) are very well adapted
to model Real Time Systems, as these allow for a
good representation of conflict situations, shared re-
sources, synchronous and asynchronous communica-
tion, precedence constraints and explicit quantitative
time constraints in the time Petri net case. Petri nets
can also be an efficient tool for the modeling and anal-
ysis of Workflow Management Systems, as these have
a graphic representation, are easy to learn, can be
used as a communication language between special-
ists from different areas, allow static and dynamic de-
scription of systems to be represented, and also have
a mathematical formalism that enables the use of im-
portant analysis methods (Murata, 1989). The Petri
nets that model Workflow processes are defined in
(Van Der Aalst et al., 2004) and are called Workflow
nets.
Time management of a Workflow process is an
important aspect in the study of processes due to the
fact that there exist many types of time restrictions in
business processes. A study of Workflow time man-
agement is concentrated mainly on the planning of
Workflow time execution, on the estimation of activ-
ity durations, on avoiding time restriction violations
in activities or processes, and on the treatment of time
restriction violation exceptions.
In the real world, due to dynamic features of re-
sources and activities in business processes, the ma-
jority of information is uncertain and cannot be pre-
cisely described. In this study, a Workflow net model
with time interval constraints, defined by minimum
and maximum bounds for each activity duration and
waiting time between activities, is presented. In order
to compute minimum and maximum bounds corre-
sponding to the beginning dates of the activities, two
different time constraint propagation mechanisms are
proposed: one to find the earliest start dates of the
process activities, and the other to find the latest start
dates of process activities.
The proposed work presents an approach based on
Linear Logic to prove the Soundness correctness cri-
terion defined for Workflow nets and, based on the re-
sulting proof tree, computes symbolic formulas based
on (max, +) or (min, −) operators that express the
possible beginning dates of process activities. Such
symbolic expressions will then be used to define the
numerical time constraints associated to specific cases
treated by the Workflow process and will be consid-
Bruno, L. and Julia, S.
A Symbolic Time Constraint Propagation Mechanism Proposal for Workflow Nets.
DOI: 10.5220/0011064400003179
In Proceedings of the 24th International Conference on Enterprise Information Systems (ICEIS 2022) - Volume 1, pages 537-544
ISBN: 978-989-758-569-2; ISSN: 2184-4992
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
537

ered in the Planning/Scheduling problem of resources
associated with the activities linked to the process.
2 TIME WORKFLOW NET
2.1 Workflow Net
A Petri net that models a Workflow process is called
a Workflow net (Van Der Aalst et al., 2004). A Work-
flow net satisfies the following properties:
• It has only one source place named Start and only
one sink place named End. These are special
places, such that the place Start has only outgoing
arcs and the place End has only incoming arcs.
• A token in Start represents a case that needs to be
handled and a token in End represents a case that
has been handled.
• Every task t (transition) and condition p (place)
should be in a path from place Start to place End.
2.2 Process
A process defines which tasks need to be executed and
in which order (Van Der Aalst et al., 2004). Model-
ing a Workflow process in terms of a Workflow net is
rather straightforward: transitions are active compo-
nents and models the tasks, places are passive compo-
nents and model conditions (pre and post), and tokens
model cases (Van Der Aalst et al., 2004).
In order to illustrate the mapping of a process
into a Workflow net, the process for handling com-
plaints, shown in (Van Der Aalst et al., 2004) can
be understood as follows: an incoming complaint is
first recorded. Then the client who has complained
along with the department affected by the complaint
are contacted. The client is approached for more in-
formation. The department is informed of the com-
plaint and may be asked for its initial reaction. These
two tasks may be performed in parallel, i.e. simulta-
neously or in any order. After that, data is gathered
and a decision is made. Depending upon the decision,
either a compensation payment is made or a letter is
sent. Finally, the complaint is filed. In Fig. 1, a Work-
flow net that correctly model this process is shown.
2.3 Time Petri Net
Time and Timed Petri nets can associate time stamps
to places (p-time and p-timed Petri net) or transi-
tions (t-time and t-timed Petri nets). In the p-timed
Figure 1: Handle Complaint Process.
Petri net case, according to (Sifakis, 1979), time con-
straints are represented by durations (positive ratio-
nal numbers) associated with places. In the t-timed
Petri net case, according to (Ramamoorthy and Ho,
1980), time constraints are represented by durations
(positive real numbers) associated with transitions. In
the t-time Petri net case, time constraints are repre-
sented by an interval [δ
min
, δ
max
] associated with each
transition; the time interval associated with a specific
transition corresponds to an imprecise enabling du-
ration, according to (Merlin, 1974) and (Menasche,
1982). For example, the interval [8, 12] associated
with a transition indicates that the transition will be
fired at least eight time units after it has been enabled
and, at the most, twelve time units after its enabling
instant.
3 LINEAR LOGIC
Linear Logic (Girard, 1987) was proposed by Jean-
Yves Girard in 1987. In Linear Logic, the propo-
sitions are considered as resources which are con-
sumed and produced in each change of state, which is
different from classic logic where propositions have
Boolean values (true or false) (Pradin-Ch
´
ezalviel
et al., 1999). The Linear Logic introduces seven new
connectors divided into three groups, but in this pa-
per, just two of these connectives will be used: times,
denoted by ⊗ and linear implies, denoted by (. The
first symbol represents the simultaneous availability
of resources; for example, A ⊗ B represents simulta-
neous availability of resources A and B. The second
symbol represents a possible change of state; for in-
stance A ( B means that B is produced when A is
consumed.
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
538

The translation of a Petri net into formulas of Lin-
ear Logic is performed as presented in (Riviere et al.,
2001). A marking M is a monomial in ⊗, which is
represented by M = A1 ⊗ A2 ⊗ ... ⊗ Ak in which Ai
are place names. In Fig.1, the initial marking is just
Start because of the token in place Start. A transition
is an expression of the form M1 ( M2 where M1 and
M2 are markings. For instance, the transition Record
of the Workflow net in Fig.1 can be represented as
Record = Start ( p1 ⊗ p2.
A sequent represents the triggering of a transition
(or a sequence of possible transitions). The sequent
M, t
i
` M
0
represents a scenario where M is the initial
marking, M
0
is the final marking, and t
i
is a set of
non-ordered transitions. To prove the correctness of
a sequent, a proof tree should be built by applying
the rules of sequent calculus. According to (Girault
et al., 1997) the proof of a sequent in linear logic is
equivalent to the corresponding reachability problem
in the Petri net theory.
In this paper, only some of the Linear Logic rules
will be considered. These rules will be used to build
the proof trees in the context of the reachability prob-
lem of the Petri net theory. For such, F, G and H
are considered as formulas and, Γ and ∆ are blocks
of formulas. The following rules will be used in this
paper:
• The (
L
rule,
Γ`F ∆,G`H
Γ,∆,F(G`H
(
L
expresses a transi-
tion firing and generates two sequents. The left se-
quent represents the tokens consumed by the tran-
sition firing and the right sequent represents the
subsequent that still needs to be proved.
• The ⊗
L
rule,
Γ,F,G`H
Γ,F⊗G`H
⊗
L
, transforms a marking
into an atom list.
• The ⊗R rule,
Γ`F ∆`G
∆,Γ`F⊗G
⊗
R
, transforms a sequent
such as A, B ` A⊗B into two identity sequents A `
A and B ` B.
A Linear Logic proof tree is read from bottom-up.
The proof stops when the identity sequent End ` End
is produced, when there is no longer any rule that can
be applied, or when all the leaves of the proof tree are
identity sequent.
4 TIME CONSTRAINT
PROPAGATION MECHANISM
Typically, the time required to execute an activity in a
Workflow process is non-deterministic. According to
(Riviere et al., 2001), explicit time constraints, which
exist in systems with real-time characteristics, can be
formally specified using a static time interval associ-
ated to each task (transition) of the model. The dy-
namic behavior of the corresponding time Petri net
thus depends on the marking of the network, as well
as on the tokens temporal situation that is given by a
visibility interval (dos Santos Soares et al., 2008). A
visibility interval [(δ
p
)
min
, (δ
p
)
max
] associated with a
token in a place p of a time Petri net specified the min-
imum date (δ
p
)
min
at which a token is available in p
to trigger an output transition of p (earliest start date
of an activity), and the maximum date after which the
token becomes unavailable (dead) and cannot be used
to trigger any transition (latest start date of the corre-
sponding activity).
In a Workflow Management System, the visibility
interval depends on a global clock connected to the
entire net which calculates the passage of time from
date δ = 0, which corresponds to the start of system
operations. In particular, the existing waiting time be-
tween sequential activities will be represented by a
visibility interval, for which the minimum and maxi-
mum bounds will depend on the earliest and latest de-
livery of a case process by the Workflow net. Through
knowledge of the beginning date and the maximum
duration of a case, it should be possible to calculate
the visibility intervals associated with the tokens in
the waiting places.
The calculus of the visibility intervals associated
with the tokens in the waiting places will be real-
ized in this proposal by considering the different kinds
of routes that can exist in a Workflow process, and
which can be expressed through the sequents of Lin-
ear Logic. An iterative route can be replaced by a
global activity as shown in (Soares Passos and Julia,
2016) and will not be considered in this work.
The constraint propagation technique proposed in
this article is based on two different approaches: a
forward reasoning to produce the minimum bounds
of the visibility intervals (earliest dates to initiate the
activities of the process), and a backward reasoning
to produce the maximum bounds of the visibility in-
tervals (latest dates to initiate the activities of the pro-
cess). The produced visibility intervals will be given
through symbolic date expressions instead of numeri-
cal ones. The main advantage of using symbolic dates
is that once the expressions have been calculated for a
specific Workflow process, these can be used for any
case that will be handled by the same Workflow pro-
cess.
In this paper, D
i
will denote a date and d
i
a du-
ration associated with a transition (t
i
) firing. A pair
(D
p
, D
c
) will be associated with each token of the
proof tree and represents respectively the production
and consumption date of a token. As transition firings
A Symbolic Time Constraint Propagation Mechanism Proposal for Workflow Nets
539

are instantaneous ones in t-time nets (there is no to-
ken reservation), the following definition can be pro-
duced:
Definition 1. The production date D
p
of a token is
equal to the firing date of the transition which has
produced it and the consumption date D
c
is equal to
the firing date of the transition which has consumed
it.
For each triggered activity on the t-Time Work-
flow net analyzed, the dates of production D
p
and
consumption D
c
of the atoms that represents the pre-
conditions of the activity should be extracted. The
date of production of the atom D
p
, corresponds to the
start execution of the activity associated with the tran-
sition and the date of consumption, D
c
, corresponds to
its conclusion. Thus, an interval of dates [D
p
, D
c
] will
be generated, and the resource that will handle the re-
ferred activity will be able to be requested within the
calculated interval.
Since production and consumption dates depend
on d
i
(duration associated to a transition firing)
and take there values within time intervals ∆
i
=
[δ
imin
, δ
imax
], many tasks execution intervals can be
considered according to a strategic planning. For in-
stance, the execution interval I
Exec
= [D
Pmin
, D
Cmax
]
considers that the allocation of resources to handle the
task can occur between the earliest beginning and the
latest conclusion of this activity. To illustrate the pro-
posal of this work, the Workflow net shown in Fig. 1
is considered.
4.1 Forward Propagation
The forward propagation consider the Workflow net
in its normal flow, which is a case represented by a
token that begins in place Start and finishes in place
End, while following the ordered places and transi-
tions.
The date computation in the canonical proof for
the Workflow net is then the following one:
• Assign a production date D
i
to the initial token in
place Start (initial marking of the t-Time Petri net
model).
• For each ( L, compute the firing date of the cor-
responding transition: it is equal to the maximum
of the production dates of the consumed atoms,
increased by the enabling duration d
j
associated
with the considered transition.
• Update all the temporal stamps of the atoms
which have been consumed and produced.
As in t-Time Petri net model (Merlin, 1974), an
enabling duration d
i
takes its values from within a
time interval ∆
i
= [δ
imin
, δ
imax
]. The computed sym-
bolic dates depend on d
i
and its domains will depend
on time interval.
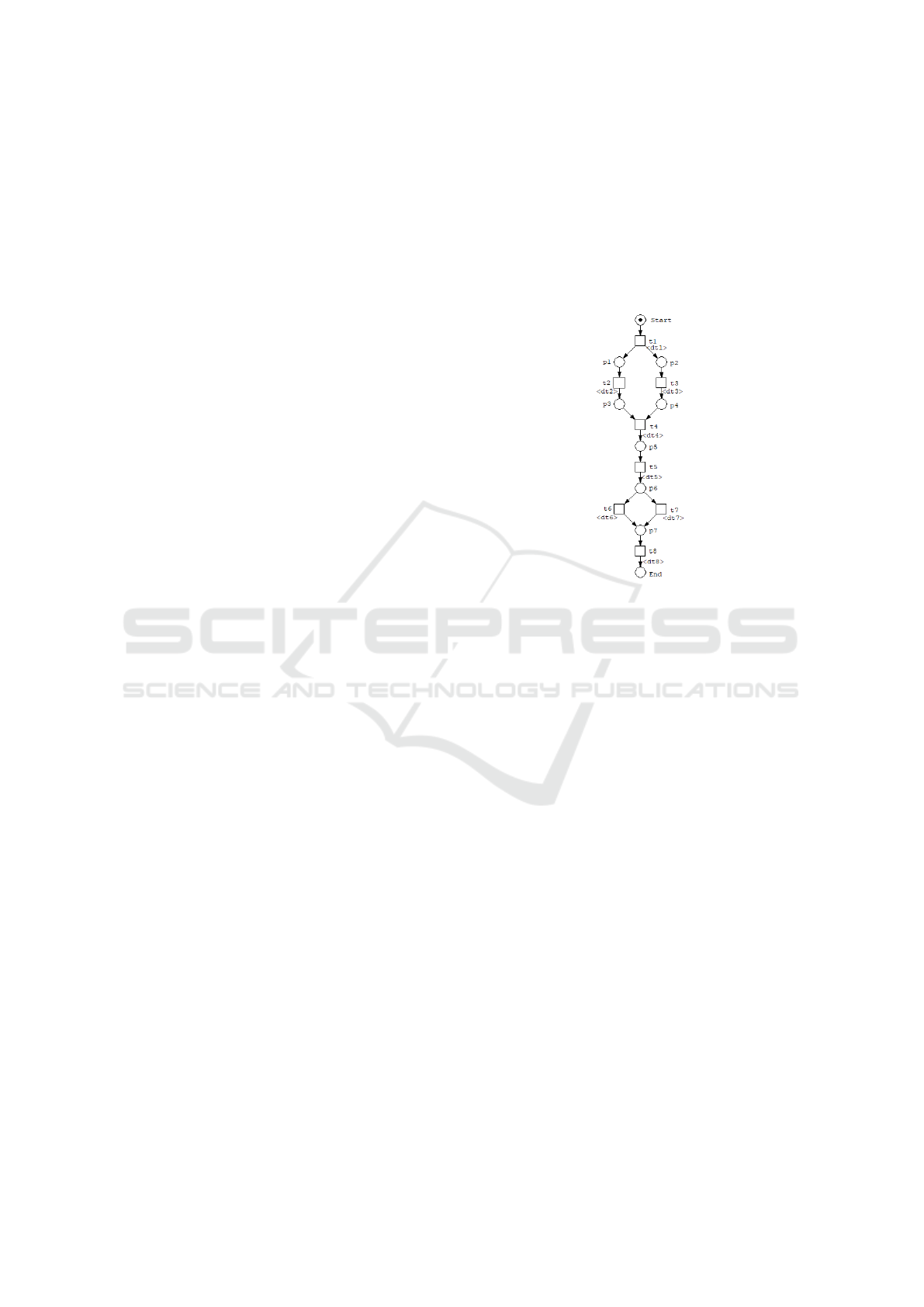
Considering Fig. 2, two linear sequents must be
proved, where each one represents a different sce-
nario. Such linear sequents can be obtained automati-
cally applying a t-invariant algorithm (linear equation
solving) as proposed in (Oliveira and Julia, 2020).
Figure 2: t-Time Workflow net - Forward Propagation.
For scenario S
c1
, the following sequent has to be
proved:
Start, t1, t2, t3, t4, t5, t6, t8 ` End (1)
For scenario S
c2
, the following sequent has to be
proved:
Start, t1, t2, t3, t4, t5, t7, t8 ` End (2)
The transitions of the Workflow net are repre-
sented by the following formulas of Linear Logic:
t
1
= Start ( p1 ⊗ p2; t
2
= p1 ( p3; t
3
= p2 ( p4;
t
4
= p3 ⊗ p4 ( p5; t
5
= p5 ( p6; t
6
= p6 ( p7;
t
7
= p6 ( p7; t
8
= p7 ( End.
Considering Seq = D
S
+d
t1
+max{d
t2
, d
t3
}+d
t4
,
the proof tree with dates corresponding to scenario
S
c1
is represented in Equation 3. The proof tree with
dates for scenario S
c2
, represented by the Equation 4,
is similar to the one for S
c1
, the only difference is that
in the first lines of the proof, instead of d
t6
(duration of
the transition firing t6), it is d
t7
(duration of the transi-
tion firing t7) which is considered. The entire proofs
can be found in (Soares Passos and Julia, 2016).
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
540

p7(Seq+d
t5
+d
t6
,Seq+d
t5
+d
t6
+d
t8
)`p7 End(Seq+d
t5
+d
t6
+d
t8
,.)`End
(
L
p6(Seq+d
t5
,Seq+d
t5
+d
t6
)`p6 p7(Seq+d
t5
+d
t6
,.), p7(End`End
(
L
. . .
Start(D
S
,.),Start( p1⊗p2,t2,t3,t4,t5,t6,t8`End
(3)
p7(Seq+d
t5
+d
t6
,Seq+d
t5
+d
t7
+d
t8
)`p7 End(Seq+d
t5
+d
t7
+d
t8
,.)`End
(
L
p6(Seq+d
t5
,Seq+d
t5
+d
t7
)`p6 p7(Seq+d
t5
+d
t7
,.), p7(End`End
(
L
. . .
Start(D
S
,.),Start( p1⊗p2,t2,t3,t4,t5,t7,t8`End
(4)
The symbolic dates obtained from the proof tree
of forward propagation mechanism are shown in the
Table 1.
4.2 Backward Propagation
From the proof tree obtained by the forward propaga-
tion model, considering the start date D
S
, it is possi-
ble to determine part of the visibility intervals to trig-
ger the tasks (represented by a token in P
i
). As in
(Soares Passos and Julia, 2016), the forward propaga-
tion technique allows us to find the minimum bounds
of the visibility intervals.
Backward propagation is used to calculate the
maximum bounds of the same visibility interval. To
accomplish this goal, the approach is based on an in-
verted model as those presented in (Khalfhoui et al.,
2002) and (Oliveira and Julia, 2020). In (Khalfhoui
et al., 2002), a backward reasoning was applied on a
Petri net model with all the arcs reversed in order to
identify feared scenarios in mechatronic systems. Pa-
per (Oliveira and Julia, 2020) also proposed a back-
ward reasoning applied on a Workflow net with all
arcs inverted in order to diagnose the causes of dead-
lock situations in Service-Oriented Architectures.
For the backward propagation technique proposed
in this article, the arcs of the Workflow net are then
inverted in such a way that the initial marking starts in
place End and reaches the Start place at the end of the
execution of the inverted Workflow net, as illustrated
in Fig. 3.
The proof of a sequent on the inverted Workflow
net is obtained using the same proof algorithm as in
(Soares Passos and Julia, 2016) for the applied rules
of linear logic, but with different computation of tem-
poral stamps. We denote D
i
for dates and d
i
for dura-
tions.
When the consumption date is not fully computed,
some pairs are denoted (D
p
, .) will appear in the proof
tree. Identity sequents generated on the left side of the
tree will produce pair stamps (D
p
, D
c
) completely de-
Figure 3: t-Time Workflow net - Backward Propagation.
fined. These final leaves stamps will correspond to the
main temporal results (maximum bound of visibility
intervals) of the backward propagation mechanism.
The date computation in the canonical proof tree
for the inverted Workflow net is then the following
one:
• Assign a production date D
i
to the initial token in
place End (initial marking of the inverted net).
• For each ( L, compute the firing date of the cor-
responding transition: it is equal to the minimum
of the production dates of the consumed atoms,
decreased by the enabling duration d
j
associated
with the considered transition.
• Update all the temporal stamps of the atoms
which have been consumed and produced.
The rest of the process to prove the sequent is the
same as the one presented in the forward propagation
mechanism.
Considering the Workflow net in Fig. 3, the proof
of correctness on this inverted model corresponds to
two different scenarios given by the following se-
quents:
A Symbolic Time Constraint Propagation Mechanism Proposal for Workflow Nets
541

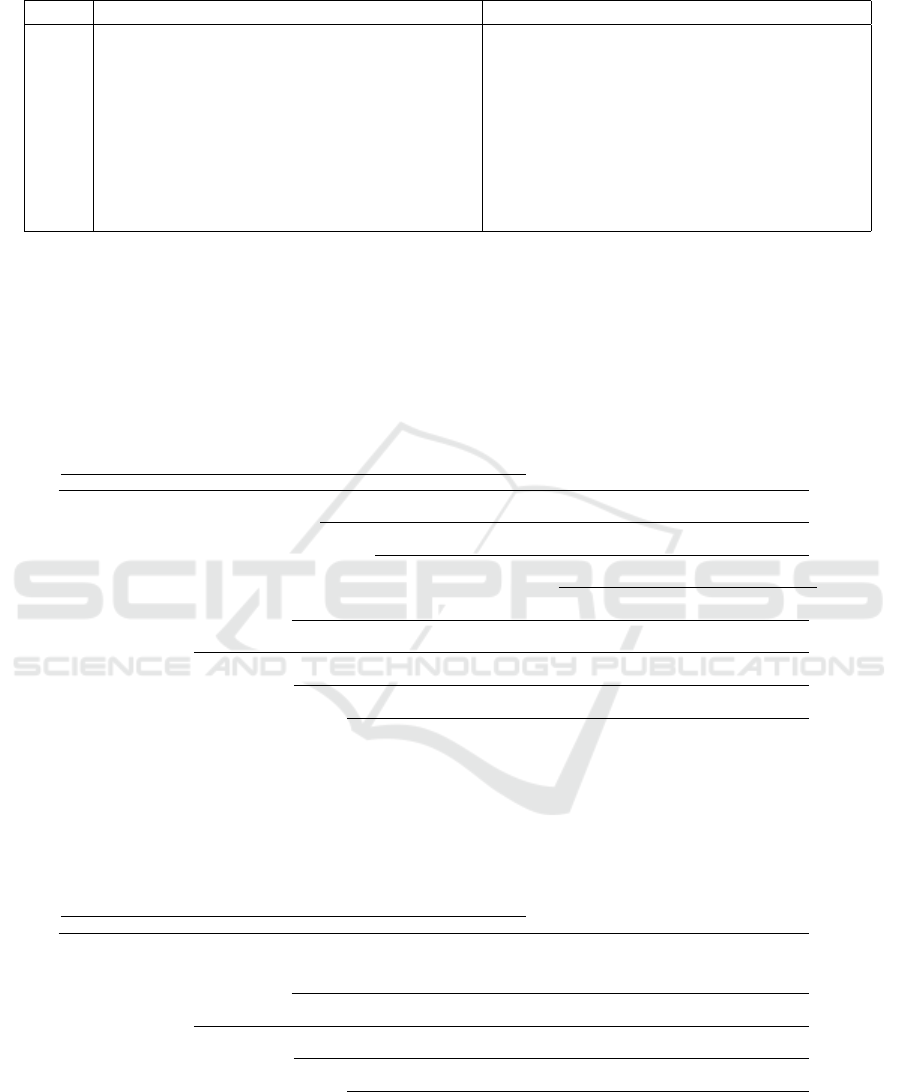
Table 1: Symbolic date intervals for forward propagation in scenario S
c1
.
Tasks Production Date Consumption Date
Start D
s
D
s
+ d
t1
p1 D
s
+ d
t1
D
s
+ d
t1
+ d
t2
p2 D
s
+ d
t1
D
s
+ d
t1
+ d
t3
p3 D
s
+ d
t1
+ d
t2
D
s
+ d
t1
+ max(d
t2
, d
t3
) + d
t4
p4 D
s
+ d
t1
+ d
t3
D
s
+ d
t1
+ max(d
t2
, d
t3
) + d
t4
p5 D
s
+ d
t1
+ max(d
t2
, d
t3
) + d
t4
D
s
+ d
t1
+ max(d
t2
, d
t3
) + d
t4
+ d
t5
p6 D
s
+ d
t1
+ max(d
t2
, d
t3
) + d
t4
+ d
t5
D
s
+ d
t1
+ max(d
t2
, d
t3
) + d
t4
+ d
t5
+ d
t6
p7 D
s
+ d
t1
+ max(d
t2
, d
t3
) + d
t4
+ d
t5
+ d
t6
D
s
+ d
t1
+ max(d
t2
, d
t3
) + d
t4
+ d
t5
+ d
t6
+ d
t8
End D
s
+ d
t1
+ max(d
t2
, d
t3
) + d
t4
+ d
t5
+ d
t6
+ d
t8
D
End
For scenario S
c1
:
End, t8, t6, t5, t4, t3, t2, t1 ` Start (5)
and for scenario S
c2
:
End, t8, t7, t5, t4, t3, t2, t1 ` Start (6)
The transitions of the Workflow net are repre-
sented by the following formulas of Linear Logic:
t
8
= End ( p7; t
7
= p7 ( p6; t
6
= p7 ( p6;
t
5
= p6 ( p5; t
4
= p5 ( p3 ⊗ p4; t
3
= p4 ( p2;
t
2
= p3 ( p1; t
1
= p1 ⊗ p2 ( Start.
Considering Seq
1
= D
End
− d
t8
− d
t6
− d
t5
− d
t4
the proof tree with dates for S
c1
is the following:
p1(Seq
1
−d
t2
,Seq
1
−min{d
t2
,d
t3
}−d
t1
)`p1 p2(Seq
1
−d
t3
,Seq
1
−min{d
t2
,d
t3
}−d
t1
)`p2
p1(Seq
1
−d
t2
,Seq
1
−min{d
t2
,d
t3
}−d
t1
), p2(Seq
1
−d
t3
,Seq
1
−min{d
t2
,d
t3
}−d
t1
)`p1⊗p2
⊗
R
Start(Seq
1
−min{d
t2
,d
t3
}−d
t1
,.)`Start
(
L
p3(Seq
1
,Seq
1
−d
t2
)`p3 p1(Seq
1
−d
t2
,.), p2(Seq
1
−d
t3
,.), p1⊗p2(Start`Start
(
L
p4(Seq
1
,Seq
1
−d
t3
)`p4 p3(Seq
1
,.), p2(Seq
1
−d
t3
,.), p3( p1,t1`Start
(
L
p4(Seq
1
,.), p3(Seq
1
,.), p4( p2,t2,t1`Start
⊗
L
p5(D
End
−d
t8
−d
t6
−d
t5
,D
End
−d
t8
−d
t6
−d
t5
−d
t4
)`p5 p3⊗p4, p4( p2,t2,t1`Start
(
L
p6(D
End
−d
t8
−d
t6
,D
End
−d
t8
−d
t6
−d
t5
)`p6 p5(D
End
−d
t8
−d
t6
−d
t5
,.), p5( p3⊗p4,t3,t2,t1`Start
(
L
p7(D
End
−d
t8
,D
End
−d
t8
−d
t6
)`p7 p6(D
End
−d
t8
−d
t6
,.), p6( p5,t4,t3,t2,t1`Start
(
L
End(D
End
,D
End
−d
t8
)`End p7(D
End
−d
t8
,.), p7( p6,t5,t4,t3,t2,t1`Start
(
L
End(D
End
,.),End( p7,t6,t5,t4,t3,t2,t1`Start
(7)
Considering Seq
2
= D
End
− d
t8
− d
t7
− d
t5
− d
t4
,
the proof tree with dates for scenario S
c2
is similar to
the proof tree of S
c1
, the only difference is that instead
of d
t6
(duration of the transition firing t6), the duration
considered is d
t7
(duration of the transition firing t7).
p1(Seq
2
−d
t2
,Seq
2
−min{d
t2
,d
t3
}−d
t1
)`p1 p2(Seq
2
−d
t3
,Seq
2
−min{d
t2
,d
t3
}−d
t1
)`p2
p1(Seq
2
−d
t2
,Seq
2
−min{d
t2
,d
t3
}−d
t1
), p2(Seq
2
−d
t3
,Seq
2
−min{d
t2
,d
t3
}−d
t1
)`p1⊗p2
⊗
R
Start(Seq
2
−min{d
t2
,d
t3
}−d
t1
,.)`Start
(
L
. . .
p5(D
End
−d
t8
−d
t7
−d
t5
,D
End
−d
t8
−d
t7
−d
t5
−d
t4
)`p5 p3⊗p4, p4( p2,t2,t1`Start
(
L
p6(D
End
−d
t8
−d
t7
,D
End
−d
t8
−d
t7
−d
t5
)`p6 p5(D
End
−d
t8
−d
t7
−d
t5
,.), p5( p3⊗p4,t3,t2,t1`Start
(
L
p7(D
End
−d
t8
,D
End
−d
t8
−d
t7
)`p7 p6(D
End
−d
t8
−d
t7
,.), p6( p5,t4,t3,t2,t1`Start
(
L
End(D
End
,D
End
−d
t8
)`End p7(D
End
−d
t8
,.), p7( p6,t5,t4,t3,t2,t1`Start
(
L
End(D
End
,.),End( p7,t7,t5,t4,t3,t2,t1`Start
(8)
The symbolic dates obtained from the proof tree
of backward propagation mechanism are shown in the
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
542

Table 2: Symbolic date intervals for backward propagation in scenario S
c1
.
Tasks Production Date Consumption Date
End D
End
D
End
− d
t8
p7 D
End
− d
t8
D
End
− d
t8
− d
t6
p6 D
End
− d
t8
− d
t6
D
End
− d
t8
− d
t6
− d
t5
p5 D
End
− d
t8
− d
t6
− d
t5
D
End
− d
t8
− d
t6
− d
t5
− d
t4
p4 D
End
− d
t8
− d
t6
− d
t5
− d
t4
D
End
− d
t8
− d
t6
− d
t5
− d
t4
− d
t3
p3 D
End
− d
t8
− d
t6
− d
t5
− d
t4
D
End
− d
t8
− d
t6
− d
t5
− d
t4
− d
t2
p2 D
End
− d
t8
− d
t6
− d
t5
− d
t4
− d
t3
D
End
− d
t8
− d
t6
− d
t5
− d
t4
− min(d
t2
, d
t3
) − d
t1
p1 D
End
− d
t8
− d
t6
− d
t5
− d
t4
− d
t2
D
End
− d
t8
− d
t6
− d
t5
− d
t4
− min(d
t2
, d
t3
) − d
t1
Start D
End
− d
t8
− d
t6
− d
t5
− d
t4
− min(d
t2
, d
t3
) − d
t1
D
s
Table 2.
Finally, symbolic visibility intervals can be pro-
duced for the tokens in each places of the Workflow
net of Fig. 2. The minimum bounds correspond to
the production dates D
p
of Table 1, and the maximum
bounds correspond to the production dates of Table 2.
5 NUMERICAL RESULTS FOR
RESOURCE PLANNING
Considering the fact that the process in Fig. 1 starts at
date 0 (i.e. D
s
= 0), the maximum time for it to com-
plete is 105, and the operation duration are the ones
presented in Table 3. Visibility intervals for task ex-
ecution can be calculated by replacing the symbolic
visibility production dates presented on Tables 1 and
2 with the numerical values of Table 3. The mini-
mum duration of operation (minimum bound of op-
eration duration intervals in Table 3) are used to re-
place the symbolic production date values produced
by the forward mechanism (Table 1), and the maxi-
mum duration of operation (maximum bounds of op-
eration duration intervals in Table 3) are used to re-
place the symbolic production date values produced
by the backward mechanism (Table 2).
Table 3: Transition duration interval.
Transition Imprecise Duration
t1 [5,10]
t2 [20,30]
t3 [25,35]
t4 [0,0]
t5 [15,25]
t6 [5,15]
t7 [20,30]
t8 [0,0]
We can then calculate the visibility intervals by
considering the production date values given in Ta-
ble 1 for the forward propagation, as the minimum
bounds of the visibility interval, because it simulates
the normal task propagation flow of the process, and
the production date values given in Table 2 for the
backward propagation as the maximum bounds of the
visibility interval, because it simulates the task prop-
agation inverse flow. The result is presented in Table
4.
As it can be seen in Table 4, considering the latest
date of completion of the process at date 0 (start date
of the process) +105 (maximum duration of the pro-
cess) = 105, and the symbolic formulas produced by
the backtrack mechanism, it is possible to reach the
place Start considering the inverted process at date
+20 for scenario 1, and at date +5 for scenario 2,
which means that if the initial marking in place Start
at the beginning of the process is trigger with a de-
lay of five time units, even so the task can be finished
on time, no matter the scenario in order to end the
process at the latest date 105 (maximum duration for
process completion).
In order to validate this new approach, it can be
observed that the visibility intervals produced in Ta-
ble 4 are the same as the ones presented in (dos San-
tos Soares et al., 2008) where the visibility intervals
were produced for the same t-time Workflow net us-
ing a pure numerical approach based on the graph of
the corresponding Petri net model.
Table 4: Numerical visibility intervals for task execution.
Tasks S
c1
S
c2
Min Max Min Max
Start 0 20 0 5
p1 5 35 5 20
p2 5 30 5 15
p3 25 65 25 50
p4 30 65 30 50
p5 30 65 30 50
p6 45 90 45 75
p7 50 105 65 105
End 50 105 65 105
A Symbolic Time Constraint Propagation Mechanism Proposal for Workflow Nets
543

6 CONCLUSIONS
In this study, a Workflow net model incremented with
symbolic date intervals for describing activity dura-
tions and waiting times was presented. In order to
produce the minimum and maximum intervals for
the execution of activities, two constraint propagation
mechanisms based on the sequent calculus of Linear
Logic were proposed. The first is a forward mecha-
nism that uses (max,+) operators to produce formu-
las that indicate the earliest dates for the beginning
of the activities of the cases treated by the Workflow
process. The second is a backward mechanism that
uses (min,−) operators to produce formulas that in-
dicate the latest dates for the beginning the activities
of those cases dealt with by the Workflow net pro-
cess. The particular case of the backward mechanism
is to prove the Soundness property of the Workflow
net considering an inverted model with all arcs re-
versed. Due to the sequent calculus being based on
such a model, this corresponds to a kind of go back
in time each time a transition is fired, thus the time is
decreased on the corresponding formula.
The computation of symbolic dates for the execu-
tion of each activity mapped into a time Workflow net,
using the proof trees of Linear Logic, allows the plan-
ning of the utilization of the resources. These are the
resources involved in the activities of the Workflow
process for any case handled by the corresponding
Workflow process, since the computed dates are sym-
bolic instead of numerical. This kind of reuse is not
provided when an approach based on a graph-oriented
method (as the conventional ones) is considered.
As a future study, the authors intend to combine
the time constraint propagation mechanisms with a
formal definition of a resource allocation mechanism,
as that presented in (Medeiros and Julia, 2017), and
propose a conflict resolution mechanism with the aim
of calculating a sequence of activities that respects
the disjunctive constraints (resource allocation mech-
anisms) as well as the time constraints (date inter-
vals).
ACKNOWLEDGEMENTS
The authors would like to thank FAPEMIG, CNPq
and CAPES for the financial support provided.
REFERENCES
dos Santos Soares, M., Julia, S., and Vrancken, J. (2008).
Real-time scheduling of batch systems using petri nets
and linear logic. Journal of Systems and Software,
81(11):1983–1996.
Girard, J.-Y. (1987). Linear logic. Theoretical computer
science, 50(1):1–101.
Girault, F., Pradier-Chezalviel, B., and Valette, R. (1997).
A logic for petri nets. Journal europ
´
een des syst
`
emes
automatis
´
es, 31(3):525–542.
Khalfhoui, S., Demmou, H., Guilhem, E., and Valette, R.
(2002). An algorithm for deriving critical scenarios
in mechatronic systems. In IEEE International Con-
ference on Systems, Man and Cybernetics, volume 3,
pages 6–pp. IEEE.
Medeiros, F. F. and Julia, S. (2017). Constraint analysis
based on energetic reasoning applied to the problem
of real time scheduling of workflow management sys-
tems. In ICEIS (3), pages 373–380.
Menasche, M. (1982). Analyse des r
´
eseaux de Petri tempo-
ris
´
es et application aux syst
`
emes distribu
´
es.
Merlin, P. M. (1974). A study of the recoverability of com-
puting systems. University of California, Irvine.
Murata, T. (1989). Petri nets: Properties, analysis and ap-
plications. Proceedings of the IEEE, 77(4):541–580.
Oliveira, K. S. and Julia, S. (2020). Detection and removal
of negative requirements of deadlock-type in service-
oriented architectures. In 2020 International Confer-
ence on Computational Science and Computational
Intelligence.
Pradin-Ch
´
ezalviel, B., Valette, R., and Kunzle, L. A.
(1999). Scenario durations characterization of t-timed
petri nets using linear logic. In Proceedings 8th In-
ternational Workshop on Petri Nets and Performance
Models (Cat. No. PR00331), pages 208–217. IEEE.
Ramamoorthy, C. and Ho, G. S. (1980). Performance evalu-
ation of asynchronous concurrent systems using petri
nets. IEEE Transactions on software Engineering,
(5):440–449.
Riviere, N., Pradin-Chezalviel, B., and Valette, R. (2001).
Reachability and temporal conflicts in t-time petri
nets. In Proceedings 9th International Workshop on
Petri Nets and Performance Models, pages 229–238.
IEEE.
Sifakis, J. (1979). Use of petri nets for performance evalu-
ation. Acta Cybernetica, 4(2):185–202.
Soares Passos, L. M. and Julia, S. (2016). Linear logic
as a tool for qualitative and quantitative analysis of
workow processes. International Journal on Artificial
Intelligence Tools, 25(03):1650008.
Van Der Aalst, W., Van Hee, K. M., and van Hee, K. (2004).
Workflow management: models, methods, and sys-
tems. MIT press.
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
544