Reversible Fragile Medical Image Watermarking Scheme Resistant to

Malicious Tampering Attacks

Victor Fedoseev

1,2 a

and Anna Denisova

1,2 b

Samara National Research University, Samara, Russia

Image Processing Systems Institute, Branch of the Federal Scientific Research Centre “Crystallography and Photonics”

of Russian Academy of Sciences, Samara, Russia

Keywords: Fragile Digital Watermark, Medical Images, Quantization Index Modulation, Reversible Watermarking.

Abstract: Paper is aimed to eliminate a significant drawback of existing schemes for protecting medical images from

tampering using fragile watermarking: instability to “malicious tampering attacks”. In such attacks, an

intruder, while tampering image content, keeps unchanged an inconspicuous additional component that

contains a fragile watermark. In watermarking schemes based on least significant bit (LSB) embedding or

quantization index modulation (QIM), such a component is the remainder of dividing pixel values by some

number corresponding to embedding parameters. In this paper, we present a QIM-based fragile watermarking

method resistant to malicious tampering due to variation in quantization steps. This fact is justified

theoretically and confirmed experimentally. For use in real systems for processing and analyzing medical

images, a reverse watermarking scheme based on this method is proposed. The reversibility property is

achieved by the division of an image into a region of interest (ROI) and a region of noninterest (RONI) and

dual watermarking.

1 INTRODUCTION

Digital medical images (CT, X-ray, MRI and other)

stored as DICOM along with patient data are usually

transmitted via unsafe networks and can be

vulnerable to falsification and tampering (Memon,

2020). This could lead to misdiagnosis and have

serious consequences. Hence, medical image

protection from tampering is a crucial problem

requiring modern solutions. Since the mid-2000s a

significant number of watermarking methods have

been developed for tampering detection and

localization in medical images (Giakoumaki, 2006),

Coatrieux, 2006), (Memon, 2008).

It is important to note that an essential feature of

the use of watermarking methods for medical data is

the inadmissibility of introducing distortions into

image fragments significant for diagnostics. This

limitation explains the fact that most of the existing

watermarking schemes use image segmentation into

the region of interest (ROI) – a part used for medical

diagnostics – and the remaining region of noninterest

https://orcid.org/0000-0003-1750-1920

https://orcid.org/0000-0002-2297-758X

(RONI). We can specify the following classes of

watermarking schemes for ROI protection against

tampering:

1) Fragile reversible watermarking in ROI or

whole image (Al-Qershi, 2011), (Liu, 2019).

2) Fragile watermarking in ROI along with robust

watermarking in RONI. The robust watermark may

contain data to recover the introduced ROI error

(Mousavi, 2014), (Khor, 2017), (Memon, 2020).

3) Robust watermarking in RONI, where the

watermark should contain some ROI data (its hash

and/or hash of its parts) to detect tampering (Swaraja,

2018), (Alshanbari, 2021), (Balasamy, 2021).

All three classes have their pros and cons, as well

as efficient implementations described in the

literature. However, unfortunately, a significant

vulnerability, which is a characteristic of classes 1-2

(which involve ROI watermarking), remains outside

the scope of known research.

Our paper discusses this vulnerability in detail and

proposes its own watermarking algorithm, and a

specific scheme related to class 2, which is free from

Fedoseev, V. and Denisova, A.

Reversible Fragile Medical Image Watermarking Scheme Resistant to Malicious Tampering Attacks.

DOI: 10.5220/0011067200003209

In Proceedings of the 2nd International Conference on Image Processing and Vision Engineering (IMPROVE 2022), pages 57-65

ISBN: 978-989-758-563-0; ISSN: 2795-4943

this vulnerability. The rest of the paper includes three

sections. Section 2 introduces us to the current state

of research on this topic. Then Section 3 describes the

proposed scheme. Finally, Section 4 provides some

experimental results and gives a brief discussion.

2 RELATED WORK

First of all, let us take a closer look at a typical class

2 scheme. It involves dividing the image into ROI and

RONI and further embedding digital watermarks of

different content and purpose into each of them. In

ROI, a fragile watermark for tampering localization

is embedded. As a rule, this watermark does not carry

any meaningful information and can be generated

using a pseudo-random generator based on a secret

key. Being fragile, this watermark is designed to

break when the image changes and the positions of

incorrectly extracted watermark bits allow us to

estimate the local area of changes. Thus, the recipient

of the image extracts the fragile watermark and

compares it with the reference watermark data

generated using the secret key known to him. The

extraction procedure is usually computationally

efficient since fragile watermarking uses simple

algorithms in the spatial domain (or less often, a

simple spatial data transformation is performed

before embedding). If the extracted watermark is

completely correct, then the image is considered

suitable for further diagnostics. Otherwise, a

distortion map is built to identify the nature of the

distortion and investigate its causes.

Fragile watermarking usually does not cause

significant distortion, but for medical images, it is

advisable to exclude even the slightest possibility of

misdiagnosis. Therefore, the error introduced into the

ROI as a result of fragile watermarking is embedded

in the RONI area as a separate watermark. This

watermark is embedded using a robust method to

protect this information from distortion, which can

also be caused by random factors, such as noise in the

data transmission channel. Thus, if the received

image was found suitable for diagnosis as a result of

checking the correctness of the extracted fragile

watermark, the extraction of the ROI error from the

robust watermark is performed. Then the ROI area is

corrected, and the image is transferred to medical

specialists. It is also worth noting that, in addition to

the ROI error, the robust watermark may include

patient data, other metadata, and data for image

recovery after malicious distortion. Watermark

robustness is provided by using DWT (Al-Qershi,

2011), DWT-SVD (Priyanka, 2017), (Alshanbari,

2021), block-DCT (Parah, 2017) or any other

transform domain. In addition, error-correcting codes

may also be used.

An important practical issue in the

implementation of the described scheme is how to

segment the image into ROI and RONI. In some

studies focusing on a particular type of medical data

(e.g., ultrasound data), the ROI and RONI areas are

considered deterministic and do not change for

different images (Khor, 2017), (Alshanbari, 2021). A

number of papers propose automatic ROI extraction

algorithms based on image analysis or machine

learning technologies, such as edge detection, active

contours and others. Examples of such algorithms can

be found in (Memon, 2008), (Memon, 2020),

(Balasamy, 2021). Other papers (Al-Qershi, 2011),

(Eswaraiah, 2015), (Priyanka, 2017), (Golea, 2019)

indicate that ROI/RONI segmentation should be

carried out by a physician before the embedding

procedure. Finally, some authors do not address this

issue at all (Liu, 2019). In our study, we also do not

consider it necessary to choose any specific

segmentation method, believing that a specific

solution should be chosen in practice from the options

described above based on the specifics of the

particular medical images.

In this paper, we want to draw attention to an

important vulnerability of the currently existing

algorithms of the considered class. It is related to the

fact that for fragile watermarking, researchers use

solutions based on least significant bit (LSB)

watermarking or quantization index modulation

(QIM). For example, papers (Memon, 2008),

(Memon, 2009), (Memon, 2020) present dual

watermarking schemes where fragile watermarking is

based on LSB embedding into ROI (region of

interest). (Eswaraiah, 2014) proposes an LSB-based

fragile watermarking technique. In (Priyanka, 2017)

two LSBs of ROI are replaced at the protection stage

by some bits. (Liu, 2019) uses a QIM-based

reversible watermarking. More examples of LSB and

QIM based watermarking for tamper localization can

be found in (PhadiKar, 2012), (Shehab, 2018), (Su,

2020) and other papers.

The vulnerability mentioned above is that LSB

and QIM may be a subject of “malicious tampering

attacks”. In such attacks, an intruder, while tampering

image content, keeps unchanged an inconspicuous

additional component that contains a fragile

watermark. In watermarking schemes based on LSB

and QIM watermarking, such a component is a matrix

of remainders of dividing pixel values by some

number depending on the quantization step value

IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering

used at watermark embedding. If data is embedded in

the first LSB, this value equals 2.

Unfortunately, in the literature on fragile

watermarking for medical image protection, this

vulnerability is not considered at all, despite its

obviousness and vivid consequences. This was the

reason for conducting the present study. In our paper,

we propose a new QIM based fragile watermarking

method resistant to the malicious tampering attack,

and specify a medical image protection scheme based

on dual watermarking in ROI and RONI.

3 PROPOSED WATERMARKING

SCHEME

In this section, we define a new fragile watermarking

algorithm based on scalar QIM watermarking and a

complete medical protection scheme that uses this

algorithm. In addition to fragile watermarking, this

scheme contains RONI watermarking as any other

class 2 implementation (see Introduction).

The main feature of our fragile watermarking

approach is that it uses a range of quantization steps

when embedding watermark bits into ROI pixels. The

value of the quantization step for each particular pixel

is generated using a pseudorandom number generator

using a secret key unknown to an intruder. The

number of possible quantization step values is limited

due to the requirement of watermark imperceptibility.

Nevertheless, it is very hard for the intruder to save

the residue of pixel brightness on several quantization

steps and at the same time meaningfully modify an

image region.

3.1 Main Features

Let 𝑆



be the ROI area and 𝑆



be the RONI area.

The sum of 𝑆



and 𝑆



is equal to 𝑁



𝑁



, where

𝑁



is a height and 𝑁



is a width of the image. We

denote a number of bits per pixel (pixel depth) as 𝐷.

For DICOM images, pixel depth can take values from

a set 𝐷∈



8,10,12,14,16



, depending on image type.

For example, 𝐷16 is usual for computer

tomography and 𝐷12 is used for digital

radiography (Mildenberger, 2002).

The fractions of pixels belonging to ROI and

RONI are

𝑘





𝑆



𝑁



𝑁



,𝑘





𝑆



𝑁



𝑁



𝑘



𝑘



1.

(1)

Thus, ROI capacity can be calculated as 𝐼





𝑆



𝐷. Similarly, RONI capacity 𝐼



𝑆



𝐷.

As mentioned below, we do not specify how to

separate ROI and RONI. However, we supply that

both ROI and RONI are defined on an 𝑟𝑟 block

grid. In practice, it is reasonable to use 𝑟8.

The same grid of pixel blocks is used to localize

tampering. If at least one pixel in an 𝑟𝑟 block is

found as tampered then we decide the whole block is

tampered. To solve the authentication problem, we

embed 𝑐 pseudorandom watermark bits into 𝑐 pixels

of each block. The bigger value of 𝑐 is used the lower

probability of skipping a tampered block is achieved.

The distorted block may not be identified if the

extracted watermark bits occasionally match to the

embedded sequence. This situation is possible with

the probability 1/2



. On the other hand, the bigger 𝑐

corresponds to the bigger distortions in the

watermarked image.

3.2 Embedding and Extraction

Formulae

The embedding and extraction formulae for a pixel



𝑛



,𝑛





are written as follows:

𝐶





𝑛



,𝑛







𝐶



𝑛



,𝑛





2∆





,



⋅2∆





,





𝑊



𝑛



,𝑛





⋅∆





,





𝐶



𝑛



,𝑛





mod ∆





,



;

)

𝑊





𝑛



,𝑛







𝐶





𝑛



,𝑛





∆





,







mod 2



)

where 𝐶



𝑛



,𝑛





is the original image pixel,

𝑊



𝑛



,𝑛





is the bit of watermark, ∆





,



is the

quantization step varying from 1 to ∆



, 𝑎 mod b

calculates the remainder from division of 𝑎 on b,

⌊

𝑎

⌋

is the closest integer value less than 𝑎, 𝐶





𝑛



,𝑛





the watermarked image pixel, 𝑊





𝑛



,𝑛





is the

extracted watermark bit.

Equation (2) describes a supervised scalar

quantization of matrix 𝐶



𝑛



,𝑛





with quantization

step 2∆





,



, which varies depending on the pixel

coordinates



𝑛



,𝑛





according to the secret key. As a

result, the distortion of each particular pixel is equal

to 0 or ∆





,



. Watermark extraction is performed

according formula (3).

Reversible Fragile Medical Image Watermarking Scheme Resistant to Malicious Tampering Attacks

3.3 Resistance to Malicious Tampering

Attacks: Theoretical Analysis

The main goal of tampering attacks on medical

images is to obstruct making a correct diagnosis.

Common methods include image slicing, image

retouching, copy-move etc. In research papers (see,

for example, (Kaur, 2016)), tampering attacks are

usually modeled using common image processing

operations like average or median filtering, noise

addition, JPEG compression and others. However,

they model a blind intruder who does not know the

image protection scheme and does not make any

efforts to preserve a fragile watermark that may be

embedded into the image.

Since most tamper protection schemes for

medical images are based on fragile LSB or QIM

watermarking as shown in Introduction, an intruder

can try to implement a malicious tampering scenario:

both change the image contents and preserve the

watermark. For this purpose, he needs to allocate an

imperceptible signal component containing a

watermark, to make changes into the visible

component and then to re-add the allocated

component containing the watermark. In classical

LSB or QIM schemes, this component is the

remainder of a division each pixel value by 2∆, where

∆ has the same meaning as in (2)-(3) but does not

change for different pixel positions. We will call as

the simple malicious tampering attack this kind of

attack where ∆ is supposed to be guessed by an

intruder and equal to the real value used for image

protection (if it is a constant value).

This attack has common features with a vector

quantization (VQ) attack described in (Holliman,

2000) and later used in many papers on tamper

detection (Su, 2020). In VQ, entire image blocks are

replaced using samples from protected images in

order to save the watermark.

Since in (2)-(3) we see ∆





,



instead of constant

∆, theoretically, this attack should be ineffective for

our method. To adopt the attack, the intruder has to

keep unchanged C











mod 2∆





,



 for all

possible values of ∆





,



from 1 to ∆



. One way to

do that is to find least common multiple of the

numbers from 2 to 2∆



: 𝐿𝐶𝑀2,...,2∆



 and

then use it instead of the constant 2∆. We call this

version of attack as the advanced malicious

tampering attack.

Table 1 shows the 𝐿𝐶𝑀 values for each particular

∆



and corresponding bit lengths to store them.

Based on the values given in Table 1, we can estimate

the value of ∆



, which is sufficient to protect the

image from the advanced attack: corresponding 𝐿𝐶𝑀

should be comparable with 2



. More precisely, we

can recognize the attack as not applicable in practice

if 𝐿𝐶𝑀



…



 2



. This empirical rule leads to the

estimations of safe ∆



values shown in Table 2.

Table 1: Adequate dividers to perform a malicious attack

on the proposed watermarking method.

∆



LCM



2,…,2∆





∆



LCM



2,…,2∆





1 2 7 840

2 4 8 1680

3 12 9 5040

4 24 10 5040

5 120 11 55440

6 120 12 55440

Table 2: Adequate ∆



values for different 𝐷.

𝐷 ∆



Free bits

available for

an intrude

Distortions in

watermarked

ixels

85 1 0,5

10 7 0 0,7

12 8 1

0,8

16 11 0 0,11

3.4 Reversibility of ROI

Table 2 demonstrates that we may use relatively sall

∆



to prevent the described attacks and guarantee

watermark invisibility. Nevertheless, even small

changes in ROI should be removed before medical

diagnostics. To restore the original image, we use the

second part of our scheme: RONI watermarking,

where the difference between original ROI and ROI

of the watermarked image is used as the second

watermark. For each pixel, this difference equals zero

or ∆





,



(and we unambiguously define the sign of

nonzero difference). Thus, to restore the original pixel

value, we need only one bit meaning that the pixel

value is changed. As a result, the volume of the

restoration watermark equals

𝐼



𝑘



𝑁



𝑁



∙







bits.

)

The ratio of RONI capacity to 𝐼



𝐼



𝐼





𝑘



𝑁



𝑁



𝐷

𝑘



𝑁



𝑁



∙

𝑐

𝑟





𝑟



𝑐



𝑘



1𝐷.

)

Let us analyze this product. The first multiplier is

not less than one. Table 3 presents typical values of

the second multiplier. Finally, 𝐷∈



8,10,12,14,16



Thereby it is evident that the capacity of RONI is

enough to store the second watermark for ROI

IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering

restoration. For example, if 𝑟2, 𝑐1, 𝑘





1/4 then the watermark can be stored 12 times in one

LSB plane of RONI.

Table 3: Typical values of the second multiplier in (4).

𝑘



1/𝑘



1

1/10 9

1/5 4

1/4 3

1/3 2

1/2 1

3.5 RONI Watermarking Method

To determine the second watermarking method for

RONI, we need to analyze possible attacks on RONI.

Intuitively, we may suppose that we need a robust

watermarking method. However, what is the aim of

attacking RONI? If an intruder attacked ROI and we

identified and localized tampering by means of ROI

watermarking then ROI restoring becomes

unnecessary. Otherwise, if tampering is not detected,

then the attacker does not need to make changes in

RONI to keep tampering unknown. Thus, RONI

tampering in combination with ROI tampering has no

sense.

In the case of RONI tampering without distorting

ROI, the attacker's goal is to leave the ROI noisy and

simply complicate the doctor’s work without

“pushing” him to misdiagnose with meaningful

changes. But it is obvious that the potential danger of

such an attack is not so significant.

Thus, we come to the conclusion that we do not

need a robust RONI watermarking and can use even

LSB watermarking with a shuffle. In practice, we set

a number of bit planes 𝑃 used for RONI

watermarking equal to 2 for 𝐷8, 3 for 𝐷∈



10,12



and 4 for 𝐷∈



14,16



3.6 Pixel Selection for ROI

Watermarking

Although the changes in ROI caused by watermark

embedding are reversible, this does not entail the

acceptability of significant changes in the ROI. Such

distortions can be seen visually and misinterpreted by

participants in the data transfer process. Moreover,

significant distortions may help an attacker to reveal

the quantization steps for particular pixels. Therefore,

the ROI should not contain obvious artifacts. Further,

we consider the question how to select watermarked

pixel positions to reduce ROI distortions.

The first approach to select 𝑐 pixel positions is

random selection using a secret key. This approach is

very simple. However, it is not the best choice in

terms of visual quality because it does not take into

account original pixel values. If the pixel has low

value and corresponding ∆





,



is high then the pixel

has a high distortion relative to other pixels.

To reduce such distortions, we propose a second

approach. Its key point is to define positions for

embedding as pixels with the smallest ∆





,



among

all pixels in a block 𝑟𝑟. It is possible to achieve

the uniqueness of determining such points in each

block when we generate the whole matrix ∆





,



This approach requires big enough values of 𝑐 and 𝑟

to prevent a possible artificial decrease in ∆



4 EXPERIMENTAL RESEARCH

In this section, we describe the results of three

experiments. The first two ones investigate tampered

area localization quality in two tampering scenarios,

while the third one researches visual quality after ROI

watermark embedding. The RONI watermarking

procedure is quite clear so we did not investigate it

numerically.

As test data, we used four DICOM images from a

dataset presented in (Rutherford, 2021). Table 4

specifies the key characteristics of these images. The

first two letters in the image name stand for image

modality: CR is Computed Radiography, DX is

Digital X-ray and CT is Computed Tomography.

Table 5 shows ROI parameters for these images

(𝑦



,𝑥



are the coordinates of the left-upper corner of

the ROI and ℎ,𝑤 denote height and width of the

ROI).

Table 4: Test image parameters.

Name Image size D Body

Part

PHI-001-1.dc

1760×2140 10 Chest

DX_PHI-002-4.dc

2022×2022 14 Chest

PHI-006-1.dc

1760×1760 12 Uterus

PHI-014-2.dc

1211×888 16 Bladde

Table 5: ROI parameters.

Name

𝑦



,𝑥



,ℎ,𝑤

PHI-001-1.dc

[200,200,1023,1023]

PHI-002-4.dc

[400,400,1023,1023]

CR_PHI-006-1.dc

[300,300,1023,1023]

CT_PHI-014-2.dc

[150,150,1023,511]

Reversible Fragile Medical Image Watermarking Scheme Resistant to Malicious Tampering Attacks

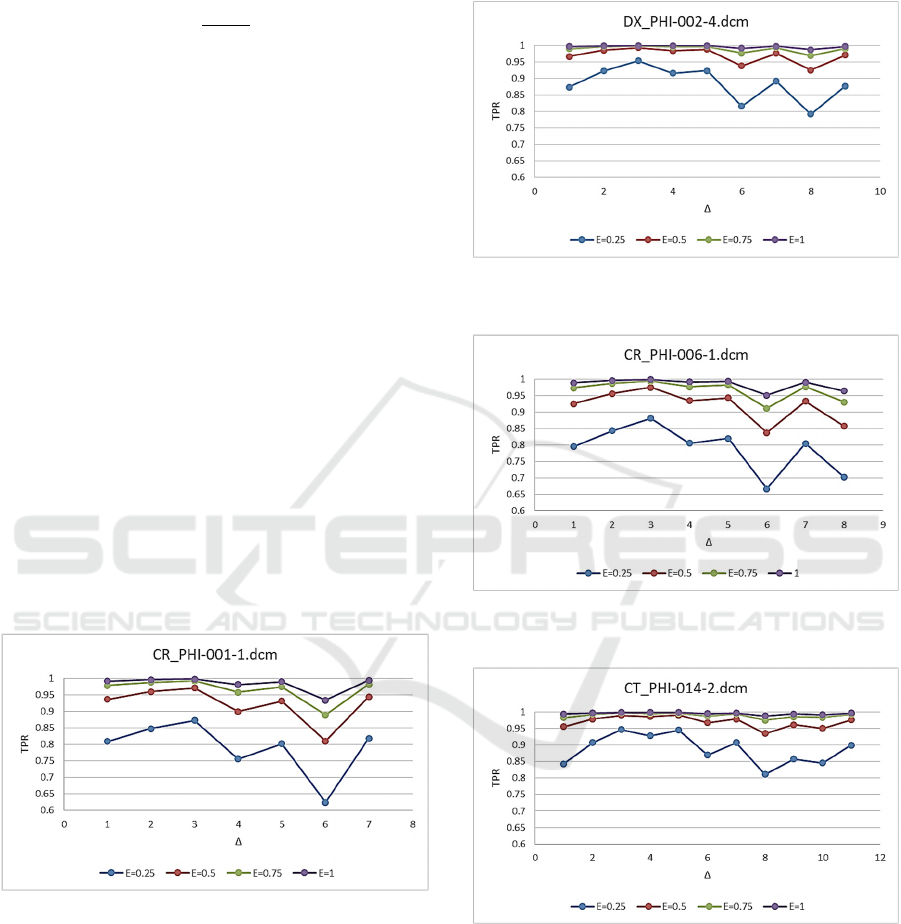
To estimate the quality of tampered area

localization, we use a true positive rate (TPR)

measure defined as follows:

𝑇𝑃𝑅

𝑄



𝑄



(6)

where 𝑄



is the number of blocks correctly

determined as tampered, 𝑄



is the total number of

changed blocks. To estimate the visual quality of

images after embedding, we compute mean square

error (MSE).

4.1 Localization of the Simple

Tampering

In our first experiment, we model the attack described

in Section 2.3. We suppose that an intruder modifies

a specific number of pixels in each block. The

modification consists in replacing 𝐶





𝑛



,𝑛





with 𝑥

which has the same remainder from the division on

2∆:

𝑥



mod 2∆



𝐶





𝑛



,𝑛





mod 2∆



)

In this experiment, ∆ is fixed for the whole image

and acts as a parameter varying from 1 to ∆



. Thus,

we consider a scenario in which the intruder tries to

save the remainder of a division by 2∆ and does not

know the valid quantization step values used at the

embedding procedure and the positions of protected

pixels.

Figure 1: Tamper localization quality for CR_PHI-001-

1.dcm, 𝑀𝑅0.5.

We tested our method for 𝑀𝑅 



0.5,0.75



(number of modified pixels divided by the total

number of pixels), 𝑟



4,8



and 𝐸



0.25,0.5,0.75,1



, where 𝐸𝑐𝑟



⁄

. The average

results for different images and different 𝑀𝑅 values

are shown in Figures 1-4. These figures demonstrate

that more than 90% of tampered blocks are detected

if we embed watermark bits into half pixels of each

block or more. The worst result (60-90% of correctly

identified blocks) corresponds to the case of 𝐸 

0.25 for CR_PHI-001-1.dcm. As a result, we

recommend to use 𝐸 greater than 0.5.

Figure 2: Tamper localization quality for DX_PHI-002-

4.dcm, 𝑀𝑅0.75.

Figure 3: Tamper localization quality for CR_PHI-006-

1.dcm, 𝑀𝑅0.5.

Figure 4: Tamper localization quality for CT_PHI-014-

2.dcm, 𝑀𝑅0.75.

We should also stress that the quality of the

resulting mask of unauthorized tampering can be

additionally improved by post processing. In this

procedure, we applied morphological closing with a

square structural element of size 3𝑟  3𝑟. Our

experiments showed that average 𝑇𝑃𝑅 value

obtained in the worst case (𝐸 0.25, 𝐶𝑅0.5 for

IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering

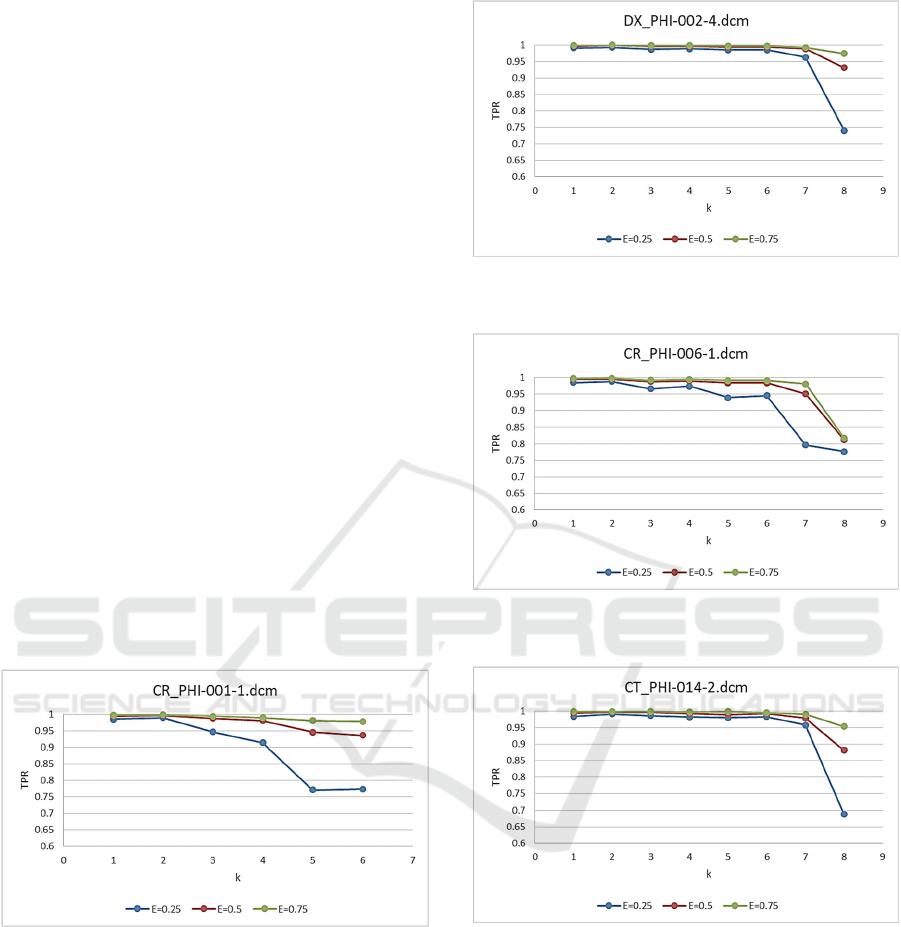
image CR_PHI-001-1.dcm) rose to 0.98. To sum up,

the proposed method in combination with post

processing provides 𝑇𝑃𝑅0.98.

4.2 Localization of the Advanced

Tampering

In our second experiment, we modeled a more

advanced tampering attack when an intruder

substitutes a pixel 𝐶





𝑛



,𝑛





mod δ



with 𝑥 such

𝑥



mod δ



 𝐶





𝑛



,𝑛





mod δ



)

where 𝛿LCM2,4…,2k and k varies from 1 to

∆



. Some of k values were not considered because

the resulting LCM was too big and changes exceeded

the dynamic range of the image.

For this experiment, we decided to use post

processing for all δ values. The other parameters of

the method are: 𝑀𝑅 



0.5,0.75



, 𝑟



4,8



and

𝐸



0.25,0.5,0.75



. Figures 5-8 show the results for

our four DICOM images. They demonstrate that our

watermark remains resistant to the second attack.

𝑇𝑃𝑅 starts to degrade only for

𝑘

more than 7.

However, in this case the changes made by the

intruder became visible because the LCM2,4…,2k

value become too big (more than 840) and an

authorized user can detect the changes visually.

Figure 5: Tamper localization quality for CR_PHI-001-

1.dcm, 𝑀𝑅0.5, for different k, after post processing.

4.3 Visual Quality Examination

In our third experiment, we assessed visual

degradation of images after watermarking. In

Section 2.6, we presented two approaches to select

positions for embedding. The first one is random,

while the second one embeds watermark bits in pixels

with the smallest ∆





,



values in the block.

Figure 6: Tamper localization quality for DX_PHI-002-

4.dcm, 𝑀𝑅0.75, for different k, after post processing.

Figure 7: Tamper localization quality for CR_PHI-006-

1.dcm, 𝑀𝑅0.5, for different k, after post processing.

Figure 8: Tamper localization quality for CT_PHI-014-

2.dcm, 𝑀𝑅0.75, for different 𝑘, after post processing.

The embedding method was tested under the

following parameters: 𝑀𝑅0.5, 𝑟



4,8



and 𝐸



0.25,0.5,0.75



. MSE values obtained for both

approaches are shown in Tables 4 and 5. The tables

show that the second approach produces less MSE

error than the first one. Specifically, the second

approach reduces the RMSE value in 1.81 times in

average.

Reversible Fragile Medical Image Watermarking Scheme Resistant to Malicious Tampering Attacks

Table 6: MSE of watermarked images (first pixel selection

approach).

Image E=0.25 E=0.5 E=0.75

CR_PHI-001-1.dcm 2.97 4.20 5.14

CR_PHI-006-1.dcm 3.39 4.80 5.87

CT_PHI-014-2.dcm 4.38 6.21 7.61

DX_PHI-002-4.dcm 3.68 5.21 6.38

Table 7: MSE of watermarked images (second pixel

selection approach).

Image E=0.25 E=0.5 E=0.75

CR_PHI-001-1.dcm 1.25 2.60 4.11

CR_PHI-006-1.dcm 1.36 2.86 4.64

CT_PHI-014-2.dcm 1.64 3.65 6.04

DX_PHI-002-4.dcm 1.45 3.12 5.10

As the experiment showed, due to the wide

dynamic range of the images, the embedded

watermark is imperceptible. Examples of a source

image, a corresponding watermarked image and their

difference shown in Figure 9 illustrate that watermark

traces are very hard to locate visually. Moreover, we

should not forget (according to Section 2.5) that the

watermarking method is reversible, and the

watermark can be removed from the image after its

detection.

a) b)

Figure 9: Watermark embedding effect for DX_PHI-002-

4.dcm: (a) source image, (b) watermarked image, (c)

absolute value of their difference.

Figure 10 illustrates an example of tampering

localization for the same image. Although the

tampered area is imperceptible by human eye, our

algorithm gives a good approximation of this area.

Moreover, a post-processing morphological closing

procedure let us improve this approximation (we used

a 9×9 window in this example).

a) b)

c) d)

Figure 10: Tampering localization for DX_PHI-002-4.dcm:

a) tampered image, b) correct map of tampered values, c)

map of tampered values estimated by our algorithm, d)

estimated map after post-processing.

5 CONCLUSION

In this paper, we have addressed the issue of the

vulnerability of the known fragile watermarking

methods for medical images to malicious tampering.

To fix this issue, we have proposed a new QIM-based

fragile digital watermarking method. This method

embeds a digital watermark into ROI. The method is

based on random generation of the quantization steps

for each pixel of the ROI using a secret key. The

variation of quantization steps protects the image

from malicious tampering when an intruder tries to

keep unchanged the invisible image component

containing the watermark. To make the scheme

reversible, the embedding error is stored in RONI.

The experimental results approved the efficiency

of the proposed approach to malicious tampering and

demonstrated visual imperceptibility of the

watermark.

IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering

ACKNOWLEDGEMENTS

The reported study was funded by RFBR, project

number 19-29-09045.

REFERENCES

Al-Qershi, O. M., & Khoo, B. E. (2011). Authentication

and Data Hiding Using a Hybrid ROI-Based

Watermarking Scheme for DICOM Images. Journal of

Digital Imaging, 24(1), 114–125.

Alshanbari, H. S. (2021). Medical image watermarking for

ownership & tamper detection. Multimedia Tools and

Applications, 80(11), 16549–16564.

Balasamy, K., & Suganyadevi, S. (2021). A fuzzy based

ROI selection for encryption and watermarking in

medical image using DWT and SVD. Multimedia Tools

and Applications, 80(5), 7167–7186.

Coatrieux, G., Lecornu, L., Sankur, B., & Roux, Ch. (2006).

A Review of Image Watermarking Applications in

Healthcare. 2006 International Conference of the IEEE

Engineering in Medicine and Biology Society, 4691–

4694.

Eswaraiah, R., & Reddy, E. S. (2014). A Fragile ROI-Based

Medical Image Watermarking Technique with Tamper

Detection and Recovery. 2014 Fourth International

Conference on Communication Systems and Network

Technologies, 896–899.

Eswaraiah, R., & Sreenivasa Reddy, E. (2015). Robust

medical image watermarking technique for accurate

detection of tampers inside region of interest and

recovering original region of interest. IET Image

Processing, 9(8), 615–625.

Giakoumaki, A., Pavlopoulos, S., & Koutsouris, D. (2006).

Multiple Image Watermarking Applied to Health

Information Management. IEEE Transactions on

Information Technology in Biomedicine, 10(4), 722–

732.

Golea, N. E. H., & Melkemi, K. (2019). ROI-based fragile

watermarking for medical image tamper detection.

International Journal of High Performance Computing

and Networking, 13, 199.

Holliman, M., & Memon, N. (2000). Counterfeiting attacks

on oblivious block-wise independent invisible

watermarking schemes. IEEE Transactions on Image

Processing, 9(3), 432–441.

Kaur, A., & Rani, J. (2016). Digital Image Forgery and

Techniques of Forgery Detection: A brief review.

International Journal of Technical Research & Science,

1(4), 18–24.

Khor, H. L., Liew, S.-C., & Zain, J. Mohd. (2017). Region

of Interest-Based Tamper Detection and Lossless

Recovery Watermarking Scheme (ROI-DR) on

Ultrasound Medical Images. Journal of Digital

Imaging, 30(3), 328–349.

Liu, X., Lou, J., Fang, H., Chen, Y., Ouyang, P., Wang, Y.,

Zou, B., & Wang, L. (2019). A Novel Robust

Reversible Watermarking Scheme for Protecting

Authenticity and Integrity of Medical Images. IEEE

Access, 7, 76580–76598.

Memon, N. A., & Gilani, S. A. M. (2008). NROI

watermarking of medical images for content

authentication. 2008 IEEE International Multitopic

Conference, 106–110.

Memon, N. A., Gilani, S. A. M., & Qayoom, S. (2009).

Multiple watermarking of medical images for content

authentication and recovery. 2009 IEEE 13th

International Multitopic Conference, 1–6.

Memon, N. A., & Alzahrani, A. (2020). Prediction-Based

Reversible Watermarking of CT Scan Images for

Content Authentication and Copyright Protection.

IEEE Access, 8, 75448–75462.

Mildenberger, P., Eichelberg, M., Martin, E. (2002).

Introduction to the DICOM standard. European

radiology, 12(4), 920-927.

Mousavi, S. M., Naghsh, A., & Abu-Bakar, S. A. R. (2014).

Watermarking Techniques used in Medical Images: a

Survey. J Digit Imaging, 27, 714-729.

Parah, S. A., Sheikh, J. A., Ahad, F., Loan, N. A., & Bhat,

G. M. (2017). Information hiding in medical images: A

robust medical image watermarking system for E-

healthcare. Multimedia Tools and Applications, 76(8),

10599–10633.

Phadikar, A., Maity, S. P., & Mandal, M. (2012). Novel

wavelet-based QIM data hiding technique for tamper

detection and correction of digital images. Journal of

Visual Communication and Image Representation,

23(3), 454–466.

Priyanka, & Maheshkar, S. (2017). Region-based hybrid

medical image watermarking for secure telemedicine

applications. Multimedia Tools and Applications,

76(3), 3617–3647.

Rutherford, M., Mun, S. K., Levine, B., Bennett, W., Smith,

K., Farmer, P., Jarosz, Q., Wagner, U., Freyman, J.,

Blake, G., Tarbox, L., Farahani, K., Prior, F. (2021). A

DICOM dataset for evaluation of medical image de-

identification. Scientific Data, 8(1), 1-8.

Shehab, A., Elhoseny, M., Muhammad, K., Sangaiah, A.

K., Yang, P., Huang, H., & Hou, G. (2018). Secure and

Robust Fragile Watermarking Scheme for Medical

Images. IEEE Access, 6, 10269–10278.

Su, G.-D., Chang, C.-C., & Lin, C.-C. (2020). Effective

Self-Recovery and Tampering Localization Fragile

Watermarking for Medical Images. IEEE Access, 8,

160840–160857.

Swaraja K. (2018). Medical image region based

watermarking for secured telemedicine. Multimedia

Tools and Applications, 77(21), 28249–28280.

Reversible Fragile Medical Image Watermarking Scheme Resistant to Malicious Tampering Attacks