A New Approach for Analyzing Financial Markets using Correlation

Networks and Population Analysis

Zahra Hatami

1 a

, Hesham Ali

1 b

,David Volkman

2 c

and Prasad Chetti

3 d

College of Information Science & Technology, University of Nebraska at Omaha,Omaha, U.S.A.

College of Business Administration, University of Nebraska at Omaha,Omaha, U.S.A.

School of Computer Science & Information Systems,Northwest Missouri State University, Maryville, U.S.A.

Keywords:

Financial Markets, Population Analysis, Network Models.

Abstract:

With the availability of massive data sets associated with stock markets, we now have opportunities to apply

newly developed big data techniques and data-driven methodologies to analyze these complicated markets.

Correlation network analysis makes it possible to structure large data in ways that facilitate ﬁnding common

patterns and mine-hidden information. In this study, we developed the population analysis with utilizing a

correlation network model to conduct a study on stock market data on companies for the years 2000 through

2004. We utilized companies’ parameters for behavior assessment based on the population analysis. After

creating the network model, we employed graph-based community algorithms, such as GLay, to identify

communities and stocks with similar features associated with their excess returns. Our analysis of the top

two communities revealed that companies in the ﬁnance sector have the highest share in the market, and

companies with a low amount of capitalization have a high excess return, similar to large companies. The

proposed correlation network model and the associated population analysis show that investing in companies

with high capitalization does not always guarantee higher rates of return on investment. Based on the proposed

approach, investors could get similar returns by investing in certain small companies.

1 INTRODUCTION

Investing in stock markets has continued to represent

challenges for many investors around the world. At-

tempting to understand the key aspects of stock mar-

kets, like when to buy or sell stocks or whether stocks

are performing well or poor, remains extremely dif-

ﬁcult. Although many studies have addressed these

issues, they primarily focused on using simple sta-

tistical models. Fundamental analysis and technical

analysis are two ways to analyze stock markets from

a ﬁnancial perspective (Bettman et al., 2009). The

fundamental analyst is to calculate the stock’s intrin-

sic value with the company’s information, analyze the

ﬁnancial statements, and compare it with the current

value to make the right decision about buying and

selling the stock of the company. Technical analysis is

applied to ﬁnd the right time to buy or sell a share by

https://orcid.org/0000-0002-6344-4421

https://orcid.org/0000-0002-8016-6144

https://orcid.org/0000-0002-7988-3517

https://orcid.org/0000-0002-3838-5781

observing and analyzing stock price behavior in the

past and using the patterns to predict the future price

movements. Researchers have analyzed the ﬁnancial

markets from big data analytical perspective using

various computational and statistical methodologies,

including Artiﬁcial Intelligence, Machine Learning,

Artiﬁcial Neural Networks, Fuzzy Logic, and Support

Vector Machines(Gupta and Dhingra, 2012).

The ﬁnancial market brings the opportunity for in-

vestors to have access to the large and complex daily

and monthly data. This data can be used by big data

analytical tools, such as network models and corre-

lation analysis. This study aims to use a population

analysis and correlation network model (CNM) ap-

proach to determine the speciﬁc sector that dominates

in the stock market. The purpose of applying pop-

ulation analysis is to compare different clusters, or

groups, of stocks with respect to a particular parame-

ter such as companies’ returns, economic sectors, and

companies’ capitalization. The network models allow

researchers to analyze each element in the network

and look for networks’ characteristics and features

that are not possible under traditional approaches.

Hatami, Z., Ali, H., Volkman, D. and Chetti, P.

A New Approach for Analyzing Financial Markets using Correlation Networks and Population Analysis.

DOI: 10.5220/0011073800003179

In Proceedings of the 24th International Conference on Enterprise Information Systems (ICEIS 2022) - Volume 1, pages 569-577

ISBN: 978-989-758-569-2; ISSN: 2184-4992

569

The general objective of this research is to demon-

strate how network and community analysis can be

applied to stock market data. We propose to employ

CNM to create a correlation network of companies

based on the time-series data of companies’ excess

returns(ER). After creating a correlation network, we

applied the GLay clustering algorithm, which is a

community detection algorithm(Su et al., 2010), to

obtain a set of companies that have similarities in

their ER. Based on different communities from the

network, we identiﬁed the top two communities pro-

duced by the clustering algorithm for further anal-

ysis. We then identiﬁed the economic sectors that

dominated the market between the years 2000 through

2004 and also found their relevant capitalization. The

experimental results from the network suggested that,

in the short term, the ER for small-size companies

(low total capitalization) is the same as the large-size

companies. In other words, in order to have more

proﬁt, investors should focus on small size companies

that can bring the same, or more, proﬁt as large size

companies. In this study, we aimed to answer the fol-

lowing questions: What type of companies have the

similar behavior during 2000-2004 based on their ER

and amount of capitalization (Research Question 1:

RQ1), and Does any other factor affect their behav-

ior outside of network analysis (Research Question 2:

RQ2)? The remainder of this paper is organized as

follows. First, we comprise a literature review of re-

lated studies in different disciplines and ﬁnancial mar-

ket analysis. The following section gives an overview

of correlation networks, graph models, and cluster-

ing analysis. Then, we explain the methodology and

discuss the implementation of the proposed approach.

Next, the experimental results of the study, and lastly,

we present our conclusion and offer recommendations

for future work.

2 LITERATURE REVIEW

Analysis of the network involves the recognition of

which entities are connected to others in a graph.

The entities and how they affect each other are im-

portant in ﬁnding the most inﬂuential entities in the

network. The strength of the relationships (i.e., the

strength of the edges) can be measured with differ-

ent kinds of correlation coefﬁcients such as Pearson,

Kendall, and Spearman. The coefﬁcient of continu-

ity is always between -1 and 1. A correlation coef-

ﬁcient above 0 means that there is a positive corre-

lation; the closer the coefﬁcient to +1, the stronger

the positive correlation. A correlation coefﬁcient be-

low 0 means that there is a negative correlation be-

tween the two variables, and the closer the number

is to -1, the stronger the negative correlation. Vari-

ous correlation coefﬁcients can be used as measure-

ments depending on the nature of the data that creates

the correlation network. For example, if the data are

normally distributed, the Pearson correlation coefﬁ-

cient will be used to establish the edges’ connections.

Pearson correlation-based network is an unweighted/

undirected network that constructs and measures the

network using Pearson correlation coefﬁcients.

2.1 Correlation Networks in Various

Disciplines

Different research domains such as social comput-

ing (Hatami et al., 2021), bio-sciences, and civil en-

gineering used correlation networks in their analysis

(Chetti and Ali, 2020; Chetti and Ali, 2019; Cooper

et al., 2019; Dempsey and Ali, 2014; Fuchsberger and

Ali, 2017; Kim et al., 2018; Rastegari et al., 2019).

The theoretical framework behind the correlation net-

works can address different problems in different do-

mains. Another beneﬁt of using the correlation net-

work is extracting hidden information by using ad-

vanced visualization tools such as clustering (Ba-

tushansky et al., 2016). In bio-science, using cluster-

ing methods on the complex network created based on

biological entities could help researchers recognize

active genes associated with various stages of disease

progression(Dempsey et al., 2011). The outcome of

the research could detect different early health condi-

tions in different patients. They also allow researchers

to utilize advanced visualization tools at different

granularity levels(Batushansky et al., 2016; Lancel-

lotta et al., 2018). Recently, researchers used the cor-

relation network in the civil engineering domain in

order to assess the safety, deterioration, and perfor-

mance of bridges and their infrastructures(Chetti and

Ali, 2020; Chetti and Ali, 2019; Fuchsberger and Ali,

2017).

2.2 Correlation Network Model in

Financial Domain

Financial markets have been analyzed by researchers

in the big data domain using different computa-

tional and statistical methodologies, such as Artiﬁ-

cial Intelligence, Machine Learning, Artiﬁcial Neu-

ral Networks, Fuzzy Logic and Support Vector Ma-

chines(Gupta and Dhingra, 2012), minimum span-

ning trees (MSTs), and Planar Maximally Filtered

Graph, which is a topological generalization of the

MSTs(Bonanno et al., 2004; Tumminello et al.,

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

570

2007). Financial markets bring the opportunity for in-

vestors to have access to the large and complex daily

and monthly data. This data can be used by big data

analytical tools such as network models and correla-

tion analysis. Correlation network modeling is one of

the computational methods that researchers apply to

the ﬁnancial/stock market(Bonanno et al., 2004; Chi

et al., 2010; Hatami et al., 2022). The correlation

network in the ﬁnancial domain can be created based

on different input variables such as prices or compa-

nies’ returns. A correlation network model (CNM)

can be built by assuming that each company/stock is

a node (a vertex) in the graph model, and two nodes

are connected by a directed/undirected edge if and

only if their correlation coefﬁcient is above a partic-

ular threshold (such as 0.75 or above). In(Bonanno

et al., 2004; Chi et al., 2010), researchers established

the networks based on similarities between compa-

nies’ prices. In networks, companies are represented

by nodes, and similarities between companies’ prices

are represented by edges. The result of the study

revealed that ﬁnance sector

dominated the market

compared to other economic sectors

. In other stud-

ies (Chi et al., 2010), researchers established the net-

work as a worldwide network based on a few entities

such as price indices, companies, and stocks. The cor-

relation network analysis brings opportunities to the

researchers to uncover hidden information from the

network. For example, in(Gupta and Dhingra, 2012),

researchers could predict the next day’s events using

time series data in the correlation network using Hid-

den Markov Models to forecast the stock market. The

result of different studies using big data techniques

showed that governments could make use of the re-

sults of correlation networks while making economic

decisions(Kenett et al., 2012).

3 MATERIAL AND METHODS

Different data sets were used in this study. One

set of data was collected from the Center for Re-

search in Security Prices (CRSP). In addition, an-

other data set was collected from the Fama-French

(FF) data library. The CRSP dataset contained a list

of stocks/companies with their monthly information.

After data cleaning and ﬁltering, we looked at com-

panies’ Standard Industrial Classiﬁcation (SIC), ER,

and total capitalization (TCap) for all available stocks

A ﬁnance sector is a group of companies that ﬁt into

one of the main categories such as banks and ﬁnancial ser-

vices

Economic Sectors are large groups of the economy that

categorized according to their place in the production chain

in the U.S.. SIC is a code used to group companies

with similar products or services at the end of the re-

porting period. SIC is used to identify companies’

economic sectors. Economic sectors are groups that

are categorized according to their place in the pro-

duction chain. TCap results from the multiplication

of price and number of shares (in 1000s) for each

company. Based on the companies’ capitalization,

the companies’ size will be divided into ten categories

called deciles. In this study, companies that belong to

decile 1-5 are called small-size, and companies that

belong to decile 6-10 are called big-size companies.

ER was obtained by subtracting the return value (a

parameter in the CRSP data set) from the risk-free

value

(from the FF data set).

Under population analysis, correlation network

analysis is applied in time-series data in order to ﬁnd

hidden information when it cannot be found using tra-

ditional approaches (Mi

skiewicz, 2012; Hatami et al.,

2022). In this study, cluster analysis was applied on

the network in order to group different companies

whose degree of correlation between two companies

is above a threshold.

After creating the communities/clusters, all the

parameters from CRSP were added to the companies

in each community for further analysis to do cluster

enrichment for that speciﬁc community. As the com-

munities are formed with high correlations among the

nodes, we can infer that the overall behavior of the

nodes within each community is the same.

3.1 Data Acquisition and Filtering

Two separate data sets were utilized in this research.

The Center for Research in Security Prices (CRSP)

is a variation of the research-quality stock database,

which contains monthly data of all companies from

1926 to 2018. This data set includes ﬁve parame-

ters/variables (Companies’ ID (CUSIP), date, return,

SIC, TCap). Another data set was collected from the

Fama-French (FF) data library. Risk-free was the only

parameter that was used from FF data set. As a major

parameter in this study, ER reﬂects the overall perfor-

mance of companies based on different factors such

as economic sectors and capitalization. ER values

range between -1 and 2. A value of -1 means 100%

loss, and a value of 2 means 200% gain. To study

the features of the correlation network for companies,

we should ﬁrst establish the correlation network by

extracting data from different data sets. A network,

represented by a graph, is a collection of nodes and

risk-free is the rate of return of a hypothetical invest-

ment with no risk of ﬁnancial loss over a given period of

time

A New Approach for Analyzing Financial Markets using Correlation Networks and Population Analysis

571

edges, N = (V, E), where each node represents a com-

pany, and an edge between two nodes reﬂects the re-

lationship between the corresponding companies. We

established the pilot study for the years 2000 to 2004

(inclusively). The reason for selecting these years is

because the 9/11 attacks happened during this period,

and the authors would like to study what sectors of

companies are better to invest in case of having an

unexpected event.

During the time period 2000 to 2004, some com-

panies had not existed for ﬁve years, resulting in some

missing data points for those companies. Therefore,

to avoid any biased results for this pilot study, only

companies with all data points for 12 months in these

ﬁve years were extracted. At the end of the data ﬁl-

tering, out of 5280 companies, 3427 companies were

extracted for further analysis.

3.2 Population Analysis

The term ”population analysis” in the correlation net-

works analysis refers to comparing the group/cluster

of nodes/companies with respect to various param-

eters. Some parameters may be highly enriched in

one cluster compared to another cluster. Applying a

novel population analysis helps us compare individual

data points with other data points in different clusters

or populations regarding different performance lev-

els. In other words, population analysis allows us to

compare two or more clusters of companies with re-

spect to one or more enriched parameters. The results

of this analysis will allow us to discover the parame-

ters that signiﬁcantly affect the cluster. For example,

if companies are enriched with company size in one

cluster, then we can recognize other factors related to

the companies for further analysis.

3.3 Correlation Networks and

Community Detection

The correlation network was created based on the ER.

The time-series data of ER for the 3427 companies

was recorded as an input matrix. In the matrix, there

were 60 data points (time-series data of 60 months)

for each company. Since the data set is normally dis-

tributed, we applied the Pearson correlation coefﬁ-

cient to the ER matrix. In the constructed correla-

tion network, each company as a node (vertex) is con-

nected to another company with an undirected edge if

their correlation coefﬁcient is 0.75 or more and their

signiﬁcance of correlation is less than or equal to 0.05.

This creates a correlation network with companies as

nodes along with highly correlated companies con-

nected by edges, as shown in Figure 1.

Figure 1: Correlation network of companies’ data between

2000 and 2004.

In this study, due to the high similarity between

companies’ ER, cluster analysis was applied on the

network as a data analysis shortcut tool in order to

group different companies whose degree of correla-

tion between two companies is above a threshold.

Cluster analysis, or clustering, is a process by which

a set of objects can be separated into groups. Each

partition is called a cluster. The members of each

cluster are very similar to each other in terms of their

properties, and, in turn, the similarity between clus-

ters is minimal. In this case, the purpose of cluster-

ing is to assign similar objects into one cluster and

label with object’s membership in the cluster. The

ﬁnancial market network is one of the most com-

plex networks, which brings signiﬁcant challenges to

visualization. Creating clusters from this complex

network consumes considerable time and computa-

tional resources, and the results are not always use-

ful. By using a speciﬁc topology, we have an op-

portunity to visualize the clusters from the commu-

nity structure. Therefore, for this project, we ap-

plied GLay community structure detection algorithm

(available in Cytoscape(Shannon et al., 2003) tool)

that identiﬁed as an efﬁcient layout for very large

networks. GLay community clustering was applied

to the network with all default parameters in Cy-

toscape(Shannon et al., 2003) on the obtained correla-

tion network to produce communities/clusters. GLay

clustering was used since it has the ability for disin-

tegration and could be used for large and complex

networks that contain a large number of nodes and

edges(Su et al., 2010). In this study, from 3427 com-

panies, 2580 companies were involved in the network

based on the above-referenced network criteria. Out

of 2580 companies, 2477 nodes were placed in two

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

572

communities (communities one and two). The subset

of these two large communities are shown in Figure

2 and 3. Hence, communities one and two were con-

sidered for further analysis, and various experiments

were conducted on these two communities.

Figure 2: Subset-Community one network with 1402 nodes

and 156778 edges.

Figure 3: Subset-Community two network with 1075 nodes

and 307087 edges.

4 EXPERIMENTAL RESULTS

This section discusses various network properties and

the application of the population analysis on the cor-

relation network.

4.1 Network Properties of the

Communities

The correlation network in Figure 1 represents 3427

companies (nodes) and 657890 relationships (edges).

This network has 25 communities that are formed

with a correlation of 0.75 or greater between edges.

This network is a scale-free network that follows a

power-law node degree distribution. The power-law

degree distribution means there are many nodes with

fewer degrees and fewer number of nodes with more

degrees. Two top communities (with respect to the

number of nodes) were selected from this network,

and the communities’ statistics are shown in Table 1.

Community 1 has 1402 nodes and 156778 edges, and

Community 2 has 1075 nodes and 307087 edges.

Some of the network statistics/properties of the

top two clusters are shown in Table 1. The aver-

age degree of each cluster is the average number of

edges of all nodes.The cluster density describes the

potential number of edges present in the sub-network

compared to the possible number of edges in the sub-

network. The higher the clustering coefﬁcient, the

higher the degree to which nodes in a graph are in-

clined to cluster together(Watts and Strogatz, 1998).

The higher values of the average clustering coefﬁcient

for each cluster/sub-network indicate that the nodes

inside each cluster tend to be part of that cluster only.

Table 1 shows that Community 2 has fewer nodes but

has the highest clustering coefﬁcient of 0.85. Once

again, Community 2 has a higher density (0.532)

compared to Community 1.

Table 1: Network statistics of top two communities.

4.2 Cross-tabulation Properties

In this study, the data set obtained from communi-

ties was analyzed based on various parameters, such

as economic sectors, companies’ capitalization, and

their degrees. Economic sectors are large groups of

the economy, grouped according to their place in the

production chain, by their kind of work (product or

service) or ownership. There are 12 economic sec-

tors in the economic era: consumer staples (NoDur),

consumer discretionary (Durbl), industrial (Manuf),

basic materials (Chems), energy (Energy), informa-

tion technology (BusEq), communications (Telcm),

utility (Util), real estate (Shops), health (Hlth), ﬁ-

nance(Finance), and other(Other).

The degree indicates how many times each com-

pany is connected to other companies based on sim-

ilarities in their ER. According to the degree range

for the companies, we ranked the number of degrees

into ﬁve categories. For example, rank one shows de-

grees between 1-200, and rank ﬁve shows degrees be-

tween 800-1000. The higher rank means more simi-

larity with other companies within the cluster.

Companies’ capitalization results from the multi-

plication of price and number of shares (in 1000s) for

each company. In the ﬁnancial domain, a company’s

capitalization is divided into ten categories that are

called deciles. A decile is a quantitative method of

splitting up a set of ranked data into ten equally large

A New Approach for Analyzing Financial Markets using Correlation Networks and Population Analysis

573

subsections

. The ﬁrst category has the lowest, and

the tenth category has the highest amount of capital-

ization.

4.3 Cross-tabulation Results for

Communities One and Two

Since Communities 1 and 2 have the highest num-

ber of companies in their community, in this sec-

tion, we report the result of the cross-tabulation analy-

sis between degree-ranked, capitalization-ranked and

economic sectors for companies belonging to these

communities. In 2000-2004, the ﬁnance sector dom-

inated the market with 36%, and consumer discre-

tionary with 2% had the lowest share in the market.

The cross-tabulation analysis shows that, for ranked

degrees one through ﬁve, the ﬁnance sector had the

highest number of companies in the market followed

by the information technology sector (Table 2 & Fig-

ure 4).

Table 2: Sector statistics for 2526 companies in 2000-2004.

Sector Frequency Percent

Consumer Staples 127 5%

Industrial 230 9%

Energy 90 4%

Basic Materials 50 2%

Information Technology 314 12%

Communications 55 2%

Utility 99 4%

Real Estate 223 9%

Health 85 3%

Finance 899 36%

Consumer Discretionary 44 2%

Other 310 12%

Total 2526 100%

Applying cross-tabulation between economic sec-

tors and capitalization (deciles) shows that companies

belonging to the ﬁnance sector for all ten deciles have

the highest share in the market during the time period

2000-2004 (Figure 5).

Finally, a cross-tabulation analysis between

degree-ranked and capitalization shows that the high-

est number of degrees belongs to companies that have

the lowest amount of capitalization (ranked 1-4). In

other words, companies that have a low amount of

capitalization (deciles 1-4) have the most similarity in

their ER with other companies. That means they have

the same ER as other companies considered large

companies (Figure 6).

As a result of this analysis, we can say that com-

panies belonging to the ﬁnance sector from 2000 to

https://cleartax.in/g/terms/decile

Figure 4: Cross-tabulation between economic sectors and

ranked degrees.

Figure 5: Cross-tabulation between economic sectors and

ranked capitalization in 2000-2004.

2004 have the highest degree of relationship (simi-

larity in their ER) with other companies while they

have the lowest amount of capitalization. Further-

more, based on this analysis, we can say that compa-

nies that have the most similarities in their ER move-

ments compared to others in the community are those

that even have the lowest amounts of capitalization.

4.3.1 Analysis of 50 Randomly Picked

Companies in Community One with

Respect to Input Capitalization and

Economic Sectors

For this part of analysis, we randomly picked the 50

companies in Community 1 as one of the largest com-

munities in the correlation network for analyzing cap-

italization movements. In this community, 80% of

companies belonged to the ﬁnance sector with cap-

italization ranked 1-4, and the remaining 20% were

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

574

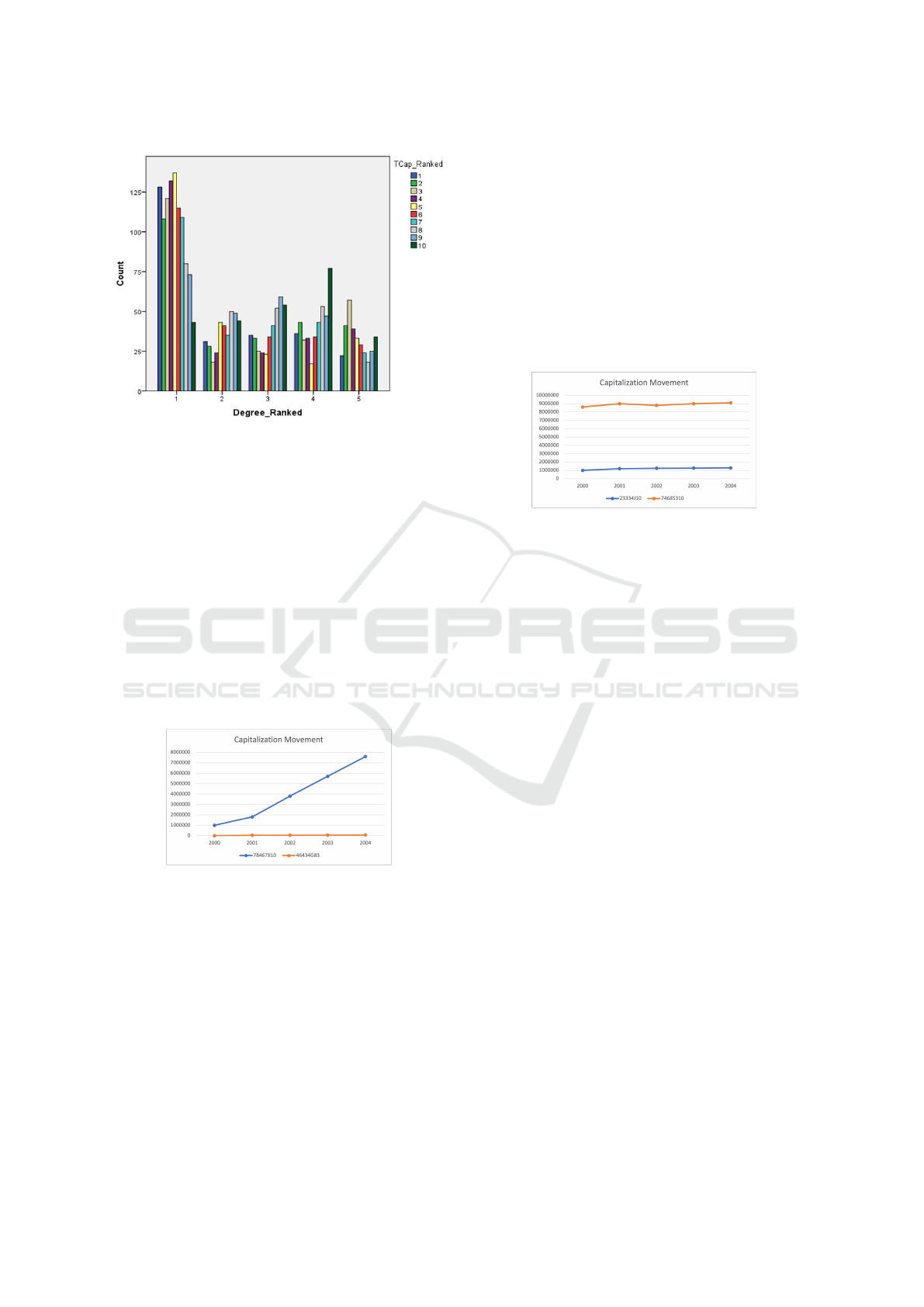
Figure 6: Cross-tabulation between ranked degree and

ranked capitalization in 2000-2004.

companies belonging to other economic sectors.

As another comparison in Community 1, we com-

pared the behavior of one high degree and one low

degree company in the ﬁnance sector. The company

ID ”46434G83” belonged to the highest-degree com-

pany and the company ID ”78467X10” belonged to

the lowest-degree company. Tracking their capitaliza-

tion showed that company 46434G83, belongs to the

lowest-ranked capitalization decile (decile 2), while it

has the most similarity in its ER compared to com-

pany 78467X10 as one of the largest size companies

in the market (decile 9). Figure 7 shows the capital-

ization trend for these two companies in the ﬁnance

sector in Community 1 during 2000-2004.

Figure 7: Comparison of average capitalization val-

ues of two companies from Community one in 2000-

2004(Horizontal axis stands for ”year” and vertical axis is

”amount of capitalization”).

4.3.2 Analysis of 50 Randomly Picked

Companies in Community Two with

Respect to Input Capitalization and

Economic Sectors

We applied the same analysis procedure on the next

largest community (Community 2), and again, 50

companies were randomly picked. In this community,

96% of companies are in the ﬁnance sector, and from

this 96%, 69% belong to capitalization rank of 1-4.

As another comparison in Community 2, we com-

pared the behavior of one high-degree and one low-

degree company in the ﬁnance sector. The com-

pany with CUSIP ”23334J10” and the company

with CUSIP ”74685310” were selected. Tracking

their capitalization showed that company 23334J10

belongs to the lowest-ranked capitalization decile

(decile 3), while it has the most similarity in its ER

compared to company 74685310 as one of the largest

sized companies in the market (decile 7). Figure 8

shows the capitalization trend for these two compa-

nies in the ﬁnance sector in Community 2.

Figure 8: Comparison of average capitalization values of

two companies from Community two in 2000-2004 (Hori-

zontal axis stands for ”year” and vertical axis is ”amount of

capitalization”).

5 CONCLUSION

With the growing availability of ﬁnancial data, new

approaches are needed to take full advantage of such

data and provide investors insightful knowledge about

the behavior of companies in the ﬁnancial markets.

This research proposes a new approach for analyz-

ing ﬁnancial markets and extracting useful informa-

tion from the large amount of ﬁnancial data. Due to

the complexity of ﬁnancial market data, the proposed

approach that utilizes the concept of population anal-

ysis and correlation networks, along with associated

enrichment analysis, allowed us to identify behavioral

patterns of the ﬁnancial market that are difﬁcult to

identify using traditional approaches.

To test our proposed approach, we conducted a

case study on the stock market data of the United

States for the years 2000-2004. We proposed a cor-

relation network model along with population analy-

sis to conduct the study. We constructed a correla-

tion network based on companies’ ER. After creating

the network and applying clustering algorithms, we

extracted the top two communities and analyzed the

associated companies. We collected various relevant

information about the companies, such as the amount

of their capitalization and economic sectors. Based

on the clustering analysis, we found that companies

in ﬁnance sectors have the highest share in the market

A New Approach for Analyzing Financial Markets using Correlation Networks and Population Analysis

575

as compared to other sectors. We also showed that

companies in the ﬁnance sector have similarities in

their ER movements as to that of big-size companies,

even though they mostly had the lowest capitalization.

Based on the obtained results, it can be concluded that

investment in a small company with low capitaliza-

tion in the ﬁnance sector, even during the crises, may

yield a higher return than investment in large compa-

nies. From 2000 to 2004, companies in the ﬁnance

sector kept their consistency with low capitalization

and got the same ER as big companies with high cap-

italization (RQ1). Using the population analysis, we

did not ﬁnd any parameters outside network charac-

teristics that signiﬁcantly affected the behavior of the

companies under study (RQ2).

The proposed model and the reported results rep-

resent a starting point for a new direction in analyz-

ing ﬁnancial markets. The results show the viabil-

ity of this new approach. However, additional studies

with larger and more diverse data sets are necessary

to make a case for utilizing the concept of population

analysis in making important ﬁnancial decisions. The

limitation of this study is that we analyzed the market

for a limited sample during the 2000-2004 time pe-

riod. To further validate the obtained results, we plan

to conduct a more comprehensive study using the pro-

posed approach for different time periods and utiliz-

ing different types of data sets. We intend to apply

the concept of population analysis on different sets of

data tied to independently-established major crises in

order to recognize the patterns that may be otherwise

obfuscated. In addition to ER, future studies also in-

clude exploring other indicators such as different eco-

nomic sectors and companies’ sizes for comparing the

behavior of companies in ﬁnancial markets.

REFERENCES

Batushansky, A., Toubiana, D., and Fait, A. (2016).

Correlation-based network generation, visualization,

and analysis as a powerful tool in biological studies:

a case study in cancer cell metabolism. BioMed re-

search international, 2016.

Bettman, J. L., Sault, S. J., and Schultz, E. L. (2009). Fun-

damental and technical analysis: substitutes or com-

plements? Accounting & Finance, 49(1):21–36.

Bonanno, G., Caldarelli, G., Lillo, F., Micciche, S., Vande-

walle, N., and Mantegna, R. N. (2004). Networks of

equities in ﬁnancial markets. The European Physical

Journal B, 38(2):363–371.

Chetti, P. and Ali, H. (2019). Analyzing the structural health

of civil infrastructures using correlation networks and

population analysis. In Proceedings of the Eighth In-

ternational Conference on Data Analytics, pages 12–

19.

Chetti, P. and Ali, H. (2020). Estimating the inspection

frequencies of civil infrastructures using correlation

networks and population analysis. International Jour-

nal on Advances in Intelligent Systems, 13(1&2):125–

136.

Chi, K. T., Liu, J., and Lau, F. C. (2010). A network per-

spective of the stock market. Journal of Empirical

Finance, 17(4):659–667.

Cooper, K., Hassan, W., and Ali, H. (2019). Identiﬁcation

of temporal network changes in short-course gene ex-

pression from c. elegans reveals structural volatility.

International Journal of Computational Biology and

Drug Design, 12(2):171–188.

Dempsey, K., Thapa, I., Bastola, D., and Ali, H. (2011).

Identifying modular function via edge annotation in

gene correlation networks using gene ontology search.

In 2011 IEEE International Conference on Bioinfor-

matics and Biomedicine Workshops (BIBMW), pages

255–261. IEEE.

Dempsey, K. M. and Ali, H. H. (2014). Identifying aging-

related genes in mouse hippocampus using gateway

nodes. BMC systems biology, 8(1):62.

Fuchsberger, A. and Ali, H. (2017). A correlation network

model for structural health monitoring and analyzing

safety issues in civil infrastructures. In Proceedings of

the 50th Hawaii International Conference on System

Sciences.

Gupta, A. and Dhingra, B. (2012). Stock market predic-

tion using hidden markov models. In 2012 Students

Conference on Engineering and Systems, pages 1–4.

IEEE.

Hatami, Z., Chetti, P., Ali, H., and Volkman, D. (2022).

A novel population analysis approach for analyzing

ﬁnancial markets under crises – 2008 economic crash

and covid-19 pandemic.

Hatami, Z., Hall, M., and Thorne, N. (2021). Identifying

early opinion leaders on covid-19 on twitter. In In-

ternational Conference on Human-Computer Interac-

tion, pages 280–297. Springer.

Kenett, D. Y., Preis, T., Gur-Gershgoren, G., and Ben-

Jacob, E. (2012). Dependency network and node in-

ﬂuence: Application to the study of ﬁnancial mar-

kets. International Journal of Bifurcation and Chaos,

22(07):1250181.

Kim, S., Thapa, I., and Ali, H. H. (2018). A graph-theoretic

approach for identifying bacterial inter-correlations

and functional pathways in microbiome data. In 2018

IEEE International Conference on Bioinformatics and

Biomedicine (BIBM), pages 405–411. IEEE.

Lancellotta, P. I., Str

oele, V., Braga, R. M., David, J. M. N.,

and Campos, F. (2018). Semantic analysis and com-

plex networks as conjugated techniques supporting

decision making. In ICEIS (2), pages 195–202.

skiewicz, J. (2012). Analysis of time series correlation.

the choice of distance metrics and network structure.

Acta Phys. Pol. A, 121:B–89.

Rastegari, E., Azizian, S., and Ali, H. (2019). Machine

learning and similarity network approaches to support

automatic classiﬁcation of parkinson’s diseases using

accelerometer-based gait analysis. In Proceedings of

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

576

the 52nd Hawaii International Conference on System

Sciences.

Shannon, P., Markiel, A., Ozier, O., Baliga, N. S., Wang,

J. T., Ramage, D., Amin, N., Schwikowski, B., and

Ideker, T. (2003). Cytoscape: a software environment

for integrated models of biomolecular interaction net-

works. Genome research, 13(11):2498–2504.

Su, G., Kuchinsky, A., Morris, J. H., States, D. J., and

Meng, F. (2010). Glay: community structure analysis

of biological networks. Bioinformatics, 26(24):3135–

3137.

Tumminello, M., Di Matteo, T., Aste, T., and Mantegna,

R. N. (2007). Correlation based networks of equity

returns sampled at different time horizons. The Euro-

pean Physical Journal B, 55(2):209–217.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynam-

ics of ‘small-world’networks. nature, 393(6684):440–

442.

A New Approach for Analyzing Financial Markets using Correlation Networks and Population Analysis

577