How Can Autonomous Road Vehicles Coexist with Human-Driven

Vehicles? An Evolutionary-Game-Theoretic Perspective

Isam Bitar

, David Watling

and Richard Romano

Institute for Transport Studies, University of Leeds, 34-40 University Rd, Leeds, LS2 9JT, U.K.

Keywords: Autonomous Vehicles, Game Theory, Evolution, Evolutionarily Stable Strategies, Fitness.

Abstract: The advent of highly automated vehicles in the form of autonomous road vehicles (ARVs) is bound to bring

about a paradigm shift in road user interaction, especially that between ARVs and human-driven vehicles

(HDVs). Previous literature on the game-theoretic interaction between ARVs and HDVs tends to focus on

working out the best possible strategy for a single interaction, i.e. the Nash equilibrium. This position paper

sets out to demonstrate the importance and potential impact of applying evolutionary game theoretic principles

to what is effectively a dynamic population driven by evolutionary forces – the population of road users. We

demonstrate using theoretical scenarios that simply maintaining Nash equilibria does not guarantee

evolutionary success. Instead, ARVs must enjoy a demonstrable advantage over other road users when few

in numbers. Otherwise, their uptake will slow down and eventually reverse. We argue that the same selection

factors which influence the success of living populations in the natural world also influence the success of the

different vehicle types and driving styles in the road user population, including ARVs. We demonstrate this

by assigning an expected fitness score to each vehicle in a one-to-one interaction, such as at a junction. This

fitness score is dependent on driver, rider and economic costs incurred by the vehicle and/or its occupant(s)

during interaction. In turn we show that ARV and transport system designers need to ensure that the fitness

score of their systems create evolutionary stability.

1 INTRODUCTION

Road transport is a highly interactive activity in

which road users must compete for space and priority.

This is done through a vast array of competitive,

cooperative, and communicative behaviours in which

road users engage to facilitate their distribution in

space and time. These behaviours are defined as road

user interactions (Markkula et al., 2020). As

autonomous road vehicles (ARV) reach market

maturity and begin using the road network, their

interaction with human-driven vehicles (HDV) will

strongly influence the success of ARVs in the short

and long term. In this position paper, we argue that

this extends beyond the one-on-one interaction

between ARVs and HDVs to include the population-

level interaction between the two distinct groups of

road users, each with their own inherent properties.

https://orcid.org/0000-0002-5130-0148

https://orcid.org/0000-0002-6193-9121

https://orcid.org/0000-0002-2132-4077

There are fundamental differences between

ARVs and HDVs that set them apart as distinct road

user populations. These differences include

differences in the decision-making mechanism

(Elvik, 2014; Fox et al., 2018; Harris, 2017; Kang &

Rakha, 2020; Meng, Su, Liu, & Chen, 2016),

attention span, driving behaviour (Millard-Ball,

2018; van Loon & Martens, 2015) and over-all

communication and interaction capabilities (C. Liu,

Lin, Shiraishi, & Tomizuka, 2018). Many researchers

believe that HDVs and human road users in general

are likely to learn the nuances of ARV behaviour and

subsequently take advantage of them to force ARVs

to yield at every interaction (Cooper et al., 2019; Fox

et al., 2018; Millard-Ball, 2018). Indeed, experiments

on humans and AI have demonstrated that whilst

humans expect cooperative behaviour from

machines, they are rarely willing to reciprocate

(Karpus, Krüger, Verba, Bahrami, & Deroy, 2021). If

376

Bitar, I., Watling, D. and Romano, R.

How Can Autonomous Road Vehicles Coexist with Human-Driven Vehicles? An Evolutionary-Game-Theoretic Perspective.

DOI: 10.5220/0011079500003191

In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2022), pages 376-383

ISBN: 978-989-758-573-9; ISSN: 2184-495X

ARVs are pushed to yield at most interactions, they

will be unable to make significant progress on the

road network (Cooper et al., 2019; Fox et al., 2018;

Millard-Ball, 2018). This would in turn cause

significant traffic safety and efficiency issues and

damage the uptake of ARVs.

Various solutions have been proposed in the

literature, including building larger, more imposing

ARVs or mounting loud sirens or water pistols to

“punish” transgressors (Fox et al., 2018). Going

further, some suggested programming ARVs with a

non-zero probability to cause collision as a form of

credible threat to dissuade would-be exploiters

(Camara, Dickinson, Merat, & Fox, 2019). Others

have programmed a Stackelberg game in which the

bullied virtual ARV actively punishes the human

player if they behaved antisocially in previous

interactions (Cooper et al., 2019). Setting aside their

ethical and practical ramifications, such measures

merely offer reactionary solutions to a fundamental

problem and are unlikely to work in the long term.

Instead, one must look to other environments in

which we can observe competition and cooperation

between fundamentally different populations. One

such environment is the natural world. There,

members of different animal species (and within the

same species) interact, compete, and cooperate with

each other to share limited resources. Such resources

include food, shelter, and mates. These are resources

each individual needs to maximise its own fitness and

ensure survival and reproduction. Yet, despite the

prevalent scarcity of these resources in most natural

settings, cooperative behaviour is widely spread in

animal populations and fatal conflicts are rare outside

of predation (J. Maynard Smith & Price, 1973;

Wilkinson, 1984).

Animal cooperation in nature can evolve and

persist through means of natural selection (Hamilton,

1964). Evolutionary game theory provides the ideal

theoretical framework for understanding the

dynamics that lead to the evolution of cooperation

(Bendor & Swistak, 1995; John Maynard Smith,

1982). Once evolved, cooperation persists through

means of evolutionary stability. Evolutionary

stability is a state in which most or all members of a

population of individuals interact in a way where a

new, small group of mutant individuals cannot invade

and dominate the population (John Maynard Smith,

1982). A set of behaviours that fits this description is

known as an evolutionarily stable strategy (ESS).

ESSs have been used to describe emergent

cooperative and competitive behaviours in animal

populations (Sirot, 2000; Wilkinson, 1984). The

classic Hawk-Dove game provides a conceptual

illustration of the evolution of cooperation (J.

Maynard Smith & Price, 1973). Many animal

behaviours in nature have been shown to conform to

the categorical paradigm of Hawk-Dove games.

Examples include nesting habits of digger wasps

(Brockmann, Grafen, & Dawkins, 1979), food

sharing in vampire bats (Wilkinson, 1984) and

territorial conflicts in funnel web spiders

(Hammerstein & Riechert, 1988).

Beyond the natural world, several studies exist on

the applicability of ESSs in other disciplines. One

such example is the work of Altman, El-Azouzi,

Hayel, and Tembine (2009) who use a variant of the

Hawk-Dove game to predict the success and

evolutionary stability of different Internet transport

protocols (TCPs) and provide guidelines for the

introduction and upgrade of evolutionarily-stable

TCPs. Other such studies exist in the fields of

economics (Friedman, 1991; Kandori, 1996), policy

making (da Silva Rocha & Salomão, 2019; Xu,

Wang, Wang, & Ding, 2019) and stakeholder conflict

(L. Liu, Zhu, & Guo, 2020; Yu, Zhao, Huang, &

Yang, 2020).

Several studies have also been conducted in the

field of transport. Some applications include route

and mode choice modelling (Lei & Gao, 2019; Wu,

Pei, & Gao, 2015). Others have used evolutionary

game theory as a predictor and facilitator of effective

implementation of government subsidies and

compliance monitoring in transport. Examples

include new-energy vehicles (Wang, Fan, Zhao, &

Wu, 2015) and public transport (Zhang, Long, Huang,

Li, & Wei, 2020). Some road user interaction models

have also made use of evolutionary game theory to

predict driver attention, simulate driver cooperation

and address social dilemmas (Chatterjee & Davis,

2013; Iwamura & Tanimoto, 2018). One exploratory

study has investigated the aggressiveness of driving

behaviour from a Hawk-Dove standpoint (Free,

2018). To the authors’ knowledge, however, this

concept is yet to be expanded to draw larger-scale

conclusions on the evolutionary stability of road user

populations. More specifically, evolutionary game

theory has not yet been used as a framework for

ARVs’ interaction with HDVs.

2 CONCEPTUAL

DEMONSTRATION

There are parallels to be drawn between the

competition for resources in nature and the interaction

between vehicles on the road network. Whilst animals

How Can Autonomous Road Vehicles Coexist with Human-Driven Vehicles? An Evolutionary-Game-Theoretic Perspective

377

in nature compete for food, territory and mates,

vehicles (both human-driven and autonomous)

compete for road space and priority on the road

network. In both worlds, competitors can either

cooperate to share the contested resource or expend

energy fighting for it. Only the “fittest” individuals

will succeed in reproduction and proliferation. This

fitness can be loosely defined by the individual’s

success in securing a viable amount of the contested

resources without compromising one’s viability.

Thus, the use of the concept of fitness ensures that

strategies adopted do not endanger the safety of the

agent (and by extension, its opponent). This is crucial

for ARVs since one of the main motivations for their

development is the elimination of human-related

safety risks. In terms of reproduction, animals

reproduce genetically via procreation, whereas

vehicles and driving styles “reproduce” memetically

(Dawkins, 2016) through increased sales and

imitation, respectively. This parallel is possible

because as far as behaviour is concerned, an ARV is

a living organism, whose goal is to “reproduce”

through selling more models (copies) of itself, which

it can achieve by being successful in the road space

and enticing potential customers to buy in.

Game-theoretic ARV models in the literature are

often validated against opponents playing by the same

rules (Kang & Rakha, 2020; Meng et al., 2016) In

reality, such results are only valid against a static,

homogenous population. The road user population,

however, is dynamic, varied and constantly evolving.

More importantly, road users have the capacity to

adjust their behaviour based on the characteristics of

their opponents. This is known as a conditional

strategy in game theory (Gross & Repka, 1998). We

envisage that, unlike model simulations in the

literature, HDVs will react to the introduction of

ARVs by adjusting their behaviour to maximise their

benefit. Primarily, HDVs will look to exploit ARVs’

propensity to be risk averse and their ability to

maintain permanent rationality and attention. Unless

ARVs can adapt in turn, they risk developing

strategies that are evolutionarily unstable and thus fail

in penetrating the population of road users.

2.1 Theoretical Formulation

As ARVs mature and make their way to the market,

they will begin their entry into the road user

population gradually. These ARVs will likely operate

within a connected environment in which ARV-ARV

interactions are concluded more efficiently and

effectively (Hancock, Nourbakhsh, & Stewart, 2019;

Wadud, MacKenzie, & Leiby, 2016).

As with the traditional Hawk-Dove game,

vehicles interact to share road space. Interaction costs

energy. Conceptually, there are three elements to an

interaction cost function: the economic costs (fuel

consumption, tyre wear, etc.), the driver costs

(increased demand on attention, planning, decision-

making, etc.) and the rider costs (safety, delay, ride

comfort, etc.). All costs traditionally apply to an

HDV. In contrast, ARVs arguably bear no driver

costs since ARV controllers are expected to be ever-

attentive and ever-processing. Thus, it makes no

difference to an ARV whether an interaction is

required and to what level of sophistication.

There are two key concepts to understand in how

vehicle interactions are represented in this paper.

Vehicles can either choose to facilitate an interaction

(Dove-like behaviour) or escalate in a bid to win

priority (Hawk-like behaviour). Facilitation can be

thought of as cooperation between the two vehicles to

conclude the interaction with the maximum (Pareto

efficient) payoff for both vehicles. Escalation, on the

other hand, constitutes competitive behaviour whose

aim is to maximise individual payoff at the expense

of the other vehicle. Therefore, if both vehicles

choose to facilitate, they interact to share priority

equitably, i.e., it goes to the vehicle which, by

convention, has right of way. We assume that, on

average, a vehicle would have right of way half of the

time. This is conceptualised as an interaction reward

𝑅0.5. If one vehicle escalates and the other

facilitates, the escalating vehicle forcibly takes

priority ( 𝑅1). If both escalate, both vehicles

attempt to forcibly win priority, expending

considerable energy in the process, but will determine

priority by convention in the end ( 𝑅0.5).

Facilitation incurs the least interaction cost ( 𝐶 ),

typically thought of as the mere cost of engaging in

an interaction with another vehicle. Escalation incurs

greater cost as that would likely involve aggressive

manoeuvring or excessive acceleration. Mutual

escalation incurs the greatest cost as both vehicles are

assumed to maintain their escalation for longer.

Table 1 below demonstrates the concepts discussed.

Table 1: Normal-form the road user interaction game.

Veh 2

Veh 1

Facilitate

(F)

Escalate

(E)

Facilitate

(

)

0.5 - 𝐶



, 0.5 - 𝐶



0 - 𝐶



, 1 - 𝐶



Escalate

(E)

1 - 𝐶



, 0 - 𝐶



0.5 - 𝐶



, 0.5 - 𝐶



𝐶



𝐶



𝐶



𝐶



VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

378

John Maynard Smith (1982) established two

conditions that a strategy must meet in order to be

evolutionarily stable. For a resident strategy, this

means the ability to resist invasion by new strategies.

For a new strategy, this means the ability to invade a

population of resident strategies.

 The subject strategy must do better against

itself than any other strategy could

 If a strategy exists which could do equally well

against the subject strategy, the subject strategy

must do better against the other strategy than

the other strategy could against itself

This can be mathematically expressed as follows

𝐸



𝑆



,𝑆





𝐸𝑆



,𝑆



 OR

(1)

𝐸



𝑆



,𝑆





𝐸𝑆



,𝑆



 AND

𝐸𝑆



,𝑆



𝐸𝑆



,𝑆





(2)

where

𝑆



,𝑆



are the subject strategy and the set of all

other strategies, respectively

𝐸𝑆



,𝑆



 is the total expected payoff for 𝑆



against 𝑆



These broad conditions can be adapted and

applied to the situation where ARVs are introduced to

the market. The current resident population in the

road network is that of HDVs. As of 2022, they

comprise well over 99% of all vehicular road traffic.

Therefore, any new fleet of ARVs which wish to

establish a meaningful foothold in the road user

network must satisfy one of the below two conditions

𝐸



𝑆



,𝑆





𝐸



𝑆



,𝑆





(3)

𝐸



𝑆



,𝑆





𝐸



𝑆



,𝑆





AND

𝐸



𝑆



,𝑆





𝐸𝑆



,𝑆





(4)

where

𝑆



,𝑆



are the interaction strategy sets

available to ARVs and HDVs, respectively

𝐸𝑆



,𝑆



 is the total expected payoff for each

strategy in Strategy Set 𝑥 against each strategy in

Strategy Set 𝑦 and can be calculated as follows

𝐸𝑆



,𝑆



 𝑢



𝑖



𝜎𝑖







(5)

where

𝑖 ∈ 1,2,3,… ,𝑛 is an outcome of the normal-

form game between Strategy Sets 𝑆



and 𝑆



𝑢𝑖 is the utility (payoff) of Outcome 𝑖, which is

calculated as 𝑅𝐶

𝜎𝑖 is the probability of Outcome 𝑖

Looking back at Table 1, 𝑖 in this scenario can be

one of four outcomes: 𝑖 ∈ 𝐹𝐹,𝐹𝐸,𝐸𝐹,𝐸𝐸. As

such, the total expected payoff for ARVs can be

thought of as the weighted sum of the ARV payoff of

each of these four outcomes weighted against each

outcome’s probability. This probability will depend

on the strategy employed by both ARVs and HDVs.

Substituting Equation 5 into the inequalities in 3

and 4 yields the following inequalities





𝑅



𝐶





𝜎



𝑖







𝑅



𝐶



𝜎𝑗







)

where

𝑖 ∈ 𝐹𝐹,𝐹𝐸,𝐸𝐹,𝐸𝐸 is an outcome of the game

between Strategy Sets 𝑆



and 𝑆



𝑗 ∈ 𝐹𝐹,𝐹𝐸,𝐸𝐹,𝐸𝐸 is an outcome of the game

between Strategy Sets 𝑆



and 𝑆







𝑅



𝐶





𝜎



𝑖







𝑅



𝐶



𝜎𝑗





AND





𝑅



𝐶





𝜎



𝑘











𝑅



𝐶





𝜎𝑙





)

where

𝑘 ∈ 𝐹𝐹,𝐹𝐸,𝐸𝐹,𝐸𝐸 is an outcome of the game

between Strategy Sets 𝑆



and 𝑆



𝑙 ∈ 𝐹𝐹,𝐹𝐸,𝐸𝐹,𝐸𝐸 is an outcome of the game

between Strategy Sets 𝑆



and 𝑆



Fulfilling the inequalities in 6 and 7 require the

optimisation of three variables

 Maximisation of 𝑅



/𝑅



 Minimisation of 𝐶



/𝐶



 Maximisation of 𝜎



𝑖



/𝜎



𝑘



where 𝑅



𝐶



𝑅



𝐶



is at a maximum

The solution(s) to this optimisation problem will

vary greatly in the real world based on ARV

application, the driving culture of the local existing

road user population, traffic rules and regulations, and

other considerations. However, the approaches

available to implement such solutions can generally

be grouped into three categories.

 External measures to provide greater incentive

for customers to adopt ARVs

 Capitalisation on inherent ARV behavioural,

computational, and sensory strengths

 Creation of a cooperative ARV subcommunity

where ARVs work together to maximise the

subcommunity’s over-all fitness

In the following section, we provide an example

of how some of these categorical solutions can be

used to optimise the problem.

How Can Autonomous Road Vehicles Coexist with Human-Driven Vehicles? An Evolutionary-Game-Theoretic Perspective

379

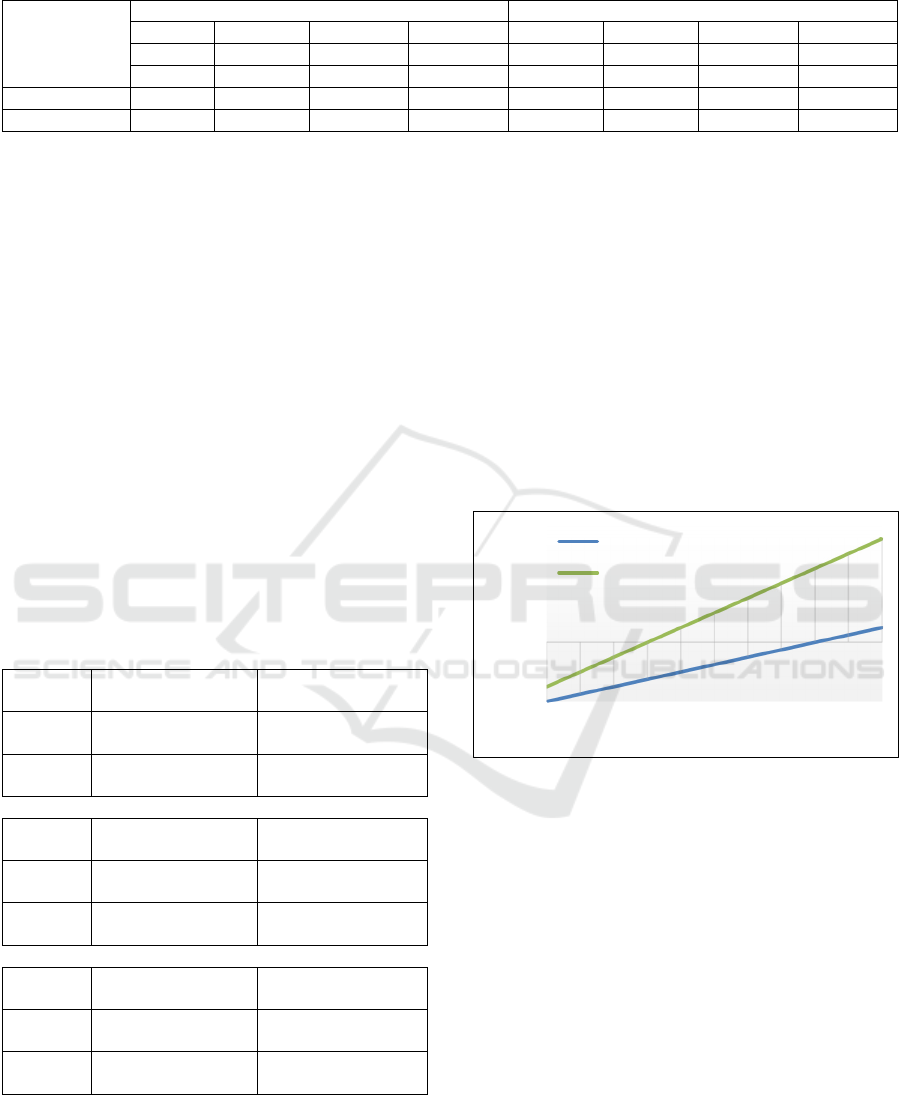
Table 2: Reward and cost parameters for road user interaction demonstration.

ARV HDV

𝐶



𝐶



𝐶



𝐶



𝐶



𝐶



𝐶



𝐶



0.2 0.2 0.55 0.85 0.3 0.3 0.65 1.05

𝑅



𝑅



𝑅



𝑅



𝑅



𝑅



𝑅



𝑅



vs ARV 0.5 0 1 0.5 0.5 0 1 0.8

vs HDV 0.5 0 1 0.2 0.5 0 1 0.5

2.2 Demonstrative Example

We continue with the set-up described in Section 2.1

with an initial introduction of a small population of

ARVs. Table 2 gives an overview of the chosen

parameters which correspond to the different costs

and rewards associated with vehicle interaction.

These values are simplified to illustrate the

concept of evolutionary stability. In the real world,

the parameters would be subject to a range of traffic,

policy, vehicle, and human factors which would

together make up the cost and reward functions.

The cost parameters outlined in Table 2 for ARVs

are lower than the cost parameters for HDVs. This is

to account for the fact that ARVs bear no driver costs

associated with the interaction. Hence, the over-all

cost for interacting with other vehicles is smaller.

Table 3: Normal-form of the ARV-ARV game (top), HDV-

HDV game (middle) and HDV-ARV game (bottom).

Fractions under actions denote each action’s probability

based on the game’s Nash equilibrium.

ARV 2

ARV 1

0.5

0.3, 0.3 -0.2, 0.45

0.5

0.45, -0.2 -0.35, -0.35

HDV 2

HDV 1

0.5

0.1, 0.1 -0.4, 0.35

0.5

0.35, -0.4 -0.65, -0.65

ARV

HDV

0.1, 0.3 -0.4, 0.45

0.35, -0.2 -0.35, -0.65

The reward parameter for mutual escalation for

HDVs ( 𝑅



 has been increased from 0.5 (equal

distribution of priority) to 0.8 (80-20 distribution of

priority to HDVs’ benefit). The reason for this is that

this scenario echoes the research findings discussed

in the introduction with regards to HDVs taking

advantage of and pushing ARVs to yield at most

interactions. The result of this asymmetry creates a

game matrix in which HDVs’ best strategy against

ARVs is to escalate with 100% probability. In turn,

this pushes ARVs to adopt a 100% probability to

facilitate. This creates a unique Nash equilibrium in

HDV-ARV interactions of EF. Table 3 illustrates this

in normal form.

HDVs’ exploitation of ARVs puts ARVs at an

immediate disadvantage. This is clearly demonstrated

in Figure 1, which illustrates the average expected

payoff profile for each of the two populations across

all possible proportions of ARVs out of the entire

population.

Figure 1: Average expected payoff profile for ARVs and

HDVs under the conditions set out in Table 3.

Under the currently set circumstances, HDVs

enjoy a significant advantage over ARVs across the

board. At lower proportions, ARVs receive the least

possible expected payoff. This will result in ARVs

failing to enter the road user population. Using the

figures in Table 3, we can calculate the total expected

payoff for each strategy pair at 𝑝𝐴𝑅𝑉  0 as follows

𝐸



𝑆



,𝑆





= 0.05 𝐸



𝑆



,𝑆





= 0.35

𝐸



𝑆



,𝑆





= -0.2 𝐸



𝑆



,𝑆





= -0.15

Therefore

𝐸



𝑆



,𝑆





𝐸



𝑆



,𝑆





Which means that the current set of HDV

strategies is evolutionarily stable, thus ARVs will not

be able to invade the population.

To combat this, we introduce two measures

inspired by the three solution categories outlined in

‐0,2

‐0,1

0,1

0,2

0,3

0,4

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

Averageexpectedpayoff

ProportionofARVs

ARVs

HDVs

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

380

Section 2.1. Namely, we allow ARVs to

communicate with each other via V2V channels. This

allows ARVs to adopt a 100% probability to facilitate

when interacting with one another, thus maximising

the payoff for both vehicles (Pareto efficient).

Second, we introduce a subsidy function which

offsets the economic costs of operating an ARV.

Subsidies can take many different forms and have

varying effects on both ARVs and HDVs in the target

population. Evolutionary game theory has already

been used to model the likely reaction of new-energy

car manufacturers to government subsidies and

penalties (Zhang et al., 2020). In this paper, we focus

on modelling the effect of a hypothetical subsidy on

the over-all fitness of ARVs in the population. The

subsidy is granted in a manner that is inversely

proportional to the proportion of ARVs in the

population so that maximum subsidy is given when

ARV population is at a minimum. Equation 8

illustrates how the subsidy is applied in this example.

𝐶





 𝐶



1  𝑄  𝑝𝐴𝑅𝑉

(8)

where

𝐶



is the ARV’s economic cost of interaction

𝐶





is the ARV’s economic cost of interaction

after subsidy

𝑝𝐴𝑅𝑉 is the

proportion

of ARVs in the population

𝑄 is a constant which determines the magnitude

of the subsidy and its effect on the given cost. For

example, a 𝑄 equal to 𝐶



offsets the entire economic

cost of interaction at 𝑝𝐴𝑅𝑉 = 0

We choose a 𝑄 value of 0.75, which provides a

net economic benefit (incentive) to ARVs. The

subsidy is terminated once the ARV proportion

reaches one half (𝑝𝐴𝑅𝑉  0.5). The resultant change

in normal-form payoffs is shown in Table 4.

Figure 2 illustrates the average expected payoff

profile for each of the two populations following the

application of the two measures.

Figure 2: Average expected payoff profile for ARVs and

HDVs under the conditions set out in Table 4.

Table 4: Normal-form of the ARV-ARV game (top), HDV-

HDV game (middle) and HDV-ARV game (bottom) after

applying V2V communication and government subsidy.

Fractions under actions denote each action’s probability

based on the game’s Nash equilibrium.

ARV 2

ARV 1

0.413, 0.413 -0.09, 0.75

0.75, -0.09 0.1, 0.1

HDV 2

HDV 1

0.5

0.1, 0.1 -04., 0.35

0.5

0.35, -0.4 -0.65, -0.65

ARV

HDV

0.1, 0.413 -0.4, 0.75

0.35, -0.09 -0.35, -0.2

The application of V2V communication has the

positive effect of improving the average expected

payoff for ARVs as their numbers grow. This helps

close the gap between ARVs and HDVs in terms of

over-all fitness. Applying the subsidy has the added

benefit of offsetting some of the costs incurred by

ARVs. This in turn offsets the average expected

payoff for ARVs to levels above that of HDVs across

the population proportion to which a subsidy applies.

Using the figures in Table 4, we can calculate the

total expected payoff for each strategy pair at

𝑝𝐴𝑅𝑉  0 as follows

𝐸



𝑆



,𝑆





= 0.41 𝐸



𝑆



,𝑆





= 0.35

𝐸



𝑆



,𝑆





= -0.09 𝐸



𝑆



,𝑆





= -0.15

Therefore

𝐸



𝑆



,𝑆





𝐸



𝑆



,𝑆





Which means that the new set of ARV strategies

is evolutionarily stable, thus ARVs will be able to

invade the population and reach an evolutionarily

stable state at the population proportion at which the

average expected payoff of ARVs equals that of

HDVs. This can be graphically identified in Figure 2

as the point of intersection between the two curves, at

approximately 𝑝𝐴𝑅𝑉  0.5.

‐0,2

‐0,1

0,1

0,2

0,3

0,4

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

Averageexpectedpayoff

ProportionofARVs

ARVs

HDVs

How Can Autonomous Road Vehicles Coexist with Human-Driven Vehicles? An Evolutionary-Game-Theoretic Perspective

381

3 CONCLUSIONS

The relationship between ARVs and HDVs is a

complex, dynamic, and evolving one. Evolutionary

game theory gives us a nature-based understanding of

a living, constantly evolving population: the

population of road users. Members of this population

interact with one another and compete for the finite

resources of space and priority. A vehicle or driving

style’s over-all performance in the daily task of

interactive driving dictates whether it continues to be

adopted or gets dropped in favour of an alternative.

This process of memetic reproduction is analogous to

genetic reproduction (Dawkins, 2016). Therefore,

without proper understanding of the evolutionary

dynamics of this population, ARV manufacturers and

policymakers may find that their ARVs are unable to

keep a meaningful presence within the road user

population. Cooperative behaviour between selfish

individuals in the natural world can only be

adequately explained using evolutionary game theory

(John Maynard Smith, 1982; J. Maynard Smith &

Price, 1973). Similarly, we argue that cooperative

behaviour in a naturally evolving road user

population with autonomous entities can only be

ensured if these entities are programmed in line with

the principles of evolutionary game theory.

The fitness and therefore success of ARVs is

governed by a cost and reward function. The

particulars of such a function vary greatly and depend

on the class of ARV in question, the prevalent driving

culture and road etiquette, and the traffic rules and

policies in place. For example, heavy goods vehicles

will skew considerably towards faster, more efficient

transport, whilst passenger vehicles may be more

sensitive to passenger comfort and satisfaction. The

values used in the examples described in this paper

have been chosen to demonstrate how the dynamic

may look under certain conditions and behavioural

patterns. However, if the road user population were to

behave differently or the network conditions be

different, it is highly probable that the resulting

dynamic will not produce evolutionarily stable

outcomes that allow for a viable ARV sub-

population. The topic of characterising and tuning the

reward and cost functions of ARVs is a subject that

requires further research.

Future research will investigate developing a

methodology by which ARVs can dynamically adapt

to changes in policy, HDV strategies, and other

factors to ensure evolutionary stability is maintained

throughout the course of ARV introduction and

beyond.

REFERENCES

Altman, E., El-Azouzi, R., Hayel, Y., & Tembine, H.

(2009). The evolution of transport protocols: An

evolutionary game perspective. Computer Networks,

53(10), 1751-1759. doi:https://doi.org/10.1016/

j.comnet.2008.12.023

Bendor, J., & Swistak, P. (1995). Types of evolutionary

stability and the problem of cooperation. Proceedings

of the National Academy of Sciences of the United

States of America, 92(8), 3596-3600.

doi:10.1073/pnas.92.8.3596

Brockmann, J. H., Grafen, A., & Dawkins, R. (1979).

Evolutionarily stable nesting strategy in a digger wasp.

Journal of Theoretical Biology, 77(4), 473-496.

doi:https://doi.org/10.1016/0022-5193(79)90021-3

Camara, F., Dickinson, P., Merat, N., & Fox, C. W. (2019).

Towards game theoretic AV controllers: measuring

pedestrian behaviour in Virtual Reality. Paper

presented at the Proceedings of TCV2019: Towards

Cognitive Vehicles.

Chatterjee, I., & Davis, G. A. (2013). Evolutionary Game

Theoretic Approach to Rear-End Events on Congested

Freeway. Transportation Research Record, 2386(1),

121-127. doi:10.3141/2386-14

Cooper, M., Lee, J. K., Beck, J., Fishman, J. D., Gillett, M.,

Papakipos, Z., Littman, M. L. (2019, 2019//).

Stackelberg Punishment and Bully-Proofing

Autonomous Vehicles. Paper presented at the Social

Robotics, Cham.

da Silva Rocha, A. B., & Salomão, G. M. (2019).

Environmental policy regulation and corporate

compliance in evolutionary game models with well-

mixed and structured populations. European Journal of

Operational Research, 279(2), 486-501.

doi:https://doi.org/10.1016/j.ejor.2019.05.040

Dawkins, R. (2016). The selfish gene (4th ed.). Oxford:

Oxford University Press.

Elvik, R. (2014). A review of game-theoretic models of

road user behaviour. Accident Analysis & Prevention,

62, 388-396. doi:https://doi.org/10.1016/j.aap.20

13.06.016

Fox, C., Camara, F., Markkula, G., Romano, R., Madigan,

R., & Merat, N. (2018). When Should the Chicken Cross

the Road? - Game Theory for Autonomous Vehicle -

Human Interactions. Paper presented at the

Proceedings of the 4th International Conference on

Vehicle Technology and Intelligent Transport Systems.

Free, C. (2018). How does Aggressive Driving Respond to

Passenger Load and Type.

Friedman, D. (1991). Evolutionary Games in Economics.

Econometrica, 59(3), 637-666. doi:10.2307/2938222

Gross, M. R., & Repka, J. (1998). Stability with Inheritance

in the Conditional Strategy. J Theor Biol, 192(4), 445-

453. doi:10.1006/jtbi.1998.0665

Hamilton, W. D. (1964). The genetical evolution of social

behaviour. I. Journal of Theoretical Biology, 7(1), 1-16.

doi:https://doi.org/10.1016/0022-5193(64)90038-4

Hammerstein, P., & Riechert, S. E. (1988). Payoffs and

strategies in territorial contests: ESS analyses of two

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

382

ecotypes of the spiderAgelenopsis aperta. Evolutionary

Ecology, 2(2), 115-138. doi:10.1007/BF02067272

Hancock, P. A., Nourbakhsh, I., & Stewart, J. (2019). On

the future of transportation in an era of automated and

autonomous vehicles. Proceedings of the National

Academy of Sciences, 116(16), 7684.

doi:10.1073/pnas.1805770115

Harris, C. M. (2017, 2017//). Autonomous Vehicle

Decision-Making: Should We Be Bio-inspired? Paper

presented at the Towards Autonomous Robotic

Systems, Cham.

Iwamura, Y., & Tanimoto, J. (2018). Complex traffic flow

that allows as well as hampers lane-changing

intrinsically contains social-dilemma structures.

Journal of Statistical Mechanics: Theory and

Experiment, 2018, 023408. doi:10.1088/1742-

5468/aaa8ff

Kandori, M. (1996). Evolutionary game theory in

economics.

Kang, K., & Rakha, H. A. (2020). A Repeated Game

Freeway Lane Changing Model. Sensors, 20(6), 1554.

Retrieved from https://www.mdpi.com/1424-

8220/20/6/1554

Karpus, J., Krüger, A., Verba, J. T., Bahrami, B., & Deroy,

O. (2021). Algorithm exploitation: Humans are keen to

exploit benevolent AI. iScience, 24(6), 102679.

doi:https://doi.org/10.1016/j.isci.2021.102679

Lei, L., & Gao, S. (2019). Transportation network

companies and drivers dilemma in China: an

evolutionary game theoretic perspective. Transport, 34,

1-12. doi:10.3846/transport.2019.11105

Liu, C., Lin, C., Shiraishi, S., & Tomizuka, M. (2018, 27-

29 June 2018). Improving Efficiency of Autonomous

Vehicles by V2V Communication. Paper presented at

the 2018 Annual American Control Conference (ACC).

Liu, L., Zhu, Y., & Guo, S. (2020). The Evolutionary Game

Analysis of Multiple Stakeholders in the Low-Carbon

Agricultural Innovation Diffusion. Complexity, 2020,

6309545. doi:10.1155/2020/6309545

Markkula, G., Madigan, R., Nathanael, D., Portouli, E.,

Lee, Y. M., Dietrich, A., . . . Merat, N. (2020). Defining

interactions: A conceptual framework for

understanding interactive behaviour in human and

automated road traffic. PsyArXiv Preprints.

doi:10.31234/osf.io/8w9z4

Meng, F., Su, J., Liu, C., & Chen, W. (2016, 31 Aug.-2

Sept. 2016). Dynamic decision making in lane change:

Game theory with receding horizon. Paper presented at

the 2016 UKACC 11th International Conference on

Control (CONTROL).

Millard-Ball, A. (2018). Pedestrians, Autonomous

Vehicles, and Cities. Journal of Planning Education

and Research, 38(1), 6-12.

doi:10.1177/0739456x16675674

Sirot, E. (2000). An evolutionarily stable strategy for

aggressiveness in feeding groups. Behavioral Ecology,

11(4), 351-356. doi:10.1093/beheco/11.4.351

Smith, J. M. (1982). Evolution and the Theory of Games.

Cambridge: Cambridge University Press.

Smith, J. M., & Price, G. R. (1973). The Logic of Animal

Conflict. Nature, 246(5427), 15-18.

doi:10.1038/246015a0

van Loon, R. J., & Martens, M. H. (2015). Automated

Driving and its Effect on the Safety Ecosystem: How

do Compatibility Issues Affect the Transition Period?

Procedia Manufacturing, 3, 3280-3285.

doi:https://doi.org/10.1016/j.promfg.2015.07.401

Wadud, Z., MacKenzie, D., & Leiby, P. (2016). Help or

hindrance? The travel, energy and carbon impacts of

highly automated vehicles. Transportation Research

Part A: Policy and Practice, 86, 1-18.

doi:https://doi.org/10.1016/j.tra.2015.12.001

Wang, S., Fan, J., Zhao, D., & Wu, Y. (2015). The Impact

of Government Subsidies or Penalties for New-energy

Vehicles A Static and Evolutionary Game Model

Analysis. Journal of Transport Economics and Policy

(JTEP), 49(1), 98-114. Retrieved from

https://www.ingentaconnect.com/content/lse/jtep/2015

/00000049/00000001/art00006

Wilkinson, G. S. (1984). Reciprocal food sharing in the

vampire bat. Nature, 308(5955), 181-184.

doi:10.1038/308181a0

Wu, C., Pei, Y., & Gao, J. (2015). Evolution Game Model

of Travel Mode Choice in Metropolitan Beijing.

Discrete Dynamics in Nature and Society, 2015,

638972. doi:10.1155/2015/638972

Xu, R., Wang, Y., Wang, W., & Ding, Y. (2019).

Evolutionary game analysis for third-party governance

of environmental pollution. Journal of Ambient

Intelligence and Humanized Computing, 10(8), 3143-

3154. doi:10.1007/s12652-018-1034-6

Yu, Y., Zhao, R., Huang, Y., & Yang, L. (2020). An

Evolutionary Game Theoretical Analysis to Conflicts

among Stakeholders Involved in the Operation of

Municipal Waste Incineration. Complexity, 2020,

8825284. doi:10.1155/2020/8825284

Zhang, L., Long, R., Huang, Z., Li, W., & Wei, J. (2020).

Evolutionary game analysis on the implementation of

subsidy policy for sustainable transportation

development. Journal of Cleaner Production, 267,

122159. doi:10.1016/j.jclepro.2020.122159

How Can Autonomous Road Vehicles Coexist with Human-Driven Vehicles? An Evolutionary-Game-Theoretic Perspective

383