A Data-driven Energy Estimation based on the Mixture of Experts

Method for Battery Electric Vehicles

Patrick Petersen

, Thomas Rudolf

and Eric Sax

FZI Research Center for Information Technology,

Haid-und-Neu-Straße 10-14, 76131 Karlsruhe, Germany

Keywords:

Battery Electric Vehicle, Energy Estimation, Machine Learning.

Abstract:

Battery electric vehicles (BEVs) are an immediate solution to the reduction of greenhouse gas emissions.

However, BEVs are limited in their range by the battery capacity. An accurate estimation of BEV’s range and

its energy consumption have become a signiﬁcant factor in eliminating customers “range anxiety”. To over-

come range anxiety, advanced algorithms can predict the remaining capacity, estimate the range and inform

the driver. Algorithms need to consider various inﬂuencing factors for their range estimation. A crucial part

for an accurate range estimation is the energy consumption modeling itself. Thus, machine learning-based

approaches are highly investigated which are able to learn nonlinear relations between relevant features and

the energy consumption. In this paper, we propose a data-driven approach for the energy estimation of BEVs

by utilizing ensemble learning to achieve a feature-speciﬁc estimation. In this paper, we trained neural net-

works on different road types independently. We improve the overall estimation by combining models via

the mixture of experts method compared to a monolithic trained neural network. The results demonstrate that

specialized neural networks for the energy estimation of BEVs are beneﬁcial for the energy estimation. This

approach contributes to reducing range anxiety and therefore helping toward elevated adoption of BEVs.

1 INTRODUCTION

The electriﬁcation of the automotive industry has be-

come the solution for future sustainable transport and

contributes to the reduction of air pollution and the

dependency on fossil fuels (Arif et al., 2021). Es-

pecially BEVs have become popular as alternative

for conventional internal combustion engine vehicles.

The reason for this is that BEVs offer zero local

emissions in combination with reduced noise pollu-

tion (Mahmoudzadeh Andwari et al., 2017; Sanguesa

et al., 2021; Hua et al., 2021). Due to their simpler de-

sign with regard to required parts for building them,

they are easier and cheaper to build, easier to maintain

and moreover more efﬁcient than combustion vehi-

cle counterparts (Sanguesa et al., 2021). Despite the

environmental beneﬁts of BEVs, customers are still

reluctant to fully accept and adept the electriﬁcation

trend in the transport sector. The reason for this cus-

tomer behavior is the limited charging infrastructure

and lower driving range of BEVs (Eisel et al., 2016;

https://orcid.org/0000-0003-3203-5470

https://orcid.org/0000-0002-6020-2611

https://orcid.org/0000-0003-2567-2340

Thorgeirsson et al., 2020). This causes one of the ma-

jor concerns of drivers, called ”range anxiety”, which

is deﬁned as the anxiety that drivers experiences when

worrying about whether the battery of their BEVs

runs out of power before arriving at the destination

or before a suitable charging point is reached (Noel

et al., 2019). In consequence, automakers are expand-

ing the range of BEVs by incorporating higher density

batteries and advanced technology to reduce charg-

ing times as well as support the deployment of appro-

priate charging infrastructure. However, drivers still

do not fully trust the displayed range of their vehicle,

which leads to a safety margin of roughly 27% (Yuan

et al., 2018). To achieve greater customer acceptance

of sustainable electriﬁed mobility and trust in the dis-

played range, an accurate estimation of the remaining

range of BEVs is essential to eliminate range anxiety

and increase the everyday usability. An accurate es-

timation of the energy consumption is also important

for the whole energy management strategy of BEVs

(Rudolf et al., 2021). However, determining the en-

ergy consumption and estimating range remains is a

non-trivial task. The actual energy consumption of a

BEV is inﬂuenced by many factors such as driving

384

Petersen, P., Rudolf, T. and Sax, E.

A Data-driven Energy Estimation based on the Mixture of Experts Method for Battery Electric Vehicles.

DOI: 10.5220/0011081000003191

In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2022), pages 384-390

ISBN: 978-989-758-573-9; ISSN: 2184-495X

style, road topology, weather and trafﬁc conditions.

Thus, for an accurate estimation, advanced algorithms

are required to take all these factors into account and

try to reduce uncertainties for the estimation (Krup-

pok et al., 2018).

Current estimation algorithms utilize data-driven

methods such as machine learning to accurately es-

timate the energy consumption of BEVs. Often, a

single monolithic neural network architecture with re-

spect to the available data features is used. However,

over the last couple of decades, research has shown

that combining multiple machine learning models

have a beneﬁcial impact on the predictive perfor-

mance compared to a single model (Sagi and Rokach,

2018).

Ensemble learning has already been used for en-

ergy estimation BEVs (Chung et al., 2019; Ullah

et al., 2021). Each model of the ensemble approach

is trained on the same data, thus each model is able

to give an overall estimation in every upcoming sit-

uation. The ﬁnal estimation result is computed by

combining the results of each individual model esti-

mations. However, no detailed studies have yet been

performed how ensemble learning can beneﬁt if each

individual model is specialized for certain conditions

e.g. road types or driver-styles. Thus, the goal of this

paper is to extend the mentioned related work by pre-

senting a methodology on how specialized neural net-

works can be utilized in an ensemble learning manner

for the energy estimation of BEVs.

The remaining sections are set out as follows: A

literature review on related works is presented in sec-

tion 2. In section 3 we present our methodology for

utilizing an ensemble neural network for the energy

consumption estimation specialized on road types. In

section 4, we show and discuss results of our imple-

mented energy consumption estimation method and

provide results and discussion. Finally, section 5

gives concluding remarks and an outlook.

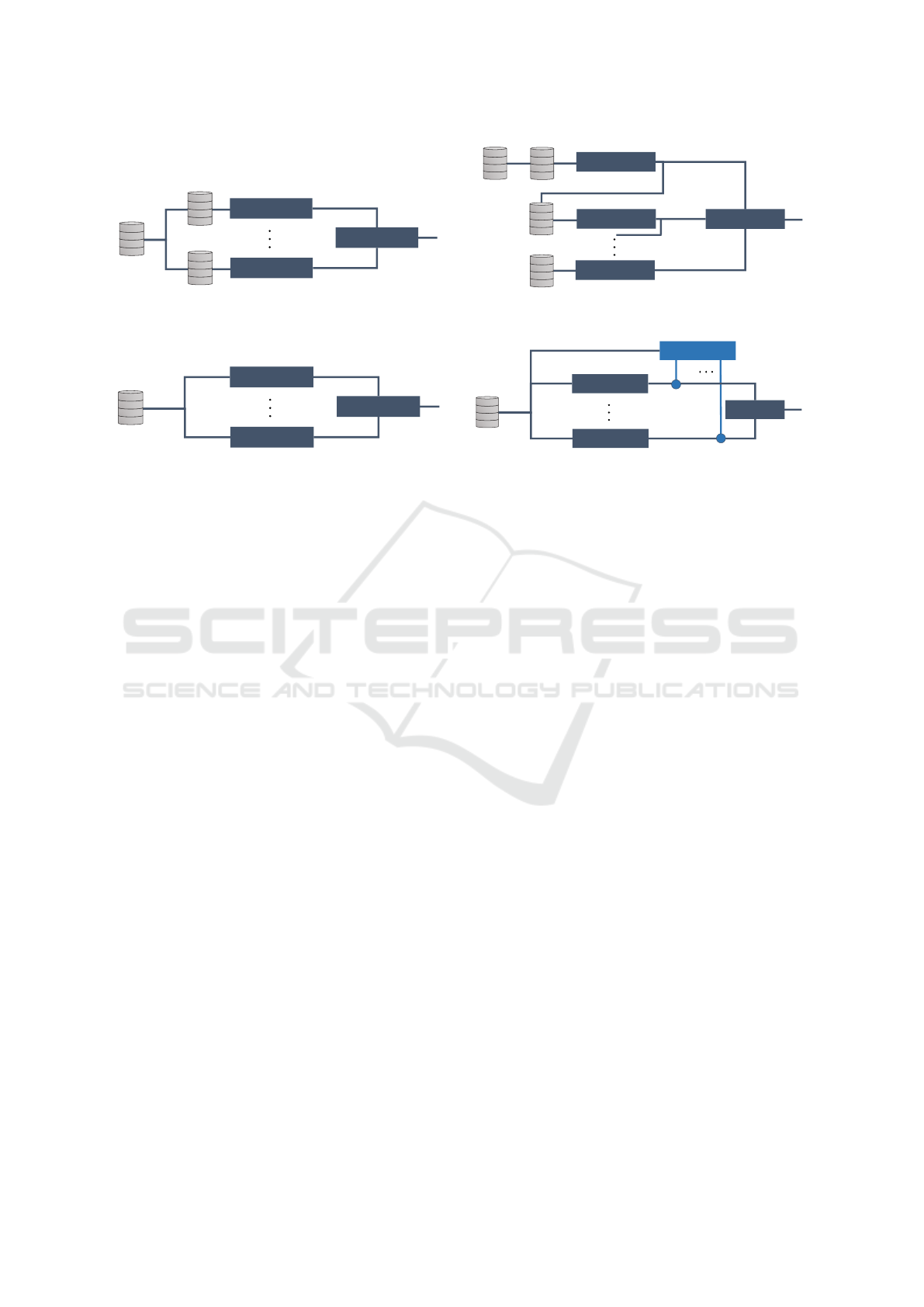
2 ENSEMBLE LEARNING

Ensemble learning is a ﬁeld of extensive research,

showing potential performance increment for estima-

tion applications. In general, the primary concept

of ensemble learning is “the wisdom of the crowd”

meaning that, based on the implemented ensemble

learning methods, the predictions of several base

models are combined for a ﬁnal prediction. Ensem-

ble learning can be either homogeneous or heteroge-

neous. A homogeneous ensemble is a collection of

base models of the same type built on different data

sets, whereas a heterogeneous ensemble is a collec-

tion of base models of different types built on the

same data set. In the following we want to give a

brief introduction to four common ensemble learning

methods (bagging, boosting, stacking and mixture of

experts) (Zhang and Ma, 2012). Describing their in-

dividual approach on how base models are used for

improving the ﬁnal prediction. Figure 1 shows an

overview of the common ensemble learning methods.

Bagging

Bootstrap aggregating, or more commonly known by

the acronym bagging, belongs to the homogeneous

ensemble learning methods (Breiman, 1996). It cre-

ates individual base models M

, . . . , M

for its en-

semble by training each model on a random dis-

tributed subset of the data. However, sampling is

done with replacements, thus samples are likely to

appear more than once. The ﬁnal output y(x) is re-

trieved by combining the outputs of each base models

(X), . . . , M

(X) (see Figure 1a). For classiﬁcation,

this can be done by a simple majority vote for class

c ∈ C (see the following equation):

y(x) = arg max

c∈C

∑

i=1

1(M

(x) = c) (1)

For regression, the ﬁnal output y(x) is retrieved via

averaging each individual output, as seen in the fol-

lowing equations:

y(x) =

∑

i=1

(x) (2)

Boosting

Boosting revolves around the idea of creating a

“strong” learner from a set of “weak” homogeneous

learners (Schapire, 1990; Freund and Schapire, 1999).

A weak learner is a model which achieves an accuracy

slightly better than random guessing. On the other

hand, a strong learner refers to a model which pro-

duces close to perfect outputs. For applying the boost-

ing method, models are trained sequentially (see Fig-

ure 1b). The ﬁrst weak learner is trained on a random

subset from the data. Every following weak learner

is trained on the previous output, thus trying to cor-

rect its predecessors. This is done by redistribution

of the previous weights of the preceding weak learn-

ers, to focus the resources of the following models

on tougher data for the output. A strong learner uses

weighted aggregation of the particular outputs of each

weak learner to get the ﬁnal output. Adaptive boost-

ing (AdaBoost) is a popular representative for the en-

semble learning boosting method. It uses a weighted

majority vote, which weights w

, . . . , w

are based on

the premise of giving the more accurate weak learner

A Data-driven Energy Estimation based on the Mixture of Experts Method for Battery Electric Vehicles

385

Data

M(x)

Combina�on

M(x)

(a) Bagging

Data

M(x)

Combine

M(x)

(b) Boosting

Data

M(x)

Meta Model

M(x)

Data

M(x)

Combine

M(x)

Gate

G(x)

(d) Mixture of experts

Figure 1: Graphical illustration of the four common ensemble learning methods.

outputs M

(X), . . . , M

(X) a greater inﬂuence for the

ﬁnal output y(x). The following equation shows the

basic formula for AdaBoost:

y(x) = sign

∑

i=1

(x)

(3)

Stacking

Stacking (or stacked generalization) relies on a meta

model, which tries to improve the ﬁnal output y(x) by

inducing which base models M

(X), . . . , M

(X) pro-

duce an accurate output (Smyth and Wolpert, 1997).

In contrast to bagging and boosting, the stacking

method often uses different learning algorithms such

as decision trees and neural networks within the en-

semble, thus following a heterogeneous approach for

the ensemble. Similar to cross-validation, the whole

data is split in k subsets, one for validation and the

remaining k − 1 for training. Each base model is then

trained on a different set of k − 1 subsets and after-

wards validated on the unseen k

subsets. The output

of each base model is then used as the training data

for a meta model, which learns on how to combine the

outputs of each base model (see Figure 1c). Thus, re-

sulting in learning weights w

, . . . , w

for the outputs

of each base model. After ﬁnished training for the

meta model all the previously trained base models are

discarded to retrain on the combined entire training

data (Rincy and Gupta, 2020). The following equa-

tion demonstrates the combination rule for the meta

model output y(x):

y(x) =

∑

i=1

(x) (4)

Mixture of Experts

Mixture of experts relies on the idea of divide-and-

conquer as the problem space is “divided” and then

“conquered” by combining experts for the output (see

Figure 1d) (Sagi and Rokach, 2018). It trains models

, . . . , M

on separated subsets of the training data,

which are derived by separating different regions of

the feature space (Jacobs et al., 1991). Hence, each

model becomes an expert on its individual feature

space. However, there is no general rule on how to

create the subsets, and they are even allowed to over-

lap. After each model becomes an expert for its sub-

space of the problem, it is responsible for its special-

ized subset. An additional learning model is then used

as a “gate” to learn and apply a weighted combination

rule for the outputs of each expert M

(X), . . . , M

(X).

Thus, the weights w

, . . . , w

are determined by the

gate and the ﬁnal output y(x) is aggregated by the fol-

lowing equation:

y =

∑

i=1

(x)M

(x) (5)

3 METHODOLOGY

Our proposed methodology for the application of en-

semble learning for energy estimation is based on the

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

386

mixture of experts method. Thus, experts are com-

bined to improve the estimation of energy usage for

a given trip. These experts apply a machine learn-

ing technique on real-world driving-data which is en-

riched by external data sources such as data from

navigation providers (e.g. Google or HERE) (Pe-

tersen et al., 2019). The input data for the experts

is aggregated by GPS information, based on links

from the navigation provider. This is reasonable due

to common eco-routing systems which rely on road

segments or links for their routing algorithms (Ku-

cukoglu et al., 2021). In this study, data from the nav-

igation provider HERE is used, which distinguishes

5 different road types. For each road type, an expert

model is trained by selecting corresponding link-wise

data. Thus, due to the nature of this methodology,

we call this approach Mixture of Road Energy Ex-

perts (MORE). An illustration of MORE is given in

Figure 2.

Selector

Combina�on

Data

1 2 3 4 5

Figure 2: Graphical illustration of the postulated methodol-

ogy MORE. Consisting of 5 road experts (RE) and a road-

based selector for combining the estimations.

It is important to note, that in contrast to the stan-

dard mixture of experts method, we don’t incorporate

weights for each expert. Since the approach is a link-

wise estimation method, based on routing informa-

tion, the composition of the trip is known. Thus, it is

known to the algorithm when to apply which road ex-

pert RE

, . . . , RE

for a link to beneﬁt from its exper-

tise. In the remaining part of this section, we will give

a description of the available data, presenting the se-

lected features as well as the energy estimation model.

3.1 Description of Real-world Driving

Data

Data-driven approaches such as MORE learn the re-

lationship between different real-world driving sig-

nals such as velocity and the energy consumption. In

this study, data from 152 real-world test drives of a

Porsche Taycan were used. The test drives were con-

ducted under real-world conditions in Europe, mainly

in Germany, and consists of an accumulated length

of approximately 7500 km. All signals on the Con-

troller Area Network (CAN) were sampled at 10 Hz.

As mentioned in the beginning of this section, the ex-

isting CAN data was enriched by trafﬁc and road data

from the navigation provider HERE and segmented

based on the link information. Yielding roughly

40000 road segments as the data input for the mod-

els used in MORE.

3.2 Machine Learning-based Energy

Consumption Model

The proposed methodology consists of ﬁve expert

models for the estimation of the energy consumption

on different road types. Research has shown that Mul-

tilayer Perceptron (MLP) architectures achieve high

accuracy when used in ensembles for time series es-

timation (Mahalakshmi et al., 2016), thus it was cho-

sen as an initial expert model type. Even tough newer

and more complex models for time series estimation

exist, MLPs yield sufﬁcient estimation accuracy and

can be used in a variety of different circumstances.

Thus, MLPs can be used as a baseline to investigate

the MORE approach. For the input of the MLPs var-

ious statistical features (e.g. mean and standard de-

viation) were calculated on the recorded signals for

each road segment. By applying a correlation-based

feature selection, 6 relevant features were deduced to

have a high impact on the energy consumption. Ta-

ble 1 gives an overview of the selected features as the

input for the expert models of MORE.

Table 1: Input data for the expert models.

Feature Description

mean

Mean speed of the ego vehicle

neg

% of negative slope

base

Base speed of road participants

l Length of the road segment

RT Road type of the current road segment

out

Outside temperature

4 EXPERIMENT AND

DISCUSSION

In this study, we evaluate the performance of MORE

and its individual road experts RE

, . . . , RE

against

the performance of a general monolithic model G

which is trained on all the training data. The orig-

inal data is split into training and testing by apply-

ing an 80/20 split. For verifying the robustness of

the models, we conducted a 5-fold cross-validation

experiment on the training data. Figure 4 illustrated

the 5-fold cross-validation procedure. For evaluation

A Data-driven Energy Estimation based on the Mixture of Experts Method for Battery Electric Vehicles

387

0 100 200 300 400 500

Epoch

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.10

RMSE Loss in kWh

Mean Training Loss

5-Fold Training Loss Spread

Mean Validation Loss

5-Fold Validation Loss Spread

(a) Model G

0 100 200 300 400 500

Epoch

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.10

RMSE Loss in kWh

Mean Training Loss

5-Fold Training Loss Spread

Mean Validation Loss

5-Fold Validation Loss Spread

(b) Model RE

0 100 200 300 400 500

Epoch

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.10

RMSE Loss in kWh

Mean Training Loss

5-Fold Training Loss Spread

Mean Validation Loss

5-Fold Validation Loss Spread

0 100 200 300 400 500

Epoch

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.10

RMSE Loss in kWh

Mean Training Loss

5-Fold Training Loss Spread

Mean Validation Loss

5-Fold Validation Loss Spread

(d) Model RE

0 100 200 300 400 500

Epoch

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.10

RMSE Loss in kWh

Mean Training Loss

5-Fold Training Loss Spread

Mean Validation Loss

5-Fold Validation Loss Spread

(e) Model RE

0 100 200 300 400 500

Epoch

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.10

RMSE Loss in kWh

Mean Training Loss

5-Fold Training Loss Spread

Mean Validation Loss

5-Fold Validation Loss Spread

(f) Model RE

Figure 3: Training and validation loss for applied 5-fold cross-validation.

Training Data

It .1

Training Folds

Valida�on Fold

It .2

It .3

It .4

It .5

Test Data

Original Data

Overall Model

Mean Performance

80 %

20 %

Test Data

Final Evalua�on

Figure 4: 5-Fold cross-validation for the training and test

data.

of each model, we used the root mean squared error

(RMSE) (see equation 6).

RMSE =

∑

i=1

− ˆy

)

(6)

Each model was trained for 500 epochs on its dedi-

cated data. Thus, road experts RE

were trained and

validated on the subset of road type n. As a result,

model G had the most data for the training and valida-

tion process compared to the individual road experts.

Table 2 give an overview of the composition of the

data in regard to the road types.

Table 2: Proportions of road types on the total distance.

Road Type v in data Percentage of data

1 90 kmh

−1

41 %

2 60 kmh

−1

35 %

3 57 kmh

−1

17 %

4 45 kmh

−1

4 %

5 28 kmh

−1

3 %

HERE deﬁnes the road types as ”used to classify

roads depending on the speed, importance and con-

nectivity of the road” (HERE, 2022). A lower number

indicates a higher priority, thus higher speed and im-

portance of that road type. Figure 3 shows the mean

training and validation loss, as well as the loss spread

across the folds for each model. It can be seen that

during the process, no model underﬁtted or overﬁt-

ted. However, the spread of the validation loss is

much higher for the road expert models RE

, . . . , RE

compared to the general monolithic model G. This

is due to the decreased data for the cross-validation

approach for the road expert models. Table 3 sum-

marizes the best mean validation loss of the cross-

validation approach.

The results indicate that besides RE

each road expert

yield a smaller RMSE for its individual road type. For

a ﬁnal evaluation of the combined road experts as our

proposed MORE we compare it to the general mono-

lithic model G on the test data which was not used

for the cross-validation. Table 4 compares the two

models on the whole test data, as well as a detailed

comparison of each road type within the test data.

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

388

Table 3: Cross-validation results of each model.

Model RMSE [kWh]

G 0.052

0.056

0.045

0.048

0.041

0.034

Table 4: Comparison of general monolithic model G and

MORE on test data.

Data RMSE

[kWh] RMSE

[kWh]

All test data 0.053 0.049

Road type 1 0.048 0.045

Road type 2 0.048 0.044

Road type 3 0.051 0.047

Road type 4 0.055 0.052

Road type 5 0.052 0.051

It can be seen that MORE has an overall better

performance on each road type. Each individual road

expert RE

of MORE has an better estimation perfor-

mance on its dedicated part of the test data compared

to the general monolithic model G. In total, MORE

has an 7.5% improvement over the performance of

model G for the whole test data. It illustrates the po-

tential on how ensemble learning can improve the en-

ergy estimation for BEVs.

5 CONCLUSION

This paper presents a data-driven approach for the en-

ergy estimation of BEVs based on ensemble learning,

utilizing the mixture of experts method to specialize

models on speciﬁc road types. It is found that, the

proposed method MORE with 5 specialized road ex-

perts improves the RMSE of the energy estimation by

roughly 7.5% compared to the estimation of a mono-

lithic model. The results show that, energy estima-

tion beneﬁts from utilizing an ensemble neural net-

work approach. However, testing this concept in live

operation on a BEV may yield additional insights on

the applied advantages of MORE.

The research shown in this paper could be ex-

tended in the future in different aspects. Different spe-

cializations for the mixture of experts method should

be investigated, e.g. for different driver styles. Fur-

ther work could incorporate advanced methods for a

robust and reliable classiﬁcation of different driver-

styles, which will be used for the experts. A fur-

ther study could assess the impact of individual fea-

tures for each specialized neural network due to their

importance for the energy estimation, e.g. on dif-

ferent road types or for different driver-styles. Si-

multaneously investigating different combinations of

neuronal network architectures (e.g. RNN, CNN or

Transformer) might also optimize the overall accu-

racy and data efﬁciency of utilizing heterogeneous

models to beneﬁt from their individual traits.

REFERENCES

Arif, S. M., Lie, T. T., Seet, B. C., Ayyadi, S., and Jensen,

K. (2021). Review of Electric Vehicle Technologies,

Charging Methods, Standards and Optimization Tech-

niques. Electronics, 10(16):1910.

Breiman, L. (1996). Stacked regressions. Machine Learn-

ing, 24(1):49–64.

Chung, Y. W., Khaki, B., Li, T., Chu, C., and Gadh, R.

(2019). Ensemble machine learning-based algorithm

for electric vehicle user behavior prediction. Applied

Energy, 254(April):113732.

Eisel, M., Nastjuk, I., and Kolbe, L. M. (2016). Understand-

ing the inﬂuence of in-vehicle information systems on

range stress – Insights from an electric vehicle ﬁeld

experiment. Transportation Research Part F: Trafﬁc

Psychology and Behaviour, 43:199–211.

Freund, Y. and Schapire, R. E. (1999). A Short Introduction

to Boosting. In Proceedings of the 16th International

Joint Conference on Artiﬁcial Intelligence - Volume 2.

HERE (2022). FunctionalClassType. https:

//developer.here.com/documentation/routing/

dev guide/topics/resource-type-functional-class.html

[Online; Accessed: 2022-01-22].

Hua, X., Thomas, A., and Shultis, K. (2021). Re-

cent progress in battery electric vehicle noise,

vibration, and harshness. Science Progress,

104(1):003685042110052.

Jacobs, R. A., Jordan, M. I., Nowlan, S. J., and Hinton, G. E.

(1991). Adaptive Mixtures of Local Experts. Neural

Computation, 3(1):79–87.

Kruppok, K., Kriesten, R., and Sax, E. (2018). Calcu-

lation of route-dependent energysaving potentials to

optimize EV’s range. In Bargende, M., Reuss, H.-

C., and Wiedemann, J., editors, 18. Internationales

Stuttgarter Symposium, pages 1349–1363. Springer

Fachmedien Wiesbaden, Wiesbaden.

Kucukoglu, I., Dewil, R., and Cattrysse, D. (2021). The

electric vehicle routing problem and its variations: A

literature review. Computers & Industrial Engineer-

ing, 161:107650.

Mahalakshmi, G., Sridevi, S., and Rajaram, S. (2016). A

survey on forecasting of time series data. In 2016

International Conference on Computing Technologies

and Intelligent Data Engineering, ICCTIDE 2016. In-

stitute of Electrical and Electronics Engineers Inc.

Mahmoudzadeh Andwari, A., Pesiridis, A., Rajoo, S.,

Martinez-Botas, R., and Esfahanian, V. (2017). A re-

view of Battery Electric Vehicle technology and readi-

ness levels. Renewable and Sustainable Energy Re-

views, 78(May):414–430.

A Data-driven Energy Estimation based on the Mixture of Experts Method for Battery Electric Vehicles

389

Noel, L., Zarazua de Rubens, G., Sovacool, B. K., and

Kester, J. (2019). Fear and loathing of electric vehi-

cles: The reactionary rhetoric of range anxiety. Energy

Research & Social Science, 48:96–107.

Petersen, P., Thorgeirsson, A. T., Scheubner, S., Otten, S.,

Gauterin, F., and Sax, E. (2019). Training and vali-

dation methodology for range estimation algorithms.

In Proceedings of the 5th International Conference

on Vehicle Technology and Intelligent Transport Sys-

tems, VEHITS 2019, Heraklion, Crete, Greece, May

3-5, 2019, pages 434–443. SciTePress.

Rincy, T. N. and Gupta, R. (2020). Ensemble Learn-

ing Techniques and its Efﬁciency in Machine Learn-

ing: A Survey. In 2nd International Conference on

Data, Engineering and Applications (IDEA), pages 1–

6, Bhopal, India. IEEE.

Rudolf, T., Schurmann, T., Schwab, S., and Hohmann,

S. (2021). Toward Holistic Energy Management

Strategies for Fuel Cell Hybrid Electric Vehicles in

Heavy-Duty Applications. Proceedings of the IEEE,

109(6):1094–1114.

Sagi, O. and Rokach, L. (2018). Ensemble learning: A sur-

vey. WIREs Data Mining and Knowledge Discovery,

8(4).

Sanguesa, J. A., Torres-Sanz, V., Garrido, P., Martinez, F. J.,

and Marquez-Barja, J. M. (2021). A Review on Elec-

tric Vehicles: Technologies and Challenges. Smart

Cities, 4(1):372–404.

Schapire, R. E. (1990). The strength of weak learnability.

Mach. Learn., 5(2).

Smyth, P. and Wolpert, D. (1997). Stacked Density Esti-

mation. In Advances in Neural Information Process-

ing Systems 10, [NIPS Conference, Denver, Colorado,

USA, 1997], pages 668–674. The MIT Press.

Thorgeirsson, A. T., Scheubner, S., Funfgeld, S., and Gau-

terin, F. (2020). An Investigation Into Key Inﬂuence

Factors for the Everyday Usability of Electric Vehi-

cles. IEEE Open Journal of Vehicular Technology,

1(Xx):348–361.

Ullah, I., Liu, K., Yamamoto, T., Zahid, M., and Jamal, A.

(2021). Electric vehicle energy consumption predic-

tion using stacked generalization: An ensemble learn-

ing approach. International Journal of Green Energy,

18(9):896–909.

Yuan, Q., Hao, W., Su, H., Bing, G., Gui, X., and Saﬁkhani,

A. (2018). Investigation on Range Anxiety and Safety

Buffer of Battery Electric Vehicle Drivers. Journal of

Advanced Transportation, page 12.

Zhang, C. and Ma, Y. (2012). Ensemble Machine Learning.

Springer US, Boston, MA.

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

390