A Hybrid Genetic Algorithm using Progressive Alignment and

Consistency based Approach for Multiple Sequence Alignments

Vitoria Zanon Gomes

1 a

, Matheus Carreira Andrade

1 b

, Anderson Rici Amorim

2,1 c

and Geraldo Francisco Doneg

a Zafalon

1,3 d

Department of Computer Science and Statistics, Universidade Estadual Paulista (UNESP), Rua Crist

ao Colombo, 2265,

Jardim Nazareth, S

ao Jos

e do Rio Preto - SP, 15054-000, Brazil

Department of Computer and Digital Systems Engineering, Universidade de S

ao Paulo (USP) - Escola Polit

ecnica,

Av. Prof. Luciano Gualberto, Travessa 3, 158, Butant

a, S

ao Paulo - SP, 05508-010, Brazil

Department ICET, Universidade Paulista, Avenida Presidente Juscelino Kubitschek de Oliveira, s/n, Jardim Tarraf II,

ao Jos

e do Rio Preto-SP, 15091-450, Brazil

Keywords:

Bioinformatics, Multiple Sequence Alignment, Genetic Algorithm, Hybrid Multiple Sequence Alignment.

Abstract:

The multiple sequence alignment is one of the most important tasks in bioinformatics, since it allows to analyze

multiple sequences at the same time. There are many approaches for this problem such as heuristics and meta-

heuristics, that generally lead to great results in a plausible time, being among the most used approaches.

The genetic algorithm is one of the most used methods because of its results quality, but it had a problematic

disadvantage: it can be easily trapped in a local optima result, not being able to reach better alignments. In

this work we propose a hybrid genetic algorithm with progressive and consistency-based methods as a way to

smooth the local optima problem and improve the quality of the alignments. The obtained results show that

our method was able to improve the quality of AG results 2 a 27 times, smoothing the local maximum problem

and providing results with more biological signiﬁcance.

1 INTRODUCTION

Due to the increasing importance of Next Generation

Sequencing (NGS) techniques, the amount of biolog-

ical data is in constant growth nowadays (Amorim

et al., 2018; Bawono et al., 2017), leading to a cres-

cent need to faster and more accurate biological anal-

ysis, so the computational support became essential to

help on those biological tasks (Baxevanis et al., 2020).

At the begining, pairwise alignment algorithms

were created, aligning two sequences at once.

Needleman and Wunsch (1970) created an algorithm,

known as Needleman-Wunsch algorithm, able to gen-

erate the optimal alignment for the given sequences

by dynamic programming (DP). However, if the input

has three or more sequences the execution time grows

prohibitively due the use of DP and the nature of the

problem. The so-called multiple sequence alignment

(MSA) is an NP-Complete (Non-Polynomial) prob-

https://orcid.org/0000-0003-4176-566X

https://orcid.org/0000-0002-1670-266X

https://orcid.org/0000-0001-7862-7530

https://orcid.org/0000-0003-2384-011X

lem (Wang and Jiang, 1994), which means that, until

now, there is no deterministic method able to ﬁnd the

optimal solution for it in a polynomial time, that is, a

reasonable execution time (the P versus NP problem)

(Cook, 2006).

So, the development of MSA algorithms came as a

way to analyze many sequences simultaneously (Ba-

wono et al., 2017) through a stochastic approach, be-

ing able to produce results with relevant biological

signiﬁcance in a timely manner (Nute et al., 2019). A

MSA algorithm rearranges DNA or protein sequences

through gap insertions, following a predeﬁned crite-

ria (Bawono et al., 2017; Edgar and Batzoglou, 2006)

as a way to maximize the similar residues that are

matched (Mount, 2001).

There are many approaches to perform MSA, such

as progressive alignment (Lassmann, 2020; Sievers

and Higgins, 2018; Thompson et al., 1994), Fast-

Fourier Transform (Katoh et al., 2002, 2019), simu-

lated annealing (Correa et al., 2012; Kim et al., 1994),

Tabu Search (Riaz et al., 2004), artiﬁcial bee colony

(Rubio-Largo et al., 2016), genetic algorithm (GA)

(Gondro and Kinghorn, 2007; Kaya et al., 2016),

Gomes, V., Andrade, M., Amorim, A. and Zafalon, G.

A Hybrid Genetic Algorithm using Progressive Alignment and Consistency based Approach for Multiple Sequence Alignments.

DOI: 10.5220/0011082900003179

In Proceedings of the 24th International Conference on Enterprise Information Systems (ICEIS 2022) - Volume 2, pages 167-174

ISBN: 978-989-758-569-2; ISSN: 2184-4992

167

among others.

Progressive alignment is the base of many well-

known tools, such as the Clustal family (Sievers and

Higgins, 2018; Thompson et al., 1994), Kalign (Lass-

mann, 2020) and MUSCLE (Edgar, 2004), and it’s

very fast when compared with other methods (Rubio-

Largo et al., 2016). However, a great accuracy is not

guaranteed since errors occurred in the ﬁrst steps of

the algorithm can not be repaired, causing error prop-

agation (Bawono et al., 2017; Gondro and Kinghorn,

2007; Rubio-Largo et al., 2016).

GA, on the other hand, does not have this disad-

vantage, since it is an iterative algorithm (Gondro and

Kinghorn, 2007), which means that errors occured in

a certain iteration can be repaired in the next one (Ba-

wono et al., 2017).

The Genetic Algorithm is a sthocastic method in-

spired by the evolution theory (Amorim et al., 2021;

Chowdhury and Garai, 2017). It is also a population-

based method, where the individuals represent a can-

didate solution for the problem (Kaya et al., 2016). In

each generation, these individuals are exposed to mu-

tation and recombination operators (Lee et al., 2008)

and evaluated by a ﬁtness function, so the best indi-

viduals will produce a offspring and the worst ones

are discarded (Kaya et al., 2016).

The GA is frequently used for solving MSA prob-

lems (Chowdhury and Garai, 2017) since the qual-

ity and biological signiﬁcance from its results tends

to be better when compared to progressive methods

(Gondro and Kinghorn, 2007). SAGA (Notredame

and Higgins, 1996) and MSA-GA (Gondro and

Kinghorn, 2007) are well known tools that apply GA

for MSA. The ﬁrst one has 22 complex operators for

mutation and recombination, but even getting good

results, further studies shown that the complexity of

the operators does not inﬂuence on the quality of the

ﬁnal result (Thomsen and Boomsma, 2004). The sec-

ond one, on the other hand, is a simpler version of

GA, being able to produce great results when com-

pared to other well known tools, such as Clustal W

(Gondro and Kinghorn, 2007).

However, the GA also has its disadvantages. Due

to its greedy nature, the algorithm can be trapped in

a local optima result, which means that the solution

is nott the global optima and could be improved (Lee

et al., 2008).

Thus, this work aims to develop a new hy-

brid approach using the progressive alignment and a

consistenc-based heuristic, so we can improve even

more the GA-based tools results, avoiding the local

optima problem without increasing prohibitively the

computational cost of the method.

This work is organized as follows: in section 2, the

Multiple Sequence Alignment is explained, in section

3 the related works are shown, in section 4 we de-

scribe the materials used and show our methodology,

in section 5 we show the tests and discuss about the

obtained results and in section 6, we show our con-

clusions.

2 MULTIPLE SEQUENCE

ALIGNMENT

As mentioned before, a Multiple Sequence Alignment

is the rearrange of sequences following a pre-deﬁned

criteria. Given a set of sequences S =

{

s1, s2, ..., sn

}

deﬁned over an alphabet

∑

, where

∑

= {A, T, C, G}

for DNA sequences and

∑

= {A, C, D, E, F, G, H,

I, K, L, M, N, P, Q, R, S, T, V, W, Y} for protein se-

quences, a MSA is a set S’ =

{

, s2

, ..., sn

}

deﬁned

over an alphabet

∑

’ where

∑

’ =

∑

∪ (−), which is the

gap symbol (Rubio-Largo et al., 2016). A gap repre-

sents insertions and/or deletions on the sequences.

In a practical way, a MSA is a matrix, where the

rows represent the sequences and the columns repre-

sent the aligned bases. This matrix is generated by

the insertion of gaps along the sequences following a

given criteria, not allowing columns with only gaps,

equaling the sequences length and optimizing quality

metrics.

3 RELATED WORKS

The local optima problem in GA is well-known in the

literature, and many published works try to resolve

it. Lee et al. (2008) describes the GA-ACO: a hybrid

GA with Ant Colony Optimization (ACO) algorithm,

which helps GA to escape from local optima, improv-

ing the quality of the results. But, since ACO has

a greater computational cost than other approaches,

like the progressive ones, the total computational cost

of GA-ACO becomes exorbitant (Rubio-Largo et al.,

2016).

Nonetheless, recent works show that hybrid differ-

ent heuristics and metaheuristics is important. Chat-

terjee et al. (2019) use the Chemical Reaction Opti-

mization (CRO) algorithm to help GA to achieve bet-

ter results. The CRO is executed at the end of every

GA generation, looking for alignments better than the

current population. Even with good results achieved,

producing better results in 47% when compared to

other well-known tools, the authors warned that the

method has some difﬁculties when dealing with less

similar sequences.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

168

Figure 1: An example of multiple sequence alignment.

Zafalon et al. (2021) also describe a hybrid ap-

proach to solve the GA local optima problem us-

ing Kalign (Lassmann, 2020), a progressive approach.

The method was able to get better results when com-

pared to GA by itself, but the authors describe that

the method still having some difﬁculties when deal-

ing with less similar sequences, suggesting that other

heuristics could help to improve even more the align-

ments.

Rubio-Largo et al. (2016) used a hybrid-

progressive approach to solve the local optima prob-

lem too, but this time in the Artiﬁcial Bee Colony al-

gorithm (ABC). Due to its evolutionary nature, the

ABC have the same disadvantage as GA, so the

Kalign tool (Lassmann, 2020) is applied to execute

a local search in stagnated bees (individuals) as a way

to improve the quality of the results at a viable run

time. The authors show that the method got better

results when compared to the existing GA tools for

MSA, and its results are statistically relevant in rela-

tion to other well-known tools.

Once the less similar sequences generally implies

noisy alignments, the hybridization with consistency-

based methods may overcome this drawback. As

we can see, Amorim et al. (2015) use the COF-

FEE, a consistency-based function (Notredame et al.,

1998), instead of the Weighted Sum-of-Pairs (WSP)

in MSA-GA tool (Gondro and Kinghorn, 2007). The

results obtained with the COFFEE objective function

were better than the results with WSP, and improve-

ments on this method can be seen in Amorim et al.

(2018).

Do et al. (2005) proposed a new approach called

ProbCons to the MSA problem, using consistency as

its objective function. It works creating a guide tree

using probability matrices and the consistency func-

tion, so the progressive alignment can be executed,

resulting in more accurate and statistically relevant

alignments in relation to other tool.

Thus, a hybrid approach is a effective way to deal

the local optima problem, and when combined with a

consistency based method it may result in alignments

with better quality and smooth any difﬁculties that

might occur due to the use of progressive alignment.

4 THE PROPOSED METHOD

4.1 MSA-GA

The MSA-GA tool was chosen as the GA in this work

due its simplicity when compared to other GA tools

and for the quality of its results that are better than the

most used MSA methods such as Clustal W (Gondro

and Kinghorn, 2007).

The execution starts initializing the population. It

can be done by pre-alignment ﬁles or based in pair-

wise alignment with the Needleman-Wunsch algo-

rithm (Needleman and Wunsch, 1970). Then, each

individual is evaluated with the WSP, the worst ones

will be discarded and the best ones will be exposed to

genetic operators: crossover and mutation, as a way

to diversify the population and to possibly produce

better individuals.

The crossover operators work using two individu-

als to generate an offspring. The MSA-GA uses two

of these operators: horizontal recombination and ver-

tical recombination. Both operators deﬁne cut points

on both parents, separating them in two parts, and

combine their parts into new alignments, but the ﬁrst

one deﬁnes a horizontal cut point and the second one

a vertical cut pont.

The mutation operators modify a individual align-

ment, creating a new individual. MSA-GA uses three

mutation operators to optimize gap positions: gap

opening, that selects randomly a position and inserts

a block of gaps into the sequence; gap extension, that

selects a block of gaps and adds a gap at its end; and

gap reduction, that deletes a gap from a block of gaps

selected randomly.

After that, we have a new population and the in-

dividuals are evaluated by the WSP again. Each it-

eration follows these steps until a pre-deﬁned criteria

is reached, such as a limit of iterations or a certain

individual score. 2 shows the MSA-GA execution.

A Hybrid Genetic Algorithm using Progressive Alignment and Consistency based Approach for Multiple Sequence Alignments

169

Knowing that, our method will be executed after

the tournament end, modifying the new population

before the next tournament begins.

4.2 First Reﬁnement Step: Local

Realignment with Kalign

As a way to smooth the local optima, the local realign-

ment with a progressive method is executed when the

GA reaches n iterations without any improvement in

the best individual, which is the individual with best

score (evaluated by WSP), being n a user-deﬁned pa-

rameter. Initially, a portion of the best individual

is randomly selected to be realigned by Kalign. Its

length is also randomly deﬁned over an interval be-

tween 5%-25% of the individual size, since Rubio-

Largo et al. (2016) showed that this interval is efﬁ-

cient for a local reﬁnement. Then, the gaps of this

portion are removed and it is written in a fasta ﬁle

that is the input for Kalign.

After the realignment, the output ﬁle produced by

Kalign is read and the sequences portions are rein-

serted at the original individual, replacing the old por-

tion. Then, the new individual has its score evaluated,

and if there is any improvement, it replaces the best

individual on the GA population, and the execution

continues. Figure 3 shows how this step works.

Despite the good results obtained with the ﬁrst

step by itself, it may have some difﬁculties when deal-

ing with less similar sequences due to the propagation

error problem from the progressive method. Looking

for solve that while improving even more the quality

of the GA results and solving its local optima prob-

lem, a second step is added to the hybrid method.

4.3 Second Reﬁnement Step: A

Consistency-based Realignment

As shown in section 3, a consistency-based approach

helps to achieve better alignments without signiﬁcant

disadvantages, so this work added to the hybrid GA

a second step as a way to deal with less similar se-

quences, smoothing the local optima problem even

more: the realignment of the worst individual using

the T-COFFEE

tool (Notredame et al., 2000). T-

COFFEE is an open-source package for MSA, and it

is well known by the quality of its results, the reason

why it was chosen as the consistency-based method

for this work.

This routine is executed at the end of the genera-

tion after n iterations, being n a user-deﬁned param-

eter. However, unlike the ﬁrst reﬁnement step of our

http://www.tcoffee.org/

algorithm, it does not use the non improvement con-

dition, and it works with the worst individual in the

population. We show in Figure 4 the execution of the

consistency-based realignment step. Basically, we ex-

ecute the processes as follows:

1. First of all, the search for the worst individual in

the population takes place. The routine starts by

checking the population score array and ﬁnding

the smallest value. Then, its index leads to its

respective individual in the population. If there

is more than one individual with the same worst

score, then the ﬁrst found is the chosen one.

2. After that, the selected individual has its gaps

deleted and it is written in a new ﬁle. This ﬁle

is used as the input to T-COFFEE, which will re-

align this individual, creating a new alignment as

the output.

3. Back in the GA, the output ﬁle is read, and the

WSP function evaluates the new individual. If

there is any improvement when compared to the

original individual, the new one replaces it, and

the GA execution continues, starting a new gener-

ation. If the new alignment has a score better than

the actual best score, it becomes the best individ-

ual in the population.

If both steps are going to be executed in a same

generation, the progressive method is processed ﬁrst,

followed by the consistency method.

5 RESULTS AND DISCUSSION

5.1 Benchmark and Test Parameters

In this work, we used the test cases from BAliBase

(Thompson et al., 2005). This benchmark contains

sequences sets, organized in different families with

different characteristics, such as biological similarity

and size. BAliBase also contains the reference align-

ments, so we can compare the obtained results with

the ideal ones.

We have executed cases from RV11, RV12, RV20,

RV30, RV40 and RV50 families. The ﬁrst one con-

tains sequence sets with less than 20% of similarity;

the second one is related to sequences sets which at

least two sequences are between 20% and 40% simi-

lar; the third one contains sequence sets with similar-

ity between 20% and 40%; the fourth one is related

to sets with, at least, one divergent sequence; the ﬁfth

one contains sequence sets with more than 40% of

similarity, but less than 20% when compared to the

other families; last but not least, the sixth one is re-

lated to sequences with many insertions.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

170

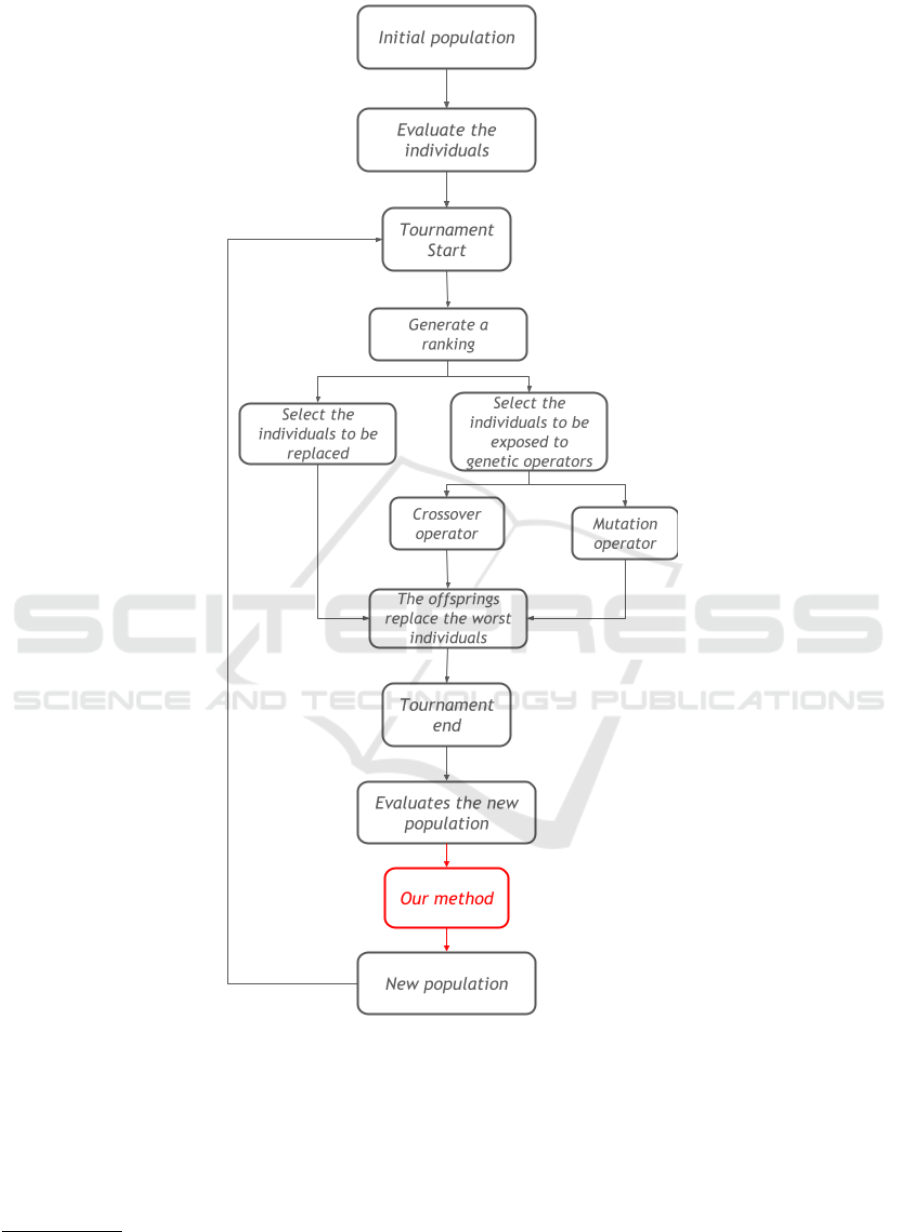
Figure 2: Flowchart of MSA-GA execution.

To measure the quality of the results, we used the

Qscore tool

to calculate the Q (Quality) and TC (to-

tal column) scores, which are metrics related to the

biological signiﬁcance of the alignment when com-

pared to the reference alignment. The scores values

are between 0 and 1, so the greater the score, more

https://www.drive5.com/qscore/

biologically signiﬁcant is the alignment and better the

produced MSA.

All the tests were executed using a computer with

Windows 10 Home 64 bits, Intel Core i7-8565U CPU

4.60GHz processor and 12GB of RAM. The parame-

ters of MSA-GA were the default values described by

Gondro and Kinghorn (2007) and the n parameter for

both progressive and consistency reﬁnement routines

A Hybrid Genetic Algorithm using Progressive Alignment and Consistency based Approach for Multiple Sequence Alignments

171

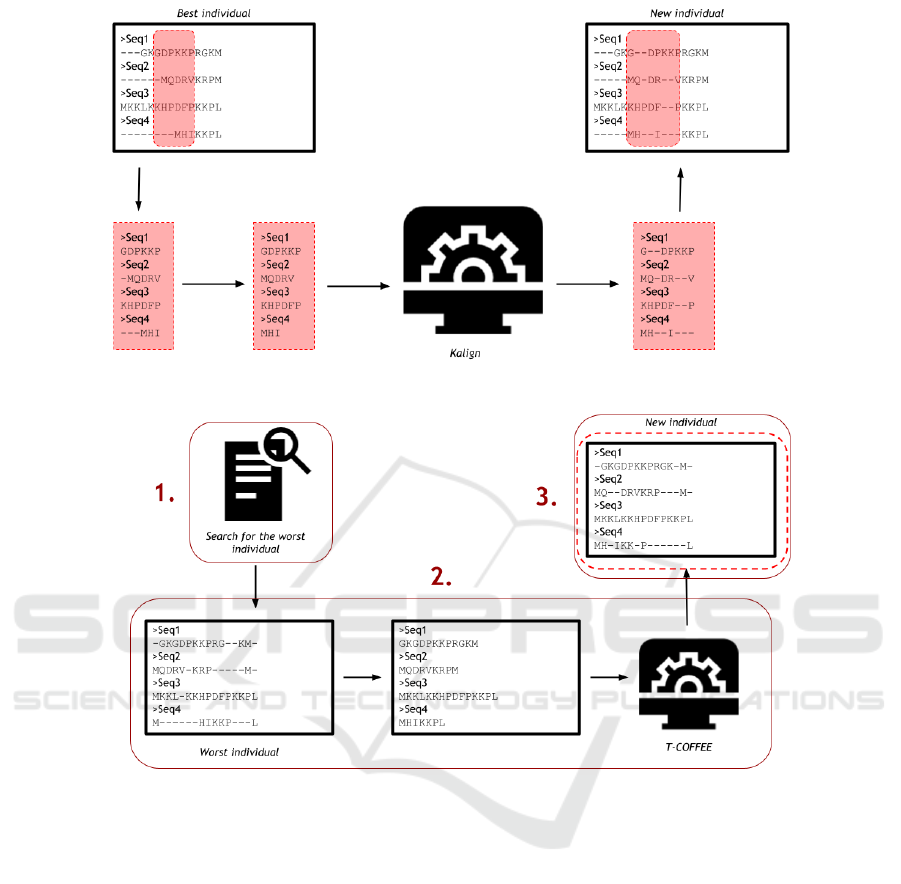
Figure 3: The local realignment using Kalign.

Figure 4: The realignment using T-COFFEE.

was 500.

5.2 Results

Due to the stochastic nature of GA, each test case was

executed ﬁve times and the average value was calcu-

lated. The results were compared with the original

MSA-GA and three well-known tools: Kalign (Lass-

mann, 2020), Clustal Omega (Sievers and Higgins,

2018) and MUSCLE (Edgar, 2004).

In Table 1 the average values of Q score for each

family are presented. We can notice that our hybrid

method has a better performance in ﬁve of the six

families, being the family RV30 the one where Clustal

Omega performed better, but yet our method aver-

age value in this family has less than 5% of differ-

ence compared to the Clustal Omega values. When

comparing to the original MSA-GA, our method is

able to increase the quality of the ﬁnal alignments in

290%, suggesting that the changes proposed in this

work were effectively able to smooth the maximum

local problem.

We can see in Table 2 the average TC scores for

all the families. This time, our method was able to

increase the AG results in 2769% in compare with

the original one, showing that the proposed method is

able to reﬁne the alignments and even beat the well-

known tools in most cases.

We can observe in Table 3 and Table 4 the aver-

age standard deviation calculated for all tools and all

families from BAliBase. The method proposed in this

work has the least average standard deviation, which

indicates a better statistical consistency when com-

pared to the others.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

172

Table 1: Q scores obtained for all families of BAliBase.

RV11 RV12 RV20 RV30 RV40 RV50 Average

MSA-GA 0.2375 0.3497 0.3082 0.2657 0.3569 0.3261 0.2989

Kalign 0.6397 0.8873 0.9230 0.8020 0.8947 0.8643 0.8352

Clustal Omega 0.6359 0.8910 0.9265 0.8723 0.9073 0.8680 0.8502

MUSCLE 0.6033 0.8960 0.8845 0.8290 0.8977 0.9010 0.8352

Our method 0.6904 0.9130 0.9500 0.8330 0.9120 0.8963 0.8658

Table 2: TC scores obtained for all families of BAliBase.

RV11 RV12 RV20 RV30 RV40 RV50 Average

MSA-GA 0.0971 0.0893 0.0000 0.0000 0.0000 0.0135 0.0221

Kalign 0.4376 0.8045 0.5640 0.5830 0.6780 0.5363 0.6006

Clustal Omega 0.4473 0.8167 0.6435 0.7147 0.7500 0.5502 0.6537

MUSCLE 0.3349 0.8177 0.2760 0.5843 0.7147 0.5605 0.5605

Our method 0.4649 0.7147 0.6545 0.5093 0.7277 0.6007 0.6120

Table 3: Average Standard Deviation of Q score for each tool.

MSA-GA Kalign Clustal Omega MUSCLE Our Method

Average Standard Deviation 0.1300 0.1080 0.1083 0.1158 0.0945

Table 4: Average Standard Deviation of TC score for each tool.

MSA-GA Kalign Clustal Omega MUSCLE Our Method

Average Standard Deviation 0.2102 0.2115 0.2095 0.2564 0.2093

6 CONCLUSIONS

In this work we presented a new hybrid method for

multiple sequence alignment, combining both pro-

gressive and consistency-based techniques to smooth

the local maximum problem in AG and increase the

quality of the results. The Kalign tool was used

to perform a local realignment when the algorithm

shows stagnation signs, and the T-COFFEE tool re-

align globally individuals that would be discarted

from the population as a way to avoid degradation that

may result from the use of a progressive approach,

since it is known for its difﬁcult when dealing with

less similar sequences.

The results shown that the given hypothesis was

correct, since the hybrid proposed AG was able to ob-

tain results 2 a 27 times better than the original one,

indicating the smooth of the local maximum problem.

Our method also was able to beat the quality of align-

ments realized by well-known tools 5 out of 6 times,

encouraging its use in situations when the quality of

the result is prioritized over the execution time.

We propose, as future work, combining the ad-

vantages of hybridization techniques with parallel ap-

proaches as a way to obtain a better execution time,

balancing the quality/time ratio.

ACKNOWLEDGEMENTS

The authors would like to thank S

ao Paulo Research

Foundation (FAPESP) for the ﬁnancial support,

under grant 2019/00030-3, Universidade Paulista

(Unip/ICET) to partially support this research un-

der grant number 7-03-1169/2021, and Coordenac¸

de Aperfeic¸oamento de Pessoal de N

ıvel Superior -

Brasil (CAPES) for the partial ﬁnancial support.

REFERENCES

Amorim, A. R., Neves, L. A., Val

encio, C. R., Roberto,

G. F., and Zafalon, G. F. D. (2018). An approach

for coffee objective function to global dna multiple se-

quence alignment. Computational biology and chem-

istry, 75:39–44.

Amorim, A. R., Zafalon, G. F. D., de Godoi Contessoto, A.,

Val

encio, C. R., and Sato, L. M. (2021). Metaheuristics

for multiple sequence alignment: a systematic review.

Computational Biology and Chemistry, page 107563.

Amorim, A. R., Zafalon, G. F. D., Neves, L. A., Pinto, A.,

Val

encio, C. R., and Machado, J. M. (2015). Improve-

ments in the sensibility of msa-ga tool using coffee ob-

jective function. In Journal of Physics: Conference Se-

ries, volume 574, page 012104. IOP Publishing.

A Hybrid Genetic Algorithm using Progressive Alignment and Consistency based Approach for Multiple Sequence Alignments

173

Bawono, P., Dijkstra, M., Pirovano, W., Feenstra, A., Abeln,

S., and Heringa, J. (2017). Multiple sequence alignment.

In Bioinformatics, pages 167–189. Springer.

Baxevanis, A. D., Bader, G. D., and Wishart, D. S. (2020).

Bioinformatics. John Wiley & Sons.

Chatterjee, S., Hasibuzzaman, M., Iftiea, A., Mukharjee,

T., Nova, S. S., et al. (2019). A hybrid genetic algo-

rithm with chemical reaction optimization for multiple

sequence alignment. In 2019 22nd International Confer-

ence on Computer and Information Technology (ICCIT),

pages 1–6. IEEE.

Chowdhury, B. and Garai, G. (2017). A review on multi-

ple sequence alignment from the perspective of genetic

algorithm. Genomics, 109(5-6):419–431.

Cook, S. (2006). The p versus np problem. The millennium

prize problems, pages 87–104.

Correa, J. M., de Melo, A. C. M. A., Jacobi, R. P., and

Boukerche, A. (2012). Parallel simulated annealing for

fragment based sequence alignment. In 2012 IEEE 26th

International Parallel and Distributed Processing Sym-

posium Workshops & PhD Forum, pages 641–648. IEEE.

Do, C. B., Mahabhashyam, M. S., Brudno, M., and Bat-

zoglou, S. (2005). Probcons: Probabilistic consistency-

based multiple sequence alignment. Genome research,

15(2):330–340.

Edgar, R. C. (2004). Muscle: multiple sequence align-

ment with improved accuracy and speed. In Proceed-

ings. 2004 IEEE Computational Systems Bioinformatics

Conference, 2004. CSB 2004., pages 728–729. IEEE.

Edgar, R. C. and Batzoglou, S. (2006). Multiple se-

quence alignment. Current opinion in structural biology,

16(3):368–373.

Gondro, C. and Kinghorn, B. P. (2007). A simple genetic

algorithm for multiple sequence alignment. Genetics and

Molecular Research, 6(4):964–982.

Katoh, K., Misawa, K., Kuma, K.-i., and Miyata, T. (2002).

Mafft: a novel method for rapid multiple sequence align-

ment based on fast fourier transform. Nucleic acids re-

search, 30(14):3059–3066.

Katoh, K., Rozewicki, J., and Yamada, K. D. (2019). Mafft

online service: multiple sequence alignment, interactive

sequence choice and visualization. Brieﬁngs in bioinfor-

matics, 20(4):1160–1166.

Kaya, M., Kaya, B., and Alhajj, R. (2016). A novel multi-

objective genetic algorithm for multiple sequence align-

ment. International Journal of Data Mining and Bioin-

formatics, 14(2):139–158.

Kim, J., Pramanik, S., and Chung, M. J. (1994). Multiple

sequence alignment using simulated annealing. Bioinfor-

matics, 10(4):419–426.

Lassmann, T. (2020). Kalign 3: multiple sequence align-

ment of large datasets.

Lee, Z.-J., Su, S.-F., Chuang, C.-C., and Liu, K.-H. (2008).

Genetic algorithm with ant colony optimization (ga-aco)

for multiple sequence alignment. Applied Soft Comput-

ing, 8(1):55–78.

Mount, D. W. (2001). Bioinformatics. In Bioinformatics,

pages 564–564.

Needleman, S. B. and Wunsch, C. D. (1970). A general

method applicable to the search for similarities in the

amino acid sequence of two proteins. Journal of molec-

ular biology, 48(3):443–453.

Notredame, C. and Higgins, D. G. (1996). Saga: sequence

alignment by genetic algorithm. Nucleic acids research,

24(8):1515–1524.

Notredame, C., Higgins, D. G., and Heringa, J. (2000).

T-coffee: A novel method for fast and accurate multi-

ple sequence alignment. Journal of molecular biology,

302(1):205–217.

Notredame, C., Holm, L., and Higgins, D. G. (1998). Cof-

fee: an objective function for multiple sequence align-

ments. Bioinformatics (Oxford, England), 14(5):407–

422.

Nute, M., Saleh, E., and Warnow, T. (2019). Evaluating

statistical multiple sequence alignment in comparison to

other alignment methods on protein data sets. Systematic

biology, 68(3):396–411.

Riaz, T., Wang, Y., and Li, K.-B. (2004). Multiple sequence

alignment using tabu search. In Proceedings of the sec-

ond conference on Asia-Paciﬁc bioinformatics-Volume

29, pages 223–232.

Rubio-Largo,

A., Vega-Rodr

ıguez, M. A., and Gonz

alez-

Alvarez, D. L. (2016). Hybrid multiobjective artiﬁcial

bee colony for multiple sequence alignment. Applied Soft

Computing, 41:157–168.

Sievers, F. and Higgins, D. G. (2018). Clustal omega for

making accurate alignments of many protein sequences.

Protein Science, 27(1):135–145.

Thompson, J. D., Higgins, D. G., and Gibson, T. J. (1994).

Clustal w: improving the sensitivity of progressive mul-

tiple sequence alignment through sequence weighting,

position-speciﬁc gap penalties and weight matrix choice.

Nucleic acids research, 22(22):4673–4680.

Thompson, J. D., Koehl, P., Ripp, R., and Poch, O.

(2005). Balibase 3.0: latest developments of the multi-

ple sequence alignment benchmark. Proteins: Structure,

Function, and Bioinformatics, 61(1):127–136.

Thomsen, R. and Boomsma, W. (2004). Multiple sequence

alignment using saga: investigating the effects of oper-

ator scheduling, population seeding, and crossover op-

erators. In Workshops on applications of evolutionary

computation, pages 113–122. Springer.

Wang, L. and Jiang, T. (1994). On the complexity of multi-

ple sequence alignment. Journal of computational biol-

ogy, 1(4):337–348.

Zafalon, G. F. D., Gomes, V. Z., Amorim, A. R., and

Val

encio, C. R. (2021). A hybrid approach using progres-

sive and genetic algorithms for improvements in multi-

ple sequence alignments. In 23rd International Confer-

ence on Enterprise Information Systems (ICEIS 2021),

volume 2, pages 384–391. SciTePress.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

174