Metrics of Parallel Complexity of Operational Business Processes

Andrea Chiorrini, Claudia Diamantini, Alex Mircoli and Domenico Potena

Department of Information Engineering, Polytechnic University of Marche, Ancona, Italy

Keywords:

Business Modelling, Business Process Management, Metrics and Evaluation of Processes, Degree of

Parallelism, Instance Graphs.

Abstract:

This paper addresses the problem of quantifying the parallelism in a business process. Having a synthetic

metric to quantify the parallelism of a process may provide an assessment of the complexity of the process and

guide certain design choice. In the present paper we discuss the advantages and disadvantages of two metrics

presented in the literature, as well of two novel metrics that leverage on the notion of Instance Graph. Analysis

is performed by means of use cases that are representative of operational business processes. The proposed

metrics show to provide a sensible way to evaluate the overall parallel complexity of a process model.

1 INTRODUCTION

A business process is a ﬂow of related activities ex-

ecuted by people and/or machines to achieve a spe-

ciﬁc goal for a client. Activities can be executed

sequentially, or in parallel, and cycles may exist as

well. Business process modelling is a fundamental

task in business management since it allows to de-

sign, analyse and improve process efﬁciency. Sev-

eral metrics have been devised to measure relevant

aspects of business processes (Radu Mateescu, 2014;

Mao, 2010). Among them, one of particular interest

is how much parallel a process is. It is acknowledged

that increasing the number of activities performed in

parallel is a way to improve the performance of a

business process (Davenport, 1993), although this im-

provement comes at the cost of a more complex pro-

cess design, development, and maintenance. Hav-

ing a synthetic metric to quantify the parallelism of

a process may thus provide an assessment of the pro-

cess and guide certain design choices. In the litera-

ture, a widely adopted metric is the Degree of Par-

allelism (DoP), deﬁned as the maximum number of

parallel activities that can be executed in that process

(Radu Mateescu, 2014; Sun and Su., 2011). In par-

ticular, (Sun and Su., 2011) proposes different algo-

rithms to compute the DoP for three classes of BPMN

processes. In (Radu Mateescu, 2014) it is observed

that the DoP, theoretically, can be computed by deter-

mining the bound of a Petri net, which is the maxi-

mum number of tokens in a marking of the net. The

computation of such bound requires the construction

of the reachability graph, whose derivation is known

to be an NP-complete problem or ever harder for some

classes of Petri nets (Esparza, 1998; Mayr., 1984).

A more efﬁcient general procedure is then proposed

for a wide class of BPMN processes, which exploits

the notion of Labeled Transition System and model

checking. An extension (Dur

an et al., 2018) con-

siders timed business processes modeled in BPMN,

where execution times are associated to BPMN con-

structs such as activities and ﬂows. The DoP metric

is concerned with the “worst” case scenario. Other

metrics aimed at assessing the overall complexity of

a business process are discussed in (Mao, 2010). In

particular, it is argued that complexity of the paral-

lelism of a process can be measured by the Average

Degree of Transitions (ADT) which is the average

number of incoming and outgoing arcs of transitions

in a Petri net. In the present paper we discuss the ad-

vantages and disadvantages of these two metrics and

we propose two novel metrics to measure the over-

all parallel complexity of a process by leveraging on

the notion of Instance Graph (IG). We show that these

two novel metrics manage to capture the advantages

of both DoP and ADT and we discuss their pros and

cons by means of use cases that are representative of

operational business processes modelled by a class of

Petri Nets called Workﬂow Nets (Aalst, 1997).

The rest of the paper is organised as follows: in

Section 2 we brieﬂy recall the notions of Petri Nets

and IGs. Section 3 describes the set of processes con-

sidered as use cases for assessment purpose. Then,

Section 4 is devoted to the deﬁnition and comparison

Chiorrini, A., Diamantini, C., Mircoli, A. and Potena, D.

Metrics of Parallel Complexity of Operational Business Processes.

DOI: 10.5220/0011084200003179

In Proceedings of the 24th International Conference on Enterprise Information Systems (ICEIS 2022) - Volume 2, pages 561-566

ISBN: 978-989-758-569-2; ISSN: 2184-4992

561

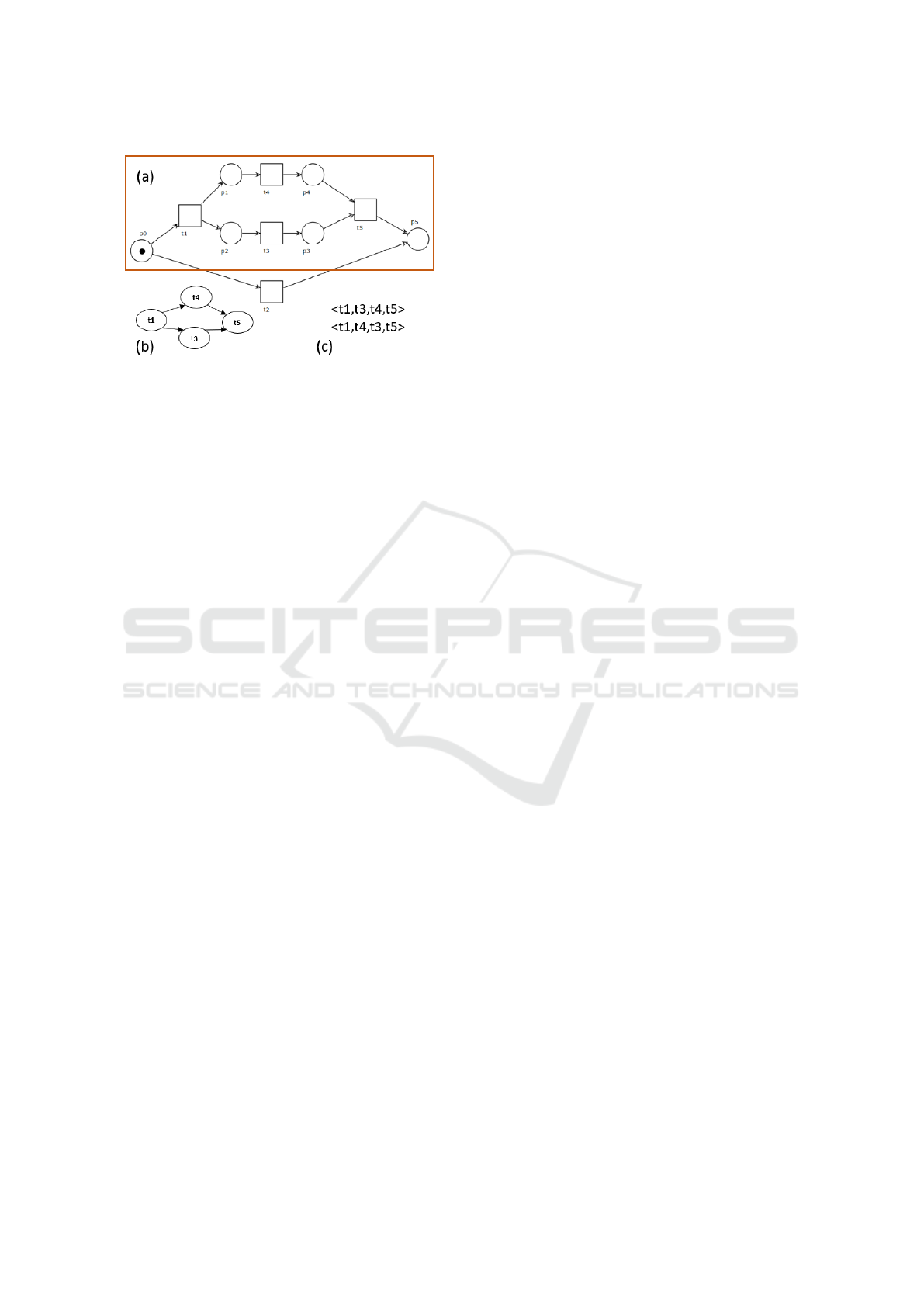
Figure 1: An example of: Petri net (a), Instance Graph (b),

variants (c).

of DoP, ADT and the two novel metrics. Finally, Sec-

tion 5 provides some ﬁnal remarks and sketches future

work.

2 PRELIMINARIES

A business process is a ﬂow of related activities exe-

cuted by people and/or machines to achieve a speciﬁc

output for a client. Activities can be executed sequen-

tially, or in parallel and loops can exist. In the present

paper we will focus on loop-free processes. A process

model is a general description of the ﬂow of activities.

Several notations exist to describe a process model,

like Petri nets (van der Aalst and van Hee, 1996), or

BPMN (van der Aalst, 2018). In the following we

will discuss the properties of the different metrics on

a set of paradigmatic processes described in Petri nets

notation.

Figure 1(a) shows a simple Petri net. Squares rep-

resent transitions, that is well-deﬁned activities that

have to be performed within the process. Circles rep-

resent places, that can be informally interpreted as re-

sources or pre-conditions enabling transitions. The

availability of a set of resources is denoted by a mark-

ing (the black dot in the ﬁgure). Arcs connecting

places to transitions describe the set of resources that

must be available in order to perform the activity,

while arcs connecting transitions to places describe

the set of resources enabled by the effect of activity

execution. Hence, from the marking shown, only one

between the activity t1 and t2 can be performed at

each process execution (we say that t1 and t2 are al-

ternative choices). If t1 is performed then t3 and t4

are both enabled, this represents an interleaving be-

haviour that allow to perform in parallel the two ac-

tivities. Finally, their execution enables t5 which ends

the process. Note that we focus on operational busi-

ness processes, that are represented by a sub-class of

Petri nets called Workﬂow nets (WF-net). A WF-net

has one start place, one end place, and all transitions

and all places are on a path from start to end.

A speciﬁc execution of the process generates a so-

called process instance, which is the partially ordered

set of activities that are performed to achieve the com-

pletion of a single execution of a process. A process

instance can be modelled by an IG. In an IG each node

represents an activity, and an edge between activity A

and activity B denotes the existence of a causal rela-

tion between A and B, namely the fact that B cannot

be executed until A is terminated; in other words, the

execution of B depends on the execution of A. For a

more formal deﬁnition of IGs and causal relations see

(van Dongen and van der Aalst, 2004). The IG cor-

responding to the upper part of the Petri net in Figure

1(a) (marked by a square) is shown in 1(b), while the

IG for the lower part is simply a node labelled t2. In

an IG, all control-ﬂow structures are represented ex-

cept for choices. This is obvious, since in each single

execution choices have already been made. Activities

that can be done in parallel within one instance can be

executed in any order. As a consequence, an IG is rep-

resentative of one or more variants that differ exactly

in the interleaving of parallel activities. The variants

for the IG in Figure 1(b) are reported in Figure 1(c).

The relation between an IG and its underlying variants

is the basic property underpinning the development of

the metrics proposed in this work.

3 USE CASES DESCRIPTION

In this section we introduce 7 use cases, in the form

of Petri nets. Although simple, these processes have

been designed to capture some paradigmatic situa-

tions allowing to enlighten the properties of the dif-

ferent metrics, and can be easily scaled. Table 1 de-

scribes the characteristics of the processes. The pro-

cesses are shown in Figures 2-8. In particular, we de-

signed use case 1 (Fig. 2), as a simple starting base

case so to compare the added structural complexity of

the other models with it. Use case 2, (Fig. 3) only

adds to use case 1 a sequence of transitions after the

parallelism. Hence, for this model, it is desirable that

a metric lowers its score. Concerning use case 3 (Fig.

4), we designed it to highlight the opposite behaviour:

it is basically a sequence of two use case 1, so it would

be reasonable to see an increase in the metric score.

Use case 4 (Fig. 5), has been designed so to compare

it with both use cases 2 and 3. We expect to see an

increased score w.r.t. the former, while it is more dif-

ﬁcult to compare the quantity of parallelism with the

latter. Indeed, use case 4 has a greater number of ac-

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

562

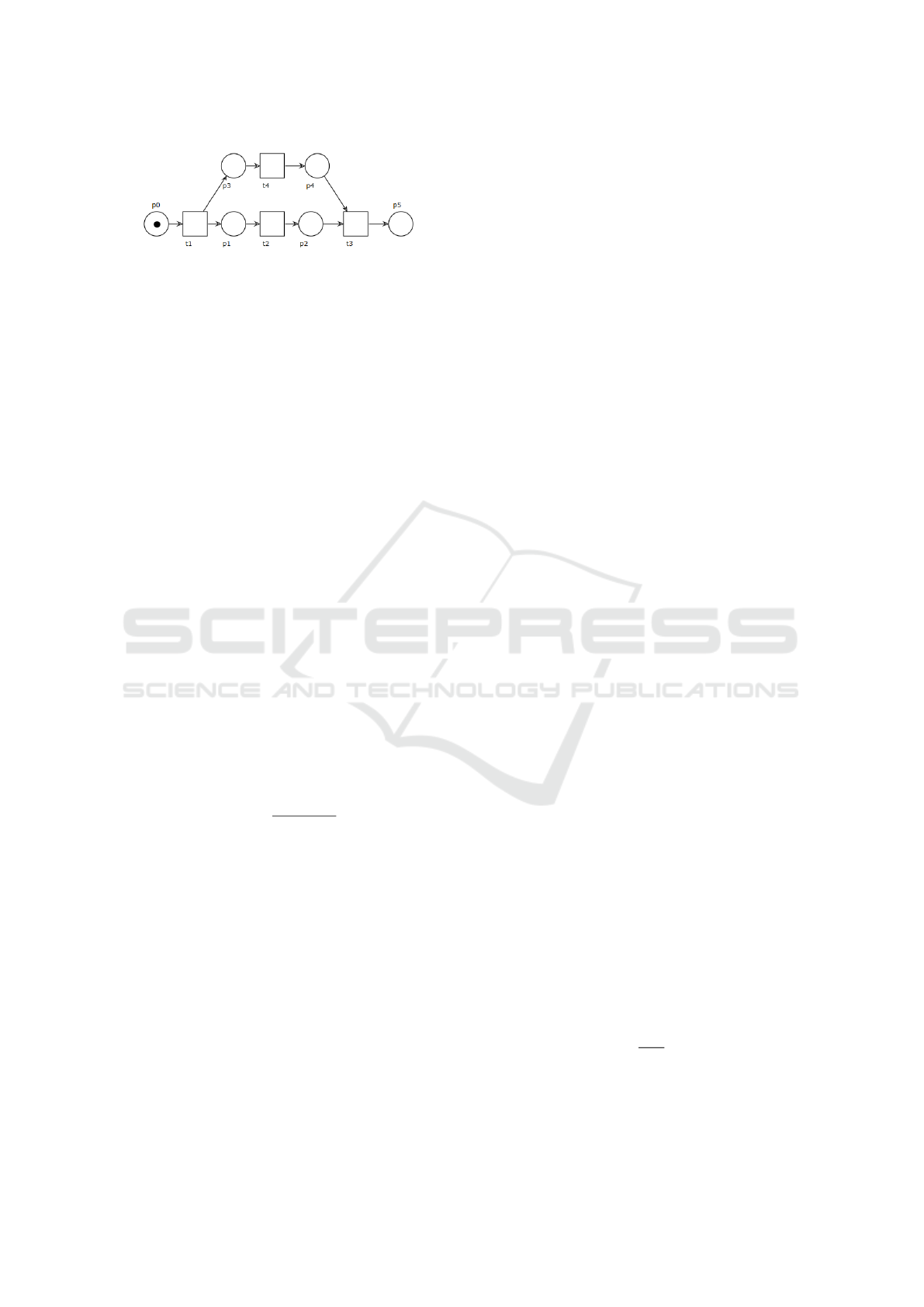
Figure 2: Use case 1.

tivities that can be performed simultaneously, while

use case 3 has a greater number of parallelisms. Sim-

ilarly, we designed use case 5 (Fig. 6) as a problem-

atic example to compare with use cases 1 and 2, since

there are a greater number of activities in the parallel

branch. Use case 6 (Fig. 7) is introduced to show the

effect of synchronisation on the parallel complexity

of the process with respect to use case 5. Lastly, we

consider use case 7 (Fig. 8) to show the effects of an

or split on the various metrics.

4 METRICS FOR PROCESS

PARALLELISM EVALUATION

4.1 Metrics based on Model Perspective

In this subsection we introduce two popular metrics,

whose values are calculated directly from the struc-

ture of the process.

4.1.1 Average Degree of Transition

The Average Degree of Transition (ADT) has been

introduced in the context of Petri net-based business

process as a mean to measure control ﬂow parallel

complexity (Mao, 2010). It is deﬁned as:

ADT =

∑

deg(t

)

|T |

(1)

where T is the set of all transitions in the Petri net, and

deg : T → N is the function that associates to a transi-

tion the number of its incoming and outgoing arcs. It

is relevant to notice that such metric assumes values

in [2;+∞), a value of 2 represents a purely sequen-

tial process whereas bigger values indicate the pres-

ence of more parallelism. As examples, considering

use case 1 we can compute the ADT as 10/4 = 2.5

whereas for the use case 2 it is 16/7 = 2.29.

4.1.2 Degree of Parallelism

The most commonly used metric to quantify the par-

allelism of a process is the maximum number of ac-

tivities that can be executed in parallel, called Degree

of Parallelism (DoP). It is computed by evaluating the

number of activities enabled by a marking of the Petri

net. For examples, for the use case 1 the value of DoP

is 2 due to the marking

p1, p3

which enables both

transitions t2 and t4; for the process in Figure 5 the

DoP is 3 since the marking

p1, p6, p8

enables the

maximum number of transitions, namely t2,t7 and t8.

Techniques to calculate the DoP have been proposed

in (Radu Mateescu, 2014; Sun and Su., 2011).

4.1.3 Comparison between DoP and ADT

First of all we notice that as the DoP calculate a max-

imum parallelism, it is hence suited to assess peak be-

haviours, whereas ADT shows a more comprehensive

average complexity of the process. In order to high-

light this fact, let us consider use cases 2 and 3. The

value of the DoP metric is 2 for both processes, but the

latter clearly shows a more complex behaviour due to

the presence of a second parallelism. This is captured

by ADT whose value is increased from 2.29 to 2.5.

Clearly DoP is able to capture the difference between

processes in Figures 3 and 5 passing from 2 to 3. ADT

also detect the increased complexity, although with a

slightly minor relative increment passing from 2.29 to

2.5. We remark that the ADT metric returns the same

value for use cases 3 and 4, demonstrating that ADT

is unable to capture the increased complexity inherent

to a parallelism with a higher number of parallel activ-

ities. The values of DoP and ADT metrics for all the

use cases are shown in the last two columns of Table

2. The limits discussed for the two metrics motivated

us to focus on a different aspect of a process model to

deﬁne a metric. Speciﬁcally, in the following subsec-

tion we describe two metrics which take into account

the number of variants represented by an IG.

4.2 Metrics based on Instance Graphs

We can say that each IG represents a speciﬁc set of

parallel branches that exist in the process and that the

parallel complexity of such set is as high as the num-

ber of variants represented by the IG. On this basis

we introduce a metric called Parallel Complexity, and

a scaled variant, designed to overcome the limits of

both ADT and DoP being more sensitive to both over-

all and maximum parallelism.

4.2.1 Parallel Complexity (PC)

This metric is deﬁned as:

PC =

|V |

|IG|

− 1 (2)

where |V | is the number of distinct variants allowed

by the process model and |IG| is the number of dis-

tinct IGs that represents those variants. The minus 1

Metrics of Parallel Complexity of Operational Business Processes

563

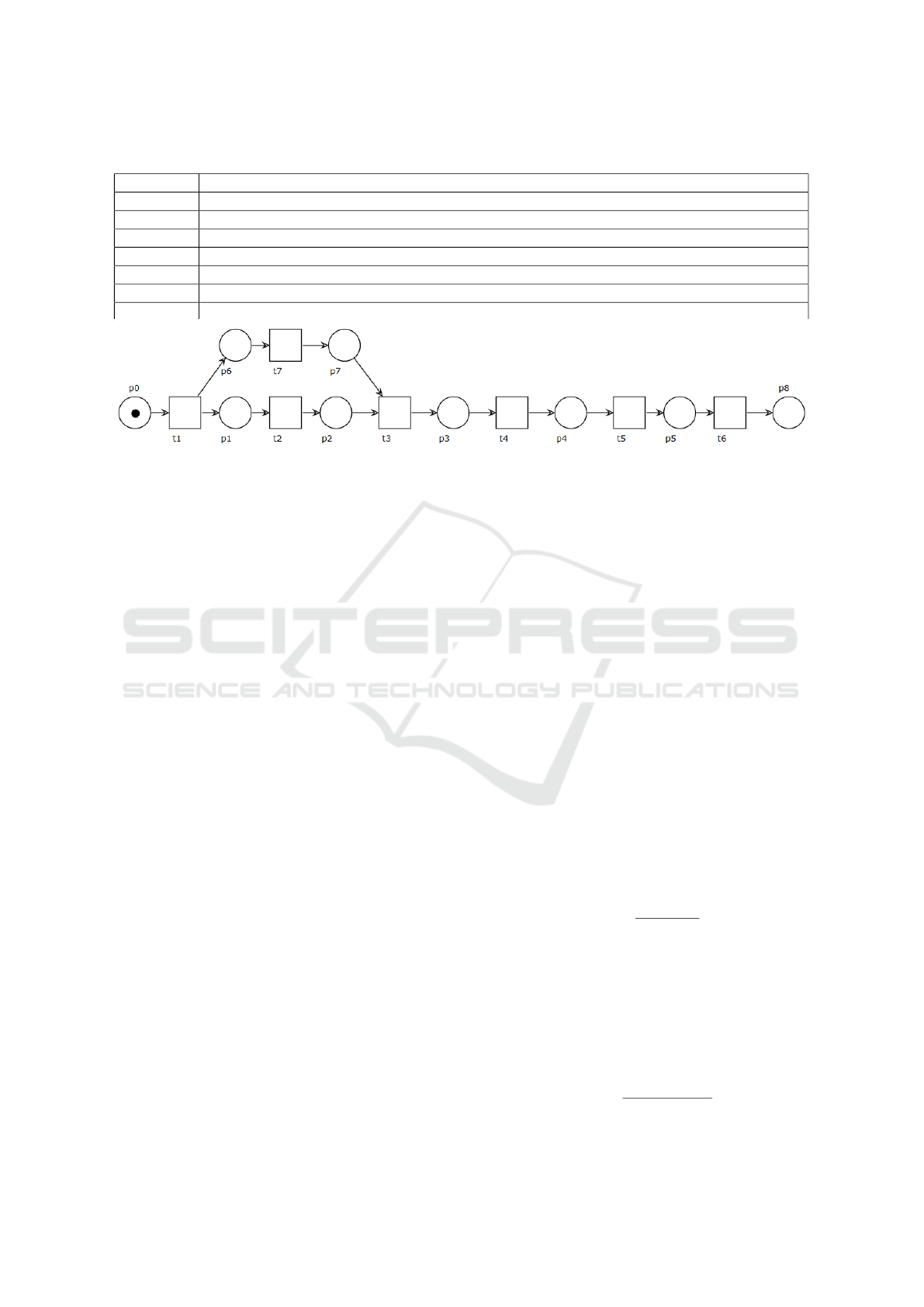
Table 1: Use case descriptions.

Process Description

Use case 1 a process with 2 parallel activities (simple parallelism)

Use case 2 a process with 2 parallel activities followed by a sequence

Use case 3 a process with a sequence of 2 simple parallelisms

Use case 4 a process with 3 parallel activities followed by a sequence

Use case 5 a process with two parallel sequences followed by a further sequence

Use case 6 use case 5 with a synchronisation between activities t7 and t3

Use case 7 a process with an alternative choice between use case 1 and use case 5

Figure 3: Use case 2.

is a scaling parameter used to reduce to 0 the Paral-

lel Complexity in case of strictly sequential processes.

Given a process model, the set of IGs can be easily ob-

tained by a two-step procedure. First, the variants of a

process are generated (play-out). Then, using causal

relations of the model, an IG is generated for each

variant. Computing such metric for the provided use

cases, we can see that the metric shows an hybrid be-

haviour with respect to DoP and ADT, i.e., it is sen-

sitive to both overall parallelism and maximum paral-

lelism. On the one hand, as regards the use cases 2

and 3 we can notice that PC scores respectively 1 and

3 managing to reﬂect the increased overall parallelism

as ADT does, but DoP does not. On the other hand,

for use cases 3 and 4, PC takes the values 3 and 5

respectively, highlighting the difference between the

two examples as DoP does but ADT does not. Agree-

ing behaviours are displayed considering use cases 2

and 4 as both ADT and DoP detect the increment.

However, it should be noted that PC scores a bigger

relative increase. Indeed, the percentage increment of

ADT, DoP and PC are 9.2%, 50% and 400%, respec-

tively. This is due to the fact that adding a branch

to a parallelism does not increase linearly its com-

plexity as the possible actual executions of such par-

allelism grow combinatorially. A relevant advantage

of the PC metric is shown comparing use case 6 with

use case 5. The former adds to the latter a synchro-

nisation place p9 which locks the execution of t3 to

t7, therefore reducing the existing parallelism. In this

situation, ADT, instead of a reduction, even scores an

increment due to the arcs used to connect p9. DoP ig-

nore the change altogether. On the contrary we note

that PC correctly reﬂects the change passing from 5

of Figure 6 to 4 of Figure 7. A similar situation is

displayed by use cases 3 and 5, where ADT lowers

its value instead of increasing it. Use case in Figure

8 shows that PC also works well if choices exist in

the process model, giving rise to more than one IG.

Since this use case is composed by a choice between

1 and 5, PC correctly returns a score of 3 which is the

average of its values for these two use cases. A simi-

lar behaviour is displayed by ADT which scores 2.33

which is in-between the composing use cases ADT

values. The main limit of PC is that it doesn’t scale

well with respect to process length. To explain the

point, let us consider use cases 1 and 2. The former

shows a higher overall parallelism, since a larger por-

tion of process 2 is strictly sequential. Instead, PC

values for both processes is 1, whereas this difference

is captured by ADT. This motivates the introduction

of a scaled variant of the PC.

4.2.2 Scaled Parallel Complexity (SPC)

In order to overcome the described limit of the pro-

posed metric, we devised a scaling mechanism that

takes into account the number of activities.

SPC =

(|T | − |S|)

(3)

where |T | is the total number of transitions in the

model and |S| is the number of transitions that have

more than one outgoing or incoming arcs. They in

fact represent the point where a parallel branch starts

(AND split) and where a parallel branch synchronises

(AND merge) respectively. From equation (2) we can

also write SPC as:

SPC =

|V | − |IG|

|IG|(|T | − |S|)

(4)

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

564

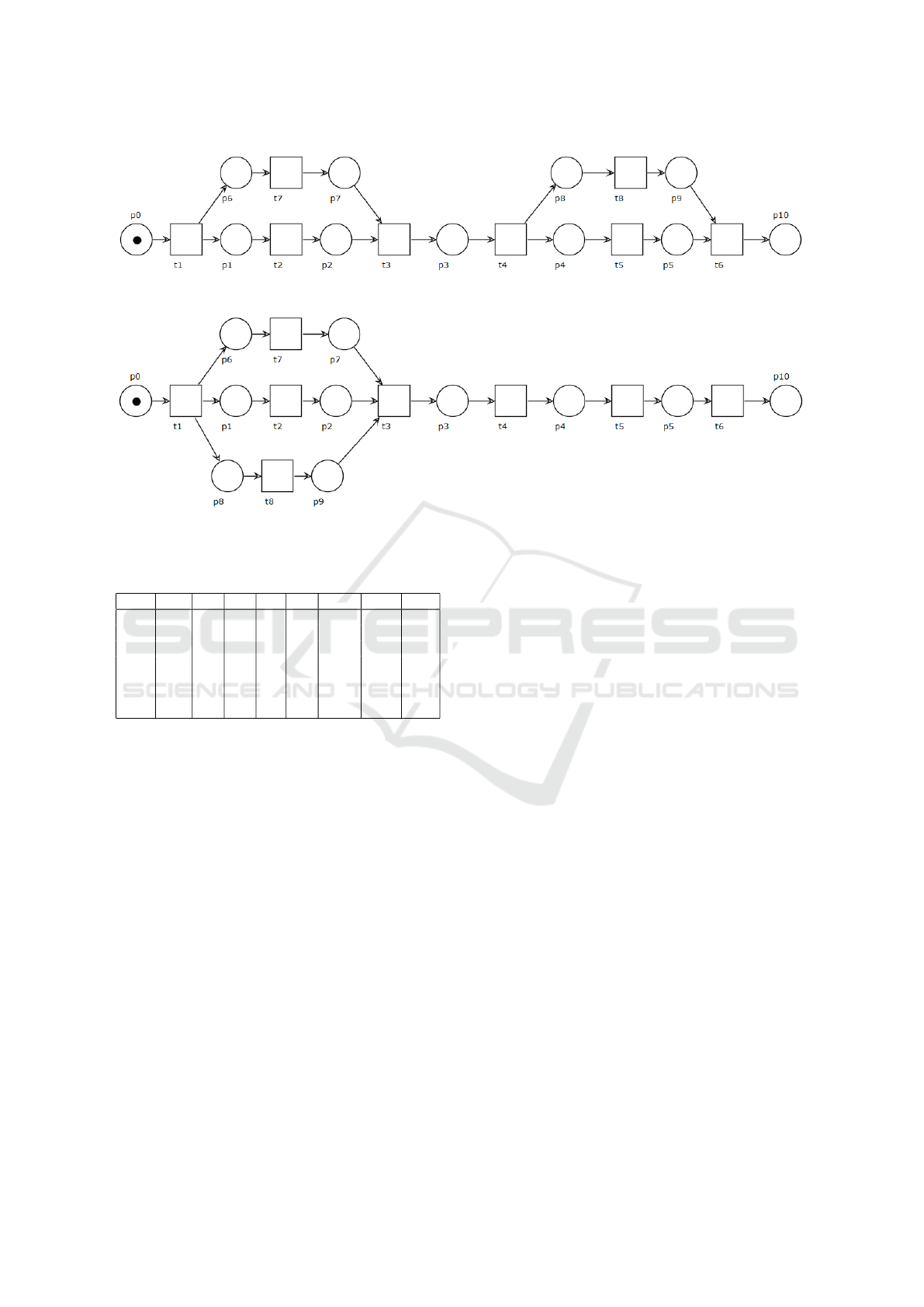
Figure 4: Use case 3.

Figure 5: Use case 4.

Table 2: Metrics for all use cases.

Case |IG| |V | |T | |S| PC SPC ADT DoP

1 1 2 4 2 1 0.5 2.5 2

2 1 2 7 2 1 0.2 2.29 2

3 1 4 8 4 3 0.75 2.5 2

4 1 6 8 2 5 0.83 2.5 3

5 1 6 8 2 5 0.83 2.25 2

6 1 5 8 3 4 0.8 2.5 2

7 2 8 12 4 3 0.375 2.33 2

We can see from Table 2 that this new metric main-

tains all the good behaviours that PC has. It also dis-

plays the desired behaviour that PC does not have:

when considering use cases 1 and 2, we can note that

SPC decreases as required thanks to the scaling factor

that takes into account the presence of the sequence

in use case 2. We also notice that this scaling leads to

smaller relative increment with respect to PC. In con-

trast to PC, when considering use case 7 we see that

SPC fails to produce a coherent value. Indeed, use

case 7 is a process with an alternative choice between

use case 1 and use case 5. Nevertheless, SPC score

drops to 0.375 which is not in the range of scores for

use cases 1 and 5. This is due to how the scaling is

implemented. Currently the mechanism considers all

transitions in the process model even though the num-

ber of transitions in the derived IG could be far less.

This is because an IG only displays the activities from

one of the optional branches of the process. This over-

reduces the score by over-estimating the denominator

of SPC formula.

5 DISCUSSION AND

CONCLUSIONS

This paper addresses the problem of evaluating the

level of parallelism in a business process. We discuss

the limits of the two best known metrics in the liter-

ature and we introduce the Process Complexity met-

ric, and its scaled variant, based on the notion of In-

stance Graph. The idea underlying the proposed met-

ric is that the parallel complexity of a process linearly

depends on the number of distinct variants allowed

by each IG, representing the possible executions of

the process. This metric provides a sensible way to

evaluate the overall complexity of the process model

due to the number and structural relations among par-

allel activities. None of the metrics, on the other

hand, is fully satisfactory showing some incoherent

behaviours with respect to the number of activities

or the presence of alternative branches. One possi-

ble conclusion is that more than one metric should be

taken into account when evaluating the parallelism of

a process. The results are not conclusive as they have

been obtained on a set of synthetic use cases. Future

works will be devoted to conﬁrm the result both the-

oretically and empirically on a larger set of process

models. Another research direction is toward the in-

troduction of different scaling mechanisms that takes

the length of a sequence of activities into due consid-

eration.

Metrics of Parallel Complexity of Operational Business Processes

565

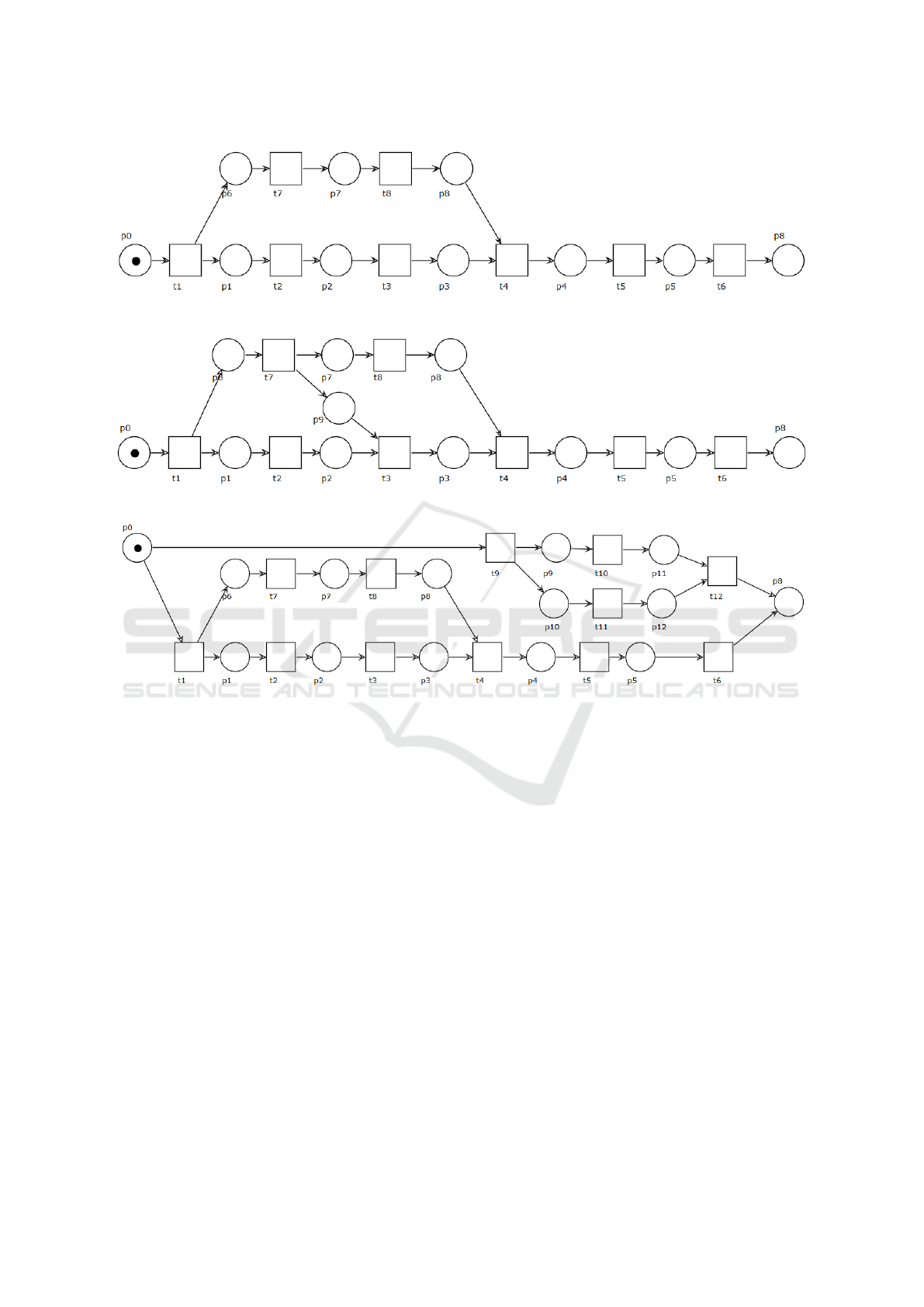
Figure 6: Use case 5.

Figure 7: Use case 6.

Figure 8: Use case 7.

REFERENCES

Aalst, W. (1997). Veriﬁcation of workﬂow nets. In ICATPN,

pages 407–426.

Davenport, T. H. (1993). Process innovation: reengineering

work through information technology. Harvard Busi-

ness Press.

Dur

an, F., Rocha, C., and Sala

un, G. (2018). Comput-

ing the parallelism degree of timed bpmn processes.

In Software Technologies: Applications and Founda-

tions, pages 320–335, Cham. Springer International

Publishing.

Esparza, J. (1998). Reachability in live and safe free-choice

Petri Nets is NP-complete. Theoretical Computer Sci-

ence.

Mao, C. (2010). Control ﬂow complexity metrics for Petri

Net-based web service composition. Journal of Soft-

ware, 5:1292–1299.

Mayr., E. (1984). An algorithm for the general Petri Net

reachability problem. SIAM Journal on Computing.

Radu Mateescu, Gwen Sala

un, L. Y. (2014). Quantify-

ing the parallelism in BPMN processes using model

checking. In The 17th International ACM Sigsoft Sym-

posium on Component-Based Software Engineering

(CBSE 2014).

Sun, Y. and Su., J. (2011). Computing degree of parallelism

for BPMN processes. In Springer, editor, Proceedings

of ICSOC’11, page 1–15.

van der Aalst, W. (2018). Business process modeling nota-

tion. In Liu, L. and

Ozsu, M. T., editors, Encyclopedia

of Database Systems, pages 382–383. Springer New

York, New York, NY.

van der Aalst, W. and van Hee, K. (1996). Business process

redesign: A petri-net-based approach. Computers in

Industry, 29(1):15–26.

van Dongen, B. F. and van der Aalst, W. M. P.

(2004). Multi-phase process mining: Building in-

stance graphs. In Conceptual Modeling – ER 2004,

pages 362–376, Berlin, Heidelberg. Springer Berlin

Heidelberg.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

566