Sequencing and Recommending Pedagogical Activities from Bloom’s

Taxonomy using RASI and Multi-objective PSO

Denis Jos

e Almeida

1 a

, M

arcia Aparecida Fernandes

1 b

and Newarney Torrez

ao da Costa

2 c

Department of Computing, Federal University of Uberl

andia, Av. Jo

ao Naves de

Avila, Uberl

andia, Brazil

Department of Computing, Federal Institute of Goi

as, Ipor

a, Brazil

Keywords:

Sequencing of Pedagogical Activities, Pedagogical Recommendation, Bloom’s Taxonomy, RASI, PSO,

Multi-objective Optimization.

Abstract:

According to student needs, learning can be supported and enhanced through structured and personalized

instruction. This paper presents an approach to personalized pedagogical recommendations based on the stu-

dent’s cognitive proﬁle, given by the Revised Approaches to Studying Inventory (RASI). The recommended

pedagogical actions follow the hierarchy of Revised Bloom’s Taxonomy. We model the sequencing of ped-

agogical actions as a multi-objective optimization problem. This problem solution was implemented using a

Particle Swarm Optimization (PSO) algorithm. The optimized objectives in this problem are the similarity

between the student’s proﬁle and the sequence of actions, and the number of actions appropriate to the stu-

dent’s proﬁle. Experiments conducted with students in higher education institutions suggest that the proposed

approach using PSO presents solutions that are better accepted by students than the randomized pedagogical

recommendation.

1 INTRODUCTION

Learning is a continuous and natural process that oc-

curs in both organized situations and everyday activ-

ities Huang et al. (2019). According to Brown et al.

(2020), teaching and learning is a human effort car-

ried out by people for the beneﬁt of others, and Woolf

(2010) argues that learning is more efﬁcient when stu-

dents are motivated to learn. In addition, Huang et al.

(2019) state that learning, when intentional and de-

ﬁned in an institutional context with explicit goals

and objectives, is generally supported by structured

sequences of instructions designed to support, facili-

tate or improve learning and performance.

Traditional teaching models are dependent on

course content and are teacher-centered; therefore, the

teaching strategies are based on the teacher’s under-

standing of the course. Because classes are hetero-

geneous, adjustments must be made to the content or

pedagogical strategies to help students perform better

and reach a different level in the learning process.

The student’s cognitive proﬁle is an example of

an attribute that can be considered to make the learn-

https://orcid.org/0000-0003-3224-8249

https://orcid.org/0000-0003-3572-612X

https://orcid.org/0000-0002-4954-176X

ing process student-centered. With this type of in-

formation, teachers can plan learning activities that

are more appropriate for students. Moreover, technol-

ogy can play a crucial role in developing personalized

and individualized learning activities (Huang et al.,

2019), which largely determines student satisfaction

and teaching efﬁciency.

Automation of the teaching process in formal

learning can collaborate with teaching methodologies

that put the student in a more active role in the learn-

ing process. Teaching can be customized in intelli-

gent and adaptive virtual platforms by recommending

tailored activities to students. This can be done by

considering the student’s cognitive proﬁle or prefer-

ences to meet individual needs, providing stimuli that

guide the student, and allowing everyone to learn in

their own time (Sunaga and Carvalho, 2015).

Student performance in Virtual Learning Envi-

ronments (VLEs) can be improved by recommend-

ing teaching strategies customized and individualized.

With the support of these environments, it is possi-

ble to provide personalized and more appropriate se-

quences of pedagogical activities for each predomi-

nant learning style of students, which is impossible in

mass or conventional education (Moran, 2015). The

relevance of VLEs leads to the exploration and de-

Almeida, D., Fernandes, M. and Torrezão da Costa, N.

Sequencing and Recommending Pedagogical Activities from Bloom’s Taxonomy using RASI and Multi-objective PSO.

DOI: 10.5220/0011090000003182

In Proceedings of the 14th International Conference on Computer Supported Education (CSEDU 2022) - Volume 2, pages 105-116

ISBN: 978-989-758-562-3; ISSN: 2184-5026

105

velopment of new tools to adapt and respond to the

student.

Considering the previous scenario, this work

presents a proposal for sequencing pedagogical ac-

tions to be recommended to students. The sequenc-

ing problem is formulated as a multi-objective opti-

mization problem, and the solution is obtained by a

discrete binary approach of the Particle Swarm Op-

timization (PSO) algorithm. The pedagogical ac-

tions are those from Bloom’s Taxonomy, and the stu-

dent model is the cognitive proﬁle of Revised Ap-

proaches to Studying Inventory (RASI). Experiments

have been conducted and the results are promising in

terms of student satisfaction and sequence quality.

The paper is organized as follows. Section 2

presents previous work that used PSO for pedagog-

ical sequencing. Bloom’s Taxonomy, RASI proﬁles,

the relationships between both theories, and a gen-

eral view of PSO are described in Section 3. The

multi-objective optimization problem for sequencing

and the search for a solution by a PSO algorithm are

described in Section 4. Experiments and the analysis

of the results are presented in Section 5. Section 6

contains the conclusion and further work.

2 RELATED WORKS

Meta-heuristics based on Evolutionary Computing

(EC) have been used to cope with pedagogical se-

quencing since is a hard problem (Al-Muhaideb and

Menai, 2011), especially when it considers some

student characteristics to propose an adaptive se-

quencing. In this sense, Al-Muhaideb and Menai

(2011) provide an overview of EC approaches — such

as Ant Colony Optimization (ACO), Genetic Algo-

rithm (GA), Parallel Memetic Algorithm, and Particle

Swarm Optimization (PSO) — for solving the Cur-

riculum Sequencing problem.

De-Marcos et al. (2009) proposed the automatic

sequencing process of learning objects in the e-

learning content creation. The sequencing problem

was transformed into a constraint satisfaction prob-

lem, and two optimization agents were designed, de-

veloped, and tested: a discrete PSO and a GA. The

results showed that both can solve the problem and

PSO implementation outperforms GA.

In Chu et al. (2011), PC

PSO was proposed to

select appropriate e-learning materials for individual

learners in a personalized e-course. In this approach,

a binary multi-objective PSO was used, considering

four different factors as optimization objectives: the

learning concept covered, the difﬁculty level of the

e-learning materials, the total learning time required,

and the balance among the weighs of the learning con-

cepts.

In Smaili et al. (2020), a solution was proposed

to dynamically adapt the content offered in distance

learning courses based on student proﬁles. Student

proﬁles are generated from personal data collected in

virtual learning environments, forums and social net-

works. Starting from the identiﬁcation of the proﬁles,

a PSO-based approach is used to select activities and

recommend them in an order to be followed in the

course.

The research conducted by Subiyantoro et al.

(2021) proposed a model for recommending learning

paths based on the cognitive classiﬁcation of Revised

Bloom’s Taxonomy and an ontology of learning ob-

jects. To determine the most appropriate learning path

for the student’s cognitive abilities, the Hybrid PSO

method was used, which consists of a Binary PSO to

represent the cognitive classes and a Discrete PSO to

Table 1: Summary of researches using meta-heuristics to sequencing problem.

Paper Metaheuristic algorithms Student Model Pedagogical Theories

De-Marcos et al. (2009) Discrete PSO, GA Competencies -

Chu et al. (2011) Binary PSO Ability level, expected

learning targets, expected

learning time of an e-course

Smaili et al. (2020) PSO Objectives, preferences,

level of knowledge, learn-

ing styles and academic

motivations

Subiyantoro et al. (2021) Hibrid PSO (Binary and

Discrete)

Cognitive classes based on

Martins et al. (2021) AG, Binary PSO, Prey

Predator Algorithm, Differ-

ential Evolution

Previous knowledge, time

availability, learning prefer-

ences based on ILS

Learning Style and prior

knowledge (ILS), Felder

and Silverman Learning

Style Model (FSLSM)

CSEDU 2022 - 14th International Conference on Computer Supported Education

106

represent the learning objects of an ontology.

Martins et al. (2021) presented a procedure for

generating synthetic data sets to evaluate approaches

used in the Adaptive Curriculum Sequencing prob-

lem. The generated datasets were used to investi-

gate the contribution of four metaheuristic techniques:

Genetic Algorithms (GA), Particle Swarm Optimiza-

tion (PSO), Prey Predator Algorithm, and a proposed

technique based on Differential Evolution. The indi-

vidual sequencing approach was modeled as a multi-

objective problem using information from the stu-

dents, the learning materials (difﬁculty, content, and

style), and the course (target concepts).

Table 1 provides an overview of researches ad-

dressing the pedagogical sequencing problem using

metaheuristics.

3 BACKGROUND

In this section, the Revised Approaches to Studying

Inventory and Bloom’s Taxonomy theories are intro-

duced and the mapping created between them is pre-

sented. Such mapping is the basis for pedagogical

sequencing and allows automatic sequencing of ped-

agogical actions in a way that is independent of the

curriculum and takes into account the learning pro-

cess. In addition, the metaheuristic approach used to

determine optimal sequences of actions is described.

3.1 Student’s RASI Proﬁle

An essential requirement for customizing the se-

quencing of pedagogical actions is the student’s pro-

ﬁle. Several student characteristics can be used. In

Pireva and Kefalas (2017), learning style and VLE’s

metadata were used to provide a personalized learning

path for the student. In work proposed by Smaili et al.

(2020), learning style and knowledge level were used

to provide a course tailored to the student’s needs.

Thus, the student is classiﬁed under the surface,

strategic or deep dimensions. According to this study,

the student classiﬁed in the surface category, presents

a preference for directing the learning process to the

requirements of the evaluation. The student whose

category is deﬁned as strategic is motivated by per-

sonal satisfaction, that is, he or she prioritizes achiev-

ing the best results by means of organized study and

optimizing time. On the other hand, the student iden-

tiﬁed in the deep category directs his study toward

challenging teaching activities, that is, that aim at re-

searching the meaning of things.

The Revised Approaches to Studying Inventory

(RASI) deﬁnes the student’s cognitive proﬁle from

the perspective of three axes (Surface, Strategic, and

Deep), as described by Tait and Entwistle (1996).

Thus, the student is classiﬁed under the surface,

strategic or deep dimensions. According to this study,

the student classiﬁed in the surface category, presents

a preference for directing the learning process to the

requirements of the evaluation. The student whose

category is deﬁned as strategic is motivated by per-

sonal satisfaction, that is, he or she prioritizes achiev-

ing the best results by means of organized study and

optimizing time. On the other hand, the student iden-

tiﬁed in the deep category directs his study toward

challenging teaching activities, that is, that aim at re-

searching the meaning of things.

The RASI establishes a relationship with the BT

since each axes presents an evolution in the student’s

cognitive proﬁle, from Lower Order Cognitive Skills

(LOCS) to Higher-Order Cognitive Skills (HOCS)

just as occurs with the educational objectives in the

BT. This characteristic led us to decide by using the

RASI as a student model to provide the personaliza-

tion of pedagogical actions based on the BT.

The RASI was developed for use with students

in higher education. It is also widely used in sev-

eral works, such as Entwistle (2018), in which the

RASI is one of the dimensions of the Approaches and

Study Skills Inventory for Students (ASSIST). Its use

can also be seen in Fusilier et al. (2021), whose goal

was to identify students’ study approaches to sug-

gest adaptations in the delivery of educational con-

tent. The RASI in its original version is composed

of 52 objective questions, with answers on a 5-point

Likert

scale. A short version of the RASI consisting

of 18 questions is used in Entwistle and Tait (2013),

which was also used in this work since the chance

of student engagement and attention when answering

this questionnaire may be increased.

3.2 Bloom’s Taxonomy

In Krathwohl (2002), BT was extended by the in-

troduction of a second dimension, deﬁning a two-

dimensional BT composed of Cognitive Process Di-

mension (CPD) and Knowledge Dimension (KD).

Then the taxonomy’s educational objectives are

placed in a matrix. CPD has six levels (Remember,

Understand, Apply, Analyze, Evaluate, Create) and

KD into four levels (Factual, Conceptual, Procedural,

and Metacognitive). As the ﬂow through these levels

follows a hierarchy from LOCS to HOCS, which is

also observed in RASI, it is possible to deﬁne peda-

gogical actions from the BT and RASI perspectives.

Likert, R. (1932). A technique for the measurement of

attitudes. Archives of psychology.

Sequencing and Recommending Pedagogical Activities from Bloom’s Taxonomy using RASI and Multi-objective PSO

107

Thus, we deﬁned 24 pedagogical actions, as shown in

Table 2.

Table 2: Pedagogical actions deﬁned according to BT.

Source: Adapted from da Costa and Fernandes (2021).

FA CO PR ME

CPD

Remember A1 A2 A3 A4

Understand A5 A6 A7 A8

Apply A9 A10 A11 A12

Analyze A13 A14 A15 A16

Evaluate A17 A18 A19 A20

Create A21 A22 A23 A24

Subtitle: FA. Factual; CO. Conceptual; PR. Procedural;

ME. Metacognitive; A. Action.

On Table 2, 24 actions are arranged, one for each

educational objective of the BT. These actions follow

the hierarchy proposed in the BT in which they de-

velop from actions close to LOCS (concrete actions)

to actions close to HOCS (abstract actions), in the or-

der A1, A2, ..., A24. Note also that such a hierar-

chy allows for supplanting actions according to the

student’s needs. In this way, a pedagogical sequence

would not necessarily contemplate the 24 proposed

actions. Thus, there are 2

sequencing possibilities,

which makes manual customization difﬁcult. In this

sense, a contribution of this work is the automation of

this process, based on the student’s RASI proﬁle.

For the sequencing of pedagogical actions (educa-

tional objectives), as proposed in this work to be pos-

sible, it is essential to associate activities with peda-

gogical actions. Several works structure activities or

digital tools to the educational objectives of the BT. In

Schrock (2011), for each of the levels of CPD in BT,

technologies capable of meeting such requirements

are listed. In work proposed by Go

stautait

e (2019),

digital activities indexed by BT are used to select an

optimal set of activities to enhance the learning of a

group of students.

In Churches (2010), Bloom’s Digital Taxonomy

(BDT) was developed to index digital activities to

CPD levels to make the pedagogical recommendation

based on BT actions feasible. da Costa and Fernandes

(2021) extended this indexing to the KD, making it

feasible to use the BDT as support for the recommen-

dation of digital activities from the pedagogical goals

structured by the two dimensional BT. In this work,

we have chosen to use such a framework because it

enables the recommendation from the sequencing of

pedagogical actions.

3.3 Relationship between RASI and BT

Both RASI and BT present a hierarchy based on the

evolution of the student’s cognitive level from LOCS

to HOCS. da Costa and Fernandes (2021) proposed

a mapping that establishes this relationship based on

this principle. Figure 1 shows the inﬂuence of each

CPD level on each RASI axis. The framework formu-

lated according to Figure 1 is essential for developing

this proposal since it allows comparisons between a

sequence of actions based on the BT and the student’s

RASI proﬁle. From this, our goal is to ﬁnd, in an au-

tomated way, a sequence of actions that are as close

as possible to the student’s needs, considering his/her

RASI proﬁle.

Figure 1: Mapping RASI versus BT. Source: Adapted from

da Costa and Fernandes (2021).

3.4 Particle Swarm Optimization

Optimization problems can consider one or more ob-

jective functions, which represent the criteria to be

optimized (minimized or maximized) and are directly

related to the problem to be solved. These functions

can be inﬂuenced by independent variables that affect

the evaluation of the solutions.

An efﬁcient stochastic optimization method is Par-

ticle Swarm Optimization (PSO), which is modeled

from the emergent social behavior of a birds’ ﬂock.

Then, each bird is represented by a particle and as the

birds are changing their positions during the ﬂight, the

particle position is the information to be considered

by PSO and the search process in the solution space

CSEDU 2022 - 14th International Conference on Computer Supported Education

108

is performed on a swarm of particles. Each particle

position is associated with a candidate solution for the

optimization problem and its representation is a vec-

tor d-dimensional where each dimension is a compo-

nent of the solution.

The particles’ positions are adjusted toward an op-

timal position (optimal solution) by the inﬂuence of

their own particle experience (the cognitive compo-

nent) and by the experience of their neighborhood in

the swarm (the social component). These components

enable the particles to move toward an optimal solu-

tion as they explore the space around the best solu-

tion found so far. The PSO algorithm was originally

proposed by Kennedy and Eberhart (1995) as a ro-

bust approach to the optimization of problems char-

acterized by nonlinearity and nondifferentiability, op-

timal multiples, and high dimensionality, and accord-

ing to Kennedy et al. (2001) is highly resistant to be-

ing trapped in local optima.

During the optimization process, the PSO main-

tains a swarm of particles and iteratively updates their

positions by adding a new velocity v

t+1

to their cur-

rent position x

. The update of the position x

of each

particle i in the search space at time t + 1 depends on

the calculation of the velocity and is given by Eq. 1.

t+1

= x

+ v

t+1

(1)

The optimization process is driven by the veloc-

ity vector, which reﬂects the particle’s experiential

knowledge and information exchanged with neigh-

boring particles about promising areas in the search

space. The particle velocity (v

) update consists of the

sum of three main terms and is calculated, by dimen-

sion d, according to Eq. 2:

t+1

= wv

+ c

− x

] + c

− x

] (2)

The previous velocity v

represents the memory of

the previous direction of the particle and prevents it

from drastically changing its direction. This compo-

nent is weighted by the inertia w, which determines

how much it affects the new velocity. The cogni-

tive component c

− x

] quantiﬁes the parti-

cle’s performance with respect to its previous perfor-

mance, attracting it back to its personal best position

found since the ﬁrst-time step. The social com-

ponent quantiﬁes the particle’s performance with re-

spect to the particles in its neighborhood, resulting in

each particle also being attracted to the best position

found so far by that group of particles. The cogni-

tive and social components are weighted by the posi-

tive acceleration coefﬁcients c

and c

and the random

values r

and r

. The values of r

and r

control the

stochastic inﬂuence of each component on the general

velocity of the particles and are obtained for each time

step from a uniform distribution ∈ [0,1].

Since optimization problems with real-valued do-

mains can easily be converted to binary domains (En-

gelbrecht, 2006), a discrete version was developed

by Kennedy and Eberhart (1997) to work in binary

search spaces. In this version, the particles represent

positions in binary space, where each element of the

position vector can take the values 0 and 1 (Engel-

brecht, 2006). The position of the particle changes

when any bit of the position vector ﬂips its value from

one value to another. In this way, the velocity of a

particle can be interpreted as the Hamming distance

between its previous and its current position.

The binary PSO is a binary decision model cal-

culated as a function of social and personal factors

Kennedy et al. (2001). The new velocity v

t+1

is de-

ﬁned as the probability that a bit is in one state or the

other, and its value represents the probability that the

bit value is 1. The previous velocity v

measures the

predisposition (or current probability) to choose the

next bit value 1.

In this probabilistic view, velocity must be nor-

malized to be conﬁned to the interval [0, 1]. This nor-

malization is achieved by using the sigmoid function

presented in Eq. 3. The parameter V

max

= ±4 was

set to limit the particle velocity to the interval [−4, 4]

to ensure that there is always the possibility of a bit

changing state.

sig(v

t+1

) =

1 + e

−v

(3)

The normalized velocity is now the probability

with the d-th bit of position vector will be set to 1.

The position x

t+1

of the particle is changed stochas-

tically by comparing, at each iteration, the result of

sig(v

t+1

) with a random number ρ from a uniform

distribution ∈ [0,1], according to Eq. 4. Due to the

random number, the new bit position can be changed

even if the velocity does not change.

t+1

(

1, if ρ

< sig(v

t+1

)

0, otherwise

(4)

4 PROPOSED METHOD

This section describes the pedagogical sequencing of

actions which is formulated as a multi-objective op-

timization problem since the goal is to recommend

a sequence of actions that best ﬁt student’s cognitive

proﬁle. As previously mentioned, metaheuristics such

as PSO are suitable to a such problem. Hence, the

Sequencing and Recommending Pedagogical Activities from Bloom’s Taxonomy using RASI and Multi-objective PSO

109

(a) Particle representation vector

(b) Recommended Sequence

Figure 2: Positions vector of a particle and corresponding recommendation sequence with 11 actions.

proposal consists of a multi-objective PSO for the se-

quencing.

In the proposed model, a particle is represented

by a vector sized 24 as pictured in Figure 2a, where

each position is associated with a pedagogical action

according to Table 2. If an action is present in the se-

quence, the corresponding bit is set to 1, otherwise,

0. Formally, the problem is deﬁned as the minimiza-

tion of the objective function f (x) as given by Eq. 5,

where x is a sequence represented by a particle, F

measures the similarity between the sequence RASI

index R

RASI

and the student’s RASI proﬁle S

RASI

and

the sequence size. The weights ω

were adopted to

weigh the contribution of each criterium and then the

multi-objective aspect was considered as the weighed

sum of criteria. After simulations performed on the

RASI proﬁles of 156 students, the weights were ad-

justed to ω

= 0.7 and ω

= (1 − ω

) as the best

values for minimizing f .

f (x) =

∑

i=1

(x) (5)

checks whether the sequence matches the RASI

proﬁle of the student. Therefore, the RASI indices

of the sequence must be determined, expressing the

strength of each CPD level (Remember, ..., Create) in

the sequence weighted by the relevance of that level

to each RASI axis (Surface, Strategic and Deep). For-

mally, the index of each RASI axis that makes up

RASI

is calculated by the product between the weight

of the inﬂuence of each CPD level for the RASI axis

(Figure 1) and the number of bits set to 1 in that BT

level multiplied by 1/4. The S

RASI

index is obtained

from students’ responses to the RASI questionnaire.

Notice in Figure 1 that the Apply level does not inﬂu-

ence the Surface and Deep axes, just as the Evaluate

level has no inﬂuence on the Deep axis.

The R

RASI

index of the sequence represented by

the vector in Figure 2a is [0.438, 0.484, 0.475], where

the value for each axis is Surface = 0.438, Strategic =

0.484, and Deep = 0.475. To illustrate the calculation

of the value of each axis, we can take the value for the

Surface axis of this sequence, which is the result of

the calculation of Equation 6.

Sur f ace

RASI

2 ∗ 0.625

2 ∗ 0.125

1 ∗ 0.000

0 ∗ 0.125

4 ∗ 0.000

2 ∗ 0.125

(6)

Finally, the similarity between the RASI index of

the sequence and the RASI proﬁle of the student is

given by the Euclidean distance D between R

RASI

and

RASI

. Note that the Euclidean distance alone is not

sufﬁcient to determine whether the sequence is close

to the student’s proﬁle with respect to each RASI axis.

Then P adds a penalty to F

(x) for each RASI axis

that is violated. Assume that the Deep axis is more

relevant to the student and the Surface axis is more

relevant to the sequence. This relevance is attributed

to each axis according to w

= 1 for the least relevant

axis, w

= 2 for the intermediate axis, and w

= 3 for

the most relevant axis. At each RASI axis where there

is a divergence of relevance between the student and

the sequence, the corresponding weight is multiplied

by 1/6 of the Euclidean distance. Thus, the penalty

is at most the Euclidean distance and consequently,

(x) is at most twice the Euclidean distance. If there

is no difference in the order of relevance on any of the

RASI axes, w

, w

, and w

are set to 0. The objective

function F

and the penalty P are given by Eq. 7 and

Eq. 8, respectively.

(x) = D (S

RASI

, R

RASI

) + P (7)

P =

∑

i=1

∗

(8)

CSEDU 2022 - 14th International Conference on Computer Supported Education

110

Through experiments conducted by da Costa and

Fernandes (2021), the appropriate number of actions

for each predominant RASI proﬁle was deﬁned and it

is used in this study as a reference value for the se-

quence size (re f ): 9 for Surface, 13 for Strategic, and

11 for Deep. Thus, the objective function F

has the

task of optimizing the number of activities that make

up the sequence, minimizing the difference between

the sequence size and the reference value. Eq. 9 de-

ﬁnes F

(x) =











re f −size(x)

re f −1

, if size(x) < re f

size(x)− re f

24− re f

, otherwise

(9)

We can assume that the problem of sequencing

pedagogical actions allows one to ﬁnd more than one

appropriate sequence for a student. Hence, some PSO

properties were deﬁned to make this metaheuristic

more adherent to the sequencing problem. Then, a

lbest PSO was developed using a ring social network

topology, where the information exchange in the so-

cial component of the particle is realized with only a

small neighborhood (two other particles). Updating

the best particle positions is done asynchronously, as

this is more suitable for the lbest PSO.

The recommended sequence is composed of digi-

tal activities according to the BDT. Then, for each bit

set to 1 in the sequence returned by the PSO, a BDT

activity is assigned (see Figure 2b). This attribution

was performed according to the mapping presented

by da Costa and Fernandes (2021) between BDT and

BT. So, in effect, the recommendation is a sequence

of digital activities.

5 RESULTS AND DISCUSSION

A total of 979 higher education students at three edu-

cational institutions were invited to participate in the

experiments. Distance learning and presential course

of a Federal Institute of Education, Science and Tech-

nology and Distance Learning Center of a Federal

University are in Minas Gerais, Brazil. Also, a Fed-

eral Institute is in Goi

as, Brazil. The experiments took

place in the period from May to December 2021.

The experiments were divided into three phases: i)

Application of the RASI questionnaire; ii) Sequenc-

ing of pedagogical actions; and iii) Recommendation

of pedagogical activities. The research participants

were divided into two groups: a control group, which

received random sequences of activities; and the ex-

perimental group, that received sequenced activities

through the PSO algorithm.

The student’s participation in each phase was vol-

untary. In addition, they were informed that the col-

lected data would be anonymized, and that no per-

sonal information would be disclosed under any cir-

cumstances. Thus, we had 182 participants in Phase

i, and of these, 50 participated in Phase iii. In the next

subsections, we will discuss the results obtained in the

experiments.

The questions asked in the questionnaires of

phases i and iii of the experiment are listed in Table 3,

and the groups of response options are shown in Table

5.1 Students’ Proﬁles

We used a free translation of the short version of the

RASI questionnaire into Portuguese in Phase i of the

experiments. One hundred eighty-two students an-

swered the RASI questionnaire. For each student, the

values for the RASI axes were calculated according

to the respective answer to the questionnaire. The dis-

tribution of the participants’ proﬁles according to the

predominant RASI axis was Surface = 9%, Strategic

= 25%, and Deep = 66%.

In addition, 100 of these participants answered a

questionnaire stating how much they agreed with the

obtained RASI indices. For this, six objective ques-

tions with answer options on a 5-point Likert scale

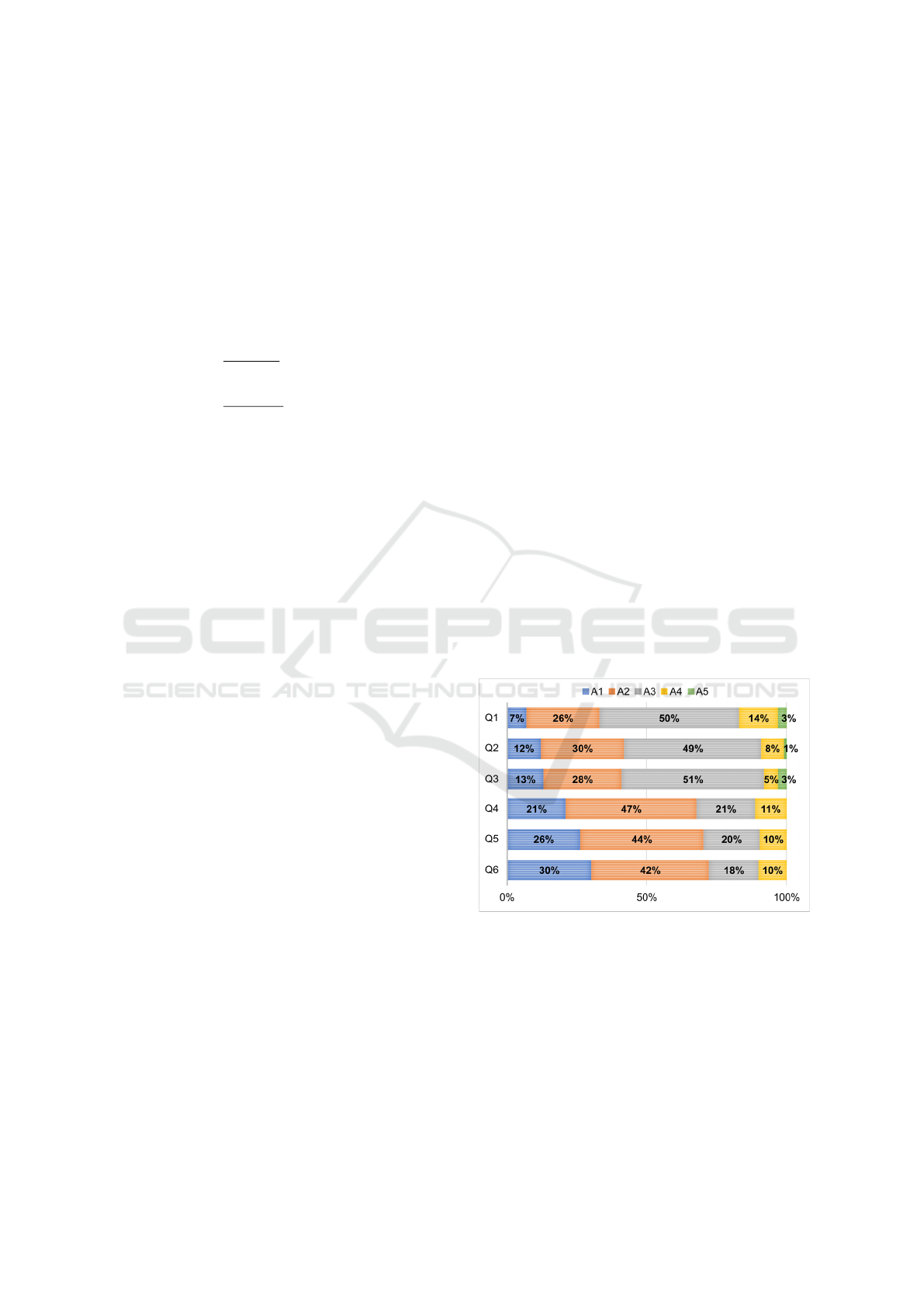
were asked, as shown in Figure 3.

Figure 3: Students’ perception of the indices obtained by

the RASI proﬁle.

In Figure 3, Q1 to Q6 questions are intended to

know about the students’ agreement with their RASI

proﬁle obtained from their questionnaire answers. Q1

to Q3 asked the student if the percentage for Surface,

Strategic, and Deep, respectively, should be less or

more signiﬁcant. Q4 to Q6 intended to conﬁrm the

answers from Q1 to Q3. It was only asked if the stu-

dent agreed with the percentual of each axis. Most

of the answers for Q1 to Q3 were Higher, Equal, or

Sequencing and Recommending Pedagogical Activities from Bloom’s Taxonomy using RASI and Multi-objective PSO

111

Table 3: Questionnaire questions and their answer groups.

QUESTION AG

∗

Q1. I consider that the percentage assigned to me on the SURFACE axis should be: G1

Q2. I consider that the percentage assigned to me on the STRATEGIC axis should be: G1

Q3. I believe that the percentage assigned to me on the DEEP axis should be: G1

Q4. I consider that the percentage assigned to me on the SURFACE axis is in line with my learning proﬁle. G2

Q5. I consider that the percentage assigned to me on the STRATEGIC axis is in line with my learning proﬁle. G2

Q6. I consider that the percentage assigned to me on the DEEP axis is in line with my learning proﬁle. G2

Q7. Do you think the number of activities is: G3

Q8. The sequence of activities is comfortable to lead you in learning a new content or subject. G2

Q9. What is the probability that you will complete all the activities in this sequence? G4

Q10. The total number of recommended activities is too many. G2

* Answer Group

Table 4: Questionnaire answer groups.

∗

A1 Much higher (from 7%

more)

Agree Very High (at least 6

more than ideal)

Very High (above 80%)

A2 Higher (3% to 6% more) Partially Agree High (between 3 and 5

more than ideal)

High (between 61% and

80%)

A3 Equal (up to 2% more or

less)

Indifferent Sufﬁcient (up to 2 more

or fewer than ideal)

Moderated (between

41% and 60%)

A4 Smaller (from 3 to 6%

less)

Partially Disagre Low (between 3 and 5

less than ideal)

Low (between 20% and

40%)

A5 Much Smaller (from 7%

less)

Disagree Very Low (at least 6

fewer than ideal)

Very Low (below 20%)

* Answer Number; ** Answer Group

Smaller, with a higher concentration on the Equal an-

swer. This result suggests a certain degree of student

awareness while taking the RASI questionnaire. The

results show that most of the answers from Q4 to Q6

focused on Agree and Partially Agree, conﬁrming the

students’ attention to answer the RASI questionnaire

and, therefore, the quality of this questionnaire’s an-

swers.

5.2 Sequencing Analysis Regarding the

Student’s Proﬁle

The optimization process was performed for the par-

ticipants of Phase i of the experiment. Based on the

sequences generated in the process, the distribution of

pedagogical actions was observed for each predomi-

nant RASI proﬁle according to CPD levels.

Compared to the mapping RASI performed to TB,

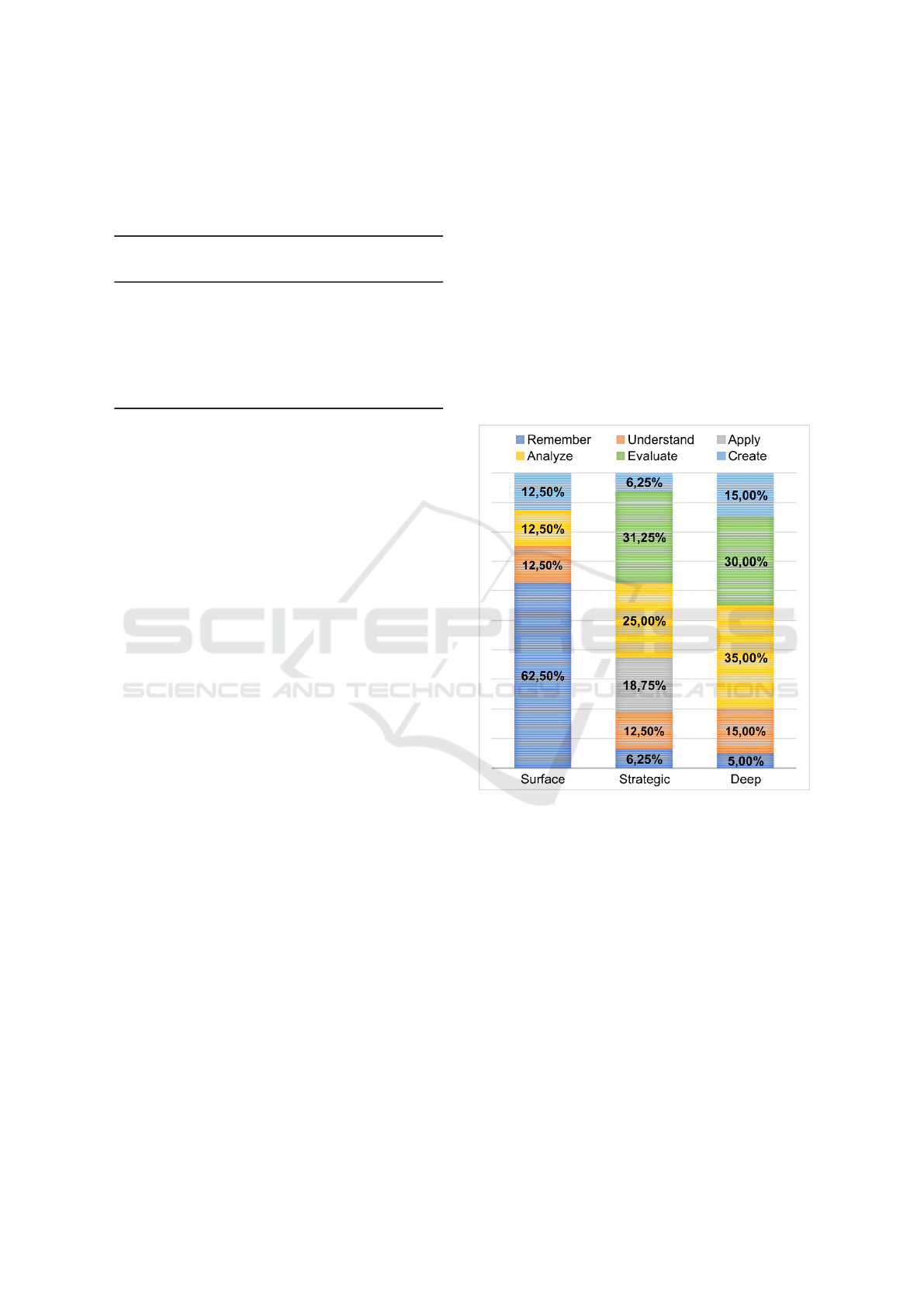
it can be seen in Figure 4 that the actions for the Sur-

face proﬁle were mostly distributed across the pro-

ﬁle’s preference levels, with recommendations for an

unexpected level (Evaluate) and no recommendation

for the Understand level; for the Strategic proﬁle, no

action was recommended for the Create level; and

for the Deep proﬁle, all recommendations were dis-

tributed across the assigned levels.

Table 5: Relevance of BT levels for each RASI axis.

Surface Strategic Deep

High Remember

Analyze

Evaluate

Analyze

Evaluate

Moderate

Understand

Analyze

Create

Understand

Apply

Understand

Create

Low

Apply

Evaluate

Remember

Create

Remember

Apply

In F

, the predominant RASI axis of the student’s

proﬁle is used to calculate the penalty. However, the

similarity between the sequence and the student’s pro-

ﬁle considers all the axes that make up the proﬁle. In

this sense, the analysis of the quality of the recom-

mendation distribution can be performed by grouping

CSEDU 2022 - 14th International Conference on Computer Supported Education

112

Figure 4: Recommended actions by CPD levels for each

RASI proﬁle.

the CPD levels according to the degree of relevance

(High, Moderate, and Low) for each RASI proﬁle.

The relevance of the CPD levels for each RASI proﬁle

can be seen in Table 5.

Thus, Figure 5 shows the distribution of recom-

mendations by the degree of relevance, the average

number of recommended actions, and the reference

values for each predominant proﬁle. As can be seen,

most of the recommended actions are concentrated

at BT levels that are more relevant to the predomi-

nant proﬁle, and the average of the number of recom-

mended actions for each predominant proﬁle is equal

to the reference values, showing the convergence of

the F

and F

functions, respectively.

5.3 Students’ Perception about the

Recommended Sequences of

Activities

In Phase iii of the experiments, sequenced activi-

ties were recommended. Two groups received the

pedagogical recommendations generated by differ-

ent methods. The ﬁrst group, with 41 participants,

was presented with sequences of pedagogical activ-

ities generated using the PSO algorithm. The sec-

ond group, called the control group, with 15 partici-

pants, was presented with randomly sequenced activ-

ities. Figures 6 and 7 show the students’ perceptions

regarding the pedagogical recommendations in each

of these groups.

Q7 is related to the students’ perception regard-

Figure 5: Recommended actions by the degree of relevance

for each RASI proﬁle.

Figure 6: Satisfaction questionnaire for activities sequenced

using the PSO algorithm (41 attendees).

ing the number of recommended activities. In Figure

6 (PSO), 7% of the participants consider the number

of activities Very High, while in Figure 7 (random),

14% of the participants consider this number Very

High. This item is directly related to the quality of the

second objective of the PSO algorithm since it seeks

to optimize the number of sequenced actions accord-

ing to the student’s proﬁle. Compared to randomly

sequenced activities, the results of Q7 for PSO are

better since the percentage of participants who con-

sider the number of answers Sufﬁcient is higher than

each other answers. Also, in the recommendation of

randomly sequenced activities, the number of partici-

pants who consider the number of activities Very high

Sequencing and Recommending Pedagogical Activities from Bloom’s Taxonomy using RASI and Multi-objective PSO

113

Figure 7: Satisfaction questionnaire for randomly se-

quenced activities (15 attendees).

is higher. We observe that the PSO algorithm fulﬁlls

the requirement of controlling the number of activi-

ties. However, a more detailed analysis of the results

is necessary to adapt better the reference values of the

number of activities for each student proﬁle.

In ﬁgures 6 and 7, Q8 is related to the quality of

the sequence of activities offered to the student since

the student answers how comfortable he considers the

pedagogical recommendation to be for learning new

content. In Figure 6, 85% of the participants agreed

or partially agreed with the statement of Q8 for the

PSO algorithm. This result is better than that ob-

served for randomly generated sequencing. This re-

sult directly evaluates the ﬁrst objective of the PSO

algorithm since this objective seeks to sequence ped-

agogical actions compatible with the student’s RASI

proﬁle.

The Q9 in ﬁgures 6 and 7 mixed evaluate the

quality of the recommendation and the number of se-

quenced activities. Most of the answers (78%) fo-

cused on Very High, High, or Moderated for the PSO

Algorithm. Again, these results are better than those

observed in the recommendation of randomly gener-

ated activities. Q10 presents a statement related to

the high quantity of recommended activities. In this

item, the percentage of Agree is lower for the PSO

algorithm than for the randomly generated sequence.

While noting the need for adjustments in the number

of sequenced actions, these results conﬁrm the effec-

tiveness of the proposed algorithm.

In Figure 8, the results of the satisfaction ques-

tionnaire shown in Figure 6 are presented, that is, for

the PSO algorithm, but grouped by the predominant

RASI axis of the participant. The number of partici-

pants per proﬁle was Surface = 5, Strategic = 7, and

Deep = 29. Note that the results for the Deep group

tend to resemble the results in Figure 6, as there is a

signiﬁcant number of participants with a predominant

Deep proﬁle.

Figure 8: Satisfaction questionnaire layered by predomi-

nant RASI axis, for activities sequenced by the PSO algo-

rithm (41 attendees).

Regarding question Q7, there is a lower tendency

for participants with Surface and Strategic proﬁles to

consider the number of actions Very High. Also, at

this point, the low number of participants with Sur-

face or Strategic proﬁle may explain why this is these

groups with the lowest rate of Very High answers. In

question Q8, which analyzes how comfortable the stu-

dents consider the sequence of activities received, we

observed that the results were satisfactory, with a pos-

itive highlight for Surface and Strategic groups.

In question Q9, students in the Strategic group

showed better results regarding the probability of per-

forming all the recommended activities. Thus, we see

better performance of the PSO algorithm concerning

the quality of the pedagogical recommendation for the

Strategic proﬁle. In question Q10, we observe that

10% disagree or partially disagree that the quantity of

activities is high for the Deep group. This result may

suggest better adequacy of the algorithm to Deep pro-

ﬁles. However, it should be noted that the low number

of participants with a Surface or Strategic proﬁle may

have distorted the results.

In general, we noticed that grouping the results al-

lows us to better understand the PSO algorithm’s be-

CSEDU 2022 - 14th International Conference on Computer Supported Education

114

havior for each proﬁle. In this sense, the proposal

of this work satisfactorily meets the need and per-

sonalizes personalized pedagogical actions in an au-

tomated manner. From this, we understand that in

future works, it is necessary to improve the adapta-

tion functions (F

and F

) to provide pedagogical se-

quences more adjusted to the students’ proﬁles.

6 CONCLUSIONS

This paper presents an approach to automatically se-

quencing customized pedagogical actions to the stu-

dent. Using two cognitive theories, such as the Re-

vised Bloom Taxonomy and the student’s RASI pro-

ﬁle, it was possible to sequence actions in an inde-

pendent way of the curriculum structure, considering

the learning process. Using digital activities provided

by Bloom’s Digital Taxonomy, a satisfaction experi-

ment was carried out in which sequences of activities

were recommended for students from the sequences

of actions generated by the PSO.

An important ﬁnding of this work concerns the

feasibility of personalized pedagogical recommenda-

tions through digital activities that consider a student

RASI proﬁle. Thus, it was shown that the relation-

ship established between the BT and the RASI is an

effective approach to solve this problem. From the

results of the experiment, it was concluded that stu-

dents were satisﬁed with the quantity and quality of

activities recommended by the PSO.

In this sense, the binary PSO developed from the

proposed methodology proved to be an efﬁcient ap-

proach to solve the sequencing problem. The op-

timization process was able to ﬁnd sequences com-

posed of actions that were relevant and in adequate

quantity for each student. A limitation in this study

is the discrepancy between the predominant proﬁles

of the students who participated in the experiment,

which requires a more in-depth statistical analysis of

the data obtained. As future works, we intend to feed-

back the reference values of the optimization objec-

tives from the satisfaction survey results and carry out

the integration with a Virtual Learning Environment

in order to automate the recommendation process.

ACKNOWLEDGMENT

The authors thank the Federal University of

Uberl

andia, the Goiano Federal Institute, and the Fed-

eral Institute of Tri

angulo Mineiro for supporting this

research.

REFERENCES

Al-Muhaideb, S. and Menai, M. E. B. (2011). Evolutionary

computation approaches to the curriculum sequencing

problem. Natural Computing, 10(2):891–920.

Brown, M., McCormack, M., Reeves, J., Brook, D. C., Gra-

jek, S., Alexander, B., Bali, M., Bulger, S., Dark, S.,

Engelbert, N., et al. (2020). 2020 educause horizon

report teaching and learning edition. Technical report,

EDUCAUSE.

Chu, C.-P., Chang, Y.-C., and Tsai, C.-C. (2011). Pc 2 pso:

personalized e-course composition based on particle

swarm optimization. Applied Intelligence, 34(1):141–

154.

Churches, A. (2010). Bloom’s digital taxonomy.

da Costa, N. T. and Fernandes, M. A. (2021). Sequenci-

amento de ac¸

oes pedag

ogicas baseadas na taxonomia

de bloom usando planejamento automatizado apoiado

por algoritmo gen

etico. Revista Brasileira de In-

form

atica na Educac¸

ao, 29:485–501.

De-Marcos, L., Mart

ınez, J. J., Guti

errez, J. A., Barchino,

R., and Guti

errez, J. M. (2009). A new sequenc-

ing method in web-based education. In 2009 IEEE

Congress on Evolutionary Computation, pages 3219–

3225. IEEE.

Engelbrecht, A. P. (2006). Fundamentals of Computational

Swarm Intelligence. John Wiley & Sons, Inc., Hobo-

ken, NJ, USA.

Entwistle, N. (2018). Student learning and academic under-

standing: A research perspective with implications for

teaching. Academic Press.

Entwistle, N. and Tait, H. (2013). Approaches and study

skills inventory for students (assist) (incorporating the

revised approaches to studying inventory - rasi). Edin-

burgh: Centre for Research on Learning and Instruc-

tion, University of Edinburgh.

Fusilier, M., Bhuyan, R., Russell, J., Lin, S., and Yang,

S. (2021). Studying approaches: samples in china,

kuwait, and usa. Journal of Applied Research in

Higher Education, ahead-of-print.

stautait

e, D. (2019). Principal component analysis

and bloom taxonomy to personalise learning. In

EDULEARN19 Proceedings 11th International Con-

ference on Education and New Learning Technolo-

gies: Palma, Spain. 1-3 July, 2019, pages 2910–2920.

IATED Academy.

Huang, R., Spector, J. M., and Yang, J. (2019). Educational

technology: a primer for the 21st century. Springer.

Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-

mization. In Proceedings of ICNN’95 - International

Conference on Neural Networks, volume 4, pages

1942–1948 vol.4.

Kennedy, J. and Eberhart, R. C. (1997). A discrete bi-

nary version of the particle swarm algorithm. In 1997

IEEE International conference on systems, man, and

cybernetics. Computational cybernetics and simula-

tion, volume 5, pages 4104–4108. IEEE.

Kennedy, J. F., Eberhart, R. C., and Shi, Y. (2001). Swarm

intelligence. The Morgan Kaufmann series in evo-

Sequencing and Recommending Pedagogical Activities from Bloom’s Taxonomy using RASI and Multi-objective PSO

115

lutionary computation. Morgan Kaufmann Publishers,

San Francisco.

Krathwohl, D. R. (2002). A revision of bloom’s taxonomy:

An overview. Theory Into Practice, 41(4):212–218.

Martins, A. F., Machado, M., Bernardino, H. S., and

de Souza, J. F. (2021). A comparative analysis

of metaheuristics applied to adaptive curriculum se-

quencing. Soft Computing, pages 1–16.

Moran, J. (2015). Educac¸

ao h

ıbrida: um conceito-

chave para a educac¸

ao, hoje. Ensino h

ıbrido:

personalizac¸

ao e tecnologia na educac¸

ao. Porto Ale-

gre: Penso, pages 27–45.

Pireva, K. and Kefalas, P. (2017). A recommender system

based on hierarchical clustering for cloud e-learning.

In Intelligent Distributed Computing XI, pages 235–

245.

Schrock, K. (2011). Bloomin’ Apps: Kathy Schrock’s

Guide to Everything.

Smaili, E. M., Khoudda, C., Sraidi, S., and Charaf, M. E. H.

(2020). An optimized method for adaptive learning

based on pso algorithm. In 2020 IEEE 2nd Interna-

tional Conference on Electronics, Control, Optimiza-

tion and Computer Science (ICECOCS), pages 1–5.

IEEE.

Subiyantoro, E., Ashari, A., and Suprapto, S. (2021).

Learning Path Recommendation using Hybrid Particle

Swarm Optimization. Advances in Science, Technol-

ogy and Engineering Systems Journal, 6(1):570–576.

Sunaga, A. and Carvalho, C. S. (2015). As tecnolo-

gias digitais no ensino h

ıbrido. In Bacich, L., Neto,

A. T., and Trevisani, F. d. M., editors, Ensino h

ıbrido:

personalizac¸

ao e tecnologia na educac¸

ao. Penso Edi-

tora. Cap

ıtulo 7.

Tait, H. and Entwistle, N. (1996). Identifying students at

risk through ineffective study strategies. Higher Edu-

cation, 31:97–116.

Woolf, B. P. (2010). Building intelligent interactive tu-

tors: Student-centered strategies for revolutionizing

e-learning. Morgan Kaufmann.

CSEDU 2022 - 14th International Conference on Computer Supported Education

116